八年级数学上册《轴对称》知识归纳
8年级上册数学第三单元《第十三章 轴对称》知识点总结

第十三章轴对称一、概念1.把一个图形沿着一条直线折叠,如果直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
这时我们也说这个图形关于这条直线(成轴)对称。
2. 把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图关于这条直线对称。
这条直线叫做对称轴。
折叠后重合的点是对应点,叫做对称点3、让学生知道轴对称图形(一个图形,有一条或多条对称轴)和轴对称(两个图形,只有一条对称轴)的区别与联系4.轴对称的性质①关于某直线对称的两个图形是全等形。
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
③轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
④如果两个图形的对应点连线被同条直线垂直平分,那么这两个图形关于这条直线对称。
二、线段的垂直平分线1.经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2.线段垂直平分线上的点与这条线段的两个端点的距离相等3.与一条线段两个端点距离相等的点,在线段的垂直平分线上三、用坐标表示轴对称小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为(x,- y).点(x, y)关于y轴对称的点的坐标为(-x, y).注意:像类似点(x,y)关于X=1对称的题目要学会做法2.三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等注意:知道角平分线交点(到边相等)和垂直平分线交点(到点相等)的区别四、等腰三角形1.等腰三角形的性质①.等腰三角形的两个底角相等。
(等边对等角)②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
(三线合一)2、等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(等角对等边)注意:三线合一不能直接来判定等腰三角形,需要证明全等。
最新人教版初中八年级上册数学《轴对称》知识归纳

第十三章轴对称
13.1 轴对称(对称点)
轴对称图形:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合。
这条直线就是它的对称轴。
垂直平分线:经过线段中点并且垂直于这条线段的直线。
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
线段垂直平分线的性质:垂直平分线上的点到两端的距离相等。
若PA=PB,点C为AB中点,则PC⊥AB或点P在线段AB的垂直平分线上。
13.2 画轴对称图形
先画对称点(过该点画对称轴的垂线,取等长),然后连接对称点,形成轴对称图形。
13.3 等腰三角形
概念:有两边相等的三角形。
性质:等边对等角,三线合一(顶角平分线、底边上的中线、底边上的高)。
判定:等角对等边
等边三角形:三边都相等的特殊的等腰三角形。
三个内角都相等,每个内角60º。
(判定:三个角都相等的三角形;有一个角是60º的等腰三角形。
)
在RtΔ中,如果一个锐角等于30º,那么它所对的直角边等于斜边的一半。
(在RtΔ中,斜边上的中线等于斜边的一半。
)
13.4 课题学习最短路径问题
利用轴对称、平移作出最短路径选择。
(两点之间线段最短)
作者留言:
非常感谢!您浏览到此文档。
为了提高文档质量,欢迎您点赞或留言告诉我文档的不足之处,以便于对该文档进行完善优化,在此本人深表感
谢!祝您天天快乐!。
人教八年级数学上册第十三章轴对称知识点常见考点例析

第十三章轴对称知识点常见考点例析一.知识框架图二.轴对称和轴对称图形1、有一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.2、轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
(对称轴必须是直线)3、对称点:折叠后重合的点是对应点,叫做对称点。
4、轴对称图形的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
类似的,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
连接任意一对对应点的线段被对称轴垂直平分.轴对称图形上对应线段相等、对应角相等。
5.画一图形关于某条直线的轴对称图形步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
三.轴对称与轴对称图形的区别和联系区别:轴对称是指两个图形之间的形状与位置关系,成轴对称的两个图形是全等形;轴对称图形是一个具有特殊形状的图形,把一个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.联系:1:都是折叠重合 2;如果把成轴对称的两个图形看成一个图形那么他就是轴对称图形,反之亦然。
线段的垂直平分线经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线)(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,与一条线段两个端点距离相等的点在这条线段的垂直平分线上.(证明是必须有两个点)因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.四.用坐标表示轴对称1、点(x,y)关于x轴对称的点的坐标为(-x,y)2、点(x,y)关于y轴对称的点的坐标为(x,-y);五.关于坐标轴夹角平分线对称点P(x,y)关于第一、三象限坐标轴夹角平分线y=x对称的点的坐标是(y,x)点P(x,y)关于第二、四象限坐标轴夹角平分线y=-x对称的点的坐标是(-y,-x)六.关于平行于坐标轴的直线对称点P(x,y)关于直线x=m对称的点的坐标是(2m-x,y);点P(x,y)关于直线y=n对称的点的坐标是(x,2n-y);。
八年级上册数学轴对称知识点总结

八年级上册数学轴对称知识点总结
八年级上册数学轴对称的知识点总结如下:
1. 轴对称图形:如果一个图形可以折叠成两半,使得两半完全重合在一起,则这个图形是轴对称的。
轴对称图形具有轴对称轴,也称为镜像轴。
2. 轴对称图形的性质:
- 图形的每个点关于轴对称轴对应有另一个点。
- 图形的每一对对称点与轴对称轴的距离相等。
- 图形的任意两点关于轴对称轴的连线垂直于轴对称轴。
3. 轴对称图形的判断方法:
- 观察图形是否可以折叠成两半,使得两半完全重合。
- 观察图形是否和它自己的镜像一样。
4. 轴对称图形的绘制方法:
- 给出轴对称轴,沿着轴对称轴将图形折叠。
- 给定部分图形的对称点,通过连接对称点来绘制完整的轴对称图形。
5. 轴对称图形的性质的应用:
- 可以通过找到轴对称图形的对称点来绘制完整的图形。
- 可以通过轴对称图形的性质来解决有关对称点的问题,如求解距离、面积等。
这些都是八年级上册数学轴对称的知识点的总结,希望对你有所帮助!。
轴对称(全章知识梳理与考点分类讲解)(人教版)(教师版) 2024-2025学年八年级数学上册基础

专题13.12轴对称(全章知识梳理与考点分类讲解)第一部分【知识点归纳】【知识点一】轴对称1.轴对称图形和轴对称(1)轴对称图形如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.(2)轴对称定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.(3)轴对称图形与轴对称的区别和联系区别:轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的.联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.2.线段的垂直平分线线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.反过来,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.【知识点二】作轴对称图形(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.【知识点三】等腰三角形1.等腰三角形(1)定义:有两边相等的三角形,叫做等腰三角形.(2)等腰三角形性质①等腰三角形的两个底角相等,即“等边对等角”;②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.(3)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).2.等边三角形(1)定义:三条边都相等的三角形,叫做等边三角形.(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.(3)等边三角形的判定:①三条边都相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;③有一个角为60°的等腰三角形是等边三角形.3.直角三角形的性质定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.第二部分【题型展示与方法点拨】【题型1】利用轴对称的性质求值【例1】(2024八年级上·江苏·专题练习)如图,点P 在四边形ABCD 的内部,且点P 与点M 关于AD 对称,PM 交AD 于点G ,点P 与点N 关于BC 对称,PN 交BC 于点H ,MN 分别交AD BC ,于点E F ,.(1)连接PE PF ,,若12cm MN =,求PEF !的周长;(2)若134C D ∠+∠=︒,求HPG ∠的度数.【答案】(1)12cm (2)134°【分析】本题主经考查了轴对称与多边形综合.熟练掌握轴对称性质,多边形内角和公式,是解决问题的关键.n 边形内角和公式()2180n -⋅︒.(1)根据轴对称性质得到,PE ME =,PF NF =,得到PEF !的周长等于线段MN 的长度,为12cm .(2)根据轴对称性质得到,PM AD ⊥,90PGA ∠=︒,PN BC ⊥,90PHB ∠=︒,根据四边形ABCD 内角和为360︒与134C D ∠+∠=︒,得到226A B ∠+∠=︒,根据五边形ABFPE 内角和为540︒,得到134HPG ∠=︒.解:(1)如图,∵点P 与点M 关于AD 对称,∴PE ME =,∵点P 与点N 关于BC 对称,∴PF NF =,∵12ME EF FN MN ++==,∴PEF !的周长为12cm .(2)解:∵点P 与点M 关于AD 对称,∴PM AD ⊥,即90PGA ∠=︒,∵点P 与点N 关于BC 对称,∴PN BC ⊥,即90PHB ∠=︒,∵360A B C D ∠+∠+∠+∠=︒,134C D ∠+∠=︒,∴226A B ∠+∠=︒,∵540A B PHB HPG PGA ∠+∠+∠+∠+∠=︒,∴134HPG ∠=︒.【变式1】(23-24七年级下·广东深圳·期末)如图,四边形ABCD 中,AB AD =,将ABC V 沿着AC 折叠,使点B 恰好落在CD 上的点B '处,若110BAD ∠=︒,则ACB =∠()A .55︒B .45︒C .40︒D .35︒【答案】D 【分析】本题主要考查了轴对称的性质,四边形内角和以及三角形外角性质的运用,解决问题的关键是作辅助线构造四边形AOB E ',解题时注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.连接AB ',BB ',过A 作AE CD ⊥于E ,依据BAC B AC '∠=∠,DAE B AE '∠=∠,即可得出12CAE BAD ∠=∠,再根据四边形内角和以及三角形外角性质,即可得到1902ACB ACB BAD '∠=∠=︒-∠.解:如图,连接BB ',过A 作AE CD ⊥于E ,点B 关于AC 的对称点B '恰好落在CD 上,AC ∴垂直平分BB ',AB AB '∴=,BAC B AC '∴∠=∠,AB AD = ,AD AB '∴=,又AE CD ⊥Q ,DAE B AE '∴∠=∠,1552CAE BAD ∴∠=∠=︒,又90AEC =︒∠ ,35ACB ACB '∴∠=∠=︒,故选:D .【变式2】(22-23八年级上·江苏镇江·阶段练习)如图,APT △与CPT △关于直线PT 对称,A APT ∠=∠,延长AT 交PC 于点F ,当A ∠=︒时,FTC C ∠=∠.【答案】36【分析】本题考查轴对称的性质,三角形内角和定理,三角形的外角的性质等知识,证明2APF AFP A ∠∠∠==,利用三角形内角和定理构建方程求解即可.解:APT 与CPT △关于直线PT 对称,A C TA TC APT CPT ∠∠∠∠∴===,,,A APT ∠∠= ,A C APT CPT ∠∠∠∠∴===,FTC C ∠∠= ,22AFP C FTC C A ∠∠∠∠∠∴=+==,180A APF AFP ∠∠∠++=︒ ,5180A ∴∠=︒,36A ∴∠=︒,故答案为:36.【题型2】利用折叠的特征求值【例2】(23-24七年级下·河南新乡·期末)如图,在长方形纸片ABCD 中,点E 在边AD 上,点F 在边BC 上,四边形CDEF 沿EF 翻折得到四边形C D EF ''且点D ¢恰好落在边AB 上;将AED '△沿ED '折叠得到A ED ''△且点A '恰好落在边BC 上.(1)若77BFE ∠=︒,则BFC '∠=.(2)若50A D B '∠='︒,求A EF '∠的度数.【答案】(1)26︒(2)52.5A EF '∠=︒【分析】本题考查了折叠的性质,熟练用折叠的性质进行角度的转换是解题的关键.(1)根据折叠的性质可得EFC EFC '∠=∠,设BFC x '∠=,则可得77EFC x '∠=+︒,根据180EFB EFC ∠+∠=︒列方程,即可解答;(2)根据50A D B '∠='︒可求得EA F '∠,再求出AED '∠和D EA ''∠,利用折叠的性质即可得到D EF '∠,即可解答.解:(1) 四边形CDEF 沿EF 翻折得到四边形C D EF ''且点D ¢恰好落在边AB 上,EFC EFC '∴∠=∠,设BFC x '∠=,则可得77EFC EFC x '∠=∠=+︒,根据180EFB EFC ∠+∠=︒可得7777180x ︒++︒=︒,解得26x =︒,故答案为:26︒;(2)解:在A D B '' 中,∵50A D B '∠='︒,90B Ð=°,40D A B ''∴∠=︒,∵点A '恰好落在边BC 上,90D A E A ''∴∠=∠=︒.180904050EA F ∴∠=︒-︒-︒='︒,AD BC ∥ ,50AEA EA F ''∴∠=∠=︒,1252AED A ED AEA ∴︒''''∠=∠=∠=由折叠的性质,知()1180257752D EF DEF ∠=∠=⨯︒-︒=︒'.52.5A EF D EF A ED ∴∠=∠-'='∠''︒.【变式1】(23-24九年级上·山东枣庄·开学考试)如图,四边形ABCD 为一矩形纸带,点E F 、分别在边AB CD 、上,将纸带沿EF 折叠,点A D 、的对应点分别为A ''、D ,若235∠=︒,则1∠的度数为()A .62.5︒B .72.5︒C .55︒D .45︒【答案】B 【分析】本题考查了邻补角的性质,折叠的性质及平行线的性质,由235∠=︒可得145AEA '∠=︒,再利用折叠的性质求得AEF ∠的度数,然后利用平行线性质即可求得答案,掌握折叠的性质是解题的关键.解:∵235∠=︒,∴18035145AEA ∠=︒-︒='︒,由折叠性质可得,172.52AEF A EF AEA ∠='∠='∠=︒,∵AB CD ∥,∴272.5AEF ∠=∠=︒,故选:B .【变式2】(2024八年级上·江苏·专题练习)如图,在ABC V 和DCB △中,90,,A D AC BD ∠=∠=︒相交于点E ,AE DE =.将CDE 沿CE 折叠,点D 落在点D ¢处,若30BED ∠='︒,则BCD '∠的大小为.【答案】22.5︒【分析】本题主要考查了翻折变换(折叠问题),全等三角形的判定与性质等知识点,解决本题的关键是掌握翻折的性质.证明()ASA ABE DCE ≌,得,ABE DCE BE CE ∠=∠=,然后由翻折的性质和三角形内角和定理即可解决问题.解:在ABE 和DCE △中,90A D AE DE AEB DEC ∠==︒⎧⎪=⎨⎪∠=∠⎩,∴()ASA ABE DCE ≌,∴,ABE DCE BE CE ∠=∠=,∴EBC ECB ∠=∠,由翻折可知:,D CE DCE D EC DEC ''∠=∠∠=∠,∵30BED ∠='︒,∴()118030752D EC DEC AEB ∠=∠=∠=︒-︒='︒,∴907515ABE ∠=︒-︒=︒,∴15ABE DCE D CE '∠=∠=∠=︒,∵,75BE CE AEB =∠=︒,∴37.5EBC ECB ∠=∠=︒,∴37.51522.5BCD EBC D CE ∠=∠-∠=︒-︒=''︒,故答案为:22.5︒.【题型3】线段垂直平分线的性质与判定求值【例3】(23-24八年级上·江苏宿迁·期中)如图,AD 是ABC 的角平分线,DE DF 、分别是ABD △和ACD 的高.(1)试说明AD 垂直平分EF ;(2)若8628ABC AB AC S === ,,,求DE的长.【答案】(1)详见解析(2)4【分析】此题考查了角平分线的性质、全等三角形的判定和性质、垂直平分线的判定等知识,证明()Rt Rt HL AED AFD ≌是解题的关键.(1)利用角平分线的性质证明DE DF =,证明()Rt Rt HL AED AFD ≌,则AE AF =,即可证明结论;(2)根据28ABC S =△列式计算即可.解:(1)证明:∵AD 是ABC ABC △△的角平分线,DE DF 、分别是ABD △和ACD 的高.∴DE DF =,在Rt AED △与Rt AFD △中,AD AD DE DF =⎧⎨=⎩,∴()Rt Rt HL AED AFD ≌,∴AE AF =,∵DE DF =,∴AD 垂直平分EF ;(2)解:∵DE DF =,∴()11128222ABD ACD S S AB ED AC DF DE AB AC +=⋅+⋅=+= ,∵14AB AC +=,∴4DE =.【变式1】(23-24八年级上·四川巴中·期末)如图,在ABC V 中,分别以点A 和点B 为圆心,大于12AB长为半径画弧,两弧相交于点M 、N ,作直线MN ,交BC 于点D ,连接AD .若7AC =,12BC =,则ADC △的周长为()A .12B .14C .19D .26【答案】C【分析】由作图可知,MN 是线段AB 的垂直平分线,根据垂直平分线的性质,可得DA DB =,通过等量代换即可求解,本题考查了垂直平分线的判定和性质,解题的关键是:从作图方法中识别出垂直平分线的作法.解:由题意可得,MN 是线段AB 的垂直平分线,DA DB ∴=,71219ABC C AC AD CD AC CD BD AC BC =++=++=+=+= ,故选:C .【变式2】(23-24九年级上·重庆·期末)如图在ABC V 中,D 为AB 中点,DE AB ⊥,180ACE BCE ∠+∠=︒,EF BC ⊥交BC 于F ,8AC =,12BC =,则BF 的长为.【答案】10【分析】本题考查了线段垂直平分线的性质定理,全等三角形的判定及性质,角平分线的性质定理等;连接AE ,过点E 作EG AC ⊥交AC 的延长线于点G ,由线段垂直平分线的性质得EA EB =,由角平分线的性质得EG EF =,由HL 得Rt Rt EFC EGC ≌ 由全等三角形的性质得CF CG =,同理可得BF AG =,即可求解;掌握相关的判定方法及性质,能根据题意作出恰当的辅助线,构建全等三角形是解题的关键.解:如图,连接AE ,过点E 作EG AC ⊥交AC 的延长线于点G ,D 为AB 中点,DE AB ⊥,EA EB ∴=,180ACE BCE ∠+∠=︒ ,180ACE ECG ∠+∠=︒,ECG BCE ∴∠=∠,EF BC ⊥ ,EG AC ⊥,EG EF ∴=,在Rt EFC △和Rt EGC 中,CE CE EF EG=⎧⎨=⎩,Rt Rt EFC EGC ∴≌ (HL ),CF CG ∴=,同理可得:Rt Rt BFE AGE ≌ ,BF AG ∴=,BC CF AC CG ∴-=+,128CF CF ∴-=+,解得:2CF =,12210BF ∴=-=,故答案:10.【题型4】利用等腰三角形的性质与判定求值或证明【例4】(2024八年级上·江苏·专题练习)如图,在ABC V 中,AC BC =,120ACB ∠=°,CD 是AB 边上的中线,BD 的垂直平分线EF 交BC 于点E ,交AB 于点F ,15CDG ∠=︒.(1)求证:AD AG =;(2)试判断CDE 的形状,并说明理由.【答案】(1)见解析;(2)等边三角形,见解析【分析】本题考查了等腰三角形的性质与判定,线段垂直平分线的性质,等边三角形的判定,掌握等腰三角形的性质与判定是解题的关键.(1)根据等腰三角形的性质得出CD AB ⊥,30A B ==︒∠∠,AD DB =,进而根据15CDG ∠=︒,得出AGD ADG ∠=∠,根据等角对等边即可得证;(2)根据EF 是BD 的垂直平分线,得出DE EB =,根据等边对等角得出30EDB B ∠=∠=︒,进而得出60DCE CDE ∠=∠=︒,可得CDE 是等边三角形.(1)证明:∵AC BC =,120ACB ∠=°,CD 是BC 边上的中线,∴CD AB ⊥,()1180302A B ACB ∠=∠=︒-∠=︒,AD BD =,∴90ADC CDB ∠=∠=︒,∵15CDG ∠=︒,∴9075ADG CDG ∠=︒-∠=︒,∵18075AGD A ADG ∠=︒-∠-∠=︒,∴AGD ADG ∠=∠,∴AD AG =;(2)结论:CDE 是等边三角形.∵EF 垂直平分线段BD ,∴DE EB =,∵30B ∠=︒,∴30EDB B ∠=∠=︒,∴9060CDE EDB ∠=︒-∠=︒,又∵AC BC =,120ACB ∠=°,CD 是BC 边上的中线,∴1602DCB ACB ∠=∠=︒,∴60DCE CDE ∠=∠=︒,∴CDE 是等边三角形.【变式1】(23-24八年级上·湖南株洲·期末)在ABC V 中,36A ∠=︒,72B ∠=︒,则ABC V 是()A .钝角三角形B .等腰三角形C .等边三角形D .等腰直角三角形【答案】B 【分析】本题考查三角形的内角和,等腰三角形的判定,根据三角形的内角和求出72C B ∠=∠=︒即可判断.解:在ABC V 中,36A ∠=︒,72B ∠=︒,∴18072C A B B ∠=︒-∠-∠=︒=∠,∴ABC V 是等腰三角形,故选:B .【变式2】(23-24八年级上·重庆沙坪坝·期末)如图,在ABC ∆中,AB AC =,AD BD =,DE AB ⊥于点E ,若4BC =,BDC 的周长为10,则AE 的长为.【答案】3【分析】本题考查等腰三角形的性质,熟练掌握等腰三角形三线合一是解题的关键.根据已知可得6BD CD +=,从而可得6AB AC ==,然后利用等腰三角形三线合一性质计算解答.解:4BC = ,且BDC 的周长为10,1046BD CD ∴+=-=,AD BD = ,6AD DC ∴+=,6AC ∴=,AB AC = ,6AB ∴=,AD DB = ,DE AB ⊥,132AE AB ∴==.故答案为:3.【题型5】利用等边三角形的性质与判定求值或证明【例5】(2024八年级上·江苏·专题练习)如图,已知Rt ABC △中,90ACB ∠=︒,CD AB ⊥于D ,BAC ∠的平分线分别交BC ,CD 于E 、F .(1)试说明CEF △是等腰三角形.(2)若点E 恰好在线段AB 的垂直平分线上,试说明线段AC 与线段AB 之间的数量关系.【答案】(1)见解析(2)12AC AB =【分析】(1)首先根据条件90ACB ∠=︒,CD AB ⊥,可证出90B BAC ∠+∠=︒,90CAD ACD ∠+∠=︒,再根据同角的补角相等可得到ACD B ∠=∠,再利用三角形的外角性质可得到CFE CEF ∠=∠,最后利用等角对等边即可得出答案;(2)由线段垂直平分线的性质得到AE BE =,根据等腰三角形的性质得到EAB B ∠=∠,由AE 是BAC ∠的平分线,得到CAE EAB ∠=∠,根据直角三角形的性质即可得到结论.解:(1)∵90ACB ∠=︒,∴90B BAC ∠+∠=︒,∵CD AB ⊥,∴90CAD ACD ∠+∠=︒,∴ACD B ∠=∠,∵AE 是BAC ∠的平分线,∴CAE EAB ∠=∠,∵EAB B CEA CAE ACD CFE ∠+∠=∠∠+∠=∠,,∴CFE CEF ∠=∠,∴CF CE =,∴CEF △是等腰三角形;(2)∵点E 恰好在线段AB 的垂直平分线上,∴AE BE =,∴EAB B ∠=∠,∵AE 是BAC ∠的平分线,∴CAE EAB ∠=∠,∴2CAB B ∠=∠,∵90ACB ∠=︒,∴90CAB B ∠+∠=︒,∴30B ∠=︒,∴12AC AB =.【点拨】此题主要考查了直角三角形综合,熟练掌握直角三角形性质,角平分线性质,三角形外角性质,等腰三角形的判定和性质,线段垂直平分线的性质,是解题的关键.【变式1】(23-24八年级上·福建福州·期末)如果,,a b c 为三角形的三边长,且满足()()()0a b b c c a ---=,那么该三角形的形状为()A .等腰三角形B .等边三角形C .不等边三角形D .无法确定【答案】D【分析】本题考查了等腰三角形和等边三角形的判定,掌握等腰三角形和等边三角形的判定方法是解题关键.根据()()()0a b b c c a ---=得到a b =或a c =或b c =或a b c ==,从而可以判定该三角形的形状.解:∵()()()0a b b c c a ---=,∴0a b -=或0b c -=或0c a -=或0a b b c c a -=-=-=,解得a b =或a c =或b c =或a b c ==,∴该三角形的形状为等腰三角形或等边三角形,故选:D .【变式2】(23-24九年级上·河北邯郸·期末)如图1,ABC V 和ADE V 是等边三角形,连接BD ,CE 交于点F .(1)BD CE 的值为;(2)BFC ∠的度数为︒.【答案】160【分析】本题考查了全等三角形的判定及性质,等边三角形的性质.(1)根据等边三角形的性质得出AB AC =,AD AE =,BAC DAE ∠=∠,再由DAE BAE BAC BAE ∠+∠=∠+∠,得出CAE BAD ∠=∠,利用SAS 可证得CAE BAD ≌△△,从而可得出结论;(2)由()SAS CAE BAD △≌△,可得ABD ACE ∠=∠,再根据AOC BOF ∠=∠,结合三角形内角和即可求解.解:(1)∵ABC V 和ADE V 是等边三角形,∴AB AC =,AD AE =,BAC DAE ∠=∠,∵DAE BAE BAC BAE ∠+∠=∠+∠,∴CAE BAD ∠=∠,∴()SAS CAE BAD △≌△,∴BD CE =,则1BD CE=,故答案为:1;(2)由()SAS CAE BAD △≌△,可得ABD ACE ∠=∠,∵AOC BOF ∠=∠,AOC ACE BAC BOF ABD BFC ∠+∠+∠=∠+∠+∠,∴60CFB BAC ∠=∠=︒,∴60BFC ∠=︒,故答案为:60.【题型6】利用30度所对的直角边等于斜边一半求值或证明【例6】(2024八年级上·江苏·专题练习)在Rt ABC △中,90ACB ∠=︒,M 是边AB 的中点,CH AB ⊥于点H ,CD 平分ACB ∠.(1)求证:CD 平分MCH ∠;(2)过点M 作AB 的垂线交CD 的延长线于点E ,求证:CM EM =;(3)AEM △是什么三角形?证明你的猜想.【答案】(1)见解析(2)见解析(3)AEM △是等腰直角三角形,证明见解析【分析】(1)根据直角三角形斜边上的中线等于斜边的一半得到AM CM BM ==,由等腰三角形的性质得到CAB ACM ∠=∠,由余角的性质得到CAB BCH ∠=∠,等量代换得到BCH ACM ∠=∠,根据角平分线的性质得到ACD BCD ∠=∠,即可得到结论;(2)根据EM AB ⊥,CH AB ⊥,得到EM AB ∥,由平行线的性质得到HCD MED ∠=∠,由于HCD MCD ∠=∠,于是得到MCD MED ∠=∠,即可得到结论;(3)根据CM EM =,AM CM BM ==,于是得到EM AM BM ==,由EM AB ⊥,推出AEM △是等腰直角三角形.(1)证明:Rt ABC △中,90ACB ∠=︒,M 是AB 边的中点,AM CM BM ∴==,CAB ACM ∴∠=∠,90CAB ABC ∴∠=-∠,CH AB ⊥ ,90BCH ABC ∴∠=-∠,CAB BCH ∴∠=∠,BCH ACM ∴∠=∠,CD 平分ACB ∠,ACD BCD ∴∠=∠,ACD ACM BCD BCH ∴∠-∠=∠-∠,即MCD HCD ∠=∠,CD ∴平分MCH ∠;(2)证明:EM AB ⊥ ,CH AB ⊥,∴EM CH ∥,HCD MED ∴∠=∠,HCD MCD ∠=∠ ,MCD MED ∴∠=∠,CM EM ∴=;(3)解:AEM △是等腰直角三角形,CM EM = ,AM CM BM ==,EM AM BM ∴==,EM AB ⊥ ,AEM ∴△是等腰直角三角形.【点拨】本题考查了直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的判定和性质,角平分线的定义,等腰三角形的性质,熟练掌握各定理是解题的关键.【变式1】(23-24九年级上·安徽合肥·期末)如图,ABC V 中,9030ACB A ∠=︒∠=︒,,CD AB ⊥于点D ,若1BD =,则AD 的长度为()A .5B .4C .3D .2【答案】C 【分析】本题主要考查直角三角形的性质,熟练运用“在直角三角形中,30︒角所对的直角边等于斜边的一半”是解题的关键.由含30︒角的直角三角形的性质可分别求得BC 和AB 的长,进而求得AD 的长.解:∵在ABC V 中,9030ACB A ∠=︒∠=︒,,∴=60B ∠︒,∵CD AB ⊥,∴30BCD ∠=︒,∴在Rt BCD △中,22BC BD ==,∴在Rt ABC △中,24AB BC ==,∴413AD AB BD =-=-=.故选:C .【变式2】(23-24七年级下·陕西西安·阶段练习)如图,在Rt ABC △中,90C ∠=︒,AD 是CAB △的平分线,DE 垂直平分AB ,若3CD =,则BD =.【答案】6【分析】本题主要考查线段垂直平分线的性质、30︒所对的直角边是斜边的一半,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.由角平分线和线段垂直平分线的性质可求得30B CAD DAB∠=∠=∠=︒,在Rt ACD△中,根据直角三角形的性质可求得AD,则可得出BD的长.解:DE垂直平分AB,DA DB∴=,B DAB∴∠=∠,AD平分CAB∠,CAD DAB∴∠=∠,90C∠=︒,390CAD∴∠=︒,30CAD∴∠=︒,26AD CD∴==,6BD AD∴==.故答案为:6.第三部分【中考链接与拓展延伸】1、直通中考【例1】(2024·四川巴中·中考真题)如图,在ABCV中,D是AC的中点,CE AB⊥,BD与CE交于点O,且BE CD=.下列说法错误的是()A.BD的垂直平分线一定与AB相交于点EB.3BDC ABD∠=∠C.当E为AB中点时,ABCV是等边三角形D.当E为AB中点时,34BOCAECSS=△△【答案】D【分析】连接DE ,根据CE AB ⊥,点D 是AC 的中点得12DE AD CD AC ===,则BE DE =,进而得点D 在线段BD 的垂直平分线上,由此可对选项A进行判断;设ABD α∠=,根据BE DE =得EDB ABD α∠=∠=,的2AED EDB ABD α∠=∠+∠=,再根据DE AD =得2A AED α∠=∠=,则3BDC A ABD α∠=∠+∠=,由此可对选项B进行判断;当E 为AB 中点时,则12BE AB =,CE 是线段AB 的垂直平分线,由此得AC BC =,然后根据12BE AB =,12CD AC =,BE CD =得AB AC =,由此可对选项C进行判断;连接AO 并延长交BC 于F ,根据ABC V 是等边三角形得30OBC OAC ∠=∠=︒,则OA OB =,进而得2OB OF =,3AF OF =,由此得12OBC S BC OF ∆=⋅,1322ABC S BC AF BC OF ∆=⋅=⋅,由此可对选项D进行判断,综上所述即可得出答案.解:连接DE ,如图1所示:CE AB ⊥ ,点D 是AC 的中点,DE ∴为Rt AEC △斜边上的中线,12DE AD CD AC ∴===,BE CD = ,BE DE ∴=,∴点D 在线段BD 的垂直平分线上,即线段BD 的垂直平分线一定与AB 相交于点E ,故选项A 正确,不符合题意;设ABD α∠=,BE DE = ,EDB ABD α∴∠=∠=,2AED EDB ABD α∴∠=∠+∠=,DE AD = ,2A AED α∴∠=∠=,3BDC A ABD α∴∠=∠+∠=,即3BDC ABD ∠=∠,故选B 正确,不符合题意;当E 为AB 中点时,则12BE AB =,CE AB ⊥ ,CE ∴是线段AB 的垂直平分线,AC BC ∴=,12BE AB = ,12CD AC =,BE CD =,AB AC ∴=,AC BC AB ∴==,ABC ∴ 是等边三角形,故选C 正确,不符合题意;连接AO ,并延长交BC 于F ,如图2所示:当E 为AB 中点时,点D 为AC 的中点,∴根据三角形三条中线交于一点得:点F 为BC 的中点,当E 为AB 中点时,ABC V 是等边三角形,60ABC BAC ∴∠=∠=︒,AF BC ⊥,AF 平分OAC ∠,BD 平分ABC ∠,30OBC OAC ∴∠=∠=︒,OA OB ∴=,在Rt OBF △中,2OB OF =,2OA OB OF ∴==,3AF OA OF OF ∴=+=,12OBC S BC OF ∆∴=⋅,1322ABC S BC AF BC OF ∆=⋅=⋅,∴13OBC ABC S S ∆∆=,故选项D 不正确,符合题意.故选:D .【点拨】此题主要考查了直角三角形斜边上的中线,线段垂直平分线的性质,等腰三角形的判定与性质,等边三角形的判定和性质,理解直角三角形斜边上的中线,线段垂直平分线的性质,熟练掌握等腰三角形的判定与性质,等边三角形的判定和性质是解决问题的关键.【例2】(2024·江苏宿迁·中考真题)如图,在ABC V 中,5030B C ︒∠∠=︒=,,A 是高,以点A 为圆心,A 长为半径画弧,交AC 于点E ,再分别以B 、E 为圆心,大于12BE 的长为半径画弧,两弧在BAC ∠的内部交于点F ,作射线AF ,则DAF ∠=.【答案】10︒/10度【分析】本题主要考查角平分线的作法及三角形内角和定理,根据题意得出AF 平分BAC ∠,然后利用三角形内角和定理求解即可.解:因为5030B C ∠=︒∠=︒,,所以1805030100BAC ∠=︒-︒-︒=︒,根据题意得:AF 平分BAC ∠,所以1502BAF BAC ∠==︒,因为AD 为高,所以90BDA ∠=︒,所以180509040BAD ∠=︒-︒-︒=︒,所以504010DAF BAF BAD ∠=∠-∠=︒-︒=︒,故答案为:10︒.2、拓展延伸【例】(22-23八年级上·吉林长春·阶段练习)在等腰ABC V 中,CA CB =,30B ∠=︒,将一块足够大的直角三角尺PMN (90M ∠=︒、30MPN ∠=︒)按如图所示放置,顶点P 在线段AB 上滑动,三角尺的直角边PM 始终经过点C ,并且与CB 的夹角PCB α∠=,斜边PN 交AC 于点D .(1)当P 运动到AB 中点时,α=__________度;(2)当45α=︒时,请写出图中所有的等腰三角形(ABC V 除外)__________.(3)在点P 的滑动过程中,当PCD △的形状是以PC 为底的等腰三角形时,请在指定位置画出此时形成的图形,并指出此时图中的所有直角三角形(PMN 除外).不用说明理由.【答案】(1)60;(2)ACP △和PCD △;(3)此时图中的所有直角三角形是PBC △和APD △.【分析】本题属于三角形综合题,考查了全等三角形的判定与性质,等腰三角形的判定,外角性质,直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.(1)根据等腰三角形的性质得到CP AB ⊥,求得90BPC ∠=︒,根据三角形的内角和定理即可得到结论;(2)根据三角形的内角和定理得到120BCA ∠=︒,求得1204575ACP ∠=︒-︒=︒,根据等腰三角形的判定定理得到ACP △是等腰三角形,求得PDC PCD ∠=∠,根据等腰三角形的判定定理得到PCD △是等腰三角形(3)当PD CD =时,PCD △以PC 为底的等腰三角形,根据等腰三角形的性质得到30PCD CPD ∠=∠=︒,即12030α-=°°,推出PBC △是直角三角形,根据三角形的内角和定理得到60CPB ∠=︒,求得603090BPD ∠=︒+︒=︒,于是得到APD △是直角三角形.解:(1)AC BC = ,点P 为AB 中点,CP AB ∴⊥,90BPC ∴∠=︒,30B ∠=︒ ,903060α∴=︒-︒=︒,故答案为:60;(2)CA CB = ,30B ∠=︒,30A B ∴∠=∠=︒,120BCA ∴∠=︒,45BCP α∠==︒ ,1204575ACP ∴∠=︒-︒=︒,75APC BCP B ∠=∠+∠=︒ ,ACP APC ∴∠=∠,ACP ∴△是等腰三角形,30CPD ∠=︒ ,45APD ∴∠=︒,75CDP A APD ∴∠=∠+∠=︒,PDC PCD ∴∠=∠,PCD ∴ 是等腰三角形,故答案为:ACP △和PCD △;(3)如图,120ACB ∠=︒ ,120PCD α∴∠=︒-,当PD CD =时,PCD △以PC 为底的等腰三角形,30PCD CPD ∴∠=∠=︒,即12030α-=°°,90α∴=︒;PBC ∴△是直角三角形,60CPB ∴∠=︒,6030BPD ∴∠=︒+︒,90APD ∴∠=︒,APD ∴ 是直角三角形,综上所述,此时图中的所有直角三角形是PBC △和APD △.。
八年级上册数学轴对称知识点

八年级上册数学轴对称知识点在初中数学中,轴对称是一个非常重要的知识点。
轴对称是指在一个平面上,如果有一条直线,把这个平面分成两个对称的部分,那么我们就说这个平面是轴对称的。
八年级上册的数学课程中,轴对称被涉及到了,下面我们来详细地探讨一下轴对称的相关知识点。
一、轴对称的定义和性质轴对称的定义如上所述,即沿着一条直线进行对称,这条直线就称为轴线或者对称轴。
在轴对称的情况下,通过轴对称得到的镜像图形和原图形完全重合,这也就是轴对称的性质。
轴对称有如下的性质:(1)轴对称图形共有或自成一类轴对称得到的镜像图形和原图形完全重合,因此当把某个图形做轴对称后,得到的图形和原图形形状相同,只是位置不同。
所以,轴对称得到的镜像图形和原图形共有或自成一类。
(2)轴对称的两个对称图形的距离等于轴到这两个图形的距离我们知道,轴对称的求法是以轴线为轴进行对称,而轴线到对称位置不同的点的距离不同,因此,轴对称的两个对称图形的距离等于轴到这两个图形的距离。
(3)轴对称保持长度、角度不变轴对称能够保持长度和角度不变的原因是,轴对称的两个对称图形都是完全重合的,所以它们的长度和角度是相同的。
二、轴对称的基本步骤下面我们来看轴对称的基本步骤:(1)确定轴对称的轴线首先,要确定轴对称的轴线,它必须是平面内的一条直线。
(2)确定轴对称的中心点确定轴对称的中心点,这个点一般都在轴线上,它是轴线的中点。
(3)确定轴对称的象限确定轴对称的象限,即确定轴对称得到的镜像图形和原图形的位置关系。
(4)确定轴对称的顺序确定轴对称的顺序,从哪一端开始进行对称。
一般情况下,我们可以从离中心点近的位置开始对称。
三、轴对称的应用轴对称的应用十分广泛,下面我们来看一下轴对称在实际生活中的应用:(1)轮子的轴对称自行车、汽车等车辆的轮子都采用了轴对称的原理。
(2)建筑物的轴对称建筑物在建造过程中也采用了轴对称的方法,比如古希腊罗马建筑中的神殿、半圆形壳体建筑等。
初二数学知识点详解之轴对称

初二数学知识点详解之轴对称一、轴对称图形1.把一个图形沿着一条直线折叠,如果直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
这时我们也说这个图形关于这条直线(成轴)对称。
2.把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图关于这条直线对称。
这条直线叫做对称轴。
折叠后重合的点是对应点,叫做对称点3、轴对称图形和轴对称的区别与联系4.轴对称与轴对称图形的性质①关于某直线对称的两个图形是全等形。
②如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
③轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
④如果两个图形的对应点连线被同条直线垂直平分,那么这两个图形关于这条直线对称。
⑤两个图形关于某条直线成轴对称,如果它们的对应线段或延长线相交,那么交点在对称轴上。
二、线段的垂直平分线1.定义:经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2.性质:线段垂直平分线上的点与这条线段的两个端点的距离相等3.判定:与一条线段两个端点距离相等的点,在线段的垂直平分线上三、用坐标表示轴对称小结:1.在平面直角坐标系中①关于x轴对称的点横坐标相等,纵坐标互为相反数;②关于y轴对称的点横坐标互为相反数,纵坐标相等;③关于原点对称的点横坐标和纵坐标互为相反数;④与X轴或Y轴平行的'直线的两个点横(纵)坐标的关系;⑤关于与直线X=C或Y=C对称的坐标点(x,y)关于x轴对称的点的坐标为_(x,-y)_____.点(x,y)关于y轴对称的点的坐标为___(-x,y)___.2.三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等四、(等腰三角形)知识点回顾1.等腰三角形的性质①.等腰三角形的两个底角相等。
(等边对等角)②.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
(三线合一)理解:已知等腰三角形的一线就可以推知另两线。
人教八年级数学上册《全等三角形》、《轴对称》知识要点归纳
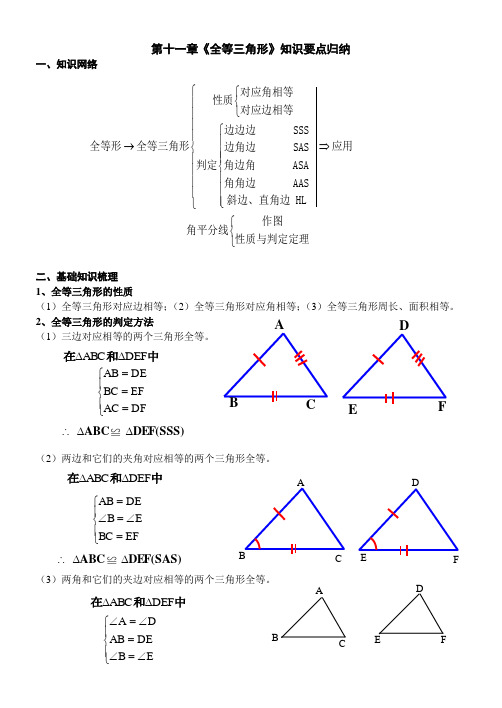
第十一章《全等三角形》知识要点归纳一、知识网络二、基础知识梳理 1、全等三角形的性质(1)全等三角形对应边相等;(2)全等三角形对应角相等;(3)全等三角形周长、面积相等。
2、全等三角形的判定方法 (1)三边对应相等的两个三角形全等。
(2)两边和它们的夹角对应相等的两个三角形全等。
(3)两角和它们的夹边对应相等的两个三角形全等。
⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪→⇒⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎨⎩对应角相等性质对应边相等边边边 SSS 全等形全等三角形应用边角边 SAS 判定角边角 ASA 角角边 AAS 斜边、直角边 HL 作图 角平分线性质与判定定理A B C D E F 中和在DEF ABC ∆∆⎪⎩⎪⎨⎧===DF AC EF BC DEAB DEF(SSS) ABC ∆∆∴≌ A B C D EF中和在DEF ABC ∆∆⎪⎩⎪⎨⎧=∠=∠=EF BC E B DE AB DEF(SAS) ABC ∆∆∴≌ AB CDE F中和在DEF ABC ∆∆⎪⎩⎪⎨⎧∠=∠=∠=∠E B DE AB D A(4)两角和其中一角的对边对应相等的两个三角形全等。
(5)斜边和一条直角边对应相等的两个直角三角形全等。
注意:①全等三角形问题中,找准对应点,对应边,对应角。
(突出对应) ②题中已知平移、翻折、旋转相当已知全等;③判定两个三角形全等的定理中,必须具备三个条件,且至少要有一组边对应相等,因此在寻找全等的条件时,总是先寻找边相等的可能性。
④要善于发现和利用隐含的等量元素,如公共角、公共边、对顶角等。
⑤要善于灵活选择适当的方法判定两个三角形全等。
其中:一般三角形有四 种判定方法 。
直角三角形有五 种判定方法。
3、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上DEF(ASA)ABC ∆∆∴≌ A B C DE F中和在DEF ABC ∆∆⎪⎩⎪⎨⎧=∠=∠∠=∠EF BC E B D A DEF(AAS)ABC ∆∆∴≌ A C BEFD中和在DEF Rt ABC Rt ∆∆⎩⎨⎧==DF AC DE AB )HL (DEF Rt ABC Rt ∆∆∴ ≌ ·ADP COB角平分线的性质)平分PD(PC OAPD OB PC AOB OP =∴⊥⊥∠ ·ADP CBAOB∠∠=∠∴=⊥⊥平分或:角平分线的判定)OP BOP(AOP PD PC OA PD OB PC注:①性质与判定都是由三个条件推出一个结论,要正确应用; ②会用尺规做一个角的平分线,依据为“边边边”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作品编号:522325647891253697158
学校:朝阳岗市溪边镇柳树小学*
教师:谢德刚*
班级:蝴蝶叁班*
第十三章轴对称
13.1 轴对称(对称点)
轴对称图形:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合。
这条直线就是它的对称轴。
垂直平分线:经过线段中点并且垂直于这条线段的直线。
图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
线段垂直平分线的性质:垂直平分线上的点到两端的距离相等。
若PA=PB,点C为AB中点,则PC⊥AB或点P在线段AB的垂直平分线上。
13.2 画轴对称图形
先画对称点(过该点画对称轴的垂线,取等长),然后连接对称点,形成轴对称图形。
13.3 等腰三角形
概念:有两边相等的三角形。
性质:等边对等角,三线合一(顶角平分线、底边上的中线、底边上的高)。
判定:等角对等边
等边三角形:三边都相等的特殊的等腰三角形。
三个内角都相等,每个内角60º。
(判定:三个角都相等的三角形;有一个角是60º的等腰三角形。
)
在RtΔ中,如果一个锐角等于30º,那么它所对的直角边等于斜边的一半。
(在RtΔ中,斜边上的中线等于斜边的一半。
)
13.4 课题学习最短路径问题
利用轴对称、平移作出最短路径选择。
(两点之间线段最短)。
