第2章0和1语义符号化、符号计算化与计算自动化练习题复习资料分析
2010计算机导论Chapter2复习提纲
任课教师：战德臣，聂兰顺
2.2 基本思想与基本过程
1. 语义符号化思想 语义符号化是指将现实世界的语义用符号表达，进而进行基于符号的计算的一种思维， 将符号赋予不同语义，则能计算不同的问题。 例如， 《易经》将现实世界分为阴和阳，阴即０，阳即１，进一步用阴阳的组合与变化， 即０,1 的组合与变化来反映大千世界的变化规律，例如八卦，用三位０,1 码的组合，每一种 组合抽象于一种自然现象，如“乾卦”抽象于天，表达具有天的特性的事物，则天为乾卦的 本体语义，而如果将乾卦放在“家庭空间”中，则表征“父” ，而如果放在“身体空间”中， 则表征“首” ，因此，符号可以被绑定不同的语义。由此符号化，则二十四节气的演变、生 命规律的演变等都可以用 0 和１，即阴和阳的变化来反映了。 2. 计算的实现：电子电路级的实现，即基于 0 和 1 的电子实现； 现实世界的各种信息可表示成０和１， 可基于０和１进行算术运算和逻辑运算， 在实现 过程中，能够表示０和１的元器件有很多，典型的如继电器开关：开(表示１)、关(表示０)， 电路中的电信号：低电平(表示０)、高电平(表示１)，二极管、三极管等不仅实现表示，还 实现控制。 利用基本元器件，如二极管、三极管可封装集成后制造“与”门、 “或”门、 “非”门等 门电路，并能确认这些基本门电路的正确性。 再将“与”门、 “或”门、 “非”门等门电路进行组合，形成更为复杂的组合电路。布尔 代数与数字逻辑是判断组合电路正确性的工具。 微处理器、内存储器等就是不断组合已有的门电路、组合电路，并将其集成在一块芯片 上所形成的。 3. 计算的实现：程序级的实现，即图灵机 图灵认为：所谓计算就是计算者(人或机器)对一条两端可无限延长的纸带上的一串 0 或 1，执行指令一步一步地改变纸带上的 0 或 1，经过有限步骤最后得到一个满足预先规定的 符号串的变换过程。基本思想： “基本动作”就是机器将输入转变为输出， “指令”是对基本 动作的控制， “程序”是有先后次序关系的指令串即控制规则， “自动执行”是依控制规则自 动将输入处理为输出， “输入/输出”及“程序”均用符号表达及最终由 0 和 1 表达。 上述思想可用形式化模型表达。图灵机是一个七元组 P = (Q, , , , q0, B, F )，其中 Q 是有穷状态集，是有穷输入字符集， 是有穷输入带字符集，＝<q,X,Y,R/L/N,p>是状 态转移函数，表示：在当前状态 q 下，将字符 X 转换为字符 Y,同时，控制纸带向左、向右 移动或不动，然后将状态改为 p。q0 是初始状态，B 是空格符，F 是有穷终结状态集。 图灵机模型被认为是计算机的基本理论模型， 即计算机是使用相应的程序来完成任何设 定好的任务，是一种离散的、有穷的、构造性的问题求解思路，一个问题的求解可以通过构 造其图灵机(即程序)来解决。图灵认为：凡是能用算法方法解决的问题也一定能用图灵机解 决; 凡是图灵机解决不了的问题任何算法也解决不了，此即图灵可计算性问题。 4. 冯.诺依曼计算机和存储程序思想 冯.诺依曼计算机的五大基本部件：运算器、控制器、存储器、输入设备和输出设备。 其中运算器负责执行逻辑运算和算术运算，控制器负责读取指令、分析指令并执行指令，以 调度运算器进行计算， 存储器负责存储数据和指令， 输入设备负责将程序和指令输入到计算 机中，输出设备是将计算机处理结果显示或打印出来。 冯.诺依曼计算机的基本思想是存储程序的思想，即程序在执行之前事先存储在存储器 中，这样机器就可连续地从存储器中读取指令执行指令，实现连续自动的计算。 2-4
编译原理_第1-5章习题课答案
（1）以01结尾的二进制数串。 (0 | 1)*01
（2）能被5整除的十进制数。
0|5
| (1|2|3|4|5|6|7|8|9)
（3）包含奇數個1或奇數個0的二進制串
0*1(0|10*1)*|1*0(0|10*1)*
（4）英文字母组成的所有符号串，要求符号串中的 字母按字典序排列。
(A | a)* (B | b)* (C | c)*… (Z | z)*
I00
0 ΦC
0
B {c,d} 1 0
E
1
{c,d} D
{c,d,f}
1
1
{c,d}
{c,d,f}
chapter1~5习题
I1 {b,c,d} 1 {c,dF,e}
{c,d,e} 0 {c,d,e} {c,d,e,g}
{c,d,e}
S
0
A(始态)
Φ
B
C
C
C
D
E
E
C
F(终态)
E
1 B D D D F(终态) D
1(0|1)*101 1(0|1)*101
chapter1~5习题
g
1
a
(0|1)* b
101
d
g
1 a
0
ε
ε
b
c
1
1
0
1
d
e
f
g
编译原理
②.状态转换矩阵
1 a
0
ε
ε
b
c
1
chapter1~5习题
1
0
1
d
e
f
g
I {a} {b,c,d} {c,d} {c,d,e} {c,d,f} {c,d,e,g}
北航计算机学院编译习题讲解
北航计算机学院编译习题讲解习题课 (1-3章）1、复习2、习题讲解北京航空航天大学计算机科学与工程系2008年6月27日1第一章概论(介绍名词术语、了解编译系统的结构和编译过程）北京航空航天大学计算机科学与工程系2008年6月27日21.2 编译过程所谓编译过程是指将高级语言程序翻译为等价的目标程序的过程。
习惯上是将编译过程划分为5个基本阶段：词法分析语法分析语义分析、生成中间代码代码优化生成目标程序北京航空航天大学计算机科学与工程系2008年6月27日 3典型的编译程序具有7个逻辑部分 S.P 词法分析程序符号表管理语法分析程序语义分析、生成中间代码代码优化生成目标程序 O.P 出错处理北京航空航天大学计算机科学与工程系2008年6月27日4第二章? 掌握符号串和符号串集合的运算、文法和语言的定义? 几个重要概念：递归、短语、简单短语和句柄、语法树、文法的二义性、文法的实用限制等。
? 掌握文法的表示：BNF、扩充的BNF范式、语法图。
? 了解文法和语言的分类北京航空航天大学计算机科学与工程系2008年6月27日 5第三章:词法分析3.1 词法分析的功能 3.2 词法分析程序的设计与实现–状态图3.3 词法分析程序的自动生成–有穷自动机、LEX北京航空航天大学计算机科学与工程系2008年6月27日6补充正则文法正则文法 1 2 4 NFA NFA 3 DFA DFA 最小化北京航空航天大学计算机科学与工程系2008年6月27日 75 6 正则表达式正则表达式习题1－3章北京航空航天大学计算机科学与工程系2008年6月27日8第一章2．典型的编译程序可划分为哪几个主要的逻辑部分？各部分的主要功能是什么？北京航空航天大学计算机科学与工程系2008年6月27日91.2 编译过程所谓编译过程是指将高级语言程序翻译为等价的目标程序的过程。
习惯上是将编译过程划分为5个基本阶段：词法分析语法分析语义分析、生成中间代码代码优化生成目标程序北京航空航天大学计算机科学与工程系2008年6月27日 10典型的编译程序具有7个逻辑部分 S.P 词法分析程序符号表管理语法分析程序语义分析、生成中间代码代码优化生成目标程序 O.P 出错处理北京航空航天大学计算机科学与工程系2008年6月27日11P19：4.试证明：A+ =AA*=A*A 证：∵ A*=A0∪A+，A+=A1∪A2∪…∪An∪… 得：A*=A0∪A1∪A2∪…∪An∪… ∴ AA*=A（A0∪A1∪A2∪…∪An∪…）= AA0∪AA1∪AA2∪…∪A An∪… =A∪A2∪A3∪An +1∪… = A+ 同理可得：A*A =(A0∪A1∪A2∪…∪An∪…)A =A0 A∪A1A∪A2A∪…∪AnA∪… = A∪A2∪A3∪An+1∪… = A+ 因此： A+ =AA*=A*A北京航空航天大学计算机科学与工程系2008年6月27日 12P26:1.设G[〈标识符〉]的规则是：〈标识符〉::=a|b|c| 〈标识符〉a|〈标识符〉c| 〈标识符〉0|〈标识符〉1 试写出VT和VN，并对下列符号串a,ab0,a0c01,0a,11,aaa给出可能的一些推导。
编译原理教程课后习题答案第二章
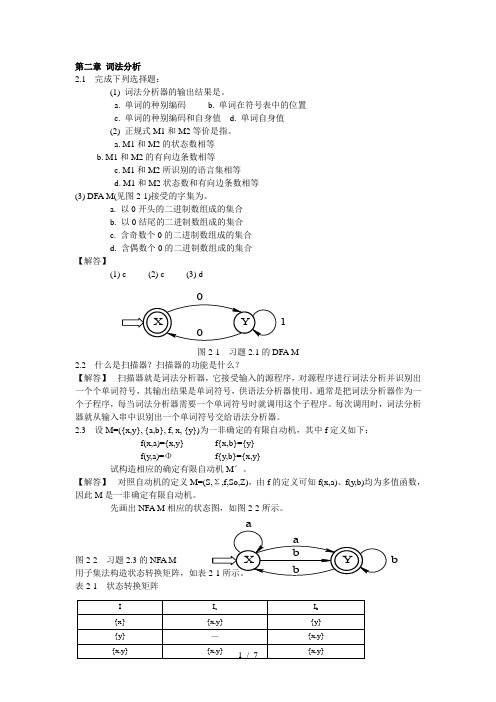
第二章 词法分析2.1 完成下列选择题：(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器？扫描器的功能是什么？【解答】 扫描器就是词法分析器，它接受输入的源程序，对源程序进行词法分析并识别出一个个单词符号，其输出结果是单词符号，供语法分析器使用。
通常是把词法分析器作为一个子程序，每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时，词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机，其中f 定义如下：f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z)，由f 的定义可知f(x,a)、f(y,b)均为多值函数，因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图，如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵，如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名，形成表2-2所示的状态转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。
第二讲：符号化,计算化,自动化
思路：语义符号化--符号计算化--计算01化--01自动化--分层构造化--构造集成化1。
语义符号化定义：将现象定义为符号，进行符号组合，利用符号组合表达自然现象。
解释：将现象符号化为01及其组合，再进行01组合的变化以及进行基于01的计算，最后语义化为现象变化规律。
目的：进行基于符号的演算，即符号组合的变化方式。
关键：区分与命名，形成术语体系。
本质：抽象与具体化。
例子：易经。
天为现象，乾为本体，用体可为父，首，马等。
2。
符号计算化（思维符号的表达与计算）逻辑：世物因果之间所遵循的规律，视线始终普适的思维方式。
逻辑的基本表现形式是命题与推理。
命题是一个判断语句，内容为真或假。
推理是由简单命题判断推导得出复杂命题判断结论的过程。
四种基本逻辑运算（1为真，0为假）与AND：全真才真，有假则假。
0AND0=0，0AND1=0，IAND0=0，1AND1=1或OR：有真则真，全假才假。
0OR0=0，0OR1=1，1OR0=1，1OR1=1非NOT：非真则假，非假则真。
NOT0=1，NOT1=0异或XOR：相同为假，不同为真。
0XOR0=0，1XOR1=0，0XOR1=1，1XOR0=13。
计算01化（处理数值性信息即算术运算，处理非数值性信息即编码）数值性信息进位制：用数码和带有权值的数位来表示有大小关系的数值性信息的表示方法。
为啥用二进制：可与逻辑运算统一，元器件容易实现二进制：01八进制：01234567十进制：0123456789十六进制：0123456789ABCDEF（分别代表10，11，12，13，14，15）例如：(11110101)2=（365）8=(245)10=(F5)16=(0F5)16,表示数时，前面可以加无数个零，不影响数的大小。
符号咋办呢？----机器数的原码，反码，补码。
机器数：n+1位二进制数中第n+1位表示符号，0表示正数，1表示负数。
真实数值（真值）：带符号的n位二进制数正数的原码，反码，补码是一样的。
自动机理论、语言和计算导论课后习题答案(中文版)
Solutions for Section 2.2Exercise 2.2.1(a)States correspond to the eight combinations of switch positions, and also must indicate whether the previous roll came out at D, i.e., whether the previous input was accepted. Let 0 represent a position to the left (as in the diagram) and 1 a position to the right. Each state can be represented by a sequence of three 0's or 1's, representing the directions of the three switches, in order from left to right. We follow these three bits by either a indicating it is an accepting state or r, indicating rejection. Of the 16 possible states, it turns out that only 13 are accessible from the initial state, 000r. Here is the transition table:杠杆可能出现8种情况，影响着最终状态。
并且也要说明，前面一个大理石球是否从D滚出，也就是说，前一个输入是否被接受。
令0 代表向左方的状态（如图表），1 代表向右方。
这三个杠杆的每一个状态都可以用三个数（0或1）组成的序列表示。
这个序列后面跟着字母a或者r。
举出计算机符号化的例子
举出计算机符号化的例子
0和1的思维概述
语义符号化;符号计算化;计算0(和)1化;0(和)1自动化;分层构造化;构造集成化
上述这段文字虽然很拗口，但是我们要理解其中的含义。
符号语义化
是指自然中的现象和思维均可以表达为0和1，具体可参见《易经》，其中对阴阳八卦的阐述确实与0和1的思想很相似。
符号计算化
是指用0和1可以进行算数和逻辑计算，其中的思想可参见数电的中逻辑运算，有“与”，“或”，“非”，“异或”运算。
计算0(和)1化
是指0和1可用电子技术实现，在大学会学习一门《数字电路基础》的课程，会对相应的电路进行介绍，到时候会更加深刻得感受0和1的魅力。
0(和)1自动化
是指电子技术实现逻辑运算，根据电路设计出可以实现逻辑运算的电路，同上可在数电中进一步认识与了解。
分层构造化
这里分层构造实现复杂运算，让“与”，“或”，“非”，“异或”运算组合成更多功能的电路，如加法器。
构造集成化
芯片–集成的复杂组合逻辑电路，让电路实现的功能更为强大。
计算机化工运用复习题+答案
第一、二章 matlab 向量与矩阵 1、变量名由字母、数字和下划线组成。
2、利用冒号生成向量：x ＝x0:step:xn 3、向量的数乘、数组乘和向量乘。
4、Matlab 的流程控制语句。
5、矩阵的生成方式(直接输入、M 文件、冒号表达式)，矩阵拆分。
6、矩阵的运算包括基本算术运算：＋(加)、－(减)、*(乘)、/(右除)、\(左除)、^(乘方)和点运算.*、./、.\和.^。
（两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维参数相同）7. 矩阵分析（a.矩阵的转置；b.矩阵的逆inv(A)与伪逆pinv(A)；c.方阵的行列式det(A)；d.矩阵的秩rank(A)）。
1、标点符号 （ ）可以使命令行不显示运算结果，（ ） 用来表示该行为注释行。
2、下列变量名中 （ ） 是合法的。
(A) char_1 ; (B) x*y ; (C) x\y ; (D) _end例1． 已知0.30.30.3sin(0.3)ln 22a a e e ay a --+=++，当a 取1和2时，求各点的函数值。
>> y1=(exp(0.3*1)-exp(-0.3*1))*sin(1+0.3)+log((0.3+1)/2) y1= 0.1561>> y2=(exp(0.3*2)-exp(-0.3*2))*sin(2+0.3)+log((0.3+2)/2) y2= 1.0893例2．当a＝[1:1:3]; b=[2:2:6]时，以下命令的运行结果是什么？1)>>a1=2*a 2) >> a2=a.*b 3) >>a3=a*b>> a＝[1:1:3]; b=[2:2:6];>> a1=2*a, a2=a.*b, a3=a*ba1 = 2 4 6a2 = 2 8 18Error using例3.已知12345678910111213141516A⎛⎫⎪⎪=⎪⎪⎪⎝⎭，求（1）A(3,4)；（2）A（7）；（3）取A矩阵第1～3行内，并在第2～4列中的所有元素组成B矩阵。
编译原理复习汇总
复习汇总一、第一章概述1.文法与自动机的等价1)0型文法—图灵机2)1型文法—线性有界非确定图灵机3)2型文法—非确定下推自动机4)3型文法—有限状态自动机2.编译技术的应用1)语法制导的结构化编辑器2)程序格式化工具3)软件测试工具4)程序理解工具5)高级语言的翻译工具6)等等3.从面向机器的语言到面向人类的语言（结合第二章第9小点理解）1)面向机器的语言：机器指令，汇编语言2)面向人类的语言：通用程序设计语言，数据查询语言，形式化描述语言（正规式,产生式）等等。
4.各语言的分类（结合第二章第9小点理解）1)过程式语言，面向对象语言：通用程序设计语言。
2)函数语言：面向特点领域的，递归特性。
例如LISP语言3)说明性，非算法式语言：LEX/YACC,SQL。
4)脚本式语言：Shell语言5.语言之间的转换（李静PPT41）1)高级语言之间的转换一般称为预处理或转换。
2)高级语言翻译成汇编语言或机器语言称之为编译。
3)把汇编语言翻译成机器语言称之为汇编。
4)将一个汇编语言程序汇编为可在另一台机器上运行的机器指令称之为交叉汇编。
5)把机器语言翻译成汇编语言称之为反汇编。
6)把汇编语言翻译成高级语言称之为反编译。
6.编译器和解释器1)编译器●源程序的翻译和翻译后的程序的运行是两个不同的阶段。
◆编译阶段：用户输入源程序，经过编译器的处理，生成目标程序。
◆目标程序的运行阶段：根据要求输入数据，得出结果。
2)解释器（凡是可以采用编译器的地方均可以采用解释器）●解释器把翻译和运行结合到一起，编译一段源程序，紧接着就执行它。
这种方式称为解释。
7.解释器的优点（对比与编译器）1)具有较好的动态特性。
2)具有较好的移植特性。
8.解释器的缺点（对比于编译器）1)相比于编译器需花费大量的时间。
2)占用更多的内存空间。
9.编译器的工作阶段（结合第二章6小点红色部分理解）1)源程序->词法分析器->语法分析器->语义分析器->中间代码生成器->代码优化器->目标代码生成器->目标代码2)工作过程中的每个阶段均采用了符号表管理器，出错处理器。
【2024版】人工智能及其应用蔡自兴)课后答案
可编辑修改精选全文完整版人工智能及其应用(蔡自兴)课后答案第二章知识表示方法2-1 状态空间法、问题归约法、谓词逻辑法和语义网络法的要点是什么？它们有何本质上的联系及异同点?答：状态空间法：基于解答空间的问题表示和求解方法，它是以状态和算符为基础来表示和求解问题的。
一般用状态空间法来表示下述方法：从某个初始状态开始，每次加一个操作符，递增的建立起操作符的试验序列，直到达到目标状态为止。
问题规约法：已知问题的描述，通过一系列变换把此问题最终变成一个子问题集合：这些子问题的解可以直接得到，从而解决了初始问题。
问题规约的实质：从目标出发逆向推理，建立子问题以及子问题的子问题，直至最后把出示问题规约为一个平凡的本原问题集合。
谓词逻辑法：采用谓词合式公式和一阶谓词算法。
要解决的问题变为一个有待证明的问题，然后采用消解定理和消解反演莱证明一个新语句是从已知的正确语句导出的，从而证明这个新语句也是正确的。
语义网络法：是一种结构化表示方法，它节点和弧线或链组成。
节点用于表示物体、概念和状态，弧线用于表示节点间的关系。
语义网络的解答是一个经过推理和匹配而得到的具有明确结果的新的语义网络。
语义网络可用于表示多元关系，扩展后可以表示更复杂的问题2-2 设有3个传教士和3个野人来到河边，打算乘一只船从右岸渡到左岸去。
该船的负载能力为两人。
在任何时候，如果野人人数超过传教士人数，那么野人就会把传教士吃掉。
他们怎样才能用这条船安全地把所有人都渡过河去?用Si(nC, nY) 表示第i次渡河后，河对岸的状态，nC表示传教士的数目，nY表示野人的数目，于总人数的确定的，河对岸的状态确定了，河这边的状态也即确定了。
考虑到题目的限制条件，要同时保证，河两岸的传教士数目不少于野人数目，故在整个渡河的过程中，允许出现的状态为以下3种情况： 1. nC=0 2. nC=33. nC=nY>=0 (当nC不等于0或3)用di(dC, dY)表示渡河过程中，对岸状态的变化，dC表示，第i次渡河后，对岸传教士数目的变化，dY表示，第i次渡河后，对岸野人数目的变化。
《计算机专业导论》1-4讲练习题答案【杨上卿制作】
1计算机包括_____。
A.软件B.台式机、便携机C.嵌入在各种设备中的芯片D.以上所有正确答案：D你选对了2人类应具备的三大思维能力是指_____。
A.抽象思维、逻辑思维和形象思维B.实验思维、理论思维和计算思维C.逆向思维、演绎思维和发散思维D.计算思维、理论思维和辩证思维正确答案：B你选对了3本课程中拟学习的计算思维是指_____。
A.计算机相关的知识B.算法与程序设计技巧C.蕴含在计算学科知识背后的具有贯通性和联想性的内容D.知识与技巧的结合4如何学习计算思维？_____。
A.为思维而学习知识而不是为知识而学习知识B.不断训练，只有这样才能将思维转换为能力- 1 -C.先从贯通知识的角度学习思维，再学习更为细节性的知识，即用思维引导知识的学习D.以上所有5计算学科的计算研究什么? _______。
A.面向人可执行的一些复杂函数的等效、简便计算方法B.面向机器可自动执行的一些复杂函数的等效、简便计算方法C.面向人可执行的求解一般问题的计算规则D.面向机器可自动执行的求解一般问题的计算规则正确答案：D你选对了6“人”计算与“机器”计算有什么差异? _______。
A.“人”计算宁愿使用复杂的计算规则，以便减少计算量能够获取结果，“机器”计算则需使用简单的计算规则，以便于能够做出执行规则的机器B.“机器”计算使用的计算规则可能很简单但计算量却很大，尽管这样，对越来越多的计算，机器也能够完成计算结果的获得C.“机器”可以采用“人”所使用的计算规则，也可以不采用“人”所使用的规则D.上述说法都正确正确答案：D你选对了7自动计算需要解决的基本问题是什么？_______。
A.数据的表示，数据和计算规则的表示B.数据和计算规则的表示与自动存储C.数据和计算规则的表示、自动存储和计算规则的自动执行D.上述说法都不正确- 2 -8计算机器的基本目标是什么？_______。
A.能够辅助人进行计算，能够执行简单的四则运算规则B.能够执行特定的计算规则，例如能够执行差分计算规则等C.能够执行一般的任意复杂的计算规则D.上述说法都不正确正确答案：C你选对了9电子计算机器的基本特征是什么？_______。
慕课测试题答案
1计算之树中，通用计算环境的演化思维是怎样概括的？________。
A.程序执行环境—由CPU-内存环境，到CPU-存储体系环境，到多CPU-多存储器环境，再到云计算虚拟计算环境B.网络运行环境---由个人计算机、到局域网广域网、再到InternetC.元器件---由电子管、晶体管、到集成电路、大规模集成电路和超大规模集成电路D.上述全不对正确答案：A2计算之树中，网络化思维是怎样概括的________。
A.局域网、广域网和互联网B.机器网络、信息网络和人-机-物互联的网络化社会C.机器网络、信息网络和物联网D.局域网络、互联网络和数据网络正确答案： B3人类应具备的三大思维能力是指_____。
A.抽象思维、逻辑思维和形象思维B.实验思维、理论思维和计算思维C逆向思维、演绎思维和发散思维D.计算思维、理论思维和辩证思维正确答案：B4如何学习计算思维？_____。
A.为思维而学习知识而不是为知识而学习知识B.不断训练，只有这样才能将思维转换为能力C.先从贯通知识的角度学习思维，再学习更为细节性的知识，即用思维引导知识的学习D.以上所有正确答案：D5自动计算需要解决的基本问题是什么？_______。
A.数据的表示，数据和计算规则的表示B.数据和计算规则的表示与自动存储C数据和计算规则的表示、自动存储和计算规则的自动执行D.上述说法都不正确正确答案：C6计算机器的基本目标是什么？ _______。
A.能够辅助人进行计算，能够执行简单的四则运算规则B.能够执行特定的计算规则，例如能够执行差分计算规则等C.能够执行一般的任意复杂的计算规则D.上述说法都不正确正确答案：C7摩尔定律是指_______。
A.芯片集成晶体管的能力每年增长一倍，其计算能力也增长一倍B.芯片集成晶体管的能力每两年增长一倍，其计算能力也增长一倍C.芯片集成晶体管的能力每18个月增长一倍，其计算能力也增长一倍D.芯片集成晶体管的能力每6个月增长一倍，其计算能力也增长一倍正确答案：C8计算之树概括了计算学科的经典思维，它从几个维度来概括的？________。
第2章作业及参考答案
第2章作业及参考答案形式语言与自动机理论课程是计算机科学与技术专业的一门很基础的课程。
这套课件由于各种原因,我以后可能不再用了。
但这份付出了我心血的成果愿意献出来,供大家共享。
4题：文法G的产生式集合如下，试给出句子aaabbbccc的一个推导和一个归约S→aBC | aSBCCB→BCaB→abbB→bbbB→bbC→bccC→ccC→cc6题：文法G的产生式集合如下，请给出G中每个语法范畴代表的集合S→aSa|aaSaa|aAaA→bA|bbbA|bBB→cB|cCC→ccC|DDD→dD|d7题: 给定如下文法，请用自然语言描述它们定义的语言（4）S→aB|bAA→a|aS|BAAB→b|bS|ABB8题: 设∑={0,1}, 请给出∑上下列语言的文法（3）所有以11开头, 以11结尾的串;（6）所有长度为偶数的串9题: 设∑={a,b,c}, 构造下列语言的文法（2）L2={anbm|n,m≥1}（3）L3={anbnan|n≥1}（4）L4={anbmak|n,m,k≥1}（6）L6={xwxT| x,w∈∑+}（7）L7={w | w = wT, w∈∑+}补充：对给定RGS→abA|baBA →abA|abB →baB|ba构造等价文法，新文法的产生式形如：A→a，A→aB，A,B∈V，a∈T形式语言与自动机理论课程是计算机科学与技术专业的一门很基础的课程。
这套课件由于各种原因,我以后可能不再用了。
但这份付出了我心血的成果愿意献出来,供大家共享。
参考答案4、文法G的产生式集合如下，试给出句子aaabbbccc的一个推导和一个归约S→aBC | aSBCCB→BCaB→abbB→bbbB→bbC→bccC→ccC→cc答：S aSBCaaSBCBCaaaBCBCBCaaabCBCBCaaabBCCBCaaabbCCBCaaabbCBCCaaabbBCCCaaabbbCCCaaabbbccCaaabbbccc6、文法G的产生式集合如下，请给出G中每个语法范畴代表的集合S→aSa|aaSaa|aAaA→bA|bbbA|bBB→cB|cCC→ccC|DDD→dD|d解：(注意方法)Set(D)= {dm| m≥1}set(C)= {c2ndm| n≥0,m≥2}(注意：d只要大于2，不一定是偶数，可以没有c)set(B)= {cndm| n≥1,m≥2}set(A)= {bkcndm| k≥1,n≥1,m≥2}set(S)= {apbkcndmap| p≥1,k≥1,n≥1,m≥2}问题：不可写作：S={。
编译原理第四版课后答案
编译原理第四版课后答案第一章简介1.1 编译原理的定义编译原理是计算机科学中一个重要的领域，它涉及到将高级程序语言转化为机器语言的过程。
编译原理的目标是设计和实现一个能够将源代码转化为机器语言的编译器。
1.2编译器的结构和功能编译器一般包含以下几个部分：词法分析器、语法分析器、语义分析器、中间代码生成器、代码优化器和目标代码生成器。
这些部分协同工作，将源代码转化为可执行的机器语言。
1.3 编译原理的应用编译原理广泛应用于各个领域，如操作系统、数据库、嵌入式系统等。
在这些领域中，编译原理被用于将高级程序语言转化为机器语言，以在计算机上执行。
第二章词法分析2.1 词法分析的基本概念词法分析是编译器中的第一步，它将源代码划分为一个个的词法单元，如标识符、关键字、常量等。
词法分析器通过对源代码进行扫描和解析，生成词法单元的序列。
2.2 正则表达式正则表达式是一种用于描述字符串模式的工具。
在词法分析中，正则表达式常被用于识别和匹配不同的词法单元。
例如，正则表达式[a-z]+可以用来匹配一个或多个小写字母组成的标识符。
2.3 有限自动机有限自动机是一种用于识别和处理正则表达式的工具。
它由状态和转移函数组成，能够根据输入字符的不同改变状态，并最终确定是否接受输入。
有限自动机常被用于实现词法分析器。
第三章语法分析3.1 语法分析的基本概念语法分析是编译器中的第二步，它将词法单元序列转化为一棵语法树。
语法树是一种树形结构，用于表示源代码的语法结构。
语法分析器通过对词法单元序列进行解析和归约，生成语法树。
3.2 上下文无关文法上下文无关文法是用于描述程序语言语法的形式化工具。
它由一个或多个产生式组成，每个产生式包含一个非终结符和一串终结符或非终结符。
上下文无关文法常被用于定义编程语言的语法规则。
3.3 语法分析算法语法分析算法有多种，如递归下降分析、LL(1)分析、LR(1)分析等。
这些算法都是基于上下文无关文法的语法规则进行解析和归约，并生成语法树。
编译原理 第二章习题答案
第2章习题解答1.文法G[S]为：S->Ac|aBA->abB->bc写出L(G[S])的全部元素。
[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}==============================================2. 文法G[N]为：N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么？[答案]G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D===============================================3.已知文法G[S]：S→dAB A→aA|a B→ε|bB问：相应的正规式是什么？G[S]能否改写成为等价的正规文法？[答案]正规式是daa*b*；相应的正规文法为(由自动机化简来)：G[S]:S→dA A→a|aB B→aB|a|b|bC C→bC|b也可为(观察得来):G[S]:S→dA A→a|aA|aB B→bB|ε===================================================================== ==========4.已知文法G[Z]：Z->aZb|ab写出L(G[Z])的全部元素。
[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}===================================================================== =========5.给出语言{a n b n c m|n>=1,m>=0}的上下文无关文法。
人工智能教程习题及答案第2章习题参考解答
第二章知识表示习题参考解答2.3 练习题2.1 什么是知识?它有哪些特性?有哪几种分类方法?2.2 何谓知识表示? 陈述性知识表示法与过程性知识表示法的区别是什么?2.3 在选择知识的表示方法时，应该考虑哪些主要因素?2.4 一阶谓词逻辑表示法适合于表示哪种类型的知识?它有哪些特点?2.5 请写出用一阶谓词逻辑表示法表示知识的步骤。
2.6 设有下列语句，请用相应的谓词公式把它们表示出来：（1）有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。
（2）他每天下午都去玩足球。
（3）太原市的夏天既干燥又炎热。
（4）所有人都有饭吃。
（5）喜欢玩篮球的人必喜欢玩排球。
（6）要想出国留学，必须通过外语考试。
2.7 房内有一只猴子、一个箱子，天花板上挂了一串香蕉，其位置关系如图2. 11所示，猴子为了拿到香蕉，它必须把箱子推到香蕉下面，然后再爬到箱子上。
请定义必要的谓词，写出问题的初始状态（即图2.16所示的状态）、目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。
图2.11 猴子摘香蕉问题2.8 对习题2.7中的猴子摘香蕉问题，利用一阶谓词逻辑表述一个行动规划，使问题从初始状态变化到目标状态。
2.9 产生式的基本形式是什么？它与谓词逻辑中的蕴含式有什么共同处及不同处？2.10 何谓产生式系统？它由哪几部分组成？2.11 产生式系统中，推理机的推理方式有哪几种？在产生式推理过程中，如果发生策略冲突，如何解决？2.12 设有下列八数码难题：在一个3×3的方框内放有8个编号的小方块，紧邻空位的小方块可以移入到空位上，通过平移小方块可将某一布局变换为另一布局（如图2.12所示）。
请用产生式规则表示移动小方块的操作。
2831231684754765S0S g图2.12 习题2.12的图图2.13 习题2.13的图2.13 推销员旅行问题：设有五个相互可直达且距离已知的城市A、B、C、D、E，如图2.13所示，推销员从城市A出发，去其它四城市各旅行一次，最后再回到城市A，请找出一条最短的旅行路线。
SPOC 单元测验2-符号化、计算化与自动化
题型题目内容单选题以二进制和程序控制为基础的计算机结构是由__________最早提出来的。
冯·诺依曼布尔卡诺图灵单选题计算机中采用二进制，是因为__________。
可降低硬件成本，两个状态的系统具有稳定性，以及二进制的运算法则简单。
可降低硬件成本。
两个状态的系统具有稳定性。
二进制的运算法则简单。
单选题将十进制数215转换成二进制数是__________。
11010111111010111110101011010110单选题机器数可以有三种表示形式，分别是原码、反码和__________。
补码ASCII码国标码BCD码单选题ASCII码值排列有如下规律__________。
小写字母的码值比其对应大写字母的码值大32小写字母的码值小于大写字母的码值大小写字母的码值按字母表顺序依次递增2数字的码值大于小写字母的码值单选题每个ASCII码由__________个二进制位组成。
7568单选题逻辑运算是最基本的基于“真/假”值的运算，也可以被看作是基于“1/0”的运算，1为真，0为假。
关于基本逻辑运算，下列说法不正确的是__________。
“异或”运算是“相同为1，不同为0”“与”运算是“有0为0，全1为1”“或”运算是“有1为1，全0为0”“非”运算是“非0则1，非1则0”单选题将十六进制数586转换成16位的二进制数，应该是__________。
0101 1000 0110 00000000 0101 1000 01100110 1000 0101 00000000 0110 1000 0101单选题在计算机中，引入十六进制，主要目的是__________。
缩短二进制字串的长度，简化书写计算机中的数据存储采用十六进制计算机中的数据运算采用十六进制十六进制更加容易实现，运算高效单选题下列说法不正确的是__________。
视频信息不能进行符号化现实世界的任何事物，若要由计算机系统计算，首先需要将其语义符号化汉字、声音、图像等都可以进行符号化，并由计算机进行各种处理将符号赋予不同的语义，则能计算不同的现实世界问题单选题下列关于《易经》的说法不正确的是__________。
计算思维-符号化-计算化-自动化..
《易经》是什么? 八卦？ 预测与占卜？算命？ 自然现象及其变化规律 人事现象及其变化规律 其他现象及其变化规律
天
日
风 泽
月
雷 山ቤተ መጻሕፍቲ ባይዱ
地
？
0和1与易经---语义符号化表达与计算 (2) 易经怎样表达自然现象?
将现象抽象为符号，进行符号组合，利用符号组合表达自然现象
0和1与易经---语义符号化表达与计算 (2) 易经怎样表达自然现象?
更多的组合，更多的语义，更多的变化
符号化的六十四卦图
0和1与易经---语义符号化表达与计算 (3) 易经怎样区分各种组合要素?
符号化的关键是区分与命名---术语体系
待区分的
命名 阴 (六 ) 阳 (九 )
三个阴阳构成的一个组合
卦
一个组合中的某一位置
三画阴阳可能出现的八种组合 一卦中的三个位置 一个位置可能出现阴和阳 一个位置可能出现阴和阳，结合卦 中不同位置组合
冬至一阳生
生命演化规律
0和1与易经---语义符号化表达与计算 (5) 易经中为什么称乾坤而不称天地?
将符号再赋予语义 ---“本”与“用”：抽象与具体化
现象 本体 用体
天(自然空间)
乾(抽象空间)
父(家庭空间)， 首 (身体空间)，马 (动物空间)
0和1与易经---语义符号化表达与计算 (6) 小结?
由“易经”看“符号化及符号计算”? 自然/社 会现象
符号化
0/1及其 组合
计算化
再语义化 自然/社会 0/1组合的变化/ 现象变化 基于0/1的计算 规律
符号
组合
命名
“本体” “用体”
0和1与易经---语义符号化表达与计算 (6) 易经在“符号化-计算化-自动化”思维中的位置?
第2章0和1 语义符号化符号计算化与计算自动化练习题答案解析
第2章0和1 语义符号化符号计算化与计算自动化练习题答案解析第2章0和1-语义符号化、符号计算化与计算自动化练习题答案解析第2章符号化、计算化与自动化1、易经就是用0和1符号化自然现象及其变化规律的典型案例。
以下观点不恰当的就是_____。
(a)易经既是用0和1来抽象自然现象，同时又不单纯是0和1，起始即将0和1与语义“阴”和“阳”绑定在一起；(b)易经本质上就是关于0和1、0和1的三画(或六画)女团、以及这些女团之间相互变化规律的一门学问；(c)易经仅仅是以自然现象为依托，对人事及未来进行占卜或算卦的一种学说；(d)易经通过“阴”“阳”(即0和1)符号化，既反映了自然现象及其变化规律，又能将其映射到不同的空间，反映不同空间事务的变化规律，例如人事现象及其变化规律。
2、易经的符号化案例，救赎我们________。
(a)社会/自然规律的一种研究方法是符号化，即利用符号的组合及其变化来反映社会/自然现象及其变化，将看起来不能够计算的事物转换为可以计算的事物；(b)任何事物只要符号化，就可以被排序；(c)符号化，不仅仅是数学符号化；任何事物都可以符号化为0和1，也就能进行基于0和1的运算；(d)符号的排序不仅仅就是数学计算，符号的女团及其变化同样也就是一种排序，这种排序可以基于0和1去同时实现。
(e)上述全部。
3、逻辑运算就是最基本的基于“真/假”值的运算，也可以被看做就是基于“1/0”的运算，1为真，0为假。
关于基本逻辑运算，以下观点不恰当的就是_____。
(a)“与”运算是“有0为0，全1为1”；(b)“或”运算是“有1为1，全0为0”；(c)“非”运算是“非0则1，非1则0”；(d)“异或”运算是“相同为1，不同为0”。
4、假设m=真，n=假，k=真，问以下逻辑运算式的计算结果就是真还是假？(1)(mand(notk))or((notm)andk)。
_____。
(a)真；(b)假(2)(mandn)and((notm)and(notn))。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2章符号化、计算化与自动化1、易经是用0和1符号化自然现象及其变化规律的典型案例。
下列说法不正确的是_____。
(A)易经既是用0和1来抽象自然现象，同时又不单纯是0和1，起始即将0和1与语义“阴”和“阳”绑定在一起；(B)易经本质上是关于0和1、0和1的三画(或六画)组合、以及这些组合之间相互变化规律的一门学问；(C)易经仅仅是以自然现象为依托，对人事及未来进行占卜或算卦的一种学说；(D)易经通过“阴”“阳”(即0和1)符号化，既反映了自然现象及其变化规律，又能将其映射到不同的空间，反映不同空间事务的变化规律，例如人事现象及其变化规律。
答案：C解释：本题考核内容：考核0和1与易经A．A的描述完全正确；B．B的叙述也完全正确；C．不正确，易经不仅仅以自然现象为依托，对事及未来进行占卜或算卦的一种学说，他还是将现象抽象为符号，进行符号组合，利用符号组合表达自然现象；D．D的表述完全正确，易经既反映了自然现象及其变化规律，还反映不同空间事物的变化规律；具体内容请参考第二章视频“2. 0和1与易经”的“1.1～1.4”视频。
2、易经的乾卦是从“天”这种自然现象抽象出来的，为什么称其为“乾”而不称其为“天”呢？_____。
(A)易经创作者故弄玄虚，引入一个新的名词，其实没有必要；(B)易经的“乾”和“天”是不同的，“乾”是一种比“天”具有更丰富语义的事物；(C)“天”是一种具体事物，只能在自然空间中应用，若变换到不同空间应用，可能会引起混淆；而“乾”是抽象空间中的概念，是指具有“天”这种事务的性质，应用于不同的空间时不会产生这种问题；(D)易经创作者依据阴阳组合的符号特征，选择了更符合该符号的名字“乾”。
答案：C解释：本题考核内容：考核0和1与易经A不正确，易经并不是故弄玄虚的；B不正确，易经中“乾”为“天”，“乾”是抽象空间中的概念，是指具有“天”这种事务的性质所以B并不正确；C完全正确，“天”是具体事物，“乾”是抽象概念；D不正确，“乾”并不是因为阴阳组合而命名的；具体内容请参考第二章视频“2. 0和1与易经”的“1.1～1.4”视频。
3、易经的符号化案例，启示我们________。
(A)社会/自然规律的一种研究方法是符号化，即利用符号的组合及其变化来反映社会/自然现象及其变化，将看起来不能够计算的事物转换为可以计算的事物；(B)任何事物只要符号化，就可以被计算；(C)符号化，不仅仅是数学符号化；任何事物都可以符号化为0和1，也就能进行基于0和1的运算；(D)符号的计算不仅仅是数学计算，符号的组合及其变化同样也是一种计算，这种计算可以基于0和1来实现。
(E)上述全部。
答案：E解释：本题考核内容：考核0和1与易经A说法完全正确；B的说法也正确，只要被符号化，就可以被计算；C完全正确，任何事物都可以符号化为0和1，也就能进行基于0和1的运算；D正确，符号的计算不仅仅是数学计算，符号的组合及其变化同样也是一种计算，这种计算可以基于0和1来实现；E．鉴于ABCD都正确，所以选择E；具体内容请参考第二章视频“2. 0和1与易经”的“1.1～1.4”视频。
4、逻辑运算是最基本的基于“真/假”值的运算，也可以被看作是基于“1/0”的运算，1为真，0为假。
关于基本逻辑运算，下列说法不正确的是_____。
(A)“与”运算是“有0为0，全1为1”；(B)“或”运算是“有1为1，全0为0”；(C)“非”运算是“非0则1，非1则0”；(D)“异或”运算是“相同为1，不同为0”。
答案：D解释：本题考核内容：考核与或非等逻辑运算A正确，与运算确实是“有0为0，全1为1”B正确，或运算确实是“有1为1，全0为0”C正确，非运算确实是“非0则1，非1则0”D不正确，异或运算应该是“相同为0，不同为1”具体内容请参考第二章视频“2. 0和1与逻辑”的“2.1～2.4 ”视频。
5、假设M=真，N=假，K=真，问下列逻辑运算式的计算结果是真还是假？(1) (M AND (NOT K)) OR ((NOT M) AND K)。
_____。
(A) 真；(B) 假答案：B(2) (M AND N) AND ((NOT M) AND (NOT N))。
_____。
(A) 真；(B) 假答案：B(3) (M OR N) AND ((NOT M) OR (NOT N))。
_____。
(A) 真；(B) 假答案：A(4) (M OR (NOT N) OR K) AND ((NOT M) OR (N AND (NOT K)))。
_____。
(A) 真；(B) 假答案：B解释：本题是使学生体验逻辑运算，把真——1，假——0（1）化为0，1，表达式为：（1 and 0）or （0 and 1）=0 假选B；（2）化为0，1，表达式为：（1 and 0）and （0 and 1）=0假选B；（3）化为0，1，表达式为：（1 or 0）and（0 or 1）=1真选A；（4）化为0，1，表达式为：（1 or 1 or 1）and （0 or （0 and 0））=0假选B；具体内容请参考第二章视频“2. 0和1与逻辑”的“2.1～2.4 ”视频。
6、假设M=1，N=0，K=1，问下列运算式的计算结果是0还是1？(1) (M AND (NOT K)) OR ((NOT M) AND K)。
_____。
(A) 1；(B) 0答案：B(2) (M AND N) AND ((NOT M) AND (NOT N))。
_____。
(A) 1；(B) 0答案：B(3) (M OR N) AND ((NOT M) OR (NOT N))。
_____。
(A) 1；(B) 0答案：A(4) (M OR (NOT N) OR K) AND ((NOT M) OR (N AND (NOT K)))。
_____。
(A) 1；(B) 0答案：B解释：本题是使学生体验基于逻辑的0、1运算。
（1）表达式为：（1 and 0）or （0 and 1）=0 选B；（2）表达式为：（1 and 0）and （0 and 1）=0 选B；（3）表达式为：（1 or 0）and（0 or 1）=1 选A；（4）表达式为：（1 or 1 or 1）and （0 or （0 and 0））=0 选B；具体内容请参考第二章视频“2. 0和1与逻辑”的“2.1～2.4 ”视频。
7、已知：M、N和K的值只能有一个1，其他为0，并且满足下列所有逻辑式：((M AND (NOT K)) OR ((NOT M) AND K)) = 1；(NOT N) AND ((M AND (NOT K)) OR ((NOT M) AND K))) = 1；(NOT N) AND (NOT K) = 1；问：M、N、K的值为__________。
(A)0，1，0；(B)1，0，0；(C)0，0，1；答案：B解释：本题考核内容：考核与或非等逻辑运算A不正确，将M,N,K分别以0，1，0带入，第一个式子不满足；B正确，将M,N,K分别以1，1，0带入，第一个式子不满足三个式子均满足；C不正确，将M,N,K分别以0，0，1带入，第三个式子不满足具体内容请参考第二章视频“2. 0和1与逻辑”的“2.1～2.4 ”视频8、已知：关于S i和C i+1的逻辑运算式如下：S i = ((A i XOR B i) XOR C iC i+1 = ((A i AND B i) OR ((A i XOR B i) AND C i) ，问：(1) 如果A i = 1，B i = 0，C i = 1，则S i，C i+1 的值为________。
(A)0，0；(B)0，1；(C)1，0；(D)1，1；答案：B(2) 如果A i = 1，B i = 1，C i = 1，则S i，C i+1 的值为________。
(A)0，0；(B)0，1；(C)1，0；(D)1，1；答案：D解释：本题是使学生体验逻辑的0，1运算（1）将A i = 1，B i = 0，C i = 1带入，得S i =（1 XOR 0）XOR 1=0；C i+1 =（1 and 0）or （（1 XOR 0）and 1）=1，选B;（2）将A i = 1，B i = 1，C i = 1带入，得S i =（1 XOR 1）XOR 1=1；C i+1 =（1 and 1）or （（1 XOR 1）and 1）=1，选D;9、逻辑的符号化案例，启示我们________。
(A)逻辑运算可以被认为是基于0和1的运算，其本质是一种基于位的二进制运算；(B)形式逻辑的命题与推理可以基于0和1的运算来实现；(C)硬件设计的基础理论--布尔代数，即是将逻辑与0和1的运算结合起来的一种数字电路设计理论；(D)人的基本思维模式和计算机的0和1运算是相通的。
(E)上述全部。
答案：E解释：本题考核内容：0和1与逻辑A逻辑的基本表现形式是推理和命题，推理即判断，命题简单来所是表现真假，因此可用0与1来表现。
B形式逻辑的命题与推理都是判断事物真假，两种状态可用0和1的运算来实现。
C硬件设计可实现布尔代数与或非运算，将逻辑与0和1的运算结合起来。
D人的基本思维模式可通过语义符号化为“真”与“假”的逻辑思维具体参考：第二章视频2.1“0和1与易经”，2.2“0和1与逻辑”，2.5“0和1与电子元件”10、将十进制数126.375转换成二进制数，应该是_____。
(A) 0111 1110.0110 (B) 0111 1110.1110(C) 0111 1100.0110 (D) 0111 1100.1110答案：A解释：本题考核内容：0和1与数值运算思考过程：27=128>126.425>26=64，2-1=0.5>0.375整数部分：126=128-2=27-2=1000 0000-0000 0010=0111 1110也可采用除2取余。
小数部分：0.375*2=0.75,取整0, 0.75*2=1.5取整1，小数位余数:0.5*2=1.0,取整1，小数位余0,结束，结果为0.0110具体参考：第二章视频2.3“0和1与非数值性信息”11、将十六进制数586转换成16位的二进制数，应该是。
(A) 0000 0101 1000 0110 (B) 0110 1000 0101 0000(C) 0101 1000 0110 0000 (D) 0000 0110 1000 0101解释：本题考核内容：0和1与数值运算过程：十六进制数1位对应4位二进制数，5为0101,8为1000,6为0110,连在一起就是0000 0101 1000 0110，当然也可采用数值计算的方法，重在理解数值转换。