基尔霍夫定律的相量表达式
最新电工学电力学课程第八章《电路定律的相量形式》

由相量形式KVL有 : V V 1 V 2 600 8090 (V)
(2)相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式
UR RIR
U L jL IL
1
UC
j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C
U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路(旁路作用);
(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源(线性)的控制电压或电流是正弦量, 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示,反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°,当电容电压由负值增加经过零点时,其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义:
X
C
定义
1
C
(1) 表示限制电流的能力;
相量关系
+
U R R I
U R
-
有效值关系:UR = RI 相位关系:u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)
基尔霍夫定律的相量形式.

电压相量,如图(c)所示,从相量图上容易看出各正弦电压
的相位关系。
值得注意的是回路中全部电压有效值之代数和并不一
定等于零,本题中 US=10U1+U2+U3=6+8+12=26
即一般说来
n
Uk 0
k 1Biblioteka 关于复数的几个公式1. 假设复数 c rθ a jb
则有 c a2 b2 θ arctan b a
uk (t) Re[U kme jt ] Re[ 2U k e jt ]
代入KVL方程中得到
n uk (t) n Re[Ukmejt ] 0
k 1
k 1
n
n
uk (t) Re[
2Uke jt ] 0
k 1
k 1
由于上式适用于任何时刻t,其相量关系也必须成立,
j ej180 cos180 jsin180 1 1 j2 ej180 1180
模型,图中各电流参考方向均与时域模型相同,仅将
时域模型中各电流符号 iS、i、i1、i2 用相应的相量符
号 IS、I、I1、I2 表示,并计算出电流相量 。
I1 1060 A
I2 5 90 A
列出图(b)相量模型中结点1的KCL方程,其相量形式
为
I I1 I2 0
§8-3 基尔霍夫定律的相量形式
一、基尔霍夫电流定律的相量形式
基尔霍夫电流定律(KCL)叙述为:对于任何集中参数 电路中的任一结点,在任何时刻,流出该结点的全部支路 电流的代数和等于零。其数学表达式为
n
ik (t) 0
k 1
假设电路中全部电流都是相同频率ω的正弦电流,则 可以将它们用振幅相量或有效值相量表示为以下形式
45相量形式的基尔霍夫定律
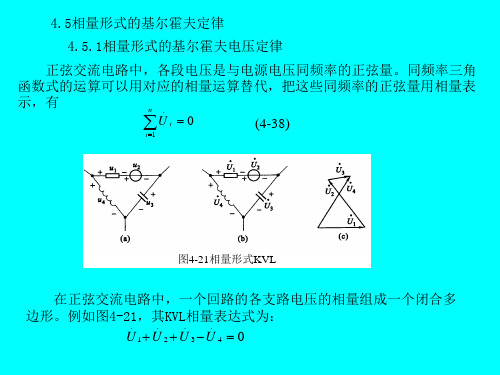
4.6.1用相量法分析串联电路 对于RLC串联电路来说,其阻抗为
Z = Z R + Z L + Z C = R + jωL + 1 jωC
1 = R + j ωL − ωC
1 = R 2 + ωL − ωC
2
ωL −
arctg R
1 ωC
(4-53)
0 • •
=U L =UC
•
•
为参考向量,相量图如
故电流表的读数为 即(1) (2)
2 A = I R + (I C − I L ) 2 A
A = 5 2 + (25 − 20) 2 = 7.07 A
图4-26 例4-9相量图
A = 5 + ( 25 − 10) = 40.31A
2 2
从【例4-9】题的解法二,可以体会到应用向量图分析电路的要点,那就是: (1)首先要选好一个参考相量,这个参考相量的选择,必须能方便地将电路 中其它电压、电流相量,根据电路的具体结构及参数特点逐一画出,把所给的 条件转化成相量图中的几何关系。 (2)最后根据相量图中的相量关系,使问题得到解决。一般对串联电路,选 电流作参考方向较方便,如【例4-8】题。对并联电路,则选电压作参考相量较 方便,如【例4-9】题。有些问题通过相量图分析将很直观和简便。
2 2 U S = U R + U L = 30 2 + 60 2 = 67.08V
图4-24例4-8解法二图
由题解图4-24b)可得
2 U S = U R + (U C − U L ) 2 = 15 2 + (100 − 80) 2 = 258V
电路相量图的原理及应用

电路相量图的原理及应用1. 什么是电路相量图电路相量图是一种用于表示电路中电压、电流及其相位信息的图形工具。
相量图使用矢量的长度和角度来表示电压和电流的振幅和方向。
通过使用相量图,我们可以更直观地理解和分析电路中的信号传输和变换。
2. 电路相量图的原理在电路相量图中,电压和电流被表示为复数的形式,其中实部表示振幅,虚部表示相位。
根据欧姆定律和基尔霍夫定律,我们可以推导出电阻、电容和电感的相量图表示。
•电阻的相量表示为:Z R=R•电容的相量表示为:$Z_C = \\frac{1}{j\\omega C} = \\frac{-j}{\\omega C}$•电感的相量表示为:$Z_L = j\\omega L$3. 电路相量图的应用3.1 直流电路分析通过使用电路相量图,我们可以更加简洁和方便地分析直流电路。
相量图可以帮助我们计算电流和电压的大小和方向,从而更好地理解和解决直流电路中的问题。
例如,当我们需要计算电阻串联电路中总电阻时,可以将每个电阻的相量图相加得到总阻抗。
3.2 交流电路分析在交流电路中,相量图发挥着重要的作用。
交流电压和电流的相量图可以用于计算电路中电压的幅值、相位和频率响应。
通过将电路的各个元件转换为相量图形式,我们可以方便地计算电路中电压和电流的大小和相位差,进而计算功率、阻抗和电流的分布。
3.3 三相电路分析在三相电路分析中,电路相量图也是必不可少的工具。
通过将三相电压和电流表示为相量的形式,我们可以更好地理解和分析三相电路中的功率传输、电压平衡和相序问题。
3.4 系统稳定性分析电路相量图可以用于分析系统的稳定性。
通过计算电路的传输函数,并绘制相量图,我们能够评估系统的稳定性和抗干扰能力。
相量图可以帮助我们观察电路中的衰减、相位移和共振频率。
4. 总结电路相量图是一种重要的工程工具,它帮助我们直观地理解和分析电路中的信号传输和变换。
通过使用电路相量图,我们可以更好地计算电压和电流的大小、相位差和频率响应。
正弦交流电的相量表示法(2)

正弦量的表示法:
解析式: i(t ) I m sin(t ) A
i
Im
最大值相量: I m I m
有效值相量: I I
最大值: I m
I
Im
I
有效值: I
平均值:
I
I
电工基础
例:写出下列正弦量的相量形式:
i1 (t ) 5 2 sin(t 53.1) A
2
虚数
用 j 代替
虚部 实部
i
B a jb
j
复数 A a jb 代数式
0
D
b
A
C a jb
D a jb
复数的模
r
0
1
r a 2 b2
复数矢量与实轴正方向的夹角
a
C
0
取值在正180度到负180度之间
a r cos
0
电工基础
三、正弦量的相量表示法: re j r cos jr sin
Im
t
正弦交流电
I me j (t ) I m cos(t ) jI m sin(t )
用 I me
I me
j (t )
代
jt
替
I m sin(t ) I mt
加减用代 数式运算
A B a1 jb1 a2 jb2 (a1 a2 ) j (b1 b2 ) A B a1 jb1 (a2 jb2 ) (a1 a2 ) j (b1 b2 )
A B
A
A B
A
B B
1
1
基本元件的相量形式(3)

电流与电压同相
电工基础
三、电感元件的相量形式: 电感元件的相量形式:
i
L
Z L = ωL∠90 = jωL = j 2πfL
ɺ I
ZL
相量图
+
u
−
ɺ U
ϕi
ɺ I
+
ɺ U
−
i (t ) = I m sin(ωt + ϕi ) A u (t ) = U m sin(ωt + ϕ u )V
u(t ) = L ⋅
Q=
ωt
t
2 UC
XC
电 源
i 电
源
(var) : 电容元件 电
u
电工基础
例:求电流及电容元件的电压和无功功率,并画相量图。 求电流及电容元件的电压和无功功率,并画相量图。 ɺ ZC C = 10µF i C I
+
u
解: X C =
− u (t ) = 100 2 sin(1000t + 30 )V
ɺ UC
电工基础
u (t ) = U m sin(ωt + ϕ u )V
ϕ
ɺ I +1
电流与电压同相
ɺ I = I∠ϕi (A) ɺ U = U∠ϕ u (V )
ɺ U Z= ɺ = Z ∠ϕ z I
u(t ) = R ⋅ i(t )
= R ⋅ I m sin(ωt + ϕ i )
大小关系: 大小关系: m = R ⋅ I m U
ϕ z = ϕu − ϕi
电工基础
电感元件的功率: 电感元件的功率:
1)瞬时功率: 瞬时功率:
p ( t ) = u ( t )i ( t )
电工学第六版课后答案
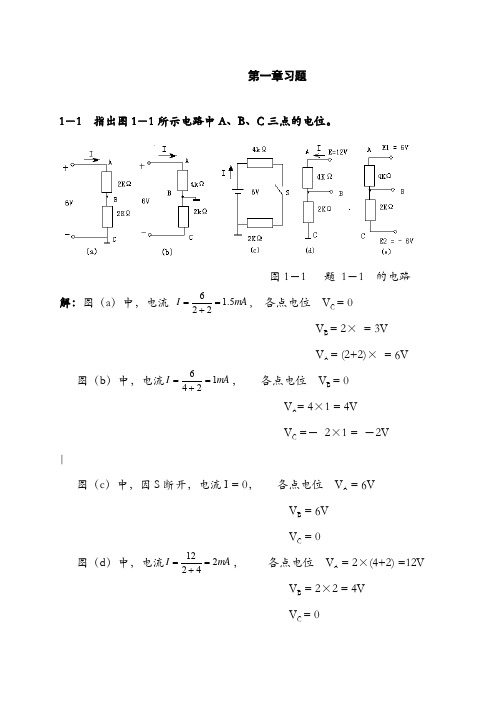
第一章习题1-1 指出图1-1所示电路中A 、B 、C 三点的电位。
图1-1 题 1-1 的电路解:图(a )中,电流 mA I 51226.=+=, 各点电位 V C = 0 V B = 2× = 3V V A = (2+2)× = 6V图(b )中,电流mA I 1246=+=, 各点电位 V B = 0 V A = 4×1 = 4V V C =- 2×1 = -2V|图(c )中,因S 断开,电流I = 0, 各点电位 V A = 6VV B = 6V V C = 0图(d )中,电流mA I 24212=+=, 各点电位 V A = 2×(4+2) =12V V B = 2×2 = 4V V C = 0图(e )的电路按一般电路画法如图,电流mA I 12466=++=, 各点电位 V A = E 1 = 6VV B = (-1×4)+6 = 2V ?V C = -6V1-2 图1-2所示电路元件P 产生功率为10W ,则电流I 应为多少 解:由图1-2可知电压U 和电流I 参考方向不一致,P = -10W =UI 因为U =10V, 所以电流I =-1A )图 1-2 题 1-2 的电路1-3 额定值为1W 、10Ω的电阻器,使用时通过电流的限额是多少 解:-根据功率P = I 2 R A R P I 3160101.===1-4 在图1-3所示三个电路中,已知电珠EL 的额定值都是6V 、50mA ,试问哪个电珠能正常发光图 1-3 题 1-4 的电路解:图(a )电路,恒压源输出的12V 电压加在电珠EL 两端,其值超过电珠额定值,不能正常发光。
图(b )电路电珠的电阻Ω=Ω==120120506K R .,其值与120Ω电阻相同,因此电珠EL 的电压为6V ,可以正常工作。
图(c )电路,电珠与120Ω电阻并联后,电阻为60Ω,再与120Ω电阻串联,电珠两端的电压为V 4126012060=+⨯小于额定值,电珠不能正常发光。
电路基本定律的相量形式

i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
?
?
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 (正方向) 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程: 其KVL相量表达式为:
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I
