基尔霍夫定律的应用和例题
基尔霍夫简单练习题

基尔霍夫简单练习题一、基尔霍夫电流定律(KCL)相关题目1. 已知电路中某节点有三个支路电流分别为I1、I2和I3,求该节点的总电流。
2. 在一个电路节点处,已知有两个电流分别为5A和3A,求第三个电流的大小。
3. 四个电流分别为2A、4A、6A和8A,通过一个节点,求这四个电流的代数和。
4. 若一个节点处的总电流为10A,其中两个支路电流分别为4A和6A,求第三个支路电流。
5. 在一个节点处,已知三个支路电流之和为15A,其中一个支路电流为7A,求另外两个支路电流之和。
二、基尔霍夫电压定律(KVL)相关题目1. 已知一个闭合回路中有三个电阻,分别为R1、R2和R3,求该回路中的总电压。
2. 一个闭合回路中有两个电压源,分别为10V和15V,求该回路中的总电压。
3. 在一个闭合回路中,已知三个电阻上的电压分别为5V、8V和12V,求该回路中的总电压。
4. 若一个闭合回路中的总电压为24V,其中两个电阻上的电压分别为6V和9V,求第三个电阻上的电压。
5. 在一个闭合回路中,已知四个电阻上的电压之和为50V,其中三个电阻上的电压分别为10V、15V和20V,求第四个电阻上的电压。
三、基尔霍夫定律综合应用题目1. 一个电路包含三个节点和四个电阻,已知节点A的总电流为8A,节点B的总电流为6A,求节点C的总电流。
2. 一个闭合回路中有两个电压源和一个电阻,已知电压源分别为10V和15V,电阻上的电压为5V,求电阻的阻值。
3. 一个电路包含两个节点和三个电阻,已知节点A的总电流为12A,节点B的总电流为8A,求三个电阻上的电压。
4. 一个电路包含四个节点和五个电阻,已知节点C的总电流为10A,节点D的总电流为6A,求节点A和节点B的总电流。
5. 一个闭合回路中有三个电阻和两个电压源,已知电压源分别为20V和30V,电阻上的电压分别为10V、15V和20V,求三个电阻的阻值。
四、基尔霍夫定律与欧姆定律结合应用题目1. 在一个电路中,已知一个电阻R1的电流为3A,另一个电阻R2的电压为6V,若R1和R2串联,求R2的电流。
基尔霍夫定律练习题

基尔霍夫定律练习题基尔霍夫定律练习题基尔霍夫定律是电路分析中的重要原理,它可以帮助我们解决复杂的电路问题。
在这篇文章中,我将为大家提供一些基尔霍夫定律的练习题,帮助大家更好地理解和应用这个定律。
练习题一:简单电路假设有一个简单的电路,由一个电源和两个电阻组成。
电源的电压为12伏特,电阻1的阻值为4欧姆,电阻2的阻值为6欧姆。
我们需要求解电路中的电流。
解答:根据基尔霍夫定律,我们可以得到以下方程:12 = I1 * 4 + I2 * 6其中,I1和I2分别代表电流通过电阻1和电阻2的大小。
通过解这个方程组,我们可以得到I1和I2的值。
练习题二:复杂电路现在考虑一个稍微复杂一些的电路,由一个电源和三个电阻组成。
电源的电压为24伏特,电阻1的阻值为8欧姆,电阻2的阻值为12欧姆,电阻3的阻值为16欧姆。
我们需要求解电路中的电流。
解答:同样根据基尔霍夫定律,我们可以得到以下方程:24 = I1 * 8 + I2 * 12 + I3 * 16其中,I1、I2和I3分别代表电流通过电阻1、电阻2和电阻3的大小。
通过解这个方程组,我们可以得到I1、I2和I3的值。
练习题三:并联电路考虑一个并联电路,由一个电源和两个并联的电阻组成。
电源的电压为20伏特,电阻1的阻值为10欧姆,电阻2的阻值为15欧姆。
我们需要求解电路中的电流。
解答:在并联电路中,电流会分流,通过每个电阻的电流之和等于总电流。
根据基尔霍夫定律,我们可以得到以下方程:I = I1 + I2其中,I代表总电流,I1和I2分别代表通过电阻1和电阻2的电流。
另外,根据欧姆定律,我们还可以得到以下方程:20 = I1 * 1020 = I2 * 15通过解这个方程组,我们可以得到I1和I2的值,从而求解出总电流I。
通过以上的练习题,我们可以看到基尔霍夫定律在解决电路问题中的重要性。
无论是简单的电路还是复杂的电路,基尔霍夫定律都能够帮助我们找到解决问题的方法。
_基尔霍夫定律

§10-4 含源电路欧姆定律 *基尔霍夫定律1. 一段含源电路的欧姆定律如果研究的电路中包含电源,则在欧姆定律中应包含非静电场强,即将欧姆定律的微分形式推广为)(k E E ���+=γδA BCRi R ,εI即kE E ���−=γδA BCRi R ,εI 电源放电电源充电积分得∫⋅B A l E ��d l E l B Ak B A ����d d ⋅−⋅=∫∫γδ欧 姆A BC RiR ,εI A BCRi R ,εI 电源放电电源充电∫⋅BA l E ��d lE l l B A k B C C A ������∫∫∫⋅−⋅+⋅=d d d γδγδ 电源放电时,电流密度与积分方向相反;电源充电时,电流密度与积分方向相同,且BA BA V V l E −=⋅∫��d ε−=⋅=⋅∫∫l E l E C A k B A k ����d d SI =δ代入上式,则一段含源电路的欧姆定律εγγ++=−∫∫)d d (B C C A B A SlI S l I V V ∓∫⋅BA l E ��d l E l lB A kB C C A ������∫∫∫⋅−⋅+⋅=d d d γδγδε++=−)(i B A IR IR V V ∓A BCRi R ,εI A BCRi R ,εI 电源放电电源充电电流与电动势方向相同时,取负号,反之取正号。
上式称为一段含源电路的欧姆定律。
一段含源电路的欧姆定律•若I =0,则i B A IR V V −=−ε电源放电,端电压低于电动势。
iB A IR V V +=−ε电源充电,端电压高于电动势。
•若R =0,则ε=−B A V V 电路断开,端电压等于电动势。
•若AB 接在一起,形成闭合电路,则ABRiR ,εIiR R I +=εiR R +总电阻 闭合电路中的电流等于电源的电动势与总电阻之比。
一段含源电路的欧姆定律•一段含多个电源的电路的欧姆定律ABC 2R 22,i R ε1I 1R 3R 2I 3I 11,i R ε33,i R ε∑∑−=−εIR V V B A 正负号选取规则:任意选取线积分路径方向,写出初末两端点的电势差;电流的方向与积分路径方向相同,电流取正号,反之为负;电动势指向与积分路径同向,电动势取正号,反之为负。
基尔霍夫定律
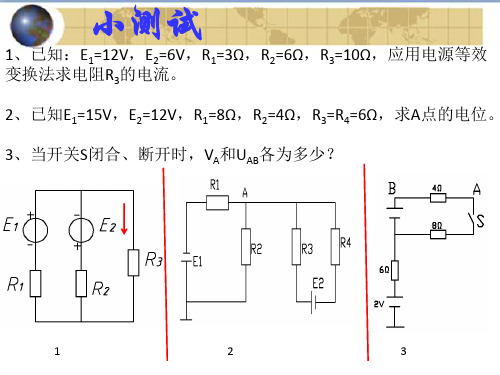
解:(1)设各支路电流方向如图(a)所示。 (2)作出每个电源单独作用时的分图,有几个电动势就 分解为几个具有单一电动势的简单电路,并标出各电流参考 方向。如图(b)和(c)所示。 (3)求出各分图中单一电动势作用时的各支路电流。
R
+
+R
_E1 _E2
R
+
R1
_E3
图C 电流定律的推广(3)
上一节点页电流定律下的推一广 页 结束
节点电流定律的推广
(3) 晶体管电极之间的电流关系,也可以由节点电流定律判定,
如图C中对于NPN型晶体管有 IB+ IC = IE
IB
IC
s
IE
图c 电流定律的推广(3)
上一节点页电流定律下的推一广 页 结束
主要贡献: 1、电路设计:1845年,21岁时他发表了第一篇论文,提出了著 名的基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL), 解决了电器设计中电路方面的难题 2、热辐射:1859年,基尔霍夫做了用灯焰烧灼食盐的实验。得 出了关于热辐射的定律,后被称为基尔霍夫定律 3、化学:在海德堡大学期间制成光谱仪,与化学家本生合作创 立了光谱化学分析法,从而发现了元素铯和铷。 4、光学理论:给出了惠更斯-菲涅耳原理的更严格的数学形式, 对德国的理论物理学的发展有重大影响。著有《数学物理学讲 义》4卷 5、薄板直法线理论:1850年,在柏林大学执教的基尔霍夫发表 了他关于板的重要论文《弹性圆板的平衡与运动》
解:对节点a:I1=I2+I3 则 I2=I1I3=2516=9mA 对节点d:I4+I5= I1 则 I5=I1I4=2512=13mA 对节点c:I6+I3=I4 则 I6=I4 I3= 1216= -4mA
根据基尔霍夫定律简单计算题

根据基尔霍夫定律简单计算题根据基尔霍夫定律,电流是在节点之间分割和合并的。
根据这个定律,我们可以求解电流和电压的分配情况。
下面是几个根据基尔霍夫定律进行简单计算的例题。
1. 求解电流分配已知一个电路有三个并联的电阻,电阻值分别为R₁=10Ω,R₂=20Ω,R₃=30Ω。
求解电流分配情况。
解答:根据基尔霍夫定律,电流在节点上分割后再合并。
根据并联电路的性质,每个电阻上的电流相等。
设电流I为总电流,则电流在R₁上为I₁,电流在R₂上为I₂,电流在R₃上为I₃。
根据欧姆定律,电流与电阻之间的关系为U = I * R。
结合基尔霍夫定律可以得出以下等式:I = I₁ + I₂ + I₃根据电流分配定律,每个电阻上的电流之和等于总电流。
因此有以下等式:I = I₁ + I₂ + I₃ = I₁ + I + I₂ + I + I₃化简得到:I = (R₁/(R₁+R₂+R₃)) * I + (R₂/(R₁+R₂+R₃)) * I +(R₃/(R₁+R₂+R₃)) * I整理得到:I = I * (R₁+R₂+R₃) / (R₁+R₂+R₃)化简后得到:I = I因此,每个电阻上的电流相等,都等于总电流I。
在本例中,每个电阻上都有相同的电流,都等于总电流I。
即 I₁ = I₂ = I₃ = I。
2. 求解电压分配已知一个电路有两个串联的电阻,电阻值分别为R₁=10Ω,R₂=20Ω,电源电压为U=100V。
求解电压分配情况。
解答:根据基尔霍夫定律,电压在串联电阻之间分割后再合并。
根据串联电路的性质,总电压等于电阻之和。
设电压U₁为电阻R₁上的电压,电压U₂为电阻R₂上的电压。
根据基尔霍夫定律和欧姆定律可以得出以下等式:U = U₁ + U₂U = I * R₁ + I * R₂由此可以解出电流I:I = U / (R₁ + R₂)将电流代入电压分配的等式可以得到:U₁ = I * R₁ = U * R₁ / (R₁ + R₂)U₂ = I * R₂ = U * R₂ / (R₁ + R₂)因此,在本例中,电阻R₁上的电压为U₁ = U * R₁ / (R₁ +R₂) = 100 * 10 / (10 + 20) = 33.33V电阻R₂上的电压为U₂ = U * R₂ / (R₁ + R₂) = 100 * 20 / (10+ 20) = 66.66V以上就是根据基尔霍夫定律进行简单计算的例题解答。
基尔霍夫第二定律

1 + 11 + 22 + 2 + 33 − 44 = 0
01知识抢答
题五
基尔霍夫第二定律只适用于线性电路,不
适用于非线性电路。
02
实验探究
02实验探究
实验电路原理图
实验电路 小组操作
展示操作
数据分析
实验电路实物图
实验小结
02实验探究
实验电路 小组操作
展示操作
任务一
VD
R1
于不闭合的假想回路。
实验小结
03
综合应用
03综合应用
例1
如图二极管应用电路,试分析电路:
1.判断二极管的状态
2.求输出电压UCO
3.计算流过二极管的电流
03综合应用
举一反三 练一练
如图二极管应用电路,已知测得LED两端的
电压为2V,试求:
1.输出电压UCO
2.流过LED的电流
04课堂小结ຫໍສະໝຸດ 04课堂小结勤思考
提出问题
敢探究
探究定律
能总结
实验总结
会应用
电路分析
05
自我评价
05课堂评价
学生自评
各任务是否掌握
组内互评
教师评价
任务完成情况
课中活动参与情况
06
课后作业
06课后作业
如图二极管应用电路,试求:
1.输出电压UCO
2.流过二极管的电流
专业强则自强
谢谢
数据分析
实验小结
任务三
1.运用基尔霍夫第二定律
识元件
测电压
析数据
计算任意两点间的电压
2.对比测试数据
02实验探究
基尔霍夫定律的应用和例题

上一页
下一页
2
返回
一、基尔霍夫电流定律(KCL)
1、KCL定律: 描述1:对任何结点,在任一瞬间,流入节点的电流等于由节 点流出的电流。I入=I出
描述2:在任一瞬间,一个节点上电流的代数和为 0。∑I=0
即: I =0 设:流入结点为正,流出结点为负。
I2
I1 I3 I2 I4
I1
I4 I3
某个封闭面。
◆ 注意: 对已知电流,一般按实际方向标示; 对未知电流,可任意设定方向,由计算结果确
定 未知电流的方向,即正值时,实际方向与假定 方பைடு நூலகம்一致,负值时,则相反。
6
例2 一个晶体三极管有三个电极,各极电流的方向 如图3所示。各极电流关系如何?
解:晶体管可看成一个闭合面,则:
IE=IB+IC
作 业:
第43页2-19、2-29
15
基尔霍夫定律
制作:浙江广厦建设职业技术学院 信息与控制工程学院
1
1.支路(Branch)——无分支的一段电路。支路中各处电流 相等,称为支路电流。
2.节点(Node)——三条或三条以上支路的联接点。 3.回路(Loop)——由一条或多条支路所组成的闭合电路。
右图中有三条支路:ab、acb和adb; 两个节点:a和b; 三个回路:adbca、abca和abda。
解:对左回路应用基尔霍夫电压定律列出:
E1=I(R1+R2)+U1
得
I E1 U1 4 10 1A
R1 R2 4 2
再对右回路列出:
E1-E2=IR1+U2
得
U2=E1-E2-IR1=4-2-(-1)×4=6V
图7
基尔霍夫定律全

1.2 基尔霍夫定律
上式中各电压和电动势的正、负符号的确定方法如下: (1)首先标明各支路电流的参考方向。 (2)确定回路的绕行方向是顺时针方向,还是逆时
针方向 (3)确定电阻上电压的符号:若通过电阻的电流参
和R2、US2支路分别含有电源US1和US2,称为有源支路 ;R3支路中不含有电源,称为无源支路
(2)节点 电路中三条或三条以上支路的连接点叫作节点。
(3)回路 电路中任意闭合路径叫作回路。
1.2 基尔霍夫定律
1.2.1 基尔霍夫电流定律(KCL)
基尔霍夫电流定律也称节点电流定律,应用于电路 中的节点。它的内容是:在任一瞬间,流入某节点的电 流之和等于流出该节点的电流之和,即
或者说在任一瞬间,某一节点上的电流代数和为零,即
1.2 基尔霍夫定律
它体现了电流连续性的原理,在电路中的任何一点 都不会发生电荷堆积。
1.2 基尔霍夫定律
【例1.2】图1.13为某电路中的一个节点,已知I1=2A, I2=3A,I3=-4A,I5=7A,求电流I4。 【解】 设流进节点的电流为正,流出节点的电流为负,由 基尔霍夫电流定律得
图1.15 某闭合回路
1.2 基尔霍夫定律
【解】 (1)由基尔霍夫电压定律可列出
得UCD=2V (2)ABCA不是闭合回路,也可应用基尔霍夫定律列出
即
得
UCA=-1V
1.2 基尔霍夫定律
【例1.4】图1.16所示电路中,已知 RB=20kΩ,R1=10kΩ,EB=6V,US=6V,UBE=-0.3V,试求 电流IB、I2及I1。
式中的正、负号是由基尔霍夫电流定律根据电流的 参考方向确定的。括号内的正、负号是电流本身数值的 正负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2 一个晶体三极管有三个电极,各极电流的方向 如图3所示。各极电流关系如何? 解:晶体管可看成一个闭合面,则:
IE=IB+IC
图3 晶体管电流流向图
上一页
下一页
返 回
例3 两个电气系统若用两根导线联接,如图4 (a)所示,电流I1和I2的关系
如何?若用一根导线联接,如图4 (b)所示,电I是否为零?
基尔霍夫定律
制作:浙江广厦建设职业技术学院 信息与控制工程学院
1.支路(Branch)——无分支的一段电路。支路中各处电 流相等,称为支路电流。 2.节点(Node)——三条或三条以上支路的联接点。 3.回路(Loop)——由一条或多条支路所组成的闭合电路。
右图中有三条支路:ab、acb和adb; 两个节点:a和b; 三个回路:adbca、abca和abda。
对图6(b)的电路可列出 U=E-IR0
列电路的电压与电流关系方程时,不论是应用 基尔霍夫定律或欧姆定律,首先都要在电路图上标 出电流、电压或电动势的正方向。 上一页 下一页
返 回
例4 在图7所示电路中,已知U1=10V,E1=4V,E2=2V,R1=4, R2=2,
R3=5,1、2两点间处于开路状态,试计算开路电压U2。
图4 两个电气系统联接图
解:将A电气系统视为一个广义节点,则
对图4(a):I1=I2
对图4(b):I= 0
上一页 下一页 返 回
二、基尔霍夫电压定律(KVL)
1、KVL定律 对电路中的任一回路,沿任意循行方向的各段电压 的代数和等于零。 即:
U 0 E IR
在任一回路的循行方向上,电动势的代数和等于电 阻上电压降的代数和。 即:
E、U和IR与循行方向相同为正,反之为负。
以图5所示的回路adbca为例,图中电源电动势、电
流和各段电压的正方向均已标出。按照虚线所示方向循 行一周,根据电压的正方向可列出:
U1+U4=U2+U3
或将上式改写为:
U1-U2-U3+U4=0 即 U=0
图5 在任一瞬时,沿任一回路循行方向(顺时针方向或逆时针方向),回路中 各段电压的代数和恒等于零。如果规定电位升取正号,则电位降就取负号。
图2 基尔霍夫电流定律应用于闭合面
可见,在任一瞬时,通过任一闭合面的电流的代数和也恒等于零。
上一页 下一页 返 回
由上面的例子,可知: • 节点电流定律不仅适用于节点,还可推广应用到 某个封闭面。 ◆ 注意: 对已知电流,一般按实际方向标示; 对未知电流,可任意设定方向,由计算结果 确定 未知电流的方向,即正值时,实际方向与假 定方向一致,负值时,则相反。
解:对左回路应用基尔霍夫电压定律列出: E1=I(R1+R2)+U1
得
E1 U1 4 10 I 1A R1 R 2 42
再对右回路列出: E1-E2=IR1+U2 得 U2=E1-E2-IR1=4-2-(-1)×4=6V
图7
上一页
下一页
返 回
小结:
1、支路:电路中流过同一电流的每一个分支 2、节点:电路中三条或三条以上支路的连接点。 3、回路:电路中任一闭合路径,回路内不含支路的回路叫网孔。 4、KCL定律内容: 表述1:在任一时刻,流入某一节点的电流之和等于从该节点流出的 电流之和。表达式为∑I入=∑I出 表述2:在任一时刻,流入(或流出)电路中任一节点的各电流的代 数和等于零。表达式为∑I=0 5、KCL定律可应用于电路中任一假设的封闭面。 6、KVL定律内容: 表述1:在任一时刻,沿闭合回路绕行一周,各段电压的代数和等于 零,表达式为:∑U=0 表述2:在任一时刻,沿任一回路绕行一周,各电阻上电压的代数的 和等于各电动势的代数和。表达式为∑IR=∑E
上一页
下一页
返 回
一、基尔霍夫电流定律(KCL)
1、KCL定律:
描述1:对任何结点,在任一瞬间,流入节点的电流等于
由节点流出的电流。I入=I出 描述2:在任一瞬间,一个节点上电流的代数和为 0。∑I=0 即: I =0 设:流入结点为正,流出结点为负。
I2
I1
I1 I 3 I 2 I 4
作 业: 第43页2-19、2-29
上一页 下一页 返 回
图5所示的adbca回路是由电源电动势和电阻构成 的,上式可改写为:
E1-E2-I1R1+I2R2=0
或 即
E1-E2=I1R1-I2R2 E=(IR)
图5
上一页
下一页
返 回
2、基尔霍夫电压定律的推广应用
图6
上一页 下一页 返 回
对图6(a)所示电路(各支路的元件是任意的) 可列出 U=UAB-UA+UB=0 或 UAB=UA-UB
I4
I3
或:
I1 I 3 I 2 I 4 0
基氏电流定律的依据:电流的连续性
在图1所示的电路中,对节点a可以写出: I1+I2=I3 或将上式改写成: I1+I2-I3=0 即 I=0 图1
上一页
下一页
返 回
2、KCL定律的推广应用 例1 图2所示的闭合面包围的是一个三角形电路,它有三 个节点。求流入闭合面的电流IA、IB、IC之和是多少? 解:应用基尔霍夫电流定律可列出 IA=IAB-ICA IB=IBC-IAB IC=ICA-IBC 上列三式相加可得 IA+IB+IC=0 或 I=0
