1—7基尔霍夫定律1
电路基础-电压源和电流源-受控源-基尔霍夫定律

电路基础-电压源和电流源-受控源-基尔霍夫定律————————————————————————————————作者:————————————————————————————————日期:2第一章电路模型和基尔霍夫定律3讲授板书1、掌握电压源、电流源的概念、用法及特性;2、熟悉受控源的用法;3、掌握基尔霍夫定律的应用。
1、电压源、电流源用法及特性2、基尔霍夫定律的应用受控源的概念及用法1. 组织教学 5分钟3. 讲授新课70分钟1)电压源及电流源25 2)受控源15 3)基尔霍夫定律302. 复习旧课5分钟电路元件特性4.巩固新课5分钟5.布置作业5分钟34一、学时:2二、班级:06电气工程(本)/06数控技术(本)三、教学内容:[讲授新课]:第一章电路模型和电路定律(电压源和电流源的概念及特点受控源的概念及分类基尔霍夫定律)§1-8电源元件(independent source)1. 理想电压源1)定义:其两端电压总能保持定值或一定的时间函数,且电压值与流过它的电流i 无关的元件叫理想电压源。
2)电路符号3)理想电压源的电压、电流关系(1)电源两端电压由电源本身决定,与外电路无关;与流经它的电流方向、大小无关。
(2)通过电压源的电流由电源及外电路共同决定。
伏安关系曲线如下图示:实际电流源可由稳流电子设备产生,如晶体管的集电极电流与负载无关;光电池在一定光线照射下光电池被激发产生一定值的电流等。
4)电压源的功率在电压、电流的非关联参考方向下;P = us i56物理意义:电流(正电荷 )由低电位向高电位移动,外力克服电场力作功电源发出功率。
例1-3图示电路,当电阻R 在0~∞之间变化时,求电流的变化范围和电压源发出的功率的变化。
解:(1)当电阻为R 时,流经电压源的电流为: 电源发出的功率为:表明当电阻由小变大,电流则由大变小,电源发出的功率也由大变小。
(2)当,则(3)当,则由此例可以看出:理想电压源的电流随外部电路变化。
基尔霍夫定律及电路元件
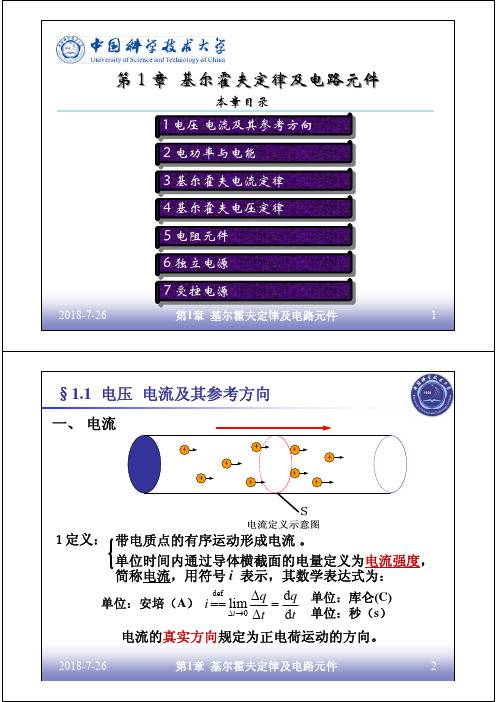
i + u – +
i u –
图(a)关联参考方向
图(b)非关联参考方向
注意:以后讨论均在参考方向下进行,不考虑真实方向。
2018-7-26
第1章 基尔霍夫定律及电路元件
11
§1.2 电功率与电能
一、电功率
1 定义:电功率[常简称功率(power)]是用以衡量电能转换或 传输速率的物理量,可用下式表达: 单位: (瓦特)W 2 功率与电压电流关系 由于 所以
2018-7-26 第1章 基尔霍夫定律及电路元件 2
§1.1 电压 电流及其参考方向
问
题
10Ω
7Ω
4Ω 1Ω
8Ω 5Ω 2Ω
9Ω 6Ω 3Ω
i
R
t
O
(1) 在有些复杂电路中,电流的真实方向事先很难确定。 (2) 电路中有些电流的真实方向随时间变化,无法标出 真实方向。
2018-7-26 第1章 方向
3 直流电流与交变电流 大小和方向不随时间变化的电流称为直流 。(DC) 随时间作周期性变化且平均值为零的电流称为交流。(AC)
i
t
i
ωt
O
O
π
2π
2018-7-26
第1章 基尔霍夫定律及电路元件
6
§1.1 电压 电流及其参考方向
二、电压
1 定义:电场力把单位正电荷从一点移动到另一点所作的功。 用符号 u 表示,其数学表达式为:
10Ω
§1.1 电压 电流及其参考方向
(2)电流参考方向的两种表示: • 用箭头表示:箭头的指向为电流的参考方向。
i a b
• 用双下标表示:如iab,电流的参考方向由a点指向b点。
注意:
1-6,7,8基尔霍夫定律

I2 b I5
I2=I5-I4 =[8-(-5 ) ]A =13 A
I6 I3 c
I3=I6-I5 = (-8-8 ) A = - 16 A
或由广义结点得 I3=-I1-I2= (-3-13 ) A =-16 A
8
第 1
章 二、基尔霍夫电压定律(KVL)
直 流
由电路元件组成的闭
+ I1
电 路
合路径称为回路。
直
代入数据
流
I3
I1
I2
I4
R1
R2
电 路
I1+I2-I3 -I4 =0
R3
+
+
R4
US1
US2
I1+2I3-12=0
-
-
I1 - 2I2-12+12 =0
2I2+4I4-12=0
I1=4 A, I2=2 A, I3=4 A, I4=2 A
20
第
1
章
1.8 叠加定理
直 流
叠加定理是分析线性电路最基本的方
第 1
1.6 基尔霍夫定律
章
本节问题?
直 流
欧姆定理:u=iR 电阻元件的电压电
电
流特性
路
基尔霍夫定律的目的:解决多回路的
电路。
基尔霍夫定律第一和第二定理? 描述系统中各元件的电压和电流之间的约束关系
如何使用基尔霍夫定律第一和第二定理?
1
第 1 章
直 流
基尔霍夫定律用来描述电路中各部分电压或
电 路
独立的结点方程式。
I3
I2 +
E2
R3
-
R2
结点 a : I1+I2-I3 =0 只有1个方程是独立的
§1—7基尔霍夫定律(1)
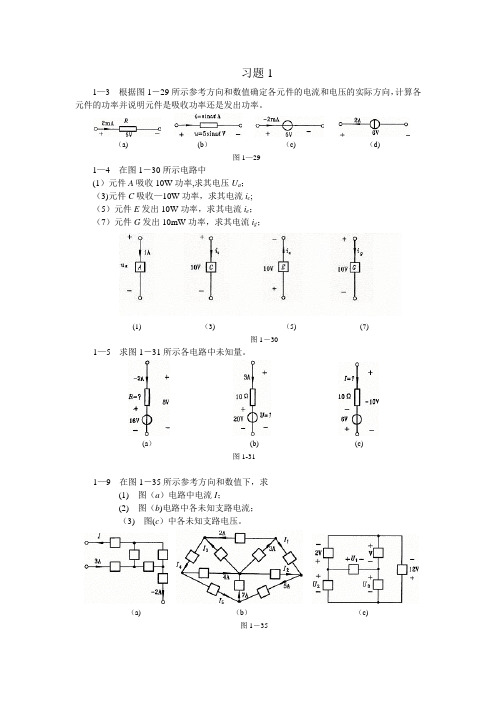
习题11—3 根据图1-29所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是吸收功率还是发出功率。
(a) (b)(c) (d)图1—291—4 在图1-30所示电路中(1)元件A吸收10W功率,求其电压U a;(3)元件C吸收—10W功率,求其电流i c;(5)元件E发出10W功率,求其电流i e;(7)元件G发出10mW功率,求其电流i g;(1) (3) (5) (7)图1-301—5 求图1-31所示各电路中未知量。
(a)(b) (c)图1-311—9 在图1-35所示参考方向和数值下,求(1) 图(a)电路中电流I;(2) 图(b)电路中各未知支路电流;(3) 图(c)中各未知支路电压。
(a) (b)(c)图1-351—11 求图1-37所示电路中电压U1、U ab、U cb。
图1-371—13 求图1-39所示电路中电压U1和电流I2。
图1-391—14 求图1-40所示电路中电压U s和电流I。
图1-40习题22—l 电路如图2-22所示,已知R1=1Ω,R2=2Ω,R3=4Ω,求各电路的等效电阻R ab.(c)(d) (e)(f)图2-222—3 电路如图2-24所示,已知R=2Ω,求开关打开和闭合时等效电阻R ab。
图2-242—9 电路如图2-30所示:(1)开关K打开时,求电压U ab;(2)开关K闭合时,求流过开关电流I ab。
(a)图2-302-13 求图2-34所示各电路的最简单的等效电路.(a)(b) (c)图2-342—14 求图2-35所示各电路的最简单的等效电路。
(b)(d)(f)图2-352-18 求图2-39所示各含受控源电路的输入电阻R i。
(b)图2-392-19 求图2-40所示各电路中的电压比Uσ/ U s。
(b)图2-402-23 电路如图2-44所示,求:(1)如果电阻R=4Ω,计算电压U和电流I。
(2)如果电压U=− 4V,计算电阻R。
1-8基尔霍夫电流定律
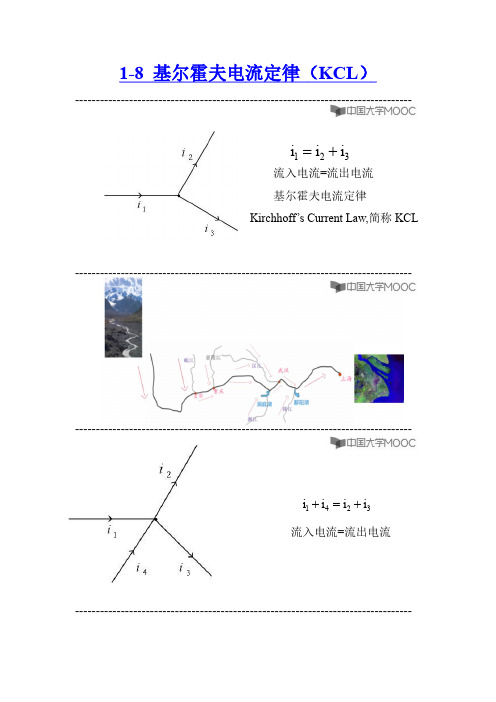
--------------------------------------------------------------------- 基尔霍夫电流定律 Kirchhoff ’s Current Law,简称 KCL
-----------------------------------------------------------------------------------
结点 1KCL 方程: 结点 2KCL 方程:
iS iR 0
结点 1KCL 方程: 结点 2KCL 方程: 结点 3KCL 方程:
---------------------------------------------------------------------------------
---------------------------------------------------------------------------------
流入电流前面的符号取+ 流出电流前面的符号取— 反过来定义也可以
i1 i2 i3
i1 i2 i3 0
i1 i4 i2 i3
i1 i2 i3 0
i1 i2 i3 i4 0
i1 i2 i3 0
基尔霍夫电流定律 Kirchhoff ’s Current Law,简称 KCL 电路中任一结点上所有电流的代数和为零
iS i R 0
is1 iR1 iR3 is 2 0 is1 iR1 iR 2 0
i R 2 i R 3 is 2 0
两个结点的 KCL 方程 只有一个 KCL 方程是独立的!
基尔霍夫电流定律

一、电路的常用术语
1.支路:一个或几个二端元件串联构成的一段电路称为支路。
I3
E4
E3
_
+
R3
R6
+
R4
R5
R1
R2
a
b
c
d
I1
I2
I5
I6
I4
-
ab、ac、ad、bc、bd、cd
一、复杂电路中的几个基本概念
1、支路:由一个或几个元件首尾相接构成的无分支电路。
右图中有 条支路:
E1和R1串联构成一条支路
E2和R2串联构成一条支路
R3单独构成另一条支路
3
R1
E1
E2
R2
R3
A
B
思考
同一支路中的电流有什么关系?
相同
2.节点:电路中三条及三条以上支路的连接点.
a b c d
I3
E4
E3
_
+
R3
R6
+
R4
R5
R1
R2
a
b
c
d
I1
I2
I5
I6
I4
-
一、电路的常用术语
-3A
10A
5A
10A
2A
I1
I2
A
B
解:
对节点A:
I1 = -3A + 10A + 5A
对节点B:
5A = I2 + 2A + 10A
= 12A
整理:
I2 = 5A - 2A - 10A
= -7A
注意:应用基尔霍夫电流定律时必须首先假设电流的参考方向,然后列写方程并代入电流数值计算。若求出电流为负值,则说明该电流实际方向与假设的参考方向相反。
第1章 基尔霍夫定律与电路元件

1.6
独立电源
基本要求:掌握电压源和电流源的基本特性。
1. 电压源
US
US
直流电压源
(a) (b)
uS
+ (c)
uS
(d)
电压源的符号
输出电压可调的 直流电压源
按任意规律变化 的电压源
交流电压源
特性:电压源能够提供确定的电压uS(称为源电压)。所谓“确 定”是指源电压uS 与流过电压源的电流无关,电压源的电流将由 与其相连的外电路来确定。
u ab ( l )是电场力将单位正电荷由 a 点沿路线 l 移动到 b 点所作
l l
的功,称为由 a 点到 b 点沿路线 l 的电压:
u ab (l ) F dl
l
注意:在集中参数电路中,a, b 两点之间的电压与计算路径无 关,称为端电压。
电位:
任选一点G作为电位参考点,电路中某点与参考点之间的电压称
2 . 基尔霍夫电流定律
基尔霍夫电流定律(Kirchhoff‘s Current Law,简称KCL) : 在集中参数电路中,任一时刻流出(或流入)任一节点的支路电 流代数和为零,即
i
k
0
( ik 表示第 k 条支路电流)
约定: ik 参考方向为流出节点时, ik 前面取“+”号; 流入 节点时, ik 前面取“-”号。 ① 在集中参数电路中,任一时刻流出(或流 入)任一闭合边界 S 的支路电流代数和等于 KCL的其他 表述
回路l1: 回路l2: 回路l3: 回路l4:
u1 6V 4V 10V
4V ④ u3 l1 6V l3
u2 u1 2V 8V
u3 6V 8V 14V
基尔霍夫第一定律课件

学习目标: 1、使学生理解和掌握基尔霍夫定律的 内容,能运用定律解决问题。 2、培养学生分析、思考、概括的能力 3、通过引导学生进行思考,及表达式 学习难点: 基尔霍夫第一定律的具体应用
什么是简单直 流电路?
凡是运用欧姆定律 及电阻串并联能进 行化简计算的直流 电路
加油 加油
如图所示,I1=2A, I2= -3A, I3=-2A, 试求I4
解:根据基尔霍夫第一定律, I1+I3=I2+I4 代入数据,2+(-2)= (-3)+I4 I4= 3A
3、第一定律的应用
用第一定律可以列出 IA=IAB-ICA IB=IBC-IAB IC=ICA-IBC
+
IA +IB +IC =0
小结:
• 四个名词的含义 支路,节点,回路,网孔 • 基尔霍夫第一定律内容 • 基尔霍夫第一定律应用
谢 谢!
2、基尔霍夫第一定律
我们来做个小实验,如图接线
测出I1,I2,I3并记录数值
• 名称:节点电流定律
• 定律内容:在任一瞬间,流进某一节点 对于 的电流之和恒等于流出该节点电流之和。 O点, 即 ΣI进 =ΣI出
ΣI进 =I1+I2 ΣI=I 3+I4+I5 ΣI进 I1+I2= I3+I4+I5 =ΣI 出 I1+I2- I3-I4-I5=0 因此我们可以得到ΣI=0
1、几个名词
支路:电路中的每一个分支 E1-R1,E2-R2,R3 节点:三条或三条以上支路的汇 交点 A,B 回路:电路中任一闭合电路 E1-R1-R3 ,E2-R2-R3, E1-R1-R2-E2 网孔:最简单的,不可再分的回 路 E1-R1-R3 ; E2-R2-R3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题11—3 根据图1-29所示参考方向和数值确定各元件的电流和电压的实际方向,计算各元件的功率并说明元件是吸收功率还是发出功率。
(a) (b) (c) (d)图1-291—4 在图1-30所示电路中(1)元件A吸收10W功率,求其电压U a;(3)元件C吸收-10W功率,求其电流i c;(5)元件E发出10W功率,求其电流i e;(7)元件G发出10mW功率,求其电流i g;(1) (3) (5) (7)图1-301—5 求图1-31所示各电路中未知量。
(a) (b) (c)图1-311—9 在图1-35所示参考方向和数值下,求(1) 图(a)电路中电流I;(2) 图(b)电路中各未知支路电流;(3) 图(c)中各未知支路电压。
(a) (b) (c)图1-351—11 求图1-37所示电路中电压U1、U ab、U cb。
图1-371—13 求图1-39所示电路中电压U1和电流I2。
图1-391—14 求图1-40所示电路中电压U s和电流I。
图1-40习题22—l 电路如图2-22所示,已知R1=1Ω,R2=2Ω,R3=4Ω,求各电路的等效电阻R ab。
(c)(d) (e)(f)图2-222—3 电路如图2-24所示,已知R=2Ω,求开关打开和闭合时等效电阻R ab。
图2-242—9 电路如图2-30所示:(1)开关K打开时,求电压U ab;(2)开关K闭合时,求流过开关电流I ab。
(a)图2-302-13 求图2-34所示各电路的最简单的等效电路。
(a) (b) (c)图2-342—14 求图2-35所示各电路的最简单的等效电路。
(b)(d)(f)图2-352-18 求图2-39所示各含受控源电路的输入电阻R i。
(b)图2-392-19 求图2-40所示各电路中的电压比Uσ/ U s。
(b)图2-402—23 电路如图2-44所示,求:(1)如果电阻R=4Ω,计算电压U和电流I。
(2)如果电压U=− 4V,计算电阻R。
图2-44习题33—4用网孔电流法求解图3-18所示电路中各支路电流。
(b)图3-183-6 用网孔电流法求图3-20所示电路中电流i、受控源发出的功率。
图3-203-12 列写图3-25所示电路的节点电压方程。
(b) (c)图3-253-14 用节点电压法求图3-26所示电路的节点电压。
(b)图3-263-15 用节点电压法计算题3-5。
图3-193-19 电路如图3-28所示,分别用节点法和回路电流法求支路电流I1。
图3-283-20 电路如图3-29所示,列写其回路电流方程和节点电压方程,尽量使方程列写简捷。
(d)图3-29习题44—l 试用叠加定理求图4-29所示电路的电流i。
(b)图4-294—5 已知图4-33所示电路中支路电流i=0.5A,用替代定理求电阻R。
图4-334—7 求图4-35所示各一端口网络的戴维南等效电路或诺顿等效电路。
(a) (b)(c) (d)图4-354—10 图4-38所示各电路中负载电阻R L可变,问R L何值时它吸收的功率最大?此最大功率等于多少?(b) (c)图4-384—12 求图4-40所示电路的戴维南或诺顿等效电路。
(b)图4-404—16 图4-44所示电路中,N0由线性电阻组成。
已知R1=1Ω,R2=2Ω,R3=3Ω,U s1=18V。
进行两次测量,第一次测量时把U s2短路,由U s1作用。
测得U1=9V,U2=4V;第二次测量时由U s1和U s2共同作用,测得U3=−30V。
用特勒根定理求电压源值U s2。
图4-444—20 电路如图4-48所示,当电流源i s1和电压源u s1反向而电压源u s2不变时,电压u0是原来的1/2倍;当i s1和u s2反向而u s1不变时,电压u0是原来的3/10倍。
如果仅i s1反向而u s1和u s2不变时,电压u0应是原来的多少倍?图4-484—24 无源双端口网络N R如图4-52所示。
(1)当输入电流i1=2A时,u1=10V,输出端开路电压=u25V。
如果输入电流源移到输出端口2-2′,同时在输入端口1-1′跨接电阻5Ω,求5Ω电阻中电流。
(2)当输入电压u1=10V时,输入端电流i1=5A,而输出端的短路电流1A,如果把电压源移到输出端,同时在输入端跨按2Ω电阻,求2Ω电阻的电压。
(提示:用互易定理和戴维南定理)。
图4-524—26 对图4-54所示电路进行两次测量:图(a)电路中,u2(1)=0.45u s,i4(1)=0.25 u s;对题4-23图(b)电路,u2(2)=0.15u s,i4(2)=0.25 u s。
(1)应用互易定理求R1;(2)设有两个电压源同时作用于该电路,如图(c)所示,应用叠加定理确定使R3中无电流时的k值。
(1)计算R2、R3与R4。
(提示:参考题4-25)。
(a) (b) (c)图4-54习题55—l 图5-61所示,试求(2) x=u C (图(b),x的波形见图e,f,试作出电流i的波形。
(3) x=u L (图(c),x的波形见图d,e,试作出电流i的波形。
(d) (e) (f)图5-615—2 图5-62所示电路原来处于稳态,t=0时开关S打开。
求换路后t=0+时刻各支路电流与动态元件电压(电流)的初始值。
(a) (b)图5-625-5 图5-65所示电路中开关S在l位置已长久,t=0时合向2位置,求换路后u C (t)与i (t)。
图5-655—6 如图5-66所示电路中开关S在1位置已长久,t=0时合向2位置,求换路后i(t)与u L(t)。
图5-665—7 如图5-67所示电路原处稳态,t=0时把开关S合上,求换路后i (t)和i1(t)。
图5-675—8 如图5-68所示电路中电容原来不带电荷,t=0时合上开关S,已知经过1.5ms 时电流为0.11A。
求电容C值、电流的初始值和电容电压u C (t)。
图5-685—10 如图5-70所示电路原处稳态,t=0时合上开关S。
求换路后的i L(t)和电压源发出的功率。
图5-705-11 如图5-71所示电路原处稳态,t=0时合上开关S,求换路后的i L(t)和i (t)。
图5-715—12 求图5-72所示电路零状态响应i (t)。
(a) (b)图5-725—15 如图5-75所示电路中开关S在1位置已长久,t=0时合向2位置,求换路后电流i (t)和i L(t)。
图5-755—16 如图5-76所示电路原处稳态,t=0时打开开关S,已知u C (0−)=2V,求全响应i (t)、i C(t)和u C (t)。
图5-765—21 已知图5-79(a)所示电路中N0为电阻电路,u s (t)=ε(t) V,C=2F,其零状态响应u2 (t)=(0.5+0.125e−0. 25) ε(t)V如果用L=2H的电感代替电容C,见附图(b),求其零状态响应u2 (t),并选择合适的元件组成电路N0。
(a) (b)图5-795-25 图5-83(a)所示电路中开关S在1位置已长久,t=0时合到2位置,求换路后电流i1和i2。
(1) u s为2V直流电压源;(2) u s波形如图(b)所示。
(a) (b)图5-835—26 图5-84(a)所示电路原处稳态,t=0时合上开关S,求换路后响应u L(t)和电流i L (t)。
(1) u s=δ(t);(2) u s = e−1t V;(3) u s波形如图(b)所示。
图5-845—30 电路如图5-88所示,已知i L(0+)=3A,u C(0+)=4V,求t≥0时电压u C (t)。
图5-885-32 图5-90所示电路原处稳态,t=0时开关S闭合。
设u C (0−)=100V,求换路后的电流i L(t)。
图5-90习题66—1 已知电压u1=2202cos(314t+120˚)Vu2=2202sin(314 t−30˚)V(1)确定它们的有效值、频率和周期井画出其波形;(2)写出它们的相置,决定它们的相位差,画出相量图。
6-3 已知某一支路的电压和电流在关联参考方向下分别为u(t)=311.1sin(314 t+30˚)Vi(t)=14.1cos(314 t−120˚)A(1) 确定它们的周期、频率与有效值;(2) 画出它们的波形,求其相位差并说明超前与滞后关系;(3)若电流参考方向与前相反,重新回答(2)。
6—4 已知两个正统电压分别为u1=2202(ωt +30˚)Vu2=2202(ωt +150˚)V试分别用相量作图法和复数计算法求。
U1+。
U2和。
U1−。
U2。
6—9 并联正弦电流电路如图6-25所示,图中电流表A1读数为5A,A2为20A,A3为25A。
(1)图中A的读数是多少?(2)如果维持第一只表A1读数不变,而把电路的频率提高一倍,再求其它表读数。
图6-256—13 图6-27所示电路中,i s=10cos100t A,R=10Ω,L=100mH,C=500μF,试求电压u R(t)、u L(t)、u C(t)、和u(t),并画出电路的相量图。
图6-276—14 图6-28所示电路中,u s(t)=100cos100t V,R=10Ω,L=0.1H,C=500μF,试求各支路电流i R (t)、i L (t)、i C (t)、和i (t),并画出电路相量图。
图6-28习题77—6 正弦电流电路如图7-42所示,已知.U=10 /45ºV,R=2Ω,ωL=3Ω,1/ωC=1/2Ω,求各元件的电压、电流,并画出电路的相量图。
图7-427—7 列写如图7-43所示各电路的输入阻抗Z和导纳Y的表达式(不必化简)。
(a) (b)(c)(d)图7-437—8 求如图7-44所示各电路的输入阻抗Z ab。
(b)(c)图7-447—11 如图7-47所示电路为测量线圈参数常用的实验线路,已知电源频率为50Hz,电压表读数为100V,电流表读数为5A,功串表读数为400W,根据上述数据计算线圈的电阻和电感。
图7-477—15 电路如图7-48所示,已知端电压U=100V,ω=1000rad/s。
两个并联负载的电流和功率因数分别为I l=10A,cosφ1=0.8(φ1<0=;I2=20A,cosφ2=0.5(φ2>o)。
(1)试求图中电流表和功率表的读数以及电路的功率因数;(2)如果电源的额定电流为30A,那么还能并联多大的电阻?试求并上该电阻后,电流表和功率表的读数以及电路的功率因数;(3)如果要使原电路的功率因数提高到0.9,需要并联多大的电容?图7-487—16 电路如图7-49所示,已知Z1吸收功率P1=200W,功率因数cosφ1=0.83(容性);Z2吸收功率P2=180W,功率因数cosφ2=0.5(感性);Z3吸收功率P3=200W,功率因数cosφ3=0.7(感性),电源电压U=200V,频率f=50Hz。
