基尔霍夫定律及支路电流法
2.1 基尔霍夫定律 2.2 叠加定理与等效电源定理

所有独立源置零后 b
所得无源二端网络。
2.诺顿定理
任何一个含独立电源、线性电阻和线性受控源的单口网络N, 可以用一个电流源和电阻的并联组合来等效;
电流源的电流 = 单口网络的端口短路电流ISC ,
而并联电阻 = 单口网络的所有独立源置零后的输入电阻。 a a ISC b a ISC R0 b N0为将N中 所有独立源置零后 所得无源二端网络。
1.戴维宁定理
任何一个含有独立电源、线性电阻和线性受控源的 线性二端网络可以用一个理想电压源(UOC)和电阻R0的串联 组合来等效; 等效电压源的电压 = 二端网络的端口开路电压UOC , 而等效电阻 = 二端网络中所有独立源置零后的输入电阻。 i=0 a i a a + R0 N U N N OC 0 _ b b b N0为将N中 a + UOC_ R0
i1 + i2+ i3 = 0
i1
i1
uS1 + _ uS2 R2 + _ R3
R1
i1 + i 2 = 0
i2
2沿任一闭合路径(循行方向), 各支路电压的代数和为零,即 u 0 R2 + US1 _ I2 (1)选定一个绕行方向:顺时针 –R1I1–US1+R2I2–R3I3+R4I4+US4= 0 电流与绕行方向一致,用“+”; R3 I4 _ U + S4 R4 I3 不一致,用“-”。 (2)也可写成:
a +
_
1.结点 (node): 三条或三条以上支路的连接点。 2 R3 3 2.支路 (branch): 电路中通过同一电流的每个分支。 3.回路(loop): 由支路组成的闭合路径。
支路电流法基尔霍夫第一定律
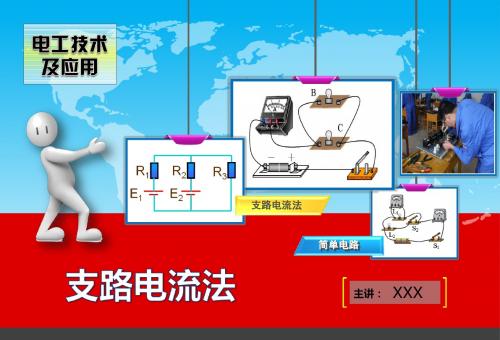
R1
E1 E2
R2
R3
支路电流法
假定各支路电流的方向和回路方向。
R1
E1 E2
R2
R3
支路电流法
用基尔霍夫电流定律列出独立 节点方程
节点a:I1+I2=I3 R1 E1 E2 R2 R3 若节点有 n 个。那么节 点电流方程 的个数应该 为(n-1) 个。
节点b:I3=I1+I2
支路电流法
用基尔霍夫电压定律列出独立回路方程。
R1
E1 E2
R2
R3
-E1+I1R1-I2R2+E2=0 -E1+I1R1-I2R2+E2=0
I3R3-E2+I2R2=0
支路电流法
代入已知数,解联立方程式,求出各 支路的电流。
I1+I2=I3 -E1+I1R1-I2R2+E2=0 I3R3-E2+I2R2=0 I1+I2=I3
-130+I1-0.6I2+117=0
24I3-117+0.6I2=0
I1=10A I2=-5A I3=5A
确定各支路电流的实际方向。当支路电流计算结 果为正值时,其方向和假设方向相同;当支路电流计 算结果为负值时,其方向和假设方向相反。
支路电流法
用支路电流法解题的步骤:
1 2 3 4 5 6
假定各支路电流的方向和回路方向。 用基尔霍夫电流定律列出独立节点方程。 用基尔霍夫电压定律列出独立回路方程 。 代入已知数,解联立方程式,求出各支路的电流。
作业
巩固复习本节课的
知识及内容。 预习下节课的内容,与 支路电流法比较有什么 异同。
支路电流法
基尔霍夫定律、支路电流法

支路电流法简介
支路电流法是电路分析中另一种广泛应用的方法,它可以简化复杂电路的分析过程。
1 假设与规则
通过在每个支路上引入一个未知的电流变量,我们可以编写一组方程来解析电路。
2 应用范围
支路电流法适用于复杂的多支路电路,尤其适用于由电流源驱动的电路。
3 实例分析
我们将通过一个由多个支路组成的电路来演示支路电流法的应用。
电路图示例
我们将通过一个包含电阻、电流源和电压源 的电路示例来分析基尔霍夫定律和支路电流 法。
结果分析
我们将计算电路中的未知电流和电压,并解 释结果的物理意义。
结论和要点
本演示总结了基尔霍夫定律和支路电流法的关键概念和应用。
基尔霍夫定律
节点定律和回路定律帮助我们分析电路中的电流和电压。
支路电流法
通过引入支路电流变量,我们可ቤተ መጻሕፍቲ ባይዱ简化电路的分析过程。
基尔霍夫定律、支路电流 法
本演示将介绍基尔霍夫定律和支路电流法,两个在电路分析中至关重要的概 念。
基尔霍夫定律简介
基尔霍夫定律是电路分析的基础,它可以帮助我们理解和计算电路中的电流和电压分布。
1 第一定律
电流在交汇节点的总 和为零。
2 第二定律
在闭合回路中,电压 的总和等于零。
3 应用实例
我们将通过一个实际 的电路图示例来演示 如何应用基尔霍夫定 律进行分析。
1 共同点
两种方法都基于电路中电流和电压的守恒原理。
2 适用范围
基尔霍夫定律适用于任何电路,而支路电流法更适用于复杂的多支路电路。
3 实例分析
我们将通过一个实际的电路图例来阐述基尔霍夫定律和支路电流法的关系。
基尔霍夫定律和支路电流法的实例分 析
第二单元复杂直流电路一轮复习

第一讲:基尔霍夫定律及支路电流法点击考纲:熟练掌握基尔霍夫定律的内容和适用场合。
熟练运用支路电流法求解电路中的电流和电压。
(一)课前尝试练习:1、看书P40-43完成下课知识准备(1)基尔霍夫电流定律指出流过任一节点的________________为零,其数学表达式为________________或,该定律也可推广应用于。
(2)基尔霍夫电压定律指出从电路上的任一点出发绕任意回路一周回到该点时________________为零,其数学表达式为________________,该定律也可推广应用于求两点之间的。
(3)几个或多个元件首尾相连构成的无分支电路称为,此支路上流过任意元件的电流。
2、如图所示,为一网络的一部分。
则I1= ,I2= 。
3、某电路用支路电流法解的方程组如下:I1+I2+I3+I4=0I1R1-I4R4+E1=0I2R2-I4R4-E1-E2=0-I2R2+I3R3+E2+E3=0那么该电路的节点数为______________,网孔数为______________,支路数为______________,回路数为______________,并画出电路图。
4、判断下列说法是否正确(1)基尔霍夫电流定律是指沿任意回路绕行一周,各段电压的代数和一定等于零。
()(2)任意的闭合电路都是回路。
()(3)回路电流和支路电流是同一电流。
()(4)在电路中任意一个节点上,流入节点的电流之和,一定等于流出该节点的流之和。
()(5)基尔霍夫定律只适用于线性电路的计算。
()5、如图2-3所示网络N1、N2,已知I1=5A,I2=6A,则I3为()A、11AB、-11AC、1AD、-1AI1图2-4图2-36、如图2-4所示,电流I的值为()Us的值为()A、1AB、-2AC、2AD、-1AE、3VF、-3VG、2VH、-2V (二)课堂探究1、如图所示的电桥电路中,已知电阻R1、R2和R3中的电流分别是25mA、15mA和10mA,方向如图中所示,那么电阻R4、R5和R6中的电流分别是_____、______和_____,并在图上标出电流方向。
基尔霍夫定律及支路电流法

一、复习提问(2分钟)◆教师提问◆学生回答二、提出任务:(5分钟)◆勾起同学们求知欲望(新课引入)二、链接知识:(60分钟)◆基尔霍夫电流定律讲授(出示标题)◆与学生互动问答◆与学生互动问答◆知识延伸◆基尔霍夫电压定律讲授(出示标题)◆与学生互动问答三、运用知识完成任务(5分钟)◆知识延伸四、分析归纳支路电流法解题步骤(5分钟)五、课堂练习、讨论与答疑(8分钟)六、小结、布置作业(5分钟)1、什么叫关联参考方向和非关联参考方向。
(请一学生回答)2、写出关联参考方向和非关联参考方向下欧姆定律表达式(请一学生回答)注: 新课要用到的相关知识,为新课的学习打下基础。
任务:图1已知R1=4Ω,R2=6Ω, R3=1Ω,U1=10V,U2=20V,试求I1、I2、I3。
请问哪一位同学会解这道题?(停顿片刻,让同学们充分思考)这道题目不光同学们不会解,欧姆也不会解。
这道题目用我们中学学到的知识——欧姆定律和电阻的串、并联关系是无法求解的。
如何解这道题就是我们今天这两节课的任务。
也就是说今天的课程学完后,同学们会解这道题就完成了今天这两节课的教学任务。
既然这道题目欧姆不会解,我们就需要请教另外一位高人。
这位高人在他还是21岁大学生时,提出了以他的名字命名的两大定律——电流和电压定律。
(停顿片刻)他就是基尔霍夫(G.R. Kirchhoff)。
那么,当时21岁的德国小伙基尔霍夫,他提出的电流定律是什么?“小基”说,对一个节点来说,节点无电荷聚集。
在任一时刻,流入电路中某一节点的电流等于流出这个节点的电流。
数学表达式为:∑I入=∑I出。
这就是基尔霍夫电流定律(Kirchhoff’s Current Law)简称 KCL。
那么,什么叫节点(Node)?三条以上支路的连接点。
什么叫支路(Branch)?流过同一电流的每个分支。
有几个电流就有几个支路。
请问同学们:图1中有几条支路?有几个节点?(学生答:有3条支路,2个节点)下面运用KCL,列出KCL方程式:大家看,上面这两个方程式有什么不同?是否是一回事呀?(学生答:一样的),对于两个节点只有1个独立的KCL方程式,对于3个节点只有2个独立的KCL方程式……,由此我们可以说,对于n个节点可以列几个独立的KCL方程式呀?(学生答:n-1个)KCL推广:由节点推广到任意封闭的面。
支路电流法讲解
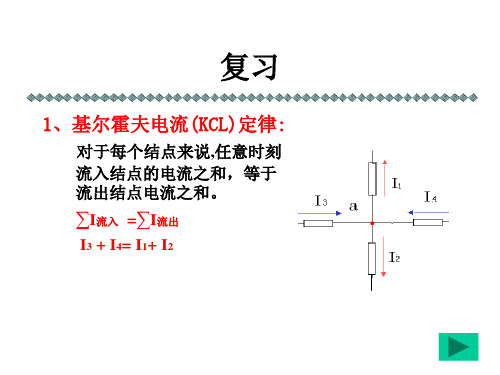
对网孔L1可列出 对网孔L2可列出
R1I1+R3I3-US1=0 R2I2+R3I3-US2=0
可见,对有2个网孔的电路,用基尔霍夫电压定律可列出2 个独立的KVL方程。
推广:对于n个结点,b条支路组成的电路中,可列出b-(n-1) 个网孔电压方程。
结论:应用KCL和KVL,一共列出[(n一1)+b一(n一1)]=b 个独立方程,故可解出b个支路电流。
+ I1
I2 + 分析:以支路电流为未知量,需要3个独
US1
-
I3 R3
US2 立方程方可求解出3个未知电流。
-
b
首先,用基尔霍夫电流定律列写结点KCL方程 对结点a列出KCL方程 I1+I2=I3
对结点b列出KCL方程 I3=I1+I2
可见,对具有两个结点的电路,应用基尔霍夫电流定律 只能列出2-1=1个独立方程。
解:
4、联立方程组,代入参数求解。
I1+I2=I3 (1) R1I1+R3I3-US1=0 (2) R2I2+R3I3-US2=0 (3)
将(1)式代入(2)、(3)式,整理可得
I1+I2=I3 (1) 20I1+6I3-140=0 (2) 5I2+6I3-90=0(3)
R1 a R2
+ I1
US1
I3
-
L1
解:
I2 R3
b L2
图中:若已知
+
US2
US1=140V,US2=90V, R1=20Ω, R2=5Ω, R3=6Ω。
- 求:各支路电流
4、联立方程组,代入参数求解。
13I1+3I2-70=0 6I1+11I2-90=0
第五节 支路电流法

i2 1
R1
1 i1 34
R6
R3 2
应用欧姆定律消去支路电压得: 3
i R5 5 i6 uS – +
厚德 笃行 务实 创新
小结
(1)支路电流法的一般步骤: ①标定各支路电流(电压)的参考方向; ②选定(n–1)个节点,列写其KCL方程; ③选定b–(n–1)个独立回路,指定回路绕行方 向,结合KVL和支路方程列写;
R2=0.6Ω, R3=24Ω,求各支路电流。 US1 –
R1
a点KCL方程:
1
b
2
–
+
+
I1
R2
Us2
a I3
2个KVL方程:
I2
R3 整理3个方程得到:
厚德 笃行 务实 创新
b
2
–
Us2
–
1
+ +
R1
I1
R2
a
I2
R3
I2
解方程组得:
I1=-10A,I2= 5A,I3=-5A
厚德 笃行 务实 创新
支路数: 节点数:
b=6条 n=4个
节点电流方程:
4
i6
想一想
这4个KCL方程相互独立吗?来自厚德 笃行 务实 创新
所有KCL方程相加:
注意:其中任意3个方程之和不等以0 即 :任意 1 个节点的电流方程都可以由其他
3个节点电流方程推导得出 ,那么4个节 点电流方程中有3个是互相独立的。
结论
n个结点的电路, 独立的KCL方程为n-1个。
厚德 笃行 务实 创新
2.KVL的独立方程数 i1 i2
1
包含网 孔1和3
i1 i3
基尔霍夫定律及支路电流法

4k B
I 6 1mA
2k
42
C
U BC 2I 2V
U AB 4I 4V
VB U BC VC 2V
VA 6V
例2: Uab 10 6 60V
UU
ca da
4 20 80V 6 5 30V
Ucb 140V
Udb 90V
c 4A
a 6A 5 d
20 10A
E1 140V
或:∑U=0
与绕行方向一致者取“+”,其中回 路 的绕行方向可任意选取
c I1 R1 a
+
U1 I2
US1 -
R2
U2
b
I3 d R3 IS3
如图沿回路abca,有:
U1 U2 US1
电位降 电位升
或 U 2 U S1 U1 0
电位降为正,电位升为负
KVL的另一种形式: 针对只含电阻、电压源的电路
a I1
b
I4 R4
R1 I2
R2
E4
E2
d
I3 R3
c
电流参考方向与回路的绕行方向一致:
RkIk 项前取“+”,反之 “-”;
绕行过电压源US:若从“-”→“+”(电位升),
取“+”,反之“-”。
四、基尔霍夫定律的适用范围及注意事项
1.不仅适用于直流电路,也可适用于任何变 化的电压和电流,即:
时的Vb
解:1)S闭合时,Vb 0
+10V 1kΩ b 2kΩ -5V
a I1
S I2 c
2)S断开时, I1 I2
例3:分别计算开关S合上及断开时的VA=?
2k B 4k
A
2k B 4k
A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、复习提问(2分钟)◆教师提问
◆学生回答
二、提出任务:
(5分钟)
◆勾起同学们求知欲望(新课引入)
二、链接知识:
(60分钟)
◆基尔霍夫电流定律讲授(出示标题)1、什么叫关联参考方向和非关联参考方向。
(请一学生回答)
2、写出关联参考方向和非关联参考方向下欧姆定律表达式(请一学生
回答)
注: 新课要用到的相关知识,为新课的学习打下基础。
任务:
图1
已知R1=4Ω,R2=6Ω, R3=1Ω,U1=10V,U2=20V,试求I1、I2、I3。
请问哪一位同学会解这道题?(停顿片刻,让同学们充分思考)
这道题目不光同学们不会解,欧姆也不会解。
这道题目用我们中学学到的知识——欧姆定律和电阻的串、并联关系是无法求解的。
如何解这道题就是我们今天这两节课的任务。
也就是说今天的课程学完后,同学们会解这道题就完成了今天这两节课的教学任务。
既然这道题目欧姆不会解,我们就需要请教另外一位高人。
这位高人在他还是21岁大学生时,提出了以他的名字命名的两大定律——电流和电压定律。
(停顿片刻)他就是基尔霍夫(G.R. Kirchhoff)。
那么,当时21岁的德国小伙基尔霍夫,他提出的电流定律是什么?
“小基”说,对一个节点来说,节点无电荷聚集。
在任一时刻,流入电路中某一节点的电流等于流出这个节点的电流。
数学表达式为:∑I入=∑I出。
这就是基尔霍夫电流定律(Kirchhoff’s Current Law)简称 KCL。
◆与学生互动问答
◆与学生互动问答
◆知识延伸
◆基尔霍夫电压定律
讲授(出示标题)
那么,什么叫节点(Node)?三条以上支路的连接点。
什么叫支路(Branch)?流过同一电流的每个分支。
有几个电流就有几个支路。
请问同学们:图1中有几条支路?有几个节点?(学生答:有3条支路,2个节点)
下面运用KCL,列出KCL方程式:
大家看,上面这两个方程式有什么不同?是否是一回事呀?(学生答:一样的),对于两个节点只有1个独立的KCL方程式,对于3个节点只有
2个独立的KCL方程式……,由此我们可以说,对于n个节点可以列几个
独立的KCL方程式呀?(学生答:n-1个)
KCL推广:由节点推广到任意封闭的面。
对于图1所示电路,求I1、I2、I3共3个未知数,需要列3个方程式,而我们运用KCL只列了1个方程式,另外两个方程式需要基尔霍夫电压定律
来解决。
基尔霍夫电流定律是对节点来说,那么,基尔霍夫电压定律,则是对回路来讲的。
“小基”说,对任意回路,任意时刻,沿一定方向绕行一周,各元件上电压降的代数和为零。
即∑u = o这就是基尔霍夫电压定律(Kirchhoff’s
◆与学生互动问答
Voltage Law)简称 KVL。
那么,什么叫回路((Loop))?由支路构成的闭合路径。
通俗地说,就是能够回去的路.
请问同学们:图1中有几条回路呢?(学生答:有3条回路)
“沿一定方向绕行”,既可以顺时针,也可以逆时针绕行。
各元件上电压降的代数和为零。
“代数和”表示有正有负,绕行方向与经过电阻的电流方向相同,电阻电压降取正号;绕行方向与经过电阻
的电流方向相反,是电压升,电阻电压降取负号。
绕行方向经过理想电压源时,从-到+,是电压升,取负号;从+到-,是电压降,取正号。
下面运用KVL,列出KVL方程式:
回路#1 : I1 R1 +I3 R3-U1 =0
回路#2 :- I2 R2 +U2-I3 R3 =0
回路#3 : I1 R1 –I2 R2+U2 -U1 =0
由上面3个方程式可知:
回路#1方程式+回路#2方程式=回路#3方程式。
上面3个方程式只有任意2个方程式是独立的。
以后为了列方程的方便,我们只列回路#1、回路#2的方程式。
象回路#1、回路#2这样的回路内
部不含支路的回路,或者说是单孔回路,它形如鱼网孔,故称为网孔回路。
以后我们只列网孔回路的方程式。
三、运用知识完成任务 (5分钟)
◆知识延伸
四、分析归纳支路电流法解题步骤(5分钟)
五、课堂练习、讨论与答疑(8分钟)
六、小结、布置作业(5分钟)
至此,我们可以完成上课前布置的任务了,应用KCL 、KVL 列方程:
回路#1 : I 1 R 1 +I 3 R 3-U 1 =0 回路#2 :- I 2 R 2 +U 2-I 3 R 3 =0
3个方程式3个未知数,联列方程求解即可。
这种方法叫支路电流法。
KVL 推广:KVL 通常用于闭合回路,但也可推广应用到任一不闭合的电
路上。
支路电流法的解题步骤:
1. 在图中标出各支路电流的参考方向,对选定的回路标出
回路绕行方向。
2. 应用 K C L 对节点列出 ( n -1 )个独立的K C L 方程式。
3. 应用 K V L 对网孔回路列出K V L 方程式.
4. 联立求解方程,求出各支路电流。
课堂练习第29页习题2-7,前后左右可以讨论,教师走下讲
台巡回答疑,个别点拨。
对于普遍问题集中答疑。
布置课后作业第29页习题2-11.
+ -
I 5
+ U ab
- + -
I 3
I 1
I 2
R 3 R 1
R 2 U S1 U S3 +
U S2 - I 4
b
a
111222333=----++s s s ab U R I U R I R I U U
教后小结
讲课时,同学们鸦雀无声、全神贯注、兴致勃勃,一个个头似麦斗,眼似钢铃,二眸子烁烁放光,认真听讲;启发教学,师生互动时,一唱一和,同学们积极响应,声音洪亮,课堂气氛热烈而活跃。
课后作业批改显示,全体学生都正确地完成了课后作业。
本次课达到了预期的教学目的,取得了圆满成功,
本次课的成功在于,以求解一道具体的电路计算题为任务,指出这道题欧姆不会解,需要请教1位21岁的大学生基尔霍夫(注:基尔霍夫21岁还是大学生时,提出了基尔霍夫定律),很好地抓住了学生的好奇心和兴奋点,以此为线索,将基尔霍夫电流定律、电压定律、支路电流法隐含其中,整个课程内容紧凑,环环紧扣,一气呵成。
“趁热打铁”的课堂练习、讨论与答疑,进一步巩固了教学效果。
