最新中考数学证明题综合训练试题精品版

合集下载

2023年数学中考试题精选：几何综合证明(一)

1.（2023.营口24题）在平行四边形ABCD中，∠ADB=90°,点E在CD 上，点G在AB上，点F在BD的延长线上，连接EF，DG, ∠FED=∠ADG，ADBD =DG EF=k.（1）如图1，当k=1时，请用等式表示线段AG与线段DF的数量关系________；（2）如图2，当k=√(3)时，写出线段AD，DE和DF之间的数量关系,并说明理由；（3）在（2）的条件下，当点G是AB的中点时，连接BE，求tan∠EBF的值2.（2023.本溪铁岭辽阳25题）在Rt△ABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上（不与点A，B重合），连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G.（1）如图1，当点D与点O重合时，请直接写出线段AD与线段EF 的数量关系；（2）如图2，当点D在线段AB上时，求证：CG+BD=√2BC；（3）连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值.3.(2023.大连25题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质。

已知AB=AC，∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折，同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB.”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长.”补足探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC，∠A>90°，△BDE由△ABE翻折得到.（1）如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；（2）如图2，若点E为AC中点，AC=4，CD=3，求BE的长.问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以问题进一步拓展.问题2：如图3，在等腰△ABC中，∠A<90°，AB=AC=BD=4，2∠D=∠ABD.若CD=1，则求BC的长.4.(2023.牡丹江26题)平行四边形ABCD中，AE⊥BC，垂足为E，连接DE，将ED绕点E逆时针旋转90°，得到EF，连接BF.（1）当点E在线段BC上，∠ABC=45°时，如图1，求证：AE+EC=BF；（2）当点E在线段BC延长线上，∠ABC=45°时，如图2，当点E在线段CB延长线上，∠ABC=135°时，如图3，请猜想并直接写出线段AE，EC,BF的数量关系；（3）在（1）、（2）的条件下，若BE=3，DE=5，则CE=______.5.（2023.贵州省25题）如图1，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°,过点B作射线BD⊥AB，垂足为B，点P在CB上.（1）【动手操作】如图2，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形，图中∠PBE的度数为______度；（2）【问题探究】根据（1）所画图形，探究线段PA与PE的数量关系，并说明理由；（3）【拓展延伸】如图3，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD将于点E，探究线段BA，BP，BE之间的数量关系，并说明理由.6.(2023.沈阳24题)如图1.在平行四边形纸片中，AB=10，AD=6，∠DAB=60°，点E为BC边上的一点（点E不与点C重合），连接AE，将平行四边形ABCD纸片沿AE所在直线折叠，点C，D的对应点分别为C`，D`，射线C`E与射线AD将于点F.（1）求证：AF=EF；（2）如图2，当EF⊥AF时，DF的长为______;（3）如图3，当CE=2时，过点F作FM⊥AE，垂足为点M，延长FM 交C`D`于点N，连接AN，EN，求△ANE的面积。

中考数学三角形全等证明习题50题

中考数学三角形全等证明习题50题第一篇：中考数学三角形全等证明习题50题探索三角形全等的条件练习题1、已知AD是⊿ABC的中线，BE⊥AD，CF⊥AD，问BE=CF吗？说明理由。

A BCB CC2、已知AC=BD，AE=CF，BE=DF，问AE∥CF吗？3、已知AB=CD，BE=DF，AE=CF，问AB∥CD吗？4、已知在四边形ABCD中，AB=CD，AD=CB，问AB∥CD吗？说明理由。

CEA5、已知∠BAC=∠DAE，∠1=∠2，BD=CE，问ABD≌⊿ACE.吗？为什么？6、已知CD∥AB，DF∥EB，DF=EB，问AF=CE吗？说明理由。

7、已知BE=CF，AB=CD，∠B=∠C.问AF=DE吗？D AB F M CBE B8、已知AD=CB，∠A=∠C，AE=CF，问EB∥DF吗？说明理由。

9、已知，M是AB的中点，∠1=∠2，MC=MD，问∠C=∠D吗？说明理由。

F D A BAA CC10、已知，AE=DF，BF=CE，AE∥DF，问AB=CD吗？说明理由。

11、已知∠1=∠2，∠3=∠4，问AC=AD吗？说明理由。

12、已知∠E=∠F，∠1=∠2，AB=CD，问AE=DF吗？说明理由。

13、已知ED⊥AB，EF⊥BC，BD=EF，问BM=ME吗？说明理由。

C EM E FA C D D14、在⊿ABC中，高AD与BE相交于点H，且AD=BD，问⊿BHD≌⊿ACD，为什么？15、已知∠A=∠D，AC∥FD，AC=FD，问AB∥DE吗？说明理由。

16、已知AC=AB，AE=AD，∠1=∠2，问∠3=∠4吗？A AF E EE D C DDB C17、已知EF∥BC，AF=CD，AB⊥BC，DE⊥EF，问⊿ABC≌⊿DEF吗？说明理由。

18、已知AD=AE，∠B=∠C，问AC=AB吗？说明理由。

19、已知AD⊥BC，BD=CD，问AB=AC吗？20、已知∠1=∠2，BC=AD，问⊿ABC≌⊿BAD吗？D A D B B C E21、已知AB=AC，∠1=∠2，AD=AE，问⊿ABD≌⊿ACE.说明理由。

中考数学精选汇编几何证明---13道题目(含答案)(优选.)

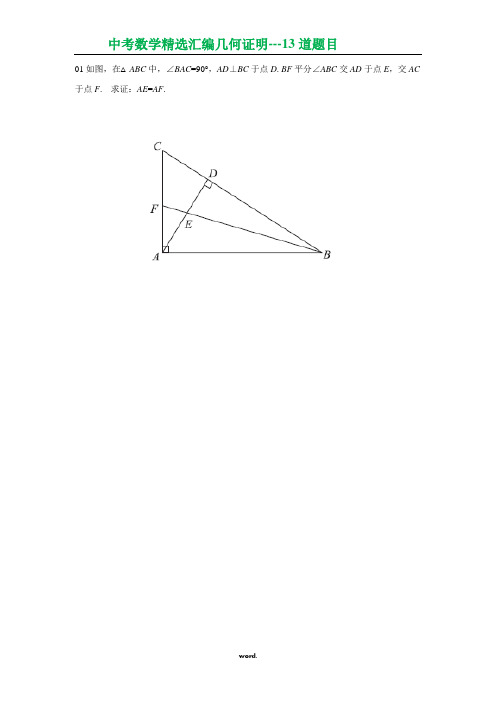
01如图，在△ABC中，∠BAC=90°，AD⊥BC于点D. BF平分∠ABC交AD于点E，交AC 于点F. 求证：AE=AF..证明：∵∠BAC=90°，∴∠FBA+∠AFB=90°.-------------------1分∵AD⊥BC，∴∠DBE+∠DEB=90°．---------------- 2分∵BE平分∠ABC,∴∠DBE=∠FBA. -------------------3分∴∠AFB=∠DEB.-------------------4分∵∠DEB=∠FEA，∴∠AFB=∠FEA.∴AE=AF.-------------------5分02如图，AD平分BAC∠，BD AD⊥于点D，AB的中点为E，AE AC<．（1）求证：DE AC∥．（2）点F在线段AC上运动，当AF AE=时，图中与ADF△全等的三角形是__________．ED CBA【解析】（1）证明：∵AD 平分BAC ∠， ∴12∠=∠， ∵BD AD ⊥于点D ， ∴90ADB ∠=︒， ∴ABD △为直角三角形． ∵AB 的中点为E ， ∴2AB AE =，2ABDE =， ∴DE AE =， ∴13∠=∠， ∴23∠=∠， ∴DE AC ∥．（2）ADE △．321ECBA03如图，△ABC 中，90ACB ∠=︒，D 为AB 的中点，连接CD ，过点B 作CD 的平行线EF ，求证：BC 平分ABF ∠．FE DCBA证明：∵90ACB ∠=︒，D 为AB 的中点，12CD AB BD==∴ABC DCB ∠=∠.…………… ∵DC EF ∥，∴CBF DCB ∠=∠.∴CBF ABC ∠=∠. ∴BC 平分ABF ∠.FE DCBA04如图，在△ABC中，AB = AC，D是BC边上的中点，DE⊥AB于点E，DF⊥AC于点F．求证：DE = DF．AEFBC证明：连接AD.∵AB＝BC，D是BC边上的中点，∴∠BAD=∠CAD. ………………………3分∵DE⊥AB于点E，DF⊥AC于点F，∴DE＝DF．………………………5分（其他证法相应给分）AE FB C05问题:将菱形的面积五等分．小红发现只要将菱形周长五等分，再将各分点与菱形的对角线交点连接即可解决问题．如图，点O 是菱形ABCD 的对角线交点，5AB =，下面是小红将菱形ABCD 面积五等分的操作与证明思路，请补充完整.（1）在AB 边上取点E ，使4AE =，连接OA ，OE ；（2）在BC 边上取点F ，使BF = ，连接OF ；（3）在CD 边上取点G ，使CG = ，连接OG ；（4）在DA 边上取点H ，使DH = ，连接OH ．由于AE = ＋ = ＋ = ＋ = . 可证S △AOE ==EOFB FOGC GOHD S S S ==四边形四边形四边形S △HOA .OH GFE DCBA解：3，2，1；………………2分EB、BF；FC、CG；GD、DH；HA.………………4分06如图，在△ACB中，AC=BC，AD为△ACB的高线，CE为△ACB的中线.求证：∠DAB=∠ACE.证明：∵AC＝BC，CE为△ACB的中线，∴∠CAB＝∠B，CE⊥AB.……………………………………………2分∴∠CAB＋∠ACE＝90°.………………………………………………3分∵AD为△ACB的高线，∴∠D＝90°.∴∠DAB＋∠B＝90°. ……………………………………………………4分∴∠DAB＝∠ACE. ………………………………………………………5分07文艺复兴时期，意大利艺术大师达．芬奇研究过用圆弧围成的部分图形的面积问题。

初三数学证明题试卷

一、选择题（每题5分，共25分）1. 已知三角形ABC中，∠A=90°，∠B=30°，则∠C的度数是：A. 60°B. 45°C. 30°D. 75°2. 在直角坐标系中，点A（2，3），点B（4，6），则线段AB的中点坐标是：A. （3，4）B. （5，4）C. （3，5）D. （5，6）3. 已知等腰三角形ABC中，AB=AC，∠B=40°，则∠C的度数是：A. 40°B. 50°C. 60°D. 70°4. 一个正方形的对角线长为8cm，则这个正方形的周长是：A. 16cmB. 24cmC. 32cmD. 40cm5. 在等腰三角形ABC中，若AB=AC，且∠B=50°，则∠A的度数是：A. 50°B. 60°C. 70°D. 80°二、填空题（每题5分，共25分）6. 已知等边三角形ABC的边长为a，则它的周长为______。

7. 在直角坐标系中，点P（-3，4），点Q（2，-1），则线段PQ的长度为______。

8. 在等腰三角形ABC中，AB=AC，若∠B=70°，则∠A的度数为______。

9. 一个圆的半径为r，则它的直径为______。

10. 在等腰梯形ABCD中，AD=BC，AB∥CD，若AB=6cm，CD=10cm，则梯形的高为______。

三、解答题（共50分）11. （10分）证明：等腰三角形的底角相等。

证明：已知等腰三角形ABC中，AB=AC。

要证明：∠B=∠C。

证明过程如下：由等腰三角形的定义，可知∠B=∠C。

因此，等腰三角形的底角相等。

12. （15分）已知：在三角形ABC中，AB=AC，D为BC的中点。

（1）证明：AD⊥BC；（2）若∠B=30°，求∠BAC的度数。

证明：（1）由等腰三角形的性质，可知∠B=∠C。

中考几何证明题及答案

中考几何证明题及答案几何证明练题及答案知识要点：1.掌握直角三角形的性质并能熟练应用；2.能写出较难证明的求证；3.证明要合乎逻辑，能应用综合法证明几何命题。

概念回顾：1.全等三角形的性质：对应边、对应角、对应高线、对应中线、对应角的角平分线。

2.在Rt△ABC中，∠C=90°，∠A=30°，则BC：AC：AB=？例题解析：题1：已知在ΔABC中，A=108°，AB=AC，BD平分ABC。

求证：___。

题2：如图，点E为正方形ABCD的边CD上一点，点F 为CB的延长线上的一点，且EA⊥AF。

求证：DE=BF。

题3：如图，AD为ΔABC的角平分线且BCBD=CD。

求证：AB=AC。

题4：已知：如图，点B、F、C、E在同一直线上，BF=CE，AB∥ED，AC∥FD，证明AB=DE，AC=DF。

题5：已知：如图，△ABC是正三角形，P是三角形内一点，PA=3，PB=4，PC=5.求∠APB的度数。

题6：如图：△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足是F，过B作BD⊥BC交CF的延长线于D。

1）求证：AE=CD；2）若AC=12 cm，求BD的长。

题7：等边三角形CEF于菱形ABCD边长相等。

求证：（1）∠AEF=∠AFE；（2）角B的度数。

题8：如图，在△ABC中，∠C=2∠B，AD是△ABC的角平分线，∠1=∠B。

求证：___。

题9：如图，在三角形ABC中，AD是BC边上的中线，E是AD的中点，BE的延长线交AC于点F。

求证：___。

题10：如图，将边长为1的正方形ABCD绕点C旋转到A'B'CD'的位置，若∠B'CB=30°，求AE的长。

题11：AD,BE分别是等边△ABC中BC,AC上的高。

M,N 分别在AD,BE的延长线上，∠___∠ACN。

求证：AM=BN。

题12：已知：如图，AD、BC相交于点O，OA=OD，OB=OC，点E、F在AD上，且AE=DF，∠ABE＝∠DCF。

中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道

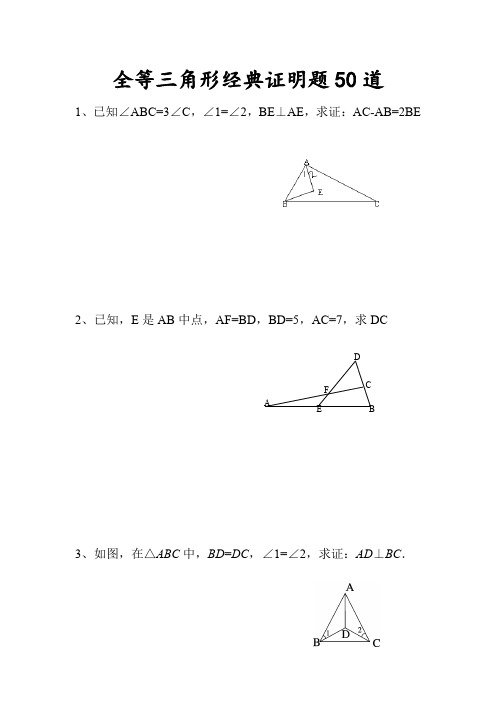
全等三角形经典证明题50道1、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE2、已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC3、如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ．FAEDC B4．如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA5．（5分）如图，已知AD∥BC，∠P AB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．PCEDBA6．（6分）如图①，E、F分别为线段AC上的两个动点，且DE ⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．7．已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点，（1）求证：△AED ≌△EBC ．（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：8．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．OEDCB AFE D CB A25、如图：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

证明：∵DF=CE ， ∵DF-EF=CE-EF ，即DE=CF ，在∵AED 和∵BFC 中，∵ AD=BC ， ∵D=∵C ，DE=CF ∵∵AED ∵∵BFC （SAS ）26、（10分）如图：AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

中考数学专项练习命题与证明(含解析)

中考数学专项练习命题与证明(含解析)本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March中考数学专项练习命题与证明（含解析）【一】单项选择题1.以下命题中正确的选项是〔〕A. 对角线相等的四边形是矩形B. 对角线互相垂直的四边形是菱形C. 对角线互相垂直平分且相等的四边形是正方形D. 一组对边相等，另一组对边平行的四边形是平行四边形2.以下四个命题：⑴数据5、2、﹣3、0的极差是8；⑵方差越大，说明数据就越稳定；⑶不在同一直线上的三点确定一个圆；⑷在半径为5的⊙O中，弦AB∥CD，且AB=6，CD=8，那么AB与CD之间距离为7其中真命题的个数为〔〕A. 4个B. 3个C. 2个D. 1个3.以下定理中，没有逆定理的是〔〕①内错角相等，两直线平行②等腰三角形两底角相等③对顶角相等④直角三角形的两个锐角互余．A. 1个B. 2个C. 3个D. 4个4.以下命题中，是假命题的是〔〕A. 平方根等于本身的数是B. 如果a，b都是无理数，那么a+b也一定是无理数C. 坐标平面内的点与有序实数对一一对应 D. 与6 可以合并同类项5.以下命题中，是真命题的是〔〕A. 有理数都是有限小数B. 同旁内角互补C. 函数y= 自变量x的取值范围是x≥3D. 假设甲、乙两组数据中各有20个数据，平均数= ，方差S 甲2=1.25，S乙2=0.96，那么说明乙组数据比甲组数据稳定6.下面说法正确的选项是( )A. 定理一定是命题B. 定理一定有逆定理C. 命题一定是定理 D. 逆命题一定正确7.以下命题是真命题的是〔〕A. 不相交的两条直线叫做平行线 B. 经过直线外一点，有且只有一条直线与直线平行C. 两直线平行，同旁内角相等 D. 两条直线被第三条直线所截，同位角相等8.以下命题为真命题的是〔〕A. 假设a2=b2 ，那么a=bB. 等角的补角相等C. n边形的外角和为〔n﹣2〕•180° D. 假设x甲= x乙， S2甲＞S2乙，那么甲数据更稳定【二】填空题9.指出以下命题的条件和结论，并改写成〝如果…，那么…〞的形式．〔1〕两直线平行，内错角相等；〔2〕三角形内角和等于180°．10.〝同位角相等〞的逆命题是________．11.请把命题〝对顶角相等。

中考数学证明题练习模拟试题

中考数学证明题练习模拟试题1. 选择题：在直角三角形ABC中，∠C=90°，AB=c，AC=b，BC=a，且a²+b²=c²。

如果a=3，b=4，那么c的值为？A. 5B. 6C. 7D. 82. 填空题：已知等腰三角形的底边长为8cm，两腰相等且各为5cm，求顶角的正弦值为____。

3. 简答题：证明勾股定理：在一个直角三角形中，两条直角边的平方和等于斜边的平方。

4. 计算题：在△ABC中，D是BC的中点，AD⊥BC，且AD=6cm，BC=12cm。

求△ABC的面积。

5. 选择题：下列哪个图形一定可以被分割成若干个全等的直角三角形？A. 正方形B. 长方形C. 平行四边形D. 菱形6. 填空题：若梯形的上底、下底、高分别为a、b、h，那么梯形的面积公式为____。

7. 简答题：证明：在一个三角形中，任意两边之和大于第三边。

8. 计算题：已知矩形的长为10cm，宽为6cm，求其对角线的长度。

9. 选择题：在等边三角形ABC中，点D在边BC上，且BD=DC，连接AD，那么∠BAD=？A. 30°B. 45°C. 60°D. 90°10. 填空题：正方形的对角线长度为10cm，则该正方形的面积为____平方厘米。

11. 简答题：证明：等腰三角形底边上的中线也是它的高。

12. 计算题：直角三角形的两直角边分别是3cm和4cm，求斜边上的高。

13. 选择题：在△ABC中，若∠A=∠B=∠C，则△ABC是？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等边三角形14. 填空题：若一个三角形的三边长分别为3, 4, 5单位长度，则此三角形的类型为____三角形。

15. 简答题：证明：平行四边形的对角线互相平分。

16. 计算题：梯形的上底为6cm，下底为10cm，高为8cm，求梯形的面积。

17. 选择题：在△ABC中，若∠A>∠B>∠C，且∠A+∠B+∠C=180°，则△ABC是？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形18. 填空题：正n边形的每个内角大小为____度（用n表示）。

初三数学证明题练习题

初三数学证明题练习题1. 设直角三角形ABC中，∠B = 90度。

则有结论：AB² + BC² = AC²。

证明：先证∠ACB = ∠ABC。

已知∠B = 90度，而直角三角形中，两个锐角互余。

所以∠ACB + ∠ABC = 90度，而直角三角形中，角之和为180度，所以∠ACB + ∠ABC + ∠B = 180度，即∠ACB + ∠ABC + 90度 = 180度，化简得∠ACB + ∠ABC = 90度，所以∠ACB = ∠ABC。

根据正弦定理，有sin∠ACB / BC = sin∠ABC / AC由于∠ACB = ∠ABC，所以sin∠ACB / BC = sin∠ACB / AC即BC / AC = sin∠ACB / sin∠ACB由于sin∠ACB ≠ 0，所以BC / AC = 1即BC = AC将BC代入AB² + BC² = AC²中，得AB² + AC² = AC²再次化简得AB² = 0由于AB是一条线段，所以长度不可能等于0，所以上述等式不成立。

综上所述，结论“AB² + BC² = AC²”不成立。

2. 设正方体ABCD-A'B'C'D'的边长为a，连接DD'并延长至交于点P。

证明：首先，观察正方体ABCD-A'B'C'D'的几何性质。

由于正方体的六个面都是正方形，所以对于任意两点A和B，有AB平行于正方体的某个棱长，并且AB = 2a，其中a是正方体边长。

同理，对于任意两点A'和B'，有A'B'平行于另一个棱长，并且A'B' = 2a。

在正方体ABCD-A'B'C'D'中，连接AP。

考虑四边形ABCP。

初中中考数学24题几何证明综合学习练习

每一个为梦想奋斗的日子，都值得被仰慕！综合练习【练习1】如图，AC是正方形ABCD 的对角线，点E为线段CB上一个动点（点E不与点C、B重合），连结AE，点F在直线AC上，且EF=AE。

（1）若∠BAE=10°，求∠CEF的度数；（（2）求证：2CECF2CD图难于其易为大于其细1【练习2】在菱形ABCD 中，∠ABC=60°，BD为菱形的一条对角线。

（1）如图1，过点 A作AE⊥BC于点E，交BD于点F，若EF=2，求菱形ABCD 的面积；（2）如图2，M为菱形ABCD 外一点，过A作AN⊥BM交BM的延伸线于点N，连结 AM，DM，AG⊥DM于点G，且∠AMN=∠AMD，求证：DM BM 3AM图难于其易为大于其细2【练习3】如图，在正方形ABCD 中，对角线AC、BD订交于点O，以AD为边向外作等边三角形ADE，连结CE，交BD于F。

（1）如图1，若AE 6，求DF的长；（2）如图2，点M为AB的延伸线上一点，连结CM，连结FM且FM均分∠AMC，求证：CM 3MF AM图难于其易为大于其细3【练习4】已知在平行四边形 ABCD中，点E为AB边上一点，过点E作EF⊥BC于点F。

（1）如图1，连结EC，若点E为AB中点，tanB 410，EC45，求平行四边形，AB3ABCD的面积；（2）如图2，作∠AEF的均分线交CD于点G，连结FG，若EGF2GFC，EGH为等边三角形，且FG⊥HG，求证：AE+BF=AG。

图难于其易为大于其细4每一个为梦想奋斗的日子，都值得被仰慕！【练习5】如图，四边形ABCD是平行四边形，连结对角线AC，AE⊥BC于点E，F为EA延伸线上一点，且BE=EF，连结CF。

1）如图1，若AB⊥AC，AB=4，AC=3，求AF的长度；（2）如图2，若CD⊥CF，求证：AD 2AC AF。

图1 图2图难于其易为大于其细5每一个为梦想奋斗的日子，都值得被仰慕！【练习6】如图，平行四边形 ABCD中，点O是对角线AC的中点，点M为BC上一点，连结AM，且AB=AM，AE为△ABM边BM的中线，AF⊥AB，EG⊥DG，延伸FO交AB于点N。

(完整版)中考数学-圆的切线证明综合试题

专题-------圆的切线证明我们学习了直线和圆的位置关系，就出现了新的一类习题，就是证明一直线是圆的切线.在我们所学的知识范围内，证明圆的切线常用的方法有：一、若直线l 过⊙O 上某一点A ，证明l 是⊙O 的切线，只需连OA ，证明OA⊥l 就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1 如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于D ，交AC 于E ，B 为切点的切线交OD 延长线于F.求证：EF 与⊙O 相切.证明：连结OE ，AD. ∵AB 是⊙O 的直径， ∴AD⊥BC. 又∵AB=BC， ∴∠3=∠4. ∴BD=DE，∠1=∠2. 又∵OB=OE，OF=OF ， ∴△BOF≌△EOF（SAS ）. ∴∠OBF=∠OEF. ∵BF 与⊙O 相切， ∴OB⊥BF. ∴∠OEF=900.∴EF 与⊙O 相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD 是∠BAC 的平分线，P 为BC 延长线上一点，且PA=PD.求证：PA 与⊙O 相切.证明一：作直径AE ，连结EC. ∵AD 是∠BAC 的平分线， ∴∠DAB=∠DAC.⌒⌒∵PA=PD， ∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB， ∴∠1=∠B. 又∵∠B=∠E， ∴∠1=∠E∵AE 是⊙O 的直径， ∴AC⊥EC，∠E+∠EAC=900. ∴∠1+∠EAC=900. 即OA⊥PA.∴PA 与⊙O 相切.证明二：延长AD 交⊙O 于E ，连结OA ，OE. ∵AD 是∠BAC 的平分线，∴BE=CE，∴OE⊥BC.∴∠E+∠BDE=900. ∵OA=OE， ∴∠E=∠1. ∵PA=PD， ∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA 与⊙O 相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用.例3 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM⊥AC 于M求证：DM 与⊙O 相切.证明一：连结OD. ∵AB=AC， ∴∠B=∠C.⌒⌒∵OB=OD，∴∠1=∠B.∴∠1=∠C. ∴OD∥AC. ∵DM⊥AC，∴DM⊥OD.∴DM 与⊙O 相切证明二：连结OD ，AD.∵AB 是⊙O 的直径，∴AD⊥BC.又∵AB=AC,∴∠1=∠2. ∵DM⊥AC，∴∠2+∠4=900∵OA=OD，∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM 是⊙O 的切线说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.例4 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上.求证：DC 是⊙O 的切线证明：连结OC 、BC.∵OA=OC，∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600. 又∵OC=OB，∴△OBC 是等边三角形.∴OB=BC.∵OB=BD， ∴OB=BC=BD. ∴OC⊥CD. ∴DC 是⊙O 的切线.说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好.例5 如图，AB 是⊙O 的直径，CD⊥AB，且OA 2=OD·OP.求证：PC 是⊙O 的切线.证明：连结OC∵OA 2=OD·OP ，OA=OC ， ∴OC 2=OD·OP ，.OCOPOD OC 又∵∠1=∠1， ∴△OCP∽△ODC. ∴∠OCP=∠ODC. ∵CD⊥AB， ∴∠OCP=900. ∴PC 是⊙O 的切线.说明：此题是通过证三角形相似证明垂直的例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.求证：CE 与△CFG 的外接圆相切.分析：此题图上没有画出△CFG 的外接圆，但△CFG 是直角三角形，圆心在斜边FG 的中点，为此我们取FG 的中点O ，连结OC ，证明CE⊥OC 即可得解.证明：取FG 中点O ，连结OC.∵ABCD 是正方形，∴BC⊥CD，△CFG 是Rt△∵O 是FG 的中点， ∴O 是Rt△CFG 的外心. ∵OC=OG， ∴∠3=∠G，∵AD∥BC，∴∠G=∠4.∵AD=CD，DE=DE，∠ADE=∠CDE=450，∴△ADE≌△CDE（SAS）∴∠4=∠1，∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵D F⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二：连结DE，AD，作DF⊥AC，F是垂足.∵AB与⊙D相切，∴DE⊥AB.∵AB=AC，BD=CD，∴∠1=∠2.∴DE=DF.∴F 在⊙D 上.∴AC 与⊙D 相切.说明：证明一是通过证明三角形全等证明DF=DE 的，证明二是利用角平分线的性质证明DF=DE 的，这类习题多数与角平分线有关.例8 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC∥BD，若∠COD=900.求证：CD 是⊙O 的切线.证明一：连结OA ，OB ，作OE⊥CD，E 为垂足.∵AC，BD 与⊙O 相切， ∴AC⊥OA，BD⊥OB. ∵AC∥BD，∴∠1+∠2+∠3+∠4=1800. ∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900. ∵∠4+∠5=900. ∴∠1=∠5.∴Rt△AOC∽Rt△BDO.∴.ODOCOB AC = ∵OA=OB， ∴.ODOCOA AC = 又∵∠CAO=∠COD=900， ∴△AOC∽△ODC，∴∠1=∠2.又∵OA⊥AC，OE⊥CD, ∴OE=OA. ∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明二：连结OA ，OB ，作OE⊥CD 于E ，延长DO 交CA 延长线于F.∵AC，BD 与⊙O 相切，O∵AC∥BD，∴∠F=∠BDO.又∵OA=OB，∴△AOF≌△BOD（AAS ）∴OF=OD.∵∠COD=900，∴CF=CD，∠1=∠2.又∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线.证明三：连结AO 并延长，作OE⊥CD 于E ，取CD 中点F ，连结OF.∵AC 与⊙O 相切，∴AC⊥AO.∵A C∥BD，∴AO⊥BD.∵BD 与⊙O 相切于B ，∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC∥BD，OA=OB ，CF=DF ，∴OF∥AC，∴∠1=∠COF.∵∠COD=900，CF=DF ，∴.CF CD OF ==21∴∠2=∠COF.∴∠1=∠2.∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.此题较难，需要同学们利用所学过的知识综合求解.以上介绍的是证明圆的切线常用的两种方法供同学们参考.以下是武汉市2007----2010中考题汇编：（2007中考）22．(本题8分)如图，等腰三角形ABC 中，AC ＝BC ＝10，AB ＝12。

初三数学证明题练习(3套)含答案

证明（一）一、选择题1. 下列句子中，不是命题的是（）（A ）三角形的内角和等于180度（B ）对顶角相等（C ）过一点作已知直线的平行线（D ）两点确定一条直线 2. 下列说法中正确的是（）（A ）两腰对应相等的两个等腰三角形全等（B ）两锐角对应相等的两个直角三角形全等（C ）两角及其夹边对应相等的两个三角形全等（D ）面积相等的两个三角形全等 3. 下列命题是假命题的是（）（A ）如果∥a b ，∥b c ，那么∥a c （B ）锐角三角形中最大的角一定大于或等于60° （C ）两条直线被第三条直线所截，内错角相等（D ）矩形的对角线相等且互相平分 4. △ABC 中，∠∠+=A B 120，∠∠=C A ，则△ABC 是（）．（A ）钝角三角形（B ）等腰直角三角形（C ）直角三角形（D ）等边三角形5. 在△ABC 中，∠A ，∠B 的外角分别是120°、150°，则∠=C （）．（A ）120°（B ）150°（C ）60°（D ）90°6．如图1，l 1∥l 2，∠1=50°, 则∠2的度数是（）（A ）135° （B ）130° （C ）50° （D ）40° 7．如图2所示，不能推出∥AD BC 的是（）（A ）∠∠+=DAB ABC 180 （B ）∠∠=24（C ）∠∠=13 （D ）∠∠=CBE DAE8. 如图3，∥a b ，⊥c a ，∠=1130，则∠2等于（）（A ）30°（B ）40°（C ）50°（D ）60°9. 如图4，∥AB CD ，⊥AC BC ，图中与∠CAB 互余的角有（）1（A ）1个（B ）2个（C ）3个（D ）4个10．若三角形的一个外角等于和它相邻的内角，则这个三角形是（）（A ）锐角三角形（B ）直角三角形（C ）钝角三角形（D ）都有可能二、填空题11．将命题“对顶角相等”改写成“如果……，那么……”的形式：如果，那么．12．如图5所示，如果BD 平分∠ABC ，补上一个条件作为已知，就能推出∥AB CD ．13．如图6，∥AB CD ，AF 交AB 、CD 于，A C ，CE 平分∠DCF ，∠=1120，则∠=2 ．14. 如图7，一个顶角为40°的等腰三角形纸片，剪去顶角后，得到一个四边形，则∠∠+=12 ．15. 若一个三角形的三个内角之比为4∶3∶2，则这个三角形的最大内角的外角为．三、解答题16. 如图8，直线AB 、CD 相交与点O ，∠AOD =70º，OE 平分∠BOC ，求∠DOE 的度数。

2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)

2024年中考数学复习重难点题型训练—简单几何证明题（含答案解析）类型一三角形全等1.(2022·西藏)如图，已知AD平分∠BAC，AB=AC.求证：△ABD≌△ACD．【答案】证明：∵AD平分∠BAC，∴∠BAD=∠CAD，在△ABD和△ACD中，AB=AC∠BAD=∠CADAD=AD，∴△ABD≌△ACD(SAS)．2.(2022·湖南省益阳市)如图，在Rt△ABC中，∠B=90°，CD//AB，DE⊥AC于点E，且CE=AB.求证：△CED≌△ABC．【答案】证明：∵DE⊥AC，∠B=90°，∴∠DEC =∠B =90°，∵CD//AB ，∴∠A =∠DCE ，在△CED 和△ABC 中，∠DCE =∠A CE =AB ∠DEC =∠B ，∴△CED≌△ABC(ASA)．3.(2022·江苏省南通市)如图，AC 和BD 相交于点O ，OA =OC ，OB =OD ．(1)求证：∠A =∠C ；(2)求证：AB//CD ．【答案】证明：(1)在△AOB 和△COD 中，OA =OC ∠AOB =∠COD OB =OD ,∴△AOB≌△COD(SAS)，∴∠A =∠C ；(2)由(1)得∠A =∠C ，∴AB//CD ．4.(2022·上海市)如图所示，在等腰三角形ABC 中，AB =AC ，点E ，F 在线段BC 上，点Q 在线段AB 上，且CF =BE ，AE 2=AQ ⋅AB ．求证：(1)∠CAE =∠BAF ；(2)CF ⋅FQ =AF ⋅BQ ．【答案】证明：(1)∵AB=AC，∴∠B=∠C，∵CF=BE，∴CF−EF=BE−EF，即CE=BF，在△ACE和△ABF中，AC=AB∠C=∠BCE=BF，∴△ACE≌△ABF(SAS)，∴∠CAE=∠BAF；(2)∵△ACE≌△ABF，∴AE=AF，∠CAE=∠BAF，∵AE2=AQ⋅AB，AC=AB，∴AE AQ=AC AF，∴△ACE∽AFQ，∴∠AEC=∠AQF，∴∠AEF=∠BQF，∵AE=AF，∴∠AEF=∠AFE，∴∠BQF=∠AFE，∵∠B=∠C，∴△CAF∽△BFQ，∴CF BQ=AF FQ，即CF⋅FQ=AF⋅BQ．5.(2022·贵州省铜仁市)如图，点C在BD上，AB⊥BD，ED⊥BD，AC⊥CE，AB=CD.求证：△ABC≌△CDE．【答案】证明：∵AB⊥BD，ED⊥BD，AC⊥CE，∴∠B=∠D=∠ACE=90°，∴∠DCE+∠DEC=90°，∠BCA+∠DCE=90°，∴∠BCA=∠DEC，在△ABC和△CDE中，∠BCA=∠DEC∠B=∠DAB=CD，∴△ABC≌△CDE(AAS)．6.(2022·广东省云浮市)如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E.求证：△OPD≌△OPE．【答案】证明：∵∠AOC=∠BOC，PD⊥OA，PE⊥OB，∴PD=PE，在Rt△OPD和Rt△OPE中，OP=OPPD=PE，∴Rt△OPD≌Rt△OPE(HL)．7.(2022·四川省宜宾市)已知：如图，点A、D、C、F在同一直线上，AB//DE，∠B=∠E，BC=EF.求证：AD=CF．【答案】证明：∵AB//DE，∴∠A=∠EDF．在△ABC和△DEF中，∠A=∠EDF∠B=∠EBC=EF，∴△ABC≌△DEF(AAS)．∴AC=DF，∴AC−DC=DF−DC，即：AD=CF．8.(2022·陕西省)如图，在△ABC中，点D在边BC上，CD=AB，DE//AB，∠DCE=∠A.求证：DE=BC．【答案】.证明：∵DE//AB，∴∠EDC=∠B，在△CDE和△ABC中，∠EDC=∠BCD=AB∠DCE=∠A，∴△CDE≌△ABC(ASA)，∴DE=BC．9.(2022·湖南省衡阳市)如图，在△ABC中，AB=AC，D、E是BC边上的点，且BD=CE.求证：AD=AE．【答案】证明：∵AB=AC，∴∠B=∠C，在△ABD和△ACE中，AB=AC∠B=∠CBD=CE，∴△ABD≌△ACE(SAS)，∴AD=AE．10.(2022·四川省乐山市)如图，B是线段AC的中点，AD//BE，BD//CE.求证：△ABD≌△BCE．【答案】证明：∵点B为线段AC的中点，∴AB=BC，∵AD//BE，∴∠A =∠EBC ，∵BD//CE ，∴∠C =∠DBA ，在△ABD 与△BCE 中，∠A =∠EBC AB =BC ∠DBA =∠C ，∴△ABD≌△BCE.(ASA)．11.（2021·湖南衡阳市·中考真题）如图，点A 、B 、D 、E 在同一条直线上，,//,//AB DE AC DFBC EF =．求证：ABC DEF △≌△．【答案】见解析【分析】根据//,//AC DF BC EF ，可以得到,A FDE ABC DEF ∠=∠∠=∠，然后根据题目中的条件，利用ASA 证明△ABC ≌△DEF 即可．【详解】证明：点A ，B ，C ，D ，E 在一条直线上∵//,//AC DF BC EF∴,A FDE ABC DEF∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△【点睛】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS 、ASA 、SAS 、SSS ，直角三角形可用HL 定理，但AAA 、SSA ，无法证明三角形全等，本题是一道较为简单的题目．12.（2021·四川乐山市·中考真题）如图，已知AB DC =，A D ∠=∠，AC 与DB 相交于点O ，求证：OBC OCB ∠=∠．【答案】证明见解析【分析】根据全等三角形的性质，通过证明ABO DCO △≌△，得OB OC =，结合等腰三角形的性质，即可得到答案．【详解】∵A D AOB DOC AB DC ∠=∠∠=∠=⎧⎪⎨⎪⎩，∴ABO DCO △≌△（AAS ），∴OB OC =，∴OBC OCB ∠=∠．【点睛】本题考查了全等三角形、等腰三角形的知识；解题的关键是熟练掌握全等三角形、等腰三角形的性质，从而完成求解．13.（2021·四川泸州市·中考真题）如图，点D 在AB 上，点E 在AC 上，AB=AC ，∠B=∠C ，求证：BD=CE【答案】证明见详解．【分析】根据“ASA”证明△ABE ≌△ACD ，然后根据全等三角形的对应边相等即可得到结论.【详解】证明：在△ABE 和△ACD 中，∵A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩,△ABE ≌△ACD (ASA)，∴AE=AD ，∴BD=AB–AD=AC-AE=CE ．【点睛】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．14.（2021·云南中考真题）如图，在四边形ABCD 中，,,AD BC AC BD AC ==与BD 相交于点E ．求证：DAC CBD ∠=∠．【答案】见解析【分析】直接利用SSS 证明△ACD ≌△BDC ，即可证明．【详解】解：在△ACD 和△BDC 中，AD BC AC BD CD DC =⎧⎪=⎨⎪=⎩，∴△ACD ≌△BDC （SSS ），∴∠DAC=∠CBD ．【点睛】本题考查了全等三角形的判定和性质，解题的关键是根据题意灵活运用SSS 的方法．15.（2020•菏泽）如图，在△ABC 中，∠ACB ＝90°，点E 在AC 的延长线上，ED ⊥AB 于点D ，若BC ＝ED ，求证：CE ＝DB．【分析】由“AAS ”可证△ABC ≌△AED ，可得AE ＝AB ，AC ＝AD ，由线段的和差关系可得结论．【解答】证明：∵ED ⊥AB ，∴∠ADE ＝∠ACB ＝90°，∠A ＝∠A ，BC ＝DE ，∴△ABC ≌△AED （AAS ），∴AE ＝AB ，AC ＝AD ，∴CE ＝BD ．16.（2020•南充）如图，点C 在线段BD 上，且AB ⊥BD ，DE ⊥BD ，AC ⊥CE ，BC ＝DE ．求证：AB ＝CD ．【分析】证明△ABC≌△CDE（ASA），可得出结论．【解答】证明：∵AB⊥BD，ED⊥BD，AC⊥CE，∴∠ACE＝∠ABC＝∠CDE＝90°，∴∠ACB+∠ECD＝90°，∠ECD+∠CED＝90°，∴∠ACB＝∠CED．在△ABC和△CDE中，∠ACB=∠CEDBC=DE∠ABC=∠CDE，∴△ABC≌△CDE（ASA），∴AB＝CD．17.（2020•硚口区模拟）如图，点D在AB上，点E在AC上，AB＝AC，∠B＝∠C，求证：BD＝CE．【分析】要证BD＝CE只要证明AD＝AE即可，而证明△ABE≌△ACD，则可得AD＝AE．【解答】证明：在△ABE与△ACD中∠A=∠AAB=AC∠B=∠C，∴△ABE≌△ACD．∴AD ＝AE ．∴BD ＝CE ．18.（2020•铜仁市）如图，∠B ＝∠E ，BF ＝EC ，AC ∥DF ．求证：△ABC ≌△DEF ．【分析】首先利用平行线的性质得出∠ACB ＝∠DFE ，进而利用全等三角形的判定定理ASA ，进而得出答案．【解答】证明：∵AC ∥DF ，∴∠ACB ＝∠DFE ，∵BF ＝CE ，∴BC ＝EF ，在△ABC 和△DEF 中，∠B =∠E BC =EF ∠ACB =∠DFE ，∴△ABC ≌△DEF （ASA ）．19.（2020•无锡）如图，已知AB ∥CD ，AB ＝CD ，BE ＝CF ．求证：（1）△ABF ≌△DCE ；（2）AF ∥DE ．【分析】（1）先由平行线的性质得∠B ＝∠C ，从而利用SAS 判定△ABF ≌△DCE ；（2）根据全等三角形的性质得∠AFB ＝∠DEC ，由等角的补角相等可得∠AFE ＝∠DEF ，再由平行线的判定可得结论．【解答】证明：（1）∵AB ∥CD ，∴∠B ＝∠C ，∵BE ＝CF ，∴BE ﹣EF ＝CF ﹣EF ，即BF ＝CE ，在△ABF 和△DCE 中，∵AB =CD ∠B =∠C BF =CE ，∴△ABF ≌△DCE （SAS ）；（2）∵△ABF ≌△DCE ，∴∠AFB ＝∠DEC ，∴∠AFE ＝∠DEF ，∴AF ∥DE ．20.（2020•台州）如图，已知AB ＝AC ，AD ＝AE ，BD 和CE 相交于点O ．（1）求证：△ABD ≌△ACE ；（2）判断△BOC 的形状，并说明理由．【分析】（1）由“SAS ”可证△ABD ≌△ACE ；（2）由全等三角形的性质可得∠ABD ＝∠ACE ，由等腰三角形的性质可得∠ABC ＝∠ACB ，可求∠OBC＝∠OCB，可得BO＝CO，即可得结论．【解答】证明：（1）∵AB＝AC，∠BAD＝∠CAE，AD＝AE，∴△ABD≌△ACE（SAS）；（2）△BOC是等腰三角形，理由如下：∵△ABD≌△ACE，∴∠ABD＝∠ACE，∵AB＝AC，∴∠ABC＝∠ACB，∴∠ABC﹣∠ABD＝∠ACB﹣∠ACE，∴∠OBC＝∠OCB，∴BO＝CO，∴△BOC是等腰三角形．21.如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．（1）求证：AB＝CD；（2）若AB＝CF，∠B＝40°，求∠D的度数．【分析】（1）根据平行线的性质求出∠B＝∠C，根据AAS推出△ABE≌△DCF，根据全等三角形的性质得出即可；（2）根据全等得出AB＝CD，BE＝CF，∠B＝∠C，求出CF＝CD，推出∠D＝∠CFD，即可求出答案．【解答】（1）证明：∵AB∥CD，∴∠B＝∠C，在△ABE和△DCF中，∠A=∠D∠B=∠CAE=DF，∴△ABE≌△DCF（AAS），∴AB＝CD；（2）解：∵△ABE≌△DCF，∴AB＝CD，BE＝CF，∠B＝∠C，∵∠B＝40°，∴∠C＝40°∵AB＝CF，∴CF＝CD，∴∠D＝∠CFD=12×（180°﹣40°）＝70°．类型二特殊四边形判定及性质22.(2022·广西壮族自治区河池市)如图，点A，F，C，D在同一直线上，AB=DE，AF=CD，BC=EF．(1)求证：∠ACB=∠DFE；(2)连接BF，CE，直接判断四边形BFEC的形状．【答案】(1)证明：∵AF=CD，∴AF+CF=CD+CF，即AC=DF，在△ABC和△DEF中，AB=DEBC=EFAC=DF，∴△ABC≌△DEF(SSS)，∴∠ACB=∠DFE；(2)解：如图，四边形BFEC是平行四边形，理由如下：由(1)可知，∠ACB=∠DFE，∴BC//EF，又∵BC=EF，∴四边形BFEC是平行四边形．23.(2022·青海省西宁市)如图，四边形ABCD是菱形，AE⊥BC于点E，AF⊥CD于点F．(1)求证：△ABE≌△ADF；(2)若AE=4，CF=2，求菱形的边长．【答案】(1)证明：∵四边形ABCD 是菱形，∴AB =BC =CD =AD ，∠B =∠D ，∵AE ⊥BC ，AF ⊥CD ，∴∠AEB =∠AFD ，在△ABE 和△ADF 中，∠AEB =∠AFD ∠B =∠D AB =AD ，∴△ABE≌△ADF(AAS)；(2)解：设菱形的边长为x ，∵AB =CD =x ，CF =2，∴DF =x −2，∵△ABE≌△ADF ，∴BE =DF =x −2，在Rt △ABE 中，根据勾股定理得，AE 2+BE 2=AB 2，即42+(x −2)2=x 2，解得x =5，∴菱形的边长是5．24.(2022·江苏省无锡市)如图，已知四边形ABCD为矩形，AB=22，BC=4，点E在BC 上，CE=AE，将△ABC沿AC翻折到△AFC，连接EF．(1)求EF的长；(2)求sin∠CEF的值．【答案】解：(1)∵CE=AE，∴∠ECA=∠EAC，根据翻折可得：∠ECA=∠FCA，∠BAC=∠CAF，∵四边形ABCD是矩形，∴DA//CB，∴∠ECA=∠CAD，∴∠EAC=∠CAD，∴∠DAF=∠BAE，∵∠BAD=90°，∴∠EAF=90°，设CE=AE=x，则BE=4−x，在△BAE中，根据勾股定理可得：BA2+BE2=AE2，即：(22)2+(4−x)2= x2，解得：x=3，在Rt△EAF中，EF=AF2+AE2=17．(2)过点F作FG⊥BC交BC于点G，设CG=x，则GB=3−x，∵FC=4，FE=17，∴FG2=FC2−CG2=FE2−EG2，即：16−x2=17−(3−x)2，解得：x=43，∴FG=FC2−CG2∴sin∠CEF=FG EF=25.(2022·湖北省荆门市)如图，已知矩形ABCD中，AB=8，BC=x(0<x<8)，将△ACB 沿AC对折到△ACE的位置，AE和CD交于点F．(1)求证：△CEF≌△ADF；(2)求tan∠DAF的值(用含x的式子表示)．【答案】(1)证明：∵四边形ABCD是矩形，∴∠B=∠D=90°，BC=AD，根据折叠的性质得：BC=CE，∠E=∠B=90°，∴∠E=∠D=90°，AD=CE，在△CEF与△ADF中，∠ CFE=∠AFD∠D=∠E=90°AD=CE，∴△CEF≌△ADF(AAS)；(2)解：设DF=a，则CF=8−a，∵四边形ABCD是矩形，∴AB//CD，AD=BC=x，∴∠DCA=∠BAC，根据折叠的性质得：∠EAC=∠BAC，∴∠DCA=∠EAC，∴AF=CF=8−a，在Rt△ADF中，∵AD2+DF2=AF2，∴x2+a2=(8−a)2，∴a=64−x216，∴tan∠DAF=DF AD=64−x216x．26.(2022·四川省遂宁市)如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是AD的中点，连接OE，过点D作DF//AC交OE的延长线于点F，连接AF．(1)求证：△AOE≌△DFE；(2)判定四边形AODF的形状并说明理由．【答案】(1)证明：∵E是AD的中点，∴AE=DE，∵DF//AC，∴∠OAD=∠ADF，∵∠AEO=∠DEF，∴△AOE≌△DFE(ASA)．(2)解：四边形AODF为矩形．理由：∵△AOE≌△DFE，∴AO=DF，∵DF//AC，∴四边形AODF为平行四边形，∵四边形ABCD为菱形，∴AC⊥BD，即∠AOD=90°，∴平行四边形AODF为矩形．27.(2022·湖北省)如图，已知E、F分别是▱ABCD的边BC，AD上的点，且BE=DF(1)求证：四边形AECF是平行四边形；(2)若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长．【答案】(1)证明：∵四边形ABCD是平行四边形，∴AD//BC，且AD=BC，∴AF//EC，∵BE=DF，∴AF=EC，∴四边形AECF是平行四边形；(2)如图所示：∵四边形AECF是菱形，∴AE=EC，∴∠1=∠2，∵∠3=90°−∠2，∠4=90°−∠1，∴∠3=∠4，∴AE=BE，∴BE=AE=CE=12BC=5．28.(2022·云南省)如图，在平行四边形ABCD中，连接BD，E为线段AD的中点，延长BE 与CD的延长线交于点F，连接AF，∠BDF=90°．(1)求证：四边形ABDF是矩形；(2)若AD=5，DF=3，求四边形ABCF的面积S．【答案】.(1)证明：∵四边形ABCD是平行四边形，∴BA//CD，∴∠BAE=∠FDE，∵点E是AD的中点，∴AE=DE，在△BEA和△FED中，∠BAE=∠FDEAE=DE∠BEA=∠FED，∴△BEA≌△FED(ASA)，∴EF=EB，又∵AE=DE，∴四边形ABDF是平行四边形，∵∠BDF=90°．∴四边形ABDF是矩形；(2)解：由(1)得四边形ABDF是矩形，∴∠AFD=90°，AB=DF=3，AF=BD，∴AF=AD2−DF2=52−32=4，∴S矩形ABDF=DF⋅AF=3×4=12，BD=AF=4，∵四边形ABCD是平行四边形，∴CD=AB=3，∴S△BCD=12BD⋅CD=12×4×3=6，∴四边形ABCF的面积S=S矩形ABDF+S△BCD=12+6=18，答：四边形ABCF的面积S为18．29.(2022·广西壮族自治区河池市)如图，点A，F，C，D在同一直线上，AB=DE，AF=CD，BC=EF．(1)求证：∠ACB=∠DFE；(2)连接BF，CE，直接判断四边形BFEC的形状．【答案】(1)证明：∵AF=CD，∴AF+CF=CD+CF，即AC=DF，在△ABC和△DEF中，AB=DEBC=EFAC=DF，∴△ABC≌△DEF(SSS)，∴∠ACB=∠DFE；(2)解：如图，四边形BFEC是平行四边形，理由如下：由(1)可知，∠ACB=∠DFE，∴BC//EF，又∵BC=EF，∴四边形BFEC是平行四边形．30.(2022·湖南省郴州市)如图，四边形ABCD是菱形，E，F是对角线AC上的两点，且AE=CF，连接BF，FD，DE，EB.求证：四边形DEBF是菱形．【答案】证明：∵四边形ABCD是菱形，∴AB=BC=CD=AD，∠DAB=∠DCB，AC平分∠DAB，AC平分∠DCB，∴∠DAC=∠BAC=12∠DAB，∠DCA=∠ACB=12∠DCB，∴∠DAC=∠BAC=∠DCA=∠ACB，∵AE=CF，∴△DAE≌△BAE≌△BCF≌△DCF(SAS)，∴DE=BE=BF=DF，∴四边形DEBF是菱形．31.(2022·山东省聊城市)如图，△ABC中，点D是AB上一点，点E是AC的中点，过点C 作CF//AB，交DE的延长线于点F．(1)求证：AD=CF；(2)连接AF，CD.如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF 是菱形，证明你的结论．【答案】(1)证明：∵CF//AB，∴∠ADF=∠CFD，∠DAC=∠FCA，∵点E是AC的中点，∴AE=CE，∴△ADE≌△CFE(AAS)，∴AD=CF；(2)解：当AC⊥BC时，四边形ADCF是菱形，证明如下：由(1)知，AD=CF，∵AD//CF，∴四边形ADCF是平行四边形，∵AC⊥BC，∴△ABC是直角三角形，∵点D是AB的中点，∴CD=12AB=AD，∴四边形ADCF是菱形．32.(2022·北京市)如图，在▱ABCD中，AC，BD交于点O，点E，F在AC上，AE=CF．(1)求证：四边形EBFD是平行四边形；(2)若∠BAC=∠DAC，求证：四边形EBFD是菱形．【答案】证明：(1)在▱ABCD中，OA=OC，OB=OD，∵AE=CF．∴OE=OF，∴四边形EBFD是平行四边形；(2)∵四边形ABCD是平行四边形，∴AB//DC，∴∠BAC=∠DCA，∵∠BAC=∠DAC，∴∠DCA=∠DAC，∴DA=DC，∵OA=OC，∴DB⊥EF，∴平行四边形EBFD是菱形．33.(2022·湖南省张家界市)如图，菱形ABCD的对角线AC、BD相交于点O，点E是CD的中点，连接OE，过点C作CF//BD交OE的延长线于点F，连接DF．(1)求证：△ODE≌△FCE；(2)试判断四边形ODFC的形状，并写出证明过程．【答案】.(1)证明：∵点E是CD的中点，∴CE=DE，又∵CF//BD∴∠ODE=∠FCE，在△ODE和△FCE中，∠ODE=∠FCEDE=CE∠DEO=∠CEF，∴△ODE≌△FCE(ASA)；(2)解：四边形ODFC为矩形，证明如下：∵△ODE≌△FCE，∴OE=FE，又∵CE=DE，∴四边形ODFC为平行四边形，又∵四边形ABCD为菱形，∴AC⊥BD，即∠DOC=90°，∴四边形ODFC为矩形．34.(2022·四川省内江市)如图，在▱ABCD中，点E、F在对角线BD上，且BE=DF．求证：(1)△ABE≌△CDF；(2)四边形AECF是平行四边形．【答案】证明：(1)∵四边形ABCD为平行四边形，∴AB=CD，AB//CD，∴∠ABD=∠CDB，在△ABE和△CDF中，AB=CD∠ABE=∠CDFBE=DF，∴△ABE≌△CDF(SAS)；(2)由(1)可知，△ABE≌△CDF，∴AE=CF，∠AEB=∠CFD，∴180°−∠AEB=180°−∠CFD，即∠AEF=∠CFE，∴AE//CF，∵AE=CF，AE//CF，∴四边形AECF是平行四边形．35.(2022·湖南省长沙市)如图，在▱ABCD中，对角线AC，BD相交于点O，AB=AD．(1)求证：AC⊥BD；(2)若点E，F分别为AD，AO的中点，连接EF，EF=32，AO=2，求BD的长及四边形ABCD 的周长．【答案】(1)证明：∵四边形ABCD是平行四边形，AB=AD，∴▱ABCD是菱形，∴AC⊥BD；(2)解：∵点E，F分别为AD，AO的中点，∴EF是△AOD的中位线，∴OD=2EF=3，由(1)可知，四边形ABCD是菱形，∴AB=BC=CD=AD，AC⊥BD，BD=2OD=6，在Rt△AOD中，由勾股定理得：AD=AO2+OD2=22+32=13，∴菱形ABCD的周长=4AD=41336.（2021·四川广安市·中考真题）如图，四边形ABCD是菱形，点E、F分别在边AB、AD=．连接CE、CF．的延长线上，且BE DF求证：CE CF=．【答案】见解析【分析】根据菱形的性质得到BC=CD，∠ADC=∠ABC，根据SAS证明△BEC≌△DFC，可得CE=CF．【详解】解：∵四边形ABCD 是菱形，∴BC=CD ，∠ADC=∠ABC ，∴∠CDF=∠CBE ，在△BEC 和△DFC 中，BE DF CBE CDF BC CD =⎧⎪∠=∠⎨⎪=⎩，∴△BEC ≌△DFC （SAS ），∴CE=CF ．【点睛】本题考查了菱形的性质，全等三角形的判定和性质，解题的关键是根据菱形得到判定全等的条件．37.（2021·江苏扬州市·中考真题）如图，在ABC 中，BAC ∠的角平分线交BC 于点D ，//,//DE AB DF AC．（1）试判断四边形AFDE 的形状，并说明理由；（2）若90BAC ∠=︒，且AD =，求四边形AFDE 的面积．【答案】（1）菱形，理由见解析；（2）4【分析】（1）根据DE ∥AB ，DF ∥AC 判定四边形AFDE 是平行四边形，再根据平行线的性质和角平分线的定义得到∠EDA=∠EAD ，可得AE=DE ，即可证明；（2）根据∠BAC=90°得到菱形AFDE是正方形，根据对角线AD求出边长，再根据面积公式计算即可．【详解】解：（1）四边形AFDE是菱形，理由是：∵DE∥AB，DF∥AC，∴四边形AFDE是平行四边形，∵AD平分∠BAC，∴∠FAD=∠EAD，∵DE∥AB，∴∠EDA=∠FAD，∴∠EDA=∠EAD，∴AE=DE，∴平行四边形AFDE是菱形；（2）∵∠BAC=90°，∴四边形AFDE是正方形，∵AD=，=2，∴∴四边形AFDE的面积为2×2=4．【点睛】本题考查了菱形的判定，正方形的判定和性质，平行线的性质，角平分线的定义，解题的关键是掌握特殊四边形的判定方法．38.（2021·江苏连云港市·中考真题）如图，点C是BE的中点，四边形ABCD是平行四边形．（1）求证：四边形ACED是平行四边形；，求证：四边形ACED是矩形．（2）如果AB AE【答案】（1）见解析；（2）见解析【分析】（1）由平行四边形的性质以及点C是BE的中点，得到AD∥CE，AD=CE，从而证明四边形ACED是平行四边形；（2）由平行四边形的性质证得DC=AE，从而证明平行四边形ACED是矩形．【详解】证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC，且AD=BC．∵点C是BE的中点，∴BC=CE，∴AD=CE，∵AD∥CE，∴四边形ACED是平行四边形；（2）∵四边形ABCD是平行四边形，∴AB=DC，∵AB=AE，∴DC=AE，∵四边形ACED是平行四边形，∴四边形ACED是矩形．【点睛】本题考查了平行四边形和矩形的判定和性质，正确的识别图形是解题的关键．39.（2021·四川遂宁市·中考真题）如图，在平行四边形ABCD 中，对角线AC 与BD 相交于点O ，过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F ．（1）求证：AE ＝CF ；（2）请再添加一个条件，使四边形BFDE是菱形，并说明理由．【答案】（1）见解析；（2）EF ⊥BD 或EB ＝ED ，见解析【分析】（1）根据平行四边形的性质和全等三角形的证明方法证明AOE COF V V ≌，则可得到AE ＝CF ；（2）连接BF ，DE ，由AOE COF V V ≌，得到OE=OF ，又AO=CO ，所以四边形AECF 是平行四边形，则根据EF ⊥BD 可得四边形BFDE 是菱形．【详解】证明：（1）∵四边形ABCD 是平行四边形∴OA ＝OC ，BE ∥DF∴∠E ＝∠F在△AOE 和△COF 中E F AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴AOE COF V V ≌()AAS ∴AE ＝CF（2）当EF ⊥BD 时，四边形BFDE 是菱形，理由如下：如图：连结BF ，DE∵四边形ABCD 是平行四边形∴OB ＝OD∵AOE COFV V ≌∴OE OF=∴四边形BFDE 是平行四边形∵EF ⊥BD ，∴四边形BFDE 是菱形【点睛】本题主要考查了全等三角形的性质与判定、平行四边形的性质，菱形的判定等知识点，熟悉相关性质，能全等三角形的性质解决问题是解题的关键．40（2020•黄冈）已知：如图，在▱ABCD 中，点O 是CD 的中点，连接AO 并延长，交BC 的延长线于点E ，求证：AD ＝CE ．【分析】只要证明△AOD≌△EOC（ASA）即可解决问题；【解答】证明：∵O是CD的中点，∴OD＝CO，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D＝∠OCE，在△ADO和△ECO中，∠D=∠OCEOD=OC∠AOD=∠EOC，∴△AOD≌△EOC（ASA），∴AD＝CE．41.（2020•扬州）如图，▱ABCD的对角线AC、BD相交于点O，过点O作EF⊥AC，分别交AB、DC于点E、F，连接AF、CE．（1）若OE=32，求EF的长；（2）判断四边形AECF的形状，并说明理由．【分析】（1）判定△AOE≌△COF（ASA），即可得OE＝OF=32，进而得出EF的长；（2）先判定四边形AECF是平行四边形，再根据EF⊥AC，即可得到四边形AECF是菱形．【解析】（1）∵四边形ABCD是平行四边形，∴AB∥CD，AO＝CO，∴∠FCO＝∠EAO，又∵∠AOE＝∠COF，∴△AOE≌△COF（ASA），∴OE＝OF=32，∴EF＝2OE＝3；（2）四边形AECF是菱形，理由：∵△AOE≌△COF，∴AE＝CF，又∵AE∥CF，∴四边形AECF是平行四边形，又∵EF⊥AC，∴四边形AECF是菱形．42.（2020•青岛）如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF．（1）求证：△ADE≌△CBF；（2）连接AF，CE．当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．【分析】（1）根据四边形ABCD是平行四边形，可以得到AD＝CB，∠ADC＝∠CBA，从而可以得到∠ADE＝∠CBF，然后根据SAS即可证明结论成立；（2）根据BD平分∠ABC和平行四边形的性质，可以证明▱ABCD是菱形，从而可以得到AC ⊥BD，然后即可得到AC⊥EF，再根据题目中的条件，可以证明四边形AFCE是平行四边形，然后根据AC⊥EF，即可得到四边形AFCE是菱形．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD＝CB，∠ADC＝∠CBA，∴∠ADE＝∠CBF，在△ADE和△CBF中，AD=CB∠ADE=∠CBFDE=BF，∴△ADE≌△CBF（SAS）；（2）当BD平分∠ABC时，四边形AFCE是菱形，理由：∵BD平分∠ABC，∴∠ABD＝∠CBD，∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，AD∥BC，∴∠ADB＝∠CBD，∴∠ABD＝∠ADB，∴AB＝AD，∴平行四边形ABCD是菱形，∴AC⊥BD，∴AC⊥EF，∵DE＝BF，∴OE＝OF，又∵OA＝OC，∴四边形AFCE是平行四边形，∵AC⊥EF，∴四边形AFCE是菱形．43.（2020•新疆）如图，四边形ABCD是平行四边形，DE∥BF，且分别交对角线AC于点E，F，连接BE，DF．（1）求证：AE＝CF；（2）若BE＝DE，求证：四边形EBFD为菱形．【分析】（1）根据平行四边形的性质，可以得到AD＝CB，AD∥CB，从而可以得到∠DAE＝∠BCF，再根据DE∥BF和等角的补角相等，从而可以得到∠AED＝∠CFB，然后即可证明△ADE和△CBF全等，从而可以得到AE＝CF；（2）根据（1）中的△ADE和△CBF全等，可以得到DE＝BF，再根据DE∥BF，即可得到四边形EBFD是平行四边形，再根据BE＝DE，即可得到四边形EBFD为菱形．【解答】（1）证明：∵四边形ABCD 是平行四边形，∴AD ＝CB ，AD ∥CB ，∴∠DAE ＝∠BCF ，∵DE ∥BF ，∴∠DEF ＝∠BFE ，∴∠AED ＝∠CFB ，在△ADE 和△CBF 中，∠DAE =∠BCF ∠AED =∠CFB AD =CB ，∴△ADE ≌△CBF （AAS ），∴AE ＝CF ；（2）证明：由（1）知△ADE ≌△CBF ，则DE ＝BF ，又∵DE ∥BF ，∴四边形EBFD 是平行四边形，∵BE ＝DE ，∴四边形EBFD 为菱形．类型三与相似有关的证明44.（2021·广东中考真题）如图，边长为1的正方形ABCD 中，点E 为AD 的中点．连接BE ，将ABE △沿BE 折叠得到,FBE BF 交AC 于点G ，求CG 的长．【答案】CG =【分析】根据题意，延长BF 交CD 于H 连EH ，通过证明()Rt EDH Rt EFH HL ≌、DHE AEB ∽得到34CH =，再由HGC BGA ∽得到()34CG AC CG =-，进而即可求得CG 的长．【详解】解：延长BF 交CD 于H 连EH ，∵FBE 由ABE △沿BE 折叠得到，∴EA EF =，90EFB EAB ∠=∠=︒，∵E 为AD 中点，正方形ABCD 边长为1，∴12EA ED ==，∴12ED EF ==，∵四边形ABCD 是正方形，∴90D EFB EFH ∠=∠=∠=︒，在Rt EDH △和Rt EFH 中，ED EF EH EH=⎧⎨=⎩，∴()Rt EDH Rt EFH HL ≌，又∵AEB FEB ∠=∠，∴90DEH AEB ∠+∠=︒，∵90ABE AEB ∠+∠=︒，∴ABE DEH ∠=∠，∴DHE AEB ∽，∴12DH AE DE AB ==，∴14DH =，∴13144CH CD DH =-=-=，∵CH AB ∥，∴HGC BGA ∽，∴34CG CH AG AB ==，∴()3344CG AG AC CG ==-，∵1AB =，1CB =，90CBA ∠=︒，∴AC =，∴)34CG CG =，∴CG =．【点睛】本题主要考查了三角形全等的判定及性质、三角形相似的判定及性质以及正方形的性质，熟练掌握相关几何知识是解决本题的关键．45.（2021·湖北鄂州市·中考真题）如图，在ABCD 中，点E 、F 分别在边AD 、BC 上，（1）探究四边形BEDF的形状，并说明理由；（2）连接AC，分别交BE、DF于点G、H，连接BD交AC于点O．若23AGOG=，4AE=，求BC的长．【答案】（1）平行四边形，见解析；（2）16【分析】（1）利用平行四边形的判定定理，两组对边分别平行是平行四边形即可证明；（2）根据23AGOG=，找到边与边的等量关系，再利用三角形相似，建立等式进行求解即可．【详解】（1）四边形BEDF为平行四边形．理由如下：∵四边形ABCD为平行四边形∴ABC ADC∠=∠∵ABE CDF∠=∠∴EBF EDF∠=∠∵四边形ABCD为平行四边形∴//AD BC∴EDF DFC EBF∠=∠=∠∴//BE DF∵//AD BC∴四边形BEDF 为平行四边形（2）设2AG a =，∵23AG OG =∴3OG a =，5AO a=∵四边形ABCD 为平行四边形∴5AO CO a ==，10AC a =，8CG a=∵//AD BC,,AGE CGB AEG CBG EAG BCG ∠=∠∠=∠∠=∠，∴AGE CGB∆∆∽∴14AE AG BC GC ==∵4AE =∴16BC =．【点睛】本题考查了平行四边形的判定定理、相似三角形的判定定理，解题的关键是：熟练掌握相关定理，能进行相关的证明．46.（2021·北京中考真题）如图，在ABC 中，,,AB AC BAC M α=∠=为BC 的中点，点D 在MC 上，以点A 为中心，将线段AD 顺时针旋转α得到线段AE ，连接,BE DE ．（1）比较BAE ∠与CAD ∠的大小；用等式表示线段,,BE BM MD 之间的数量关系，并证明；（2）过点M 作AB 的垂线，交DE 于点N ，用等式表示线段NE 与ND 的数量关系，并证明．【答案】（1）BAE CAD ∠=∠，BM BE MD =+，理由见详解；（2）DN EN =，理由见详解．【分析】（1）由题意及旋转的性质易得BAC EAD α∠=∠=，AE AD =，然后可证ABE ACD △≌△，进而问题可求解；（2）过点E 作EH ⊥AB ，垂足为点Q ，交AB 于点H ，由（1）可得ABE ACD ∠=∠，BE CD =，易证BH BE CD ==，进而可得HM DM =，然后可得DMN DHE ∽，最后根据相似三角形的性质可求证．【详解】（1）证明：∵BAC EAD α∠=∠=，∴BAE BAD BAD CAD α∠+∠=∠+∠=，∴BAE CAD ∠=∠，由旋转的性质可得AE AD =，∵AB AC =，∴()ABE ACD SAS ≌，∴BE CD =，∵点M 为BC 的中点，∴BM CM =，∵CM MD CD MD BE =+=+，∴BM BE MD =+；（2）证明：DN EN =，理由如下：过点E 作EH ⊥AB ，垂足为点Q ，交AB 于点H ，如图所示：∴90EQB HQB ∠=∠=︒，由（1）可得ABE ACD △≌△，∴ABE ACD ∠=∠，BE CD =，∵AB AC =，∴ABC C ABE ∠=∠=∠，∵BQ BQ =，∴()BQE BQH ASA ≌，∴BH BE CD ==，∵MB MC =，∴HM DM =，∵MN AB ⊥，∴//MN EH ，∴DMN DHE ∽，∴12DM DN DH DE ==，∴DN EN =．【点睛】本题主要考查全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质，熟练掌握全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质是解题的关键．47.（2020•长沙）在矩形ABCD 中，E 为DC 边上一点，把△ADE 沿AE 翻折，使点D 恰好落在BC边上的点F．（1）求证：△ABF∽△FCE；（2）若AB＝23，AD＝4，求EC的长；（3）若AE﹣DE＝2EC，记∠BAF＝α，∠FAE＝β，求tanα+tanβ的值．【分析】（1）根据两角对应相等的两个三角形相似证明即可．（2）设EC＝x，证明△ABF∽△FCE，可得AB CF=BF EC，由此即可解决问题．（3）首先证明tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB，设AB＝CD＝a，BC＝AD＝b，DE＝x，解直角三角形求出a，b之间的关系即可解决问题．【解答】（1）证明：∵四边形ABCD是矩形，∴∠B＝∠C＝∠D＝90°，由翻折可知，∠D＝∠AFE＝90°，∴∠AFB+∠EFC＝90°，∠EFC+∠CEF＝90°，∴∠AFB＝∠FEC，∴△ABF∽△FCE．（2）设EC＝x，由翻折可知，AD＝AF＝4，∴BF=AF2−AB2=16−12=2，∴CF＝BC﹣BF＝2，∵△ABF∽△FCE，∴AB CF=BF EC，∴2322，∴x=∴EC=（3）∵△ABF∽△FCE，∴AF EF=AB CF，∴tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB，设AB＝CD＝a，BC＝AD＝b，DE＝x，∴AE＝DE+2CE＝x+2（a﹣x）＝2a﹣x，∵AD＝AF＝b，DE＝EF＝x，∠B＝∠C＝∠D＝90°，∴BF=b2−a2，CF=x2−(a−x)2=2ax−a2，∵AD2+DE2＝AE2，∴b2+x2＝（2a﹣x）2，∴a2﹣ax=14b2，∵△ABF∽△FCE，∴AB CF=BF EC，−(a−x)=b2−a2a−x，∴a2﹣ax=b2−a2•2ax−a2，∴14b2=b2−a2•整理得，16a4﹣24a2b2+9b4＝0，∴（4a2﹣3b2）2＝0，∴b a=233，∴tanα+tanβ=BC AB=48.（2020•怀化）如图，在⊙O中，AB为直径，点C为圆上一点，延长AB到点D，使CD ＝CA，且∠D＝30°．（1）求证：CD是⊙O的切线．（2）分别过A、B两点作直线CD的垂线，垂足分别为E、F两点，过C点作AB的垂线，垂足为点G．求证：CG2＝AE•BF．【分析】（1）连接OC，∠CAD＝∠D＝30°，由OC＝OA，进而得到∠OCA＝∠CAD＝30°，由三角形外角定理得到∠COD＝∠A+∠OCA＝60°，在△OCD中由内角和定理可知∠OCD＝90°即可证明；（2）证明AC是∠EAG的角平分线，CB是∠FCG的角平分线，得到CE＝CG，CF＝CG，再证明△AEC∽△CFB，对应线段成比例即可求解．【解答】（1）证明：连接OC，如右图所示，∵CA＝CD，且∠D＝30°，∴∠CAD＝∠D＝30°，∵OA＝OC，∴∠CAD＝∠ACO＝30°，∴∠COD＝∠CAD+∠ACO＝30°+30°＝60°，∴∠OCD＝180°﹣∠D﹣∠COD＝180°﹣30°﹣60°＝90°，∴OC⊥CD，∴CD是⊙O的切线；（2）∵∠COB＝60°，且OC＝OB，∴△OCB为等边三角形，∴∠CBG＝60°，又∵CG⊥AD，∴∠CGB＝90°，∴∠GCB＝∠CGB﹣∠CBG＝30°，又∵∠GCD＝60°，∴CB是∠GCD的角平分线，∵BF⊥CD，BG⊥CG，∴BF＝BG，又∵BC＝BC，∴Rt△BCG≌Rt△BCF（HL），∴CF＝CG．∵∠D＝30°，AE⊥ED，∠E＝90°，∴∠EAD＝60°，又∵∠CAD＝30°，∴AC是∠EAG的角平分线，∵CE⊥AE，CG⊥AB，∴CE＝CG，∵∠E＝∠BFC＝90°，∠EAC＝30°＝∠BCF，∴△AEC∽△CFB，。

中考数学证明题附答案（免费）

中考数学证明题附答案（免费）第一篇：中考数学证明题附答案(免费)中考中的“ 旋转、平移和翻折”平移、旋转和翻折是几何变换中的三种基本变换．所谓几何变换就是根据确定的法则，对给定的图形(或其一部分)施行某种位置变化，然后在新的图形中分析有关图形之间的关系．这类实体的特点是：结论开放，注重考查学生的猜想、探索能力；便于与其它知识相联系，解题灵活多变，能够考察学生分析问题和解决问题的能力．在这一理念的引导下，近几年中考加大了这方面的考察力度，特别是2006年中考，这一部分的分值比前两年大幅度提高．为帮助广大考生把握好平移，旋转和翻折的特征，巧妙利用平移，旋转和翻折的知识来解决相关的问题，下面已近几年中考题为例说明其解法，供大家参考．一．平移、旋转平移：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移．“一定的方向”称为平移方向，“一定的距离”称为平移距离．平移特征：图形平移时，图形中的每一点的平移方向都相同，平移距离都相等．旋转：在平面内，将一个图形绕一个定点沿某个方向转动一个角度成为与原来相等的图形，这样的图形运动叫做图形的旋转，这个定点叫做旋转中心，图形转动的角叫做旋转角．旋转特征：图形旋转时，图形中的每一点旋转的角都相等，都等于图形的旋转角．例1．（2006年乐山市中考题）如图（1），直线l经过点A（－3，1）、B（0，－2），将该直线向右平移2个单位得到直线l'．（1）在图（1）中画出直线l'的图象；（2）求直线l的解析式．解：（1）l'的图象如图．（2）点A向右平移两个单位得A´（－1，1），点B向右平移两个单位B´（2，－2），即直线l'经过点A´（－1，1）和B´（2，－2）设直线l的解析式为y=kx+b(k≠0)所以⎨⎧1=-k+b⎩-2=2k+b'''，解这个方程组，得k=-1，b=0∴直线l的解析式为y=-x．点评：抓住A、B两点平移前后坐标的关系是解题的例2．（2006年绵阳市中考试题）如图，将ΔABC绕顶点A顺时针旋转60º后得到ΔAB´C´，且C´为BC的中点，则C´D:DB´=（）A．1:2B．1:22C．1: 3D．1:3C´ CB 分析：由于ΔAB´C´是ΔABC绕顶点A顺时针旋转60º后得到的，所以，旋转角∠CAC′=60º，ΔAB´C´≌ΔABC，∴AC´=AC，∠CAC′=60º，∴ΔAC´C是等边三角形，∴AC´=AC´．又C´为BC的中点，∴BC´=CC´，易得ΔAB´C、ΔABC是含30º角的直角三角形，从而ΔAC´D也是含30º角的直角三角形，∴C´D=12AC´，AC´=12B´C´，∴C´D=14B´C´，故C´D:DB´= 1:3点评：本例考查灵活运用旋转前后两个图形是全等的性质、等边三角形的判断和含30 º角的直角三角形的性质的能力，解题的关键是发现ΔAC´C是等边三角形．二、翻折翻折：翻折是指把一个图形按某一直线翻折180º后所形成的新的图形的变化．翻折特征：平面上的两个图形，将其中一个图形沿着一条直线翻折过去，如果它能够与另一个图形重合，那么说这两个图形关于这条直线对称，这条直线就是对称轴．解这类题抓住翻折前后两个图形是全等的，弄清翻折后不变的要素．翻折在三大图形运动中是比较重要的，考查得较多．另外，从运动变化得图形得特殊位置探索出一般的结论或者从中获得解题启示，这种由特殊到一般的思想对我们解决运动变化问题是极为重要的，值得大家留意．例3．（2006年江苏省宿迁市）如图，将矩形ABCD沿AE折叠，若∠BAD′＝30°，则∠AED′ 等于（）A．30°B．45°C．60°D．75° 分析：由已知条件∠BAD′＝30°，易得∠DAD′=60º，又∵D、D′D′ACB关于AE对称，∴∠EAD=∠EAD′=30º，∴∠AED=∠AED′=60º．故选C点评：本例考查灵活运用翻折前后两个图形是全等的性质的能力，解题的关键是发现∠EAD=∠EAD′，∠AED=∠AED′．例4．（2006年南京市）已知矩形纸片ABCD，AB=2，AD=1，将纸片折叠，使顶点A与边CD上的点E重合．(1)如果折痕FG分别与AD、AB交与点F、G(如图1)，AF=3，求DE的长；(2)如果折痕FG分别与CD、AB交与点F、G(如图2)，△AED的外接圆与直线BC相切，求折痕FG的长．解：(1)在矩形ABCD中，AB=2，AD=1，AF=3，∠D=90º．根据轴对称的性质，得 EF=AF=∴DF=AD-AF=2212在ΔDEF中DE=()-()=(2)设AE与FG的交点为O．NAGB根据轴对称的性质，得AO=EO．取AD的中点M，连接MO．则mO=DE，MO∥DC．12x．设DE= x，则MO=在矩形ABCD中，∠C=∠D=90º，∴AE为ΔAED的外接圆的直径，O为圆心．延长MO交BC于点N，则ON∥CD ∴∠CNM=180º-∠C=90º．∴ON⊥BC，四边形MNCD是矩形．∴MN=CD=AB=2．∴ON=MN-MO=2-12x，根据轴对称的性质，得AE⊥FG．∴∠FOE=∠D=90º．∵∠FEO=∠AED，∴ΔFEO∽ΔAED．∴FOAD=OEDE．∵ΔAED的外接圆与BC相切，∴ON是ΔAED的外接圆的半径．∴OE=ON=2-12x，∴FO=OEDE•AD．可得FO=1730．AE=2ON=4-x．在RtΔAED中，AD2+DE2=AE2，∴12+x2=(4-x)又AB∥CD，∴∠EFO=∠AGO，∠FEO=∠GAO．∴ΔFEO≌ΔGAO．∴FO=GO．∴FG=2FO= 171解这个方程，得x=∴DE=158．1716．1715，OE=2-x=．∴折痕FG的长是．点评：图形沿某条线折叠，这条线就是对称轴，利用轴对称的性质并借助方程的的知识就能较快得到计算结果．由此看出，近几年中考，重点突出，试题贴近考生，贴近初中数学教学，图形运动的思想(图形的旋转、翻折、平移三大运动)都一一考查到了．因此在平时抓住这三种运动的特征和基本解题思路来指导我们的复习，将是一种事半功倍的好方法．例4．（2006年南京市）已知矩形纸片ABCD，AB=2，AD=1，将纸片折叠，使顶点A与边CD上的点E重合．(1)如果折痕FG分别与AD、AB交与点F、G(如图1)，AF=3，求DE的长；(2)如果折痕FG分别与CD、AB交与点F、G(如图2)，△AED的外接圆与直线BC相切，求折痕FG的长．：(1)在矩形ABCD中，AB=2，AD=1，AF=2，=90º．∠D根据轴对称的性质，得 EF=AF=∴DF=AD-AF=13在ΔDEF中DE=(221233)-(3)=(2)设AE与FG的交点为O．根据轴对称的性质，得AO=EO．取AD的中点M，连接MO．则mO=DE，MO∥DC．设DE= x，则MO=在矩形ABCD中，∠C=∠D=90º，∴AE为ΔAED的外接圆的直径，O为圆心．延长MO交BC于点N，则ON∥CD ∴∠CNM=180º-∠C=90º．∴ON⊥BC，四边形MNCD是矩形．∴MN=CD=AB=2．∴ON=MN-MO=2-12x，∵ΔAED的外接圆与BC相切，∴ON是ΔAED的外接圆的半径．∴OE=ON=2-12x，AE=2ON=4-x．在RtΔAED中，AD2+DE2=AE2，∴12+x2=(4-x)．解这个方程，得x=158．∴DE=1518，OE=2-2x=1716．NAGB根据轴对称的性质，得AE⊥FG．∴∠FOE=∠D=90º．∵∠FEO=∠AED，∴ΔFEO∽ΔAED．∴FOOEAD=DE．∴FO=OEDE•AD．可得FO=．又AB∥CD，∴∠EFO=∠AGO，∠FEO=∠GAO．∴ΔFEO≌ΔGAO．∴FO=GO．∴FG=2FO=1715．∴折痕FG的长是1715．解第二篇：科学证明题附答案证明题1．液体内部存在压强。

初中数学九年级中考复习三角形部分证明练习题精选

1．已知：如图点C 是AB 的中点，CD ∥BE ，且CD=BE.求证：∠D=∠E.2．已知：E 、F 是AB 上的两点，AE=BF ，又AC ∥DB ，且AC=DB.求证：CF=DE 。

3 如图，已知△ABC 和△DEC 都是等边三角形，∠ACB=∠DCE=60°，B 、C 、E 在同一直线上，连结BD 和AE.求证：BD=AE.4．如图，D 、E 、F 、B 在一条直线上，AB=CD ，∠B=∠D ，BF=DE 。

求证：⑴AE=CF ；⑵AE ∥CF ；⑶∠AFE=∠CEF 。

AC B ED A BC DE F A B C D E FA B CDE5．如图，D 是△ABC 的边BC 上一点，且CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线。

求证：AC=2AE 。

6．已知：如图∠B=∠E=90°AC=DF FB=EC ，则AB=DE.请说明理由。

7．如图，AD ∥BC ，∠A=90°，E 是AB 上一点，∠1=∠2，AE=BC 。

请你说明∠DEC=90°的理由。

AB E DC8．如图，已知：在等边三角形ABC 中，D 、E 分别在AB 和AC 上，且AD=CE ，BE 和CD 相交于点P 。

（1）说明△AD ≌△CEB（2）求：∠BPC 的度数.1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD证明: 延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD 即BE=AC=2在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6又AD 是整数,则AD=52．如图，在△ABC 中，AB=AC ，M 为BC 的中点，点D 、E 分别在AB 、AC 上，且AD=AE ．求证：MD=ME ．证明：（法一） ∵AB=AC ， ∴∠B=∠C ．∵M 为BC 的中点， ∴BM=CM ．∵AB=AC ，AD=AE ，∴BD=CE ．在△DBM 和△ECM 中，∴BD=CE ，∠B=∠C ，BM=CM ．ADBC∴△DBM ≌△ECM ． ∴MD=ME ．（法二）连接AM ，（1分）∵AB=AC ，M 为BC 的中点， ∴AM 平分∠BAC ， ∴∠BAM=∠CAM ．在△ADM 和△AEM 中，∵AD=AE ，∠DAM=∠EAM ，AM=AM ， ∴△ADM ≌△AEM ． ∴MD=ME ．4．如图所示，已知AE ⊥AB ，AF ⊥AC ，AE=AB ，AF=AC 。

初三证明题练习题及答案

初三证明题练习题及答案1. 已知直角三角形ABC中，AB = 3 cm，BC = 4 cm，求证：∠B = 90°。

证明：首先，我们知道直角三角形的定义是其中一个角为90°。

所以，我们需要证明∠B = 90°。

假设∠B ≠ 90°，即角B为锐角或钝角。

若∠B为锐角，则根据三角形内角和为180°的性质，∠A + ∠B + ∠C = 180°，因为∠B是一个锐角，所以∠A + ∠C > 90°。

但根据余弦定理，我们可以计算出AB^2 + BC^2 = AC^2：3^2 +4^2 = 9 + 16 = 25 = AC^2。

然而，当∠A + ∠C > 90°时，对于一个给定的直角三角形，AC的长度必定大于5（根据三角不等式），但根据计算结果AC = 5。

这与实际情况不符，所以假设不成立，∠B不能是一个锐角。

若∠B为钝角，则根据三角形内角和为180°的性质，∠A + ∠B + ∠C = 180°，因为∠B是一个钝角，所以∠A + ∠C < 90°。

但根据余弦定理，我们可以计算出AB^2 + BC^2 = AC^2：3^2 +4^2 = 9 + 16 = 25 = AC^2。

然而，当∠A + ∠C < 90°时，对于一个给定的直角三角形，AC的长度必定小于5（根据三角不等式），但根据计算结果AC = 5。

这同样与实际情况不符，所以假设不成立，∠B不能是一个钝角。

综上所述，假设∠B ≠ 90°不成立，所以∠B = 90°，即三角形ABC 是一个直角三角形。

2. 已知直角三角形ABC中，AC = 5 cm，BC = 12 cm，求证：AB = 13 cm。

证明：为了证明AB = 13 cm，我们可以利用勾股定理。

根据勾股定理，直角三角形的斜边平方等于两直角边平方和。

中考数学证明题模拟试题

中考数学证明题模拟试题1. 选择题：在直角三角形ABC中，∠C=90°，如果AC=6，BC=8，则AB的长度为？A) 7 B) 10 C) 12 D) 142. 填空题：已知正方形的对角线长为10cm，该正方形的面积为______cm²。

3. 简答题：证明勾股定理：在一个直角三角形中，直角两边的平方和等于斜边的平方。

4. 计算题：已知等腰三角形的底边长为12cm，两腰长度相等且为10cm，求顶角的大小。

5. 选择题：下列哪个图形不是轴对称图形？A) 正六边形 B) 平行四边形 C) 等腰梯形 D) 圆6. 填空题：若三角形ABC中，∠A = 60°，∠B = 80°，则∠C = ______。

7. 证明题：证明在一个等腰三角形中，底边上的中线也是顶角的平分线。

8. 简答题：解释什么是相似三角形，并给出两个实际生活中的相似三角形例子。

9. 计算题：在直角三角形中，若一条直角边长为5cm，斜边长为13cm，求另一条直角边的长度。

10. 选择题：下列条件中，不能确定一个唯一的三角形的是？A) 三边长确定B) 两边夹一角确定C) 一边和两个锐角确定 D) 两边及其中一边的对角确定11. 填空题：平行四边形ABCD中，对角线AC和BD交于点O，若AC=16cm，BD=12cm，且△AOB的面积为12cm²，则平行四边形ABCD的面积为______cm²。

12. 证明题：证明三角形的中位线等于第三边的一半。

13. 简答题：描述并举例说明“垂直平分线定理”。

14. 计算题：梯形ABCD中，AD∥BC，AD=6cm，BC=12cm，高为8cm，求梯形的面积。

15. 选择题：在等边三角形中，从一个顶点画到相对边的中点的线段称为？A) 高 B) 角平分线 C) 中线 D) 以上都是16. 填空题：圆的直径为10cm，那么这个圆的周长是______cm。

17. 证明题：证明圆内接四边形对角互补。

(完整word版)全等三角形证明中考题精选[有答案解析]

WORD 格式可编辑七年级数学下---全等三角形证明题1如图，已知人。

是厶ABC 勺中线，分别过点 B 、C 作BEL AD 于点E, CF 丄AD 交AD 的延长线于点F ,求证：BE=CF(1操作发现：如图2，固定△ ABC 使厶DEC 绕点C 旋转，当点D 恰好落在AB 边上时，填空:①线段DE 与 AC 的位置关系是 ____________ ;当厶DEC 绕点C 旋转到如图3所示的位置时，小明猜想(1中S i 与S 2的数量关系仍然成立，并尝试分别作出了△ BDC ffiA AEC 中BC CE 边上的高，请你证明小明的猜想.(3)拓展探究已知/ABC=60，点D 是角平分线上一点，BD=CD=,4DE// AB 交BC 于点E (如图4).若在射线BA 上2•如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中/ C=90° , ZB=Z E=30°②设△ BDC 的面积为$,△ AEC的面积为9，则S 与S 2的数量关系是 ______________ (2)猜想论证存在点F,使S A DC=&BDE,请直接写出相应的BF的长.3•如图，把一个直角三角形ACB(/ACB=90 )绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F, G分别是BD, BE上的点，BF=BG延长CF与DG交于点H. (1) 求证：CF=DG (2)求出/ FHG勺度数.4•如图所示，在△ ABC中, D E分别是AB AC上的点，DE// BC,如图①，然后将厶ADE绕A点顺时针旋转一定角度，得到图②，然后将BD CE分别延长至M N,使DM=BD, EN=CE得到图③，ba请解答下列问题：(1)若AB=AC请探究下列数量关系：①在图②中，BD与CE的数量关系是___________ ;②在图③中，猜想AM与AN的数量关系、/ MANW Z BAC的数量关系，并证明你的猜想；(2)若AB=I?AC(k>1),按上述操作方法，得到图④，请继续探究：AM与AN的数量关系、/ MAN与/BAC K数量关系，直接写出你的猜想，不必证明.£134. (1)如图，在△ABC ffiA ADE中，AB=AC AD=A£/ BAC K DAE=90 .①当点D在AC上时，如图1,线段BD CE有怎样的数量关系和位置关系？直接写出你猜想的结论;②将图1中的△ADE绕点A顺时针旋转口角(0°VaV90°)如图2,线段BD CE有怎样的数量关系和位置关系？请说明理由.⑵当厶ABC^n^ADE满足下面甲、乙、丙中的哪个条件时，使线段BD CE在(1)中的位置关系仍然成立？不必说明理由.甲：AB AC=AD AE=1, / BAC K DA字90°;乙：AB AC=AD AE M 1,6. CD经过/ BCA顶点C的一条直线，CA=CB E, F分别是直线CD上两点，且/ BEC2 CFA=（1若直线CD经过/ BCA勺内部，且E, F在射线CD上，请解决下面两个问题：①如图 1 若/ BCA=90，/ a=90°,则BE _ _ CF; EF _ _ |BE~ AF| （填“〉”，“v”或“=”）；②如图2,若0°<Z BCA< 180°，请添加一个关于/a与/ BCA关系的条件—，使①中的两个结论仍然成立，并证明两个结论成立.（2）如图3,若直线CD经过/ BCA的外部，/ a =/ BCA请提出EF, BE, AF三条线段数量关系的合理猜想（不要求证明）..WORD 完美格式.7. 如图，已知 AB=AC （1）若CE=BD 求证: ⑵若CE=m BD （ m 为正数），试猜想GE 与 GD 有何关系.（只写结论，不证明）GE=G；.WORD完美格式.8. (1)已知：如图①，在△COD中, OA=OB OC=OP / AOB M COD=60，求证：①AC=BD②/ APB=6(度；(2)如图②，在△ AOBf^A COP中，若OA=OBOC=OJP / AOB M COD a，贝U AC与BD间的等量关系式为 ____________ ; Z APB的大小为_____________ ;(3)如图③，在△ AOBf^A COD中，若OA=? OB OC=? OD( k > 1)，Z AOB Z COD a，贝U AC 与BD 间的等量关系式为 ____________ ; Z APB的大小为 _____10.已知：EG// AF, AB=AC DE=DF 求证：BE=CF参考答案与试题解析.WORD 完美格式.4、2.解：（1）①DEC 绕点C 旋转点D 恰好落在AB 边上，••• AC=CD ：/ BAC=90 -ZB=90° £0°=60°,：m CD 是等边三角形，•••/ ACD=60，又 V /CDE T T BAC=60 ,：Z ACD M CDE 二 DE// AC② V / B=30O ,/C=90° ,.QD=AC=AB, A BD=AD=AC2根据等边三角形的性质，△ ACM 边AC AD 上的高相等，•••△ BDC 勺面积和△ AEC 勺面积相等（等底等高的三角形的面积相等），即 S=S 2;故答案为：DE// AC S 1=S 2;（2）如图，•••△ DEC 是由厶ABC 绕点C 旋转得到，A BC=CE AC=CD V / ACN / BCN=90 ,ZDCM /BCN=180 -90°=90°,A / ACN / DCMI V 在厶 ACNm DCM 中,fZAC^ZDCMI ZCHD=ZN=90° ,[AC 二 CD •••△ ACN^A DCM （ AAS, A AN=DM•••△ BDC 的面积和△ AEC 的面积相等（等底等高的三角形的面积相等），即S i =S 2;3、解（1）证明：•••在厶 CBF ft^ DBG K“ f BC=BD答：口 ■ 厶顶二乙佃二柑,[BF =BG•••△ CBF^A DBG （ SAS , A CF=DQ（2）解：•••△ CBF^ADBG A / BCF / BDG 又V / CFB / DFH A / DHF / CBF=60 ,A / FHG=180 -ZDHF=180 -60°=120°.解答：解：（1）①结论：BD=CE BDL CE②结论：BD=CE BH CE 理由如下：I/ BAC K DAE=90解答：解：(1)① BD=CE ②AM=AN / MAN /BAC v/ DAE / BACCAE / BAD •••/ BAC- / DAC / DAE- / DAC 即/ BAD / CAE ft^ ABD 与△ ACE 中,在△_BADf3 CAE 中•v Z B 期二ZCAE 二△ ABD^A ACE(SAS 二 BD=CEV L AD=AE延黒二BD 交AC 于 F ,交CE 于H. • ZCAE=ZBAD •••△ CAE^ △ BAD (SAS ,在临^^与厶HCF 中，v/ ABF=/ HCF / AFB=/ HFC •/ CHF / BAF=90 • / ACE / ABD v DM=BD EN=CE • BM=C N• BDL CE(2)结论：乙.AB A C=AD AE, / BAC / DAE=90 / MAN /BAC 在厶 ABM ffiA ACN ,-(2) AM=? AN5 .6.解答：解：(1)①I/ BCA=90，/a=90°,：/BCE£ CBE=90，/BCE# ACF=90 ,•••/ CBE# ACF v CA=CB/ BEC# CFA BCE^A CAF 二BE=CF EF=|BE- AF|.②所填的条件是：#a +/ BCA=180 .证明：在厶BCE中,/ CBE/ BCE=180 -ZBEC=180 -/a.v/BCA=180 -/a,• / CBE/ BCE/ BCA 又v/ ACF/ BCE/ BCA •/ CBE/ ACF又v BC=CA / BEC/ CFA •△BCE^A CAF( AAS •- BE=CF CE=AF又v EF=C F CE, • EF=|BE- AF|.(2) EF=BE+AF7.解证明：(1)过D作DF// CE交BC于F,答: 贝U/E=/ GDF v AB=AC •/ ACB# ABC/ DF/ CE •/ DFB/ ACB•/ DFB/ ACB/ ABC • DF=DB v CE=BD •- DF=CE 在厶GDF^ GEC中, (ZE 二Z GDFI ZDGF=ZEGC ,[DF=EC•△GDF^A GEC(AAS. • GE=GD(2) GE=m GD9.解解：(1)①I/AOB M COD=60 , :-ZAOB+L BOC M COD 乂BOC 即：/ AOC M BOD 答：又T OA=OB OC=OD •••△ AOC^ABOD - AC=BD②由①得：Z OAC Z OBDT/ AEO Z PEB / APB=180 -(Z BEP+Z OBD, Z AOB=180 -(/OAC Z AEO, -Z APB Z AOB=60 .(2) AC=BD a(3) AC=? BD, 180°-a.。

最新中考数学证明题综合训练试题精品版

2023年数学中考试题精选：几何综合证明(一)

中考数学三角形全等证明习题50题

中考数学精选汇编几何证明---13道题目(含答案)(优选.)

初三数学证明题试卷

中考几何证明题及答案

中考数学全等三角形证明经典50题(含答案)+经典因式分解练习题100道

中考数学专项练习命题与证明(含解析)

中考数学证明题练习模拟试题

初三数学证明题练习题

初中中考数学24题几何证明综合学习练习

(完整版)中考数学-圆的切线证明综合试题

初三数学证明题练习(3套)含答案

最新中考数学三角形全等证明题、解答题精选30题 附解题过程

2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)

中考数学证明题附答案（免费）

初中数学九年级中考复习三角形部分证明练习题精选

初三证明题练习题及答案

中考数学证明题模拟试题

(完整word版)全等三角形证明中考题精选[有答案解析]

最新中考数学三角形全等证明题、解答题精选30题附解题过程