第10章习题解答哈工大习题册
(完整版)哈工大模电习题册答案

【2-1】 填空:1.本征半导体是 ,其载流子是 和 。
两种载流子的浓度 。
2.在杂质半导体中,多数载流子的浓度主要取决于 ,而少数载流子的浓度则与 有很大关系。
3.漂移电流是 在 作用下形成的。
4.二极管的最主要特征是 ,与此有关的两个主要参数是 和 。
5.稳压管是利用了二极管的 特征,而制造的特殊二极管。
它工作在 。
描述稳压管的主要参数有四种,它们分别是 、 、 、和 。
6.某稳压管具有正的电压温度系数,那么当温度升高时,稳压管的稳压值将 。
1. 完全纯净的半导体,自由电子,空穴,相等。
2. 杂质浓度,温度。
3. 少数载流子,(内)电场力。
4. 单向导电性,正向导通压降U F 和反向饱和电流I S 。
5. 反向击穿特性曲线陡直,反向击穿区,稳定电压(U Z ),工作电流(I Emin ),最大管耗(P Zmax )和动态电阻(r Z )6. 增大;【2-2】电路如图2.10.4所示,其中u i =20sinωt (mV),f =1kHz ,试求二极管VD 两端电压和通过它的电流。
假设电容C 容量足够大。
-+-+C R+k 5ΩV 6iu VD+-D u Di a)(图2.10.4 题2-5电路图1.静态分析静态,是指u i =0,这时u i 视作短路,C 对直流视作开路,其等效电路如图1.4.2(a)所示。
不妨设U D =0.6V则D D 6V (60.6)V1.08mA 5kU I R --===Ω 对于静态分析,也可以根据二极管的伏安特性曲线,用图解法求解。
2.动态分析对于交流信号,直流电源和电容C 视作短路;二极管因工作在静态工作点附近很小的范围内,故可用动态电阻r d 等效,且D d D1ir u ∆=∆,由此可得等效电路如图1.4.2(b)所示。
二极管伏安特性方程:)1e (TD/S D -=U u I i (1.4.1)由于二极管两端电压U D ?U T =26 mV ,故式1.4.1可简化为:TD/S D e U u I i ≈TD D Dd d d 1U I u i r ≈=Ω==≈07.241.08mA26mVD T d I U r 所以d i d d d 0.02sin (V)0.83sin (mA)24.07()u u t i t r r ωω===≈Ω 3.交流和直流相叠加)(mA sin 83.008.1d D D t i I i ω+=+=)(V sin 02.06.0d D D t u U u ω+=+=4.u D 和i D 波形如图1.4.2(c)、(d)所示。
哈尔滨工业大学理论力学课后习题答案
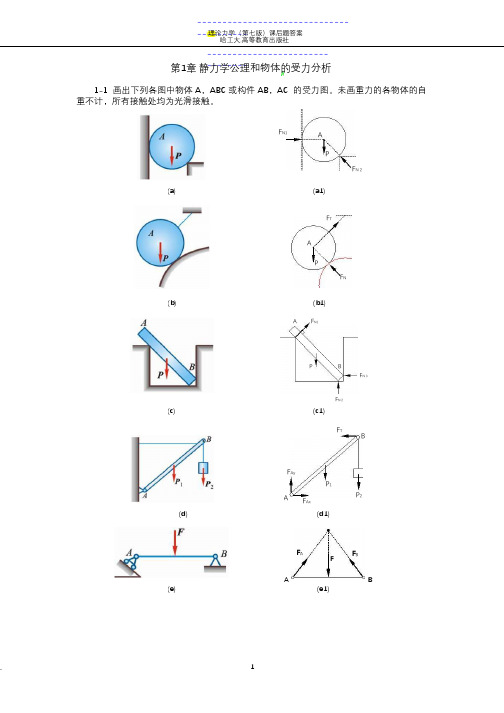
.----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
哈尔滨工业大学理论力学课后习题问题详解
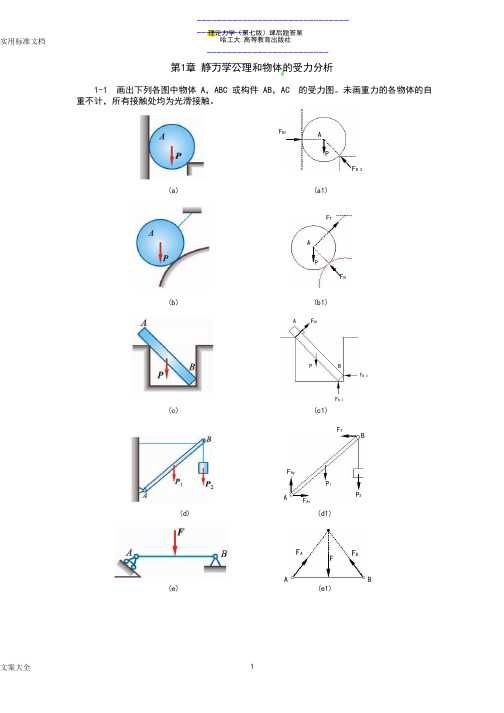
实用标准文档----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社-------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB ′ F AC CA′ F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C′ F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)′ F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxACD F N2B P2P1F N1(c) (c1)F AyF TA F AxD′FF N2 TBP1F N1 P2(c2) (c3)F AyF BqBA FAxC DF C(d) (d1)F DyF Ay F BqqD′FDxBA F Ax C F Dx D′FDyF C(d2) (d3)F Ay′FBxq BF AyF AxqA B ′FByF AxF Cx CF Cy PF BxA BPF Cx(e1)C F By F Cy(e) (e2) (e3)F1 CF2F Ay FByA BF Ax F Bx(f) (f1)F Cx′ FCxCCF 1F CyF ′ F 2 F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)′ F CyF T′FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B ′ F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC′ A F EF CyF F OyCDF OxF Cx ′EO B(i)(i1)(i2)AA ′FAx′FE′FAyFEC DF ByF ByF OyF BxF Ox F BxOB B(i3) (i4)F AyD EF CxF TA F AxF ByCCH FBy F CyB PF Bx F BxB(j) (j1) (j2)F Ay F Dy′′FEy′F CF Cx′E F AxT 2D F T 2 ′FExF Ex A D F Dx′ EF DxF T3F T1 ′FCyF Dy F Ey(j3) (j4) (j5)EF F BC ED ′ BFCxθ′′FDEFCy(k) (k1)F BFFCB FCxθ E CF Cy90°−θFDED DF AyF AyA AF Ax F Ax(k2) (k3)F B′ FBF 1F DBBDCAF AF C(l)(l1)(l2)F 2′ D F DF 1F 2D BAC EE F EF AF C F E(l3)(l4)或′ ′ F DyF 2F 1F F Dy F 2F 1B ′ DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’ (l4)’′ F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD ′(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq′ F BF N 2F N3(n2)FB D FF C F E F AF G GCEA(o)(o1)FBBDFDF BF E F F F CF D′ FEA F AF B ′ CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
哈尔滨工业大学理论力学课后习题问题详解

实用标准文档----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社-------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB ′ F AC CA′ F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C′ F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)′ F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxACD F N2B P2P1F N1(c) (c1)F AyF TA F AxD′FF N2 TBP1F N1 P2(c2) (c3)F AyF BqBA FAxC DF C(d) (d1)F DyF Ay F BqqD′FDxBA F Ax C F Dx D′FDyF C(d2) (d3)F Ay′FBxq BF AyF AxqA B ′FByF AxF Cx CF Cy PF BxA BPF Cx(e1)C F By F Cy(e) (e2) (e3)F1 CF2F Ay FByA BF Ax F Bx(f) (f1)F Cx′ FCxCCF 1F CyF ′ F 2 F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)′ F CyF T′FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B ′ F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC′ A F EF CyF F OyCDF OxF Cx ′EO B(i)(i1)(i2)AA ′FAx′FE′FAyFEC DF ByF ByF OyF BxF Ox F BxOB B(i3) (i4)F AyD EF CxF TA F AxF ByCCH FBy F CyB PF Bx F BxB(j) (j1) (j2)F Ay F Dy′′FEy′F CF Cx′E F AxT 2D F T 2 ′FExF Ex A D F Dx′ EF DxF T3F T1 ′FCyF Dy F Ey(j3) (j4) (j5)EF F BC ED ′ BFCxθ′′FDEFCy(k) (k1)F BFFCB FCxθ E CF Cy90°−θFDED DF AyF AyA AF Ax F Ax(k2) (k3)F B′ FBF 1F DBBDCAF AF C(l)(l1)(l2)F 2′ D F DF 1F 2D BAC EE F EF AF C F E(l3)(l4)或′ ′ F DyF 2F 1F F Dy F 2F 1B ′ DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’ (l4)’′ F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD ′(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq′ F BF N 2F N3(n2)FB D FF C F E F AF G GCEA(o)(o1)FBBDFDF BF E F F F CF D′ FEA F AF B ′ CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
电路基本理论课后答案(哈工大版)第10章

答案10.1解:0<t 时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u 由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t 时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A 3)363685(V45)0(=Ω+⨯++=-i ,A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得:V 24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i 由KVL 得开关电压:V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解:0<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
哈工大工程制图作业答案

3-4 已知 ABC平行于 DEFG,作出其水平投影。
′
(2) 过直线AB作一平面△ABC∥DE。
′
c
′
′
′
′
′
′ ′
′
′
′
c
第三章 直线与平面、平面与平面的相对位置
3-5 △ABC平行于△DEF,点M属于△ABC,作出其正面投影。 3-6 判别已知两平面是否平行。
a
′
c ′ ′
b
′
′ ′
′
′
′
′
e′
′
′
′
′
c′′
b a′′
e
d′ c′
′ ′
d
c
30
第三章 直线与平面、平面与平面的相对位置
3-31 在△ABC内求作一直线与MN垂直相交。
3-32 AB为一直角边作直角△ABC,斜边AC为水平线,∠C为60 。
′
′
l′
′
k′
′
′
l
k
′
′
c
c
bc
30
AC
49
第四章 投影变换
习题 4-1 习题 4-4 习题 4-7
′
′
′
′
′
第三章 直线与平面、平面与平面的相对位置
习题 3-1,2 习题 3-7,8 习题 3-13,14 习题 3-19,20 习题 3-25,26 习题 3-31,32
习题 3-3,4 习题 3-9,10 习题 3-15,16 习题 3-21,22 习题 3-27,28
习题 3-5,6 习题 3-11,12 习题 3-17,18 习题 3-23,24 习题 3-29,30
哈工大电路原理基础课后习题集
第一章习题1.1 图示元件当时间t<2s时电流为2A,从a流向b;当t>2s时为3A,从b流向a。
根据图示参考方向,写出电流的数学表达式。
1.2图示元件电压u=(5-9e-t/τ)V,τ>0。
分别求出t=0 和t→∞时电压u的代数值及其真实方向。
图题1.1 图题1.21.3 图示电路。
设元件A消耗功率为10W,求;设元件B消耗功率为-10W,求;设元件C发出功率为-10W,求。
图题1.31.4求图示电路电流。
若只求,能否一步求得?1.5 图示电路,已知部分电流值和部分电压值。
(1) 试求其余未知电流。
若少已知一个电流,能否求出全部未知电流?(2) 试求其余未知电压u14、u15、u52、u53。
若少已知一个电压,能否求出全部未知电压?1.6 图示电路,已知,,,。
求各元件消耗的功率。
1.7 图示电路,已知,。
求(a)、(b)两电路各电源发出的功率和电阻吸收的功率。
1.8 求图示电路电压。
1.9 求图示电路两个独立电源各自发出的功率。
1.10 求网络N吸收的功率和电流源发出的功率。
1.11 求图示电路两个独立电源各自发出的功率。
1.12 求图示电路两个受控源各自发出的功率。
1.13 图示电路,已知电流源发出的功率是12W,求r的值。
1.14 求图示电路受控源和独立源各自发出的功率。
1.15图示电路为独立源、受控源和电阻组成的一端口。
试求出其端口特性,即关系。
1.16 讨论图示电路中开关S开闭对电路中各元件的电压、电流和功率的影响,加深对独立源特性的理解。
第二章习题2.1 图(a)电路,若使电流A,,求电阻;图(b)电路,若使电压U=(2/3)V,求电阻R。
2.2 求图示电路的电压及电流。
2.3 图示电路中要求,等效电阻。
求和的值。
2.4求图示电路的电流I。
2.5 求图示电路的电压U。
2.6 求图示电路的等效电阻。
2.7 求图示电路的最简等效电源。
图题2.72.8 利用等效变换求图示电路的电流I。
哈尔滨工业大学理论力学课后习题答案
.----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB 2 F AC CA2 F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C2 F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)2 F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF TAF AxD2 F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD2 FDxBAF AxCF Dx D 2 FDyF C(d2) (d3)F Ay2 FBxqBF AyF AxqAB 2F ByF AxF CxC F CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx2 FCxCCF 1F CyF 2 F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)2 F CyF T2 FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B2 F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC2 A F EF CyF F OyCDF OxF Cx 2EOB(i)(i1)(i2)A A2 F Ax2 FE2 F AyFEC D F ByF ByF OyF BxF OxF BxOBB (i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F Cy BPF BxF BxB(j)(j1)(j2)F Ay F Dy 22 F Ey2 F CF Cx 2 E F AxT 2 D F T 22FExF ExA D F Dx 2E F DxF T3F T12FCyF DyF Ey(j3)(j4)(j5)EFF BCED2 BF Cx⎝2 2 F DEF Cy(k)(k1)F BF FC BF Cx⎝EC F Cy90︒ ⎝FDED DF AyF AyAAF AxF Ax(k2) (k3)F B2 FBF 1F DBBDCAF AF C(l)(l1)(l2)F 22 DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或2 2 F DyF2F 1F F Dy F 2F 1B 2 DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’2 F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD 2(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq2 F BF N 2F N3(n2)FB D FF C F EF AF G GCEA(o)(o1)FBB DFDF BF E F FF C F D2 FEA F AF B 2CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
电路基本理论课后答案(哈工大版)第10章汇总
答案10.1解:0<t 时,电容处于开路,故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得:V 20)0()0(==-+C C u u换路后一瞬间,两电阻为串联,总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得:m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解:0<t 时电容处于开路,电感处于短路,Ω3电阻与Ω6电阻相并联,所以A 3)363685(V45)0(=Ω+⨯++=-i ,A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得:V 24)0()0(==-+C C u u ,A 2)0()0(==-+L L i i 由KVL 得开关电压:V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u 答案10.3解:0<t 时电容处于开路,0=i ,受控源源电压04=i ,所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时,求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应,故电容电压为:V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为:V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解:0<t 时电感处于短路,故A 3A 9363)0(=⨯+=-L i ,由换路定律得: A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ,时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应,故电感电流为A e 3e )0()(2/t t L L i t i --+==τ)0(≥t 电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为:W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解:由换路定律得0)0()0(==-+L L i i ,达到稳态时电感处于短路,故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
哈尔滨工业大学理论力学课后习题答案
----------------------------------------理论力学(第七版)课后题答案哈工大 . 高等教育出版社--------------------------------第 1章静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
FN1 APFN 2(a)(a1)FTAPFN(b)(b1)A FN1P BFN 3FN 2(c)(c1)FTBFAyP1AP2F Ax(d) (d1)FA FBFA B (e) (e1)1理论力学(第七版)课后题答案哈工大 . 高等教育出版社qFFAy F BA FAxB(f) (f1)FBC F CF A A(g)(g1)FAy FCCA FAx BP1 P2(h)(h1)BFCF CDFAxAF Ay(i) (i 1)(j)(j1)BF B FCPF AyF AxA(k)(k1) 2理论力学(第七版)课后题答案哈工大 . 高等教育出版社FCA FABCF ACAF ABFACBA PFBA(l) (l1)(l2) (l3) 图1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
B F N1C FN 2F N P2(a)(a1)F N1BFN1C F N 2FNP2PP1FAyF Ay1FAxFAxA A(a2)(a3)FN1APBFN31P2FN 2 (b)(b1)F NA B FN3P2PF N F N 21(b2) (b3)3理论力学(第七版)课后题答案哈工大 . 高等教育出版社(c)FTDFN2 BP1F N1(c2)(d)F AyA FAxCD FN2B P2P1FN1(c1)F AyA FAxF TP 2(c3)F AyFBqAF Ax C DBFC(d1)FAy FDyqqF BDB F FDxDy (d3)(e)FC(d2)F AyqFAxA BFCyPC FCx(e1)(f)F AyFAxAF1FAyA FBqBxB FBx FCxC PFByFBy FCy(e2) (e3)CF2 FByFAx FBxB(f1)4理论力学(第七版)课后题答案哈工大 . 高等教育出版社F1FAyAFAyF AxAFCxCFCyF Ax(f2)(g)FTD CFCx(g2)CFCyFAyA FAxF BBDF 1FCxF2F ByFBxB(f3)F BCBP(g1)F CyF TC FCxP(g3)F Cy FB(h)FAyAF BBFAx(h1)AF AxFAyCF2FCx B(h2)(i)FCyFCx CF CyA F EFOyF FOxC DFCx EO B(i1) (i2)5理论力学(第七版)课后题答案 哈工大 . 高等教育出版社A AF AxFF AyF E E C DFOyFBy FB yO FOxFBx F BxB B(i3) (i4)FAyD EFCxA F Ax CC FBy F TH FBy FCy BPBFBxFB x(j )(j1) (j2)FAy F DyFDF T2F T 2 E FAx CF C x EyF Dx F Ex A D FDx E FF T1F Ey F T3ExF Dy F (j3)(j4)(j5)CyEF F B D CEF CxB F CyF(k1)DE(k)FF BFCBFCxE CFCy90FD D DEFAy AyFA FAx A FAx(k2) (k3)6理论力学(第七版)课后题答案哈工大 . 高等教育出版社AF A(l)(l1) F2F D DEFE(l3)或F 1 F B FDy F Dy F 2F DxB D F Dx DC EF ExFC F Ey(l2) ’(l3) ’F AD(m)F ADDE HF B F1FF DBBB DCF C(l2)F1 F2DBA C EFA FC FE(l4)F1F2DBAC E FExF A F C F Ey(l4) ’AFCyFCxCF1B(m1)FADF2AF E FH D FAD(m2) (m3)7理论力学(第七版)课后题答案哈工大 . 高等教育出版社A FN AF kFOyO (n)FN1B D qF BF N 2FN3(n2)BF AA(o)BFN B FOx B(n1)FD FFCFEF GG C E(o1)FB DF BD FA FA F BF CFD C(o2) (o3)图 1-2F ED F F F(o4)E8理论力学(第七版)课后题答案 哈工大 . 高等教育出版社 第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A , B 和 C 处受 3 个力作用,如图 2-1a 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)第10章 二端口网络求图示各二端口网络的Y 参数。
22u (b)图题解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222*********()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y "(b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y一个互易网络的两组测量值如图题所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题解:图(a)中 11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,?由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得222jA 1V I Y ==⨯ (3)对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 求图示各二端口网络的Z 参数。
\(b)图题解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z (b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω ~求图示各二端口网络的A 参数。
(a)-+-+2(b)u 2++--图题解 (a):列写节点电压方程121122111() (1)51010111() (2)10510U U I U U I ⎧+-=⎪⎪⎨⎪-++=⎪⎩ 由式 (2)得122310()U U I =+-(3)代入式(1)整理得1220.83()I U I =+-(4)^由式(3)和(4)得3100.8S 3Ω⎡⎤=⎢⎥⎣⎦A(b)解:根据基尔霍夫定律和理想变压器方程得1111112u R i u R i nu '=+=+ (1) 1121222//()/i u R i nu R i n ''=+=+- (2) 将式(2) 代入式(1)整理得112212(1/)(/)()u R R nu R n i =++- (3)由式(3)和(1)得 ()121211R R nR n n R n ⎡+⎤=⎢⎥⎣⎦A¥图示二端口网络。
当开关S 断开时测得3129V,5V,3V U U U ===;开关S 接通时测得38V U =,14V U =,22V U =。
求网络N 的传输参数矩阵A 。
Ω6图题解:当开关断开时 15V U =,3111A 4ΩU U I -== ,220 , 3V I U == 由传输参数方程得:11215313A A =⨯⎧⎨=⨯⎩ ⇒ 11215313A A =⎧⎨=⎩ 当开关接通时 31114V,1A 4U U U I -===Ω,22212V,A 63U U I =-==Ω 由参数方程又得?1222514233111233A A⎧=⨯+⨯⎪⎪⎨⎪=⨯+⨯⎪⎩ ⇒122221A A =⎧⎨=⎩ 所以 5/321/3S 1Ω⎡⎤=⎢⎥⎣⎦A求图示各二端口网络的H 参数。
(a)2++--1u 2图题解:(a) 列写网孔电流方程如下:()11221240(1)40100 (2)U I I U I I =+⎧⎨=+⎩由式(2)得2122112220.40.01I I U H I H U =-+=+ (3)!代入式(1)整理得 112111122240.4U I U H I H U =+=+ (4) 由式(3)和(4)得240.40.40.01S Ω⎡⎤=⎢⎥-⎣⎦H (b) 根据KVL 和理想变压器方程得1112212222 (1) (2) (3)u R i nu i ni u u R i '=+⎧⎪=-⎨⎪'=-⎩ 将式(3)及式(2)代入式(1)整理得()21121221u R n R i nu i ni ⎧=++⎪⎨=-⎪⎩ 所以 2120R n R n n ⎡⎤+=⎢⎥-⎣⎦H 已知由二端口网络组成的电路如图所示,若该二端口网络的Y 参数矩阵为0.40.2S 0.20.6-⎡⎤=⎢⎥-⎣⎦Y ,试根据已知条件求0I 。
Ω{图题解:将端口电流为变量,列写改进节电法方程n1n21n1n2211124V ()1111111()111U U I U U I +-=--++=-补充二端口网络的参数方程1122120.40.20.20.6I U U I U U =-=-+又因为 1n12n2,U U U U == 以上表达式联立求解得 n1n213V,6V U U ==n206A 1U I ==Ω、设二端口网络的阻抗参数4335⎡⎤=Ω⎢⎥⎣⎦Z 。
(1)求它的混合参数矩阵H ;(2)若110A i =,220V u =,求它消耗的功率。
解:(1)由阻抗参数方程得11221243 (1)35 (2)u i i u i i =+⎧⎨=+⎩ 由式(2)得 2120.60.2i i u =-+(3)代入式(1)得1112124 1.80.6 2.20.6u i i u i u =-+=+ (4)由式(3)和(4)得2.20.60.60.2S Ω⎡⎤=⎢⎥-⎣⎦H (2) 若110A i =,220V u =,由式(3)和(4)解得1(2.2100.620)V 34V u =⨯+⨯=|2(0.6100.220)A 2A i =-⨯+⨯=-功率1122341020(2)300W p u i u i =+=⨯+⨯-=注释:二端口消耗的功率等于两个端口消耗功率之和。
试绘出对应于下列开路阻抗矩阵的任一种二端口网络模型。
(a)3112⎡⎤Ω⎢⎥⎣⎦; (b)14/2/2/32/s s s s +⎡⎤Ω⎢⎥+⎣⎦; (c)3244⎡⎤Ω⎢⎥-⎣⎦ 解:(a)中阻抗矩阵为对称矩阵,且矩阵中元素均为实数,故可用由电阻组成的T 形电路来等效。
如图(a)所示。
其中11112312R Z Z =-=-=Ω,22212211R Z Z =-=-=Ω,3121R Z ==Ω。
](b) 阻抗矩阵也为对称矩阵,但其元素含有1/s ,因此须用含有电容的T 形电路等效,如图 (b)所示。
其中1111211()12/1/()Z s Z Z s R sC =-=+=+,222122()3Z s Z Z R =-==,3122()2/1/()Z s Z s sC ===,即 11R =Ω,23R =Ω,120.5F C C == (c)所示矩阵不是对称矩阵,对应的二端口方程可写成如下形式⎭⎬⎫-+=+=221221164223I I I U I I U虚线左侧部分可用T 形电路等效,16I 用一个电流控制电压源表示,如图 (c)所示。
(a)(b)(c)+-+2U 证明给定Y 参数可以用图题所示电路来等效,求等效电路参数。
-+U 2U +-、图题解:对该电路列写节点电压方程如下:113132113132231232131232()()()()()I Y Y U Y U gU Y Y g U Y U I Y U Y Y U gU Y g U Y Y U ⎧=+-+=++-⎨=-++-=-+++⎩ 与导纳参数标准形式对比得:1311Y Y g Y ++=,312Y Y -= 321()Y g Y -+=,2322Y Y Y +=解得:11121222123121221,,,Y Y Y Y Y Y Y Y g Y Y =+=+=-=-证明给定Z 参数可以用图题所示电路来等效,求等效电路参数。
Z Z 2;图题解:选回路如图所示,列写回路电流方程11313211333223123231331232()()()()()()U Z Z I Z I I Z Z Z I Z I U Z I Z Z I Z I Z Z I Z Z I ββββ⎧=+++=+++⎨=+++=+++⎩ 与阻抗参数标准形式对比得:11133Z Z Z Z β=++,123Z Z =2133Z Z Z β=+,2223Z Z Z =+解得:11121Z Z Z =-,22212Z Z Z =-,312Z Z =,2112/1Z Z β=-图示电路中二端口网络N 的电阻参数矩阵为4245⎡⎤=Ω⎢⎥⎣⎦R ,求二端口N 的端口电压1U 和2U 。
~14V1Ω图题解:由二端口的参数方程得:1122124245U I I U I I =+⎧⎨=+⎩ (1) 由端口特性得11221421U I U I =-⎧⎨=-⨯⎩ (2) 由式(1)和式(2)联立解得18V U =,22V U =…图示二端口网络N 的阻抗参数矩阵为6446⎡⎤=Ω⎢⎥⎣⎦Z 。
问L R 为何值时可获得最大功率,并求出此功率。
(a)(b)(c)图题解:方法一,将二端口网络用T 形电路等效,如图(b)所示。
由图(b)得a ,b 端口的开路电压OC 424V 12V 422U =⨯=++等效电阻i 14242R =⨯Ω+Ω=Ω ,戴维南等效电路如图(c)所示。
所以当4L R =Ω时它可获得最大功率。
22OC maxi 129W 444U P R ===⨯ 方法二,由二端口参数和端口条件得出戴维南等效电路。
—由二端口网络N 的阻抗参数矩阵和端口参数得:111224V 264U I I I =-Ω⨯=Ω⨯+Ω⨯ (1)21246U I I =Ω⨯+Ω (2)由式(1)得:123A 0.5I I =-代入式(2)解得:2212V 4U I =+Ω由此表达式写出戴维南等效电路如图(c)所示。
求最大功率与上述相同。
图示电路,已知S 15cos 2V u t =,二端口网络阻抗参数矩阵10j6j64⎡⎤=Ω⎢⎥⎣⎦Z 。
