运筹学导论第八版6网络模型.pptx
合集下载
运筹学课件 第六章图与网络分析(清华大学出版社)
w(P ) = min w(P) 0
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
运筹学:第6章 图与网络分析

给图中的点和边赋以具体的含义和权值,我们称 这样的图为网络图(赋权图)
2021/4/18
6
图中的点用 v 表示,边用 e 表示,对每条边可用
它所联结的点表示,如图,则有:
e1 = [v1 , v1], e2 = [v1 , v2]或e2= [v2 , v1]
2021/4/18
7
用点和点之间的线所构成的图,反映实际生产和 生活中的某些特定对象之间的特定关系。
第一种解法:
1. 在点集中任选一点,不妨取 S,令 V={S} 2. 找到和 S 相邻的边中,权值最小的 [S , A] 。
2021/4/18
22
3.V={S , A} 4. 重复第2,3步,找到下一个点。
2021/4/18
23
第二种做法求解过程:
2021/4/18
24
破圈法求解步骤:
1. 从图 N 中任取一回路,去掉这个回路中边 权最大的边,得到原图的一个子图 N1。
Dijkstra 算法假设:
1.设 dij 表示图中两相邻点 i 与 j 的距离,若 i 与 j 不相邻,令 dij =∞,显然 dii =0。 2. 设 Lsi 表示从 s 点到 i 点的最短距离。
2021/4/18
31
求从起始点 s 到终止点 t 的最短路径。 Dijkstra 算法步骤:
1.对起始点 s ,因 Lss =0 ,将 0 标注在 s 旁的小 方框内,表示 s 点已标号;
终点重合的链称为圈,起点和终点重合的路称为回
路,若在一个图中,每一对顶点之间至少存在一条
链,称这样的图为连通图,否则称该图为不连通的。
2021/4/18
12
2021/4/18
链
2021/4/18
6
图中的点用 v 表示,边用 e 表示,对每条边可用
它所联结的点表示,如图,则有:
e1 = [v1 , v1], e2 = [v1 , v2]或e2= [v2 , v1]
2021/4/18
7
用点和点之间的线所构成的图,反映实际生产和 生活中的某些特定对象之间的特定关系。
第一种解法:
1. 在点集中任选一点,不妨取 S,令 V={S} 2. 找到和 S 相邻的边中,权值最小的 [S , A] 。
2021/4/18
22
3.V={S , A} 4. 重复第2,3步,找到下一个点。
2021/4/18
23
第二种做法求解过程:
2021/4/18
24
破圈法求解步骤:
1. 从图 N 中任取一回路,去掉这个回路中边 权最大的边,得到原图的一个子图 N1。
Dijkstra 算法假设:
1.设 dij 表示图中两相邻点 i 与 j 的距离,若 i 与 j 不相邻,令 dij =∞,显然 dii =0。 2. 设 Lsi 表示从 s 点到 i 点的最短距离。
2021/4/18
31
求从起始点 s 到终止点 t 的最短路径。 Dijkstra 算法步骤:
1.对起始点 s ,因 Lss =0 ,将 0 标注在 s 旁的小 方框内,表示 s 点已标号;
终点重合的链称为圈,起点和终点重合的路称为回
路,若在一个图中,每一对顶点之间至少存在一条
链,称这样的图为连通图,否则称该图为不连通的。
2021/4/18
12
2021/4/18
链
运筹学PPT完整版

线性规划通常解决下列两类问题:
(1)当任务或目标确定后,如何统筹兼顾,合理安排,用 最少的资源 (如资金、设备、原标材料、人工、时间等) 去完成确定的任务或目标 (2)在一定的资源条件限制下,如何组织安排生产获得最 好的经济效益(如产品量最多 、利润最大.)
线性规划问题的数学模型
例1.1 如图所示,如何截取x使铁皮所围成的容积最 大?
(2)
x j 0, j 1,2,, n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 27
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
最优解:使目标函数达到最大值的可行解。
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在工商管理中的应用
运筹学简述
Page 2
运筹学(Operations Research) 系统工程的最重要的理论基础之一,在美国有人把运筹
学称之为管理科学(Management Science)。运筹学所研究的 问题,可简单地归结为一句话: “依照给定条件和目标,从众多方案中选择最佳方案” 故有人称之为最优化技术。
Page 3
运筹学的主要内容
Page 4
数学规划(线性规划、整数规划、目标规划、动态 规划等) 图论 存储论 排队论 对策论 排序与统筹方法 决策分析
本课程的教材及参考书
Page 5
❖选用教材 ➢ 《运筹学基础及应用》胡运权主编 哈工大出版社
❖参考教材 ➢ 《运筹学教程》胡运权主编 (第2版)清华出版社 ➢ 《管理运筹学》韩伯棠主编 (第2版)高等教育出版社 ➢ 《运筹学》(修订版) 钱颂迪主编 清华出版社
(1)当任务或目标确定后,如何统筹兼顾,合理安排,用 最少的资源 (如资金、设备、原标材料、人工、时间等) 去完成确定的任务或目标 (2)在一定的资源条件限制下,如何组织安排生产获得最 好的经济效益(如产品量最多 、利润最大.)
线性规划问题的数学模型
例1.1 如图所示,如何截取x使铁皮所围成的容积最 大?
(2)
x j 0, j 1,2,, n (3)
求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值。
线性规划问题的数学模型
Page 27
可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。
最优解:使目标函数达到最大值的可行解。
绪论
本章主要内容: (1)运筹学简述 (2)运筹学的主要内容 (3)本课程的教材及参考书 (4)本课程的特点和要求 (5)本课程授课方式与考核 (6)运筹学在工商管理中的应用
运筹学简述
Page 2
运筹学(Operations Research) 系统工程的最重要的理论基础之一,在美国有人把运筹
学称之为管理科学(Management Science)。运筹学所研究的 问题,可简单地归结为一句话: “依照给定条件和目标,从众多方案中选择最佳方案” 故有人称之为最优化技术。
Page 3
运筹学的主要内容
Page 4
数学规划(线性规划、整数规划、目标规划、动态 规划等) 图论 存储论 排队论 对策论 排序与统筹方法 决策分析
本课程的教材及参考书
Page 5
❖选用教材 ➢ 《运筹学基础及应用》胡运权主编 哈工大出版社
❖参考教材 ➢ 《运筹学教程》胡运权主编 (第2版)清华出版社 ➢ 《管理运筹学》韩伯棠主编 (第2版)高等教育出版社 ➢ 《运筹学》(修订版) 钱颂迪主编 清华出版社
第六章运筹学图与网络-PPT课件

C
哥尼斯堡七桥问题变为,能否从图 的某一点开始不重复地一笔画出 这个图形.你能一笔画出吗?
B 欧拉在论文中证明了这是不可 能的.为什么?
A
D
理由是:图上的每一个顶点都与 奇数条边相连接,不可能一笔画 出.
第一节 图的基本概念与基本定理 一.图的基本概念 日常生活中我们见过大量的图,如各种交通图, 各种管网图(电网图,自来水管网,煤气管网,计 算机网络).都是用点表示研究对象,用线(边) 表示这些对象间的关系.因此,图可以定义为点 和边的集合.记作G=[V,E],其中V是点的集合,E 是边的集合.在图的点和边上赋予权值(如距离, 费用,容量等)则称这样的图为网络图记为N,网 络图又可分有向网络图和无向网络图.
B
C
结果:比赛顺序 是A,C,B,F,E,D.
D
A
F
E
练习1 有甲,乙,丙,丁,戊,己六名运动员报名参 加A,B,C,D,E,F六个项目比赛.报名情况如下表, 问六个项目的比赛顺序如何安排,做到每名运 动员不连续参加两项比赛.
A 甲 乙 丙 丁 戊 己 * * * * * * * B C D * * * * * E F *
铁路的转用线,管理机构图,学科分类图,AHP决策方法 等,都可用树来表示.
树的特点:1.树是边数最多的无圈连通图,即在 树上再任意增加一条边,必定出现圈; 2.树的任意两点间,有一条且仅有一 条通路.也可以说,树是最脆弱的连通图,只要 在树中去掉任一条边,图就不连通了.
图的最小部分树(最小生成树):设 G 2 是一个图,如 果 G 1 是 G 2 的支撑子图(部分图),且 G 1 是一个树, 则称 G 1 是 G 2 的部分树.树的各条边称为树枝.在 图的每条边上赋予权值的图称为赋权图. 在 G 2 中一般含有许多部分树,其中树枝总长为 最小的部分树,称为该图的最小部分树.
哥尼斯堡七桥问题变为,能否从图 的某一点开始不重复地一笔画出 这个图形.你能一笔画出吗?
B 欧拉在论文中证明了这是不可 能的.为什么?
A
D
理由是:图上的每一个顶点都与 奇数条边相连接,不可能一笔画 出.
第一节 图的基本概念与基本定理 一.图的基本概念 日常生活中我们见过大量的图,如各种交通图, 各种管网图(电网图,自来水管网,煤气管网,计 算机网络).都是用点表示研究对象,用线(边) 表示这些对象间的关系.因此,图可以定义为点 和边的集合.记作G=[V,E],其中V是点的集合,E 是边的集合.在图的点和边上赋予权值(如距离, 费用,容量等)则称这样的图为网络图记为N,网 络图又可分有向网络图和无向网络图.
B
C
结果:比赛顺序 是A,C,B,F,E,D.
D
A
F
E
练习1 有甲,乙,丙,丁,戊,己六名运动员报名参 加A,B,C,D,E,F六个项目比赛.报名情况如下表, 问六个项目的比赛顺序如何安排,做到每名运 动员不连续参加两项比赛.
A 甲 乙 丙 丁 戊 己 * * * * * * * B C D * * * * * E F *
铁路的转用线,管理机构图,学科分类图,AHP决策方法 等,都可用树来表示.
树的特点:1.树是边数最多的无圈连通图,即在 树上再任意增加一条边,必定出现圈; 2.树的任意两点间,有一条且仅有一 条通路.也可以说,树是最脆弱的连通图,只要 在树中去掉任一条边,图就不连通了.
图的最小部分树(最小生成树):设 G 2 是一个图,如 果 G 1 是 G 2 的支撑子图(部分图),且 G 1 是一个树, 则称 G 1 是 G 2 的部分树.树的各条边称为树枝.在 图的每条边上赋予权值的图称为赋权图. 在 G 2 中一般含有许多部分树,其中树枝总长为 最小的部分树,称为该图的最小部分树.
运筹学-6(图与网络分析)PPT课件

4
3
验证:第一圈内总长:3+4+5+4+7=23 第一圈逆时针内配送路长:3+4+5=12>11.5,则不是最优方案 第二圈内配送路长:4+2+3+4=13 第二圈逆时针内配送路长:2<6.5,则是最优方案。 第二圈顺时针内配送路长:3<6.5,则是最优方案。
修正第一圈内方案,取逆时针方向最小值1,然后逆时针方向配送路线减去 1,顺时针方向配送及未走路线加上1,则得到第一圈内配送路长:5<总长 一半,则是最优方案。如图所示:
相关 成本
A 4C
E
A 5C
E F
A 6C
F I
D D, F F, I
D D I H, G
D D H, G H, J
348 291, 228 294, 258
348 291 258 288, 360
348 291 288, 360 390, 384
第n个 最近
节点
最小 成本
最新 连接
A到各 N节点 最短 路径
6.2.2 网络图的绘制原则
只能有一个始点事项和一个终点事项 不允许出现编号相同的箭线 不允许出现循环线路 作业要始于结点终于结点
网 络 规 则(2)
1、避免循环、不留缺口
2、一一对应:一道工序用两个事项表示
F 228 CF A→C→F
I
258 EI A→B→E
→I
H 288 FH A→C→F →H
步 已解点 候选点 骤
相关 成本
A C 7F I H
F 8I
H D
D D G J G, J
G J J G
348 291 360 384 336, 414 360 384 414 396
运筹学6网络模型

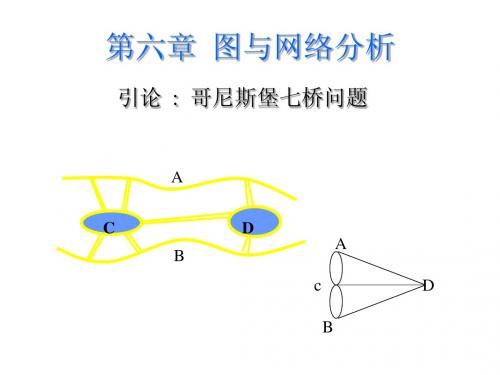
十八世纪东普鲁士哥尼斯堡城(今俄罗斯加里宁格勒)的普莱 格尔河,它有两个支流,在城市中心汇成大河,中间是岛区, 河上有7座桥,将河中的两个岛和河岸连结,如下图所示。由 于岛上有古老的哥尼斯堡大学,有教堂,还有哲学家康德的墓 地和塑像,因此城中的居民,尤其是大学生们经常沿河过桥散 步。
A
C
D
18世纪游戏: 你能从A、B、C或D任意一点出发 走遍7座桥并且每座桥只走一次最 后回到原出发点吗? A D C
e2 e 4
e5
e1 v1 e3 v3
e6
v4
e7
e8
v5
图6-1
定义2 有向图:
如果图的每条边都有一个方向则称为有向图
定义3 混合图:
如何图G中部分边有方向则称为混合图
② ⑤
① ③
④
⑥
有向图
定义4
网络(赋权图):
设图G=(V,E),对G的每一条边(vi,vj)相应的有一条数w
(vi,vj) (或记为wij),wij称为边(vi,vj)的权,赋有权的图G称为网络
几个定义:
如图6-1
V v1 , v2 ,, v5 , E e1 , e2 ,, e8
e2可记作: e2 [v1 , v2 ]
定义1 端点,关联边 若边e表示为e=[vi,vj],称vi和vj是边e v2 的端点,反之称边e为点vi或vj的关联边。 例如图6-1: v2和v4是边e6的端点,而边e6是点v2、v4的关 联边。
(赋权图)。 这里的权数可以是时间、费用、距离等,视不同背景代表不同 的含义。 15 ② 7 ⑤ 9 14 10 ④ ① 6 19 20 ⑥ ③ 25 赋权图
定义5 子图、支撑子图(生成子图) 图G1={V1、E1}和图G2={V2,E2}如果 V1 V2和E1 E2 称G1是G2的一个子图。 若有 V1=V2,E1 E2 则称 G1是G2的一个支 e1 撑子图(部分图)。 v1 e2 e e3 图6-2(a)是图 6-1的一个子图,图6-2(b) 4 v3 是图 6-1的支撑子图,注意支撑子图也是子图, v2 e1 e5 子图不一定是支撑子图。 e6 e8 e7 v1 e2 e3 e4 v2 v3 v5 v2 v3 v4 e5 图6-1 e6 e8 e6 e7
运筹学06图与网络分析PPT演示文稿
v4
v1 v2 v3 v4 v5 v1 0 1 1 0 0
起 v2 1 0 0 1 1
点 v3 1 0 0 0 1
v5
v4 0 1 0 0 1
v5 0 1 1 1 0
19
❖ 赋权无向图的邻接矩阵表示
▪ 两顶点之间有边相连的,写上其权数,无 边相连的记为∞,对角线上的数字为0。赋 权无向图对应的矩阵也是对称的。
1 图的基本概念
❖ 案例导引 ❖ 图论中的图 ❖ 图的矩阵描述
2
案例导引
❖ 图论是运筹学的一个重要分支,对其最早的 研究可以追溯到著名的哥尼斯堡七桥问题 (Konigsberg Bridges Problem)。18世纪,欧洲 的哥尼斯堡城有一条流经全城的普雷戈尔河, 河的两岸与河中两个小岛及两岛之间有七座 桥彼此相通(如左图)。
22
树及其性质
❖ 树在现实中随处可见,如电话线架设、比赛 程序、组织结构等。
❖ 树:连通的无圈的无向图称为树。
23
❖ 树的性质 ❖ 图G=(V,E),p个点、q条边,下列说法是等价
的 ▪ (1)G是一个树 ▪ (2)G连通,且恰有p-1条边 ▪ (3)G无圈,且恰有p-1条边 ▪ (4)G连通,但每舍去一边就不连通 ▪ (5)G无圈,但每增加一边即得唯一一个圈 ▪ (6)G中任意两点之间恰有一条链(简单链)
30
❖在根树中,若每个顶点的出次小于或等 于M,称这棵树为M叉树。
❖若每个顶点的出次恰好等于M或者零, 则称这棵树为完全M叉树。
❖当M=2时,称为二叉树、完全二叉树。
31
❖ 如图所示的树是根树。其 中根、分枝点、叶;各点 层次都标注在树上。
❖ 这是一棵三叉树
三叉树
根
运筹学课件 第六章图与网络分析
v 若 eij i , v j ,称 vi , v j 是边 eij 的端 点,反之,称边 eij 为点 v i 或 v j 的关联边。 若点 vi , v j 与同一条边关联,称点 vi v j 相邻; 若边 和 具有公共的端点,称 ei ei ej 和 相邻
e3 e13 v1, v3 v3 , v1 e31
2013-12-3
18
图中有些点和边的交替顺序 0 , e1 , v1 ,...,ek , vk v ,若其中各边 e1 , e2 ,...,ek 互不相同,且对 任意 vt 1 和 vt (2 t k ) 均相邻,称为 链。 上图中 1 v5 , e8 , v3, e3, v1, e2 , v2 , e4 , v3, e7 , v4
27
解
因要使上述村镇全部通上电,村镇之间必 须连通,又图中必不存在圈,否则从图中去掉一 条边图仍连通,就一定不是最短路线,故架设长 度最短的路线就是从上图中寻找一棵最小树。
2013-12-3
28
用避圈法时,先从图中任选一点 S , 令 S V ,其余点 V , V 与 V 间的最 短边为( S , A) ,将该边加粗,标志它是最小 树内的边。再令 V A V ,V V A 重复上述步骤,一直到所有点连通为止。过程 如下:
如果用点表示研究的对象,用边表示这些 对象之间的联系,则图G可以定义为点与边的集 合,记作 G , E V
V v1 , v2 ,...,vn
E e1 , e2 ,..,em
式V是点的集合,E是边的集合。
2013-12-3 13
注意,上面定义的图G区别于几何学中的图。 几何学中,图中点的位置、线的长度和斜率等都 十分重要,而这里只关心图中有多少个点以及哪 些点之间有线相连。 如果给图中的点和边以具体的含义和权数 (如距离、费用、容量等)。把这样的图称为网 络图,记作N。 图和网络分析的方法已广泛应用于物理、化 学、控制论、信息论、计算机科学和经济管理等 各领域。
#6 运筹学讲义[图与网络]
有向图
• 由点集 V {vi } 和V 中元素的有序对的一个集合
A {aij (vi , v j )}
所组成的二元组称为有向图,记为D=(V,A)。 其中 V中的元素 vi叫做顶点, A中元素aij叫做以vi为始点(尾),vj为终点 (首)的弧。 aij与aji作为具有不同指向的弧是不同的。
i 1,i k
ik
i 1,i k
x
ki
1
改写上述两个等式为:
i 1,i k
x
n
ik
x kj , xii 0
j 1
n
min Z
i , j 1
w
n
ij
xij
n x1i 1 i 1 n xin 1 i 1 n n s.t. xij x ji ,1 j n i 1 i 1 xii 0, i 1,2,..., n xij 0,1
最短路问题引例
下图为单行线交通网,每弧旁的数字表示通过这条 线所需的费用。现在某人要从v1出发,通过这个交通 网到v8去,求使总费用最小的旅行路线。
v2
6 2 3 1
1
v5
6 10 3 10
2 6
v9
3
v1
v3
2
4
v4
v6
2
v7
4
v8
v2
6 2 3 1 从v1到v8:
1
v5
6 10 3 10
2 6
2
4
7 8
1
5
10
3
6
9
图与网络优化模型
引
言
图论是应用非常广泛的运筹学分支,它 已经广泛地应用于物理学控制论,信息论,工 程技术,交通运输,经济管理,电子计算机等 各项领域。对于科学研究,市场和社会生活中 的许多问题,可以同图论的理论和方法来加以 解决。例如,各种通信线路的架设,输油管道 的铺设,铁路或者公路交通网络的合理布局等 问题,都可以应用图论的方法,简便、快捷地 加以解决。
运筹学课件-第六章图与网络分析
运筹学课件-第六章 图与网络分析
contents
目录
•的算法 • 图的应用
01
CATALOGUE
图的基本概念
图的定义
总结词
图是由顶点(或节点)和边(或弧) 组成的数据结构。
详细描述
图是由顶点(或节点)和边(或弧) 组成的数据结构,其中顶点表示对象 ,边表示对象之间的关系。根据边的 方向,图可以分为有向图和无向图。
04
CATALOGUE
图的算法
深度优先搜索
要点一
总结词
深度优先搜索是一种用于遍历或搜索树或图的算法。
要点二
详细描述
该算法通过沿着树的深度遍历树的节点,尽可能深地搜索 树的分支。当节点v的所在边都己被探寻过,搜索将回溯到 发现节点v的那条边的起始节点。这一过程一直进行到已发 现从源节点可达的所有节点为止。如果还存在未被发现的 节点,则选择其中一个作为源节点并重复以上过程,整个 进程反复进行直到所有节点都被访问为止。
物流网络设计的应用
在物流规划、供应链管理、运输优化等领域有广泛应用,例如通过物 流网络设计优化货物运输路径、提高仓储管理效率等。
生物信息学中的图分析
生物信息学中的图分析
利用图论的方法对生物信息进 行建模和分析,以揭示生物系 统的结构和功能。
生物信息学中的节点
代表生物分子、基因、蛋白质 等。
生物信息学中的边
Dijkstra算法
总结词:Dijkstra算法是一种用于在有向图中查找单源 最短路径的算法。
详细描述:Dijkstra算法的基本思想是从源节点开始, 逐步向外扩展,每次找到离源节点最近的节点,并更新 最短路径。该算法使用一个优先级队列来保存待访问的 节点,并将源节点加入队列中。然后,从队列中取出具 有最小优先级的节点进行访问,并将其相邻节点加入队 列中。这一过程一直进行,直到队列为空,即所有可到 达的节点都已被访问。Dijkstra算法的时间复杂度为 O((V+E)logV),其中V是节点的数量,E是边的数量。
contents
目录
•的算法 • 图的应用
01
CATALOGUE
图的基本概念
图的定义
总结词
图是由顶点(或节点)和边(或弧) 组成的数据结构。
详细描述
图是由顶点(或节点)和边(或弧) 组成的数据结构,其中顶点表示对象 ,边表示对象之间的关系。根据边的 方向,图可以分为有向图和无向图。
04
CATALOGUE
图的算法
深度优先搜索
要点一
总结词
深度优先搜索是一种用于遍历或搜索树或图的算法。
要点二
详细描述
该算法通过沿着树的深度遍历树的节点,尽可能深地搜索 树的分支。当节点v的所在边都己被探寻过,搜索将回溯到 发现节点v的那条边的起始节点。这一过程一直进行到已发 现从源节点可达的所有节点为止。如果还存在未被发现的 节点,则选择其中一个作为源节点并重复以上过程,整个 进程反复进行直到所有节点都被访问为止。
物流网络设计的应用
在物流规划、供应链管理、运输优化等领域有广泛应用,例如通过物 流网络设计优化货物运输路径、提高仓储管理效率等。
生物信息学中的图分析
生物信息学中的图分析
利用图论的方法对生物信息进 行建模和分析,以揭示生物系 统的结构和功能。
生物信息学中的节点
代表生物分子、基因、蛋白质 等。
生物信息学中的边
Dijkstra算法
总结词:Dijkstra算法是一种用于在有向图中查找单源 最短路径的算法。
详细描述:Dijkstra算法的基本思想是从源节点开始, 逐步向外扩展,每次找到离源节点最近的节点,并更新 最短路径。该算法使用一个优先级队列来保存待访问的 节点,并将源节点加入队列中。然后,从队列中取出具 有最小优先级的节点进行访问,并将其相邻节点加入队 列中。这一过程一直进行,直到队列为空,即所有可到 达的节点都已被访问。Dijkstra算法的时间复杂度为 O((V+E)logV),其中V是节点的数量,E是边的数量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网络是反映对象之间关系的一种工具
因此,可以说,在一般情况下,网络中点的相对位置如何, 点与点之间联线的长短曲直,对于反映对象之间的关系,并 不是重要的,例如哥尼斯堡七桥问题。 如例2,也可以用网络去反映五个球队的比赛情况,这与例 3没有本质的区别。所以,图论中的图与几何图、工程图等 是不同的。
8
6.2 最小生成树算法
最小生成树算法是以来链接一个网络所有的节点,使得树上 边的总长度最小。例如,在几个城镇之间修路,使得任意两 个城镇之间都有路相连,之间可以穿过其他城镇那么最经济 的道路网络设计方案就是道路里程最小。 令N={1,2,…,n}是网络中节点的集合,定义:
Ck 在第k步时已经连接起来的节点集合 Ck 在第k步以后需
4
例1
北京
天津
是北京、上海等十个
城市间的铁路交通图。
与此类似的还有电话 线分布图、煤气管道
郑州
图、航空路线图等。
济南 徐州
武汉
南京
青岛 连云港 上海
5
例2
分别用点v1,v2,v3,v4,v5分别代表甲、乙、 丙、丁、戊五支球队。若有两支球队之间比赛 过,就在相应的点之间联一条线,且这条线不 过其他点。如下图所示:
13
6.3 最短路径问题
6.3.1 最短路应用实例
RentCar公司开展了一项4年一周期的汽车更换政策,在每一 年的开始,消费者都可以选择继续使用购买的汽车,也可以选 择更换汽车。一辆汽车最少使用1年,最多3年,下表给出了 汽车更换的费用,它取决于车辆购置时的年数以及使用年限。 客户该如何更换汽车?
1
9
15
3
7
4
C1
迭代1
5
6
C1
2
3
5
1
9
1
6
5
3
74
6
4
C2
迭代2
C2
C3
2
3
5
1
C4
2
3
5
1
1
6
5
3
8
C3
1
6
5
3
8
C4
74 4
45
6
3
6
4
迭代3
迭代4
12
C5
2
3
5
1
1
5
6 3
C5
45
10
3
6
4
迭代5
2 1
1
5
3
45
4
3
5
可选边
3
6
迭代6 (最小生成树)
最小生成树算法在第6步给出了问题的解,要服务的电视 网络线缆长度为1+3+4+3+5=16
v1
v2
可知需要4个库房, 其中一个答案是:
v8 v7
v6
v3
{ v1 }
{ v2, v4, v7 }
v4
{ v3, v5 }
{ v6, v8 }
还有其他的答案。 7 v5
从以上几个例子可见
可以用由点及点与点的联线所构成的网络,去反映实际生活 中,某些对象之间的某个特定的关系,通常用点代表研究的 对象(如城市、球队、药品等等),用点与点的联线表示这 两个对象之间有特定的关系(如两个城市间有铁路线、两个 球队比赛过、两种药品不能存放在同一个库房里等)。
9
最小生成树算法步骤:
第0步 令 C0 ,C0 N
第1步 从 C0 中的任意一个节点i开始,令C1={i}, 那么
C1 N i ,设定 k=2.
一般的第k步 在还没有连接的节点集合 Ck1 中选择一
个节点 j*,使得j*到Ck-1中某个节点之间的弧长
最小,然后将
j*
放在Ck-1,从
Ck
中删除
2
网络模型的定义
网络是由节点(node)和弧(arc)集合组成,用符号(N,A)表示, 其中N表示节点的集合,A表示弧的集合。
1
3
5 N={1,2,3,4,5}
A={(1,2),(1,3),(2,3),(2,5),(3,4),(3,5),(4,2),(4,5)}
2
4
如果一条弧上的其中一个方向的流量是正数,相反方向就是
为零,该弧是有向的(directed),如果所有弧上的容量都是有 向的,则网络是有向网络。将两点之间链接起来,并经过其
他的一些节点的这一些列弧,称之为路径(path),如果经过路 径又能回到自身,则这些路径称之为圈(Loop),如果网络中没 有圈,网络就是树(tree),如果该树包括了图上所有的节点,则 是生成树。
开始购买汽 车的年数
给定年限的更换费用
1
2
3
1
4000
5400
9800
2
4300
6200
8700
3
4800
7100
—
4
4900
—
—
14
该问题可以描述为网络模型,节点1到5表示第1年到第5年每 年的开始。
与节点1(第1年)有弧相连的节点只有2,3,4,因为按照轨道汽车 的使用年限为1到3年。同理,可以推断出从其他节点出发的 弧。每条弧的长度等于更换费用。那么问题等价于求一条从 节点1到5的最短路径。
9800 5400
7100
1 4000 2 4300 3 4800 4 4900 5
6200 8700
可以知道,最短路是1→3→5. 这个解说明汽车在第1年购
买,然后使用2年,在第3年开始的时候更换新的汽车,一
直使用到年底。
15
例
Smart每天开车去工作,如果找最短走,会被限速因此行程 时间不是最短,如果超速会被罚款,所以最短路对smart而 言不是最好选择. 假设已知各个路段相应不被罚款的概率已 知,如下图。他想选择一条不被警察罚款的概率最大的路径, 该如何选择?
1
j*,即
Ck = Ck-1 + j* , Ck = Ck-1 j*
10
例
中西部有线电视公司正在计划为5个新的居民区提供有线电 视服务,下图给出了小区之间可以铺设电缆的情况以及相应 的距离。确定最经济的电缆铺设方案,使得5个小区可以连 接起来。
2
3
5
1
9
1
5
6 3
8
4
7
5
10
3
6
4
11
2
第6章 网络模型
1
6.1 网络模型的应用范围和定义
大量的运筹学问题都可以应用网络建模来求解: a) 在墨西哥海湾上需要设计一个海面上的天然气管道网络,
将各个井口链接到岸边的运输点,模型目标是最小化管 道建设费用。 b) 在已经存在的道路网络中,求起讫点之间的最短路径. c) 求山西煤矿到北京的发电厂的煤浆管道网络的最大运输 量 d) 给一个工程项目中的各项活动确定时间表
3
欧拉 (Euler) 在1736 年发表图论方面的第一篇论 文,解决了著名的哥尼斯堡七桥问题。哥尼斯堡城中有 一条河叫普雷格尔河,该河中有两个小岛,河上有七座 桥,参见图 5.1(a) 。
当时那里的居民热衷于这样的问题:一个散步者能 否走过七座桥,且每座桥只走过一次,最后回到出发点。
A D
C B
v1 v2
v5 v4
v3
可知各队之间的比赛情况如下: 甲—— 乙、丙、丁、戊 乙—— 甲、丙 丙—— 甲、乙、丁 丁—— 甲、丙、戊 戊—— 甲、丁
6
例3 “染色问题”
储存8种化学药品,其中某些药品不能 存放在同一个库房里。 用v1,v2,…,v8分别代 表这8种药品。规定若两种药品不能存放在 一起,则其相应的点之间联一条线。如下 图所示:
因此,可以说,在一般情况下,网络中点的相对位置如何, 点与点之间联线的长短曲直,对于反映对象之间的关系,并 不是重要的,例如哥尼斯堡七桥问题。 如例2,也可以用网络去反映五个球队的比赛情况,这与例 3没有本质的区别。所以,图论中的图与几何图、工程图等 是不同的。
8
6.2 最小生成树算法
最小生成树算法是以来链接一个网络所有的节点,使得树上 边的总长度最小。例如,在几个城镇之间修路,使得任意两 个城镇之间都有路相连,之间可以穿过其他城镇那么最经济 的道路网络设计方案就是道路里程最小。 令N={1,2,…,n}是网络中节点的集合,定义:
Ck 在第k步时已经连接起来的节点集合 Ck 在第k步以后需
4
例1
北京
天津
是北京、上海等十个
城市间的铁路交通图。
与此类似的还有电话 线分布图、煤气管道
郑州
图、航空路线图等。
济南 徐州
武汉
南京
青岛 连云港 上海
5
例2
分别用点v1,v2,v3,v4,v5分别代表甲、乙、 丙、丁、戊五支球队。若有两支球队之间比赛 过,就在相应的点之间联一条线,且这条线不 过其他点。如下图所示:
13
6.3 最短路径问题
6.3.1 最短路应用实例
RentCar公司开展了一项4年一周期的汽车更换政策,在每一 年的开始,消费者都可以选择继续使用购买的汽车,也可以选 择更换汽车。一辆汽车最少使用1年,最多3年,下表给出了 汽车更换的费用,它取决于车辆购置时的年数以及使用年限。 客户该如何更换汽车?
1
9
15
3
7
4
C1
迭代1
5
6
C1
2
3
5
1
9
1
6
5
3
74
6
4
C2
迭代2
C2
C3
2
3
5
1
C4
2
3
5
1
1
6
5
3
8
C3
1
6
5
3
8
C4
74 4
45
6
3
6
4
迭代3
迭代4
12
C5
2
3
5
1
1
5
6 3
C5
45
10
3
6
4
迭代5
2 1
1
5
3
45
4
3
5
可选边
3
6
迭代6 (最小生成树)
最小生成树算法在第6步给出了问题的解,要服务的电视 网络线缆长度为1+3+4+3+5=16
v1
v2
可知需要4个库房, 其中一个答案是:
v8 v7
v6
v3
{ v1 }
{ v2, v4, v7 }
v4
{ v3, v5 }
{ v6, v8 }
还有其他的答案。 7 v5
从以上几个例子可见
可以用由点及点与点的联线所构成的网络,去反映实际生活 中,某些对象之间的某个特定的关系,通常用点代表研究的 对象(如城市、球队、药品等等),用点与点的联线表示这 两个对象之间有特定的关系(如两个城市间有铁路线、两个 球队比赛过、两种药品不能存放在同一个库房里等)。
9
最小生成树算法步骤:
第0步 令 C0 ,C0 N
第1步 从 C0 中的任意一个节点i开始,令C1={i}, 那么
C1 N i ,设定 k=2.
一般的第k步 在还没有连接的节点集合 Ck1 中选择一
个节点 j*,使得j*到Ck-1中某个节点之间的弧长
最小,然后将
j*
放在Ck-1,从
Ck
中删除
2
网络模型的定义
网络是由节点(node)和弧(arc)集合组成,用符号(N,A)表示, 其中N表示节点的集合,A表示弧的集合。
1
3
5 N={1,2,3,4,5}
A={(1,2),(1,3),(2,3),(2,5),(3,4),(3,5),(4,2),(4,5)}
2
4
如果一条弧上的其中一个方向的流量是正数,相反方向就是
为零,该弧是有向的(directed),如果所有弧上的容量都是有 向的,则网络是有向网络。将两点之间链接起来,并经过其
他的一些节点的这一些列弧,称之为路径(path),如果经过路 径又能回到自身,则这些路径称之为圈(Loop),如果网络中没 有圈,网络就是树(tree),如果该树包括了图上所有的节点,则 是生成树。
开始购买汽 车的年数
给定年限的更换费用
1
2
3
1
4000
5400
9800
2
4300
6200
8700
3
4800
7100
—
4
4900
—
—
14
该问题可以描述为网络模型,节点1到5表示第1年到第5年每 年的开始。
与节点1(第1年)有弧相连的节点只有2,3,4,因为按照轨道汽车 的使用年限为1到3年。同理,可以推断出从其他节点出发的 弧。每条弧的长度等于更换费用。那么问题等价于求一条从 节点1到5的最短路径。
9800 5400
7100
1 4000 2 4300 3 4800 4 4900 5
6200 8700
可以知道,最短路是1→3→5. 这个解说明汽车在第1年购
买,然后使用2年,在第3年开始的时候更换新的汽车,一
直使用到年底。
15
例
Smart每天开车去工作,如果找最短走,会被限速因此行程 时间不是最短,如果超速会被罚款,所以最短路对smart而 言不是最好选择. 假设已知各个路段相应不被罚款的概率已 知,如下图。他想选择一条不被警察罚款的概率最大的路径, 该如何选择?
1
j*,即
Ck = Ck-1 + j* , Ck = Ck-1 j*
10
例
中西部有线电视公司正在计划为5个新的居民区提供有线电 视服务,下图给出了小区之间可以铺设电缆的情况以及相应 的距离。确定最经济的电缆铺设方案,使得5个小区可以连 接起来。
2
3
5
1
9
1
5
6 3
8
4
7
5
10
3
6
4
11
2
第6章 网络模型
1
6.1 网络模型的应用范围和定义
大量的运筹学问题都可以应用网络建模来求解: a) 在墨西哥海湾上需要设计一个海面上的天然气管道网络,
将各个井口链接到岸边的运输点,模型目标是最小化管 道建设费用。 b) 在已经存在的道路网络中,求起讫点之间的最短路径. c) 求山西煤矿到北京的发电厂的煤浆管道网络的最大运输 量 d) 给一个工程项目中的各项活动确定时间表
3
欧拉 (Euler) 在1736 年发表图论方面的第一篇论 文,解决了著名的哥尼斯堡七桥问题。哥尼斯堡城中有 一条河叫普雷格尔河,该河中有两个小岛,河上有七座 桥,参见图 5.1(a) 。
当时那里的居民热衷于这样的问题:一个散步者能 否走过七座桥,且每座桥只走过一次,最后回到出发点。
A D
C B
v1 v2
v5 v4
v3
可知各队之间的比赛情况如下: 甲—— 乙、丙、丁、戊 乙—— 甲、丙 丙—— 甲、乙、丁 丁—— 甲、丙、戊 戊—— 甲、丁
6
例3 “染色问题”
储存8种化学药品,其中某些药品不能 存放在同一个库房里。 用v1,v2,…,v8分别代 表这8种药品。规定若两种药品不能存放在 一起,则其相应的点之间联一条线。如下 图所示:
