习题六 简单非线性电阻电路分析.
09非线性电阻电路分析

非线性电阻电路分析一、是非题1.非线性电阻的电流增加k倍,则电压也增加k倍。
2.单调型非线性电阻,随着电压升高,动态电阻也增加。
3.非线性电阻电路小信号分析法的实质是将工作点附近的非线性伏安特性线性化。
4.半导体二极管电路模型是单调型非线性电阻,不属电压控制型、电流控制型。
5.不论非线性电阻或线性电阻串联,总功率等于各元件功率之和,总电压等于各元件电压之和。
答案部分1.答案(-)2.答案(-)3.答案(+)4.答案(-)5.答案(+)二、单项选择题1.影响非线性电阻阻值变化的因素主要是(A)时间 (B)温度 (C)电压或电流2.双向性非线性电阻的伏安特性曲线为3.有关非线性电阻电路的正确概念应是(A)不同类型的非线性电阻其动态电阻定义不同(B)单向型非线性电阻不具有单调型电阻性质(C)非线性电阻可能在有关电压下具有多个电流值(D)非线性电阻电路功率不守恒4.图示非线性电阻伏安特性曲线中的BC段对应于下列哪个等效电路?5.与图示非线性电阻伏安特性曲线AB段对应的等效电路是答案部分1.答案(C)2.答案(B)3.答案(C)4.答案(B)5.答案(B)三、填空题1.非线性电阻元件的性质一般用__________来表示。
2.图示电路中的理想二极管,流过的电流I为_______A。
3.右上图示曲线①和②为非线性电阻R1和R2的伏安特性曲线。
试画出R1、R2并联后的等效伏安特性。
4.图示隧道二极管伏安特性曲线,试分析i S=4mA、i S=1mA、i S=-2mA三种情况下,隧道二极管的工作点。
i S=4mA时____,i S=1mA时_____,i S=-2mA时____。
6.理想二极管伏安特性曲线如图(b)折线所示,试绘出图(a)所示网络的伏安特性曲线。
1.答案伏安特性曲线2.答案-13.答案4.答案当i S=4mA时,有三个工作点u=0.1V u=0.35V u=0.7Vi S=1mA时,有一个工作点u=0.05Vi S=-2mA时,无工作点6.答案1.试求图示伏安特性曲线AB、BC、CD段的动态电阻。
非线性电阻电路的分析方法

非线性电阻元件的图形符号与伏安函数关系:
i
+ u
u=f(i) i=g(u)
非线性电阻元件分类
流控电阻 压控电阻 单调型电阻
1 流控电阻:电阻两端电压是其电流的单值函数。
i
对每一电流值有唯一的电压与 之对应,
对任一电压值则可能有多个电流与之对应
(不唯一)。
某些充气二极管具有类似伏安特性。
0
u
流控电阻的伏安特性呈“S”型。
例:一非线性电阻
uf(i)10 i0 i3
(1) 分别求 i1 = 2A, i2 = 2Sin314t A, i3 = 10A时 对应电压 u1,u2,u3;
u110 i1 0i1 320 V8
u210i2 0i23
20s0i3n1t48s i3n 31t 4( s i3θ n3sθ in4s iθ 3n)
i1 G 1 ( U n1 U s )
i2 G 2( U n1 U n3 )
i3 5( U n1 U n2 )3
i4 10 ( U n 2 U n 3 )1 3
i5
15 U
15 n2
则节点方程为
i2
i3 U n1 + u 3 G 1 i1
+
Us
G2
Un2 i4
+
+
u5
i5
u4 Un3 Is
例:一非线性电阻
uf(i)10 i0 i3
(1) 分别求 i1 = 2A, i2 = 2Sin314t A, i3 = 10A时 对应电压 u1,u2,u3;
(2) 设 u12 = f (i1 + i2 ),问是否有u12= u1 + u2?
非线性电阻电路的数值解法ppt课件.ppt
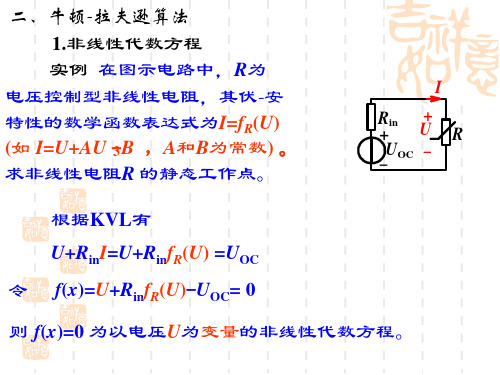
f(x (2)) f(x (3))
以 f(x (1))处的线性 方程F(x)=0(切线),使 用迭代公式逐步逼近 真解。
0
x(3)x (2) x (1) x
真 解
几点结论:
(1)牛顿-拉夫逊法是否能求得满足要求的近似解,取 决于非线性元件的伏-安特性和初始猜测值。
(2) 能得到满足要求的近似解时称为收敛,否 则称为不收敛。
10-5 非线性电阻电路的小信号分析法
一、小信号和动态电阻
1.小信号 在直流和交变电源共同激励下的非线性电路中,若交变 激励源的幅值(或有效值)远远小于直流值, 则此交变激励源称为小信号。
在非正弦激励下的非线性电路中,若交流分量的幅值(或
有效值)远远小于直流分量,则此交流分量称为小信号。
+ US +uS(t)
=
x(1) -
f (x(1)) f (x(1))
若此x不是 F(x)=0的解,可将其作为第二次猜测值x(2)
即可有
x(2)=
x(1) -
f (x(1)) f (x(1))
同理即可有
x(3)=
x(2) -
f (x(2)) f (x(2))
……
x(n+1) =
x(n) -
f (x(n)) f (x(n))
二、牛顿-拉夫逊算法
1.非线性代数方程 实例 在图示电路中,R为 电压控制型非线性电阻,其伏-安 特性的数学函数表达式为I=fR(U) (如 I=U+AU -3B ,A和B为常数) 。 求非线性电阻R 的静态工作点。
I
Rin +
+ U
R
-UOC -
根据KVL有 U+RinI=U+RinfR(U) =UOC 令 f(x)=U+RinfR(U)-UOC= 0 则 f(x)=0 为以电压U为变量的非线性代数方程。
电路原理 (1.8.7)--非线性电阻电路分析补充习题
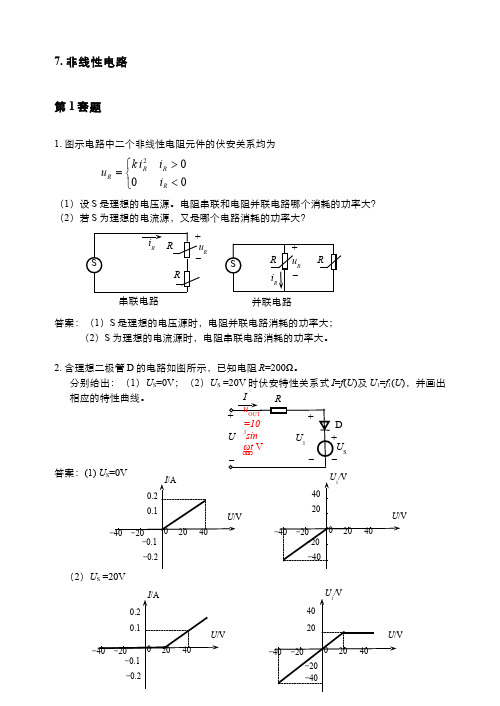
7. 非线性电路第1套题1. 图示电路中二个非线性电阻元件的伏安关系均为⎩⎨⎧<>=002R R RR i i i k u (1)设S 是理想的电压源。
电阻串联和电阻并联电路哪个消耗的功率大?(2)若S 为理想的电流源,又是哪个电路消耗的功率大?答案:(1)S 是理想的电压源时,电阻并联电路消耗的功率大;(2)S 为理想的电流源时,电阻串联电路消耗的功率大。
2. 含理想二极管D 的电路如图所示,已知电阻R =200Ω。
分别给出:(1)U S =0V ;(2)U S =20V 时伏安特性关系式I =f (U )及U 1=f 1(U ),并画出相应的特性曲线。
答案:(1) U S =0V (2)U S =20VU S DR 串联电路并联电路3. 图示电路中,二端元件N 的伏安特性为⎩⎨⎧<>+=0 0012I I I U 求电路中的电压U 、电流I 和I 1。
答案:I =1A ,U =2V ,I 1=1A 。
4.图示电路中已知电阻R 1=R 2=25Ω,R 3=50Ω,电流源I S =3.2A ,非线性电阻的伏安特性曲线如右图所示。
求:流过非线性电阻的电流I 以及电流源I S 发出的功率。
答案:I =0.2A ; P IS 发 =184w5. 图示电路中非线性电阻元件的伏安特性为:⎩⎨⎧<>=-0 001024u u u i ,直流电压U S 和小信号电压u S (t )=10-3sin(ωt )V 共同作用于电路,直流电压U S 使得非线性电阻工作在10V 电压上。
求由小信号作用在输出电压中的增量u out 。
II S8V U -+u SU u out +-答案:mV sin 5.0t u out ω=6. 已知图示电路中2个MOSFET 均工作在饱和区。
假定这2个MOSFET 的特性相同,且特性参数K =4mA/V 2,U T =1V 。
求该电路的输出电压u o 。
§6-3简单非线性电阻电路的分析

解:已知非线性电阻特性的解析表达式,可以用解析法求 已知非线性电阻特性的解析表达式, 求得l 解。由KCL求得 电阻和非线性电阻并联单口的 求得 电阻和非线性电阻并联单口的VCR 方程
i = i1 + i 2 = u − 2u + 1
2Leabharlann i = i1 + i 2 = u − 2u + 1
2
写出l 电阻和 电压源串联单口的 电压源串联单口的VCR方程 写出 电阻和3V电压源串联单口的 方程
图6-9 -
1. 将线性含源电阻单口网络用戴维宁等效电路代替 。 . 将线性含源电阻单口网络用戴维宁等效电路代替。 2.写出戴维宁等效电路和非线性电阻的VCR方程。 .写出戴维宁等效电路和非线性电阻的 方程。 方程
u = u oc − R o i i = g (u )
求得
( 6 − 1)
u = u − Ro g (u )
(6 − 2)
这是一个非线性代数方程;若已知 的解析式, 这是一个非线性代数方程;若已知i=g(u)的解析式, 的解析式 则可用解析法求解:若已知 的特性曲线, 则可用解析法求解:若已知i=g(u)的特性曲线,则可用以 的特性曲线 下图解法求非线性电阻上的电压和电流。 下图解法求非线性电阻上的电压和电流。
i = 3−u
由以上两式求得
u −u −2 = 0
2
求解此二次方程,得到两组解答: 求解此二次方程,得到两组解答:
u = 2 V , i = 1A u = −1V , i = 4 A
图6-11 -
例6-5 电路如图6-11(a)所示。已知非线性电阻特性曲线 电路如图 - 所示。 所示 如图6- 中折线所示。 和电流i。 如图 -11(b)中折线所示。用图解法求电压 和电流 。 中折线所示 用图解法求电压u和电流
第6章 简单非线性电路分析

非线性电阻并联
u u1 u2
端口特性:
i i1 i2 f1 (u1 ) f 2 (u2 ) f (u)
由两函数曲线f1(u1)和f2(u2)的纵坐标相加 即得函数f(u)的曲线。
对非线性电阻串、并联以及混联作DP图的图
解法称为曲线相加法。这种方法普遍适用于流控
电阻、压控电阻以及单调型电阻的串联、并联以
的连接方式对支路变量的约束,而与元件本身
特性无关,因而无论是线性的还是非线性的电
路,按KCL和KVL所列方程是线性代数方程。
例 如图电路,节点a和b可列出KCL方程为
i1 i2 i4 iS i3 i2 i4 0
对于回路I和II,按 KVL可列方程
i4 iS R1
R4 + u4
6.1
非线性元件与非线性电路的 基本概念
1. 非线性元件(nonlinear component ):
当元件的参数值随其端电压或端电流的数值 或方向发生变化时,这样的元件就是非线性元 件,非线性元件的伏安特性不再是通过坐标原 点的直线。 非线性元件也分为二端元件和多端元件以及 时变元件和时不变元件,本章仅讨论非线性时 不变二端电阻元件及其所构成的电路。
将电路元件方程代入所列KCL与KVL可得 :
uR1 2i 6i3 8
2 3
u 16uR1 56 0
uR1 10.828V 或 uR1 5.172V
由此可见,非线性电路的解不是唯一的 。
1. 节点法 若电路中的非线性电阻均为压控型电阻或单 调电阻,则宜选用节点法列写非线性电阻电路方 程。当电路中既有压控型电阻又有流控型电阻时, 直接建立节点电压方程的过程就会比较复杂。
电路学:第5章 非线性电阻电路分析

1 f ' (U 0 ) Gd Rd
Rd成为非线性电阻R在工作点Q(U0,I0)处的小 信号电阻,或称动态电阻。它是个常数。Gd 称为小信号电导,或动态电导。有
u1 (t ) Rd i1 (复杂得多, 所求的解也不一定是唯一的。本章只讨论简 单非线性电阻电路的分析。
5.1非线性电阻
线性电阻:元件的伏安关系为过坐标原点的直线, 可用欧姆定律描述,即u=Ri或i=Gu,且R,G为常数 。
非线性电阻:元件的伏安特性为过坐标原点的曲线( 不是直线),不满足欧姆定律,其R或G是电压或电流 的函数。若R或G不随时间而变化,则称为非线性时不 变电阻。
不难看出,这是一个线
+
uS (t)
-
+ 性电路。可见,在小信 Rd u1 号条件下,可以将非线
- 性电路分析近似转换为
线性电路分析。
这个线性电路只保留了小信号分量部分。当 然,如果需要求 u(t) 和 i(t) ,只需将上式代入 * 式即可。
i(t) u(t)
I0 U
uS (t) RS Rd
非线性电路不能用叠加定理和齐次性定理。
5.2 解析法
当电路中的非线性电阻元件的VCR的数 学函数式已知时,可使用解析法。
例:试求电路中的v和i。非线性电阻R的
VCR为i u2 u 1.。5 A
R1 2
+
R3 1 i 解:由戴维南定理 + 得:
U S 8V
-
R2 2
Ru
-
UOC 4 V , RO 2 UOC ROi u
r为非线性电阻其vcr为i当直流电压源和小信号同时起作用时即时由于信号较小即在工作点q附近可以把非线性电阻近似为一个线性电阻
非线性电阻电路的分析
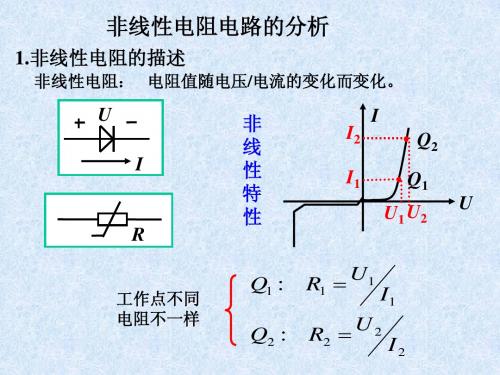
1.非线性电阻的描述 非线性电阻的描述
非线性电阻: 电阻值随电压/电流的变化而变化 电流的变化而变化。 非线性电阻: 电阻值随电压 电流的变化而变化。
U I
非 线 性 特 性
I2 I1
I Q2 Q1 U1 U2 U
R
工作点不同 电阻不一样
Q1 : Q2 :
R1 = R2 =
U1 U2
i
E/R u IQ
非线性部分
+ _ E
R
i
Q u UQ E
线性部分
u = E − iR
i = f (u )
3.动态分析 3.动态分析 -- 微变等效电路法
用动态电阻来代替非线性电阻进行分析。 用动态电阻来代替非线性电阻进行分析。
I1 I2
静态电阻U R = = tgα NhomakorabeaIQ
动态电阻
∆u r= = tgβ ∆i
Q ∆i ∆u
I
i
α
u
U
β
适用于分析微变 电压引起微变电 流的情况
适用于外加固定电压的情况
静态分析-2. 静态分析--图解法
静态分析内容:电路加上恒定直流电压时, 静态分析内容:电路加上恒定直流电压时,求各处 的电压和电流。 的电压和电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题六 简单非线性电阻电路分析
6-1 如题图6-1所示电路中,其中二极管和稳压二极管均采用理想特性,试分别画出其端口的DP 图。
题图6-1
6-2 设一混频器所用的非线性电阻特性为
2
210u a u a a i ++=
当其两端电压)()(t w A t w A u 2211cos cos +=时,求)。
(t i
6-3 试画出下列电阻元件的u -i 特性,并指出3的单调性、压控的还是流控的?
(1)u
e
i -=;
(2)2
i u =;
(3)3
01.01.0u u i +-=。
6-4 试写出题图6-4所示分段线性非线性电阻的u -i 特性表达式。
题图6-4
6-5 如题图6-5(a )所示电路为一逻辑电路,其中二极管的特性如题图6-5(b )所示。
当U 1 = 2 V ,U 2 = 3 V ,U 3 = 5 V 时,试求工作点u 。
题图6-5
6-6 如题图6-6所示电路含有理想二极管,试判断二极管是否导通?
6-7 设有一非线性电阻的特性为u u i 343
-=,它是压控的还是流控的?若)
(wt u cos =,求该电阻上的电流i 。
6-8 如题图6-8所示为自动控制系统常用的开关电路,K 1和K 2
为继电器,导通工作电
流为0.5 mA 。
D 1和D 2为理想二极管。
试问在图示状态下,继电器是否导通工作?
题图6-6 题图6-8
6-9
如题图6-9所示为非线性网络,试求工作点u 和i 。
题图6-9
6-10 如题图6-10所示网络,其中N 的A 矩阵为 A =⎥
⎦
⎤
⎢
⎣⎡Ω5.1s 05.055.2
非线性电阻的VCR 为
2
1u u i +-= 试求工作点u 和i 。
题图6-10
6-11 如题图6-11所示电路中,非线性电阻为N 形特性。
试用作图法求工作点。
题图6-11
6-12 如题图6-12所示电路,已知)(i f Φ=,试列出其状态方程。
6-13 如题图6-13所示电路,已知)(u f q =,试列出其状态方程。
题图6-12 题图6-13
6-14 如题图6-14所示电路,试列出其状态方程。
题图6-14
6-15 运算放大器的输入电压u i >0时就进入非线性区(饱和区),其输入-输出特性如题图6-15(a )所示。
试证明:当u 1≥0时,题图6-15(b )所示电路的u -i 特性为图(c )所示的分段性负阻。
题图6-15
参考答案
6-2 +++++
=]cos [2
22111222120)()()(t w A t w A a A A a a i +-++t w w A A a t w w A A a )()(1221221212cos cos
]2cos 2cos [2
2
21212)()(wt A t w A a + 6-5 u = 2.5 V , i = 2.5 mA 6-7 i = cos (3wt )
6-8 K 1不工作,K 2工作
6-9 u ≈ 5.45 V ,i ≈0.455 mA 6-10 P 1:(2 V ,3 A ),P 2:(-1.5 V ,4.75 A ) 6-11 P 1:(3 V ,7 mA ),P 2:(5 V , 5 mA ),P 3:(6.5 V , 3.5 mA ) 6-12
][1
d d S )()
(t u Ri i L t i +-= 6-13
][1
d d )(C L u f i C
t u -=, ][1d d S )
()(t u t u Ri L t i C L L +--= 6-14
][1d d )(C L C u f i C t u -=, ][1
d d S )()(t u t u Ri L
t i C L L +--=。
