人教版福建省厦门市第五中学八年级数学下册:提高题10(一次函数)
人教版福建省厦门市第五中学八年级数学下册:提高题10(一次函数)

-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点-----------------------------------------------------信达初中数学试卷初二下数学提高题10(一次函数)班级 姓名 座号1.写出两个一次函数,使这两个函数和23+-=x y ,121+=x y 在同一直角坐标系中的图象能围出 一个平行四边形 .2. 一次函数b kx y +=的图象与x 、y 轴分别交于点A (2,0),B (0,4).O 为坐标原点, 设OA 、AB 的中点分别为C 、D ,P 为OB 上一动点,则PC+PD 的最小值为 , 并求取得最小值时P 点的坐标 .3. 已知如图,直线y=-x+2与x 轴、y 轴分别交于点A 、点B ,另一直线y=kx+b (k ≠0)经过点C (1,0),且把△AOB 分成两部分.(1)若△AOB 被分成的两部分面积相等,求过点C 的直线的解析式; (2)若△AOB 被分成的两部分面积之比为1:5,求过点C 的直线的解析式.4. 已知A 、B 的坐标分别为(-2,0)、(4,0),点P 在直线y=0.5x +2上,横坐标为m , 如果△ABP 为直角三角形,求m 的值.5. 如图,一次函数33+-=x y 的图象与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作Rt △ABC ,且使∠ABC=30°.(1)求△ABC 的面积;(2)若在第二象限内有一点P (m ,23),使得△APB 与△ABC 面积相等,求m 的值;(3)是否存在使△QAB 是等腰三角形并且在坐标轴上的点Q ?若存在,请写出点Q 所有可能的坐标;若不存在,请说明理由.。
一次函数提高练习—2021—2022学年人教版数学八年级下册

一次函数一、单选题1.如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x 表示时间,y 表示小徐离他家的距离.读图可知菜地离小徐家的距离为( )A .1.1千米B .2千米C .15千米D .37千米2.函数y x 的取值范围是( ) A .x >﹣2 B .x ≥﹣2 C .x >﹣2且x ≠1 D .x ≥﹣2且x ≠1 3.如图是一次函数y=x-3的图象,若点P(2,m)在该直线的上方,则m 的取值范围是( )A .m>-3B .m>0C .m >-1D .m<34.下列图形中,表示一次函数y ax b =+与正比例函数(ax y a b =,b 为常数,且0)ab ≠的图象的是( )A .B .C .D .5.在平面直角坐标系中,一次函数y =mx+b (m ,b 均为常数)与正比例函数y =nx (n 为常数)的图象如图所示,则关于x 的方程mx =nx ﹣b 的解为( )A .x =3B .x =﹣3C .x =1D .x =﹣1 6.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )①行驶速度;①行驶时间;①行驶路程;①汽车油箱中的剩余油量A .1个B .2个C .3个D .4个7.在同一直角坐标系中,一次函数y =kx ﹣b 与正比例函数y =b kx (k ,b 是常数,且kb ≠0)的大致图象不正确的是( )A .B .C .D .8.一次函数1y x =+与一次函数3y x m =-+的图像的交点不可能在( )A .第一象限B .第二象限C .第三象限D .第四象限 9.周末,小明骑自行车从家里出发去游玩.从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程y (km )与小明离家时间x (h )的函数图象,则下列说法中正确的是( )A .小明在迪诺水镇游玩1h 后,经过512h 到达万达广场 B .小明的速度是20km /h ,妈妈的速度是60km /hC .万达广场离小明家26kmD .点C 的坐标为(2912,25) 10.一次函数的图象交x 轴于(2,0),交y 轴于(0,3),当函数值大于0时,x 的取值范围是( )A .x>2B .x<2C .x>3D .x<311.在下列各图象中,y 不是x 函数的是( )A .B .C .D .12.若点3(2,)A -,(4,3)B ,(5,)C a 在同一条直线上,则a 的值是( )A .6或6-B .6C .-6D .6或313.一次函数y =kx +b 的图象如图所示,则点(k ,﹣b )在第( )象限内.A .一B .二C .三D .四14.如果通过平移直线3x y =得到53x y +=的图象,那么直线3x y =必须( ). A .向上平移5个单位B .向下平移5个单位C .向上平移53个单位D .向下平移53个单位 15.已知一次函数(6)1y a x =-+经过第一、二、三象限,且关于x 的不等式组1()0232113a x x x ⎧-->⎪⎪⎨+⎪+≥⎪⎩恰有 4 个整数解,则所有满足条件的整数a 的值的和为( ) A .9B .11C .15D .18二、填空题 16.已知230x y +-=,用含x 的代数式表示y :__________,用含y 的代数式表示x :_________.17.已知点A (x 1,y 1)、B (x 1―3,y 2)在直线y =―2x +3上,则y 1_____y 2 (用“>”、“<”或“=”填空)18.在函数y =中,自变量x 的取值范围是___. 19.某水库的水位在一天内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,这天水库的水位高度y (米)与时间x (小时)的函数表达式是______. 20.已知P 1(1,y 1),P 2(2,y 2)在正比例函数y =﹣3x 的图象上,则y 1 ___y 2(填“>”或“<”).21.如图,两个一次函数y =kx+b 与y =mx+n 的图象分别为直线l 1和l 2,l 1与l 2交于点A (1,p ),l 1与x 轴交于点B (-2,0),l 2与x 轴交于点C (4,0),则不等式组0<mx+n <kx+b 的解集为_____.22.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在___点追上兔子.23.如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN①x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为_______.三、解答题24.已知函数y=kx+b(k≠0)的图象经过点A(﹣2,1),点B(1,52 ).(1)求直线AB的解析式;(2)若在x轴上存在点C,使S△ACO=12S△ABO,求出点C坐标.25.佳佳超市要用不超过3520元的资金采购进货价每千克4元的番茄和每千克8元的油豆角共计500千克(重量取整数),且油豆角的重量不少于番茄重量的3倍.该超市计划将所进蔬菜加价25%进行销售.(1)求超市有多少种进货方案;(2)求获利最多的方案及最多获利多少元;(3)因气温升高、品质下降和竞争需要,这两种蔬菜中有200千克最终只能以原定价的五折销售,在获利最多的方案下,超市若要取得盈利,打折销售的油豆角最多有多少千克?26.如图,一次函数y=x+3的图象1l与x轴交于点B,与过点A(3,0)的一次函数的图象2l交于点C(1,m).(1)求m的值;(2)求一次函数图象2l相应的函数表达式;(3)求ABC 的面积.27.设一次函数3y kx b =+-(k ,b 是常数,且0k ≠).(1)若该函数的图象过点(1,2)-,试判断点(4,52)P k +是否也在此函数的图象上,并说明理由.(2)已知点()1,A a y 和点()12,2B a y -+都在该一次函数的图象上,求k 的值. (3)若0k b +<,点(5,)Q m (0)m >在该一次函数图象上,求证:34k >.。
福建省厦门市第五中学八年级数学下册 19.2.3 一次函数
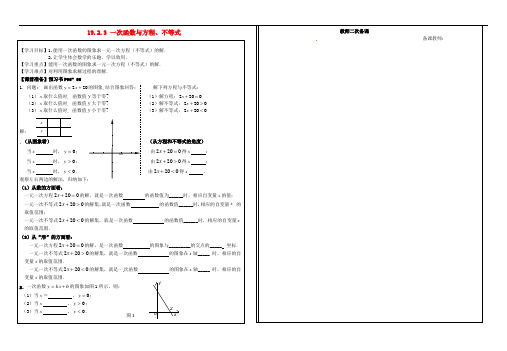
19.2.3 一次函数与方程、不等式【学习目标】1.能用一次函数的图象求一元一次方程(不等式)的解. 2.让学生体会数学的乐趣,学以致用.【学习重点】能用一次函数的图象求一元一次方程(不等式)的解. 【学习难点】对利用图象求解过程的理解. 【课前准备】预习书P96- 981.问题: 画出函数202+=x y 的图象,结合图象回答: 解下列方程与不等式: (1)x 取什么值时, 函数值y 等于零? (1)解方程:0202=+x (2)x 取什么值时, 函数值y 大于零? (2)解不等式:0202>+x (3)x 取什么值时, 函数值y 小于零? (3)解不等式:0202<+x解: (从图象看) (从方程和不等式的角度) 当x 时,0=y ; 由0202=+x 得x ; 当x 时,0>y ; 由0202>+x 得x ; 当x 时,0<y . 由0202<+x 得x . 观察左右两边的解法,归纳如下: (1)从数的方面看:一元一次方程0202=+x 的解,就是一次函数 的函数值为______时,相应自变量x 的值; 一元一次不等式0202>+x 的解集,就是一次函数 的函数值______时,相应的自变量x 的取值范围;一元一次不等式0202<+x 的解集,就是一次函数 的函数值______时,相应的自变量x 的取值范围.(2)从“形”的方面看:一元一次方程0202=+x 的解,是一次函数 的图象与_________的交点的_____ 坐标. 一元一次不等式0202>+x 的解集,就是一次函数 的图象在x 轴_____ 时,相应的自变量x 的取值范围.一元一次不等式0202<+x 的解集,就是一次函数 的图象在x 轴_____ 时,相应的自变量x 的取值范围.2.一次函数b kx y +=的图象如图1所示,则: (1)当x = ,0=y ; (2)当x ,0>y ; (3)当x ,0<y .教师二次备课备课教师:xy10 o2xy图123.如图2,是一个一次函数的图象,请问当x _______时,0≤y . 4.已知一次函数63-=x y 的图象在x 轴上方,则x 的 取值范围是( )请画示意图解答A .2>xB .2<xC .2≥xD .2≤x 【课堂探究】5.下面3个不等式什么共同点和不同点?你能从函数的角度对解这3个不等式进行解释吗? (1)223>+x (2)023<+x (3)123-<+x分析:从函数的角度看,解这3个不等式相当与在一次函数 的函数值分别大于2、 、 时,求自变量的取值范围. 如右图:由图象得(1)223>+x 的解集为 由图象得(2)023<+x 的解集为 由图象得(3)123-<+x 解集为请你从不等式的角度解这3个不等式进行验证【课堂检测】6.在直角坐标系中画出函数232-=x y 的图象,并根据图象回答下列问题: (1)函数值y 随x 增大而 ;图象从左到右 ; (2)图象与坐标轴围成的三角形面积是 ;(3)点(-2,a )和点(3,b )都在图象上,则a b ;(填“>”或“<”)(4)从图象看,方程0232=-x 的解为 ;(5)从图象看,不等式0232≤-x 的解集为 ;(6)若21≤≤-x ,求y 的取值范围.【课堂小结】用一次函数的图象来解方程或不等式未必简单,但是从函数的角度看问题,能发现一次函数、一元一次方程、一元一次不等式之间的关系,能够直观地看到怎样用图形表示方程的解或不等式的解,这种用函数观点认识问题的方法,对于继续学习数学很重要.课后作业1912--一次函数与一元一次方程(不等式)(课时12)1.如图所示,直线b kx y +=与x 轴交于点A (-4,0), 则当0>y 时,x 的取值范围是( )A .4->xB .0>xC .4-<xD .0<x 2. 一次函数b kx y +=的图象如图所示. (1)函数值y 随x 增大而 ; (2)当x = ,0=y ; (3)当x ,0<y ;(4)不等式0≥+b kx 的解集为 . 3.已知:直线42+-=x y (1)画出这条直线;(2)这条直线与坐标轴围成的三角形面积为 ; (3)直线上的一个点的横坐标为3,则该点的坐标为 ; (4)图象上有一点到x 轴的距离等于2,则该点坐标为 ;(5)根据图象回答,当x 时,0=y ,当x 时,0>y ,当x 时,0<y . 4.如图所示,平面直角坐标系中画出了函数b kx y +=的图象. (1)求k 和b 的值;(2)根据图象,求方程0=+b kx 的解; (3)根据图象,求不等式0≥+b kx 的解集.5.画出函数22+-=x y 的图象,观察图象并回答问题.(1)当x 取什么值时,函数值0=y ? 当x 取什么值时,函数值0>y ? 当x 取什么值时,函数值0<y ? (2) 当11<≤-x 时, 对应的函数值y 的取值范围; (3) 当20<<y 时, 对应的自变量x 的取值范围.6.利用函数图象......解出x ,并笔算检验:(提示:可把式子整理成一元一次方程和不等式的一般式) (1)5215+=-x x ; (2)10245+<+x x 教学反思:图2。
(人教版)厦门八年级数学下册第十九章《一次函数》经典测试卷(提高培优)

一、选择题1.若关于x 的不等式组20210x x a ->⎧⎨-+<⎩有解,则一次函数()32y a x =-+的图象一定不经过的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限2.如图,点O 为平面直角坐标系的原点,点A 在x 轴正半轴上,四边形OABC 是菱形.已知点B 坐标为(3,3),则直线AC 的函数解析式为( )A .y =33x+3 B .y =3x+23C .y =﹣33x+3 D .y =﹣3x+23 3.小明和小华同时从小华家出发到球场去.小华先到并停留了8分钟,发现东西忘在了家里,于是沿原路以同样的速度回家去取.已知小明的速度为180米/分,他们各自距离小华家的路程y (米)与出发时间x (分)之间的函数关系如图所示,则下列说法正确的是( )A .小明到达球场时小华离球场3150米B .小华家距离球场3500米C .小华到家时小明已经在球场待了8分钟D .整个过程一共耗时30分钟4.若实数k 、b 满足0k b +=,且k b >,则一次函数y kx b =+的图象可能是( )A .B .C .D .5.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )A .20210x y y x +-=⎧⎨-+=⎩B .20210x y y x -+=⎧⎨+-=⎩C .20210x y y x -+=⎧⎨--=⎩D .2010x y y x ++=⎧⎨+-=⎩6.如图,A 、M 、N 三点坐标分别为A (0,1),M (3,4),N (5,6),动点P 从点A 出发,沿y 轴以每秒一个单位长度的速度向上移动,且过点P 的直线l :y=-x+b 也随之移动,设移动时间为t 秒,若点M 、N 分别位于l 的异侧,则t 的取值范围是( )A .611t <<B .510t <<C .610t <<D .511t <<7.已知点()1,4P 在直线2y kx k =-上,则k 的值为( ) A .43B .43-C .4D .4-8.如图,已知在平面直角坐标系xOy 中.以(О为圆心,适当长为半径作圆弧,与x 轴交于点A ,与y 轴交于点,B 再分别以A B 、为圆心.大于12AB 长为半径作圆弧,两条圆弧在第四象限交于点C .以下四组x 与y 的对应值中,能够使得点(),1P x y -在射线OC 上的是( )A.2和1-B.2和2-C.2和2D.2和39.甲,乙两车分别从A,B两地同时出发,相向而行.乙车出发2h后休息,当两车相遇时,两车立即按原速度继续向目的地行驶.设甲车行驶的时间为x(h),甲,乙两车到B地的距离分别为y1(km),y2(km),y1,y2关于x的函数图象如图.下列结论:①甲车的速度是45akm/h;②乙车休息了0.5h;③两车相距a km时,甲车行驶了53h.正确的是( )A.①②B.①③C.②③D.①②③10.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为x时两种消费卡所需费用分别为y甲,y乙元,y甲,y乙与x的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算()A.甲种更合算B.乙种更合算C.两种一样合算D.无法确定11.在直角坐标系中,点P在直线x+y-4=0上,O为原点,则OP的最小值为()A.2B.2 C6D1012.如图,直线443y x =+与x 轴,y 轴分别交于A ,B 两点,点C 在OB 上,若将ABC 沿AC 折叠,使点B 恰好落在x 轴上的点D 处,则点C 的坐标是( )A .(0,1)B .20,3⎛⎫ ⎪⎝⎭C .30,2⎛⎫ ⎪⎝⎭D .(0,2)13.若点P 在一次函数31y x =-+的图象上,则点P 一定不在( ) A .第一象限B .第二象限C .第三象限D .第四象限14.如图,直线y =kx (k≠0)与y =23x+2在第二象限交于A ,y =23x+2交x 轴,y 轴分别于B 、C 两点.3S △ABO =S △BOC ,则方程组0236kx y x y -=⎧⎨-=-⎩的解为( )A .143x y =-⎧⎪⎨=⎪⎩B .321x y ⎧=-⎪⎨⎪=⎩C .223x y =-⎧⎪⎨=⎪⎩D .3432x y ⎧=-⎪⎪⎨⎪=⎪⎩15.若一次函数()231y m x =-+-的图象经过点()11,A x y ,()22,B x y ,当12x x <时,12y y >时,则m 的取值范围是( )A .32m >B .32m >-C .32m <D .32m <-二、填空题16.正方形111A B C O 、2221A B C C 、3332A B C C ……按如图的方式放置,点1A ,2A ,3A …和点1C ,2C ,3C …分别在直线()0y kx b k =+>和x 轴上,已知点1(1,1)B ,2(3,2)B ,按此规律,则点4B 的坐标是______.17.如图,两个一次函数y =kx+b 与y =mx+n 的图象分别为直线l 1和l 2,l 1与l 2交于点A (1,p ),l 1与x 轴交于点B (-2,0),l 2与x 轴交于点C (4,0),则不等式组0<mx+n <kx+b 的解集为_____.18.已知一次函数6y x =-+的图象上有两点()11,A y -,()22,A y ,则1y 与2y 的大小关系是______.19.如图,已知直线l:y =12x ,点A 1(2,0),过点A 1作x 轴的垂线交直线l 于点B 1,以A 1B 1为边,向右侧作正方形A 1B 1C 1A 2,延长A 2C 1交直线l 于点B 2;以A 2B 2为边,向右侧作正方形A 2B 2C 2A 3,延长A 3C 2交直线l 于点B 3;……;按照这个规律进行下去,点B n 的横坐标为______.(结果用含正整数n 的代数式表示)20.函数1y x =-中自变量x 的取值范围是________. 21.已知y 是x 的一次函数,下表中列出了部分对应值,则m 的值是________.x-1 0 my 1-2-522.已知一次函数(2) 3y m x m =-+-的图象经过第一、二、四象限,则化简244m m -+296m m -+=__________.23.若函数y =kx+b(k≠0)的图像平行于直线y =3x+2,且与直线y =-x -1交x 轴于同一点,则其函数表达式是_____.24.为减少代沟,增强父子感情,父子二人决定在100米跑道上,以“相向而跑”的形式来进行交流.儿子从100米跑道的A 端出发,父亲从另一端B 出发,两人同时起跑,结果儿子赢得比赛.设父子间的距离S (米)与父亲奔跑的时间(秒)之间的函数关系如图所示,则儿子奔跑的速度是______米/秒.25.已知y 是关于x 的正比例函数,当1x =-时,2y =,则y 关于x 的函数表达式为____.26.如图,平面直角坐标系中,点A 在直线333y x =+上,点C 在直线142y x =-+上,点A ,C 都在第一象限内,点B ,D 在x 轴上,若AOB 是等边三角形,BCD △是以BD 为底边的等腰直角三角形,则点D 的坐标为____________.三、解答题27.甲、乙两人计划8:00一起从学校出发,乘坐班车去博物馆参观,乙乘坐班车准时出发,但甲临时有事没赶上班车,8:45甲沿相同的路线自行驾车前往,结果比乙早1小时到达.甲、乙两人离学校的距离y (千米)与甲出发时间x (小时)的函数关系如图所示.(1)求甲、乙两人的速度. (2)求OC 和BD 的函数关系式. (3)求学校和博物馆之间的距离.28.科学研究发现.地表以下岩层的温度y (℃)与所处深度x (千米)之间近似地满足一次函数关系.经测量,在深度2千米的地方,岩层温度为90℃;在深度5千米的地方,岩层温度为195℃.(1)求出y 与x 的函数表达式;(2)求当岩层温达到1805℃时,岩层所处的深度.29.某商店需要购进甲、乙两种商品共200件,其进价和售价如表:甲 乙 进价(元/件) 14 35 售价(元/件)2045(1)若商店计划销售完这批商品后能获利1680元,问甲、乙两种商品应分别购进多少件?(2)若商店计划投入资金小于5320元,且销售完这批商品后获利大于1660元,请问有几种购货方案?并求出其中获利最大的购货方案.30.如图直线:x 6=+l y k 与x 轴、y 轴分别交于点B C 、两点,点B 的坐标是()8,0-,点A 的坐标为()6,0-.(1)求k 的值.(2)若点P 是直线l 上的一个动点且在第二象限,当PAC ∆的面积为3时,求出此时点P 的坐标.(3)在x 轴上是否存在点M ,使得BCM ∆为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.。
最新人教版八年级下册数学试题:一次函数 课后提升训练( 解析版)

解:(1)、将点A(﹣3,﹣2)代入一次函数y=kx+4,得:﹣3k+4=﹣2,
解得k=2. 所以这个一次函数的关系式为y=2x+4.
(2)、把x=﹣5代入y=2x+4中,得y=﹣6≠3,
所以B(﹣5,3)不在这个函数图象上.
19.(1) 时, 是一次函数;(2) 时,y的值为3.
【解析】
(1)由 是一次函数得 ,
A.y1<y2B.y1>y2C.y1=y2D.不能确定
9.一次函数 ymx 的图像过点(0,2),且 y 随 x 的增大而增大,则 m 的值为( )
A.1B.3C.1D.1 或 3
10.若一次函数 的函数值 随 的增大而增大,则( )
A. B. C. D.
二、填空题
11.若函数的图象经过点A(1,2),点B(2,1),写出一个符合条件的函数表达式______.
则 ,解得
故一次函数的解析式是y=-x+3.
(2)点C(4,-2)不在该一次函数的图象上.
理由:对于y=-x+3,当x=4时,y=-1≠-2,
所以点C(4,-2)不在该函数的图象上.
(3)在y=-x+3中,令y=0,得x=3,则点D的坐标是(3,0),
则S△BOD= ×OD×2= ×3×2=3.
人教版八年级下册数学试题:一次函数 课后提升训练(带解析)
一、单选题
1.下列函数:① ;② ;③ ;④ ;⑤ .其中,是一次函数的有( )
A.1个B.2个C.3个D.4个
2.一次函数 的图像与y轴交点的坐标是( )
A.(0,-4)B.(0,4)C.(2,0)D.(-2,0)
3.直线y=2x向下平移2个单位长度得到的直线是( )
人教版八年级下册数学《一次函数》提高测试

一次函数一、选择题(每小题4分,共12分)1.如图,直线AB对应的函数解析式是( )A.y=-错误!未找到引用源。
x+3B.y=错误!未找到引用源。
x+3C.y=-错误!未找到引用源。
x+3D.y=错误!未找到引用源。
x+32.有一根长40mm的金属棒,欲将其截成x根7mm长的小段和y根9mm长的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A.x=1,y=3B.x=3,y=2C.x=4,y=1D.x=2,y=33.某年的夏天,某地旱情严重.该地10号,15号的人日均用水量的变化情况如图所示.若该地10号,15号的人日均用水量分别为18kg和15kg,并一直按此趋势直线下降.当人日均用水量低于10kg时,政府将向当地居民送水.那么政府应开始送水的号数为( )A.23B.24C.25D.26二、填空题(每小题4分,共12分)4.(2013·梧州中考)若一条直线经过点(-1,1)和点(1,5),则这条直线与x轴的交点坐标为.5.(2013·包头中考)如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴,y轴分别交于点C,点D,若DB=DC,则直线CD的函数解析式为.6.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参与播种,直至完成800hm2的播种任务,播种亩数与天数之间的函数关系如图所示,那么乙播种机参与播种的天数是.三、解答题(共26分)7.(8分)已知一次函数y=kx-4,当x=2时,y=-3.(1)求一次函数的解析式.(2)将该函数的图象向上平移6个单位,求平移后的图象与x轴交点的坐标.8.(8分)(2013·临沂中考)某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:x(单位:台) 10 20 30y(单位:万元/台) 60 55 50(1)求y与x之间的函数解析式,并写出自变量x的取值范围.(2)市场调查发现,这种机器每月销售量z台)与售价a(万元/台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台(假设共生产50台机器),请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)【拓展延伸】9.(10分)如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为ts.(1)当t=3时,求l的解析式.(2)若点M,N位于l的异侧,确定t的取值范围.(3)直接写出为何值时,点M关于l的对称点落在坐标轴上.答案解析1.【解析】选A.设直线AB对应的函数解析式是y=kx+b,把A(0,3),B(2,0)代入,得错误!未找到引用源。
人教版初二数学下册一次函数的应用练习(提高)
人教版初二数学下册一次函数的应用练习(提高)1. 某中学组织初一初二先生举行〝四城同创〞宣传活动,从学校坐车动身,先上坡抵达A 地后,宣传8分钟;然后下坡到B 地宣传8分钟前往,行程状况如图.假定前往时,上、下坡速度仍坚持不变,在A 地仍要宣传8分钟,那么他们从B 地前往学校用的时间是〔 〕 A .45.2分钟 B .48分钟 C .46分钟 D .33分钟2. 小静预备到甲或乙商场购置一些商品,两商场同种商品的标价相反,而各自推出不同的 优惠方案:在甲商场累计购置满一定数额a 元后,再购置的商品按原价的90%收费;在乙商场累计购置50元商品后,再购置的商品按原价的95%收费.假定累计购物x 元,当x >a 时,在甲商场需付钱数A y =0.9x +10,当x >50时,在乙商场需付钱数为B y .以下说法: ①B y =0.95x +2.5;②a =100;③当累计购物大于50元时,选择乙商场一定优惠些; ④当累计购物超越150元时,选择甲商场一定优惠些.其中正确的说法是〔 〕A .①②③④B .①③④C .①②④D .①②③3. 绍兴黄酒是中国名酒之一.某黄酒厂的瓶酒车间先将散装黄酒灌装成瓶装黄酒,再将瓶 装黄酒装箱出车间,该车间有灌装,装箱消费线共26条,每条灌装,装箱消费线的消费流 量区分如图1,2所示.某日8:00~11:00,车间内的消费线全部投入消费,图3表示该 时段内未装箱的瓶装黄酒存质变化状况,那么灌装消费线的条数是〔 〕 A .12 B .13 C .14 D .154. 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.依据最近人体结构学的研 究效果说明,普通状况下人的身高h 是指距d 的一次函数.下表是测得的指距与身高的一组数据:依据上表处置下面这个实践效果:姚明的身高是226厘米,他的指距为〔 〕 A .26.8厘米 B .26.9厘米 C .27.5厘米 D .27.3厘米 5. 春节时期,某批发商欲将一批海产品由A 地运往B 地,汽车货运公司和铁路货运公司均 开放海产品的运输业务,两货运公司的收费项目及收费规范如下表所示.运输路程为120千米,汽车和火车的速度区分为60千米/小时,100千米/小时,请你选择一种交通工具〔 〕A.当运输货物重量为60吨,选择汽车B. 当运输货物重量大于50吨,选择汽车C. 当运输货物重量小于50吨,选择火车D. 当运输货物重量大于50吨,选择火车 6. 6月份以来,猪肉价钱一路下跌.为平抑猪肉价钱,某省积极组织货源,方案由A 、B 、C 三市区分组织10辆、10辆和8辆运输车向D 、E 两市运送猪肉,现决议派往D 、E 两地的 运输车区分是18辆、10辆,一辆运输车从A 市到D 、E 两市的运费区分是200元和800 元,从B 市到D 、E 两市的运费区分是300元和700元,从C 市到D 、E 两市的运费区分是 400元和500元.假定设从A 、B 两市都派x 辆车到D 市,那么当这28辆运输车全部派出时,总运费W 〔元〕的最小值和最大值区分是〔 〕A .8000,13200 B .9000,10000 C .10000,13200 D .13200,15400 7. 利民商店中有3种糖果,单价及重量如下表,假定商店将以上糖果配成什锦糖,那么这种什锦糖果的单价是每千克________元.8. 某公园门票价钱如下表,有27名中先生游公园,那么最少应付费______元. 〔游客只能在公园售票处购票〕9. 有一个附有进水管和出水管的容器,在单位时间内的进水量和出水量区分一定.设从某 时辰末尾的5分钟内只进水不出水,在随后的15分钟内既进水又出水,失掉容器内水量y〔升〕与时间x〔分〕之间的函数图象如图.假定20分钟后只放水不进水,这时〔x≥20时〕y与x之间的函数关系式是_________.10.如图,某公用亭打时,需付费y〔元〕与通话时间x〔min〕之间的函数关系式用图象表示为直线,小文打了2分钟,需付费__________元. 小文打了8分钟付费______元.11.甲、乙两个粮库区分存粮600吨、1400吨,A、B两市区分用粮1200吨、800吨,需从甲、乙两粮库调运,由甲库到A、B两市的运费区分为6元/吨、5元/吨;由乙库到A、B两市的运费区分是9元/吨、6元/吨,那么总运费最少需______元.12.如图,用锤子以相反的力将铁钉锤入木块,随着铁钉的深化,铁钉所受的阻力也越来越大.当铁钉进入木块局部长度足够时,每次钉入木块的铁钉长度是前一次的13.这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是αcm,如铁钉总长度是6cm,那么α的取值范围是_____________.13. 某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x〔分钟〕与收费y〔元〕之间的函数关系如下图.〔1〕有月租费的收费方式是〔填①或②〕,月租费是元;〔2〕区分求出①、②两种收费方式中y与自变量x之间的函数关系式;〔3〕请你依据用户通讯时间的多少,给出经济实惠的选择建议.14. 世界环境日的主题为〝多个物种、一颗星球、一个未来〞.为了照应节能减排的召唤,某品牌汽车4S店预备购进A型〔电动汽车〕和B型〔太阳能汽车〕两种不同型号的汽车共16辆,以满足广阔支持环保的购车者的需求.市场营销人员经过市场调查失掉如下信息:〔1〕假定运营者的购置资金不少于576万元且不多于600万元,那么有哪几种进车方案?〔2〕在〔1〕的前提下,假设你是运营者,并且所进的汽车能全部售出,你会选择哪种进车方案才干使取得的利润最大?最大利润是多少?(3)假定每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30 万公里,那么从浪费资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.15.某电器商城〝家电下乡〞指定型号冰箱、彩电的进价和售价如下表所示:〔1〕按国度政策,农民购置〝家电下乡〞产品享用售价13%的政府补贴.农民田大伯到该商场购置了冰箱、彩电各一台,可以享用多少元的补贴?〔2〕为满足农民需求,商场决议用不超越85000元推销冰箱、彩电共40台,且冰箱的数量不少于彩电数量的56. 假定使商场获利最大,请你协助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?。
厦门市第五中学八年级数学下册人教版辅导练习--一次函数作业(无答案).docx
/天t /万米3V 20040060080010001200O 5040302010初中数学试卷 桑水出品初二下数学辅导练习班级 座号 姓名一、选择题1.在平面直角坐标系中,点P (-1,3)位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.点P 在第二象限内,P 到x 轴的距离是4,到y 轴的距离是3,那么点P 的坐标为( )(A )()4,3- (B )()3,4-- (C )()3,4- (D )()3,4-3.一次函数23y x =-的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限4.点P 1(x 1,y 1),P 2(x 2,y 2)是正比例函数y = -x 图象上的两点,则下列判断正确的是( )A .y 1>y 2B .y 1<y 2C .当x 1<x 2时,y 1>y 2D .当x 1<x 2时,y 1<y 25.关于函数21y x =-+,下列结论正确的是( )A .图象必经过点(-2,1)B . y 随x 的增大而增大C .当x >12时,y <0D .图象经过第一、二、三象限6.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V (万米3)与干旱的时间t (天)的关系如图所示,则下列说法正确的是( ).A .干旱开始后,蓄水量每天减少20万米3B .干旱开始后,蓄水量每天增加20万米3C .干旱开始时,蓄水量为200万米3D .干旱第50天时,蓄水量为1 200万米3. 7.小高从家门口骑车去单位上班,先走平路到达点A ,再走上坡路到达点B ,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是() A .12分钟B .15分钟C .25分钟D .27分钟二、填空题8.点P (-2,3)关于x 轴的对称点的坐标是________.9.如图,在直角坐标平面内,线段AB 垂直于y 轴,垂足为B ,且2AB =,如果将线段AB 沿y 轴翻折,点A 落在点C 处,那么点C 的横坐标是 .10.一次函数3y x b =+的图象过坐标原点,则b 的值为 .11.、如图,当输入5x =时,输出的y = .12.直线y =k x +5经过点(2,1),则k = .13.已知一次函数21y x =+,则y 随x 的增大而_________(填“增大”或“减小”).14.将直线 y=2x-4 向上平移5个单位后,所得直线的表达式是______________.15.比较一次函数32y x =-+与122y x =+,写出它们图象的两个共同点和一个不同点: 两个共同点① ,② ;一个不同点 .16.一次函数的图象过点(0,2),且函数y 的值随自变量x 的增大而增大,请写出一个符合条件的函数解析式:_ _.17.已知关于x 、y 的一次函数()12y m x =--的图象经过平面直角坐标系中的第一、三、四象限,那么m 的取值范围是三、解答题18.已知直线y=2x-6与x 轴、y 轴分别交于A 、B 点。
人教版八年级一次函数提高练习题(附详解)
OC=8, CB=10 的矩
形纸片 ABCO.将纸片翻折后,点 B 恰好落在 x 轴上,记为 B′,折痕为 CE
( 1)求 B′点的坐标;
( 2)求折痕 CE所在直线的解析式.
13.如图, 已知函数 y
1 x b 的图像与 2
图像交于点 M,点 M的横坐标为 2.
x 轴、y 轴分别交于点
A、B,与函数 y = x的
把 x=- 4, y= 0 代人上式,得- 4k+3= 0,
k3 ∴ 4,
3 y x3 ∴4
3
3
m 13 m3
( 2)由已知得点 P 的坐标是 (1 , m),∴
4
,∴
4.
(3) 以下分三种情况讨论. i) 若∠ AP'C= 90°, P'A= P'C (如图 1),过点 P' 作 P'H⊥x轴于点 'H ,
( 1)甲乙两地之间的距离为
千米;
( 2)求快车和慢车的速度;
( 3)求线段 DE所表示的 y 与 x 之间的函数关系式,并写出自变量
x 的取值范围.
试卷第 4 页,总 4 页
参考答案
1. B
【解析】解:∵ C、D 两点坐标分别为( 1, 0)、( 2, 0).
∴按题中滚动方法点 E 经过点( 3, 0),点 A 经过点( 4,0),点 B 经过点( 5, 0), ∵点( 75,0)的横坐标是 5 的倍数,而该正五边形滚动 5 次正好一周,
FPN 90 o.
∵
2 FPN 90o
,
∴ 1 2 .∴△ PMF ≌△ PNE .
∴ PF PE .
解:②∵ CP 2 ,∴ CN CM 1.
福建省厦门市第五中学八年级数学下学期期末复习 一次函数的图象与性质(无答案) 新人教版
一次函数的图象与性质班级: 座号: 姓名:【复习要点】1.有关概念:变量、常量、函数、自变量、函数解析式;在同一个变化过程中,两个相互制约、相互依存的变量x 和y ,当x 每一个确定的值,y 都有 ,那么就说x 是 ,y 是x 的函数. 2.函数的表示方法有 种,分别是 . 3.一次函数的图象与性质;直线b kx y +=是由 直线kx y = 而得到, 当0>b 时, 平移; 当0<b 时, 平移. 4.求一次函数的解析式:待定系数法:“一设、二代、三解、四写” 【复习巩固】1.下列四条曲线中,(1) (2) (3) (4)其中能表示y 是x 的函数的是( )A .(1)(2)B .(1)(3)C .(3)(4)D .(1)(4)2.函数3-=x y ,则自变量x 的取值范围是( )A .3≥xB .3≤xC .3<xD .3>x 3.下列各点中,在直线62+=x y 上的点是( )A .(-5,-4)B .(-7,-9)C .(1,7)D .(23,328)4.周日晚饭后,小红从家中出去散步,从家中出发,到了公共阅报栏看了一会儿报后,继续往前走了一段,然后回家了;如图描述她散步过程中离家距离S (米)与散步所用时间t (分)之间的函数关系, 依据图象回答下列问题:①公共阅报栏离家 米; ②小红看报花了 分钟; ③小红离家最远 米;④小红回家的平均速度是 米/分;⑤再写出一条图象信息: . 5.根据下列条件分别确定函数的解析式.(1)y 与x 成正比例,且当5=x 时,6=y . (2)直线b kx y +=经过点(3,5)与点(-4,-9)6.在直角坐标系中画出函数232-=x y 的图象,并根据图象回答下列问题:(1)图象从左到右 (填上升或下降),函数值y 随x 增大而 ;(2)图象与坐标轴围成的三角形面积是 ;(3)点(a ,2)和点(b ,3)都在图象上,则a b .(填“>”或“<”)7.已知等腰三角形的周长为16,底边长为y ,腰长为x . (1)写出底边y 关于腰长x 的函数解析式; (2)写出自变量x 的取值范围;(3)在直角坐标系中,画出该函数图象.【课堂探究】8.一个弹簧不挂重物时长12cm ,挂上重物后伸长的长度与所挂重物的质量成正比. 如果挂上1 kg 的物体后,弹簧伸长2 cm ,(1)求弹簧总长y (单位:cm )随所挂物体质量x (单位:kg )变化的函数解析式;(2)如果所挂物体质量为4.5 kg ,此时弹簧总长是多少cm ?(3)若这个弹簧最多能伸长到22cm ,则该弹簧所挂重物质量的最大值是多少kg ?9.如图,直线6+=kx y 与x 轴、y 轴分别交于点E 、F ,点E 的坐标(-8, 0),点A 的坐标为(-6,0), (1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,当点P 运动过程中,试写出△OPA 的面积S 与 x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当点运动到什么位置时,△OPA 的面积为827,并说明理由.【课后检测】1. 在地表以下不太深的地方,温度y (℃)与所处的深度x (km )•之间的关系可近似用关系式y =35x+20表示,这个关系符合的数学模型是( )A .正比例函数B .一次函数C .不是函数D .无法确定2.关于函数12+-=x y ,下列结论正确的是( )A .图象必过点(-2,1)B .图象经过第一、二、三象限C .当x>12时,y<0; D .图象可由x y 2-=的图象向下平移1个单位的长度得到 3.已知直线43+-=x y 过点A (-2,y 1)和点(-3,y 2),则y 1和y 2的大小关系是( ) A .y 1<y 2 B .y 1>y 2 C .y 1=y 2 D .不能确定 4.过点A (0,-2),且与直线y=5x 平行的直线是( )A .y=5x+2B .y=-5x+2C .y=5x-2D .y=-5x-2 5.已知直线y=x+b ,当b<0时,直线不经过( ). A .第一象限 B .第二象限 C .第三象限 D .第四象限6.下列图象中,表示直线y=x-1的是( )7.画函数y=2x-2的图象时,取两个点,一个点的坐标为(0,_____),另一个点的坐标是(______,0). 8.把直线y=2x 向上平移3个单位,就得到直线____ _ ___,它经过______象限. 9.把一次函数y=3x+2向______ 平移______个单位得到y=3x .10.如右图所示,写出直线l 所表示的变量x ,y 之间的函数关系式____ ___ . 11.一次函数的图象过点(0,2),且函数y 的值随自变量x 的增大而增大, 请写出一个符合条件的函数解析式:_ _.12.如果点P (2,k )在直线y=2x+2k ,那么P 到x 轴的距离为____ ___.13.写一个正比例函数的解析式,使它的图象与x 轴的夹角为45°,•这个正比例函数的解析式 是______ ___.14.已知关于x 的一次函数2)73(-+-=a x a y 的图象与y 轴交点在x 轴的上方,且y 随x 的增大而减小,求a 的取值范围.15.已知一次函数的图象经过点A (2,1),B (-1,-3)(1)求此一次函数的解析式; (2)试判断点P (-2,1)是否在这个一次函数的图象上. (3)求此一次函数的图象与x 轴、y 轴的交点坐标;(4)求此一次函数的图象与两坐标轴所围成的三角形面积.16.设P (x ,0)是x 轴上的一个动点,它的x 轴上表示-3的点的距离为y ,求x 的函数y 的解析式,画出这个函数的图象.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二下数学提高题10(一次函数)
班级 姓名 座号
1.写出两个一次函数,使这两个函数和23+-=x y ,12
1
+=x y 在同一直角坐标系中的图象 能围出 一个平行四边形 .
2. 一次函数b kx y +=的图象与x 、y 轴分别交于点A (2,0),B (0,4).O 为坐标原点, 设OA 、AB 的中点分别为C 、D ,P 为OB 上一动点,则PC+PD 的最小值为 , 并求取得最小值时P 点的坐标 .
3. 已知如图,直线y=-x+2与x 轴、y 轴分别交于点A 、点B ,另一直线y=kx+b (k ≠0)经过点C (1,0),
且把△AOB 分成两部分.
(1)若△AOB 被分成的两部分面积相等,求过点C 的直线的解析式; (2)若△AOB 被分成的两部分面积之比为1:5,求过点C 的直线的解析式.
4. 已知A 、B 的坐标分别为(-2,0)、(4,0),点P 在直线y=0.5x +2上,横坐标为m ,
如果△ABP 为直角三角形,求m 的值.
5. 如图,一次函数33+-=x y 的图象与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作Rt △ABC ,且使∠ABC=30°.
(1)求△ABC 的面积;(2)若在第二象限内有一点P (m ,
2
3
),使得△APB 与△ABC 面积相等,求m 的值;
(3)是否存在使△QAB
是等腰
三角形并且在坐标轴上的点Q ?若存在,请写出点Q 所有可能的坐标;若不存在,请说明理由.。
