全国初中数学优质说课课比赛一等奖-《锐角的三角函数—正切》
合集下载
九年级数学上册第4章锐角三角函数4.2正切公开课课件省市一等奖完整版

4.2 正切
教学目标
1、理解并掌握正切的含义,能够用 tanα表示直角三 角形中两边的比值。
2、掌握特殊角的正切值。 3、能够用正切进行简单的计算。 重点: 正切定义的理解以及如何求锐角的正切值. 难点: 正切定义的理解,探索并认识正切.
新课引入
我们已经知道,在直角三角形中,当一个锐角的大 小确定时,那么不管这个三角形的大小如何,这个锐角 的对边(或邻边)与斜边的比值也就确定(是一个常 数). 那么这个锐角的对边与邻边的比值是否也是一个 常数呢?
如图,△ABC和△DEF 都是直角三角形, 其中
∠A=∠D =α ,∠C =∠F =90°, 则
BC EF AC DF
成立吗?为什么?
α
α
∵ ∠A=∠D = α,∠C =∠F = 90°, ∴ Rt△ABC∽Rt△DEF.
∴
BC AC . EF DF
即 BC·DF = AC·EF ,
∴
BC EF . AC DF
由此可得,在有一个锐角等于 α 的所有直角三角形中, 角 的对α 边与邻边的比值是一个常数,与直角三角形的大
小无关.
如何求 tan 30°,tan60°的值呢?
解: 如图,构造一个Rt△ABC,使∠C=90°,∠A=30°,
于是
BC =
1 2
AB , ∠B=60°.
从而 AC2=AB2-BC2=(2BC)2-BC2=3BC2.
(2)当 090 时, α的余弦值随着角度的增大而减小, 随着角度的减小而增大;
(3)当 090时,α的正切值随着角度的增大而增大, 随着角度的减小而减小;
3. 如图,在矩形ABCD中,E是BC边上的点,AE=BC,
DF⊥AE,垂足为点F,连接DE. (1)求证:AB=DF;
教学目标
1、理解并掌握正切的含义,能够用 tanα表示直角三 角形中两边的比值。
2、掌握特殊角的正切值。 3、能够用正切进行简单的计算。 重点: 正切定义的理解以及如何求锐角的正切值. 难点: 正切定义的理解,探索并认识正切.
新课引入
我们已经知道,在直角三角形中,当一个锐角的大 小确定时,那么不管这个三角形的大小如何,这个锐角 的对边(或邻边)与斜边的比值也就确定(是一个常 数). 那么这个锐角的对边与邻边的比值是否也是一个 常数呢?
如图,△ABC和△DEF 都是直角三角形, 其中
∠A=∠D =α ,∠C =∠F =90°, 则
BC EF AC DF
成立吗?为什么?
α
α
∵ ∠A=∠D = α,∠C =∠F = 90°, ∴ Rt△ABC∽Rt△DEF.
∴
BC AC . EF DF
即 BC·DF = AC·EF ,
∴
BC EF . AC DF
由此可得,在有一个锐角等于 α 的所有直角三角形中, 角 的对α 边与邻边的比值是一个常数,与直角三角形的大
小无关.
如何求 tan 30°,tan60°的值呢?
解: 如图,构造一个Rt△ABC,使∠C=90°,∠A=30°,
于是
BC =
1 2
AB , ∠B=60°.
从而 AC2=AB2-BC2=(2BC)2-BC2=3BC2.
(2)当 090 时, α的余弦值随着角度的增大而减小, 随着角度的减小而增大;
(3)当 090时,α的正切值随着角度的增大而增大, 随着角度的减小而减小;
3. 如图,在矩形ABCD中,E是BC边上的点,AE=BC,
DF⊥AE,垂足为点F,连接DE. (1)求证:AB=DF;
初中数学沪科版九年级上册《锐角三角函数(正切)》优质课公开课课件省级比赛获奖课件

置呢?由此你能得出什么结论?
A
C2
C1
想一想
B2
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
(2) B1C1 和 B2C2 有什么关系?
AC1 AC2
(3)如果改变B2在梯子上的位
置呢?由此你能得出什么结论?
A
C2 C1
想一想
B2
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
3) tanA不表示“tan”乘以“A ”
4)初中阶段,我们只学习直角三角形中锐角 的正切。
B
练一练: 1)在Rt△ABC中∠C=90°AC=5,
12 BC=12,tanA=( 12 )
5
A
5
C
B
练一练: 2)在Rt△ABC中∠C=90°AC=5,
13 12 AB=13,tanA=( 12 )
5
D
比眼力 比速度: 哪个梯子更陡?
A E
4m
3m
B
1.5m
F
1.3m
倾斜角越大——梯子陡
铅直高度与 水平宽度的比越大——梯子陡
想一想
B1
B2
A
C2
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
B2
A
C2
(2) B1C1 和 B2C2 有什么关系?
AC1 AC2
(3)如果改变B2在梯子上的位
置呢?由此你能得出什么结论?
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
B2
A
C2
A
C2
C1
想一想
B2
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
(2) B1C1 和 B2C2 有什么关系?
AC1 AC2
(3)如果改变B2在梯子上的位
置呢?由此你能得出什么结论?
A
C2 C1
想一想
B2
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
3) tanA不表示“tan”乘以“A ”
4)初中阶段,我们只学习直角三角形中锐角 的正切。
B
练一练: 1)在Rt△ABC中∠C=90°AC=5,
12 BC=12,tanA=( 12 )
5
A
5
C
B
练一练: 2)在Rt△ABC中∠C=90°AC=5,
13 12 AB=13,tanA=( 12 )
5
D
比眼力 比速度: 哪个梯子更陡?
A E
4m
3m
B
1.5m
F
1.3m
倾斜角越大——梯子陡
铅直高度与 水平宽度的比越大——梯子陡
想一想
B1
B2
A
C2
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
B2
A
C2
(2) B1C1 和 B2C2 有什么关系?
AC1 AC2
(3)如果改变B2在梯子上的位
置呢?由此你能得出什么结论?
C1
想一想
B1
(1)直角三角形AB1C1和直角三 角 形AB2C2有什么关系?
B2
A
C2
锐角三角函数 大赛获奖课件 公开课一等奖课件

从上面这两个问题的结论中可知,在一个 Rt△ABC 中,∠C=90°,当∠ 1 A=30°时,∠A 的对边与斜边的比都等于2,是一个固定值.当∠A=45°时, 2 ∠A 的对边与斜边的比都等于 2 ,也是一个固定值.这就引发我们产生这样一 个疑问:当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个 固定值? 探究:任意画 Rt△ABC 和 Rt△A′B′C′,使得∠C=∠C′=90°,∠ BC B′C′ A=∠A′=α,那么AB与 有什么关系?你能解释一下吗? A′B′ 分析:由于∠C=∠C=90°,∠A=∠A′=α, BC B′C′ 所以 Rt△ABC∽Rt△A′B′C′,则AB= . A′B′ 结论:在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何 改变,∠A 的对边与斜边的比都是一个固定值.
二、共同探究,获取新知 1.概念. a 师:由 sinA=c,你能得到哪些公式? 生甲:a=c·sinA. a 生乙:c=sinA. 师:我们还学习了余弦函数和正切函数,也能得到这些式子的变形.我 们知道,在直角三角形中有三个角、三条边共六个元素,能否从已知的元素 求出未知的元素呢? 教师板书: 在直角三角形中,由已知的边角关系,求出未知的边与角,叫做解直角 三角形.
重点 锐角三角函数的概念. 难点 锐角三角函数概念的理解.
一、问题引入 问题:操场上有一个旗杆,老师让小明去测量旗杆高度.(演示学校操场 上的国旗图片)小明站在离旗杆底部 10 米远处,目测旗杆的顶部,视线与水 平线的夹角为 34°,并已知目高为 1 米,然后他很快就算出旗杆的高度了.
你想知道小明是怎样算出的吗? 师:通过前面的学习,我们知道利用相似三角形的方法可以测算出旗杆 的大致高度,实际上我们还可以像小明那样通过测量一些角的度数和一些线 段的长度,来测算出旗杆的高度.这就是我们本章即将探讨和学习的利用锐 角三角函数来测算物体长度或高度的方法.下面我们一起来学习锐角三角函 数.
正弦、余弦、正切函数省公开课获奖课件说课比赛一等奖课件

cosB= 2 ,则BC旳长为________. 3
5 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA = 旳长是( )
A.2 B.8 C.2 5 D.4 5
1 2,则BC
总结
求锐角旳正弦值旳措施: 1.没有直接给出对边或斜边旳题目,一般先根据勾
股定理求出所需旳边长,再求正弦值. 2.没有给出图形旳题目,一般应根据题目,画出符
下面图1和图2中各有一种比较陡旳梯子,你能把它 们找出来吗?说说你旳理由。
图1
图2
w 一样长旳梯子旳陡、梯子旳放置角度(倾 斜角)、垂直高度和水平宽度它们之间有什么 关系?
梯子越陡——倾斜角__越_大__ 倾斜角越大——垂直高度与梯子长旳比_越_大_ 倾斜角越大——水平宽度与梯子长旳比__越_小__ 倾斜角越大——垂直高度与水平宽度旳比_越_大___
合题意旳图形,搞清所求角旳对边与斜边,再求 对边与斜边旳比. 3.题目中给出旳角不在直角三角形中,应先构造直 角三角形再求解.
延伸:由上面例1旳计算,你能猜测∠A,∠B旳正弦、余弦、正 切值有什么规律吗?
结论:一种锐角旳正弦等于它余角旳余弦,或一种锐角旳余弦 等于它余角旳正弦,两个角∠A,∠B旳正切值旳乘积等于1.
tan
A=
A的对边 A的邻边
回味无穷
• 定义中应该注意旳几种问题:
1.sinA,cosA,tanA, 是在直角三角形中定义旳, ∠A是锐 角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一种完整旳符号,表达∠A旳正切, 习惯省去“∠”号;
3.sinA,cosA,tanA, 是一种比值.注意比旳顺序,且 sinA,cosA,tanA, 均﹥0,无单位.
5 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA = 旳长是( )
A.2 B.8 C.2 5 D.4 5
1 2,则BC
总结
求锐角旳正弦值旳措施: 1.没有直接给出对边或斜边旳题目,一般先根据勾
股定理求出所需旳边长,再求正弦值. 2.没有给出图形旳题目,一般应根据题目,画出符
下面图1和图2中各有一种比较陡旳梯子,你能把它 们找出来吗?说说你旳理由。
图1
图2
w 一样长旳梯子旳陡、梯子旳放置角度(倾 斜角)、垂直高度和水平宽度它们之间有什么 关系?
梯子越陡——倾斜角__越_大__ 倾斜角越大——垂直高度与梯子长旳比_越_大_ 倾斜角越大——水平宽度与梯子长旳比__越_小__ 倾斜角越大——垂直高度与水平宽度旳比_越_大___
合题意旳图形,搞清所求角旳对边与斜边,再求 对边与斜边旳比. 3.题目中给出旳角不在直角三角形中,应先构造直 角三角形再求解.
延伸:由上面例1旳计算,你能猜测∠A,∠B旳正弦、余弦、正 切值有什么规律吗?
结论:一种锐角旳正弦等于它余角旳余弦,或一种锐角旳余弦 等于它余角旳正弦,两个角∠A,∠B旳正切值旳乘积等于1.
tan
A=
A的对边 A的邻边
回味无穷
• 定义中应该注意旳几种问题:
1.sinA,cosA,tanA, 是在直角三角形中定义旳, ∠A是锐 角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一种完整旳符号,表达∠A旳正切, 习惯省去“∠”号;
3.sinA,cosA,tanA, 是一种比值.注意比旳顺序,且 sinA,cosA,tanA, 均﹥0,无单位.
锐角三角函数优质课一等奖PPT课件

比叫做坡度,用字母i表
示,则 i h tan
l
h
l
坡度通常写成 i h tan 的形式.
l
.
12
海中有一个小岛P,它的周围18海里内有暗礁, 渔船跟踪鱼群由西向东航行,在点A测得小岛P在北 偏东60°方向上,航行12海里到达B点,这时测得小岛 P在北偏东45°方向上.如果渔船不改变航线继续向东 航行,有没有触礁危险?请说明理由.
⑶、解直角三角形在实际问题中
. 的应用。
2
B
一.锐角三角函数的概念
斜边c
对边a
A
C
邻边b
正弦:把锐角A的对边与斜边的比叫做∠A
的正弦,记作 sin A a
对这些关系式
余余弦弦: ,把 记锐 作角coAs的A 邻b边c 与斜边的要式比叫学运做会 用∠灵A的活变
c
正切:把锐角A的对边与邻边的比叫做∠A的 正切,记作 tan A a
在Rt△PAD中,∵∠PAD=90°-60°=30°,
AD 3PD, 12x 3x,
x 126( 31)1.8 31
∴渔船不改变航线继续向. 东航行,有触礁危险. 14
1.若 2si n 20,则锐角α= 45°
2.若ta n(20) 30,则锐角α= 80°
3.如果 coAs1 3tan B30
分析:作PD⊥BC,设PD=x,则 BD=x,AD=x+12,根据AD= 3 PD, 得x+12= 3 x,求出x的值,再 比较PD与18的大小关系.
D
.
13
解:有触礁危险.
D
理由:过点P作PD⊥AC于D.设PD为x,在Rt△PBD中,
∠PBD=90°-45°=45°.∴BD=PD=x,AD=12+x.
示,则 i h tan
l
h
l
坡度通常写成 i h tan 的形式.
l
.
12
海中有一个小岛P,它的周围18海里内有暗礁, 渔船跟踪鱼群由西向东航行,在点A测得小岛P在北 偏东60°方向上,航行12海里到达B点,这时测得小岛 P在北偏东45°方向上.如果渔船不改变航线继续向东 航行,有没有触礁危险?请说明理由.
⑶、解直角三角形在实际问题中
. 的应用。
2
B
一.锐角三角函数的概念
斜边c
对边a
A
C
邻边b
正弦:把锐角A的对边与斜边的比叫做∠A
的正弦,记作 sin A a
对这些关系式
余余弦弦: ,把 记锐 作角coAs的A 邻b边c 与斜边的要式比叫学运做会 用∠灵A的活变
c
正切:把锐角A的对边与邻边的比叫做∠A的 正切,记作 tan A a
在Rt△PAD中,∵∠PAD=90°-60°=30°,
AD 3PD, 12x 3x,
x 126( 31)1.8 31
∴渔船不改变航线继续向. 东航行,有触礁危险. 14
1.若 2si n 20,则锐角α= 45°
2.若ta n(20) 30,则锐角α= 80°
3.如果 coAs1 3tan B30
分析:作PD⊥BC,设PD=x,则 BD=x,AD=x+12,根据AD= 3 PD, 得x+12= 3 x,求出x的值,再 比较PD与18的大小关系.
D
.
13
解:有触礁危险.
D
理由:过点P作PD⊥AC于D.设PD为x,在Rt△PBD中,
∠PBD=90°-45°=45°.∴BD=PD=x,AD=12+x.
全国优质课一等奖人教版九年级数学下册《锐角三角函数》公开课课件

∠所邻的边
斜边
B
=
斜边
c
A
正弦和余弦的注意事项:
b
邻边
a 对边
C
1.sinA、cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA是一个比值(数值,无单位)。
3.sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。
课堂练习 (求余弦)
则 = − = − = .
=
= ,
a
b
C
课堂练习 (求余弦)
变式2-3 如图,已知Rt△ABC中,斜边BC上的高AD=4,cosB=,则AC=____.
坡面的绿地进行喷灌。现测得斜坡的仰角为30°,
【问题一】为使出水口的高度为35m,需要准备多长的水管?
∵在直角三角形中,30°角所对的边等于斜边的一边
பைடு நூலகம்
∴ =
1
2
而BC=35 m ∴AB=2BC=70 m
【问题二】如果出水口的高度为50 m,那么需要准备多长的水管?
【问题三】你发现了什么?
100 m
【解题技巧】
1)在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,
AB = c,则BC = ck,AC = ch
2)在 Rt△ABC 中,∠C = 90°,sinA = k,sinB = h,
BC=a,则 AB = a ,AC = ah .
k
k
A
b
C
02
锐角三角函数-余弦
在直角三角形中,当锐角 A 的度数一定时,
锐角三角函数PPT示范课市公开课一等奖省优质课获奖课件.pptx
第9页
解:(1)在图1中 sin A BC AB
A 45 (2)在图2中,
3 2 62
tan a AO 3OB 3 OB OB
a 60
第10页
本节课你学习了什么知识?
第11页
1?
sin 2 30 +tan 2 45 cos 2 45 +tan 30
+sin 2 60 cos30
解:原式=
1 2
2
3 2
2
1
(2)
cos45 sin45
-tan45
解: 2 2 -1 22
0
第8页
例4、(1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3 。求∠A度数。
(2)如图,已知圆锥高AO等于圆锥底面半径
OB 倍,3 求α. A
B
(2)
63
AC
(1)
O B
B
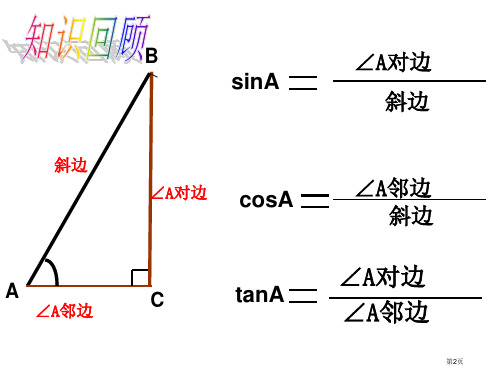
∠A对边
sinA
斜边
斜边
A
∠A邻边
∠A对边 cosA
∠A邻边 斜边
∠A对边
C
tanA
∠A邻边
第2页
1、在Rt △ABC中,∠C=90°,求∠A三角函数值。
① a=9 b=12
② a=9 b=12
2、已知∠A为锐角,sinA= 15 ,求cosA、tanA值。 17
第3页
第4页
Hale Waihona Puke 第5页特殊角三角函数值
2、已知:α为锐角,且满 足 3tan2-4ta+ n3 =0,求α度数。
第12页
3、在Rt△ABC中,∠C=90°,化简
1-2s i
第13页
4、操场里有一个旗杆,老师让小明去测量旗杆高 度,小明站在离旗杆底部10米远处,目测旗杆顶部, 视线与水平线夹角为30度,并已知目高为1.65米.然
《锐角三角函数第一课时正切》优质课获奖教学课件

2 2 1 1
一个固定值
。
=
2
A
C2 C1
1
(3) 如果改变点B2在梯子上的位置,这种关系
还成立吗?
建立模式 探求新知
正切定义
在 △ 中,如果锐角确定,
那么,∠的对边与邻边
这个比叫
的比值也随之确定,
B
做 ∠的正切. 记作:
Байду номын сангаас
斜边c
∠A的对边 a
A
∠A的邻边
b
除了∠A的对边与邻边的比值不变外,还有哪些比值也是固定
不变的?
2.观察学校及附近商场的楼梯,哪个更陡。
谢 谢
还成立吗?
建立模式 探求新知
探索思考
B1
B2
∙
(1) △ 11和 △ 22 有什么关系?
△ 11~ △ 22
(2)
2 2
1 1
2 和 1
有什么关系?
2 2 1 1
=
2
1
A
C2 C1
(3) 如果改变点B2在梯子上的位置,这种关系
还成立吗?
建立模式 探求新知
探索思考
(1) △ 11和 △ 22 有什么关系?
B1
B2
△ 11~ △ 22
∙
(2)
2 2
1 1
2 和 1
有什么关系?
2 2 1 1
=
2
1
A
C2
C1
(3) 如果改变点B2在梯子上的位置,这种关系
=
12
5
, =
5
12
B
.
13
A
12
5
C
应用巩固 形成技能
一个固定值
。
=
2
A
C2 C1
1
(3) 如果改变点B2在梯子上的位置,这种关系
还成立吗?
建立模式 探求新知
正切定义
在 △ 中,如果锐角确定,
那么,∠的对边与邻边
这个比叫
的比值也随之确定,
B
做 ∠的正切. 记作:
Байду номын сангаас
斜边c
∠A的对边 a
A
∠A的邻边
b
除了∠A的对边与邻边的比值不变外,还有哪些比值也是固定
不变的?
2.观察学校及附近商场的楼梯,哪个更陡。
谢 谢
还成立吗?
建立模式 探求新知
探索思考
B1
B2
∙
(1) △ 11和 △ 22 有什么关系?
△ 11~ △ 22
(2)
2 2
1 1
2 和 1
有什么关系?
2 2 1 1
=
2
1
A
C2 C1
(3) 如果改变点B2在梯子上的位置,这种关系
还成立吗?
建立模式 探求新知
探索思考
(1) △ 11和 △ 22 有什么关系?
B1
B2
△ 11~ △ 22
∙
(2)
2 2
1 1
2 和 1
有什么关系?
2 2 1 1
=
2
1
A
C2
C1
(3) 如果改变点B2在梯子上的位置,这种关系
=
12
5
, =
5
12
B
.
13
A
12
5
C
应用巩固 形成技能
