上海市静安区实验中学九年级上学期沪教版五四制第二十五章25.3解直角三角形

合集下载

数学25[1]3解直角三角形及其应用(沪科版九年级上)PPT课件

距离为 30米。
A
B
C 12
11、某海滨浴场的沿岸可以看成直线，如图，1号救生员在岸边的 A点看到海中的B点有人求救，便立即向前跑了300米到离B点最近的D点，再跳入海中游到B点救助；若每位救生员在岸上跑步的速度都是每秒6米，在水中游泳的速度都是每秒2米，∠BAD=45° 13
学习总结
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人：XXXXXX 时间：XX年XX月XX日
15
6
考点2 坡度（坡比）、坡角
（1）坡度也叫坡比，即i=h：m，
h是坡面的铅直高度，
h
m是对应的水平宽度。
α m
（2）坡角是坡面与水平面的夹角
（3）坡度与坡角的关系：i=tanα
7
6、在离地面高度为6米处引
拉线固定电线杆，拉线和地
面成60°角，则拉线长为ห้องสมุดไป่ตู้
（B ） A、6 3 m
C、 2 3 m
B、4 3 m D、3m
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
14
结束语
当你尽了自己的最大努力时，失败也是伟大的，所以不要放弃，坚持就是正确的。
M
N
4
5、如图，小勇想估测家门口一棵树的高度，他站在窗户C 处，观察到树顶端A正好与C
在同一水平线上，小勇测得树底B的俯角为60°，并发现B 点距墙脚D之间恰好铺设六块边长为0·5米的正方形地砖，因此测算出B点到墙脚D之间

九年级数学上册25-4解直角三角形应用(第4课时)教案沪教版五四制

教学过程设计
一、情景引入 1．观察
出示已准备的燕尾槽模型，让学生有感视印象，将其横向垂直于燕尾槽的平面切割，得横截面，请学生通过观察，认识到这是一个等腰梯形，并结合图形，向学生介绍一些专用术语，使学生知道，图中燕尾角对应哪一个角，外口、内口和深度对应哪一条线段．
2．思考怎么解决等腰梯形中的问题？
解：过点 E 作 EH 上 OG，垂足为点 H．小球在最高位置和最低位置时的高度差就是 GH 的长．根据题意，可知
∠EOH= ∠EOF=200,
在ห้องสมุดไป่ตู้Rt△EOH 中，
∵cos∠EOH=
，
∴OH＝OE·cos∠EOH＝50cos200≈46．98(厘米). ∴GH=OG-OH=50-46.98=3.02≈3.0. 答：小球在最高位置和最低位置时的高度差约为 3.0 厘米.
[说明] 这一介绍，使学生对本节课内容很感兴趣，激发了学生的学习热情．
二、学习新课
1．例题分析
例题 1 如图所示的工件叫做燕尾槽，它的横断面是一个等腰梯形，∠B 叫做燕尾角，AD 叫做外口，BC 叫做里口，AE 叫做燕尾槽深度．已知 AD 长 180 毫米，BC 长 300 毫米，AE 长 70 毫米，那么燕尾角 B 的大小是多少(精确到 1，)? 解: 根据题意，可知 BE= (BC—AD)= (300-180)=60(毫米),
答：塔的高度约为 40．5 米．
[说明]这三道例题，例题 1 是工件问题，例题 2 是摆动问题，例题 3 是测量物高问题，它们不是同一类问题但我们要看到实质：都能通过添加辅助线转化为解直角三角形的问题.
三、课堂小结
本节课教学内容仍是解直角三角形的应用的问题，遇到有关等腰梯形的问题，应考虑如何添加辅助线，将其转化为直角三角形和矩形的组合图形，从而把求等腰梯形的下底的问题转化成解直角三角形的问题．在用三角比时，要正确判断边角关系．

九年级数学上册 254 解直角三角形的应用(第1课时巩固课)教案沪教版五四制教案

25.4 解直角三角形的应用（第1课时巩固课）
教学内容分析
本节列举了解直角三角形的一类典型问题：仰角、俯角问题.让学生感受数学与生活的紧密联系，提高数学问题实际化的能力，领会数学思想.
教学重点及难点
将实际问题中的数量关系转化为直角三角形中元素间关系进行解题.
教学过程设计
一、巩固练习
1. 在离旗杆20米处的地方用测角仪测得旗杆顶的仰角为α，如果测角仪高为1.5米，那么旗杆的高为米（用含α的三角比表示）．
2.在距地面100米高的平台上，测得地面上一塔顶与塔基的俯角分别为30°和60°，则塔高为__________米;
5．如图，AB和CD是同一地面上的两座相距36米的楼房，在楼AB的楼顶A点测得楼CD的楼顶C 的仰角为45°，楼底D的俯角为30°．求楼CD的高(结果保留根号).
二、作业布置
一张试卷
36
A
B D
45°
30°
C
(第5题图)。

沪教版数学九年级上第二十五章锐角三角比25.3解直角三角形练习一和参考答案

数学九年级上第二十五章锐角三角比25.3 解直角三角形（1）一、选择题1. 在Rt △ABC 中，已知∠C ＝900，23sin =B ,32=b ,则sinA ＝ ( ) A ．23B ．21C ．22D ．422. 在△ABC 中，∠C ＝900，则下列关系式中不成立的是： ( )A ．a ＝csinAB ．b ＝ccosAC ．b ＝atanBD ．a ＝bcotC 3. 在Rt △ABC 中，已知∠C ＝900，23sin =B ,32=b ,则a 等于 ( ) A ．3 B ．1C ．2D ．3 4．已知等腰三角形底边上的高等于腰的21，则顶角为（）A. 300B. 450C. 600D. 9005．已知等腰三角形底边上的高等于底边的63，则底角为（） A. 300B. 450C. 600D. 9006. 已知在Rt △ABC 中，∠C ＝900，∠B ＝600，斜边上的高为1，则三边的长分别为（）A. 334,2,332===c b a B. 7,2,3===c b a C. 334,332,2===c b a D. 4,2,32===c b a 7. 在Rt △ABC 中，已知∠C ＝900，当已知∠B 和b 时，求c ，应选择的关系式是 ( )A ．B b c cos =B ．B b c sin =C ．B b c tan =D ．Bbc tan = 8. 在△ABC 中，∠C ＝900，∠B ，∠A 都是锐角，且21cos ,22sin ==B A ，则△ABC 是 ( ) A ．直角三角形 B ．钝角三角形 C ．锐角三角形 D ．等腰三角形二、填空题9、在Rt △ABC 中，已知∠C ＝900，a=1,b=2,则sinA= ____________。

10、在Rt △ABC 中，已知∠C ＝900，a=10,210=c ,则∠B ＝____________。

11、在Rt △ABC 中，已知∠C ＝900，a=8,54sin =A ,则c=____________。

沪教版(上海)初中数学九年级第一学期 25.4(3)解直角三角形的应用教案

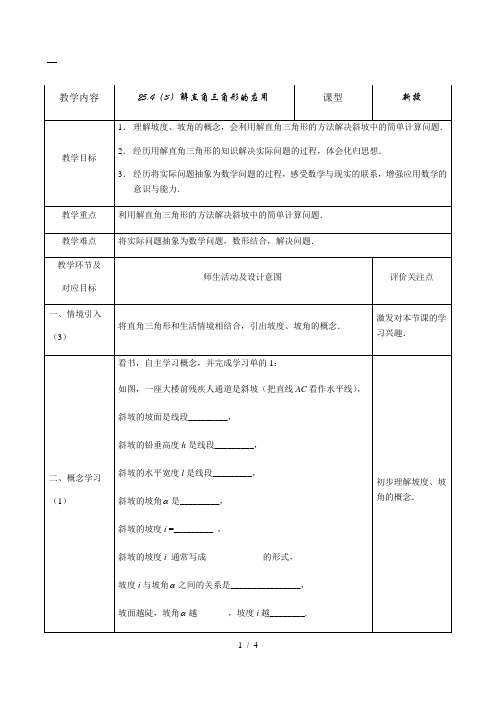
三、巩固新知（1、2）例题1如图，大楼前残疾人通道是斜坡（把直线AC看作水平线），沿着通道走8 米可进入楼厅，楼厅比楼外的地面高1 米，那么你知道该通道的坡度与坡角吗？（角度精确到1′）初步体会坡度、坡角问题转化为数学问题．完成学习单的2：巩固练习：（1）如果斜坡的坡角是30°，那么此斜坡的坡度i =___________.（保留根号）（2）如果斜坡的坡度i =1꞉12，那么此斜坡的坡角 =_________.（角度精确到1′）（3）如果斜坡的坡度i =1꞉8，水平距离是40米，那么此斜坡的铅垂高度是__________米.（4）如果斜坡的坡度i =1꞉2.35，铅垂高度是2米，那么此斜坡的水平宽度是_________米.（5）某人在坡度i =1꞉15的斜坡上走了8米，那么此人的位置高度上升了___________米.进一步理解坡度、坡角的概念，并进行简单计算．D四、新知应用（1、2）完成学习单的3：练习1如图，大楼前残疾人通道是斜坡（把直线AC 看作水平线），沿着通道走 8 米可进入楼厅，楼厅比楼外的地面高 1 米，现要把此斜坡改成 i = 1꞉16的坡道，那么地面延伸部分AD 的长是多少米？（保留根号）根据生活中的实例，再次体会将坡度、坡角的实际问题转化为解直角三角形问题的方法．五、延伸拓展（1、2、3）完成学习单的4：练习2某景区计划在观景平台两侧分别建造台阶和残疾人通道．如图，观景平台为宽是 3 米的水平面AD ，平台一侧共有十级台阶，每级台阶的高是0.15米、宽是0.4米．坡度 1 ꞉ 8 1 ꞉ 10 1 ꞉ 12 1 ꞉ 16 1 ꞉20每段允许最大铅垂高度（米）0.350.600.751.001.50（1）平台另一侧的残疾人通道AB 应该选择哪个坡度建造是符合要求的？请说明理由．（2）在(1)的坡度下，求斜坡底部点B 到台阶底部点C 的水平距离BC 的长．将实际问题抽象为数学问题，数形结合，感受数学与现实的联系，增强应用数学的意识与能力．六、总结（1、2、3）通过本节课的学习，有什么感受和收获？还有什么疑惑？提高数学概括表达能力，增强学习过程中的反思和总结意识．AB DC七、作业布置（1、2、3）1．练习册P43——习题25.4（3）．2．完成学习单上的练习3．。

九年级数学上册25-3解直角三角形(第2课时)教案沪教版五四制

0
A
B
D
C
(180 -∠A)
0 0 0
0
（180 -45 ）=67.5 =67 30’
过点 A 作 AD⊥BC，垂足为点 D ∵ AB＝AC， ∴BD= BC= ×6=3
在 Rt△ABD 中
∵cosB= ∴AB= 所以，这个等腰三角形的腰长约为 7．839，底角为 67 30’. 思考：本题如果作腰上的高，能解△ABC 吗？试一试：在等腰三角形中，已知 AB＝AC＝5，BC＝本节课我们利用直角三角形的知识将某些一般三角形问题或梯形问题中的数量关系，归结为直角三角形中元素之间的关系，从而解决问题．今后，我们还要善于用数学知识解决实际问题．四、作业布置练习册 25.3（2）
25.3 解直角三角形（第 2 课时）
教学目标设计 1．进一步运用勾股定理、锐角三角比解非直角三角形． 2．通过综合运用锐角三角比解三角形，逐步形成分析问题、解决问题的能力．教学重点及难点教学重点：学会把一般三角形转化为直角三角形解决．教学难点：如何转化为直角三角形的辅助线的做法．教学过程设计一、情景引入 1．复习 1、求下列各直角三角形中字母的值．
2、在△ABC 中，∠C 为直角，b=
，a=
，解这个三角形． =35 ，解这个三角形（精确到 0.1）．
3、在△ABC 中，∠C 为直角，且 b=20，
2．思考在一般的三角形中，如果已知适当的元素能否能求出其余相关的元素呢？ 3．讨论在一般的三角形中，已知几个元素能求出其余相关的元素呢？二、学习新课 1．例题分析例题 1 在等腰三角形 AB C 中，已知 AB=AC, ∠A=45°,BC=6,求它的腰长和底角. 分析：根据三角形内角和定理，可求得底角的大小．如图，作底边上的高，由等腰三角形“三线合一”的性质，可知底边被高平分，于是得到两个全等的直角三角形．因此在其中任意一个直角三角形中，知道了一个锐角、一条直角边，可解这个直角三角形，从而得到等腰三角形的腰长．解：在△ABC 中， ∠B= ∠C= =

九年级数学上册25-3解直角三角形(巩固课)教案沪教版五四制

4、如图所示，已知：在△ABC 中，∠A=60°，∠B=45°，AB= 8.求：△ABC 的面积(结果可保留根号).
三、作业布置一张试卷
一．问题拓展
[说明] 通过这几道例题的分析和挖掘，使学生明确可以用解直角三角形的知识解决一般三角形中的计算问题.就是要把握好转化的技巧.
二、巩固练习 1、课本 25.3（2） 2、已知等腰△比值．
3、已知在直角梯形 ABCD 中，上底 CD=4，下底 AB=10，非直角腰 BC= ，则底角∠B=；
九年级数学上册 25-3 解直角三角形（巩固课）教案沪教版五四制
教学内容分析本课时其实是安排了一个解直角三角形和应用的一节过度课，它起到了承上启下的作用 .先从
解一般的三角形或梯形的问题，寻找转化为直角三角形的方法，然后，到下一节课的应用，使学生不会有知识过度跳跃的感觉. 教学重点及难点教学重点：学会把一般三角形转化为直角三角形解决．教学难点：如何转化为直角三角形的辅助线的做法．教学过程设计

九年级数学上册 252 解直角三角形教案沪教版五四制教案

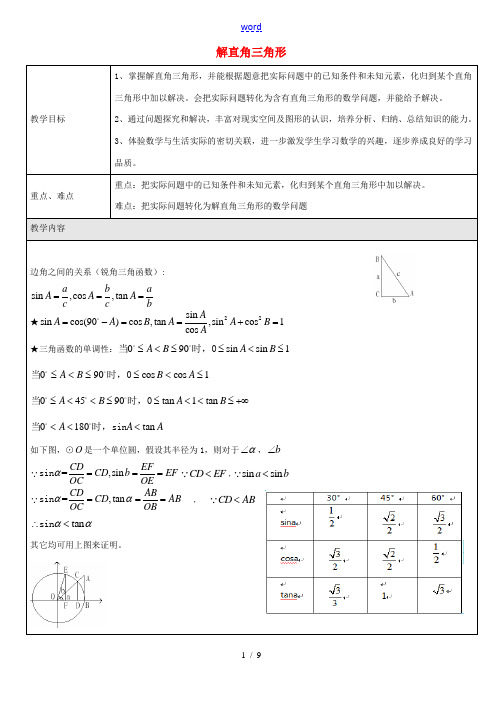
解直角三角形教学目标1、掌握解直角三角形，并能根据题意把实际问题中的已知条件和未知元素，化归到某个直角三角形中加以解决。

会把实际问题转化为含有直角三角形的数学问题，并能给予解决。

2、通过问题探究和解决，丰富对现实空间及图形的认识，培养分析、归纳、总结知识的能力。

3、体验数学与生活实际的密切关联，进一步激发学生学习数学的兴趣，逐步养成良好的学习品质。

重点、难点重点：把实际问题中的已知条件和未知元素，化归到某个直角三角形中加以解决。

难点：把实际问题转化为解直角三角形的数学问题教学内容边角之间的关系（锐角三角函数）:sin ,cos ,tan a b aA A A c c b===★22sin sin cos(90)cos ,tan ,sin cos 1cos AA AB A A B A=-==+= ★三角函数的单调性：090sin sin 1A B A B ≤<≤≤<≤当时，0090cos cos 1A B B A ≤<≤≤<≤当时，004590tan 1tan A B A B ≤<<≤≤<<≤+∞当时，0 0180tan A A A <<<当时，sin如下图，⊙O 是一个单位圆，假设其半径为1，则对于α∠，b ∠=,sin CD EFCD b EF OC OE α===sin CD EF <,sin sin a b < =,tan CD ABCD AB OC OBαα===sin ,CD AB<tan αα∴<sin其它均可用上图来证明。

30°，45°，60°的三角函数值（见右表）例（1）计算： sin60°·tan30°+cos ² 45°=（2）把Rt △ABC 各边的长度都扩大3倍得Rt △A ’B ’C ’，那么锐角A 、A ’的余弦值的关系为（3）在△ABC 中，∠C ＝90°，tan A ＝31，则sin B ＝，cosB= （4）如果1cos 3tan 302A B -+-=那么△ABC 是（5）在ABC A B C ∠∠∠中，a,b,c 分别是，，的对边，已知a=10,32,b =+32c =-，则sin sin b B c C +的值等于（6）已知cos α<0.5,那么锐角α的取值X 围是 (7)已知α为锐角，则m =sinα+cosα的值（） A ．m ＞1 B ．m =1 C ．m ＜1 D ．m ≥1在解直角三角形及应用时经常接触到的一些概念仰角和俯角（2）坡度tan i a = （3）方位角例某某市城市规划期间，欲拆除黄河岸边的一根电线杆AB(如图)，已知距电线杆AB 水平距离14米处是河岸，即BD ＝14米，该河岸的坡面CD 的坡角∠CDF 的正切值为2，岸高CF 为2米，在坡顶C 处测得杆顶A 的仰角为30°，D 、E 之间是宽2米的人行道，请你通过计算说明在拆除电线杆AB 时，为确保安全，是否将此人行道封上？(在地面上以点B 为圆心，以AB 长为半径的圆形区域为危险区域)C BAD EFG方向航行方向航行多少海里？（结果精确到400.6428≈400.7660≈400.8391≈ 1.732．CB北4030A 45°例、由于过度采伐森林和破坏植被，我国部分地区频频遭受沙尘暴侵袭。

九年级数学上册25.3解直角三角形的应用教案沪教版五四制

第（1）课时课题：书法---写字基本知识课型：新授课教学目标：1、初步掌握书写的姿势，了解钢笔书写的特点。

2、了解我国书法发展的历史。

3、掌握基本笔画的书写特点。

重点：基本笔画的书写。

难点：运笔的技法。

教学过程：一、了解书法的发展史及字体的分类：1、介绍我国书法的发展的历史。

2、介绍基本书体：颜、柳、赵、欧体，分类出示范本，边欣赏边讲解。

二、讲解书写的基本知识和要求：1、书写姿势：做到“三个一”：一拳、一尺、一寸（师及时指正）2、了解钢笔的性能：笔头富有弹性；选择出水顺畅的钢笔；及时地清洗钢笔；选择易溶解的钢笔墨水，一般要固定使用，不能参合使用。

换用墨水时，要清洗干净；不能将钢笔摔到地上，以免笔头折断。

三、基本笔画书写1、基本笔画包括：横、撇、竖、捺、点等。

2、教师边书写边讲解。

3、学生练习，教师指导。

（姿势正确）4、运笔的技法：起笔按，后稍提笔，在运笔的过程中要求做到平稳、流畅，末尾处回锋收笔或轻轻提笔，一个笔画的书写要求一气呵成。

在运笔中靠指力的轻重达到笔画粗细变化的效果，以求字的美观、大气。

5、学生练习，教师指导。

（发现问题及时指正）四、作业：完成一张基本笔画的练习。

板书设计：写字基本知识、一拳、一尺、一寸我的思考：通过导入让学生了解我国悠久的历史文化，激发学生学习兴趣。

这是书写的起步，让学生了解书写工具及保养的基本常识。

基本笔画书写是整个字书写的基础，必须认真书写。

课后反思：学生书写的姿势还有待进一步提高，要加强训练，基本笔画也要加强训练。

总第（2）课时课题：书写练习1课型：新授课教学目标：1、教会学生正确书写“杏花春雨江南”6个字。

2、使学生理解“杏花春雨江南”的意思，并用钢笔写出符合要求的的字。

重点：正确书写6个字。

难点：注意字的结构和笔画的书写。

教学过程：一、小结课堂内容，评价上次作业。

二、讲解新课：1、检查学生书写姿势和执笔动作（要求做到“三个一”）。

2、书写方法是：写一个字看一眼黑板。

九年级数学上册 25.3 解直角三角形的应用教案沪教版

锐角三角比的应用教学目标锐角三角比知识点的回顾与应用基础题型的熟练掌握重点、难点知识点的应用与总结，学生做题方法的训练考点及考试要求知识点的灵活应用教学内容【考点透视】锐角三角比的意义及特殊角的三角比值考查多以填空选择出现，属基础题集中当题，解直角三角形的应用是中考的热点． ★知识回顾1、解直角三角形的概念？2、解直角三角形的依据？（三边之间的关系；两锐角之间的关系；边角之间的关系）3、解直角三角形的类型及解法？4、仰角与俯角；坡度与坡角；方位角？问题1：某中学初三年级开展教学实践活动，测量该地电视塔的高度。

由于该塔还没有完成内外装修而周围障碍物密集，于是在它不远处的C 处测得电视塔顶点A 的仰角为45°，然后向电视塔的方向前进132米到达D 处，在D 处测得顶点A 的仰角为60°。

求：电视塔的高度约为多少米？（保留四位有效数字3 1.732≈）问题2：还有没有其它的解题方法？问题3：通过解此题我们可以得到哪些启示？总结解直角三角形的应用题的一般方法步骤：（1）认真审题；（2）建立数学模型：找出已知量与所求量并标图（即把实际问题转化为数学问题），添加必要的辅助线；（3）用方程的思想来解题，得到实际问题的答案。

二、例题（一）有关仰角、俯角的实际应用问题例1、直升飞机在跨江大桥AB 的上方P 点处，此时飞机离地面的高度PO=450米，且A 、B 、O 三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB ．1、直升飞机在长400米的跨江大桥AB 的上方P 点处，且A 、B 、O 三点在一条直线上，在大桥的两端测得飞机的仰角分别为30°和45 °，求飞机的高β αP O B A 450米例1图4530P A B D O 200变题3度PO ．2、直升飞机在高为200米的大楼AB 上方P 点处，从大楼的顶部和底部测得飞机的仰角为30°和45°，求飞机的高度PO ．3、直升飞机在高为200米的大楼AB 左侧P 点处，测得大楼的顶部仰角为45°，测得大楼底部俯角为30°，求飞机与大楼之间的水平距离．【总结：】将例1及3个相关变题中的图形加以分析，从每个问题所提供的条件特点，结合图形结构特征，可归纳出这类问题：（1）示意图为有一个公共边的两个直角三角形，分布位置有两种，位于公共边同侧或异侧；（2）所给条件一般为两角一边，且边一般为已知角的邻边或对边（非直角三角形斜边），此时选用的锐角三角比多为正切（二）有关坡度、坡角的实际应用题例2、如图，某拦水坝截面的原设计方案为：AH ∥BC,坡角∠ABC=60°，坝顶到坝脚的距离AB=6米。

2解直角三角形-沪教版(上海)九年级数学上册课件

B A
D A
P
C
B C
数学在身边
【探究2】学生小王帮在测绘局工作的爸爸买了一些仪器后
与同学在环西文化广场休息，看到濠河对岸的电视塔，他
想用手中的测角仪和卷尺不过河测出电视塔空中塔楼的高
度.现已测出∠ADB=40°，由于不能过河，因此无法知道
BD的长度，于是他向前走50米到达C处测得∠ACB=55°，
Q
30 °
P
60 °
450
A
答案：AB≈520（米）
B
C
图5
归纳与提高
α
α
β
β
450
45°
30°
45°
30°
400
O
B
AO
B
A
P
C
30°60° A
45° 22000米 45°
O
B
P 45°°
3300°°
202000米
D
O
B
练习：1、“神舟”5号载人航天飞船发射成功。当飞船完成变轨后，就在离地球表面350km的圆形轨道上运行，如图，当飞船运行到地球表面上P点的正上方时，从飞船上能直接看到地球上最远的点在什么位置？这样的最远点与P点的距离是多少？（地球半径约为6400km，Π取3.142，结果保留整数）
变题2：直升飞机在高为200米的大楼AB上方P 点处，从大楼的顶部和底部测得飞机的仰角为 30°和60°，求飞机的高度PO .
P
答案: (100 3 300 ) 米
O
C
30° A
45°
200米
B
合作与探究
变题3：直升飞机在高为200米的大楼AB左侧P 点处，测得大楼的顶部仰角为45°,测得大楼底部俯角为30°，求飞机与大楼之间的水平距离.

九年级数学上册25-4解直角三角形应用(第3课时)教案沪教版五四制

∴∠A≈7°11’. 答:残疾人通道的坡度约为 1：7.938，坡角约为 7°11’.
在 Rt△AB6BE=1.6×1.2=1.92（米）. (1)AD=AE+EF+DF=2AE+EF =2×1.92+2.8=6.64≈6.6(米) (2)设坡角为α ,则
i=tanα = ∴α ≈32°.
=0.625,
答:路基下底宽约为 6.6 米,坡角约为 32°.
三、课堂小结今天学习了什么, 你有什么收获？
四、作业布置练习册：习题 2 5.4（3）
如图，坡面的铅垂高度（h）和水平宽度（L）的比叫做坡面的坡度（或坡比），记作 i，即 i= .
坡度通常写成 1:m 的形式，如 i=1∶1.5．坡面与水平面的夹角叫做坡角,记作α .坡度 i 与坡角α 之间的关系: i= 2．例题分析例题 1 如图，一座大楼前的残疾人通表示，沿着通道走 3.2 米可进入楼厅，楼 0.4 米，那么你知道该通道的坡度与坡角 1’ ，其他近似数取四位有效数字）。提问： AB 表示什么？题中数据 3.2 什么量？如何求 i ？解过点 A 作水平线 l，再作 BC⊥l,垂足为点 C. 根据题意,可知 AB=3.2 米,BC=0.4 米. 在 Rt△ABC 中, AC= ∴i= ∴tanA= = ≈1:7.938. ≈0.1260， ≈3.175(米). 道是斜坡，若用 AB 厅比楼外的地面高吗？（角度精确到米、 0.4 米各表示 =tanα .
25.4 解直角三角形应用（第 3 课时）
教学内容分析本节教材内容主要是坡度有关概念，以及利用直角三角形边角关系，解决生产及生活中有关坡度的实际应用问题. 教学目标设计 1．理解坡度有关的概念，学会利用已学过的知识解决有关坡度的实际问题； 2．形成分析问题、解决问题的能力和运用数学的意识，感悟数学来源于实践又作用于实践．体验数学的价值. 教学重点及难点 1、学会将某些实际问题中的数量关系归结为解直角三角形中的元素之间的关系，从而解决问题； 2、掌握坡度的意义，强调坡度 i 的表示形式 1∶m．教学过程设计一、情景引入 1．思考我们知道，现在的建筑设计都很人性化，一般的大楼现在都设有残疾人通道，大家都知道残疾人通道是斜坡，若用 AB 表示，沿着通道走 3.2 米可进入楼厅，楼厅比楼外的地面高 0.4 米，那么你知道该通道的坡角吗？二、学习新课 1．概念辨析

上海市静安区实验中学九年级上学期沪教版五四制第二十五章25.4解直角三角形的应用

上海市静安区实验中学九年级上学期沪教版五四制第二十五章25.4解直角三角形的应用学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知A ，B 两点，若A 对B 的仰角为α，则B 对A 的俯角为( )A ．αB ．90°－αC ．180°－αD ．90°＋α 2．在离铁塔底部m 米的地面A 处测得铁塔塔顶的仰角为α，那么铁塔的高为（） A ．sin m α⋅ B ．cos m α⋅ C ．tan m α⋅ D ．cot m α⋅ 3．如图，为测楼房BC 的高，在距离楼房30米的A 处测得楼顶的仰角为α，则楼高BC 为（）A ．30tanα米B ．30tan α米C ．30sinα米D ．30sin α米 4．AE 、CF 是△ABC 的两条高，如果AE ：CF=3：2，则sinA ：sinC 等于（） A ．3：2 B ．2：3 C ．9：4 D ．4：9 5．如图，小雅家(图中点O 处)门前有一条东西走向的公路，经测量得知有一水塔(图中点A 处)在她家北偏东60度500 m 处，那么水塔所在的位置到公路的距离AB 是( )A ．250 mB ．mC mD ．m 6．小明同学从A 地沿北偏西60°方向走100 m 到B 地，再从B 地向正南方向走200 m 到C 地，此时小明同学离A 地 ( )A ．150 mB ．mC ．100 mD ．m 7．小明沿着与地面成30º的坡面向下走了2米，那么他下降（）A ．1米BC ．D ．3米 8．一个物体从A 点出发，在坡度为1：7和斜坡上直线向上运动到B ，当AB=30米时，物体升高（）A ．307米B ．308 米C ．D ．以上都不对 9．某人在坡角为α的山坡上种树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB 为（）A ．5cos αB ．5cos αC ．5sin αD ．5sin α二、填空题10．离旗杆20米处的地方用测角仪测得旗杆顶的仰角为α，如果测角仪高为1.5米．那么旗杆的高为__________米（用含α的三角函数表示）．11．在周一的升旗仪式时，某同学站在离旗杆12米远的地方，当国旗升起到旗杆顶时，他测得视线的仰角为30°，若这位同学的目高为1.6米，则旗杆的高度约为__________米．12．若某斜面的坡度为1:______.13．某人沿斜坡笔直向上走了100米，此时他在竖直方向上升了50米，则此斜坡的坡度为________14．一人乘雪橇沿坡角为30°的斜坡笔直滑下，滑下的距离S （米）与时间t （秒）的关系式为S=10t+t 2，若滑坡底的时间为2秒，则此人下滑的高度为________三、解答题15．如图，某电信公司计划修建一条连接B 、C 两地的电缆．测量人员在山脚A 点测得B 、C 两地的仰角分别为30°、45°，在B 处测得C 地的仰角为60°，已知C 地比A 地高200m ，求电缆BC 的长．（结果可保留根号）16．如图，AB和CD是同一地面上的两座相距36米的楼房，在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°，楼底D的俯角为30°, 求楼CD的高．17．如图，AB是江北岸滨江路一段，长为3千米，C为南岸一渡口，为了解决两岸交通困难，拟在渡口C处架桥，测量得A在C北偏西30°方向，B在C的东北方向，从C 处连接两岸的最短的桥长是多少？（结果保留根号）18．如图，某军港有一雷达站P，军舰M停泊在雷达站P的南偏东60 方向36海里处，另一艘军舰N位于军舰M的正西方向，与雷达站P相距（1）军舰N在雷达站P的什么方向？（2）两军舰M、N的距离．（结果保留根号）19．如图，斜坡AC的坡度为1AC=8米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，米，试求旗杆BC的高度．20．如图，梯形ABCD是某水库大坝的横断面，其坝顶宽5米，坝底宽33米，坝的迎水坡度是i1=1:2，背水坡的坡度i2=2:3，求：水坝横截面的面积．参考答案1．A【分析】根据俯角和仰角的定义和平行线的性质即可得到B对A的俯角为α．【详解】解：如图，∵A对B的仰角为α，∴B对A的俯角为α．故选A．【点睛】本题考查了解直角三角形的应用：向下看，视线与水平线的夹角叫俯角；向上看，视线与水平线的夹角叫仰角．2．C【分析】先画出示意图，构造直角三角形，解三角形即可表示出铁塔的高．【详解】解：如图所示：由题意得，∠A=α，AC=m，∠ACB=90°，∴BC=ACtan∠A=ACtanα=mtanα．故选C．【点睛】本题考查解直角三角形的知识，解题关键是构造直角三角形，要求同学们熟练掌握锐角三角函数的定义.3．A【详解】在Rt△ABC中，tanBCACα=，∴BC＝AC·tanα，即BC＝30tanα米．故选A．4．B【分析】根据三角函数的定义求解即可．【详解】解：如图示，sinCFCAFAC，sinAEACEAC，则sin:sin CFCF ACCAF ACEAE AEAC，又:3:2AE CF，sin:sin2:3CAF ACE．故选：B．【点睛】此题主要考查了三角函数的定义，熟悉相关性质是解题的关键．5．A【解析】解：由已知得：∠AOB=30°，OA=500m．则AB=12OA=250m．故选A．6．D 【分析】根据在Rt△ABD中利用三角函数分别求AD，BD的长，从而得到CD的长．再利用勾股定理求AC的长即可．【详解】解：如图：由B在A的北偏西60°方向可求得∠B=60°，在Rt△ABD中，AD=AB•sin60°=BD=AB•cos60°=50，∴CD=BC-BD=150．∴AC．故选D．【点睛】解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．7．A【分析】直接利用坡度的定义，坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，可画出三角形，结合图形运用三角函数求解即可．【详解】如图所示：∵AB=2，∠C=90°，∠A=30°．∴他下降的高度BC=ABsin30°=1（米）．故选A【点睛】此题主要考查了坡度的定义和特殊角的三角函数值，正确记忆特殊角的三角函数值是解题的关键.8．C【分析】先画图，由tan BC A AC ，设BC x =，7AC x ，由勾股定理得出AB ，再根据已知条件，求出BC ，即物体升高的高度．【详解】解：如图，设BC x =，7AC x ，则52AB x ，30AB =米， 5230x， 32x ，BC ∴=故选：C ．【点睛】本题考查了解直角三角形的应用，坡角的正切值等于坡度．9．B【分析】利用所给的角的余弦值求解即可．【详解】由题意可知：BC =5米，∠CBA =∠α，∴AB =BC cos α=5cos α．故选B ．【点睛】本题主要考查学生对坡度、坡角的理解及运用，熟练掌握解直角三角形的应用是解题的关键．10．1.5 +20tan【分析】由题意得，在直角三角形中，知道了已知角的邻边求对边，用正切值计算即可．【详解】根据题意可得：旗杆比仪器高20tanα，测角仪高为1.5米，故旗杆的高为(1.5+20tanα)米.故答案为1.5+20tanα【点睛】考查解直角三角形的应用，属于仰角问题，要求学生能借助仰角构造直角三角形是解题的关键.11． 1.6【分析】可由仰角的正切函数求得目高以上旗杆的高度，再加上目高即得旗杆的高度．【详解】解：由于某同学站在离国旗旗杆12米远的地方，当国旗升起到旗杆顶时，他测得视线的仰角为30，则目高以上旗杆的高度112tan3043h（米)，旗杆的高度11.6 1.643h h（米)，故答案为： 1.6．【点睛】本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．12．30°【分析】根据坡度与坡比之间的关系即可得出答案.【详解】︒==∵tan301∴坡面的坡角为30故答案为：30【点睛】本题主要考查坡度与坡角，掌握坡度与坡角之间的关系是解题的关键.13．30°【分析】根据勾股定理求出此人行走的水平距离，根据坡度的概念计算即可．【详解】053，则此斜坡的坡度50:5031:3i，即：此斜坡的坡度为30°，故答案为：30°．【点睛】本题考查的是解直角三角形的应用-坡度问题，掌握坡度是坡面的铅直高度h和水平宽度l 的比是解题的关键．14．12米【分析】由S=10t+t2可求得滑下的距离S，结合坡角为30°，通过三角函数计算从而得到答案．【详解】t=∵S=10t+t2且2∴S=20+4=24∵坡角为30°且sin30°=1 2∴此人下滑的高度为130=24122S sin⨯︒⨯=故答案为：12米．【点睛】本题考察了一元二次函数和三角函数的知识；求解的关键是结合实际问题，熟练掌握并运用一元二次函数和三角函数的性质，从而完成求解．15．电缆BC至少（200）m【分析】首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造方程关系式，进而可解即可求出答案．【详解】解：过B点分别作BE⊥CD、BF⊥AD，垂足分别为E、F．设BC=xm．∵∠CBE=60°，∴BE=12x，．∵CD=200，∴DE=200﹣2x．∴BF=DE=200，DF=BE=12x．∵∠CAD=45°，∴AD=CD=200．∴AF=200﹣12x．在Rt△ABF中，tan30°=200212002x BFAF x=-，解得x=2001）（m）．答：电缆BC至少（200）m【点睛】本题考查解直角三角形的应用-仰角俯角问题．16．楼CD的高是（【分析】在题中两个直角三角形中，知道已知角和其邻边，只需根据正切值求出对边后相加即可．【详解】延长过点A的水平线交CD于点E则有AE⊥CD，四边形ABDE是矩形，AE=BD=36∵∠CAE=45°∴△AEC是等腰直角三角形∴CE=AE=36在Rt△AED中，tan∠EAD=ED AE∴ED=36×tan30°∴答：楼CD的高是（【点睛】本题考查了解直角三角形的应用-仰角俯角问题，借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形是解题的关键．17933．【分析】本题要求的实际上是C到AB的距离，可通过构建直角三角形来求解．过点C作CD AB⊥于点D．CD就是所求的值．因为CD是直角三角形ACD和BCD的公共直角边，可用CD 表示出AD和BD的长，然后根据AB的值来求出CD的长．【详解】解：过点C作CD AB⊥于点D，CD就是连接两岸最短的桥．设CD x=千米．B在C的东北方向，A在C北偏西30°方向，45BCD∴∠=︒，30ACD∠=︒∴在直角三角形BCD中，有BD CD=，∴在直角三角形ACD中，3tan tan30AD CD ACD x x．∵AD DB AB，∴33x x，∴9332x（千米）．【点睛】本题是将实际问题转化为直角三角形中的数学问题，可通过作辅助线构造直角三角形，然后把条件和问题转化到直角三角形中进行计算．18．（1）东南方向（或南偏东45°）；（2）海里.【分析】（1）过点P 作PQ ⊥MN ，交MN 的延长线于点Q ．在Rt △PQM 中求出PQ ，进而在Rt △PQN 中求出∠QPN ；（2）在Rt △PQM 中根据三角函数求出MQ ，就得到MN 的长．【详解】解：过点P 作PQ ⊥MN ，交MN 的延长线于点Q ．（1）在Rt △PQM 中，由∠MPQ=60°，得∠PMQ=30°，又PM=36，∴PQ=12PM=12×36=18（海里）．在Rt △PQN 中，cos ∠QPN=2PQ PN ==， ∴∠QPN=45°．即军舰N 到雷达站P 的东南方向（或南偏东45°）．（2）由（1）知在Rt △PQN 为等腰直角三角形，∴PQ=NQ=18（海里）．在Rt △PQM 中，MQ=PQ•tan ∠QPM=18•tan60°=，∴MN=MQ-NQ=-18（海里）．答：两军舰的距离为(海里【点睛】解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线． 19．旗杆BC 的高度为8米【分析】如果延长BC 交AD 于E 点，则CE AD ⊥，要求BC 的高度，就要知道BE 和CE 的高度，就要先求出AE 的长度．直角三角形ACE 中有坡比，由AC 的长，那么就可求出AE 的长，然后求出BE 、CE 的高度，BC BE CE =-，即可得出结果．解：延长BC 交AD 于E 点，则CE AD ⊥．在Rt AEC ∆中，AC=8，由坡度为30CAE ∠=︒， 1sin 30842CE AC ， 3cos30843AE AC ．在Rt ABE ∆中，222283(43)12BE AB AE ． BE BC CE =+，124=8BC BE CE （米)．答：旗杆的高度为8米．【点睛】本题考查了三角函数和解直角三角形，熟悉相关性质是解题的关键．20．水坝横截面的面积为152平方米【分析】根据坝的迎水坡度是i 1=1:2，背水坡的坡度i 2=2:3，坝顶宽5米，坝底宽33米，设AE=DF=2x 米，则BE=4x 米，CF=3x 米，可得方程45333x x ++=，可以求得AE=8米，根据梯形面积公式，即可得到水坝横截面的面积．【详解】∵i 1=1:2,背水坡的坡度i 2=2:3设AE=DF=2x 米，则BE=4x 米，CF=3x 米∵AD=5米∴EF=5米∵BC=33米45333x x ++=4x =∴水坝横截面的面积为1(533)81522+⨯⨯=平方米．【点睛】本题考查了坡度的求解，根据坡度求得CF，BE的长是解题的关键．。

沪教版(上海)九年级上学期25.3第1课时解直角三角形(1)

沪教版（上海）九年级上学期25.3第1课时解直角三角形（1）学校:___________姓名：___________班级：___________考号：___________一、填空题1．在ABC ∆中，90C ∠=︒，a 、b 、c 为A ∠、B 、C ∠的对边．（1）若5cm a =，45A ∠=︒，则B ∠=______，c =______；（2）若10cm c =，30B ∠=︒，则a =______，b =______；（3）若4cm a =，8cm c =，则cos A =______，tan A =______，tan B =_____；（4）若3a b ，则sin B =______，tan A =______，tan B =_____．2．已知在ABC ∆中，8AB AC ==，30BAC ∠=．将ABC ∆绕点A 旋转，使点B 落在原ABC ∆的点C 处，此时点C 落在点D 处．延长线段AD ，交原ABC ∆的边BC 的延长线于点E ，那么线段DE 的长等于___________．二、单选题3．如图，小明为了测量其所在位置点A 到河对岸点B 之间的距离，沿着与AB 垂直的方向走了m m ，到达点C ，测得∠ACB ＝α，那么AB 等于 ( )A ．m ·sin αmB ．m ·tan αmC ．m ·cos αmD ．tan m αm 4．在Rt ABC ∆中，90C ∠=︒，2BC =，1cos 3B =，则b 等于（）．A B ．C D ．5．把两条宽度都为1的纸条交叉重叠放在一起，且它们的交角为α，则它们重叠部分（图中阴影部分）的面积为（）．A ．1sin αB ．1cos αC ．sin αD ．16．如图，在矩形ABCD 中，DE AC ⊥于E ，13EDC EDA ∠∠=∶∶，且10AC =，则DE 的长度是（）A ．3B ．5C ．D 7．如图，在ABC 中，C ∠9060B D =︒∠=︒，，是AC 上一点，DE AB ⊥于E ，且21CD DE ==，，则BC 的长为（）A ．2BC ．D ．8．如图，在△ABC 中，∠BAC ＝90°，AB ＝AC ，点 D 为边AC 的中点，DE ⊥BC 于点E ，连接BD ，则tan ∠DBC 的值为 ( )A ．13B 1C ．2D ．14三、解答题9．在ABC ∆中，90C ∠=︒，根据下列条件解直角三角形．（1）30A ∠=︒，6a =；（2）30A ∠=︒，b =．10．在ABC ∆中，已知90C ∠=︒，30b c +=，30A B ∠-∠=︒．解这个直角三角形．11．已知在ABC ∆中，::1:2:3A B C ∠∠∠=，4c b -=- 12．如图，已知ABC ∆与DFE ∆是两个全等的直角三角形，量得它们的斜边长为10cm ，较小锐角为30，将这两个三角形摆成如图（1）所示的形状，使点B 、C 、F 、D 在同一条直线上，且点C 与点F 重合，将图（1）中的ABC ∆绕点C 顺时针方向旋转到图（2）的位置，点E 在边AB 上，AC 交DE 于点G ，则线段FG 的长为______cm ．（保留根号）13．如图是直线25y x =-+的图像，求锐角α的三个三角函数值．14．如图，某种雨伞的伞面可以看成由12块完全相同的等腰三角形布料缝合而成．量得其中一个三角形OAB 的边56OA OB cm ＝＝ .(1)求AOB ∠ 的度数；(2)求OAB ∆的面积．(不计缝合时重叠部分的面积)15．阅读下列材料，并解决问题．如图（1），在锐角三角形ABC 中，A ∠、B 、C ∠的对边分别是a 、b 、c 过点A 作AD BC ⊥，垂足为D ，则sin AD B c =，sin AD C b =，即sin AD c B =，sin AD b C =，于是sin sin c B b C =，即sin sin b c B C =，同理有sin sin c a C A =，sin sin a b A B=．所以sin sin sin a b c A B C==（*）．即在一个三角形中，各边和它所对角的正弦的比相等．（1）在锐角三角形中，若已知三个元素a 、b 、A ∠，运用上述结论（*）和有关定理就可以求出其余三个未知元素c 、B 、C ∠．请你按照下列步骤填空，完成求解过程：第一步：由条件a 、b 、A ∠−−−−→用解析式______B −−−→∠求出；第二步：由条件A ∠、b 、B ∠−−−−→用解析式______C −−−→∠求出；第三步：由条件______−−−−→用解析式______c −−−→求出．（2）一货轮在C 处测得灯塔A 在货轮的北偏西30的方向上，随后货轮以28.4海里/小时的速度按北偏东45的方向航行，半小时后到达B 处，此时又测得灯塔A 在货轮的北偏西70︒的方向上（如图（2）），求此时货轮距灯塔A 的距离AB ．（结果精确到0.1）16．ABC ∆中，5AB =，8AC =，30C ∠=︒，求ABC ∆的面积．参考答案1．45︒ 5cm 12【解析】【分析】（1）利用∠A=45°，即可得出∠B 的度数，进而利用锐角三角函数关系得出c 的值；（2）利用∠B=30°，即可得出b ，c 的关系，进而利用a=10cos30°求出即可；（3）首先利用勾股定理得出b 的值，进而利用锐角三角函数关系得出即可；（4）利用3ab ，得出c=2b ，进而利用锐角三角函数关系得出即可．【详解】解：（1）∵∠C=90°，∠A=45°，∴∠B=45°，sin45°=a c，∴2（cm ）；（2）∵c=10 cm ，∠B=30°，∴b=5cm ，a=10cos30°=10（cm ）；（3）∵a=4cm ，c=8cm ，∴cm ，则=2，3；（4）∵3ab ， ∴c=2b ，则sinB=2b b =12，tanA=b故答案为：（1）45°，cm ；（2），5cm ；（3；（4）12【点睛】本题考查解直角三角形，熟练利用锐角三角函数关系求解是解题的关键．2．4【详解】解：如图，由旋转的性质知，8AD AC ==，30CAD ∠=，过C 作CF AE ⊥交AE 于F ，而142CF AC ==，AF =故8DF =-．在ABC ∆中，8AB AC ==，30BAC ∠=则75B ACB ∠=∠=，故45E ACB DAC ∠=∠-∠=，CEF ∆为等腰直角三角形，则4EF CF ==，所以4(84DE EF DF =-=--=．3．B 【解析】∵tanα=ABm，∴AB=mtanα米.故选B.点睛：熟记三角函数公式.4．B【分析】在直角三角形中，根据角的余弦值与三角形边的关系及勾股定理，即可求出b．【详解】解：在Rt△ABC中，∠C=90°，BC=a=2，CA=b，AB=c，cosB=BCAB=ac=13，∵BC=a=2，，∴c=6，∴故选：B．【点睛】本题考查解直角三角形，解题的关键是明确题意，利用锐角三角函数解答．5．A【分析】如图，过A作AE⊥BC于E，AF⊥CD于F，垂足为E，F，证明△ABE≌△ADF，从而证明四边形ABCD是菱形，再利用三角函数算出BC的长，最后根据菱形的面积公式算出重叠部分的面积即可．【详解】解：如图所示：过A作AE⊥BC于E，AF⊥CD于F，垂足为E，F，∴∠AEB=∠AFD=90°，∵AD ∥CB ，AB ∥CD ，∴四边形ABCD 是平行四边形，∵纸条宽度都为1，∴AE=AF=1，在△ABE 和△ADF 中90ABE ADF AEB AFD AE AF α∠∠∠∠︒⎧⎪⎨⎪⎩＝＝＝＝＝，∴△ABE ≌△ADF （AAS ），∴AB=AD ，∴四边形ABCD 是菱形．∴BC=AB ， ∵AE AB=sinα， ∴BC=AB=1sin α， ∴重叠部分（图中阴影部分）的面积为：BC×AE=1×1sin α=1sin α．故选：A ．【点睛】本题考查菱形的判定与性质，以及三角函数的应用，关键是证明四边形ABCD 是菱形，利用三角函数求出BC 的长．6．D【分析】根据∠EDC ：∠EDA=1：3，可得∠EDC=22.5°，∠EDA=67.5°，再由AC=10，求得DE ．【详解】∵四边形ABCD是矩形，∴∠ADC=90°，AC=BD=10，OA=OC=12AC=5，OB=OD=12BD=5，∴OC=OD，∴∠ODC=∠OCD，∵∠EDC：∠EDA=1：3，∠EDC+∠EDA=90°，∴∠EDC=22.5°，∠EDA=67.5°，∵DE⊥AC，∴∠DEC=90°，∴∠DCE=90°-∠EDC=67.5°，∴∠ODC=∠OCD=67.5°，∴∠ODC+∠OCD+∠DOC=180°，∴∠COD=45°，∴OE=DE，∵OE2+DE2=OD2，∴2DE2=OD2=25，∴DE=2，故选D．【点睛】本题主要考查了勾股定理和矩形的性质，是一道中等题．7．B【分析】由题意可知∠，即得，从而求出，再根据∠的正切函数即可求得结果.【详解】由题意得∠，，，，，，解得43 3.故选B.8．A【解析】试题分析：∵在△ABC 中，∠BAC=Rt ∠，AB=AC ，∴∠ABC=∠C=45°，AC ，又∵点D 为边AC 的中点，∴AD=DC=12AC ，∵DE ⊥BC 于点E ，∴∠CDE=∠C=45°，∴DE=EC=2DC=4AC ，∴tan ∠DBC=DE BEAC 13．故选A ．考点：1．解直角三角形；2．等腰直角三角形．9．（1）60B ∠=︒，b =12c =；（2）60B ∠=︒，10a =，20c =．【分析】（1）首先利用三角形内角和定理得出∠B 的度数，再利用三角函数关系解直角三角形即可；（2）首先利用三角形内角和定理得出∠B 的度数，再利用三角函数关系解直角三角形即可．【详解】解；（1）∵∠C=90°，∠A=30°，∴∠B=60°，∵a=6，∴c=AB=2BC=2×6=12， ∴b=12×sin60°；（2））∵∠C=90°，∠A=30°，∴∠B=60°，∵，∴c=AB=601sin ︒=20， ∴a=12c=10．【点睛】本题考查解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．利用了直角三角形中30°所对边与斜边的关系和锐角三角函数，要熟练掌握好边角之间的关系．10．60A ∠=︒，30B ∠=︒，a =10b =，20c =．【分析】根据∠C=90°可得∠A+∠B=90°，再结合∠A-∠B=30°可算出∠A 、∠B 、∠C 的度数，再根据特殊角的三角函数值计算出三边长即可．【详解】解：∵∠C=90°，∴∠A+∠B=90°，∵∠A-∠B=30°，∴∠A=60°，∠B=30°，∵sin30°=b c =12， ∴b=12c ， ∵b+c=30， ∴12c+c=30，解得c=20，则b=10，【点睛】本题考查解直角三角形，解题的关键是掌握特殊角的三角函数值．11．30A ∠=︒，60B ∠=︒，90C ∠=︒，2a =，b =4c =．【分析】根据::1:2:3A B C ∠∠∠=可得三角度数，进而得到△ABC 是直角三角形，再根据三角函数得到b 、c 之间的关系，再结合4c b -=-【详解】解：∵∠A ：∠B ：∠C=1：2：3，∴∠A=180°×1123++=30°， ∠B=60°，∠C=90°，∵sin60°=c∴b=2c ，∵4c b -=-∴c-2 解得：c=4，．【点睛】本题考查解直角三角形，涉及的知识有：勾股定理，锐角三角函数定义，以及特殊角的三角函数值，熟练掌握勾股定理，牢记特殊角的三角函数值是解题的关键．12【分析】根据直角三角形两锐角互余求出∠B=∠DEF=60°，再根据旋转的性质可得BC=CE ，然后判断出△BCE 是等边三角形，根据等边三角形的性质可得∠BCE=60°，然后求出∠EFG=30°，再求出∠EGF=90°，根据直角三角形30°角所对的直角边等于斜边的一半求出EF ，EG ，然后利用勾股定理列式计算即可得FG 的长．【详解】解：∵△ACB 与△DFE 全等，较小锐角为30°，∴∠B=∠DEF=90°-30°=60°，由旋转的性质得，BC=CE ，∴△BCE 是等边三角形，∴∠BCE=60°，∴∠EFG=90°-60°=30°，∴∠EGF=180°-30°-60°=90°，∵斜边长为10cm ，∴EF=2DE=2×10=5cm ， EG=12EF=12×5=52cm ，在Rt △EFG 中，【点睛】本题考查旋转的性质，解直角三角形，等边三角形的判定与性质，勾股定理的应用，熟记各性质并准确识图是解题的关键．13．sin α=，cos α=，tan 2α=．【分析】根据直线25y x =-+的图像，首先求出与坐标轴的两个交点坐标，根据勾股定理求得两交点之间的距离，进一步利用锐角三角函数的定义求出三角函数值即可．【详解】解：如图，直线25y x =-+的图象与x 轴的交点A 为（52，0），即OA=52；与y 轴的交点B 为（0，5），即OB=5；则2；sin α=OB AB ，5cos5OAABα===，5tan252OBOAα===．【点睛】本题考查一次函数图象上点的坐标特征，锐角三角函数的定义，解题的关键是熟知一次函数图象上点的坐标特点以及锐角三角函数的定义．14．（1）30；（2）784cm2【分析】（1）由图可得，∠AOB是360°中的十二分之一，所以用360°除以12便可得出答案（2）利用勾股定理求出OA边上的高，然后利用三角形面积公式求解即可【详解】(1)∠AOB=360°÷ 12=30°(2)如图，过B作BD⊥OA于D，在Rt BOD∆中，∠AOB=30°，∴BD=12OB=28 .∴OABs∆=12OA∙BD=12×56×28=7842cm【点睛】本题主要考查了直角三角形的相关性质与三角形面积公式，掌握以上概念是关键15．（1）sin sina bA B=，180A B C∠+∠+∠=︒，a、A∠、C∠或b、B、C∠，sin sinc aC A=或sin sinb cB C=；（2）AB约为21.3海里．【分析】（1）根据材料把已知条件代入即可，材料中的结论就是sin sin sina b cA B C==，依此就可解锐角三角形；（2）由题意求出∠ACB、∠A的度数以及BC的距离，根据材料中的结论进行计算即可．【详解】解：（1）在锐角三角形中，若已知三个元素a 、b 、A ∠，运用上述结论（*）和有关定理就可以求出其余三个未知元素c 、B 、C ∠．请你按照下列步骤填空，完成求解过程：第一步：由条件a 、b 、A ∠−−−−→用解析式sin sin a b A B=B −−−→∠求出，第二步：由条件A ∠、b 、B ∠−−−−→用解析式∠A+∠B+∠C=180°C −−−→∠求出；第三步：由条件a 、∠A 、∠C 或b 、∠B 、∠C −−−−→用解析式sin sin c a C A =或sin sin b c B C=c −−−→求出．（2）如图：由题意得：∠ACB=75°，∠FBC=180°-∠ECB=135°，∵∠FBA=70°，∴∠ABC=65°，∴∠A=180°-∠ACB-∠ABC=40°，BC=14.2．运用上述结论sin sin sin a b c A B C==可得， 14.2sin 40sin 75AB =︒︒，解得：AB≈21.3．答：货轮距灯塔A 的距离AB 约为21.3海里．【点睛】本题考查三角函数，解锐角三角形，主要是考查同学们的阅读理解能力，通过材料总结出学生们没有接触的知识，并根据此知识点解决相关的问题．16．6或6【分析】作AD ⊥BC 于D ，分两种情况：AD 在ABC ∆内和AD 在ABC ∆外，先根据含30°角的直角三角形的性质求出AD 、CD ，再根据勾股定理求出BD ，从而可得BC 的长，利用三角形的面积公式即可求出答案；【详解】解：作AD ⊥BC 于D ．分两种情况：AD 在ABC ∆内和AD 在ABC ∆外，AD 在ABC ∆内时：在Rt △ACD 中，∵∠ADC=90°， 8AC =，30C ∠=︒，∴AD=12AC=4，在Rt △ABD 中，∵∠ADB=90°，5AB =，AD=4，∴，∴∴S △ABC =12BC∙AD=12×（×4=6； AD 在ABC ∆外时：在Rt △ACD 中，∵∠ADC=90°， 8AC =，30C ∠=︒，∴AD=12AC=4，在Rt △ABD 中，∵∠ADB=90°，5AB =，AD=4，∴，∴，∴S △ABC =12BC∙AD=12×（）×4=6-．【点睛】本题考查解直角三角形的应用，含30°角的直角三角形的性质，勾股定理，根据已知构建直角三角形是解题关键．注意分类思想的运用．。