2018-2019学年天津市和平区八年级(下)期末数学试卷
2019-2020学年天津市和平区八年级第二学期期末综合测试数学试题含解析
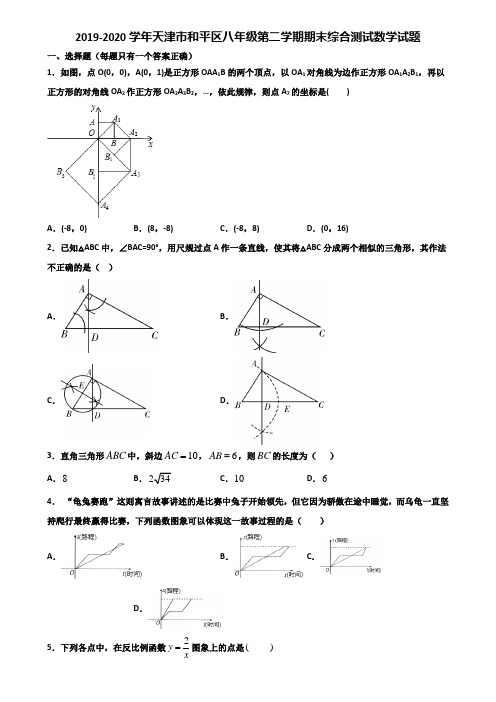
∴正方形对角线OA1= ,
∴OA2=2,
∴A2(2,0),
∴A3(2,2),
∴OA3=2 ,
∴OA4=4,
∴A4(0,-4),A5(-4,-4),A6(-8,0),A7(-8,8);
故选:C.
【点睛】
本题考查点的规律;利用正方形的性质,结合平面内点的坐标,探究An的坐标规律是解题的关键.
∴函数的图像在一三象限,在每一个象限,y随x增大而减小
∵-3<-1
∴y1<y2.
故选B.
点睛:此题主要考查了反比例函数的图像与性质,关键是利用反比例函数的系数k确定函数的图像与性质.
二、填空题
11.1﹣2a.
【解析】
【分析】
利用数轴上a的位置,进而得出a和a-1的取值范围,进而化简即可.
【详解】
由数轴可得:﹣1<a<0,
20.(6分)四边形ABCD中,AB=CB= ,CD= ,DA=1,且AB⊥CB于B.求∠BAD的度数;
21.(6分)老师随机抽査了本学期学生读课外书册数的情况,绘制成不完整的条形统计图和不完整的扇形统计图(如图所示).
(1)补全条形统计图;
(2)求出扇形统计图中册数为4的扇形的圆心角的度数;
(3)老师随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后发现册数的中位数没改变,则最多补查了.
D、以点B为圆心BA的长为半径画弧,交BC于点E,再以E点为圆心,AB的长为半径画弧,在BC的另一侧交前弧于一点,过这一点及A点作直线,该直线不一定是BE的垂线;从而就不能保证两个小三角形相似;D符合题意;
故选D.
点睛:此题主要考查了相似变换以及相似三角形的判定,正确掌握相似三角形的判定方法是解题关键.
天津市和平区2019-2020学年初二下期末综合测试数学试题含解析

【解析】
【分析】
根据点A(2,y1)与点B(3,y2)都在反比例函数 的图象上,可以求得y1、y2的值,从而可以比较y1、y2的大小,本题得以解决.
【详解】
∵点A(2,y1)与点B(3,y2)都在反比例函数 的图象上,
∴y1= ,y2= ,
∵-3<-2,
∴ ,
故选A.
【点睛】
本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.
14.五子棋的比赛规则是:一人执黑子,一人执白子,两人轮流放棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在位置用坐标表示是(-2,2),黑棋B所在位置用坐标表示是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,则点C的坐标是__________.
9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用 , 表示直角三角形的两直角边( ),下列四个说法:
① ,② ,③ ,④ .
其中说法正确的是( )
A.①②B.①②③C.①②④D.①②③④
10.到三角形三个顶点距离相等的点是( )
A.三角形三条边的垂直平分线的交点
天津市和平区2019-2020学年初二下期末综合测试数学试题
一、选择题(每题只有一个答案正确)
1.木匠有32米的木材,想要在花圃周围做边界,以下四种设计方案中,设计不合理的是( )
A. B. C.D.
2.如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
4.C
2018-2019学年天津市和平区八年级(下)期末数学试卷

2018-2019学年天津市和平区八年级(下)期末数学试卷一.选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)若在实数范围内有意义,则a的取值范围是()A.a≥﹣B.a≤﹣C.a>﹣D.a<﹣2.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为()A.4B.3C.2D.13.(3分)已知直线y=2x﹣b经过点(1,﹣1),则b的值为()A.3B.﹣3C.0D.64.(3分)设矩形的面积为S,相邻两边的长分别为a,b,已知S=2,b=,则a 等于()A.2B.C.D.5.(3分)下列说法正确的是()A.四个角都相等的四边形是正方形B.四条边都相等的四边形是正方形C.对角线相等的平行四边形是正方形D.对角线互相垂直的矩形是正方形6.(3分)若直角三角形两条直角边长分别为2,3,则该直角三角形斜边上的高为()A.B.C.D.7.(3分)晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%,小桐三项体育成绩(百分制)依次95分、90分、86分,则小桐这学期的体育成绩是()A.88分B.89分C.90分D.91分8.(3分)改革开放40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图.说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.根据上述信息,下列结论中错误的是()A.2017年第二季度环比有所提高B.2017年第三季度环比有所提高C.2018年第一季度同比有所提高D.2018年第四季度同比有所提高9.(3分)如图,直线y=kx+b过A(﹣1,2),B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为()A.x≤﹣2或x≥﹣1B.0≤y≤2C.﹣2≤x≤0D.﹣2≤x≤﹣1 10.(3分)某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是()A.每月上网不足25小时,选择A方式最省钱B.每月上网时间为30小时,选择B方式最省钱C.每月上网费用为60元,选择B方式比A方式时间长D.每月上网时间超过70小时,选择C方式最省钱11.(3分)已知直线y=﹣x+6交x轴于点A,交y轴于点B,点P在线段OA上,将△P AB 沿BP翻折,点A的对应点A′恰好落在y轴上,则的值为()A.B.1C.D.12.(3分)如图,边长为2的菱形ABCD中,∠A=60°,点M是边AB上一点,点N是边BC上一点,且∠ADM=15°,∠MDN=90°,则点B到DN的距离为()A.B.C.D.2二.填空题(本大题共6小题,每小题3分,共18分)13.(3分)如图,在Rt△ABC中,D是斜边AB的中点,AB=2,则CD的长为.14.(3分)农科院对甲、乙两个品种甜玉米各用10块试验田进行试验,得到甲、乙两个品种每公顷的平均产量相同,而甲、乙两个品种产量的方差分别为S2甲=0.01,S2乙=0.0002,则产量较为稳定的品种为(填“甲”或“乙”)15.(3分)计算(+)(﹣)的结果等于.16.(3分)若一次函数y=x+m的图象经过第一、二、三象限,写出一个符合条件的m的值为.17.(3分)一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过分钟,容器中的水恰好放完.18.(3分)图中的虚线网格是等边三角形,它的每一个小三角形都是边长为1的等边三角形.(1)如图①,连接相邻两个小正三角形的顶点A,B,则AB的长为.(2)在如图②所示的网格中,用无刻度的直尺,画一个斜边长为2的直角三角形,且它的顶点都在格点上.三.解答题(本大题共7小题,共66分,解答应写出文字说明、演算步骤或推理过程)19.(8分)计算:(1)2﹣6+3;(2)(+3)(+5).20.(8分)如图,在四边形ABCD中,AB=AD=,∠A=90°,∠CBD=30°,∠C=45°,求BD及CD的长.21.(10分)某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:(Ⅰ)本次参加跳绳测试的学生人数为,图①中m的值为;(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;(Ⅲ)根据样本数据,估计该校九年级跳绳测试中得3分的学生有多少人?22.(10分)在菱形ABCD中,AC是对角线.(1)如图①,若AB=6,则菱形ABCD的周长为;若∠DAB=70°,则∠D的度数是;∠DCA的度数是;(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD =∠EBC.23.(10分)现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.(1)根据题意,填写下表:快递物品重量(千克)0.5134…甲公司收费(元)22…乙公司收费(元)115167…(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.24.(10分)已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.(1)如图①,求证:EF∥AC;(2)如图②,EF与边CD交于点G,连接BG,BE,①求证:△BAE≌△BCG;②若BE=EG=4,求△BAE的面积.25.(10分)已知,直线y=2x﹣2与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为,点B的坐标为;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①求点C的坐标;②过动点P(m,0)且垂直于x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是;(3)若∠ABN=45°,求直线BN的解析式.。
2019学年天津市和平区八年级下学期期末数学试卷(含答案)

天津市和平区八年级(下)期末数学试卷(含答案)一、选择题(本大题共12小题,每小题3分,共36分)1.如图,在矩形ABCD 中,对角线AC ,BD 交于点O ,以下说法错误的是( )A 、∠ABC =90°B 、AC =BDC 、OA =OBD 、OA =AB2.若2)1(1 x 在实数范围内有意义,则x 的取值范围是( ) A 、x >1 B 、x ≥1C 、x ≠1D 、x >−13.下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x 与方差s 2: 甲 乙 丙 丁平均数x (cm) 561 560 561560 方差s 2 (cm 2) 3.5 3.5 15.5 16.5根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )A 、甲B 、乙C 、丙D 、丁4.某个一次函数的图象与直线y =21x 平行,并且经过点(−2,−4),则这个一次函数的解析式为( ) A 、y =−21x −5B 、y =21x +3 C 、y =21x −3 D 、y =−2x −8 5.直线y =2x +6与x 轴的交点坐标为( )A 、(−3,0)B 、(3,0)C 、(0,6)D 、(0,−3)6.下列计算错误的是( )A 、34÷211=27 B 、(8+3)×3=26+3C 、(42−36)÷22=2−323 D 、(5+7)(5−7)=−27.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是( )A 、12B 、12.5C 、13D 、148.一次函数y =kx +b 中,y 随x 的增大而增大,b <0,则这个函数的图象不经过()A、第一象限B、第二象限C、第三象限D、第四象限9.下列判断:①对角线相等的四边形是矩形②对角线互相垂直的四边形是菱形③对角线互相垂直的矩形是正方形其中,正确的有()A、0个B、1个C、2个D、3个10.在菱形ABCD中,E、F分别在BC和CD上,且△AEF是等边三角形,AE=AB,则∠BAD等于()A、95°B、100°C、105°D、120°11.一段笔直的公路AC长20千米,途中有一处休息点B,AB长15千米,甲、乙两名长跑爱好者同时从点A出发,甲以15千米/时的速度匀速跑至点B,原地休息半小时后,再以10千米/时的速度匀速跑至终点C;乙以12千米/时的速度匀速跑至终点C,下列选项中,能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(小时)函数关系的图象是()A、B、C、D、12.给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是平行四边形.(2)如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是菱形(3)在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,则中点四边形EFGH是正方形其中,正确的有()A、0个B、1个C、2个D、3个二、填空题(本大题共6小题,每小题3分,共18分)13.直角三角形斜边上的中线等于斜边的_________.14.计算:a6÷a2=________.15.已知正比例函数y=kx(k是常数,k≠0),y随x的增大而减小,写出一个符合条件的k的值为____________.16.某市广播电视局欲招聘播音员一名,对A、B两名候选人进行了两项素质测试,两人的两项测试成绩如表所示.根据实际需要,广播电视局将面试、综合知识测试的得分按3:2的比例计算两人的总成绩,那么_______(填A或B)将被录用.17.如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为___________.18.如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.在图②③④中分别画出一个以格点为顶点,边长都为整数的锐角三角形,并在每条边上标出其长度(图①−④中的三角形互不全等)三、解答题(本大题共7小题,共66分)19.计算:(1)45−20(2)27×50÷6.20.在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数0 1 2 3 4人数 3 13 16 17 1(1)求这50个样本数据的平均数、众数和中位数:(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.21.如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.(1)OA的长=_____,OE的长=______,CE的长=_____,AD的长=_____;(2)设点P在x轴上,且OP=EP,求点P的坐标.22.如图,在四边形ABCD中,∠B=∠C,点E,F分别在边AB,BC上,AE=DF=DC.(1)若∠DFC=70°,则∠C的大小=_____(度),∠B的大小=_______(度);(2)求证:四边形AEFD是平行四边形;(3)若∠FDC=2∠EFB,则四边形AEFD一定是“菱形、矩形、正方形”中的________.23.一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.(1)当0≤x≤4时,y关于x的函数解析式为__________;(2)当4<x≤12时,求y关于x的函数解析式;(3)每分钟进水升,每分钟出水升,从某时刻开始的9分钟时容器内的水量是____升.24.已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.(1)如图,点P在线段BC上,①求证:四边形APQD是平行四边形;②判断OA,OP之间的数量关系和位置关系,并加以证明;(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.25.如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E 是AB的中点,点F在BC边上,且CF=1.(1)点E的坐标为,点F的坐标为_________;(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,①点E′的坐标为______,点F′的坐标为________;②求直线E′F′的解析式;(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.。
-2018学年天津市和平区八年级(下)期末数学试卷
2017-2018学年天津市和平区八年级(下)期末数学试卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)已知△ABC 的三边分别是6,8,10,则△ABC 的面积是( ) A .24B .30C .40D .482.(3分)若√x√x −1在实数范围内有意义,则x 的取值范围是( ) A .x ≥0B .x ≥1C .x >1D .x ≥0且x ≠13.(3分)化简5x3x 的结果为( )A .3√x 5B .5x 23C .5x 3D .5√x 34.(3分)某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )A .21,21B .21,C .21,22D .22,225.(3分)下列命题正确的是( ) A .有一个角是直角的四边形是矩形 B .有三个角是直角的四边形是矩形 C .对角线相等的四边形是矩形D .对角线互相平分的四边形是矩形6.(3分)不论实数k 取何值,一次函数y =kx ﹣3的图象必过的点坐标为( )A .(0,﹣3)B .(0,3)C .(32,0)D .(−32,0)7.(3分)如图所示,菱形ABCD 中,对角线AC 、BD 相交于点O ,H 为AD 边的中点,菱形ABCD 的周长为36,则OH 的长等于( )A .B .5C .6D .98.(3分)当x =3时,函数y =x ﹣k 和函数y =kx +1的函数值相等,则k 的值为( )A .2B .12C .−12D .﹣29.(3分)关于函数y =﹣2x +1,下列结论正确的是( ) A .图象与直线y =2x +1平行 B .y 随x 的增大而增大 C .图象经过第一、二、三象限 D .当x >12时,y <010.(3分)如图是甲、乙两射击运动员的10次射击训练成绩的折线统计图,则下列说法正确的是( )A.甲比乙的成绩稳定B.乙比甲的成绩稳定C.甲、乙两人的成绩一样稳定D.无法确定谁的成绩更稳定11.(3分)如图,OB、AB分别表示两名同学沿着同一路线运动的一次函数图象,图中s和t分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:①射线AB表示甲的运动路程与时间的函数关系;②甲出发时,乙已经在甲前面12米;③8秒后,甲超过了乙;④64秒时,甲追上了乙.其中,正确结论的个数是()A.1 B.2 C.3 D.412.(3分)如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰好落在边AD上的点F处:点G在AF上,将△ABG沿BG折叠,点A恰好落在线段BF上的点H处,有下列结论:①∠EBG=45°②S△ABG=32S△FGH③AG+DF=FG④xxxx=54其中,正确结论的个数是()A.1 B.2 C.3 D.4二.填空题(本大题共6小题,每小题3分,共18分)13.(3分)计算(√5+√3)(√5−√3)的结果等于.14.(3分)某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,根据四人各自的平均成绩,公司将录取.候选人甲乙丙丁测试成绩(百分制)面试86929083笔试90838392 15.(3分)已知一次函数y=kx+2(k是常数,k≠0),y随x的增大而减小,写出一个符合条件的k的值为16.(3分)如图,E,F,G,H分别是正方形ABCD各边的中点,则四边形EFGH是形.17.(3分)如图,正方形OABC的对角线OB在直线y=−43x上,点A在第一象限.若正方形OABC的面积是50,则点A的坐标为.18.(3分)如图,在每个小正方形的边长为1的格中,点C,D,E,F,G均在格点上,DE 与FG相交于点T.(1)CD的长等于(2)在如图所的网格中,用无刻度的直尺,画出①以DE为一边的正方形②以CD,DT为邻边的矩形CDTP三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤域推理过程 19.(8分)计算:(1)(√45+√18)﹣(√8−√125) (2)(√80+√40)÷√520.(8分)某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,捐款(元)10 15 3050 60人数 3 6 1113 6因不慎,表中数据有两处被墨水污染,已无法看清,但已知全班平均每人捐款38元. (Ⅰ)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程. (Ⅱ)该班捐款金额的众数,中位数分别是多少(Ⅲ)如果用九年级(1)班捐款情况作为一个样本,请估计全校1200人中捐款在40元以上(包括40元)的人数是多少21.(10分)如图,在三角形纸片ABC 中,∠ACB =90°,BC =5,AB =13,在AC 上取一点E ,以BE 为折痕,使AB 的一部分与BC 重合,点A 与BC 延长线上的点D 重合. (1)AC 的长= . (2)求CE 的长.22.(10分)在▱ABCD中,(1)如图①,若AB=5,BC=3,则▱ABCD的周长为;若∠A=70°,则∠B的度数是,∠C的度数是;(2)如图②,点E是▱ABCD外一点,连接DB并延长交CE于点F,且CF=FE.求证DF∥AE.23.(10分)某公司计划组织员工外出,甲、乙旅行社的服务质量相问,且对外报价都是300元/人,该公同联系时,甲旅行社表示可给每人八折优惠;乙旅行社表示可免去一人的费用,其余人九折优惠.(1)根据题意,填写下表:外出人数(人)1011甲旅行社收费(元)2640乙旅行社收费(元)2430(2)设该公司此次外出有x人,选择甲旅行社的费用为y1元,选择乙旅行社的费用为y 2元,分别写出y 1,y 2关于x 的函数关系式(3)该公司外出人数在什么范围内,选甲旅行社划算24.(10分)已知,四边形ABCD 是正方形,点E 在边AD 上,点F 在边AB 的延长线上,且DE =BF ,连接EF .(1)如图①,连接CE ,CF .求证:△CEF 是等腰直角三角形;(2)如图②,BD 与EF 交于点M ,若正方形ABCD 的边长为6,DE =2,求AM 的长. (3)点G ,点H 分别在边AB ,边CD 上,GH 与EF 交于点N ,且∠GNF =45°,若正方形ABCD 的边长为6,GH =3√5,求DE 的长(直接写出结果即可)25.(10分)在平面直角坐标系中,O 为原点,已知直线y =12x +3与x 轴交于点A ,与y 轴交于点B ,点C 与点A 关于y 轴对称.(1)点A 的坐标为 ,点B 的坐标为 ,点C 的坐标为 ,直线BC 的解析式为 .(2)点M 是x 轴上的一个动点(点M 不与点O 重合),过点M 作x 轴的垂线,交直线AB 于点P .交直线BC 于点Q①如图①,当点M 在x 轴的正半轴上时,若△PQB 的面积为94,求点M 的坐标;②连接BM ,若∠BMP =∠BAC ,求点P 的坐标.2017-2018学年天津市和平区八年级(下)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【解答】解:∵62+82=102,∴△ABC是直角三角形,∴△ABC的面积=12×6×8=24.故选:A.2.【解答】解:∵√x√x−1在实数范围内有意义,∴x≥0,x﹣1>0,解得:x>1,则x的取值范围是:x>1.故选:C.3.【解答】解:3x =5x√x3x=5√x3.故选:D.4.【解答】解:这组数据中,21出现了10次,出现次数最多,所以众数为21,第15个数和第16个数都是22,所以中位数是22.故选:C.5.【解答】解:A、有一个角是直角的平行四边形是矩形,故此选项不能判定是矩形;B、有三个角是直角的四边形是矩形,能判定是矩形;C、对角线相等的平行四边形是矩形,故此选项不能判定是矩形;D、两条对角线互相平分四边形是平行四边形,故此选项不能判定是矩形.故选:B.6.【解答】解:∵一次函数y=kx﹣3,∴不论k取何值,函数图象必过点(0,﹣3).故选:A.7.【解答】解:∵四边形ABCD为菱形,且周长为36,∴AB=BC=CD=AD=9,又∵O为BD中点,H为AD的中点,∴OH为△ABD的中位线,∴OH=12AB=,故选:A.8.【解答】解:由题意:3﹣k=3k+1,∴k=12,故选:B.9.【解答】解:A.由于直线y=﹣2x+1与直线y=2x+1的k值不相等,所以它们不平行,故本选项错误;B.函数y=﹣2x+1中,k=﹣2<0,y随x的增大而减小,故本选项错误;C .函数y =﹣2x +1中,k =﹣2<0,b =1>0,此函数的图象经过一、二、四象限,故本选项错误;D .函数y =﹣2x +1可化为x =1−x 2,依据1−x 2>12,可得y <0,故本选项正确; 故选:D .10.【解答】解:由图中知,甲的成绩为7,7,8,9,8,9,10,9,9,9,乙的成绩为8,9,7,8,10,7,9,10,7,10, x 甲=(7+7+8+9+8+9+10+9+9+9)÷10=,x 乙=(8+9+7+8+10+7+9+10+7+10)÷10=, 甲的方差S 甲2=[2×(7﹣)2+2×(8﹣)2+(10﹣)2+5×(9﹣)2]÷10=,乙的方差S 乙2=[3×(7﹣)2+2×(8﹣)2+2×(9﹣)2+3×(10﹣)2]÷10= ∴S 2甲<S 2乙.故选:A .11.【解答】解:∵射线OB 所表示的速度为648=8米/秒,射线AB 所表示的速度为64−128=米/秒,而甲的速度比乙快,∴射线AB 表示乙的运动路程与时间的函数关系,所以①错误;∵乙8秒走了64﹣12=52米,甲8秒走了64米,而他们8秒时相遇,∴甲出发时,乙在甲前面12米,所以②正确;∵甲乙8秒时相遇,而甲的速度比乙快,∴8秒后,甲超过了乙,所以③正确;④错误.故选:B .12.【解答】解:∵△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上, 将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处,∴∠CBE =∠FBE ,∠ABG =∠FBG ,BF =BC =10,BH =BA =6,AG =GH ,∴∠EBG =∠EBF +∠FBG =12∠CBF +12∠ABF =12∠ABC =45°,所以①正确; 在Rt △ABF 中,AF =√xx 2−xx 2=√10−6=8,∴DF =AD ﹣AF =10﹣8=2,设AG =x ,则GH =x ,GF =8﹣x ,HF =BF ﹣BH =10﹣6=4,在Rt △GFH 中,∵GH 2+HF 2=GF 2,∴x 2+42=(8﹣x )2,解得x =3,∴GF =5,∴AG +DF =FG =5,所以③正确;∵S △ABG =12×6×3=9,S △GHF =12×3×4=6,∴S △ABG =32S △FGH .所以②正确. 设CE =EF =x ,在Rt △EFD 中,x 2=(6﹣x )2+22,解得x =103, ∴CE =103,DE =6−103=83, ∴xx xx =54,故④正确, 故选:D .二.填空题(本大题共6小题,每小题3分,共18分)13.【解答】解:原式=(√5)2﹣(√3)2=5﹣3=2,故答案为:2.14.【解答】解:甲的平均成绩=(90×4+86×6)÷10=876÷10=(分)乙的平均成绩=(83×4+92×6)÷10=884÷10=(分)丙的平均成绩=(83×4+90×6)÷10=872÷10=(分)丁的平均成绩=(92×4+83×6)÷10=866÷10=(分)∵>>>,∴乙的平均成绩最高,∴公司将录取乙.故答案为:乙.15.【解答】解:∵一次函数y随x的增大而减小,∴k<0,不妨设k=﹣1,故答案为:﹣116.【解答】解:连接AC、BD.∵E、F、G、H分别是正方形ABCD各边的中点,∴EH∥BD∥FG,EF∥AC∥HG,EH=FG=12BD,EF=HG=12AC,∴四边形EFGH为平行四边形,∵四边形ABCD是正方形,∴AC=BD,AC⊥BD,∴EF=FG,EF⊥FG,∴▱EFGH是正方形,故答案为:正方.17.【解答】解:如图作OF⊥OB,交BA的延长线于F,作BM⊥x轴于M,FN⊥x轴于N.∵四边形ABCD是正方形,∴∠OBA=45°,∵∠BOF=90°,∴△BOF是等腰直角三角形,∴OB=OF,由△BOM≌△OFN,可得BM=ON,OM=FN,∵正方形OABC的面积是50,∴OB=10,∵点B在直线y=−43上,∴B(﹣6,8),F(8,6),∵BA=AF,∴A(1,7),故答案为()18.【解答】解:(1)由勾股定理可得,CD=√12+52=√26;故答案为:√26;(2)①如图所示,四边形CDEQ即为所求;②如图所示,四边CDTP即为所求.三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤域推理过程19.【解答】解:(1)原式=3√5+3√2−2√2+5√5=8√5+√2;(2)原式=√80÷5+√40÷5=4+2√2.20.【解答】解:(I)被污染处的人数为:50﹣3﹣6﹣11﹣13﹣6=11(人),被污染处的捐款数[50×38﹣(10×3+15×6+30×11+50×13+60×6)]÷11=40,答:被污染处的人数为11人,被污染处的捐款数为40元;(Ⅱ)这组数据中50出现了13次,出现次数最多,则这组数据的众数是50;将组组数据从小到大依次排列,最中间的两数据是40,40,所以中位数为(40+40)÷2=40;(Ⅲ)因为九年级一班捐款数40元以上(包括40元)的有30人,占到60%,因此估计全校1200人捐款在40元以上(包括40元)的人数是1200×60%=720,答:全校1200人中捐款在40元以上(包括40元)的人数是720人.21.【解答】解:(1)∵∠ACB=90°,BC=5,AB=13,∴AC=12,故答案为12.(2)根据将其三角形纸片ABC 对折后点A 落在BC 的延长线上,则AB =BD =13, ∵S △ABC =S △BCE +S △BDE ,∴12×5×12=12BC ×EC +12EC ×BD , ∴30=12×EC (5+13),∴CE =103.22.【解答】解:(1)如图1中,∵四边形ABCD 是平行四边形,∴AD =BC =3,AB =CD =5,AD ∥BC ,∴∠A =∠C =70°,∠A +∠B =180°,∴∠B =110°,∴平行四边形ABCD 的周长为16.故答案为16,110°,70°.(2)如图2中,连接AC交BD于O.∵四边形ABCD是平行四边形,∴CO=OA,∵CF=FB,∴OF∥AE,即DF∥AE.23.【解答】解:(1)根据题意,甲旅行社收费为300××10=2400;甲旅行社收费为300××(11﹣1)=2700;(2)由题意可得甲旅行社的费用:y1=300×=240x乙旅行社的费用:y2=300××(x﹣1)=270x﹣270(3)当y1<y2时,240x<270x﹣270,解得x>9∴当公司外出人数大于9人时,选甲旅行社划算.24.【解答】解:(1)如图①,∵四边形ABCD是正方形,∴BC=CD,∠CBA=∠D=90°,∴∠D=∠CBF=∠BCD=90°,在△CDE和△CBF中,∵{xx =xx∠x =∠xxx xx =xx,∴△CDE ≌△CBF (SAS ),∴CE =CF ,∠DCE =∠BCF ,∴∠BCF +∠BCE =∠DCE +∠BCE =90°, ∴△CEF 是等腰直角三角形;(2)如图②,过M 作MG ⊥AF 于G , ∵DE =BF =2,AB =6,∴AE =4,AF =6+2=8,∵∠FGM =∠FAE =90°,∠FMG =∠FEA , ∴△FGM ∽△FAE ,∴xx xx =xx xx =84=2, ∴FG =2GM ,设GM =x ,则FG =2x ,∵四边形ABCD 是正方形,∴∠ABM =45°,∴△BGM 是等腰直角三角形, ∴BG =GM =x ,∴BG =BF =x =2,∴GM =2,AG =6﹣2=4,由勾股定理得:AM=√22+42=2√5;(3)如图③,过G作GP⊥CD于P,由(1)知:∠CEF=45°,∵∠GNF=∠ENM=45°,∴∠EMN=90°,∴∠D=∠EMH=90°,∴∠GHC=∠DEC,∵GP=BC=CD,∠D=∠GPH=90°,∴△GHP≌△CED,∴CE=GH=3√5,∵CD=6,在Rt△CED中,由勾股定理得:DE=√(3√5)2−62=3.25.【解答】解:(1)解:对于y =12x +3,由x =0得:y =3,∴B (0,3)由y =0得:0=12x +3,解得x =﹣6,∴A (﹣6,0),∵点C 与点A 关于y 轴对称∴C (6,0)设直线BC 的函数解析式为y =kx +b ,根据题意得:{x =36x +x =0,解得{x =−12x=3 ∴直线BC 的函数解析式为y =−12x +3.故答案为:(﹣6,0);(0,3);(6,0);y =−12x +3.(2)如图1所示:过点B 作BD ⊥PQ ,垂足为D .设M (x ,0),则P (x ,12x +3)、Q (x ,−12x +3),则PQ =x ,DB =x .∵△PQB 的面积为94,∴12BD •QP 12x •x =94,解得x =3√22(负值舍去). ∴M (3√22,0). (3)如图2所示:当点M 在x 轴的正半轴上时.∵OB ∥QP ,∴∠BMP =∠OBM .又∵∠BMP =∠BAC ,∴∠BAO =∠OBM .∴xx xx =xx xx ,即36=xx 3,解得OM =32. 将x =32代入y =12x +3得:y =154, ∴P (32,154). 如图3所示:当点M 在x 轴的负半轴上时.∵OB ∥QP ,∴∠BMP =∠OBM .又∵∠BMP =∠BAC ,∴∠BAO =∠OBM .∴xx xx =xx xx ,即36=xx 3,解得OM =32. 将x =−32代入y =12x +3得:y =94,∴P (−32,94). ∴点P 的坐标为(−32,94)或(32,154).。
(12份试卷合集)天津市重点名校2018-2019学年八下期末试卷汇总

2018-2019学年八年级下学期数学期末模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、填空题(本大题共6小题,每小题3分,满分18分)-有意义,则x的取值范围是.1.若二次根式2x2.在数轴上表示实数a的点如图所示,化简+|a﹣2|的结果为.3.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如下表所示:时间(小时) 4 5 6 7人数10 20 15 5则这50名学生一周的平均课外阅读时间是小时.4.如图,已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,若AB=6,则OE= .5.如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是.6.如图所示,四边形ABCD为矩形,点O为对角线的交点,∠BOC=120°,AE⊥BO交BO于点E,AB=4,则BE等于.二、选择题(本大题共8个小题,每小题只有一个正确选项,每小题4分,满分32分)7.下列二次根式化简后,能与合并的是()A. B.C. D.8.下列计算错误的是()A.÷=3 B.=5 C.2+=2D.2•=29.下列各组数中,不能作为直角三角形的三边长的是()A.1.5,2,3 B.6,8,10 C.5,12,13 D.15,20,2510.下列说法正确的是()A.为了解昆明市中学生的睡眠情况,应该采用普查的方式B.数据2,1,0,3,4的平均数是3C.一组数据1,5,3,2,3,4,8的众数是3D.在连续5次数学周考测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定11.如图,已知一次函数y=kx+b的图象经过点A(5,0)与B(0,﹣4),那么关于x的不等式kx+b<0的解集是()A.x<5 B.x>5 C.x<﹣4 D.x>﹣412.对于一次函数y=﹣2x+4,下列结论错误的是()A.函数的图象不经过第三象限B.函数的图象与x轴的交点坐标是(2,0)C.函数的图象向下平移4个单位长度得y=﹣2x的图象D.若两点A(x1,y1),B(x2,y2)在该函数图象上,且x1<x2,则y1<y213.如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,AC=12,菱形ABCD的面积为96,则OH的长等于()A.6 B.5 C.4 D.314.如图1反映的过程是:矩形ABCD中,动点P从点A出发,依次沿对角线AC、边CD、边DA运动至点A停止,设点P的运动路程为x,S△ABP=y.则矩形ABCD的周长是()A.6 B.12 C.14 D.15三、解答题(本大题共9个小题,满分70分.解答时必须写出必要的计算过程、推理步骤或文字说明.)15.(5分)计算:2﹣6﹣(﹣)16.(5分)计算:(7+)(7﹣)+(48﹣)÷17.(7分)重庆出租车计费的方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:(1)该地出租车起步价是元;(2)当x>2时,求y与x之间的关系式;(3)若某乘客一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?18.(8分)已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.(1)求证:CD⊥AB;(2)求该三角形的腰的长度.19.(8分)如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.(1)求证:△ABC≌△DEF;(2)求证:四边形ACFD为平行四边形.20.(7分)学生小明、小华为了解本校八年级学生每周上的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上的时间,算得这些学生平均每周上时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上的时间,算得这些学生平均每周上时间为1.2h.小明与小华整理各自样本数据,如表所示.时间段(h/周)小明抽样人数小华抽样人数0~1 6 221~2 10 102~3 16 63~4 8 2(每组可含最低值,不含最高值)请根据上述信息,回答下列问题:(1)你认为哪位学生抽取的样本具有代表性?.估计该校全体八年级学生平均每周上时间为h;(2)在具有代表性的样本中,中位数所在的时间段是h/周;(3)专家建议每周上2h以上(含2h)的同学应适当减少上的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上的时间?21.(9分)已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.(1)求证:四边形ADCE是平行四边形;(2)在△ABC中,若AC=BC,则四边形ADCE是;(只写结论,不需证明)(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.22.(9分)学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.23.(12分)如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.(1)求直线AC的函数解析式;(2)设点B(0,m),记平行四边形ABCD的面积为S,请写出S与m的函数关系式,并求当BD取得最小值时,函数S的值;(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.参考答案一、填空题(本大题共6小题,每小题3分,满分18分)1.x≤2. 2.3. 3.5.3 4.3 5. 6.2.二、选择题(本大题共8个小题,每小题只有一个正确选项,每小题4分,满分32分)7-10:CCAC 11-14:ADBC三、解答题(本大题共9个小题,满分70分.解答时必须写出必要的计算过程、推理步骤或文字说明.)15.解:原式=4﹣2﹣3+3=+.16.解:原式=49﹣5+16﹣2=42+16.17.解:(1)由函数图象知,出租车的起步价为10元,故答案为:10;(2)当x>2时,每公里的单价为(14﹣10)÷(4﹣2)=2,∴当x>2时,y=10+2(x﹣2)=2x+6;(3)当x=18时,t=2×18+6=42元,答:这位乘客需付出租车车费42元.18.解:(1)∵BC=20cm,CD=16cm,BD=12cm,∴满足BD2+CD2=BC2,∴根据勾股定理逆定理可知,∠BDC=90°,即CD⊥AB;(2)设腰长为x,则AD=x﹣12,由(1)可知AD2+CD2=AC2,即:(x﹣12)2+162=x2,解得x=,∴腰长为cm.19.(1)证明:∵AB∥DE,∴∠B=∠DEF,∵BE=EC=CF,∴BC=EF,在△ABC和△DEF中∴△ABC≌△DEF(ASA).(2)证明:∵△ABC≌△DEF∴AC=DF,∵∠ACB=∠F,∴AC∥DF,∴四边形ACFD是平行四边形.20.解:(1)小明抽取的样本太片面,信息技术兴趣小组的学生上时间相对较多,所以不具代表性,而小华抽取的样本是随机抽取具有代表性.故答案为:小华;1.2.(2)由图表可知第20和第21名同学所在的上时间段为:0~1h/周,所以中位数为:0~1h/周.故答案为:0~1.(3)随机调查的40名学生中应当减少上时间的学生的频率为:=0.2,故该校全体八年级学生中应当减少上时间的人数为:320×0.2=64(人).答:该校全体八年级学生中应当减少上时间的人数为64人.21.证明:(1)∵四边形ADCE是平行四边形∴BD∥CE,BD=CE ∵D是AB的中点∴AD=BD ∴AD=CE 又∵BD∥CE ∴四边形ADCE是平行四边形(2)在△ABC中,若AC=BC,则四边形ADCE是矩形,故答案为:矩形;(3)∵AC⊥BC ∴∠ACB=90°∵在Rt△ABC中,D是AB的中点∴CD=AD=AB ∵在△ABC中,AC=BC,D是AB的中点∴CD⊥AB ∴∠ADC=90°∴平行四边形ADCE是正方形22.解:(1)总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式分别是:y1=0.7[120x+100(2x﹣100)]+2200=224x﹣4800,(x≥50),y2=0.8[100(3x﹣100)]=240x﹣8000,(x≥50);(2)由题意,得当y1>y2时,即224x﹣4800>240x﹣8000,解得:x<200当y1=y2时,即224x﹣4800=240x﹣8000,解得:x=200当y1<y2时,即224x﹣4800<240x﹣8000,解得:x>200答:当参演男生少于200人时,购买B公司的服装比较合算;当参演男生等于200人时,购买两家公司的服装总费用相同,可任一家公司购买;当参演男生多于200人时,购买A公司的服装比较合算.23.解:(1)∵OA=3,OC=4,∴A(﹣3,0)、C(0,4).设直线AC的函数解析式为y=kx+b,将点A(﹣3,0)、C(0,4)代入y=kx+b中,得:,解得:,∴直线AC的函数解析式为y=x+4.(2)∵点B(0,m),四边形ABCD为以AC为对角线的平行四边形,∴m<4,BC=4﹣m,∴S=BC•OA=﹣3m+12(m<4).∵四边形ABCD为平行四边形,∴AD∥BC,∴当BD⊥y轴时,BD最小(如图1).∵AD∥OB,AO⊥OB,DA⊥OB,∴四边形AOBD为矩形,∴AD=OB=BC,∴点B为OC的中点,即m==2,此时S=﹣3×2+12=6.∴S与m的函数关式为S=﹣3m+12(m<4),当BD取得最小值时的S的值为6.(3)∵平行四边形ABCD是菱形,∴AB=BC.∵AB==,BC=4﹣m,∴=4﹣m,解得:m=,∴B(0,).2018-2019学年八年级下学期数学期末模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
天津市各区历年八年级下数学期末试卷真题30套

目录(1)2019-2020学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉3(2)2019-2020学年天津市东丽区八年级(下)期末数学试卷┉┉┉┉┉8(3)2019-2020学年天津市部分区八年级(下)期末数学试卷┉┉┉┉┉11(4)2019-2020学年天津市滨海新区八年级(下)期末数学试卷┉┉┉┉15(5)2018-2019学年天津市南开区八年级(下)期末数学试卷┉┉┉┉┉19(6)2018-2019学年天津市河西区八年级(下)期末数学试卷┉┉┉┉┉24(7)2018-2019学年天津市河东区八年级(下)期末数学试卷┉┉┉┉┉27(8)2018-2019学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉31(9)2018-2019学年天津市滨海新区八年级(下)期末数学试卷┉┉┉┉36(10)2017-2018学年天津市南开区八年级(下)期末数学试卷┉┉┉┉┉40(11)2017-2018学年天津市河北区八年级(下)期末数学试卷┉┉┉┉┉45(12)2017-2018学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉48(13)2017-2018学年天津市部分区八年级(下)期末数学试卷┉┉┉┉┉53(14)2017-2018学年天津市滨海新区八年级(下)期末数学试卷┉┉┉┉57(15)2016-2017学年天津市红桥区八年级(下)期末数学试卷┉┉┉┉┉61(16)2016-2017学年天津市河北区八年级(下)期末数学试卷┉┉┉┉┉65(17)2016-2017学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉69(18)2016-2017学年天津市部分区八年级(下)期末数学试卷┉┉┉┉┉75(19)2015-2016学年天津市五区县八年级(下)期末数学试卷┉┉┉┉┉80(20)2015-2016学年天津市南开区八年级(下)期末数学试卷┉┉┉┉┉84(21)2015-2016学年天津市红桥区八年级(下)期末数学试卷┉┉┉┉┉89(22)2015-2016学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉95(23)2015-2016学年天津市滨海新区八年级(下)期末数学试卷┉┉┉┉98(24)2014-2015学年天津市五区县八年级(下)期末数学试卷┉┉┉┉┉102(25)2014-2015学年天津市和平区八年级(下)期末数学试卷┉┉┉┉┉106(26)2013-2014学年天津市五区县八年级(下)期末数学试卷┉┉┉┉┉111(27)2013-2014学年天津市河西区八年级(下)期末数学试卷┉┉┉┉┉114(28)2012-2013学年天津市五区县八年级(下)期末数学试卷┉┉┉┉┉119(29)2010-2011学年天津市河西区八年级(下)期末数学试卷┉┉┉┉┉122(30)2008-2009学年天津市河西区八年级(下)期末数学试卷┉┉┉┉┉1262019-2020学年天津市和平区八年级(下)期末数学试卷1.(3分)在实数范围内有意义,则x的取值范围是()A.x≥3B.x>3C.x≤3D.x<33.(3分)如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是()A.∠ABC=90°B.AC=BD C.OA=OB D.△ABO≌△ADO 4.(3分)一次函数y=﹣5x+1的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限5.(3分)某个一次函数的图象与直线y═x+6平行,并且经过点(﹣2,﹣4),则这个一次函数的解析式为()A.y=﹣x﹣5B.y=x+3C.y=x﹣3D.y=﹣2x﹣8 6.(3分)利用勾股定理,可以作出长为无理数的线段.如图,在数轴上找到点A,使OA =5,过点A作直线l垂直于OA,在1上取点B,使AB=2,以原点O为圆心,以OB 长为半径作弧,弧与数轴的交点为C,那么点C表示的无理数是()A.B.C.7D.297.(3分)某招聘考试要进行笔试和面试,其中笔试占60%,面试占40%.孔明笔试成绩90分,面试成绩85分,那么孔明的最后成绩是()A.88.5分B.88分C.87.5分D.87分8.(3分)顺次连接菱形四边中点得到的四边形是()A.正方形B.矩形C.菱形D.等腰梯形(3分)下列命题中,是真命题的是()A.两条对角线互相平分的四边形是平行四边形B.两条对角线相等的四边形是矩形C.两条对角线互相垂直的四边形是菱形D.两条对角线互相垂直且相等的四边形是正方形9.第3题第6题第10题10.(3分)已知一次函数y=kx+b的图象如图所示,当x<2时,y的取值范围是()A.y<﹣4B.﹣4<y<0C.y<2D.y<011.(3分)甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.下列说法错误的是()A.A,B两城相距300千米B.乙车比甲车晚出发1小时,却早到1小时C.乙车出发后1.5小时追上甲车D.在一车追上另一车之前,当两车相距40千米时,t=12.(3分)如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为()A.5B.4C.3D.214.(3分)某班随机调查了10名学生,了解他们一周的体育锻炼时间,结果如表所示,则这10名学生在这一周的平均体育锻炼时间是小时.15.(3分)某次射击练习,甲、乙二人各射靶5次,命中的环数如表,通过计算可知==7,S=0.8,S=2,所以射击成绩比较稳定的是.16.(3分)若正比例函数y=kx(k为常数,且k≠0)的函数值y随着x的增大而减小,则k的值可以是.(写出一个即可)17.(3分)已知一次函数y=﹣2x+3,当0≤x≤5时,函数y的最大值是.18.(3分)如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD 于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为.20.为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:(Ⅰ)本次抽测的男生人数为,图①中m的值为;(Ⅱ)求本次抽测的这组数据的平均数、众数和中位数;(Ⅲ)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.21.如图,△ABC是一个边长为6的等边三角形,BD是△ABC的高,求BD的长.22.已知,四边形ABCD是菱形,(1)若AB=5,则菱形ABCD的周长=;(2)如图①,AC、BD是对角线,则AC与BD的位置关系是.(3)如图②,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点G、F分别在CD、BC上,MG与NF相交于点E.求证:四边形AMEN是菱形.23.甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.设原价购物金额累计为x元(x>0).(1)根据题意,填写如表:(2)设在甲商场实际购物金额为y甲元,在乙商场实际购物金额为y乙元,分别写出y甲、y乙关于x的函数解析式;(3)根据题意填空:①若在甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为元;②若在同一商场购物,商品原价购物金额累计为800元,则在甲、乙两家商场中的商场实际购物花费金额少;③若在同一商场实际购物金额为400元,则在甲、乙两家商场中的商场商品原价购物累计金额多.24.如图,P为正方形ABCD的边BC上的一动点(P不与B、C重合),连接AP,过点B 作BQ⊥AP交CD于点Q,将△BCQ沿着BQ所在直线翻折得到△BQE,延长QE交BA 的延长线于点M.(1)探求AP与BQ的数量关系;(2)若AB=3,BP=2PC,求QM的长.25.已知,直线y=3x﹣3与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为,点B的坐标为;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①点C的坐标为;②过动点P(m,0)且垂直于x轴的直线与直线AB交于点E,若点E在线段BC上,则m的取值范围是;(3)若∠ABN=45°,求直线BN的解析式.2019-2020学年天津市东丽区八年级(下)期末数学试卷2.(3分)要使二次根式有意义,则m的取值范围为()A.m<3B.m≤3C.m>3D.m≥33.(3分)直角三角形两条直角边长分别是5和12,则第三边上的中线长为()A.5B.6C.6.5D.124.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为()A.60°B.70°C.80°D.90°5.(3分)﹣3,﹣2,4,x,5,8这六个数的平均数是3,则x的值为()A.4B.5C.6D.76.有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的()A.方差B.中位数C.众数D.平均数7.(3分)下列命题中错误的是()A.对角线相等的四边形是矩形B.两组对边分别相等的四边形是平行四边形C.矩形的对角线相等D.平行四边形的对边相等8.将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为()A.y=2x﹣5B.y=2x+5C.y=2x+8D.y=2x﹣89.(3分)若一次函数y=(k﹣2)x+17,当x=﹣3时,y=2,则k的值为()A.﹣4B.8C.﹣3D.710.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是()A.平行四边形B.菱形C.矩形D.正方形11.如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是()A.x=2B.x=0C.x=﹣1D.x=﹣3第4题第11题第12题12.(3分)如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC为边作平行四边形PCQD,则对角线PQ的长的最小值是()A.3B.4C.5D.614.(3分)直角三角形的两直角边是3和4,则斜边是15.(3分)在一次函数y=3x+1中,y随x的增大而.16.(3分)一次函数y=2x﹣3与y=﹣x+1的图象的交点坐标为.17.(3分)如图,在△ABC中,AB=4,BC=2,DB=1,CD=,则AC=.18.(3分)在平行四边形ABCD中,BC边上的高为4,AB=5,AC=2,则平行四边形ABCD周长等于.20.(8分)一次函数图象经过(3,1),(2,0)两点.(1)求这个一次函数的解析式;(2)求当x=6时,y的值.21.(10分)某校八年级有500名学生,从中随机抽取了一部分学生,统计每晚写作业的时间,根据它们的时间(单位:分钟),绘制出如图的统计图①和图②请根据相关信息,解答下列问题:(1)图①中m=,n=;(2)求统计的这组数据的平均数、众数和中位数;(3)根据样本数据,估计这500名学生中,时间为120分钟的约有多少学生?22.(10分)已知:如图,在▱BEDF中,点A、C在对角线EF所在的直线上,且AE=CF.求证:四边形ABCD是平行四边形.23.(10分)如图在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.(1)请在所给的网格内画出以线段AB、BC为边的菱形,并完成填空:点D的坐标是,线段BC的长是;(2)请计算菱形ABCD的面积.24.(10分)某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)求y与x的函数表达式,其中0≤x≤21;(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.25.(10分)已知,▱ABCD中,∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.2019-2020学年天津市部分区八年级(下)期末数学试卷1.(3分)要使二次根式有意义,x必须满足()A.x≤2B.x≥2C.x>2D.x<23.(3分)由线段a,b,c组成的三角形是直角三角形的是()A.a=2,b=3,c=4B.a=3,b=4,c=5C.a=4,b=5,c=6D.a=5,b=6,c=74.(3分)下列函数中,表示y是x的正比例函数的是()A.y=x﹣1B.y=C.y=3x D.y2=x5.(3分)下列说法错误的是()A.对角线互相垂直的四边形是正方形B.对角线相等的平行四边形是矩形C.对角线互相垂直的平行四边形是菱形D.对角线互相平分的四边形是平行四边形6.如图▱ABCD的对角线交于点O,∠ACD=70°,BE⊥AC,则∠ABE的度数为()A.50°B.40°C.30°D.20°7.(3分)一次函数y=5x﹣1的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限8.(3分)已知P1(﹣1,y1),P2(1,y2)是一次函数y=﹣x﹣1的图象上的两个点,则y1和y2的大小关系是()A.y1=y2B.y1>y2C.y1<y2D.不能确定9.(3分)某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是()A.16,15B.15,15.5C.15,17D.15,1610.(3分)如图所示的正方形网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则∠BAC的大小是()A.∠BAC=30°B.∠BAC=45°C.∠BAC=60°D.∠BAC=90°第6题第9题第10题11.(3分)如图在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD 的周长为32,则OH的长等于()A.8B.6C.7D.412.(3分)如图所示的计算程序中,y与x之间的函数关系式是()A.y=﹣2x+3B.y=2x+3C.y=﹣2x﹣3D.y=2x﹣3 14.(3分)若函数y=x m﹣1+2是一次函数,则m=.15.(3分)小张和小李练习射击,两人10次射击训练成绩(环数)的统计结果如表所示,通常新手的成绩不稳定,根据表格中的信息,估计小张和小李两人中新手是.16.(3分)一次函数y1=﹣x﹣1与y2=x+4的图象如图,则﹣x﹣1>x+4的解集是.第11题第16题第17题17.(3分)如图,阴影部分是一个正方形,则这个正方形的面积为cm2.18.(3分)如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B 落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为(cm).20.(5分)某班评选一名优秀学生干部,如表是班长、学习委员和团支部书记的得分情况,假设在评选优秀干部时,思想表现、学习成绩、工作能力这三方面的比为3:3:4,通过计算说明谁应当选为优秀学生干部.21.(7分)如图,在▱ABCD中,点E、F分别在边BC和AD上,且BE=DF.(1)求证:△ABE≌△CDF.(2)求证:四边形AECF是平行四边形.22.(6分)在平面直角坐标系中,直线l与x轴、y轴分别交于点A、B(0,4)两点,且点C(2,2)在直线l上.(1)求直线l的解析式;(2)求△AOB的面积.23.(6分)为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是小时,中位数是小时;(2)计算被调查学生阅读时间的平均数;(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.24.(8分)如图,△ABC中,AB=AC,AD平分∠BAC交BC于点D,AE平分∠BAC的外角,且∠AEB=90°.求证:四边形ADBE是矩形.25.(8分)一家蔬菜公司计划到某绿色蔬菜基地收购A、B两种蔬菜共140吨,预计两种蔬菜销售后获利的情况如表所示:其中A种蔬菜的5%、B种蔬菜的3%须运往C市场销售,但C市场的销售总量不超过5.8吨.设销售利润为y元(不计损耗),设购进A种蔬菜x吨.(1)求y与x之间的函数关系式;(2)求自变量x的取值范围;(3)将这140吨蔬菜全部销售完,最多可获得多少利润?2019-2020学年天津市滨海新区八年级(下)期末数学试卷1.(3分)若是二次根式,则x的取值范围是()A.x≥1B.x≤1C.x<1D.x≥03.(3分)下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是()A.2,2,3B.2,3,4C.3,4,5D.4,5,64.(3分)下列各式中,y不是x的函数的是()A.y=x B.|y|=x C.y=2x+1D.y=x25.(3分)如图,在▱ABCD中,若∠B=70°,则∠D=()A.35°B.70°C.110°D.130°6.(3分)在平面直角坐标系中,下列各点在直线y=2x﹣1上的是()A.P(﹣2.5,﹣4)B.Q(1,3)C.M(2.5,4)D.N(﹣1,0)7.(3分)如图,下列四组条件中,不能判定四边形ABCD是平行四边形的是()A.AD=BC,AD∥BC B.AD∥BC,AB=DCC.AD=BC,AB=DC D.AD∥BC,AB∥DC8.(3分)由于台风的影响,一棵树在离地面6m处折断,树顶落在离树干底部8m处,则这棵树在折断前(不包括树根)长度是()A.8m B.10m C.16m D.18m9.(3分)下列命题中,为真命题的是()A.对角线互相垂直的四边形是菱形B.对角线相等的四边形是矩形C.一组邻边相等的菱形是正方形D.对角线相等的菱形是正方形10.(3分)关于函数y=﹣2x+1,下列结论正确的是()A.图象与直线y=2x+1平行B.y随x的增大而增大C.图象经过第一、二、三象限D.当x>时,y<011.(3分)如图所示,▱ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC =6,则OE的长为()A.2B.2.5C.3D.4第5题第7题第8题第11题12.(3分)如图所示,小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.图反映了这个过程中,小明离家的距离y(单位:km)与时间x(单位:min)之间对应关系.根据图象:下列说法错误的是()A.食堂离小明家0.6km B.小明在图书馆读报用了30minC.食堂离图书馆0.2km D.小明从图书馆回家平均速度是0.02km/min14.(3分)一次函数y=﹣x+5是由正比例函数向平移个单位得到的.15.(3分)如图,利用函数图象回答下列问题:方程组的解为.16.(3分)当x=﹣1时,代数式x2+2x+1的值是.17.(3分)如图,四边形ABCD是矩形纸片,AD=10,CD=8.在CD边上取一点E,将纸片沿AE翻折,使点D落在BC边上的点F处.则AF=;CF=;DE =.第15题第17题第18题18.(3分)在如图所示的7×7网格中,每个小正方形的边长均为1,点A、B均落在格点上.(Ⅰ)AB的长等于;(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为边的正方形ABCD,并简要说明画图的方法(不要求证明).20.(8分)如图,在▱ABCD中,点M,N分别是边AB,CD的中点.求证:AN=CM.21.(10分)如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.22.(10分)已知,矩形ABCD的对角线AC、BD相交于点O.(Ⅰ)如图①,若AB=6,BC=8,则BD=,OD=;(Ⅱ)如图②,DE∥AC,CE∥BD,求证:四边形OCED是菱形.23.(10分)已知正比例函数y=kx(k≠0)的图象经过点(3,﹣6).(Ⅰ)求这个函数的解析式;(Ⅱ)画出这个函数的图象;(Ⅲ)图象上有两点(﹣1,y1),(2,y2),比较y1与y2的大小.24.(10分)“黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.(Ⅰ)根据题意,填写下表:(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;(Ⅲ)若小张一次购买该种子花费了30元,求他购买种子的数量.25.(10分)如图,在平面直角坐标系中,O为原点,已知直线y=﹣x+4与x轴交于点A,与y轴交于点B.(Ⅰ)点A的坐标为,点B的坐标为;(Ⅱ)如图①,若点M(x,y)在线段AB上运动(不与端点A、B重合),连接OM,设△AOM的面积为S,写出S关于x的函数解析式,并写出自变量x的取值范围;(Ⅲ)如图②,若四边形OADC是菱形,求菱形对角线OD的长.2018-2019学年天津市南开区八年级(下)期末数学试卷1.(3分)下列一元二次方程中,没有实数根的是()A.2x2+3=0B.x2=2x C.x2+4x﹣1=0D.x2﹣8x+16=0 2.(3分)计算一组数据方差的算式为S2=[(x1﹣10)2+(x2﹣10)2+…+(x5﹣10)2],由比得到的信息中不正确的是()A.这组数据中有5个数据B.这组数据的平均数是10C.计算出的方差是一个非负数D.当x1增加时,方差的值一定随之增加3.(3分)用配方法解下列方程,其中应在方程左右两边同时加上4的是()A.x2﹣2x=5B.x2+4x=5C.2x2﹣4x=5D.4x2+4x=54.(3分)如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AD=8,AB=7,则BC+CD 等于()A.B.5C.4D.35.(3分)菱形和矩形一定都具有的性质是()A.对角线相等B.对角线互相垂直C.对角线互相平分D.对角线互相平分且相等6.(3分)顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是()A.平行四边形B.菱形C.矩形D.正方形7.(3分)如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程kx+b=0的解为x=2;②关于x的方程kx+b=3的解为x=0;③当x>2时,y<0;④当x<0时,y<3.其中正确的是()A.①②③B.①③④C.②③④D.①②④8.(3分)如图,在△ABC中,D,E,F分别为BC,AC,AB边的中点,AH⊥BC于H,FD=16,则HE等于()A.32 B.16C.8D.10第4题第7题第8题9.(3分)若A(x1,y1)、B(x2,y2)是一次函数y=(a﹣1)x+2图象上的不同的两个点,当x1>x2时,y1<y2,则a的取值范围是()A.a>0B.a<0C.a>1D.a<110.(3分)某地2017年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2019年在2017年的基础上增加投入资金1600万元.设从2017年到2019年该地投入异地安置资金的年平均增长率为x,则下列方程正确的是()A.1280(1+x)=1600 B.1280(1+2x)=1600C.1280(1+x)2=2880D.1280(1+x)+1280(1+x)2=288011.(3分)如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为()A.5B.4C.3D.2第11题第12题12.(3分)如图,已知直线l1:y=x+与直线l2:y=﹣2x+16相交于点C,直线l1,l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x 轴上,且点G与B点重合,那么S矩形DEFG:S△ABC=()A.1:3B.8:9C.9:16D.32:3513.(3分)某中学人数相等的甲、乙两班学生参加了同一次数学测验,两班平均分和方差分别为甲=82分,乙=82分,S甲2=245,S乙2=190.那么成绩较为整齐的是班(填“甲”或“乙”).14.(3分)如图,已知▱ABCD中,AD=8cm,AB=6cm,DE平分∠ADC交边BC于点E,则BE=cm.15.(3分)已知x=2是关于x的一元二次方程kx2+(k2﹣2)x+2k+4=0的一个根,则k的值为.16.(3分)在△ABC中,AB=,AC=5,若BC边上的高等于3,则BC边的长为.17.(3分)如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为.18.(3分)如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的三个顶点都在格点上.(Ⅰ)请你借助网格,使用无刻度的直尺在线段AC上找一点P,使得PC2﹣P A2=AB2,画出点P的位置,并简要说明画法.(Ⅱ)直接写出(Ⅰ)中线段P A的长.第14题第17题第18题19.(8分)解方程:(Ⅰ)(3x﹣1)2=(x﹣1)2(Ⅱ)3x(x﹣1)=2﹣2x20.(7分)在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m).绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:(Ⅰ)图①中a的值为;(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;(Ⅲ)根据这组初赛成绩,由高到低确定10人能进入复赛,请直接写出初赛成绩为1.65m 的运动员能否进入复赛.21.(7分)已知关于x的一元二次方程x2+x+m﹣1=0.(Ⅰ)当m=0时,求方程的实数根.(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围.22.(8分)如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,(Ⅰ)连接CC′,判断四边形CBA′C′的形状并进行证明.(Ⅱ)D为线段BC′上一动点,求AD+CD的最小值.23.(8分)某商场为了抓住夏季来临,衬衫热销的契机,决定用46000元购进A、B、C三种品牌的衬衫共300件,并且购进的每一种衬衫的数量都不少于90件.设购进A种型号的衬衣x件,购进B种型号的衬衣y件,三种品牌的衬衫的进价和售价如表所示:(Ⅰ)直接用含x、y的代数式表示购进C种型号衬衣的件数,其结果可表示为.(Ⅱ)求y与x之间的函数关系式.(Ⅲ)如果该商场能够将购进的衬衫全部售出,但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元①求利润P(元)与x(件)之间的函数关系式;②求商场能够获得的最大利润.24.(8分)如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.(Ⅰ)若△APD为等腰直角三角形①直接写出此时P点的坐标:;直线AP的解析式为.②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值;(Ⅱ)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.2018-2019学年天津市河西区八年级(下)期末数学试卷3.(3分)在下列长度的各组线段中,能组成直角三角形的是()A.1,2,3B.7,24,25C.3,3,5D.9,12,14 4.(3分)下列各点在直线y=2x+6上的是()A.(﹣5,4)B.(﹣7,20)C.(﹣5,﹣4)D.(7,﹣20)5.(3分)如果某函数的图象如图所示,那么y随x的增大而()A.增大B.减小C.不变D.有时增大有时减小6.(3分)等边三角形的边长为2,则该等边三角形的面积是()A.B.2C.1D.7.(3分)将直线y=3x+1向下平移2个单位长度,平移后直线的解析式为()A.y=3x﹣1B.y=﹣3x+1C.y=3x+3D.y=x﹣38.(3分)下列方程中,没有实数根的是()A.x2+4=4x B.x2﹣x﹣1=0C.2x2+4x+3=0D.3x﹣8=0 9.(3分)要组织一次羽毛球邀请赛,参赛的两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排6天,每天安排6场比赛,设比赛组织者应邀请x个队参赛,则x 满足的关系式为()A.x(x+1)=36 B.x(x﹣1)=36C.x(x+1)=36 D.x(x﹣1)=36 10.(3分)如图,有一正方形的纸片ABCD,边长为6,点E是DC边上一点且DC=3DE,把△ADE沿AE折叠使△ADE落在△AFE的位置,延长EF交BC边于点G,连接BF有以下四个结论:其中正确的结论序号是()①∠GAE=45°;②BG+DE=GE;③点G是BC的中点;④连接FC,则BF⊥FC;A.①②③④B.①②③C.①②D.②③第5题第10题11.(3分)方程x2=9的根是.12.(3分)在实数范围内,使得有意义的x的取值范围为.13.(3分)已知一次函数的图象经过点(0,2),且满足y随x的增大而增大,则该一次函数的解析式可以为(写出一个即可)14.一个直角三角形的两条直角边长分别为2,,直角三角形的斜边长为.15.(3分)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y 轴上,则点C的坐标是.16.(3分)如图,在每个小正方形的边长为1的网格中,点A、B、O、P均在格点上.(I)OB的长等于;(II)点M在射线OA上,点N在射线OB上,当△PMN的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出△PMN,并简要说明点M,N的位置是如何找到的(不要求证明).第15题第16题17.(6分)解方程:x2﹣4x=719.(8分)已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.20.(8分)已知函数y=3x+1,(I)画出该函数的图象;(Ⅱ)当1<x<3时,y的取值范围是;(Ⅲ)若该图象与x轴,y轴分别交于A,B两点,求AB的长度.21.(8分)用配方法解一元二次方程x2+4x+c=0(c为常数)22.(8分)用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为x(x为非负整数).(1)根据题意,填写下表:(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1,y2关于x的函数关系式;(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.23.(8分)如图①,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.(I)线段AB,BC,AC的长分别为:AB=BC=AC=;(Ⅱ)折叠△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E连接CD,如图②①求点D的坐标;②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.2018-2019学年天津市河东区八年级(下)期末数学试卷1.(3分)在实数范围内,有意义,则x的取值范围是()A.x≥0B.x≤0C.x>0D.x<02.(3分)下列各组数据中能作为直角三角形的三边长的是()A.1,2,2B.1,1,C.13,14,15D.6,8,10 3.(3分)下列函数中,y随x的增大而减小的函数是()A.y=3x B.y=4x﹣1C.y=﹣x﹣2D.y=3x﹣1 4.(3分)如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不一定能得出BE∥DF的是()A.AE=CF B.BE=DF C.∠EBF=∠FDE D.∠BED=∠BFD 5.(3分)如图,在△ABC中,∠ACB=90°,AB=15,分别以AC,BC为边向△ABC外作正方形,两个正方形的面积分别记为S1,S2,则S1+S2等于()A.30B.150C.200D.2256.(3分)已知y是x的正比例函数,且函数图象经过点(4,﹣6),则在此正比例函数图象上的点是()A.(2,3)B.(﹣4,6)C.(3,﹣2)D.(﹣6,4)7.(3分)某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为甲=82分,乙=82分,S甲2=245,S乙2=190,那么成绩较为整齐的是()A.甲班B.乙班C.两班一样整齐D.无法确定8.(3分)对于一次函数y=﹣2x+4,下列结论错误的是()A.函数的图象与x轴的交点坐标是(0,4)B.函数值随自变量的增大而减小C.函数的图象不经过第三象限D.函数的图象向下平移4个单位长度得y=﹣2x的图象9.(3分)如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是()A.20B.24C.40D.4810.(3分)如图,在矩形ABCD中,有以下结论:①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.正确结论的个数是()A.2B.3C.4D.5第4题第5题第9题第10题。
天津市和平区2018~2019学年度第二学期八年级数学学科期末质量调查试卷

和平区2018~2019学年度第二学期八年级数学学科期末质量调查试卷一. 选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若32+a 在实数范围内有意义,则a 的取值范围是 (A)a ≥23-(B) a ≤23- (C) a>23- (D) a<23- 2.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,若OA=2,则BD 的长为(A)4 (B) 3 (C)2 (D) 13.已知直线y=2x-b 经过点(1,-1),则b 的值为 (A)3 (B)-3 (C) 0 (D) 64.设矩形的面积为S ,相邻两边的长分别为a,b ,已知S=23,b=10,则a 等于(A) 230 (B)530 (C) 630 (D) 53 5.下列说法正确的是(A)四个角都相等的四边形是正方形 (B )四条边都相等的四边形是正方形 (C)对角线相等的平行四边形是正方形 (D) 对角线互相垂直的矩形是正方形 6.若直角三角形两条直角边长分别为2和3,则该直角三角形斜边上的高为 (A) 13 (B)13133 (C) 13136 (D) 1313127.晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%,小桐三项体育成绩(百分制)依次95分、90分、86分,则小桐这学期的体育成绩是(A )88 (B )89分 (C )90分 (D )91分8.改革开40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,下图为北京市统计局发布的2017年和2018年北京市居民人均教育、文化和娱乐消费支出的折线图.第2题说明:在统计学中,同比..是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较:环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较. 根据上述信息,下列结论中错误的是(A)2017年第二季度环比有所提高 (B )2017年第三季度环比有所提高 (C)2018年第一季度同比有所提高 (D) 2018年第四季度同比有所提高 9.如图,直线y=kx+b 过A(-1,2),B(-2,0)两点,则0≤kx+b ≤-2x 的解集为 (A)x ≤-2或x ≥-1 (B) 0≤y ≤2 (C) -2≤x ≤0 (D) -2≤x ≤-110.某通讯公司推出三种上网月收费方式,这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是(A)每月上网不足25小时,选项A 方式最省钱 (B )每月上网为30小时,选项B 方式最省钱(C)每月上网费用为60元,选择B 方式比A 方式时间长 (D)每月上网时间超过70小时,选择C 方式最省钱11.已知直线 y=-x+6交x 轴于点A ,交y 轴于点B ,点P 在线段OA 上,将△PAB 沿BP 翻折,点A 的对应点A ′恰好落在y 轴上,则OPPA的值为 (A)22(B) 1 (C) 2 (D) 312.如图,边长为2的菱形ABCD 中,∠A=60º,点M 是边AB 上一点,点N 是边BC 上一点,且∠ADM=15º,∠MDN=90º,则点B 到DN 的距离为 (A)22(B) 2 (C) 3 (D)2 二.填空题(本大题共6小题,每小题3分,共18分)13.如图,在Rt △ABC 中,D 是斜边AB 的中点,AB=2,则CD 的长为_____.14.农科院对甲、乙两个品种甜玉米各用10块试验田进行试验,得到甲、乙两个品种每公顷的平均产量相同,而甲、乙两个品种产量的方差分别为S 2甲=0.01,S 2乙=0.0002, 则产量较为稳定的品种为_______(填“甲”或“乙”) 15.计算(5+3)(5-3)的结果等于________.NMDCBA第12题DBCA 第13题16.已知一次函数y=x+b 的图象经过第一、二、三象限,写出一个符合条件的b 的值为_____. 17.一个装有进水管与出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟关停进水管,每分的进水量和出水量是两个常数,在打开进水管到关停进水管这段时间内,容器内的水量y (单位:升)与时间x (单位:分)之间的函数关系如图所示,关停进水管后,经过_____分钟,容器中的水恰好放完18.图中的虚线网格是等边三角形,它的每一个小三角形都是边长为1的等边三角形. (1)如图①,连接相邻两个小正三角形的顶点A ,B ,则AB 的长为_______(2)在如图②所示的网格中,用无刻度的直尺,画一个斜边长为32的直角三角形,且它的顶点都在格点上.三.解答题(本大题共7小题,共66分,解答应写出文字说明、演算步骤或推理过程) 19.(本小题8分)计算:(1)483316122+- (2) )52)(32(++20.(本小题8分)如图,在四边形ABCD 中,AB=AD=2,∠A=90º,∠CBD=30º,∠C=45º,求BD 及CD 的长.21.(本小题10分)①②某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:(1)本次参加跳绳测试的学生人数为______,图①中m 的值为_______; (2) 求本次调查获取的样本数据的平均数、众数、中位数;(3) 根据样本数据,估计该校九年级跳绳测试中得3分的学生约有多少人?22.(本小题10分)在菱形ABCD 中,AC 是对角线.(1) 如图①,若AB=6,则菱形ABCD 的周长为______;若∠DAB=70º,则∠D 的度数是_____;∠DCA 的度数是____;(2) 如图②,P 是AB 上一点,连接DP 交对角线AC 于点E,连接EB,求证: ∠APD=∠EBC.23.现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x 千克. (1)根据题意,填写下表:图②图①图①图②(2)设甲快递公司收费y 1元,乙快递公司收费y 2元,分别写出y 1,y 2关于x 的函数关系式; (3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.24.(本小题10分)已知,在正方形ABCD 中,点E 在边AD 上,点F 在边BC 的延长线上,且AE=CF,连接AC ,EF. (1)如图①,求证:EF//AC ;(2)如图②,EF 与边CD 交于点G,连接BG,BE,①求证:△BAE ≌△BCG;②若BE=EG=4,求△BAE 的面积.25.(本小题10分)已知,直线y=2x-2与x 轴交于点A ,与y 轴交于点B. (1)如图①,点A 的坐标为_______,点B 的坐标为_______; (2)如图②,点C 是直线AB 上不同于点B 的点,且CA=AB. ①求点C 的坐标;②过动点P(m,0)且垂直与x 轴的直线与直线AB 交于点E ,若点E 不在线段BC 上,则m 的取值范围是_______;F E D C B A 图①B A图②(3)若∠ABN=45º,求直线BN的解析式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年天津市和平区八年级(下)期末数学试卷一.选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)若在实数范围内有意义,则a的取值范围是()A.a≥﹣B.a≤﹣C.a>﹣D.a<﹣2.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为()A.4 B.3 C.2 D.13.(3分)已知直线y=2x﹣b经过点(1,﹣1),则b的值为()A.3 B.﹣3 C.0 D.64.(3分)设矩形的面积为S,相邻两边的长分别为a,b,已知S=2,b=,则a等于()A.2B.C.D.5.(3分)下列说法正确的是()A.四个角都相等的四边形是正方形B.四条边都相等的四边形是正方形C.对角线相等的平行四边形是正方形D.对角线互相垂直的矩形是正方形6.(3分)若直角三角形两条直角边长分别为2,3,则该直角三角形斜边上的高为()A.B.C.D.7.(3分)晨光中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%,小桐三项体育成绩(百分制)依次95分、90分、86分,则小桐这学期的体育成绩是()A.88分B.89分C.90分D.91分8.(3分)改革开放40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图.说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.根据上述信息,下列结论中错误的是()A.2017年第二季度环比有所提高B.2017年第三季度环比有所提高C.2018年第一季度同比有所提高D.2018年第四季度同比有所提高9.(3分)如图,直线y=kx+b过A(﹣1,2),B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为()A.x≤﹣2或x≥﹣1 B.0≤y≤2 C.﹣2≤x≤0 D.﹣2≤x≤﹣110.(3分)某通讯公司推出三种上网月收费方式.这三种收费方式每月所收的费用y(元)与上网时间x(小时)的函数关系如图所示,则下列判断错误的是()A.每月上网不足25小时,选择A方式最省钱B.每月上网时间为30小时,选择B方式最省钱C.每月上网费用为60元,选择B方式比A方式时间长D.每月上网时间超过70小时,选择C方式最省钱11.(3分)已知直线y=﹣x+6交x轴于点A,交y轴于点B,点P在线段OA上,将△P AB沿BP翻折,点A的对应点A′恰好落在y轴上,则的值为()A.B.1 C.D.12.(3分)如图,边长为2的菱形ABCD中,∠A=60°,点M是边AB上一点,点N是边BC上一点,且∠ADM =15°,∠MDN=90°,则点B到DN的距离为()A.B.C.D.2二.填空题(本大题共6小题,每小题3分,共18分)13.(3分)如图,在Rt△ABC中,D是斜边AB的中点,AB=2,则CD的长为.14.(3分)农科院对甲、乙两个品种甜玉米各用10块试验田进行试验,得到甲、乙两个品种每公顷的平均产量相同,而甲、乙两个品种产量的方差分别为S2甲=0.01,S2乙=0.0002,则产量较为稳定的品种为(填“甲”或“乙”)15.(3分)计算(+)(﹣)的结果等于.16.(3分)若一次函数y=x+m的图象经过第一、二、三象限,写出一个符合条件的m的值为.17.(3分)一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过分钟,容器中的水恰好放完.18.(3分)图中的虚线网格是等边三角形,它的每一个小三角形都是边长为1的等边三角形.(1)如图①,连接相邻两个小正三角形的顶点A,B,则AB的长为.(2)在如图②所示的网格中,用无刻度的直尺,画一个斜边长为2的直角三角形,且它的顶点都在格点上.三.解答题(本大题共7小题,共66分,解答应写出文字说明、演算步骤或推理过程)19.(8分)计算:(1)2﹣6+3;(2)(().20.(8分)如图,在四边形ABCD中,AB=AD=,∠A=90°,∠CBD=30°,∠C=45°,求BD及CD的长.21.(10分)某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:(Ⅰ)本次参加跳绳测试的学生人数为,图①中m的值为;(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;(Ⅲ)根据样本数据,估计该校九年级跳绳测试中得3分的学生有多少人?22.(10分)在菱形ABCD中,AC是对角线.(1)如图①,若AB=6,则菱形ABCD的周长为;若∠DAB=70°,则∠D的度数是;∠DCA 的度数是;(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD=∠EBC.23.(10分)现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.(1)根据题意,填写下表:快递物品重量(千克)0.5 1 3 4 …甲公司收费(元)22 …乙公司收费(元)11 51 67 …(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.24.(10分)已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.(1)如图①,求证:EF∥AC;(2)如图②,EF与边CD交于点G,连接BG,BE,①求证:△BAE≌△BCG;②若BE=EG=4,求△BAE的面积.25.(10分)已知,直线y=2x﹣2与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为,点B的坐标为;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①求点C的坐标;②过动点P(m,0)且垂直于x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是;(3)若∠ABN=45°,求直线BN的解析式.2018-2019学年天津市和平区八年级(下)期末数学试卷参考答案与试题解析一.选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.【解答】解:在实数范围内有意义,则2a+3≥0,解得:a≥﹣.故选:A.2.【解答】解:∵ABCD是矩形∴OC=OA,BD=AC又∵OA=2,∴AC=OA+OC=2OA=4∴BD=AC=4故选:A.3.【解答】解:将点(1,﹣1)代入y=2x﹣b得:﹣1=2﹣b,解得:b=3,故选:A.4.【解答】解:a=S÷b=2÷=,故选:B.5.【解答】解:A、四个角都相等的四边形是矩形;故错误;B、四条边都相等的四边形是菱形,故错误;C、对角线相等的平行四边形是矩形,故错误;D、对角线互相垂直的矩形是正方形,正确,故选:D.6.【解答】解:设该直角三角形斜边上的高为h,∵直角三角形的两条直角边长分别为2和3,∴斜边==,∵2×3×=×h×,∴h=,故选:C.7.【解答】解:小桐这学期的体育成绩95×20%+90×30%+86×50%=89(分),故选:B.8.【解答】解:2017年第二季度支出948元,第一季度支出859元,所以第二季度比第一季度提高,故A正确;2017年第三季度支出1113元,第二季度支出948元,所以第三季度比第二季度提高,故B正确;2018年第一季度支出839元,2017年第一季度支出859元,所以2018年第一季度同比有所降低,故C错误;2018年第四季度支出1012元,2017年第一季度支出997元,所以2018年第四季度同比有所降低,故D正确;故选:C.9.【解答】解:直线OA的解析式为y=﹣2x,当﹣2≤x≤﹣1时,0≤kx+b≤﹣2x.故选:D.10.【解答】解:A、每月上网不足25小时,选择A方式最省钱,正确;B、每月上网时间为50~70小时,选择B方式最省钱,错误;C、每月上网费用为60元,选择B方式比A方式时间长,正确;D、每月上网时间超过70小时,选择C方式最省钱,正确;故选:B.11.【解答】解:如图,y=﹣x+6,令x=0,则y=6,令y=0,则x=6,故点A、B的坐标分别为(6,0)、(0,6),则AB=6=A′B,设:P A=a=P A′,则OP=6﹣a,OA′=6﹣6,由勾股定理得:P A2=OP2+OA2,即(a)2=(6﹣6)2+(6﹣a)2,解得:a=12﹣6,则P A=12﹣,OP=6,则=,故选:C.12.【解答】解:连接BD,作BE⊥DN于E,∵边长为2的菱形ABCD中,∠A=60°,∴△ABD和△BCD是等边三角形,∴BD=AB=AD=2,∠ADB=∠CDB=60°∵∠A=60°,∴∠ADC=180°﹣60°=120°,∵∠ADM=15°,∠MDN=90°,∴∠CDN=120°﹣15°﹣90°=15°,∴∠EDB=60°﹣15°=45°,∴BE=BD=,∴点B到DN的距离为,故选:B.二.填空题(本大题共6小题,每小题3分,共18分)13.【解答】解:在Rt△ABC中,D是斜边AB的中点,∴CD=AB=1,故答案为:1.14.【解答】解:∵S2甲=0.01,S2乙=0.0002,∴S2甲>S2乙,∴产量较为稳定的品种为乙;故答案为:乙.15.【解答】解:原式=()2﹣()2=5﹣3=2,故答案为:2.16.【解答】解:∵图象经过第一、二、三象限,∴直线与y轴的交点在正半轴上,则m>0.∴符合条件的m的值大于0即可.∴m=1,故答案为1.17.【解答】解:进水管的速度为:20÷4=5(升/分),出水管的速度为:5﹣(30﹣20)÷(12﹣4)=3.75(升/分),∴关停进水管后,出水经过的时间为:30÷3.75=8分钟.故答案为:8.18.【解答】解:(1)AB=2×1×cos30°=,故答案为.(2)如图②中,△DEF即为所求.三.解答题(本大题共7小题,共66分,解答应写出文字说明、演算步骤或推理过程)19.【解答】解:(1)原式=2×2﹣6×+3×4=4﹣2+12=14;(2)原式=2+5+3+15=17+8.20.【解答】解:作DE⊥BC于E,在Rt△ABD中,BD===2,在Rt△DEB中,∠CBD=30°,∴DE=BD=1,在Rt△EDC中,∠C=45°,∴EC=DE=1,由勾股定理得,CD===.21.【解答】解:(Ⅰ)本次参加跳绳的学生人数是10+5+25+10=50(人),m=100×=10.故答案是:50,10;(Ⅱ)平均数是:(10×2+5×3+25×4+10×5)=3.7(分),众数是:4分;中位数是:4分;(Ⅲ)该校九年级跳绳测试中得3分的学生有1200×10%=120(人).答:该校九年级跳绳测试中得3分的学生有120人.22.【解答】解:(1)∵四边形ABCD是菱形∴AB=BC=CD=AD=6,∠DAB+∠ADC=180°,∠DCA=∠DCB=∠DAB=35°∴菱形ABCD的周长=4×6=24,∠ADC=110°,故答案为:24,110°,35°(2)∵四边形ABCD是菱形∴DC=BC,∠DCE=∠BCE,且CE=CE,∴△DCE≌△BCE(SAS)∴∠CDP=∠CBE∵DC∥AB∴∠CDP=∠APD∴∠CBE=∠APD23.【解答】解:(1)当x=0.5时,y甲=22×0.5=11;当x=3时,y甲=22+15×2=52;当x=4时,y甲=22+15×3=67;当x=1时,y乙=16×1+3=19.故答案为:11;52;67;19.(2)当0<x≤1时,y1=22x;当x>1时,y1=22+15(x﹣1)=15x+7.∴y1=,y2=16x+3(x>0);(3)当x>3时,当y,1>y2时,有15x+7>16x+3,解得:x<4;当y2=y2时,有15x+7=16x+3,解得:x=4;当y1<y2时,有15x+7<16x+3,解得:x>4.∴当3<x<4时,小明应选择乙公司省钱;当x=4时,两家公司费用一样;当x>4,小明应选择甲公司省钱.24.【解答】(1)证明:如图①,∵四边形ABCD是正方形,∴AE∥CF,又∵AE=CF,∴四边形AEFC是平行四边形,故EF∥AC.解:(2)如图②,∵四边形ABCD是正方形,且EF∥AC,∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;∵AD∥BF,∴∠CFG=∠DEG=45°,∵∠CGF=∠DGE=45°,∴∠CGF=∠CFG,∴CG=CF;∵AE=CF,∴AE=CG;在△ABE与△CBG中,,∴△ABE≌CBG(SAS);(3)由(2)知△DEG是等腰直角三角形,∵EG=4,∴DE=2,设AE=a,则AB=AD=a+2,Rt△ABE中,由勾股定理得:AB2+AE2=BE2,∴=42,a=4,∴S△ABE=====2.25.【解答】解:(1)如图①,令y=0,则2x﹣2=0,即x=1.所以A(1,0).令x=0,则y=﹣2,即B(0,﹣2).故答案是:(1,0);(0,﹣2);(2)①如图②,过点C作CD⊥x轴,垂足是D,∵CA=AB,∠BOA=∠ADC=90°,∠BOA=∠CAD,∴△BOA≌△CAD(ASA),∴CE=OB=2,AD=OA=1,∴C(2,2);②由①可知D(2,0),观察图②,可知m的取值范围是:m<0或m>2.故答案是:m<0或m>2;(3)如图③,作AE⊥AB,使得AE=AB,作EH⊥x轴于H,则△ABE是等腰直角三角形,∠ABE=45°.∵∠AOB=∠BAE=∠AHE=90°,∴∠OAB+∠ABO=90°,∠OAB+∠HAE=90°,∴∠ABO=∠HAE,∵AB=AE,∴△ABO≌△EAH,∴AH=OB=2,EH=OA=1,∴E(3,﹣1),设直线BE的解析式为y=kx+b,则有,解得,∴直线BE的解析式为y=x﹣2,当直线BE′⊥直线BE时,直线BE′也满足条件,直线BE′的解析式为y=﹣3x﹣2,∴满足条件的直线BE的解析式为y=x﹣2或y=﹣3x﹣2.。
