囚徒困境实验报告
囚徒困境实验报告

《实验经济学》结课论文总分囚徒困境实验报告学院财政税务学院专业12级资产评估姓名李岩学号************囚徒困境实验分析一、 实验目的根据囚徒困境经典悖论,通过实验来探寻单词与多次重复结果,分析结论。
然后通过研究“囚徒困境”,了解囚徒困境产生的原因,想出走出囚徒困境的方法,并且理解和利用囚徒困境解决生活中与经济中的实际问题。
二、 实验原理囚徒困境是博弈论的非零和博弈中具代表性的例子。
经典的囚徒困境如下:警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人入罪。
于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
若二人都互相检举(互相“背叛”),则二人同样判监2年。
用表格概述如下:三、 实验说明通过角色扮演的方式再现经典的囚徒困境。
实验者两人一组,扮演囚徒。
在甲沉默甲背叛乙沉默二人同服刑1年乙服刑10年,甲即时获释乙背叛 甲服刑10年,乙即时获释 二人同服刑8年相同的情境下看不同的实验者如何选择策略来完成实验。
实验并没有考虑其他客观因素,是在完全假设的没有任何干扰囚徒做出选择的因素的情境下进行的。
实验规则:实验参与人被随机地分配到有两个人组成的不同小组中。
如果小组中的两个成员都选择坦白,那他们将会分别获得6年的刑期;如果小组中的两个成员都选择否认,那他们将会分别获得3年的刑期;如果小组中有一个成员选择坦白、另一个选择否认,那么选择坦白的成员获得1年的刑期,选择否认的成员获得10年的刑期。
四、实验准备实验小组一共五人,通过抽签的方式分出两人,一人为囚徒一,一人为囚徒二。
实验分为两种,一个是单次,一个为多次。
另外三人分别记录单次实验与多次试验的结果,分析数据。
五、实验步骤1、在单次实验的情况下,囚徒一与囚徒二分别只有一次机会选择拒绝或坦白。
囚徒困境博弈实验

2010-11-25
1
实验说明
下面我们将进行一个博弈实验, 下面我们将进行一个博弈实验,每位同学都将 拿到2张扑克牌 一张红色,一张黑色。 张扑克牌, 拿到 张扑克牌,一张红色,一张黑色。 牌的花色和数字不重要,关键是牌的颜色。 牌的花色和数字不重要,关键是牌的颜色。 实验分为两大组同时进行, 实验分为两大组同时进行,每组中的每位同学 将会和另一组的某个同学成为“囚徒” 将会和另一组的某个同学成为“囚徒”
2010-11-25
10
下面开始第5轮实验, 下面开始第 轮实验,请在你决定出什么 轮实验 牌之后,将牌面朝下放在桌子的左( 牌之后,将牌面朝下放在桌子的左(右) 前方。 前方。 请同时公布你们的出牌, 请同时公布你们的出牌,等实验助手记 录完毕后,在表格中做好收益纪录 在表格中做好收益纪录。 录完毕后 在表格中做好收益纪录。
2010-11-257Fra bibliotek下面开始第2轮实验, 下面开始第 轮实验,请在你决定出什么 轮实验 牌之后,将牌面朝下放在桌子的左( 牌之后,将牌面朝下放在桌子的左(右) 前方。 前方。 请同时公布你们的出牌, 请同时公布你们的出牌,等实验助手记 录完毕后,在表格中做好收益纪录 在表格中做好收益纪录。 录完毕后 在表格中做好收益纪录。
如果你出红牌,另一位同学也出红牌,你将得到 如果你出红牌,另一位同学也出红牌,你将得到3 元;如果另一位同学出黑牌,你将得到0元。 如果另一位同学出黑牌,你将得到 元 如果你出黑牌,另一位同学出红牌,你将得到5元 如果你出黑牌,另一位同学出红牌,你将得到 元; 如果另一位同学出黑牌,你将得到2元 如果另一位同学出黑牌,你将得到 元。
17
下面是最后一轮实验, 下面是最后一轮实验,请在你决定出什 么牌之后, 么牌之后,将牌面朝下放在桌子的左 前方。 (右)前方。 请同时公布你们的出牌, 请同时公布你们的出牌,等实验助手记 录完毕后,在表格中做好收益纪录 录完毕后 在表格中做好收益纪录 最后将表格和扑克牌交给实验助手
经济学博弈实验实训报告

一、实验背景与目的随着经济全球化和市场经济的深入发展,博弈论在经济学中的应用日益广泛。
为了更好地理解和掌握博弈论的基本原理及其在现实经济生活中的应用,我们小组开展了为期一周的经济学博弈实验实训。
本次实训旨在通过模拟实验,使学生深入了解博弈论的基本概念、原理和策略,提高学生在实际经济活动中的决策能力。
二、实验内容与方法本次实训主要采用了以下实验内容和方法:1. 实验内容:- 独裁者博弈:通过模拟独裁者在利益分配中的决策过程,探究自主性分配地位中,不同情境下的权益分配的界限。
- 囚徒困境:模拟两个嫌疑人被关押,面临是否坦白的决策过程,分析合作与背叛的结果。
- 纳什均衡:通过模拟多个参与者之间的互动,探讨在给定条件下,每个参与者都能达到的最优策略组合。
- 宏观经济学沙盘模拟:模拟政府制定宏观经济政策,调控经济以达到预期目标。
2. 实验方法:- 实验软件:采用成都杰科力科技有限公司的《经济学综合仿真实训平台》进行模拟实验。
- 实验步骤:首先,实验指导教师介绍实验背景、目的和操作方法;然后,学生分组进行实验;最后,各组提交实验报告,进行讨论和总结。
三、实验结果与分析1. 独裁者博弈:- 实验结果显示,在独裁者博弈中,提议者往往会提出高于自己成本的价格,而响应者则接受这个价格。
- 这说明在利益分配中,独裁者会尽量争取更多的利益,而响应者则会权衡自身利益和风险。
2. 囚徒困境:- 实验结果显示,在囚徒困境中,如果两个嫌疑人都不坦白,则两人都会受到较轻的处罚;如果两人都坦白,则两人都会受到较重的处罚;如果一人坦白而另一人沉默,则坦白者会获得自由,而沉默者则会受到重罚。
- 这说明在面临困境时,合作往往比背叛更有利于双方。
3. 纳什均衡:- 实验结果显示,在纳什均衡中,每个参与者都能达到自己的最优策略组合。
- 这说明在博弈过程中,参与者会根据自身利益和预期来选择策略,以达到最优结果。
4. 宏观经济学沙盘模拟:- 实验结果显示,政府通过制定合适的宏观经济政策,可以有效地调控经济,实现经济增长和就业稳定。
囚徒困境拓展实验报告

囚徒困境拓展实验报告1. 背景介绍囚徒困境是博弈论中的一个经典问题,讲述了两名罪犯被单独审问,被告诱供出对方的情况。
在此情景下,博弈的最优策略是什么?这个问题引发了学术界广泛的探讨,而囚徒困境拓展实验也是在此背景下展开的。
2. 实验设计为了更好地研究囚徒困境的策略选择,我们设计了一个拓展实验。
实验中参与者以角色扮演的方式,扮演囚徒和警察,通过决策和博弈来模拟真实的囚徒困境。
实验的主要内容如下:2.1 参与者分组我们招募了一百名参与者,将其以随机方式分为囚徒组和警察组。
每组各有五十名参与者。
2.2 游戏规则游戏分为五轮进行。
每个回合的游戏规则如下:- 每个囚徒对每个警察进行一次选择,可以选择合作或背叛。
- 合作表示不揭发对方,获得3分。
- 背叛表示揭发对方,获得1分。
- 如果两个囚徒都选择合作,则每个人获得2分。
- 如果一个囚徒选择背叛,而另一个选择合作,则背叛的囚徒获得5分,合作的囚徒获得0分。
2.3 统计数据在游戏进行的同时,我们记录了每一轮的参与者选择和获得分数情况。
通过统计数据,我们可以分析参与者的策略选择和博弈效果。
3. 实验结果经过五轮的游戏,我们得到了如下实验结果:3.1 囚徒组策略选择分析囚徒组中,参与者的策略选择大致分为两种:- 个体理性:有一部分囚徒参与者在前几轮中选择了背叛,以追求更高的个体收益,但在后续观察到其他囚徒普遍合作后,逐渐倾向于选择合作。
- 合作主义:另一部分囚徒参与者一直坚持选择合作,始终希望通过团队合作获得更高的总体收益。
3.2 警察组策略选择分析警察组中,参与者也有两种策略选择:- 鸽派:一部分警察参与者倾向于选择合作,希望通过与囚徒团结合作,减少犯罪行为,从而获得更好的社会效益。
- 鹰派:另一部分警察参与者更倾向于选择背叛,以对付囚徒的“欺骗”,以自身利益为出发点。
3.3 获得分数统计通过实验记录的数据,我们计算了每个参与者的平均得分。
囚徒组中,个体理性囚徒的平均得分为4.2分,合作主义者的平均得分为2.8分。
简述囚徒困境及其结论

简述囚徒困境及其结论
囚徒困境是一个经典的博弈论案例,描述了两个囚犯被捕后被关进两个单独的牢房,无法通过通信相互帮助或寻求逃脱机会。
他们必须选择自己的行为,要么合作,要么互相背叛,以最大化自己的收益。
囚徒困境的假设是:两个人的行为都是理性的,不会考虑到道德或法律的因素;两个人的利益是一致的,他们背叛对方会导致自己受到更严厉的惩罚;他们无法找到第三方来帮助或合作。
在囚徒困境中,两个囚犯的最优策略是合作,这意味着他们应该将对方供出,从而各自获得一次逃脱的机会。
然而,如果他们选择合作,那么他们就必须同时供出对方,这将导致他们一起被判刑。
因此,两个囚犯都选择背叛,并各自获得了更高的收益,即逃脱了惩罚。
囚徒困境的结论是,在极端的情况下,两个人的行为取决于他们的理性和利益一致性,而不考虑道德或法律的因素。
在这种情况下,合作或背叛都是最优策略,但无法找到第三方来协助或合作。
囚徒困境的案例表明,在复杂的社会中,人们的行为往往受到理性和利益因素的影响,而不考虑道德和法律的因素。
这也提醒我们在决策时需要考虑多个因素,并做出理性的判断。
囚徒困境实验报告
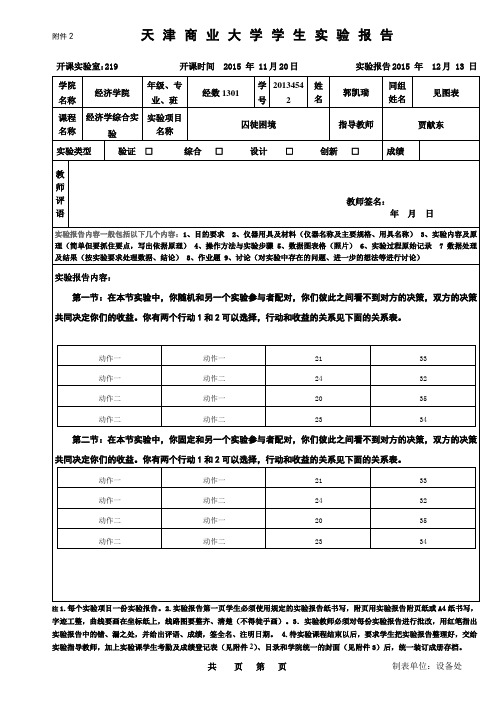
天津商业大学学生实验报告附件2开课实验室:219 开课时间 2015 年 11月20日实验报告2015 年 12月 13 日注1.每个实验项目一份实验报告。
2.实验报告第一页学生必须使用规定的实验报告纸书写,附页用实验报告附页纸或A4纸书写,字迹工整,曲线要画在坐标纸上,线路图要整齐、清楚(不得徒手画)。
3.实验教师必须对每份实验报告进行批改,用红笔指出实验报告中的错、漏之处,并给出评语、成绩,签全名、注明日期。
4.待实验课程结束以后,要求学生把实验报告整理好,交给实验指导教师,加上实验课学生考勤及成绩登记表(见附件2)、目录和学院统一的封面(见附件3)后,统一装订成册存档。
共页第页制表单位:设备处天津商业大学学生实验报告附页开课实验室: 219 开课时间2015 年月日实验报告2015 年月日因为不知道匹配者是谁,所以不知道他人品怎么样,所以比较谨慎,选择了动作一,接受者也选择了动作一,双方受益都还不错,到后面三轮我都充当的接受者,既然人家都那么大方我自己不能太小气,于是全选择动作二,双方都得到了较好收益。
最后一轮我又充当了提倡者,于是乎仍然选择了动作一。
、实验结果分析:由图表知提议者选动作一接受者大部分选动作一,只有少部分接受者选择的动作二,则说明大多数人是理性的。
当提倡者选择动作一为了是收益更大选择动作二,当提倡者选择动作二,接受者为了尽可能多收益也应该选择动作二。
作为提议者在面临“收益”时,不会考虑随机配对者如何选择策略,总是会采取作为一个“理性人”的策略,即选择利益最大化。
同样,人具有有限理性和机会主义,在利益的驱使下,可能会作出非“理性人”的抉择。
知道自己是与一个人固定搭配的,大家是要长期合作的,所以一定要让他觉得跟我合作还不赖,共页第页制表单位:设备处。
博弈论经典案例“囚徒困境”及其实证分析

博弈论经典案例“囚徒困境”及其实证分析最近三四十年,经济学经历了一场“博弈论革命”,就是引入博弈论的概念和方法改造经济学的思维,推进经济学的研究。
诺贝尔经济学奖授予包括美国普林斯顿大学的纳什博士在内的3位博弈论专家,可以看作是一个标志,这自然也激发了人们了解博弈论的热情。
博弈论作为现代经济学的前沿领域,已成为占据主流的基本分析工具。
博弈论是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡,也就是说,当一个主体的选择受到其他主体选择的影响,而且反过来影响到其他主体选择时的决策问题和均衡问题。
一个完整的博弈应当包括五个方面的内容:第一,博弈的参加者,即博弈过程中独立决策、独立承担后果的个人和组织;第二,博弈信息,即博弈者所掌握的对选择策略有帮助的情报资料;第三,博弈方可选择的全部行为或策略的集合;第四,博弈的次序,即博弈参加者做出策略选择的先后;第五,博弈方的收益,即各博弈方做出决策选择后的所得和所失。
“囚徒困境”“囚徒困境”是博弈论里最经典的例子之一。
讲的是两个嫌疑犯(A和B)作案后被警察抓住,隔离审讯;警方的政策是"坦白从宽,抗拒从严",如果两人都坦白则各判8年;如果一人坦白另一人不坦白,坦白的放出去,不坦白的判10年;如果都不坦白则因证据不足各判1年。
在这个例子里,博弈的参加者就是两个嫌疑犯A和B,他们每个人都有两个策略即坦白和不坦白,判刑的年数就是他们的支付。
可能出现的四种情况:A和B均坦白或均不坦白、A坦白B不坦白或者B坦白A不坦白,是博弈的结果。
A和B均坦白是这个博弈的纳什均衡。
这是因为,假定A选择坦白的话,B最好是选择坦白,因为B坦白判8年而抵赖却要判十年;假定A选择抵赖的话,B最好还是选择坦白,因为B坦白判不被判刑而抵赖确要被判刑1年。
即是说,不管A坦白或抵赖,B的最佳选择都是坦白。
反过来,同样地,不管B是坦白还是抵赖,A的最佳选择也是坦白。
结果,两个人都选择了坦白,各判刑8年。
囚徒困境实验报告

《实验经济学》结课论文总分囚徒困境实验报告学院财政税务学院专业 12级资产评估姓名李岩学号 201222370506囚徒困境实验分析一、 实验目的根据囚徒困境经典悖论,通过实验来探寻单词与多次重复结果,分析结论。
然后通过研究“囚徒困境”,了解囚徒困境产生的原因,想出走出囚徒困境的方法,并且理解和利用囚徒困境解决生活中与经济中的实际问题。
二、 实验原理囚徒困境是博弈论的非零和博弈中具代表性的例子。
经典的囚徒困境如下:警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人入罪。
于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
若二人都互相检举(互相“背叛”),则二人同样判监2年。
用表格概述如下:三、 实验说明通过角色扮演的方式再现经典的囚徒困境。
实验者两人一组,扮演囚徒。
甲沉默甲背叛乙沉默二人同服刑1年乙服刑10年,甲即时获释乙背叛 甲服刑10年,乙即时获释 二人同服刑8年在相同的情境下看不同的实验者如何选择策略来完成实验。
实验并没有考虑其他客观因素,是在完全假设的没有任何干扰囚徒做出选择的因素的情境下进行的。
实验规则:实验参与人被随机地分配到有两个人组成的不同小组中。
如果小组中的两个成员都选择坦白,那他们将会分别获得6年的刑期;如果小组中的两个成员都选择否认,那他们将会分别获得3年的刑期;如果小组中有一个成员选择坦白、另一个选择否认,那么选择坦白的成员获得1年的刑期,选择否认的成员获得10年的刑期。
四、实验准备实验小组一共五人,通过抽签的方式分出两人,一人为囚徒一,一人为囚徒二。
实验分为两种,一个是单次,一个为多次。
另外三人分别记录单次实验与多次试验的结果,分析数据。
五、实验步骤1、在单次实验的情况下,囚徒一与囚徒二分别只有一次机会选择拒绝或坦白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《实验经济学》结课论文总分
囚徒困境实验报告
学院财政税务学院
专业12级资产评估
姓名李岩
学号0506
囚徒困境实验分析
一、实验目的
根据囚徒困境经典悖论,通过实验来探寻单词与多次重复结果,分析结论。
然后通过研究“囚徒困境”,了解囚徒困境产生的原因,想出走出囚徒困境的方法,并且理解和利用囚徒困境解决生活中与经济中的实际问题。
二、实验原理
囚徒困境是博弈论的非零和博弈中具代表性的例子。
经典的囚徒困境如下:
警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人入罪。
于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择:若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。
若二人都保持沉默(相关术语称互相“合作”),则二人同样判监半年。
若二人都互相检举(互相“背叛”),则二人同样判监2年。
用表格概述如下:
三、 实验说
明
通过角色扮
演的方式再现经典的囚徒困境。
实验者两人一组,扮演囚徒。
在相同的情境下看不同的实验者如何选择策略来
完成实验。
实验并没有考虑其他客观因素,是在完全假设的没有任何干扰囚徒做出选择的因素的情境下进行的。
实验规则:实验参与人被随机地分配到有两个人组成的不同小组中。
如果小组中的两个成员都选择坦白,那他们将会分别获得6年的刑期;如果小组中的两个成员都选择否认,那他们将会分别获得3年的刑期;如果小组中有一个成员选择坦白、另一个选择否认,那么选择坦白的成员获得1年的刑期,选择否认的成员获得10年的刑期。
四、 实验准备
实验小组一共五人,通过抽签的方式分出两人,一人为囚徒一,一人为囚徒二。
实验分为两种,一个是单次,一个为多次。
另外三人分别记录单次实验与多次试验的结果,分析数据。
五、 实验步骤
1、在单次实验的情况下,囚徒一与囚徒二分别只有一次机会选择拒绝或坦白。
2、在多次重复实验的情况下,分为三轮,囚徒一与囚徒二分别有十次机会
甲沉默 甲背叛
乙沉默 二人同服刑1年
乙服刑10年,甲即时获释
乙背叛 甲服刑10年,乙即时获释 二人同服刑8年
来选择坦白或拒绝。
3、收集实验数据,画出折线图,并分析实验结果。
具体来说,实验分为两个阶段。
第一阶段,囚徒一和囚徒二要熟悉实验程序的实验过程和收益情况,并选择坦白或否认。
程序界面如下图所示。
第二阶段,囚徒一和囚徒二可以看到自己的选择和对方的选择,并且知道自己在本轮次获得的刑期。
程序界面如下图所示
六、实验结果分析
1、单次实验
单次实验的结果理论上有四种,即
囚徒一与囚徒二都拒绝,各判三年;
囚徒一与囚徒二都坦白,各判六年;
囚徒一坦白,判一年,囚徒二拒绝,判十年;
囚徒一拒绝,判十年,囚徒二坦白,判一年。
然而,实验的结果是,囚徒一与囚徒二均选择坦白,双方各判六年。
因为二人面对的情况一样,所以二人的理性思考都会得出相同的结论——选择坦白。
坦白是两种策略之中的支配性策略。
因此,双方坦白是这场博弈中唯一可能达到的纳什均衡。
2、多次实验
对于多次实验发生的结果。
我们一共进行了三轮实验,每轮实验均进行十次,从而来总结最后的结果,根据每轮结果的折线图和三轮总结果的折线图来看,每轮得到的实验结果均与均衡结果有偏差,但是三轮总结果的折线图却偏向于均衡结果,即两人均坦白,各判6年。
结果是纳什均衡逐渐趋于帕累托最优。
实验表格如下图所示:
第一轮实验结果折线图如下所示
第二轮试验结果折线图如下所示:
第三轮实验结果如下图所示:
三轮实验结果汇总折线图:
七、实验结论
1、单次实验结论
这场博弈的纳什均衡,显然不是顾及团体利益的帕累托最优解决方案。
以全体利益而言,如果囚徒一和囚徒二都拒绝,两人都只会被判刑3年,总体利益更高,结果也比两人都坦白,判6年的情况较佳。
但二人均为理性的个人,为实现个人利益的最大化,均衡状况会是两个囚徒都选择坦白,结果二人判决均比合作为高,总体利益较合作为低。
这证明了:在非零和博弈中,帕累托最优和纳什均衡是相冲突的。
2、多次实验结论
实验被反复地进行。
因而每个囚徒都有机会去“惩罚”另一个囚徒前一回合的不合作行为。
这时,合作可能会作为均衡的结果出现。
坦白的动机这时可能被受到惩罚的威胁所克服,从而可能导向一个较好的、合作的结果。
作为反复接近无限的数量,纳什均衡趋向于帕累托最优。
八、实际事例
上述实验结果可能过于抽象,但现实中,无类似囚徒困境的例子还是很多的。
不论是社会科学中的经济学、政治学和社会学,以及自然科学的动物行动学、进化生物学等学科,都有问题可以用囚徒困境来分析。
这种博弈方法的重要性可见一斑。
下面我就为大家举些囚徒困境的例子:
1、经济例子
中国电信与中国联通,两边都希望赚取市场利润,但是如何在话费价格定位上有着不同的选择,如果我的价格低对方价格高的话我就会占有市场,但是缺点是我会减少利润,但是如果我的价格高对方的价格低的话,我就会失去市场,在双方没有达成cartel的情况下会出现“囚徒困境”模式,就是双方都以低价位来抢占市场但是双方的利润都没有最大化。
2、政治实例
50年后军事解密,朝鲜战争的起因,因为中国和美国都有考虑,我国是怕韩国如果统一朝鲜后美军会侵略中国,而美军是怕如果朝鲜统一韩国后,中国军队会侵略日本,在占领日本后威胁美国本土。
所以双方都是以出兵和不出兵考虑,如果出兵,会有经济损失,如果不出兵会威胁自己的领土,所以双方在“囚徒困境”模式下都选择了出兵,最后两败俱伤。
3、军事例子
台湾要买美国的F16,中国希望欧洲对华军售,两个地区的政府都在为武器画着大价钱从而损失了国家的经济发展力,这也是囚徒困境的模式,都会担心如果一旦开战会对自己不利,如果我没有先进武器,你有先进武器,那么开战的话我就会吃亏。
如果我有先进武器你没有的话,我就会得利。
所以我一定要有先进武器。
殊不知如果两岸达成和平条约,双方都不购买先进武器,把资金都放在经济发展人民收入上,那才是真的双赢。
4、环法自行车赛
每年都举办的环法自由车赛中有以下情况:选手们在到终点前的路程常以大队伍(英文:Peloton)方式前进,他们采取这策略是为了令自己不至于太落后,又出力适中。
而最前方的选手在迎风时是最费力的,所以选择在前方是最差的策略。
通常会发生这样的情况,大家起先都不愿意向前(共同背叛),这使得全体速度很慢,而后通常会有二或多位选手骑到前面,然后一段时间内互相交换最前方位置,以分担风的阻力(共同合作),使得全体的速度有所提升,而这时如果前方的其中一人试图一直保持前方位置(背叛),其他选手以及大队伍就会赶上(共同背叛)。
而通常的情况是,在最前面次数最多的选手(合作)通常会到最后被落后的选手赶上(背叛),因为后面的选手骑在前面选手的冲流之中,比较不费力。
5、广告竞争
两个公司互相竞争,二公司的广告互相影响,即一公司的广告较被顾客接受则会夺取对方的部分收入。
但若二者同时期发出质量类似的广告,收入增加很少但成本增加。
但若不提高广告质量,生意又会被对方夺走。
此二公司可以有二选择:
互相达成协议,减少广告的开支。
(合作)
增加广告开支,设法提升广告的质量,压倒对方。
(背叛)
若二公司不信任对方,无法合作,背叛成为支配性策略时,二公司将陷入广告战,而广告成本的增加损害了二公司的收益,这就是陷入囚徒困境。
在现实中,要二互相竞争的公司达成合作协议是较为困难的,多数都会陷入囚徒困境中。
囚徒困境在生活中是普遍存在的,因此,我们需要在理解与互相信任的基础上达到最优合作,实现双方利益的共赢。
文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 感谢您的阅读。
