《材料科学基础》第四章习题.doc
材料科学基础习题与参考答案（doc14页）完美版
材料科学基础习题与参考答案（doc14页）完美版第⼀章材料的结构⼀、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离⼦键、⾦属键、组元、合⾦、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第⼆相强化。
⼆、填空题1、材料的键合⽅式有四类，分别是（），（），（），（）。
2、⾦属原⼦的特点是最外层电⼦数（），且与原⼦核引⼒（），因此这些电⼦极容易脱离原⼦核的束缚⽽变成（）。
3、我们把原⼦在物质内部呈（）排列的固体物质称为晶体，晶体物质具有以下三个特点，分别是（），（），（）。
4、三种常见的⾦属晶格分别为（），（）和（）。
5、体⼼⽴⽅晶格中，晶胞原⼦数为（），原⼦半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶⾯为（），晶胞中⼋⾯体间隙个数为（），四⾯体间隙个数为（），具有体⼼⽴⽅晶格的常见⾦属有（）。
6、⾯⼼⽴⽅晶格中，晶胞原⼦数为（），原⼦半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶⾯为（），晶胞中⼋⾯体间隙个数为（），四⾯体间隙个数为（），具有⾯⼼⽴⽅晶格的常见⾦属有（）。
7、密排六⽅晶格中，晶胞原⼦数为（），原⼦半径与晶格常数的关系为（），配位数是（），致密度是（），密排晶向为（），密排晶⾯为（），具有密排六⽅晶格的常见⾦属有（）。
8、合⾦的相结构分为两⼤类，分别是（）和（）。
9、固溶体按照溶质原⼦在晶格中所占的位置分为（）和（），按照固溶度分为（）和（），按照溶质原⼦与溶剂原⼦相对分布分为（）和（）。
10、影响固溶体结构形式和溶解度的因素主要有（）、（）、（）、（）。
11、⾦属化合物（中间相）分为以下四类，分别是（），（），（），（）。
12、⾦属化合物（中间相）的性能特点是：熔点（）、硬度（）、脆性（），因此在合⾦中不作为（）相，⽽是少量存在起到第⼆相（）作⽤。
13、CuZn、Cu5Zn8、Cu3Sn的电⼦浓度分别为（），（），（）。
材料科学基础习题与答案
第一章 原子排列与晶体结构1. fcc 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,晶胞中原子数为 ，把原子视为刚性球时，原子的半径r 与点阵常数a 的关系是 ；bcc 结构的密排方向是 ，密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为 ，原子的半径r 与点阵常数a 的关系是 ；hcp 结构的密排方向是 ，密排面是 ，密排面的堆垛顺序是 ，致密度为 ，配位数是 ,晶胞中原子数为 ，原子的半径r 与点阵常数a 的关系是 。
2. Al 的点阵常数为0.4049nm ，其结构原子体积是 ，每个晶胞中八面体间隙数为 ，四面体间隙数为 。
3. 纯铁冷却时在912ε 发生同素异晶转变是从 结构转变为 结构，配位数 ，致密度降低 ，晶体体积 ，原子半径发生 。
4. 在面心立方晶胞中画出）（211晶面和]211[晶向，指出﹤110﹥中位于（111）平面上的方向。
在hcp 晶胞的（0001）面上标出）（0121晶面和]0121[晶向。
5. 求]111[和]120[两晶向所决定的晶面。
6 在铅的（100）平面上，1mm 2有多少原子？已知铅为fcc 面心立方结构，其原子半径R=0.175×10-6mm 。
第二章 合金相结构一、 填空1） 随着溶质浓度的增大，单相固溶体合金的强度 ，塑性 ，导电性 ，形成间隙固溶体时，固溶体的点阵常数 。
2） 影响置换固溶体溶解度大小的主要因素是（1） ；（2） ；（3） ；（4） 和环境因素。
3） 置换式固溶体的不均匀性主要表现为 和 。
4） 按照溶质原子进入溶剂点阵的位置区分，固溶体可分为 和 。
5） 无序固溶体转变为有序固溶体时，合金性能变化的一般规律是强度和硬度 ，塑性 ，导电性 。
6）间隙固溶体是 ，间隙化合物是 。
二、 问答1、 分析氢，氮，碳，硼在α-Fe 和γ-Fe 中形成固溶体的类型，进入点阵中的位置和固溶度大小。
已知元素的原子半径如下：氢：0.046nm ，氮：0.071nm ，碳：0.077nm ，硼：0.091nm ，α-Fe ：0.124nm ，γ-Fe ：0.126nm 。
材料科学基础习题参考答案.docx
材料科学基础习题参考答案 第一章材料结构的基本知识8.计算下列晶体的离于键与共价键的相对比例。
(1) NaF (2) CaO (3) ZnS解：(1)查表得：X Na =0.93,X F =3.98--(0.93-3.98)2根据鲍林公式可得NaF 中离子键比例为：[1-e 4 ]x 100% = 90.2%共价键比例为：1-90.2%=9.8%--(1.00-3.44 )2(2) 同理，CaO 中离子键比例为：[1-e 4 ]x 100% = 77.4%共价键比例为：1-77.4%=22.6%(3) ZnS 中离子键比例为：Z“S 中离子键含量=[1 -£-1/4'2-58-165)2]x 100% = 19.44% 共价键比例为：1-19.44%=80.56%10说明结构转变的热力学条件与动力学条件的意义.说明稳态结构与亚稳态结构之间的关 系。
答：结构转变的热力学条件决定转变是否可行，是结构转变的推动力，是转变的必要条件； 动力学条件决定转变速度的大小，反映转变过程中阻力的大小。
稳态结构与亚稳态结构之间的关系：两种状态都是物质存在的状态，材料得到的结构是 稳态或亚稳态，取决于转变过程的推动力和阻力(即热力学条件和动力学条件)，阻力小时得 到稳态结构，阻力很大时则得到亚稳态结构。
稳态结构能量最低，热力学上最稳定；亚稳态 结构能量高，热力学上不稳定，但向稳定结构转变速度慢，能保持相对稳定甚至长期存在。
但在一定条件下，亚稳态结构向稳态结构转变。
1.第二章九材料中的騒須勾)与［2廊1)与［112］, (110)与［111］, (132)与［123］, (322)与［236］指数。
题: 系的 (21 在立方晶系的一个晶胞虫画出(111丄和丄112、日面.才晶系的画出同M1)、■'朋两晶面交钱亠 1]晶向。
112) d2. 有一正交点阵的a=b, c=a/2o 某晶面在三个晶轴上的截距分别为6个、2个和4个原子 间距，求该晶面的密勒指数。
材料科学基础习题第四章答案与翻译
4.2 根据本章给出的结构，画出下列链节结构：（1）聚氟乙烯：—CH2—CHF—;（2）聚三氟氯乙烯：—CF2—CFCl—（3）聚乙烯醇：—CH2—CHOH—4.3 计算下列聚合物的链节分子量（1）聚氯乙烯：—CH2—CHCl— : m = 2⨯12.011+2⨯1.008+35.453=61.491g/mol （2）聚对苯二甲酸乙二醇酯：—OCH2-CH2OCOC6H4CO—m = 10⨯12.011+8⨯1.008+4⨯15.999=192.17g/mol（3）聚碳酸酯：m = 16⨯12.011+14⨯1.008+3⨯15.999=254.285g/mol （4）聚二甲硅氧烷：C2H6OSim = 28.086+2⨯12.011+6⨯1.008+3⨯15.999 = 106.153g/mol 4.4 聚丙烯的数均分子量为1,000,000 g/mol，计算其数均聚合度。
答：链节为—CH3CH—CH2—，其分子量：m = 3⨯12.011+6⨯1.008=42.081 g/mol4.5 (a) 计算聚苯乙烯链节的分子量答：链节为-CHC6H5-CH2-，分子量：m = 8⨯12.011+8⨯1.008=104.152(b) 计算重均聚合度为25000的聚苯乙烯的重均分子量答：= 25000⨯104.152 g/mol = 2603800 g/mol4.6 下表列出了聚丙烯的分子量，计算(a) 数均分子量(b) 重均分子量(c) 数均聚合度(d) 重均聚合度分子量分布x i w i(g/mol)8,000-16,000 0.05 0.0216,000-24,000 0.16 0.1024,000-32,000 0.24 0.2032,000-40,000 0.28 0.3040,000-48,000 0.20 0.2748,000-56,000 0.07 0.21答：(a)= 0.05⨯12000+0.16⨯20000+0.24⨯28000+0.28⨯36000+0.20⨯44000+0.07⨯52000 = 600+3200+6720+10080+8800+3640 = 33040 (g/mol)(b)= 0.02⨯12000+0.1⨯20000+0.20⨯28000+0.30⨯36000+0.27⨯44000+0.21⨯52000 = 240+2000+5600+10800+11880+10920 = 41440 (g/mol)(c)聚丙烯链节的分子量：m = 42.081 g/mol(d)4.7 下表列出了某聚合物的分子量分布。
材料科学基础习题第四章答案与翻译
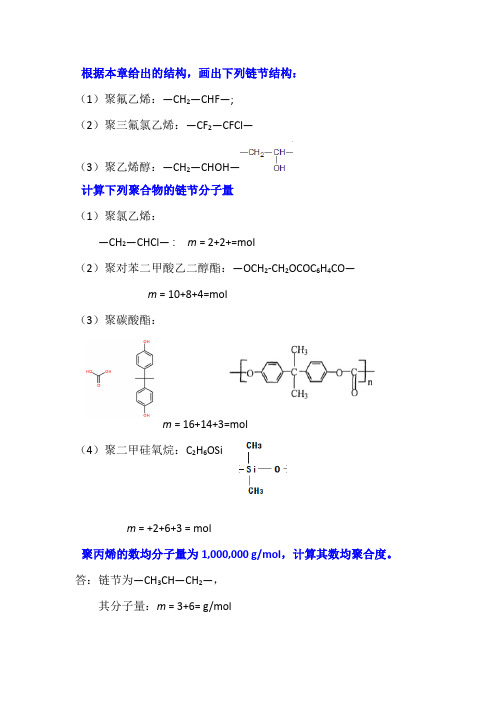
根据本章给出的结构，画出下列链节结构：（1）聚氟乙烯：—CH2—CHF—;（2）聚三氟氯乙烯：—CF2—CFCl—（3）聚乙烯醇：—CH2—CHOH—计算下列聚合物的链节分子量（1）聚氯乙烯：—CH2—CHCl— : m = 2+2+=mol（2）聚对苯二甲酸乙二醇酯：—OCH2-CH2OCOC6H4CO—m = 10+8+4=mol（3）聚碳酸酯：m = 16+14+3=mol（4）聚二甲硅氧烷：C2H6OSim = +2+6+3 = mol聚丙烯的数均分子量为1,000,000 g/mol，计算其数均聚合度。
答：链节为—CH3CH—CH2—，其分子量：m = 3+6= g/mol(a) 计算聚苯乙烯链节的分子量答：链节为CHC6H5CH2，分子量：m = 8+8=(b) 计算重均聚合度为25000的聚苯乙烯的重均分子量答：= 25000 g/mol = 2603800 g/mol下表列出了聚丙烯的分子量，计算(a) 数均分子量(b) 重均分子量(c) 数均聚合度(d) 重均聚合度x i w i 分子量分布(g/mol)8,00016,00016,00024,00024,00032,00032,00040,00040,00048,00048,00056,000答：(a)= 12000+20000+28000+36000+44000+52000 = 600+3200+6720+10080+8800+3640 = 33040 (g/mol)(b)= 12000+20000+28000+36000+44000+52000 = 240+2000+5600+10800+11880+10920 = 41440 (g/mol)(c)聚丙烯链节的分子量：m = g/mol(d)下表列出了某聚合物的分子量分布。
计算(a) 数均分子量(b) 重均分子量(c) 如果已知这一聚合物的重均聚合度为780，指出此聚合物为表所列聚合物中的哪一个为什么(d) 这一材料的数均聚合度为多少分子量分布(g/mol)x i w i15,00030,00030,00045,00045,00060,00060,00075,00075,00090,00090,000105,000105,000120,000120,000135,000答：(a)= 22500+37500+52500+67500+82500+97500+112500+127500 = 900+2625+8400+17550+19800+11700+9000+3825 = 73800 (g/mol)(b)= 22500+37500+52500+67500+82500+97500+112500+127500 = 225+1500+5775+16200+22275+15600+13500+ 6375 = 81450 (g/mol)(c)此聚合物为聚苯乙烯根据下面的分子量分布和重均聚合度为585的条件，判断是否为聚甲基丙烯酸甲酯均聚物分子量分布(g/mol)x i w i8,00020,00020,00032,00032,00044,00044,00056,00056,00068,00068,00080,00080,00092,000答：聚甲基丙烯酸甲酯链节分子式为：C5H8O2(—CH2CH3COOCH3C—)；其分子量m = 5+8+2=mol重均分子量为：=14000+26000+38000+50000+62000+74000+86000=140+1300+4560+12500+16740+15540+7740=58520与条件相符，能形成均聚物高密度聚乙烯通过诱导氯原子随机取代氢而被氯化。
《材料科学基础》第四章习题
《材料科学基础》第四章 固体中原子即分子的运动1.名词:扩散 自扩散 互扩散 扩散系数 互扩散系数 扩散激活能 扩散通量 上坡扩散 间隙扩散 空位扩散 原子迁移 界面扩散 表面扩散 柯肯达尔效应 反应扩散 稳态扩散2. 设有一条内径为30mm 的厚壁管道，被厚度为0.1mm 的铁膜隔开，通过管子的一端向管内输入氮气，以保持膜片一侧氮气浓度为1200mol/m 3，而另一侧的氮气浓度为100 mol/m 3，如在700℃下测得通过管道的氮气流量为2.8×10-8mol/s ，求此时氮气在铁中的扩散系数。
解：通过管道中铁膜的氮气通量为 )/(104.4)03.0(4108.22424s m mol J ⋅⨯=⨯⨯=--π膜片两侧氮浓度梯度为：m mol x c /101.10001.010012007-⨯=-=∆∆- 据Fick ’s First Law ： s m xc J D x c D J /104/211-⨯=∆∆-=⇒∂∂-=3. 有一硅单晶片，厚0.5mm ，其一端面上每107个硅原子包含两个镓原子，另一个端面经处理后含镓的浓度增高。
试求在该面上每107个硅原子须包含几个镓原子，才能使浓度梯度成为2×1026 atoms/m 3，硅的点阵常数为0.5407nm 。
4. 950℃下对纯铁进行渗碳，并希望在0.1mm 的深度得到w 1(C)=0.9%的碳含量。
假设表面碳含量保持在w 2(C)=1.20%，扩散系数 为D ɤ−Fe=10-10m 2/s ，计算为达到此要求至少要渗碳多少时间。
5. 在一个富碳的环境中对钢进行渗碳，可以硬化钢的表面。
已知在1000℃下进行这种渗碳热处理，距离钢的表面1-2mm 处，碳含量从x ＝ 5％减到x ＝4％。
估计在近表面区域进入钢的碳原子的流人量J （atoms/m 2s ）。
(γ-Fe 在1000℃的密度为7.63g/cm 3，碳在γ-Fe 中的扩散系数D o ＝2.0×10-5 m 2/s ，激活能Q ＝142kJ/mol)。
材料科学基础1-8章例题、作业题及其解答
第2章 例 题（A ）1. 在面心立方晶胞中画出[012]和[123]晶向。
2. 在面心立方晶胞中画出（012）和（123）晶面。
3. 右图中所画晶面的晶面指数是多少？4. 设晶面（152）和（034）属六方晶系的正交坐标表述，试给出其四轴坐标的表示。
反之，求（3121）及（2112）的正交坐标的表示。
5. （练习），上题中均改为相应晶向指数，求相互转换后结果。
答案：2. (2110) 4. （1562）， （0334） 5. [1322] [1214] （123） （212）[033] [302]第2章 例题答案(A)4. （152）)2615(6)51()(⇒-=+-=+-=v u t （034）)4303(3)30()(⇒-=+-=+-=v u t （1213）⇒ （123） （2112） ⇒ （212）5. [152]]2231[22)51(31)(313)152(31)2(311)512(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u [034]]4121[41)30(31)(312)032(31)2(311)302(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u]3121[]033[33)1(20)1(1⇒⎪⎭⎪⎬⎫===--=-==---=-=w W t v V t u U[2112]]302[20)1(13)1(2⇒⎪⎭⎪⎬⎫===---=-==--=-=w W t v V t u U第2章 例 题（B ）1. 已知Cu 的原子直径为2.56A ，求Cu 的晶格常数，并计算1mm 3Cu 的原子数。
2. 已知Al 相对原子质量Ar （Al ）=26.97，原子半径γ=0.143nm ，求Al 晶体的密度。
3. bcc 铁的单位晶胞体积，在912℃时是0.02464nm 3；fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。
【精品】材料科学基础习题及答案.doc
第一章材料的结构一、解释以下基本概念空间点阵、品格、品胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化。
二、填空题1、材料的键合方式有四类，分别是（），（），（），（）。
2、金属原子的特点是最外层电子数（），且与原子核引力（），因此这些电子极容易脱离原子核的束缚而变成（）。
3、我们把原子在物质内部呈（）排列的固体物质称为品体，品体物质具有以下三个特点，分别是（），（），（）。
4、三种常见的金属品格分别为（），（）和（）。
5、体心立方品格中，品胞原子数为（），原子半径与品格常数的关系为（），配位数是（）,致密度是（），密排品向为（），密排品面为（），品胞中八面体间隙个数为（），四面体间隙个数为（），具有体心立方晶格的常见金属有（）。
6、面心立方晶格中，品胞原子数为（），原子半径与品格常数的关系为（），配位数是（）,致密度是（），密排品向为（），密排品面为（），品胞中八面体间隙个数为（），四面体间隙个数为（），具有面心立方品格的常见金属有（）。
7、密排六方品格中，品胞原子数为（），原子半径与品格常数的关系为（），配位数是（）,致密度是（），密排品向为（），密排品面为（），具有密排六方品格的常见金属有（）。
8、合金的相结构分为两大类，分别是（）和（）。
9、固溶体按照溶质原子在品格中所占的位置分为（）和（），按照固溶度分为（）和（），按照溶质原子与溶剂原子相对分布分为（）和（）。
10、影响固溶体结构形式和溶解度的因素主要有（）、（）11、金属化合物（中间相）分为以下四类，分别是（），（），（），（）。
12、金属化合物（中间相）的性能特点是：熔点（）、硬度（）、脆性（），因此在合金中不作为（）相，而是少量存在起到第二相（）作用。
13、C uZn、Cu5Zn8x Cu3Sn 的电子浓度分别为（），（），（）。
14、如果H M表示金属，用X表示非金属，间隙相的分子式可以写成如下四种形式，分别是（）, （）,（）,（）＜,15、F e,C的铁、碳原子比为（），碳的重量百分数为（），它是（）的主要强化相。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《材料科学基础》第四章固体中原子即分子的运动
1.名词:
扩散扩散互扩散扩散系数互扩散系数扩散激活能扩散通量上坡扩散间隙扩散空位扩散原子迁移界面扩散表面扩散柯肯达尔效应反应扩散稳态扩散
2.设有一条内径为30mm的厚壁管道，被厚度为0.1mm的铁膜隔开，通过管子的一端向管内输入氮气，以保持膜片一侧氮气浓度为1200mol/m)而另一侧的
I气浓度为100 mol/m3,如在700C下测得通过管道的氮气流量为2.8xl0-8mol/s,
求此时氮气在铁中的扩散系数。
解：通过管道中铁膜的氮气通量为
J = J* ‘°——=4.4x 10 "mol/(m'・s)
jx (0.03)2
膜片两侧氮浓度梯度为：一萱二'2()()-l()() = U x]0_7m〃〃秫
Ax 0.0001
据Fick's First Law : J = -D^- n。
= ------------ -- = 4xl0-,,m2Is
ox Ac / Ax
3.有一-硅单晶片，厚0.5mm,其一端面上每10’个硅原子包含两个像原子，另一个端面经处理后含镣的浓度增高。
试求在该面上每个硅原子须包含儿个像原子，才能使浓度梯度成为2xl°26atoms/m3,硅的点阵常数为0.5407nm。
4. 950°C下对纯铁进行渗碳，并希望在0.1mm的深度得到Wi(C)=0.9%的碳含量。
假设表面碳含量保持在IA/2(C)=1.20%,扩散系数为D -Fe=1010m2/s,计算为达
到此要求至少要渗碳多少时间。
5.在-•个富碳的环境中对钢进行渗碳，可以硬化钢的表面。
己知在1000°C下进行这种渗碳热处理,距离钢的表面l-2mm处，碳含量从x= 5%减到x=4%。
估计在近表面区域进入钢的碳原子的流人量J (atoms/m2s)o (y・Fe在1000°C的密度为7.63g/cm',碳在y-Fe • | •的扩散系数D o=2.0xl0'5m2/s,激活能Q= 142kJ/mol)o
£> = 2X10-11 折
公
8.为什么钢铁零件渗碳温度
般要选择在Y ・Fe 相区中进行？若不在Y 相区进
6.有两种激活能分别为Qi = 83.7kJ/mol 和Q2 = 251kJ/mol 的扩散反应。
观察在温 度从25°C 升高到600°C 时对这两种扩散的影响，并对结果进行评述。
7.对碳的质量分数为0.1%的钢进行渗碳，渗碳时钢件表面碳的质量分数保持为
1.2% ,要求在其表面以下2mm 处碳的质量分数为0.45% ,若
,求渗碳所需的时间，若想将渗碳厚度增加一倍，需多少
渗碳时间?
行会有什么结果? 答：因a-Fe 中的最大碳熔解度(质量分数)只有0.0218% ,对于含碳质量分数大 于0.0218%的钢铁在渗碳时零件中的碳浓度梯度为零，渗碳无法进行，即使是 纯铁，在a 相区渗碳时铁中浓度梯度很小，在表也不能获得高含碳层；另外，由 于温度低，扩散系数也很小，渗碳过程极慢，没有实际意义。
v-Fe 中的碳 度高，渗碳时在表层可获得较高的碳浓度梯度使渗碳顺利进行。
N £> _ b
9.指明菲克第二定律 众 3 的适用条件。
1。
.己知铜在铝中扩散时，久=0-g 】0**, 2=136X193"
计算27°C 及527°C 时的扩散系数，并用所得数据讨论温度对扩散系数的影响。
11. 一块含0.1%C 的碳钢在930C 渗碳，渗到0.05cm 的地方碳的浓度达到0.45%o 在t>0的全部时间，渗碳气氛保持表面成分为1% ,假设
=2.0xl05exp(-140000/RT) (m 2/s),
(a) 计算渗碳时间；
(b) 若将渗层加深一倍，则需多长时间？
(c) 若规定0.3%C 作为渗碳层厚度的量度，则在930°C 渗碳10小时的渗层厚度为 870°C 渗碳10小时的多少倍?
12.设纯格和纯铁组成扩散偶，扩散lh 后,Matan 。
平面移动T 1.52xl0 3cmo 已知摩
尔分数x C r=0.478时，=126/m（z为扩散距离），互扩散系数=1.43xlO 9 m2/s,试求Matano面的移动速度和铭、铁的本征扩散系数D Cr, D Fe（实验测得Mata面移动距离的平方与扩散时间之比为常数）。
13.根据实际测定IgD和i的关系图，计算单晶体银和多晶体银在低于700 °C 温度范围的扩散激活能，并说明二者扩散激活能差异的原因.。