考研数学高等数学强化习题-定积分(应用)
高等数学第六章 定积分应用试题及答案

第六章 一元函数定积分的应用一、微元法(元素法)实际问题中可化为定积分来计算的待求量A ,一般总可按“分割、近似求和、取极限”这三个步骤导出它的积分表达式。
但为了简捷实用起见,常常采用微元法(又称元素法)。
微元法的关键就在于寻找待求量A 的微小增量(部分量)能近似表达为x ∆的线性形式,()x x f A ∆≈∆而且当0→∆x 时,()()x x x f A ∆=∆-∆0,亦即()dx x f dA =,其中()x f 为[]b a ,上的某一个连续函数。
量dA 称为待求量的微元素。
然后把()dx x f 在[]b a ,上积分,即待求量⎰=badx x f A )(。
这就是微元法。
在采用微元法时,必须注意如下几点:(1)选好坐标系,这关系到计算简繁问题。
(2)待求量A 具有以区间的可加性,即A =∑∆A ;(3)取好微元x x f d )(,经常应用“以匀代变”“以直代曲”的思想决定A ∆的线性主部,这关系到结果正确与否的问题。
定积分的几何应用一、平面图形的面积 1.直角坐标的情形求)(1x y ϕ=与)(2x y ϕ=与所围图形的面积方法(1)以x 为积分变量由)(1x ϕ)(2x ϕ=解出两个常数值a x =,b x =,面积元素dA =dx x x )]()([12ϕϕ-,面积A =x x x bad )]()([12ϕϕ-⎰,(b x a ≤≤)。
方法(2) 以y 为积分变量由)(1x y ϕ=、)(2x y ϕ=解出x 的两个表达式)(1y x ϕ=,)(2y x ϕ=,再根据)(1y ϕ)(2y ϕ=解出y 的两个常数值c y =,d y =,面积元素dA =dy y y )]()([12ϕϕ-,面积A =y y y dc d )]()([12ϕϕ-⎰,(d y c ≤≤)。
以x 还是y 为积分变量,要视具体情况分析,总之要让计算最简单。
(1)X — 型平面图形的面积 (2) Y — 型平面图形⎰-=badx x g x f S )()( ⎰-=dcdy y g y f S )()(2.参数方程情形求)(x f y =、a x =、b x =以及x 轴所围图形的面积(b a x f <≥,0)(),如果曲边)(x f y =的方程为参数方程为⎩⎨⎧==)()(t y t x φϕ,则其面积dx y A ba ⎰==dt t t )(')(ϕφβα⎰,其中)(),(βϕαϕ==b a3.极坐标情形设平面图形是由曲线 )(θϕ=r 及射线αθ=,βθ=围成的曲边扇形。
定积分及其应用练习 带详细答案

设f(x)= ,函数图象与x轴围成封闭区域的面积为( )
A.
B.
C.
D.
答案:C.
详解:
根据题意作出函数的图象:
根据定积分,得所围成的封闭区域的面积S=
故选C
变式训练二
题面:
已知函数 的图象与x轴所围成图形的面积为( )
A.
1/2
B.
1
C.
2
D.
3/2
答案:D.
详解:
由题意图象与x轴所围成图形的面积为
答案: .
详解:
设A(x0,0),则ωx0+φ= ,∴x0= - .
又y=ωcos(ωx+φ)的周期为 ,
∴|AC|= ,C .
依题意曲线段 与x轴围成的面积为
S=-∫ - + - ωcos(ωx+φ)dx=2.
∵|AC|= ,|yB|=ω,∴S△ABC= .
∴满足条件的概率为 .
变式训练二
题面:
(2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
题二
题面:
如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为().
A. B. C. D.
变式训练一
题面:
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
若在曲线段 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为________.
答案:4.
详解:
作出 在 上的图象如右
与 轴交于0、 、 ,所
求积
题二
题面:
高等数学定积分应用习题答案

第六章定积分的应用习题6-2(A) 1.求以下函数与x轴所围部分的面积:(1)y x26x8,[0,3](2)y2x x2,[0,3]2.求以下各图中暗影部分的面积:1.图6-13.求由以下各曲线围成的图形的面积:(1) y e x,y e x与 x1;(2)y lnx与x0,y lna,y lnb(ba0);(3)y2x x2与y x,y0;(4)y22x,y2(x1);(5)y24(1x)与y2x,y0;(6)y x2与y x,y2x;(7)y2sinx,y sin2x(0x);(8)y x2,x2y2(两部分都要计算);2814.求由曲线y ln x与直线y0,x e1,x e所围成的图形的面积。
5.求抛物线y x24x3及其在点(0,3)和(3,0)处的切线所围成的图形的面积。
6.求抛物线y22px及其在点(p,p)处的法线所围成的图形的面积。
27.求曲线x y a与两坐标轴所围成的图形的面积。
x2y21所围图形的面积。
8.求椭圆2b2a9.求由摆线x a(t sint),ya(1cost)的一拱(0t2)与横轴所围图形的面积。
10.求位于曲线y e x下方与由该曲线过原点的切线的左方及x轴之间的图形的面积。
11.求由以下各方程表示的曲线围成的图形的面积:(1)2asin(a0);(2)2a(2cos)(a0);(3)22cos2(双纽线);12.把抛物线y24ax及直线x x(x00)所围成的图形绕x轴旋转,计算所得旋转抛物体的体积。
13.由y x3,x2,y0所围成的图形,分别绕x轴及y轴旋转,计算所得两个旋转体的体积。
14.求以下已知曲线所围成的图形,按指定的轴旋转所产生的旋转体的体积:(1)y achx0,x a,y0,绕x轴;与xa(2)y sinx与y2x,绕x轴;(3)y sin x与y cosx(0x),绕x轴;2(4)y lnx,与x2,y0绕y轴;(5)y2x x2与y x,y0绕y轴;(6)(x5)2y216,绕y轴;15.求由抛物线y24(1x)及其在(0,2)处的切线和x轴所围的图形绕x轴旋转产生的旋转体的体积。
考研数学三(定积分及应用)模拟试卷4(题后含答案及解析)

考研数学三(定积分及应用)模拟试卷4(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.设M=cos4xdx,N=(sin3x+cos4x)dx,P=(x2sin3x-cos4x)dx,则有( ).A.N<P<MB.M<P<NC.N<M<PD.P<M<N正确答案:D解析:cos4xdx=0.N=(sin3x+cos4x)dx=cos4xdx>0,P=(x2sin3x-cos4x)dx=cos4xdx<0,则P<M<N,选D.知识模块:定积分及应用2.曲线y=x(x-1)(2-x)与x轴所围成的图形面积可表示为( ).A.-∫02x(x-1)(2-x)dxB.∫01x(x-1)(2-x)dx-∫12x(x-1)(2-x)dxC.-∫01x(x-1)(2-x)dx+∫12x(x-1)(2-x)dxD.∫02x(x-1)(2-x)dx正确答案:C解析:曲线y=x(x-1)(2-x)与x轴的三个交点为x=0,x=1,x=2,当0<x<1时,y<0;当1<x<2时,y>0,所以围成的面积可表示为C的形式,选C.知识模块:定积分及应用填空题3.=________.正确答案:解析:知识模块:定积分及应用4.∫0xxsin(x-t)2dt=________.正确答案:∫0xsinuxn-1f(xn)du+xsinxxn-1f(xn)解析:由∫0xxsin(x-t)xn-1f(xn)dt=x∫0xsin(x-t)xn-1f(xn)dtx∫0xsinuxn-1f(xn)du,得∫0xxsin(x-t)xn-1f(xn)dt=(x∫0xsinuxn-1f(xn)du)=∫0xsinuxn-1f(xn)du+xsinxxn-1f(xn).知识模块:定积分及应用5.∫02πx|sinx|dx=_________.正确答案:4π解析:∫02πx|sinx|dx=∫0πx|sinx|dx+∫π2πx|sinx|dx,∫0πx|sinx|dx=∫0πxsinxdx=∫0πsinxdx=sinxdx=π。
大学高等数学第五章 定积分及其应用答案
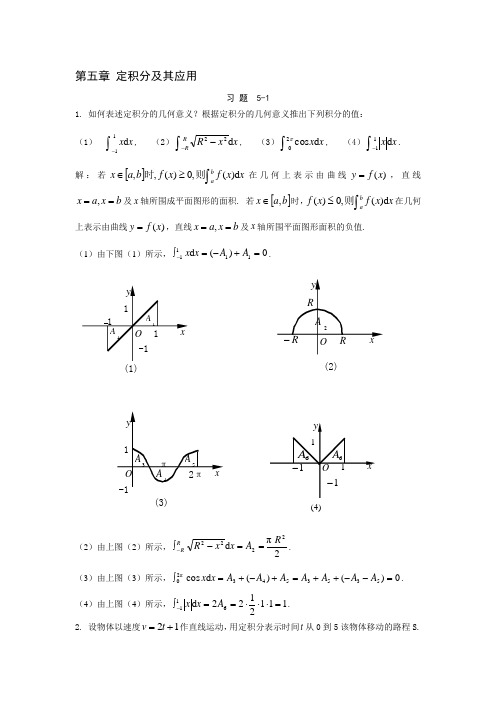
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
定积分及其应用计算题

3
(1) 求它与 x 轴所围成的面积; (2) 求它的弧长; (3) 求它与 x 轴围成区域绕 x 轴旋转而成的旋转体的体积和 表面积. 15* 设曲线 y ax a 0, x 0 与 y 1 x 相交于点 A ,过坐标原点 O 和点 A 的直线与曲线 y ax 围成一个平面图形,问 a 为何值时,该 图形绕??轴旋转一周所得的旋转体的体积最大 ?最大体积为多 少? 16. 过点 1,0 作曲线 y x 2 的切线,该切线与上述曲线及 x 轴 围成一个平面图形 A .(1) 求 A 的面积; (2) 求 A 绕 x 轴旋转 一周所成的旋转体的体积. 17* 设函数 f x 在闭区间 0,1 上连续,在开区间 0,1 内大于零, 并满足 3a xf x f x x (a 为常数);
1 2
y a1 cos t ,
(1) 求它绕 x 轴旋转一周生成的旋转体的体积与侧面积; (2) 求它绕 y 轴旋转一周生成的旋转体的体积与侧面积. 12. 13. 14.
x 2 求曲线 y 在 0 x 2 区间段的弧长. 2 x at sin t , 求外旋轮线的方程为 0 t 2 , a 0 的弧长. y a1 cos t ,
要求汽锤每次击打桩时所做的功与前一次击打时所做的功之 比为常数 r ( 0 r 1 ).问: (1) 汽锤击打 3 次后,可将桩打进地下多深? (2) 若击打次数不限,汽锤至多能将桩打进地下多深? 广义积分问题 1. 计算
3 2 1 2
dx xx
x2 0
2
.
考研数学强化班讲义-微积分第4讲(学员版)定积分应用综合

(6) 旋转体的侧面积
直角坐标系中曲线 y = f (x), a ≤ x ≤ b 绕 x 轴旋转生成的旋转体
∫ 的侧面积为
A = 2π
b
f (x)
1 + [ f ′(x)]2 dx 。
a
参数方程下曲线 x = x(t), y = y(t), α ≤ t ≤ β 绕 x 轴旋转生成的
∫ 旋转体的侧面积为
∫ 绕 x 轴旋转生成的旋转体的体积(小圆台法)Vx
=
bπ
a
f 2 (x)dx 。
∫ 绕 y 轴旋转生成的旋转体的体积(薄壁筒法)Vy
=
b 2xπ
a
f (x)dx 。
(5)平面光滑曲线的弧长
直 角 坐 标 系 中 的 光 滑 曲 线 y = f (x), a ≤ x ≤ b 的 弧 长 为
∫ l = b 1+ [ f ′(x)]2 dx 。 a
设区域的边界由曲线 L :
⎧ x = x(t)
⎨ ⎩
y
=
y(t)
(α ≤ t ≤ β ) 确定, 其中
∫ x(t), y(t) 连续可导, y(t) ≥ 0 , 则区域的面积为 A = β y(t)x′(t)dt 。 α
(3) 极坐标系下区域的面积
设 区 域 D 为 D = {(x, y) x = ρ cosϕ, y = ρ sinϕ, α ≤ ϕ ≤ β , 0 ≤ ρ ≤ ρ(ϕ)} ,
D = {(x, y) a ≤ x ≤ b, f (x) ≤ y ≤ g(x)}
∫ 的面积为 A = b [g(x) − f (x)]dx 。 a ∫b
注:若连续函数 f (x) 在区间[a, b] 上变号,则 A = f (x)dx 表示正负面 a 积的代数和,有时称为代数面积。 (2) 参数方程下区域的面积
考研高等数学重要知识点解析定积分的应用

考研高等数学重要知识点解析定积分的应用开城研究生训练营,引导学生,服务学生!高等数学考研重点知识点分析:定积分考研即将到来,不到50天,考研复习将进入冲刺阶段考生基本上已经了解了高分的总数,也许许多考点只是粗略的回顾,并不深入。
没关系。
这里的研究生入学考试导师帮助考生分析定积分的应用命题规则,并对定积分的应用进行深入分析。
定积分的应用主要是基于微分单元法,而微分单元法是基于定积分的定义。
因此,划分、逼近、总结和取极限是计算某些几何量和物理量的指导思想多年来,定积分及其应用在真问题的研究中有多种形式。
它们可以以客观问题的形式或问题的解决方式出现。
他们经常结合其他知识点来考察,如极限、导数、微分中值定理、极值等知识点来给出问题。
在这部分中,需要掌握用微元法计算的平面图形面积、平面曲线弧长、旋转体体积和侧向面积,以及已知的立体体积、功、重力、压力、质心和平行截面面积的质心。
对于三个,只需要计算平面图形的面积和旋转体的体积。
其中,旋转体体积的求解和微积分在几何中的应用与最大值问题相结合是常见试题的关键类型,应得到大多数考生的充分重视。
对于定积分的应用,首先需要掌握微元法在过去的几年里,有大量真正的研究生入学考试([微博)的试题使用微元法求解方程,而微元法的巧妙应用是写作试题的教师青睐的知识点之一。
然而,由于微元法本身思维的飞跃,灵活有效的方法只有通过充分的练习才能真正实现。
本文将功能图像与微元方法的相应核心类型相结合,总结出三种常见的微元方法:,第1页,共1页开城研究生训练营,指导学生,服务学生!2。
煎饼第2页共2页启成研究生入学考试训练营,指导学生,为他们服务!第3页,共3页开城考研训练营,指导学生,服务学生!第4页第4页第4页开城研究生训练营,指导学生,为他们服务!第5页共5页开城考研训练营指导学生并为他们服务!通过以上三个例子谈了一点对微元法特点的认识这种方法的灵活应用只能通过自助解决问题的经验来实现,因为表面上有些逻辑不符合常规思维,但这也许就是为什么研究生入学考试老师喜欢微元方法的原因。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一份好的考研复习资料,会让你的复习力上加力。
中公考研辅导老师为考生准备了【高等数学-定积分(应用)知识点讲解和习题】,同时中公考研网首发2017考研信息,2017考研时间及各科目复习备考指导、复习经验,为2017考研学子提供一站式考研辅导服务。
模块七 定积分(应用)Ⅰ经典习题一.平面图形的计算1、曲线()sin 03xy ex x π-=≤≤与x 轴所围成图形的面积可表示为()()30sin xA e xdx π--⎰ ()30sin x B e xdx π-⎰()2302sin sin sin x x x C e xdx e xdx e xdx πππππ----+⎰⎰⎰()2302sin sin xx D e xdx e xdx πππ---⎰⎰2、设b 为常数(1)求曲线321:(2)x bx L y x x ++=+的斜渐近线(记为l )的方程(2)设L 与l 从1x =延伸到x →+∞之间的图线的面积A 为有限值,求,b A3、曲线2yx =与直线2y x =+所围成的平面图形的面积为_________.4、假设曲线1L :()2101y xx =-≤≤、x 轴和y 轴所围区域被曲线2L :2y ax =分为面积相等的两部分,其中a 是大于零的常数,试确定a 的值.5、求曲线y =l ,使该曲线与切线l 及直线0,2x x ==所围成的平面图形面积最小. 6、计算抛物线22yx =与直线4y x =-所围成的图形面积。
7、求椭圆22221x y a b+=所围成图形的面积。
8、求下列各曲线围成的图形的面积 (1)2cos a ρθ=(2)()22cos aρθ=+二.简单几何体的体积9、曲线()211y x =--及直线0y =围成的图形绕y 轴旋转而成的立体的体积是( )()(2101A dy π+⎰ ()(211B dy π-⎰()((21011C dy ππ⎡⎤-⎣⎦⎰ ()((221011D dy ππ⎡⎤+-⎢⎥⎣⎦⎰ 10、设曲线方程为(0).xy e x -=≥(1)把曲线、xy ex -=轴、y 轴和直线(0)x ξξ=>所围平面图形绕x 轴旋转一周,得一旋转体,求此旋转体体积();V ξ求满足1()lim ()2V a V ξξ→+∞=的a (2)在此曲线上找一点,使过该点的切线与两个坐标轴所夹平面图形的面积最大,并求出该面积.11、设抛物线2yax bx c =++过原点,当01x ≤≤时0,y ≥又已知该抛物线与x 轴及直线1x =所围图形的面积为1.3试确定,,,a b c 使此图形绕x 轴旋转一周而成的旋转体的体积V最小.12、过坐标原点作曲线x y e =的切线,该切线与曲线xy e =以及x 轴围成的向x 轴负向无限延伸的平面图形记为D (1)求D 的面积(2)求D 饶直线1x =所成旋转体体积V13、设曲线2y ax =(0,0x a ≥>)与曲线21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一平面图形D(1)求D 饶x 轴旋转一周所成的旋转体体积()V a (2)求a 的值使()V a 为最大14、在曲线2(0)y x x =≥上某点A 处作切线,使之与曲线及x 轴所围图形的面积为1,12试求:(1)切点A 的坐标;(2)过切点A 的切线方程;(3)由上述所围平面图形绕x 轴旋转一周所成旋转体的体积。
15、过原点作曲线ln y x =的切线,该切线与曲线ln y x =以及x 围成平面图形D (1)求D 的面积(2)求D 绕直线x e =旋转一周所得旋转体的体积V16、求曲线23|1|y x =--与x 轴围成的封闭图形绕直线3y =旋转所得的旋转体体积. 17、设曲线24y ax =及直线()000x x x =>所围成图形绕x 轴旋转的体积。
三.曲线弧长(*数学一、数学二)18、曲线()0,0b r aea b θ=>>,从0θ=到()0θαα=>的弧长为()()0b A s ae αθθ=⎰ ()0B s θ=⎰()0C s θ=⎰()0b D s abe αθ=⎰19、计算曲线ln y x =x ≤≤ 20、求对数螺旋线a e θρ=,相应于0θϕ≤≤的一段弧长。
21、求曲线1ρθ=,相应于3443θ≤≤的一段弧长。
22、求心形线()1cos a ρθ=+的全长。
23、求抛物线212y x =,被圆223x y +=所截下的有限部分弧长。
四.旋转曲面面积(*数学一、数学二)24、已知摆线的参数方程为(sin )(1cos )x a t t y a t =-⎧⎨=-⎩,其中02t π≤≤,常数0a >,设摆线一拱的弧长的数值等于该弧段饶x 轴旋转一周所围成的旋转曲面面积的数值,求a25、设有曲线y =过原点作其切线,求由此曲线、切线及x 轴围成的平面图形绕x 轴旋转一周所得到的旋转体的表面积. 26、由曲线段1(02)2y x x =≤≤绕x 轴的旋转面面积.五.物理应用(*数学一、数学二)27、曲线()sin x a t t =-,()()1cos ,02y a t t π=-≤≤的质心为()4,3A a a π⎛⎫ ⎪⎝⎭ ()2,3B a a π⎛⎫ ⎪⎝⎭ ()5,4C a a π⎛⎫ ⎪⎝⎭ ()7,4D a a π⎛⎫ ⎪⎝⎭28、半径为r 的球沉入水中,球的上部与水面相切,球的密度与水相同,现将球从水中取出,需要多少功?29、一圆柱形的贮水桶高为5m ,底圆半径为3m ,桶内盛满水,试问要把桶内的水全部吸出来需要做多少的功。
30、用铁锤将一铁钉击入木板,设木板对铁钉的阻力与铁钉入木板的深度成正比,在击第一次时,将铁钉击入木板1cm 。
如果铁锤每次锤击铁钉所作的功相等,问铁锤第二次时,铁钉又击入多少?31、等腰梯形的闸门,它的两条底边各长10m 和6m ,高为20m ,较长的底边与水面相齐,计算闸门的一侧所受的水压力(重力加速度按29.8/m s 计算)。
32、一底为8cm ,高为6cm 的等腰三角形片,铅直的沉入到水中,顶在上,底在下且与水面平行,而顶离水面3cm ,试求它的每面所受的压力(重力加速度按29.8/m s 计算)。
33、求下列平面图形的形心坐标: (1)平面区域:(){}221,|1,0,0D x y xy x y =+≤≥≥;(2)曲线:221,0,0x y x y +=≥≥; (3)平面区域:(){}222,|1,11,01D x y xy x y =+≥-≤≤≤≤.Ⅱ参考答案一.平面图形的计算1、()C2、【解析】:(1)321:(2)x bx L y x x ++=+的斜渐近线为3221lim lim2(2)x x y x bx x x x →+∞→+∞++==+ 3332212124lim (2)lim [2]lim 4(2)(2)x x x x bx x bx x x y x x x x x x →+∞→+∞→+∞++++---=-==-++ 所以斜渐近线方程为:24y x =-(2)311115121(8)122[(24)][](2)(2)2A b x bx b x S x dx dx dx x x x x x x+∞+∞+∞+++++=--==++++⎰⎰⎰ 215111lim[(215)ln(2)ln ]lim[ln (2)(215)ln 3]22t b t t b x x t t b +→+∞→+∞=+++=+-+ 若21510b ++≠,即如果8b ≠-,无论8,8b b >-<-均有215lim ln (2)b t t t +→+∞+=∞ 这与A 的面积为有限值矛盾,所以当8b =-时,215lim ln (2)lim ln2b t t t t t t +→+∞→+∞+==+0,此时ln 32A S = 3、【答案】92【解析】先解出两条曲线在平面的交点,即令22x x =+解得1x =-和2x =,故所围成的平面图形如右图所示: 所求面积为 ()2212S x x dx -=+-⎰22311192.232x x x -⎛⎫=+-= ⎪⎝⎭4、【解析】先求出曲线1L 和2L 的交点,然后利用定积分求出平面图形面积1S 和2S ,如图:由()()221010y x x y ax a ⎧=-≤≤⎪⎨= >⎪⎩得 11x ,a a y .a ⎧=⎪⎪+⎨⎪=⎪+⎩所以 112120(1)S S S ydx x dx =+==-⎰⎰1301233x x ⎡⎤=-=⎢⎥⎣⎦,()()2221110111a aS x ax dx a x dx ++⎡⎤⎡⎤=--=-+⎣⎦⎣⎦⎰⎰1301331aa x x a++⎡⎤=-=⎢+⎣⎦.又因为12S S =,所以22331a=⋅+,即12a +=,解得3a .= 5、【解析】过曲线上已知点00(,)x y 的切线方程为00()y y k x x -=-,其中当0()y x '存在时,0()k y x '=.如图所示,设曲线上一点(,)t t 处的切线方程为()2y t x t t-=-,化简即得 2ty t=+. 面积 24()232t S t x dx t t t ⎡⎤⎛⎫=+-=+-⎢⎥ ⎪ ⎪⎢⎝⎭⎣⎦⎰, 其一阶导数 3/21/211()222S t t t t t--'=-+=. 令()0S t '=解得唯一驻点1t =,而且S '在此由负变正,即()S t 在(,1]-∞单调递减,在[1,)+∞单调递增,在此过程中()S t 在1t =时取极小值也是最小值,所以将1t =代入先前所设的切线方程中,得所求切线方程为122x y =+. 6、答案:187、答案:ab πy O2tt8、(1)答案:2a π(2)答案:218a π二.简单几何体的体积9、()D10、【解析】:(1)2220()(1),2x V y dx e dx e ξξξπξππ--===-⎰⎰2lim (),()(1).22a V V a e ξππξ-→+∞==-要 1()lim (),2V a V ξξ→+∞=即2(1),24a e ππ--=得1ln 2.2a = (2)设切点为(,),eαα-则切线方程为().y e e x ααα---=--令0x =得(1);y e αα-=+令0y =得1.x α=+切线与坐标轴所夹面积22111(1),(1)(1)(1)(1).222S e S e e e ααααααααα----'=+=+-+=+-令 0S '= 得1221,1().其中舍去ααα==-由于当1α<时,0;S '>当1α>时,0.S '<故当1α=时,面积S 有极大值,即最大值。
