材料力学第五章A
合集下载
05材料力学第五章
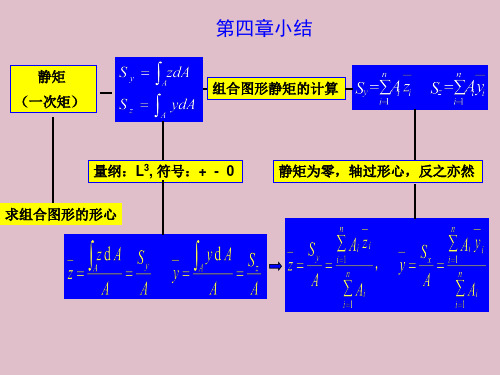
对称弯曲（平面弯曲）
一般情况下，工程中受弯杆件的横截面都至少有一个通 过几何形心的对称轴，因而整个杆件都有一个包含轴线的纵 向对称面。如下图，当作用于杆件的外力都在这个纵向对称 平面上时，可以想象到，弯曲变形后的轴线也将是位于这个 对称面内的一条曲线。这种情况的变形我们就称为平面弯曲 变形，简称为平面弯曲。 q
C A b a c D B
RA
RB
P2=P
解
(1)求支座反力
RA RB P 60 kN
(2)计算C 横截面上的剪力QSC和弯矩 MC .
看左侧
QSC P 60kN 1
M C P1 b 6.0kN.m
(3)计算D横截面上的剪力QSD 和弯矩 MD . 看左侧
QSD R A P1 60 60 0
不论在截面的左侧或右侧向上的外力均将引起正值的弯矩, 而向下的外力则引起负值的弯矩. 左侧梁段 顺时针转向的外力偶引起正值的弯矩 逆时针转向的外力偶引起负值的弯矩
右侧梁段
逆时针转向的外力偶引起正值的弯矩 顺时针转向的外力偶引起负值的弯矩
左顺右逆为正
求弯曲内力的法则
任一截面的剪力Q=∑[一侧横向力的代数和]
支座的简化
载荷的简化
对称弯曲
纵向对称面
外力作用在此 纵向对称面内
变形后的轴线仍 在纵向对称面内
简支梁：一端固定绞支座一端可动铰支座
RAx A RAy
m
A
P
B
y
RBy
求内力——截面法 RAx A
RAy
m
P
B
剪力 弯曲构件内力 弯矩 1、弯矩M 构件受弯时，横截面上其作用面垂 RAy 直于截面的内力偶矩. 2、 剪力QS 构件受弯时，横截面上其作用线平行 于截面的内力.
材料力学第五章
M O0:M dM d( x x() x )d M FQ ( (x x) - ) M M ( x 2) - M F 1 Q ( x x x ) 1 2 d F x Q - (1 2 x q )d ( x x) d x 2 0
d2d M x(2x)dF d Q x (x)q(x)
精品PPT
§5-5 剪力、弯矩和分布载荷集度间的微分关系
M图 Mmax位置
q>0 q q<0
M">0 M"<0
FQ=0
CF
+ _
FC
FQ>0 FQ<0
FQ变号处
Me C
C
Me C
紧靠C的 某一侧面
精品PPT
§5-5 剪力、弯矩和分布载荷集度间的微分关系 三、利用微分关系作剪力弯矩图
1．用微分关系判断分段点间FQ、M图形态； 2．用计算法则(或积分关系)计算分段点FQ、M值； 3．分段点间连线；
一、梁的载荷(zài hè)及支座反力
1．载荷(zà集i h中è载)：荷(集中力、集中力偶)， 分布载荷(均布载荷、分布载荷)。
名称
图示法
符号(单位)
(a)集中力 (b)分布载荷
F1 Fy2 F2 Fx2
q(x)
x
F(N)
x q(x)(N/m)
(c)均布载荷
q x q(N/m)
(d)集中力偶
Me Me
(向上的横向力、截面左侧顺时针力矩和截面右侧逆 时针力矩对该截面产生正的弯矩)
精品PPT
§5-3 剪力与弯矩
三、弯曲(wānqū)内力的计算法则
*3．判断外力产生(chǎnshēng)剪力、弯矩正负的
图例：
材料力学习题解答[第五章]
![材料力学习题解答[第五章]](https://img.taocdn.com/s3/m/5c357285a0116c175f0e48fd.png)
5-1构件受力如图5-26所示。
试：(1)确定危险点的位置；(2)用单元体表示危险点的应力状态（即用纵横截面截取危险点的单元体，并画出应力）。
题5-1图解：a) 1) 危险点的位置：每点受力情况相同，均为危险点；2）用单元体表示的危险点的应力状态见下图。
b) 1) 危险点的位置：外力扭矩3T与2T作用面之间的轴段上表面各点；2）应力状态见下图。
c) 1) 危险点：A点，即杆件最左端截面上最上面或最下面的点；2）应力状态见下图。
d) 1）危险点：杆件表面上各点；2）应力状态见下图。
5-2试写出图5-27所示单元体主应力σ1、σ2和σ3的值，并指出属于哪一种应力状态（应力单位为MPa）。
10题5-2图解：a)1σ=50 MPa,2σ=3σ=0,属于单向应力状态AAT （a）（c）（d）364dFlπτ=a) b) c) d)a) b) c)b) 1σ=40 MPa, 2σ=0, 3σ=－30 MPa ，属于二向应力状态 c) 1σ=20 MPa, 2σ=10 MPa, 3σ=－30 MPa ，属于三向应力状态5-3已知一点的应力状态如图5-28所示（应力单位为MPa ）。
试用解析法求指定斜截面上的正应力和切应力。
题5-3图解：a) 取水平轴为x 轴，则根据正负号规定可知： x σ=50MPa , y σ=30MPa , x τ=0, α=－30 带入式（5-3），（5-4）得 ατασσσσσα2sin 2cos 22x yx yx --++==45MPaατασστα2cos 2sin 2x yx +-== -8.66MPab) 取水平轴为x 轴，根据正负号规定：x σ= -40MPa , y σ=0 , x τ=20 MPa , α=120带入公式，得：240sin 20240cos 20402040---++-=ασ=7.32MPa x τ= 240cos 20240sin 2040+--=7.32MPac) 取水平轴为x 轴，则x σ= -10MPa , y σ=40MPa , x τ= -30MPa,α=30代入公式得：60sin )30(60cos 2401024010----++-=ασ=28.48MPa x τ= 60cos 3060sin 24010---=-36.65MPa5-4已知一点的应力状态如图5-29所示（应力状态为MPa ）。
材料力学 第五版 第五章
b2
15
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
(2) 圆截面
在等直圆杆扭转问题(§3-4)中已求得：
πd 4 Ip 2 d A A 32
d
o y
z
dA
z
y
而由图可见，ρ2=y2+z2 , 从而知
πd 4 Ip 2 d A y2 d A z2 d A I z I y A A A 32
梁横截面上的正应力公式。
My Iz
M为截面的弯矩，y为欲求应力点至 中性轴的距离，Iz为截面对中性轴的 惯性矩。 σ
x
注意： 1.当弯矩为正时，梁下部产 生拉应力；上部产生压应力； 弯矩为负时，则相反。一般用 计算正应力时，M与y均取正值， 而正应力的拉、压由观察判断。
M
12
材 料 力 学 Ⅰ 电 子 教 案
max
式中，[]为材料的许用弯曲正应力。
20
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
对于中性轴为横截面对称轴的梁，上述强度条件可写作
M max Wz
由拉、压许用应力[t]和[c]不相等的铸铁等脆性材 料制成的梁，为充分发挥材料的强度，其横截面上的中性 轴往往不是对称轴，以尽量使梁的最大工作拉应力t,max和
2.公式是根据纯弯曲的情形导出的，但对于横向 弯曲(即剪力、弯矩均不为零的情形)，也可以足 够精确地用来计算正应力。 3. 公式虽然是针对梁横截面有对称轴的情形 推出的，但对于不对称截面，公式的适用范围推 广到不对称截面梁,且外力作用面通过一个形心 主轴的情形。
13
材 料 力 学 Ⅰ 电 子 教 案
2.所有的纵线都弯曲 成曲线。靠近底面的 纵线伸长，靠近顶面 的纵线缩短。而位于 中间的某一条纵线O-O ，其长度不变。
15
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
(2) 圆截面
在等直圆杆扭转问题(§3-4)中已求得：
πd 4 Ip 2 d A A 32
d
o y
z
dA
z
y
而由图可见，ρ2=y2+z2 , 从而知
πd 4 Ip 2 d A y2 d A z2 d A I z I y A A A 32
梁横截面上的正应力公式。
My Iz
M为截面的弯矩，y为欲求应力点至 中性轴的距离，Iz为截面对中性轴的 惯性矩。 σ
x
注意： 1.当弯矩为正时，梁下部产 生拉应力；上部产生压应力； 弯矩为负时，则相反。一般用 计算正应力时，M与y均取正值， 而正应力的拉、压由观察判断。
M
12
材 料 力 学 Ⅰ 电 子 教 案
max
式中，[]为材料的许用弯曲正应力。
20
材 料 力 学 Ⅰ 电 子 教 案
第四章 弯曲应力
对于中性轴为横截面对称轴的梁，上述强度条件可写作
M max Wz
由拉、压许用应力[t]和[c]不相等的铸铁等脆性材 料制成的梁，为充分发挥材料的强度，其横截面上的中性 轴往往不是对称轴，以尽量使梁的最大工作拉应力t,max和
2.公式是根据纯弯曲的情形导出的，但对于横向 弯曲(即剪力、弯矩均不为零的情形)，也可以足 够精确地用来计算正应力。 3. 公式虽然是针对梁横截面有对称轴的情形 推出的，但对于不对称截面，公式的适用范围推 广到不对称截面梁,且外力作用面通过一个形心 主轴的情形。
13
材 料 力 学 Ⅰ 电 子 教 案
2.所有的纵线都弯曲 成曲线。靠近底面的 纵线伸长，靠近顶面 的纵线缩短。而位于 中间的某一条纵线O-O ，其长度不变。
材料力学-第五章
合理布置载荷
F
小结
1、熟练求解各种形式静定梁的支 座反力 2、明确剪力和弯矩的概念，理解 剪力和弯矩的正负号规定 3、熟练计算任意截面上的剪力和 弯矩的数值
4、熟练建立剪力方程、弯矩方程， 正确绘制剪力图和弯矩图
5.7 总结 回顾
毛和业，怎样快速绘制剪力图和弯
矩图，黔南民族师范学院学报， 2005，3：81-83
（ -）
1kN.m
A
FAY
1.5m
C
1.5m
D
2kN
1.5m
B
FBY
4 ．从 A 截面左测开始画 弯矩图。 从A左到A右 从A右到C左 从C左到C右 从C右到D左 从D左到D右
1.11
（+）
Fs（ kN） 0.89 M（ kN.m）
（ -）
0.330
（-）
1.330
（ -）
1.665
从D右到B左
从B左到B右
2
FS
FS x
x
0 x l 0 x l
M
ql2 / 8
依方程画出剪力图和弯矩图 ql / 2 由剪力图、弯矩图可见。最 大剪力和弯矩分别为
x
FS max＝ql
M max＝ql2 / 2
5.4
y
剪力图和弯矩图（将剪力方程和弯矩方程具体化）
q
例题 简支梁受均布载荷作用
FS ql / 2
( 2)在有均布载荷作用的 段上, 剪力图为倾斜直线, 直线由左上向右下倾斜; 弯矩图为抛物线, 抛物线 开口与均布载荷的方向一 致。
M 3ql2 / 32 x
ql2 / 8
材料力学第五章 弯曲应力分析
B
D
1m
1m
1m
y2
20
120
FRA
F1=9kN FRB F2=4kN
A C
BD
1m
1m
1m
2.5 Fs
+
+
4 kN
-
6.5 2.5
M
kNm
-
+
4
解： FRA 2.5kN FRB 10.5kN
88
52
-
+
C 2.5
4 B 80
z
20
120
20
B截面
σ t max
M B y1 Iz
4 • 52 763
20
+
-
+
10
Fs
kN
10
20
30
30
25
25
M
kNm
max
M max W
[ ]
W Mmax 30 187.5cm3
[ ] 160
1)圆 W d 3 187.5
32
d 12.4cm
A d 2 121cm2
4
2）正方形
a3 W 187.5
6
3）矩形
a 10.4cm
A a2 108cm2
压，只受单向拉压. （c）同一层纤维的变形相同。 （d）不同层纤维的变形不相同。
推论：必有一层变形前后长度不变的纤维—中性层
中性轴
中性轴⊥横截面对称轴
中性层
横截面对称轴
二、变形几何关系
dx
dx
图（a）
O
O
zb
O yx b
y
图（b）
第五章 习题解答(材料力学课件)-PPT文档资料
换后最大扭矩将由1.5kN m减小为1kN m
4. 解 ：
AC
AB
3
BC
T1 l 1 T 2 l 2 G Ip G Ip
3
1.5 1 0 1.2 0 .5 1 0 0 .8 9 4 80 10 0 .0 5 32 0 .0 4 4 8 4 ra d A、 B两 轮 互 换 位 置 后 ， 轴 两 端 的 相 对 扭 转 角 为 1.0 1 0 1.2 0 .5 1 0 0 .8 9 80 10 0 .0 5 4 32 0 .0 1 6 3 ra d
m
x
l
XT5TU1
1 0 .解 ： 轴 的 扭 矩 图 如 下 图 ， 最 大 扭 矩 T . k N m m a x 05 T m a x 由 强 度 条 件 m [] 得 轴 的 直 径 a x 3 d 1 6 1 6 T m a x 3 d 5 03 . m m []
m
A
B
m
C
D
mD
即
1 2m 解 得 m 05 . 5 7 m D 4 4 A 端 的 反 力 偶 m m .4 3m A m D 04
4
(m ) 4m D m D 2
m D 2 0
内、外层横截面上剪应力的计算公式分别为 T1 m T2 2m 1 , 2 I p1 I p1 2 I p 2 I p2 I p1 2 I p 2
1 9 .解 ： 此 为 一 次 静 不 定 问 题 。 解 除端 D 约 束 ， 代 之 以 反 力 偶 m D 由 变 形 协 调 条 件 A A 0 ， 得 D B B C C D ( m ml )A m m D B Dl B C Dl C D 0 G IpA G IpB IpC B C G D
材料力学课后习题答案5章
(b)
保留有限量，略去一阶和二阶微量后，得
足标 C 系指梁微段右端面的形心，对题图(b)亦同。 根据题图 b，由
∑F
略去微量 qdx 后，得
y
=0 ，FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b，由
(c)
∑M
C
=0 ，M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 ， M 2 有极大值，其值为 24 121 2 M 2 max = M max = ql 1152
(d)解：1．建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示，由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3．画剪力、弯矩图 依据式(c)和(e)可绘剪力图，如图 5-9b(2)所示；依据式(d)和(f)可绘弯矩图，如图 5-9b(3) 所示。 (c)解：1．求支反力
=0 ，FS左 + F + qdx − FS右 = 0
保留有限量，略去微量 qdx 后，得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况（把向下的 F 也包括在内） ，可将上式改写为
保留有限量，略去一阶和二阶微量后，得
足标 C 系指梁微段右端面的形心，对题图(b)亦同。 根据题图 b，由
∑F
略去微量 qdx 后，得
y
=0 ，FS左 + qdx − FS右 = 0
FS右 = FS左
仍据题图 b，由
(c)
∑M
C
=0 ，M 右 − M e − qdx(
dx ) − FS左 dx − M 左 = 0 2
11l 处有 FS2 = 0 ， M 2 有极大值，其值为 24 121 2 M 2 max = M max = ql 1152
(d)解：1．建立剪力、弯矩方程
8
图 5-9d 坐标如图 5-9d(1)所示，由截面法易得剪力、弯矩方程分别为
q( x1 ) ⋅ x1 qx 2 =− 1 2 l ql FS2 = − + qx2 4 qx 3 M1 = − 1 3l q 2 ql l M 2 = x2 − ⋅ ( + x2 ) 2 4 6 FS1 = −
2 q0l q 0 x2 FS = − + 4 l q x3 ql M = 0 x2 − 0 2 4 3l
l (0 ≤ x2 ≤ ) 2 l (0 ≤ x2 ≤ ) 2
(e) (f)
3．画剪力、弯矩图 依据式(c)和(e)可绘剪力图，如图 5-9b(2)所示；依据式(d)和(f)可绘弯矩图，如图 5-9b(3) 所示。 (c)解：1．求支反力
=0 ，FS左 + F + qdx − FS右 = 0
保留有限量，略去微量 qdx 后，得
FS右 − FS左 = F
为了更一般地反映 F 作用处剪力的突变情况（把向下的 F 也包括在内） ，可将上式改写为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Iz = (0.120.023)/12+(0.120.02)(0.045-0.01)2 + (0.020.123)/12+(0.120.02)(0.08-0.045)2 = 8.8410-6 m4
2. Maximum normal stresses in bending: Sections ? Points ?
max
5.3 Shearing stresses in bending
b
1. For the rectangular section:
Assumption: all shearing stresses are parallel to shearing force and uniformly distributed across the width of the section.
From the Table 3, we get: Ix : Sx = 17.2 cm, d = 7 mm
FSSz()max
50103
max =
Iz
=
= 41.5 MPa
17.210-2710-3
Average shearing stress of web is:
m = FS / h = 50103 / [(200-211.4)7] = 40.3 MPa e = 2.87 %
z
A
b
C• a zC
yC dA
zC
yC
1•
• • 2
y
z1
z z2
5.2 Normal stresses in bending
dx
1. Geometrical relation
M
M
Hypothesis of plane section
aa
(+y)d -d y
= d
=
(a)
M
d
M
2. Physical relation
y
= E =E
(b)
3. Statical relation
FN = A dA = 0
(c)
y a
a
Neutral layer
dx
Mz = A ( dA) y = M
(d)
From (b), (c), A y dA = Sz = 0
Neutral axis z must be centroidal axis.
FSSz()max
max =
Iz
z
h0 h
max
y
y
From the Table 3 in the page 351, we
can look up Ix : Sx and calculate max .
For example: calculate max of No. 20a steel I beam, if FS = 50kN.
a
Find: yC and Iz
4a
Solution:
1. Find yC
A1 = 3a2 , y1 = a / 2 ;
A2 = 3a2 , y2 = 5a / 2
yC = (A1 y1 + A2 y2) / (A1+A2) = 3a / 2 2. Find Iz
Iz1 = 3a a3/12 + 3a2 (3a/2 - a/2)2 = 13a4/4
uniformly across the width).
z
max
Limitation about the theory :
h / b 1.5
error 5 %
yy
2. For - shaped section:
b
For the web of I beam, (5.10) can be used: why ?
Chapter 5 Stresses in Bending
Contents:
1. Geometrical properties of plane areas 2. Normal stresses in bending 3. Shearing stresses in bending 4. Strength of beams 5. Principal moment of inertia 6. Unsymmetrical bending 7. Shear center
a,max = 6Fl /a3 b,max = 62Fl /a3 The strength of (a) is bigger.
Problem 5.4
Know: h, b, M, E
Find: max , EI . And compare
with that of the whole beam.
M
h h/2
3 FS 2bh
(1
-
4y2 h2 )
max =
3FS 2bh
=
3 FS 2A
(5.11) (5.12)
Analysis of error :
when h / b 2 , error 1 %
b
when h / b = 1 , error 10 %
Why ? Assumption about (distributed h FS
O
Iy = Iyc + a2 A Iz = Izc + b2 A
( 5.9a) ( 5.9b)
(2) For the composite area:
y
Iz(1) = Iz1 + y12 A1
Iz(2) = Iz2 + y22 A2
y1
Iz = Iz(1) + Iz(2)
y2
= Iz1 + y12 A1 + Iz2 + y22A2
Ip = A 2dA = A(y2 + z2)dA = Iz + Iy
(1) For the rectangular section: Iz = A y2 dA = -hh//22 y2bdy = bh3/12 Similarly, Iy = hb3/12
(2) For the circular section: From Iy = Iz , we get: Iy = Iz = Ip / 2 = d 4/64
Iz2 = a (3a)3/12 + 3a2 (5a/2 - 3a/2)2 = 21a4/4
Iz = Iz1 + Iz2 = 17a4 / 2
3a
1
yC
z 2
a y
Problem 5.2
Plot the distribution of bending normal stresses in following cross sections. If the positive moments act on the beams.
c,max= Fl y1/Iz = 150001.2(0.14-0.045)/(8.8410-6) = 193.4 MPa t,max= Fl yC /Iz= 150001.2 0.045/(8.8410-6) = 91.6 MPa
3. Maximum shearing stresses in bending:
Example 5.1
F
Know: F = 15 kN, l = 1.2 m
Find: t,max , c,max , max
Solution:
l
1. Centroid and moment of inertia:
120 z1
20
yC
120
20 y1z
y
yC = [(0.120.02)0.01+(0.020.12)(0.02+0.06)]/(20.120.02) = 0.045m
(3) For the tubular section:
Iy = Iz = D4(1- 4)/64 where = d / D .
O
z
y
z dA y
b
h
Cz y
dy y
D dd
zz C
yy
5. Moment of inertia for the composite area
(1) Parallel axis theorem:
,
For example:
yC =
Sy = Ai zi
zC =
Ai zi Ai
A1 y1 + A2 y2 A1 + A2
O
z
1• zi
y
2 y• i • • Ci n
z
y2 y1
1•
•
2•
y
z1 yC zC
z2
4. Moment of inertia of the area
Iz = A y2 dA , Iy = A z2 dA the moment of inertia of area to z and y.
M
Solution:
max = (M/2)/[b(h/2)2/6] = 12M/(bh2) EI = 2E[b(h/2)3/12] = Ebh3/48
For whole beam: w,max = 6M/ bh2 EIw = Ebh3/12
max /w,max = 2 stress
EI / EIw= 0.25 rigidity
Wz = d4/64/(d/2) = d3/32 (3) For the tubular section:
Wz = D3 (1- 4) / 32
Problems of Chapter 5 :
5 . 4 (b) 5.7
Problem 5.1
Know: a and section T shown in the Fig.
2. Maximum normal stresses in bending: Sections ? Points ?
max
5.3 Shearing stresses in bending
b
1. For the rectangular section:
Assumption: all shearing stresses are parallel to shearing force and uniformly distributed across the width of the section.
From the Table 3, we get: Ix : Sx = 17.2 cm, d = 7 mm
FSSz()max
50103
max =
Iz
=
= 41.5 MPa
17.210-2710-3
Average shearing stress of web is:
m = FS / h = 50103 / [(200-211.4)7] = 40.3 MPa e = 2.87 %
z
A
b
C• a zC
yC dA
zC
yC
1•
• • 2
y
z1
z z2
5.2 Normal stresses in bending
dx
1. Geometrical relation
M
M
Hypothesis of plane section
aa
(+y)d -d y
= d
=
(a)
M
d
M
2. Physical relation
y
= E =E
(b)
3. Statical relation
FN = A dA = 0
(c)
y a
a
Neutral layer
dx
Mz = A ( dA) y = M
(d)
From (b), (c), A y dA = Sz = 0
Neutral axis z must be centroidal axis.
FSSz()max
max =
Iz
z
h0 h
max
y
y
From the Table 3 in the page 351, we
can look up Ix : Sx and calculate max .
For example: calculate max of No. 20a steel I beam, if FS = 50kN.
a
Find: yC and Iz
4a
Solution:
1. Find yC
A1 = 3a2 , y1 = a / 2 ;
A2 = 3a2 , y2 = 5a / 2
yC = (A1 y1 + A2 y2) / (A1+A2) = 3a / 2 2. Find Iz
Iz1 = 3a a3/12 + 3a2 (3a/2 - a/2)2 = 13a4/4
uniformly across the width).
z
max
Limitation about the theory :
h / b 1.5
error 5 %
yy
2. For - shaped section:
b
For the web of I beam, (5.10) can be used: why ?
Chapter 5 Stresses in Bending
Contents:
1. Geometrical properties of plane areas 2. Normal stresses in bending 3. Shearing stresses in bending 4. Strength of beams 5. Principal moment of inertia 6. Unsymmetrical bending 7. Shear center
a,max = 6Fl /a3 b,max = 62Fl /a3 The strength of (a) is bigger.
Problem 5.4
Know: h, b, M, E
Find: max , EI . And compare
with that of the whole beam.
M
h h/2
3 FS 2bh
(1
-
4y2 h2 )
max =
3FS 2bh
=
3 FS 2A
(5.11) (5.12)
Analysis of error :
when h / b 2 , error 1 %
b
when h / b = 1 , error 10 %
Why ? Assumption about (distributed h FS
O
Iy = Iyc + a2 A Iz = Izc + b2 A
( 5.9a) ( 5.9b)
(2) For the composite area:
y
Iz(1) = Iz1 + y12 A1
Iz(2) = Iz2 + y22 A2
y1
Iz = Iz(1) + Iz(2)
y2
= Iz1 + y12 A1 + Iz2 + y22A2
Ip = A 2dA = A(y2 + z2)dA = Iz + Iy
(1) For the rectangular section: Iz = A y2 dA = -hh//22 y2bdy = bh3/12 Similarly, Iy = hb3/12
(2) For the circular section: From Iy = Iz , we get: Iy = Iz = Ip / 2 = d 4/64
Iz2 = a (3a)3/12 + 3a2 (5a/2 - 3a/2)2 = 21a4/4
Iz = Iz1 + Iz2 = 17a4 / 2
3a
1
yC
z 2
a y
Problem 5.2
Plot the distribution of bending normal stresses in following cross sections. If the positive moments act on the beams.
c,max= Fl y1/Iz = 150001.2(0.14-0.045)/(8.8410-6) = 193.4 MPa t,max= Fl yC /Iz= 150001.2 0.045/(8.8410-6) = 91.6 MPa
3. Maximum shearing stresses in bending:
Example 5.1
F
Know: F = 15 kN, l = 1.2 m
Find: t,max , c,max , max
Solution:
l
1. Centroid and moment of inertia:
120 z1
20
yC
120
20 y1z
y
yC = [(0.120.02)0.01+(0.020.12)(0.02+0.06)]/(20.120.02) = 0.045m
(3) For the tubular section:
Iy = Iz = D4(1- 4)/64 where = d / D .
O
z
y
z dA y
b
h
Cz y
dy y
D dd
zz C
yy
5. Moment of inertia for the composite area
(1) Parallel axis theorem:
,
For example:
yC =
Sy = Ai zi
zC =
Ai zi Ai
A1 y1 + A2 y2 A1 + A2
O
z
1• zi
y
2 y• i • • Ci n
z
y2 y1
1•
•
2•
y
z1 yC zC
z2
4. Moment of inertia of the area
Iz = A y2 dA , Iy = A z2 dA the moment of inertia of area to z and y.
M
Solution:
max = (M/2)/[b(h/2)2/6] = 12M/(bh2) EI = 2E[b(h/2)3/12] = Ebh3/48
For whole beam: w,max = 6M/ bh2 EIw = Ebh3/12
max /w,max = 2 stress
EI / EIw= 0.25 rigidity
Wz = d4/64/(d/2) = d3/32 (3) For the tubular section:
Wz = D3 (1- 4) / 32
Problems of Chapter 5 :
5 . 4 (b) 5.7
Problem 5.1
Know: a and section T shown in the Fig.