人教A版必修第二册《8.3 简单几何体的表面积与体积》练习卷(2)
高中数学人教A版(2019)必修 第二册第八章 立体几何初步8.3简单几何体的表面积与体积

必修第二册 8.3 简单几何体的表面积与体积一、单选题1.如图,位于贵州黔南的“中国天眼”是具有我国自主知识产权、世界最大单口径、最灵敏的球面射电望远镜,其反射面的形状为球冠,球冠是球面被平面所截后剩下的曲面,截得的圆为球冠的底,与截面垂直的球体直径被截得的部分为球冠的高,设球冠所在球的半径为R ,球冠底的半径为r ,球冠的高为h ,球冠底面圆的周长为C .已知球冠的表面积公式为2S Rh π=,若65000,500S C ππ==,则球冠所在球的表面积为( )A .1620000πB .1690000πC .1720000πD .1790000π 2.已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)813.已知ABC O 的球面上,若球O 的体积为32π3,则O 到平面ABC 的距离为( )AB .32C .1D 4.已知A ,B 是球O 的球面上两点,90AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .128πD .144π5.如图,在棱长为a 的正方体1111ABCD A B C D -中,P 在线段1BD 上,且12BP PD =,M 为线段11B C 上的动点,则三棱锥M PBC -的体积为( )A .319aB .332aC .313aD .与点M 的位置有关6.已知正四棱锥P ABCD -的所有顶点都在球O 的球面上,且正四棱锥P ABCD -的底面面积为6,侧面积为,则球O 的表面积为( )A .323πBC .16πD .32π 7.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )AB C D 8.黄金分割是指将整体一分为二,较大部分与整体的比值等于较小部分与较大部分的,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金分割比,且它们的夹角的余弦值为黄金分割比值,那么这个三角形一定是直角三角形,这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,以短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,所得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以四棱锥的高为边长的正方形面积与该四棱锥的侧面积之比为( )A B C .1 D .149.阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径.若该球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π 10.平行四边形ABCD 中,AB BD ⊥,且2224AB BD +=,沿BD 将四边形折起成平面ABD ⊥平面BDC ,则三棱锥A BCD -外接球的表面积为( )A .2πB .2πC .4πD .16π 11.已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )A .122ππ+B .144ππ+C .12ππ+ D .142ππ+ 12.已知正四棱锥的底面边长和侧棱长均为2,则该正四棱锥的体积为( )A B .C D .二、填空题13.已知圆锥的侧面积(单位:2cm ) 为2π,且它的侧面积展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.14.一个正四棱锥的顶点都在同一球面上,若该棱锥的高为2,底面边长为2,则该球的表面积为______.15.已知圆柱的轴截面(经过圆柱的轴的截面)是一个边长为2的正方形,则此圆柱的体积为________.16.若球的大圆的面积为9π,则该球的体积为________17.若五棱台11111ABCDE A B C D E -的表面积是30,侧面积是25,则两底面面积的和为______.三、解答题18.圆台的母线长为2a ,母线与轴的夹角为30,一个底面的半径是另一个底面的半径的2倍,求两底面的半径及两底面面积之和.19.将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体,O 为11A C 的中点.(1)求证://OB 平面1ACD ;(2)求几何体111ACB A D 的体积.20.如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终在桌面上,设直径AB 所在直线与桌面所成的角为α.(1)求图①中圆柱的母线与液面所在平面所成的角(用α表示);(2)要使倾斜后容器内的溶液不会溢出,求α的最大值.21.“圆锥的两条母线所作的一切截面中,以轴截面的面积最大”是否成立?答案第1页,共1页 参考答案:1.B2.D3.C4.D5.A6.C7.C8.D9.C10.C11.A12.A13.114.9π15.2π16.36π17.518.圆台上底面半径为a ,下底面半径为2a ,两底面面积之和为25a π. 19.(1)见解析;(2)4.20.(1)2πα-;(2)45°﹒21.答案见解析。
必修第二册 8.3.2 圆柱、圆锥、圆台、球的表面积和体积 习题 (新人教A版)

课时2 圆柱、圆锥、圆台、球的表面积和体积(35分钟 100分)基础 达标 了解旋转体的体积和表面积公式,并能进行简单的计算,解决球的组合体及三视图中球的有关问题 素养突破培养学生数学运算和直观想象素养1.简单组合体有两种基本形式:一种是由简单几何体拼接而成的;另一种是由简单几何体截去或挖去一部分而成的.明确组合体的结构特征,主要弄清它是由哪些简单几何体组成的.2.在处理与球有关的相接、相切问题时,一般要通过作一适当的截面,将立体问题转化为平面问题解决,而这类截面往往指的是轴截面(球的大圆)等.几个常用结论(1)球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径; (2)球外接于长方体,长方体的顶点均在球面上,长方体的对角线长等于球的直径;(3)球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径;(4)球与棱锥相切,则可利用V 棱锥=13S 底h=13S 棱锥表R ,R 为球的半径.题组一 几何体的表面积和侧面积1.(7分)某圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小的底面的半径为 ( )A .7B .6C .5D .32.(7分)一个几何体的三视图如图所示,则此几何体的表面积S= ( )A .32+πB .32+2πC .28+2πD .28+π3.(7分)如图,已知平行于圆柱轴的截面ABB 1A 1是正方形,面积为12,它与轴的距离是底面半径的一半,则圆柱的底面半径为 .4.(15分)圆锥的高为h,底面半径为r,过两条母线作一截面,截得底面圆弧的14,求该截面的面积.题组二几何体的体积5.(7分)若分别以一个锐角为30°的直角三角形的最短直角边、较长直角边、斜边所在的直线为轴旋转一周,则所形成的几何体的体积之比是()A.1∶√2∶√3B.6∶2√3∶√3C.6∶2√3∶3D.3∶2√3∶66.(7分)某几何体的三视图如图所示,则其体积为()A.3π4B.π+24C.π+12D.3π+247.(7分)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是寸(注:①平地降雨量等于盆中积水体积除以盆口面积;②1尺=10寸).题组三与球有关的切、接问题8.(7分)若球O的表面积为S1,它的内接正方体的表面积为S2,则S1S2=()A.π3B.π4C.π2D.π9.(7分)一平面截一球得到直径为2√5cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是()A.12π cm3B.36π cm3C.64√6π cm3D.108π cm310.(7分)设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为()πa2A.πa2B.73πa2D.5πa2C.11311.(7分)已知各顶点都在一个球面上的正四棱锥的高为3,体积为6,则这个球的半径为()A.2B.√5C.√6D.312.(15分)轴截面是正三角形的圆锥内有一个内切球,若圆锥的底面半径为1 cm,求球的体积.课时2 圆柱、圆锥、圆台、球的表面积和体积1.A 解析:本题考查圆台的侧面积.设圆台较小底面半径为r ,则另一底面半径为3r.由S=π(r+3r )·3=84π,解得r=7.2.A 解析:本题考查三视图与几何体的表面积.由三视图可知,此几何体的上半部分为半个球,下半部分是一个长方体,故其表面积S=4π×12+4×2×3+2×2+2×2-π=32+π.3.2 解析:本题考查圆柱的截面问题.∵正方形ABB 1A 1的面积为12,∴AA 1=AB=2√3, 设圆柱的底面半径为r ,则AB=2√r 2-(r2)2=2√3,解得r=2.4.解析:本题考查圆锥截面面积的求法.∵圆锥的高为h ,底面半径为r ,且过两条母线作一截面,截得底面圆弧的14, ∴∠AOB=π2,∴AB=√2r ;过点O 作OM ⊥AB 于点M ,连接PM ,∴PM ⊥AB , 在Rt △POM 中,OM=√22r ,∴PM=√ℎ2+(√22r )2, ∴截面△P AB 的面积为S=12AB ·PM=12×√2r×√ℎ2+(√22r )2=r√2ℎ2+r 22.5.C 解析:本题考查圆锥的体积.设Rt △ABC 中,∠BAC=30°,BC=1,则AB=2,AC=√3,求得斜边上的高CD=√32,旋转所得几何体的体积分别为V 1=13π(√3)2×1=π,V 2=13π×12×√3=√33π, V 3=13π(√32)2×2=12π,故V 1∶V 2∶V 3=1∶√33∶12=6∶2√3∶3.6.D 解析:本题考查三视图及几何体的体积.由几何体的三视图知,该几何体的一部分是以腰长为1的等腰直角三角形为底面,高为3的三棱锥,另一部分是底面半径为1,高为3的圆锥的四分之三.所以几何体的体积为13×3π4×3+13×12×1×1×3=3π4+12=3π+24,故选D 项.7.3 解析:本题考查数学史与几何体的体积.由题意知盆内所盛水的上底面直径为28+122=20寸,下底面半径为6寸,高为9寸,故体积为V=13×9×(π×102+π×62+π×10×6)=588π,又盆上口面积为π×142=196π.故平地降雨量为588π196π=3寸.8.C 解析:本题考查正方体的外接球问题.设球的内接正方体的棱长为a ,球的半径为R , 则3a 2=4R 2,所以a 2=43R 2,球的表面积S 1=4πR 2,正方体的表面积S 2=6a 2=6×43R 2=8R 2,所以S1S 2=π2.9.B 解析:本题考查球的截面问题.设球心为O ,截面圆心为O 1,连接OO 1,则OO 1垂直于截面圆O 1,如图所示.在Rt △OO 1A 中,O 1A=√5 cm,OO 1=2 cm,所以球的半径R=OA=√22+(√5)2=3 cm, 所以球的体积V=43×π×33=36π cm 3.10.B 解析:本题考查三棱柱的外接球问题.由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.如图,P 为三棱柱上底面的中心,O 为球心,易知AP=23×√32a=√33a ,OP=12a ,所以球的半径R=OA 满足R 2=(√33a )2+(12a )2=712a 2,故S 球=4πR 2=73πa 2.11.A 解析:本题考查四棱锥的外接球问题.设正四棱锥的底面边长为a , 由V=13a 2×3=a 2=6,得a=√6.由题意知球心在正四棱锥的高上,设球的半径为r ,则(3-r )2+(√3)2=r 2,解得r=2.12.解析:本题考查内切球问题.如右图所示,作出轴截面,O 是球心,与边BC ,AC 相切于点D ,E. 连接AD ,OE ,∵△ABC 是正三角形,∴CD=12AC.∵Rt △AOE ∽Rt △ACD ,∴OE AO =CDAC . ∵CD=1 cm,∴AC=2 cm,AD=√3 cm,设OE=r cm,则AO=(√3-r ) cm,∴√3-r =12,∴r=√33 cm,V 球=43π(√33)3=4√327π cm 3,即球的体积等于4√327π cm 3.。
高中数学必修二 8 3 2 圆柱、圆锥、圆台、球的表面积和体积 练习(含答案)

8.3.2 圆柱、圆锥、圆台、球的表面积和体积一、选择题1.若圆锥的高等于底面直径,则它的底面积与侧面积之比为A.1∶2B.1C.1D2【答案】C【解析】设圆锥底面半径为r,则高h=2r,∴其母线长l=r.∴S侧=πrl=πr2,S底=πr故选C.2.(2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.πB.3π4C.π2D.π4【答案】B 【解析】绘制圆柱的轴截面如图所示,由题意可得:11,2 AC AB==,结合勾股定理,底面半径2r==,由圆柱的体积公式,可得圆柱的体积是223ππ1π24V r h⎛⎫==⨯⨯=⎪⎪⎝⎭,故选B.3.圆柱的底面半径为1,母线长为2,则它的侧面积为()A.2πB.3πC.πD.4π【答案】D【解析】圆柱的底面半径为r=1,母线长为l=2,则它的侧面积为S侧=2πrl=2π×1×2=4π.故选:D.4.圆台的上、下底面半径和高的比为1:4:4,母线长为10,则圆台的侧面积为().A.81πB.100πC.14πD.169π【答案】B【解析】设圆台上底半径为r,则其下底半径为4r,高为4r,结合母线长10,可求出r=2.然后由圆台侧面积公式得,.5.(多选题)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是()A.圆柱的侧面积为22RπB.圆锥的侧面积为22RπC.圆柱的侧面积与球面面积相等D.圆柱、圆锥、球的体积之比为3:1:2【答案】CD【解析】依题意得球的半径为R,则圆柱的侧面积为2224R R Rππ⨯=,∴A错误;圆锥的侧面积为2R Rπ=,∴B错误;球面面积为24Rπ,∵圆柱的侧面积为24Rπ,∴C正确;2322V R R Rππ=⋅=圆柱,2312233V R R Rππ⋅==圆锥,343V R=π球33324:2::3:1:233:V V V R R Rπππ∴==圆柱圆锥球,∴D正确.故选:CD.6.(多选题)如图所示,ABC 的三边长分别是3AC =,4BC =,5AB =,过点C 作CD AB ⊥,垂足为D .下列说法正确的是( )A .以BC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为15πB .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为36πC .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为25πD .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为16π【答案】AD【解析】以BC 所在直线为轴旋转时,所得旋转体为底面半径为3,母线长为5,高为4的圆锥 ∴侧面积为3515ππ⨯⨯=,体积为2134123ππ⨯⨯⨯=,∴A 正确,B 错误;以AC 所在直线为轴旋转时,所得旋转体为底面半径为4,母线长为5,高为3的圆锥侧面积为4520ππ⨯⨯=,体积为2143163ππ⨯⨯⨯=,∴C 错误,D 正确.故选:AD .二、填空题7. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为____. 【答案】92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=.8.如图,若球O 的半径为5,一个内接圆台的两底面半径分别为3和4(球心O 在圆台的两底面之间),则圆台的体积为______.【答案】259π3【解析】解:作经过球心的截面(如图),由题意得13O A =,24O B =,5OA OB ==,则14OO =,23OO =,127O O =,所以()22π259347π33V ⨯⨯==.9.已知圆柱的上、下底面的中心分别为12,O O ,过直线12O O 的平面截该圆柱所得的截面是面积为4的正方形,则该圆柱的表面积为_______.【答案】6π【解析】由题意,圆柱的截面是面积为4的正方形,可得其边长为2,可得圆柱的底面半径为1r =,母线2l =,所以该圆柱的表面积为221222212216S S S rl r πππππ=+=+=⨯⨯+⨯=。
8.3.2 圆柱、圆锥、圆台、球的表面积和体积-学年人教A版(2019)高中数学必修第二册练习

圆柱、圆锥、圆台、球的表面积和体积练习一、单选题1.已知各顶点都在一个球面上的正四棱锥的高为3,体积为6,则这个球的表面积为()A. 16πB. 20πC. 24πD. 32π2.已知正方体、等边圆柱(轴截面是正方形)、球的体积相等,它们的表面积分别为S正,S柱,S球,则下列不正确的是()A. S正<S球<S柱B. S正<S柱<S球C. S球<S柱<S正D. S球<S正<S柱3.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为()A. 1B. 12C. √32D. 344.一个圆柱的底面直径与高都等于一个球的直径,则圆柱的全面积与球的表面积之比()A. 2:3B. 2:1C. 1:2D. 3:25.用与球心距离为1的平面去截球,截面面积为π,则球的体积为()A. 32π3B. 8π3C. 8√2πD. 8√2π36.祖暅是南北朝时代的伟大数学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为()A. ①②B. ①③C. ②④D. ①④7.已知某圆柱的底面周长为12,高为2,矩形ABCD是该圆柱的轴截面,则在此圆柱侧面上,从A到C的路径中,最短路径的长度为()A. 2√10B. 2√5C. 3D. 28.某几何体的三视图如图所示,其中俯视图中的半圆的直径为2,则该几何体的表面积为A. 3π+2B. 4π+2C. 3π+3D. 4π+39.如图是一个装有水的倒圆锥形杯子,杯子口径6cm,高8cm(不含杯脚),已知水的高度是4cm,现往杯子中放入一种直径为1cm的珍珠,该珍珠放入水中后直接沉入杯底,且体积不变.如果放完珍珠后水不溢出,则最多可以放入珍珠()A. 98颗B. 106颗C. 120颗D. 126颗10.若将气球的半径扩大到原来的2倍,则它的体积扩大到原来的()A. 2倍B. 4倍C. 8倍D. 16倍11.如图,在直三棱柱ABC−A1B1C1的侧面展开图中,B,C是线段AD的三等分点,且AD=3√3.若该三棱柱的外接球O的表面积为12π,则AA1=A. √2B. 2C. √5D. 2√212.将一个圆柱形钢锭切割成一个棱长为4的正方体零件,则所需圆柱形钢锭的表面积最小值为()A. 16πB. (16+16√2)πC. 16D. 16√2π二、单空题13.已知四棱锥P−ABCD的顶点都在球O的球面上,底面ABCD是边长为2的正方形,,则该球的体积为______.且PA⊥面ABCD,若四棱锥的体积为16314.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,则三棱锥D−ABC体积的最大值为.15.已知圆锥的母线长为2,高为√3,则该圆锥的外接球的表面积是______.16.将一钢球放入底面半径为3cm的圆柱形玻璃容器中,水面升高了4cm,则钢球的半径是________.三、解答题17.如图(1),在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2√2,AD=2,求四边形ABCD绕AD边所在的直线旋转一周所成几何体的表面积和体积.18.如图在底面半径为2,母线长为4的圆锥中内接一个高为√3的圆柱,求圆柱的表面积.19..某种儿童型防蚊液储存在一个容器中,该容器由两个半球和一个圆柱组成,(其中上半球是容器的盖子,防蚊液储存在下半球及圆柱中),容器轴截面如图所示,两头是半圆形,中间区域是矩形ABCD,其外周长为100毫米.防蚊液所占的体积为圆柱体积和一个半球体积之和.假设AD的长为2x毫米.(注:V k=43πR3,V柱=Sℎ,其中R为球半径,S为圆柱底面积,h为圆柱的高)(1)求容器中防蚊液的体积y关于x的函数关系式;(2)如何设计AD与AB的长度,使得y最大?答案和解析1.【答案】A【解答】解:正四棱锥的高为3,体积为6,∴底面积为6,正方形边长为√6,正方形的对角线为√(√6)2+(√6)2=2√3,设球的半径为R,则R2=(3−R)2+(√3)2,∴R=2,∴球的表面积为4πR2=4π×4=16π.2.【答案】C【解答】解:正方体的棱长为a,体积V=a3,S正=6a2=6√V23,等边圆柱(轴截面是正方形)的高为2h,体积V=π⋅ℎ2⋅2ℎ=2πℎ3,S柱=6πℎ2= 3√2πV23,球的半径为R,体积V=43πR3,S球=4πR2=√36πV23,∴S球<S柱<S正,3.【答案】D【解答】解:轴截面,圆柱为矩形,圆锥为三角形,且高相等,所以它们的底面圆的半径之比为圆柱:圆锥=1:2;所以圆柱与圆锥的底面积之比为1:4,所以圆柱与圆锥的体积之比为3:4,4.【答案】D【解答】解:设球的半径为R,则球的表面积S球=4πR2,所以圆柱的底面半径为R,高为2R,则圆柱的全面积S柱=2×πR2+2πR×2R=6πR2,则圆柱的全面积与球的表面积之比等于6πR2:4πR2=3:2.5.【答案】D【解答】解:设截面圆半径为r,截面面积为π,所以,又与球心距离d=1,所以球的半径R=√r2+d2=√2.,所以根据球的体积公式知V球=4πR33=8√2π3,6.【答案】D【解答】解:设截面与底面的距离为h,则①中截面内圆半径为h,则截面圆环的面积为π(R2−ℎ2);②中截面圆的半径为R−ℎ,则截面圆的面积为π(R−ℎ)2;③中截面圆的半径为R−ℎ2,则截面圆的面积为④中截面圆的半径为√R2−ℎ2,则截面圆的面积为π(R2−ℎ2),所以①④中截面的面积相等,故选D.7.【答案】A【解答】解:圆柱的侧面展开图如图,圆柱的侧面展开图是矩形,且矩形的长为12,宽为2,则在此圆柱侧面上从A到C的最短路径为线段AC,AC=√22+62=2√10.8.【答案】A【解析】【解答】 解:由三视图可知,这个几何体是由一个底面半径为1且高为1的半圆柱,和一个半径为1的半球的前半部分组成.所以它的下底面为半圆,面积为π2,后表面为一个矩形加半圆,面积为2×1+π2, 前表面为半个圆柱侧面加14个球面,面积为π×1×1+14×4π×1=2π. 所以其表面积为3π+2.9.【答案】D【解答】解:作出在轴截面图如图,由题意,OP =8,O 1P =4,OA =3, 设O 1A 1=x ,则48=x 3,即x =32.则最大放入珍珠的体积V =13π×32×8−13π×(32)2×4=21π,一颗珍珠的体积是43π×(12)3=π6.由21ππ6=126.∴最多可以放入珍珠126颗.10.【答案】C【解答】解:设气球原来的半径为r ,体积为V ,则V =43πr 3.当气球 的半径扩大到原来的2倍后,其体积变为43π(2r)3=8×43πr 3.11.【答案】D【解答】解:由展开图可知,直三棱柱ABC—A 1B 1C 1的底面是边长为√3的等边三角形,其外接圆的半径满足2r =√3sin60∘=2,所以r =1.由4πR 2=12π得R =√3.由球的性质可知,球心O到底面ABC的距离为d=√R2−r2=√2,结合球和直三棱柱的对称性可知,AA1=2d=2√2,12.【答案】B【解答】解:由题意,当正方体为圆柱的内接正方体时,圆柱表面积最小,所以圆柱的底面半径为正方体底面对角线的一半为2√2,圆柱高为正方体的棱长,所以圆柱的表面积最小值为.13.【答案】8√6π【解析】解:设此球半径为R,因底面ABCD是边长为2的正方形,且PA⊥面ABCD,若四棱锥的体积为163,则13×2×2×PA=163,∴PA=4,可以把四棱锥P−ABCD补成一个以ABCD为底、PA为侧棱的长方体,则这个长方体的外接球就是四棱锥P−ABCD的外接球,球心O就是PC的中点,∴(2R)2=PC2=AP2+AB2+AC2=42+22+22=24,∴R=√6,则该球的体积为4πR33=8√6π.14.【答案】18√3【解答】解:设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,∴12×AB2×sin60°=9√3,解得AB=6,球心为O,三角形ABC的外心为O′,显然D在O′O的延长线与球的交点如图:O′C=23×√32×6=2√3,OO′=√42−(2√3)2=2,则三棱锥D−ABC高的最大值为:6,则三棱锥D−ABC体积的最大值为:13×9√3×6=18√3.故答案为:18√3.15.【答案】163π【解析】解:∵圆锥的母线长为2,高为√3, ∴该圆锥的底面半径为r =√4−3=1, 由题意,圆锥轴截面的顶角为60°,设该圆锥的底面圆心为O′,球O 的半径为R , 由勾股定理可得R 2=(√3−R)2+12, 解得R =2√33, ∴球O 的表面积为4πR 2=4π×(2√33)2=163π.16.【答案】3 cm【解答】解:设钢球的半径为r ,则36π=43πr 3,解得r =3 cm .17.【答案】解:如图,∵∠ADC =135°,∴∠CDE =45°,又CD =2√2,∴DE =CE =2,又AB =5,AD =2, ∴BC =5.则圆台上底面半径r 1=2,下底面半径r 2=5,高ℎ=4,母线长l =5,圆锥底面半径r 1=2,高ℎ′=2.∴S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面=π×52+π×(2+5)×5+π×2×2√2 =(4√2+60)π;V =V 圆台−V 圆锥=13π(25+10+4)×4−13π×4×2=1483π.18.【答案】解:设圆柱的底面半径为r ,表面积为S ,则由三角形相似得r2=√16−4−√3√16−4,得r =1,∴S 底=2π,S 侧=2√3π, ∴S =2π+2√3π.19.【答案】解:(1)由2AB +2πx =100得AB =50−πx ,由AB >0得,x ∈(0,50π),所以防蚊液体积y =12×43πx 3+πx 2(50−πx)=(23π−π2)x 3+50πx 2,x ∈(0,50π);(2)求导得,令得x ⩽1003π−2;令得x ⩾1003π−2,所以y 在(0,1003π−2)上单调增,在(1003π−2,50π)上单调减, 所以当x =1003π−2时,y 有最大值, 此时AD =2x =2003π−2,AB =50π−1003π−2,答:当AD 为2003π−2毫米,AB 为50π−1003π−2毫米时,防蚊液的体积有最大值.。
高中数学人教A必修第二册精英同步卷:83简单几何体的表面积与体积 含答案
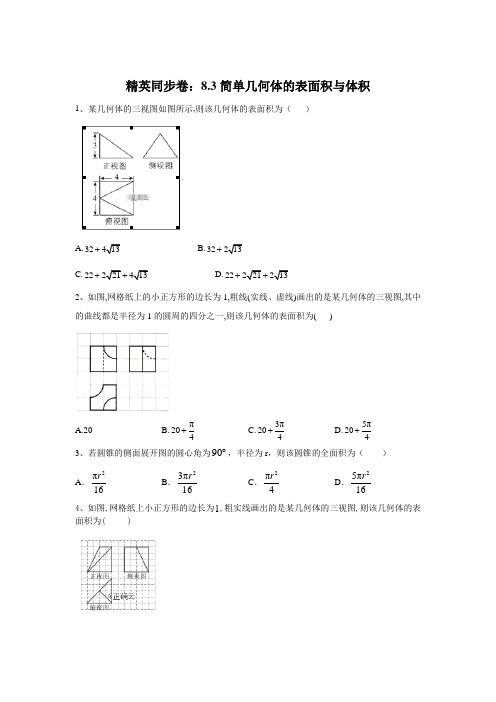
精英同步卷:8.3简单几何体的表面积与体积1、某几何体的三视图如图所示,则该几何体的表面积为()A.32413+ B.32213+C.22221413++ D.22221213++2、如图,网格纸上的小正方形的边长为1,粗线(实线、虚线)画出的是某几何体的三视图,其中的曲线都是半径为1的圆周的四分之一,则该几何体的表面积为( )A.20B.π204+ C.3π204+ D.5π204+3、若圆锥的侧面展开图的圆心角为90︒,半径为r,则该圆锥的全面积为()A.2π16rB.23π16rC.2π4rD.25π16r4、如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )A. 2843122++B. 3643122++C. 3642123++D. 44122+5、下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A. 20πB. 24πC. 28πD. 32π6、若某几何体的三视图(单位: cm )如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )A. 32cmB.33cmC. 333cmD. 33cm7、已知正三棱锥A BCD -的所有顶点都在球O 的球面上,3BC =.若球心O 在三棱锥的高AQ 的三等分点处,则球O 的半径为( )A .364B .2C .3D .48、已知正方体的体积是64,则其外接球的表面积是( ) A. 323π B. 192πC. 48πD.无法确定9、已知SC 是球 O 的直径, ,?A B 是球 O 球面上的两点,且1,3CA CB AB ==,若三棱锥S ABC -的体积为1,则球 O 的表面积为( ) A. 4π B. 13π C. 16π D. 52π10、某几何体的三视图如图2所示,则该几何体的表面积为( )A.16B.206π+C.142π+D.16π+11、如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是 。
人教版高中数学必修第二册8.3.1 棱柱、棱锥、棱台的表面积和体积 同步练习(含答案)

人教版高中数学必修第二册8.3.1棱柱、棱锥、棱台的表面积和体积同步练习一、选择题(本大题共8小题,每小题5分,共40分)1.棱长为3的正方体的表面积为()A.27B.64C.54D.362.已知高为3的三棱柱ABC-A1B1C1的底面是边长为1的正三角形(如图L8-3-1),则三棱锥B1-ABC的体积V=()图L8-3-1A.1B.12C D3.如图L8-3-2,长方体ABCD-A1B1C1D1的体积为V1,E为棱CC1上的点,且CE=13CC1,三棱锥E-BCD 的体积为V2,则 2 1=()图L8-3-2A.13B.16C.19D.1184.已知正四棱锥的底面边长为2,侧棱长为5,则该正四棱锥的体积为()A.43B.23C.43D5.已知正三棱柱的高为4,体积为43,则底面三角形的边长为()A.1B.2C.3D.46.如图L8-3-3,在正方体ABCD-A1B1C1D1中,正三棱锥D-A1BC1的表面积与正方体的表面积之比是()图L8-3-3.2B.3C.3D.27.如图L8-3-4,在三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,三棱锥P-ABC的体积为V2,则V1∶V2=()图L8-3-4A.1∶2B.1∶3C.1∶4D.1∶58.如图L8-3-5,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,水面恰好过AC,BC,A1C1,B1C1的中点,则当底面ABC水平放置时,水面的高为()图L8-3-5A.6B.7C.2D.4二、填空题(本大题共4小题,每小题5分,共20分)9.有一个正四棱台形的油槽,可以装油190L,假如它的两底面边长分别为60cm和40cm,则它的高为cm.10.已知正四棱柱的底面边长为22,体积为32,则此四棱柱的表面积为.11.已知正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别是AB,BC,CD,DA的中点,则四棱锥A1-EFGH的体积为.12.在三棱柱ABC-A1B1C1中,AB,AC,AA1两两成60°角,点E,F,G分别为AB,AC,AA1上的点,且AE=12AB,AF=13AC,AG=23AA1,则三棱锥G-AEF的体积与三棱柱ABC-A1B1C1的体积之比为.三、解答题(本大题共2小题,共20分)13.(10分)已知一个长方体共顶点的三个面的面积分别是2,3,6.(1)求这个长方体的体对角线长;(2)求这个长方体的体积.14.(10分)正四棱台ABCD-A1B1C1D1的上底面是边长为2的正方形,下底面是边长为4的正方形,侧棱长为2,侧面是全等的等腰梯形,求正四棱台的表面积.15.(5分)在《九章算术》中,堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图L8-3-6,在堑堵ABC-A1B1C1中,AC⊥BC,AA1=AB=2,则当阳马B-A1ACC1的体积最大时,堑堵ABC-A1B1C1的体积为.图L8-3-616.(15分)如图L8-3-7是一个以△A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2.(1)求该几何体的体积;(2)求截面ABC的面积.图L8-3-7参考答案与解析1.C[解析]所求表面积为6×32=54.2.D[解析]V=13×33.D[解析]由题意得,V1=S长方形ABCD·CC1,V2=13S△BCD·CE=13×12S长方形ABCD×13CC1=118S长方形ABCD·CC1,则 2 1=118.故选D.4.D[解析]由题知该正四棱锥底面的对角线的长度为22,故该正四棱锥的高h=5−2=3,所以其体积V=13×4×3=D.5.B[解析]设正三棱柱底面三角形的边长为a,则底面三角形的面积2,由正三棱柱的体积2×4=43,得a=2,故选B.6.B[解析]设正方体的棱长为1,则正方体的表面积为6,正三棱锥D-A1BC1的棱长均为2,其表面积为4×12×2sin60°×2=23,∴正三棱锥D-A1BC1的表面积与正方体的表面积之比B.7.C[解析]∵E是PC的中点,∴P,C到平面ABE的距离相等,∴V三棱锥P-ABE=V三棱锥C-ABE,又D是PB的中点,∴D到平面ABE的距离等于P到平面ABE的距离的12,∴V三棱锥D-ABE=12V三棱锥P-ABE=14V三棱锥P-ABC ,∴ 1 2= 三棱锥 - 三棱锥 - =14.故选C.8.A[解析]根据题意,当侧面AA1B1B水平放置时,有水的部分为四棱柱,其底面是梯形,设△ABC的面积为S,则S梯形=34S,水的体积V水=34S×A1A=6S.当底面ABC水平放置时,有水的部分为三棱柱,设水面的高为h,则V水=Sh=6S,故h=6,故选A.9.75[解析]设正四棱台的体积为V mL,上、下底面的面积分别为S'cm2,S cm2,高为h cm,则V=13(S+ '+S')h,即h=3×1900003600+2400+1600=75,故高为75cm.10.16+322[解析]设正四棱柱的高为h,则4,所以此四棱柱的表面积为4×4×22+2×22×22=322+16.11.43[解析]∵正方体ABCD-A1B1C1D1的棱长为2,E,F,G,H分别是AB,BC,CD,DA的中点,∴四边形EFGH是边长为2的正方形,又点A1到平面EFGH的距离d=AA1=2,∴四棱锥A1-EFGH的体积V=13×d×S正方形EFGH=13×2×2×2=43.12.127[解析]设三棱柱ABC-A1B1C1的高为H,三棱锥G-AEF的高为H',则三棱锥G-AEF的体积V=13×S△AEF×H'=13×S△AEF×23H.设△AEF的边AF上的高为h',则根据点E为AB的中点得,△ABC=12×AF×h'=12×13AC×h'=16AC×h',S△ABC=12×AC×2h'=AC×h',则三棱锥G 的边AC上的高为2h',所以S△AEF-AEF的体积V1=127AC×H×h',三棱柱ABC-A1B1C1的体积V2=AC×h'×H,故所求体积之比为127. 13.解:(1)设此长方体共顶点的三条棱的长分别为a,b,c,则ab=2,bc=3,ac=6,解得c=3,a=2,b=1.故这个长方体的体对角线长为(2)2+(3)2+12=6.(2)由(1)可知这个长方体的体积V=abc=6.14.解:∵正四棱台的上底面是边长为2的正方形,下底面是边长为4的正方形,∴上底面、下底面的面积分别是4,16.∵侧棱长为2,侧面是全等的等腰梯形,∴=3,∴一个侧面的面积为12×(2+4)×3=33,∴正四棱台的表面积为4+16+33×4=20+123.15.2[解析]设AC=x,BC=y,则由题意得x>0,y>0,x2+y2=4.阳马B-A1ACC1的体积V1=13×2x×y=23xy,∵xy≤ 2+ 22=2,当且仅当x=y=2时取等号,∴当阳马B-A1ACC1的体积最大时,AC=BC=2,此时堑堵ABC-A1B1C1的体积V2=S△ABC·AA1=12×2×2×2=2.16.解:(1)如图,过C作平行于△A1B1C1的截面A2B2C,分别交AA1,BB1于点A2,B2.由题知,该几何体的体积V=三棱柱 1 11- 2 2+ 四棱锥- 2 2=12×2×2×2+13×12×(1+2)×2×2=6.(2)在△ABC中,AB=22+(4−3)2=5,BC=22+(3−2)2=5,AC=(22)2+(4−2)2=23,则S=12×23×(5)2-(3)2=6.△ABC。
高中数学新教材必修第二册第八章 立体几何初步 8.3 简单几何体的表面积与体积(南开题库含详解)

第八章 立体几何初步 8.3 简单几何体的表面积与体积一、选择题(共40小题;共200分)1. 一个四面体的所有棱长都为 √2 ,四个顶点在同一球面上,则此球的表面积为 ( ) A. 3πB. 4πC. 3√3πD. 6π2. 有一个几何体的三视图及其尺寸如图(单位:cm ),该几何体的表面积和体积为 ( )A. 24π,12πB. 15π,12πC. 24π,36πD. 以上都不正确3. 已知下列三个命题:①若一个球的半径缩小到原来的 12,则其体积缩小到原来的 18; ②若两组数据的平均数相等,则它们的标准差也相等; ③直线 x +y +1=0 与圆 x 2+y 2=12 相切.其中真命题的序号是 ( ) A. ①②③B. ①②C. ①③D. ②③4. 如图,是一个几何体的三视图,其主视图、左视图是直角边长为 2 的等腰直角三角形,俯视图为边长为 2 的正方形,则此几何体的表面积为 ( )A. 8+4√2B. 8+4√3C. 6+6√2D. 8+2√2+2√35. 一个四棱锥的三视图如图所示,其侧视图是等边三角形.则该四棱锥的体积等于 ( )A. 8√3B. 16√3C. 24√3D. 48√36. 如图,在长方体ABCD−A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC,A1D1的两个平行截面将长方体分成三部分,其体积分别记为V1=V AEA1−DFD1,V2=V EBE1A1−FCF1D1,V3=V B1E1B−C1F1C.若V1:V2:V3=1:4:1,则截面A1EFD1的面积为( )A. 4√10B. 8√3C. 4√13D. 167. 一个几何体的三视图如图所示,则该几何体的体积(单位:cm3)为( )A. π+√33B. 2π+√33C. 2π+√3D. π+√38. 一个几何体的三视图如图所示,则该几何体的体积是( )A. 64B. 72C. 80D. 1129. 在△ABC中,AB=2,BC=1.5,∠ABC=120∘,若使该三角形绕直线BC旋转一周,则所形成的几何体的体积是( )A. 32π B. 52π C. 72π D. 92π10. 某空间几何体的三视图如图所示,则该几何体的表面积为( )A. 180B. 240C. 276D. 30011. 已知某四棱锥的三视图,如图所示.则此四棱锥的体积为( )A. 6B. 5C. 4D. 312. 正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是( )A. π3a B. π2a C. 2πa D. 3πa13. 一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )A. √3+√6B. √3+√5C. √2+√6D. √2+√514. 某几何体的三视图如图所示,则该几何体的体积为( )A. 8−2πB. 8−πC. 8−π2D. 8−π415. 直三棱柱ABC−A1B1C1的直观图及三视图如下图所示,D为AC的中点,则下列命题是假命题的是( )A. AB1∥平面BDC1B. A1C⊥平面BDC1C. 直三棱柱的体积V=4D. 直三棱柱的外接球的表面积为4π16. 如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A. 9πB. 10πC. 11πD. 12π17. 一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )A. 1+2π2πB. 1+4π4πC. 1+2ππD. 1+4π2π18. 一个几何体的三视图如图所示,则该几何体的体积是( )A. 23π+4 B. 2π+4 C. π+4 D. π+219. 在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A. 2π3B. 4π3C. 5π3D. 2π20. 如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE,△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )A. √23B. √33C. 43D. 3221. 小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )A. 16+8πB. 64+8πC. 64+8π3D. 16+8π322. 正三棱锥的底面边长为a,高为√66a,则此棱锥的侧面积为( )A. 34a2 B. 32a2 C. 3√34a2 D. 3√32a223. 已知正方形ABCD的边长为6,空间有一点M(不在平面ABCD内)满足∣MA∣+∣MB∣=10,则三棱锥A−BCM的体积的最大值是( )A. 48B. 36C. 30D. 2424. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A. 18B. 17C. 16D. 1525. 棱长为a的正方体中,连接相邻面的中心,以这些线段为棱的八面体的体积为( )A. a33B. a34C. a36D. a31226. 已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A. 2√23π B. 4√2π3C. 2√2πD. 4√2π27. 已知A,B是球O的球面上两点,∠AOB=90∘,C为该球面上的动点,若三棱锥O−ABC体积的最大值为36,则球O的表面积为( )A. 36πB. 64πC. 144πD. 256π28. 某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是( )A. 2B. 92C. 32D. 329. 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A. 500π3cm3 B. 866π3cm3 C. 1372π3cm3 D. 2048π3cm330. 一个棱锥三个侧面两两互相垂直,它们的面积分别为12cm2,8cm2,6cm2,那么这个三棱锥的体积为( )A. 8√2πB. 8√23C. 24√2D. 8√231. E,F分别是边长为1的正方形ABCD边BC,CD的中点,沿线AF,AE,EF折起来,则所围成的三棱锥的体积为( )A. 13B. 16C. 112D. 12432. 如图,三棱柱ABC−A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )A. 2:3B. 1:1C. 3:2D. 3:433. 正方体的全面积为a2,它的顶点都在同一个球面上,这个球的半径是( )A. √36a B. √24a C. √22a D. √32a34. 如图,△ABC为正三角形,AA1∥BB1∥CC1,CC1⊥底面△ABC,若BB1=2AA1=2,AB=CC1=3AA1,则多面体ABC−A1B1C1在平面A1ABB1上的投影的面积为( )A. 274B. 92C. 9D. 27235. 如图,已知直三棱柱ABC−A1B1C1,点P,Q分别在侧棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )A. 2:1B. 3:1C. 3:2D. 4:336. 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )A. 1B. 2C. 4D. 837. 如图所示,正方体ABCD−AʹBʹCʹDʹ的棱长为1,E,F分别是棱AAʹ,CCʹ的中点,过直线E F的平面分别与棱BBʹ,DDʹ交于M,N,设BM=x,x∈[0,1],给出以下四个命题:①平面MENF⊥平面BDDʹBʹ;②当且仅当x=12时,四边形MENF的面积最小;③四边形MENF周长L=f(x),x∈[0,1]是单调函数;④四棱锥Cʹ−MENF的体积V=ℎ(x)为常函数.以上命题中假命题的序号为( )A. ①④B. ②C. ③D. ③④38. 如图,正方体ABCD−A1B1C1D1的棱长为1,线段AC1上有两个动点E,F,且EF=√33.给出下列四个结论:①CE⊥BD;②三棱锥E−BCF的体积为定值;③△BEF在底面ABCD内的正投影是面积为定值的三角形;④在平面ABCD内存在无数条与平面DEA1平行的直线.其中,正确结论的个数是( )A. 1B. 2C. 3D. 439. 已知正方体ABCD−A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P−ABC的体积为( )A. 124B. 118C. 19D. 11240. 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )A. √5+3√3π2+3π2+1 B. 2√5+3√3π+3π2+1C. √5+3√3π2+3π2D. √5+3√3π2+π2+1二、填空题(共40小题;共200分)41. 已知某球体的体积与其表面积的数值相等,则此球体的半径为.42. 若一个球的体积为4√3π,则它的表面积为.43. 一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为.44. 一个正方体的各顶点均在同一球的球面上,若该球的体积为4√3π,则该正方体的表面积为.45. 某几何体的三视图如图所示,则该几何体的体积是.46. 已知某几何体的三视图如图所示,则该几何体的体积为.47. 一个几何体的三视图如图所示,则该几何体的体积为.48. 已知一个正方体的所有顶点在一个球面上,若球的体积为9π,则正方体的棱长为.249. 如图是一个几何体的三视图.若它的体积是3√3,则a=.50. 某空间几何体的三视图如图所示,则该几何体的体积为.51. 用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积是.52. 用一张长为12米,宽为8米的矩形铁皮围成圆柱的侧面,则这个圆柱的体积为.53. 有一个几何体的三视图及其尺寸(单位cm)如下图所示,则该几何体的表面积为:.54. 一个几何体的三视图如图所示(单位:m),则这个几何体的体积为m3.55. 底面是正方形,容积为256的无盖水箱,它的高为时最省材料.56. 某几何体的三视图如图所示,则该几何体的体积为.57. 一个几何体的三视图如图所示(单位:cm),则该几何体的体积为cm3.58. 已知一个四棱锥的三视图如图所示,则此四棱锥的体积为.59. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.60. 某几何体的三视图如图所示,则该几何体的体积为.61. 一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.62. 几何体的三视图如图所示,其侧视图是一个等边三角形,则这个几何体的体积是.63. 一空间几何体的三视图如图所示,则该几何体的体积为.64. 用半径为6的半圆形铁皮卷成一个圆锥的侧面,则此圆锥的体积为.65. 已知一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.66. 如图是一个几何体的三视图,则这个几何体的体积为.,则正视图与侧视图中x的值67. 一空间几何体的三视图如右图所示,该几何体的体积为12π+8√53为.68. 如图是—个几何体的三视图,则该几何体的表面积为.69. 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为.70. 如图所示,一款冰淇淋甜筒的三视图中俯视图是以3为半径的圆,则该甜筒的表面积为.71. ―个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.72. 正方体ABCD−A1B1C1D1的棱长为2√3,则四面体A−B1CD1的外接球的体积为.73. 已知正方体ABCD−A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M−EFGH的体积为.74. 如图,已知正方体ABCD−A1B1C1D1的棱长为1,则四棱锥A1−BB1D1D的体积为.75. 已知某三棱锥的三视图如图所示,则它的外接球体积为.76. 如图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:cm)可知该几何体的表面积为.77. 图中的三个直角三角形是一个体积为20cm3的几何体的三视图,该几何体的外接球表面积为cm278. 一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.79. 一个圆锥体被过其顶点的平面截去一部分,余下的几何体的三视图如图所示(单位:cm),则余下的几何体的体积为cm3.80. 棱长为1的正四面体内有一点P,由点P向各面引垂线,垂线段长度分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为.三、解答题(共20小题;共260分)81. 如图,长方体ABCD−A1B1C1D1中AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由);(2)求平面α把该长方体分成的两部分体积的比值.82. 三棱锥S−ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,求四棱锥S−BCED的体积.83. 在单位正方体AC1中,点E,F分别是棱BC,CD的中点.(1)求证:D1E⊥平面AB1F;(2)求三棱锥E−AB1F的体积;(3)设直线B1E,B1D1与平面AB1F所成的角分别为α,β,求cos(α+β)的值.84. 如图,三棱锥S−ABC内接于一个圆锥(有公共顶点和底面,侧棱与圆锥母线重合).已知AB=5cm,BC=3cm,AC=4cm,SA=SB=SC=10cm,(1)求圆锥的侧面积及侧面展开图的中心角;(2)求A经过圆锥的侧面到B点的最短距离.85. 如图,四棱锥P−ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且AMMD =PNNC=4.(1)求证:MN∥平面PAB;(2)求三棱锥P−AMN的体积.86. 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45∘,AB=2AD=2,∠BAD=60∘.(1)求证:BD⊥平面ADG;(2)求此多面体的全面积.87. 养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12(m),高4(m),养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4(m)(高不变);二是高度增加4(m)(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?88. 如图,ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC,Eʹ和Fʹ是平面ABCD内的两点,EʹE和FʹF都与平面ABCD垂直.(1)证明:直线EʹFʹ垂直且平分线段AD.(2)若∠EAD=∠EAB=60∘,EF=2,求多面体ABCDEF的体积.89. 如图,三棱锥A−BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A−MBC的体积.90. 如图,四棱锥 P −ABCD 中,底面是以 O 为中心的菱形,PO ⊥ 底面 ABCD ,AB =2,∠BAD =π3,M 为 BC 上一点,且 BM =12.(1)证明:BC ⊥ 平面 POM ; (2)若 MP ⊥AP ,求四棱锥 P −ABMO 的体积.91. 如图,平行四边形 ABCD 中,∠DAB =60∘,AB =2,AD =4,将 △CBD 沿 BD 折起到 △EBD的位置,使平面 EBD ⊥ 平面 ABD .(1)求证:AB ⊥DE ; (2)求三棱锥 E −ABD 的侧面积.92. 养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为 12 m ,高 4 m .养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大 4 m (高不变);二是高度增加 4 m (底面直径不变). (1)分别计算按这两种方案所建的仓库的体积; (2)分别计算按这两种方案所建的仓库的侧面积; (3)哪个方案更经济些?93. 如图所示,三棱柱 ABC −A 1B 1C 1 中,AA 1⊥平面ABC ,D ,E 分别为 A 1B 1,AA 1 的中点,点 F在棱 AB 上,且 AF =14AB .(1)求证:EF ∥平面BC 1D ;(2)在棱 AC 上是否存在一个点 G ,使得平面 EFG 将三棱柱分割成的两部分体积之比为 1:15,若存在,指出点 G 的位置;若不存在,请说明理由.94. 如图,四棱锥P−ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB;(2)求四面体N−BCM的体积.95. 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;,求该三棱锥的侧面积.(2)若∠ABC=120∘,AE⊥EC,三棱锥E−ACD的体积为√6396. 如图,在斜三棱柱ABC−A1B1C1中,∠A1AB=∠A1AC,AB=AC,A1A=A1B=a,侧面B1BCC1与底面ABC所成的二面角为120∘,E、F分别是棱B1C1、A1A的中点.(1)求A1A与底面ABC所成的角;(2)证明A1E∥平面B1FC;(3)求经过A1、A、B、C四点的球的体积.97. 如图1,∠ACB=45∘,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90∘(如图2所示).(1)当BD的长为多少时,三棱锥A−BCD的体积最大;(2)当三棱锥A−BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小.98. 如图,四棱锥P−ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D−AE−C为60∘,AP=1,AD=√3,求三棱锥E−ACD的体积.99. 如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.(1)证明:BD⊥PC;(2)若AD=4,BC=2,直线PD与平面PAC所成的角为30∘,求四棱锥P−ABCD的体积.100. 如图,已知正方体ABCD−A1B1C1D1的棱长为3,M,N分别是棱AA1,AB上的点,且AM= AN=1.(1)证明:M,N,C,D1四点共面;(2)平面MNCD1将此正方体分为两部分,求这两部分的体积之比.答案第一部分1. A2. A3. C4. A 【解析】由三视图知,该几何体是底面为正方形的四棱锥,其直观图如下图.所以其表面积为2×2+2×(12×2×2)+2×(12×2×2√2)=8+4√2.5. A【解析】由三视图可以看出,该几何体为四棱锥,所以V=13×12(2+4)×4×2√3=8√3.6. C7. A8. C 【解析】该几何体是由一个正方体和一个四棱锥组合而成,V=4×4×4+13×4×4×3=80.9. A 【解析】如图:△ABC中,绕直线BC旋转一周,则所形成的几何体是以ACD为轴截面的圆锥中挖去了一个以ABD为轴截面的小圆锥后剩余的部分.因为AB=2,BC=1.5,∠ABC=120∘,所以AE=ABsin60∘=√3,BE=ABcos60∘=1,设V1是以ACD为轴截面的圆锥的体积,V2是以ABD为轴截面的圆锥的体积.V1=13π⋅AE2⋅CE=52π,V2=13π⋅AE2⋅BE=π,所以V=V1−V2=32π.10. B【解析】由三视图可知,该几何体是由一个四棱锥和一个正方体组成,所以表面积=4×12×6×5+ 5×62=240.11. C 【解析】V=13×12×(2+4)×2×2=412. B 【解析】设球的半径为R,则正方体的对角线长为2R,依题意知43R2=16a,即R2=18a,所以S球=4πR2=4π⋅18a=π2a.13. C 【解析】由三视图可得:该几何体是四棱锥(如图所示),所以BA=BC=√2,BP=1,PA=PC=√3,PD=√5,可得PA⊥AD;S△PBC=S△PBA=1 2×√2×1=√22,S△PDC=S△PDA=12×√2×√3=√62,所以该几何体的侧面积S=2S△PBC+2S△PDC=√2+√6.14. B 【解析】该几何体为一个棱长为2的正方体在两端各削去一个14圆柱,V=2×2×2−2×14×(π×12×2)=8−π.15. D16. D17. A18. C19. C 【解析】提示:分析知,围成的几何体为如图所示一个圆柱挖去一个圆锥.20. A【解析】提示:如图,作AM⊥EF于点M,BN⊥EF于点N,则可将原多面体分成一个直三棱柱和两个三棱锥,然后去求其体积.21. C 【解析】由三视图可知,该建筑物由一个圆锥、一个圆柱以及一个正方体拼接而成,故所求几何体的体积V=13×π×12×2+π×12×2+4×4×4=64+8π3.22. A 【解析】利用高、底面正三角形的边心距和斜高组成的直角三角形可得斜高为√(√66a)2+(13×√32a)2=12a,于是侧面积S=3×12×a×12a=34a2.23. D24. D25. C【解析】提示:算出一个正四棱锥的体积再乘2即可.26. B27. C 【解析】在三棱锥O−ABC中,底面OAB的面积确定,所以要使O−ABC的体积最大,则C到平面OAB的距离最大,即为球的半径.设球半径为R,则三棱锥O−ABC的体积V max=13×12×R2×R=36,解得R=6,此时球的表面积S=4πR2=144π.28. D29. A30. D31. D 【解析】设AF,AE,EF折起交于点P,因为AP⊥PF,AP⊥PE,所以AP⊥面PEF,所以V P−AEF=V A−PEF=13×1×12×12×12=124.32. B【解析】不妨设此三棱柱为正三棱柱,AB=1,AA1=2,则正三棱柱的体积V=√34×2=√32,V下面部分=13×√32×32=√34,所以V上面部分=√34,所以上下两部分的体积的比为1:133. B 【解析】由正方体外接球的直径2R等于正方体的体对角线的长,得2R=√3⋅√a26,所以R=√24a.34. A35. A【解析】设B到AC的距离为m,AC=x,棱柱的高为ℎ,可得V四棱锥B−ACQP =16xℎm,V三棱柱ABC−A1B1C1=12xℎm,V四棱锥B−ACQPV三棱柱ABC−A1B1C1=13,所以平面BPQ把三棱柱分成两部分的体积比为1:2.36. B 【解析】提示:此组合体是过圆柱对称轴的平面截圆柱所得的半个圆柱和一个半球组成的组合体.37. C 【解析】因为EF⊥BD,EF⊥面BDDʹBʹ,EF⊂面EMFN,所以平面MENF⊥平面BDDʹBʹ成立;又因为四边形EMFN为菱形,∣MN∣2=(1−2x)2+2,所以S MENF=12∣EF∣×∣MN∣=1 2×√2×√4x2−4x+3,当x=12时,面积最小,所以②成立;四边形MENF的周长L=f(x)=4√4x 2−4x +3,在 (0,12) 上是单调递减函数,在 (12,1) 上是单调递增函数,所以命题③不正确;V Cʹ−MENF =2V Cʹ−MNF =2V M−CʹNF =16,所以 V =ℎ(x ) 为常函数.38. D 【解析】因为在正方体 ABCD −A 1B 1C 1D 1 中,BD ⊥平面AA 1CC 1,CE ⊂平面AA 1CC 1,所以 BD ⊥CE ,①正确;EF =√33,而 C 到 EF 的距离即为 C 到 AC 1 的距离,所以 △EFC 面积为定值,又 B点到 平面EFC 的距离为定值,所以三棱锥 E −BCF 的体积为定值,②正确;因为 EF 为定值,且在体对角线 AC 1 上,所以 EF 在底面上的投影为定值,而点 B 到 AC 的距离为定值,所以 △BEF 在底面 ABCD 内的正投影是面积为定值的三角形,③正确;因为平面 ABCD 与平面 DEA 1 不重合,显然在平面 ABCD 内存在无数条与平面 DEA 1 平行的直线,④正确.39. B 【解析】设 AP =CP =a ,在 △PAC 中,利用余弦定理有 cos∠APC =a 2+a 2−22a 2=1−1a 2,又因为当 AP ⊥BD 1 时,AP 最小,当 P 与点 D 1 重合时最大,所以 a ∈[√63,√2],所以当 AP ⊥BD 1 时,∠APC 最大,在 △BDD 1 中,BP =√33,则 P 到面 ABC 的距离为 √33√3=13.所以 V P−ABC =12×1×1×13×13=118.40. A【解析】圆锥母线为 l =√(√5)2+1=√6,高为 ℎ=√(√5)2−1=2,圆锥底面半径为 r =√l 2−ℎ2=√2,截去的底面弧的圆心角为直角,截去的弧长是底面圆周的 14,圆锥侧面剩余 34,即为 S 1=34⋅π⋅rl =34π⋅√2×√6=3√32π,截面三角形的面积为 S 2=12×2×√5=√5,底面剩余部分为S 3=34πr 2+12×√2×√2=1+3π2,所以被截后该几何体的表面积为 S =3π2+3√3π2+√5+1.第二部分 41. 3 42. 12π【解析】提示:球的半径为 √3. 43. 14π 44. 24【解析】球的半径为 √3 ,则正方体的体对角线长为 2√3 ,从而正方体的棱长为 2 ,表面积为 6×22=24 . 45. 16π−16 46. 12π【解析】提示:由三视图可知,该几何体是由左右两个相同的圆柱(底面圆半径为2,高为1)与中间一个圆柱(底面圆半径为1,高为4)组合而成.47. 12+π【解析】该几何体是一个长方体和一个圆柱的组合体.由三视图可知长方体的长、宽、高分别为4、3、1,圆柱的底面半径为1,高为1,故该组合体的体积为V=4×3×1+π×1×1=12+π.48. √349. √3【解析】三视图对应的空间几何体是以2为底、高为a的三角形作为底面,以3为高的卧放的一个三棱柱.50. 2π+2√3351. 9√3π52. 288πcm3或192πcm3.53. 24πcm2【解析】由三视图可知:该几何体是一个圆锥,其母线长是5cm,底面直径是6cm.所以该三棱锥的表面积S=π×32+12×6π×5=24πcm2.54. 6+π【解析】如图:该几何体为一个棱柱与一个圆锥的组合体.所以V=3×2×1+13π×12×3=6+π.55. 456. 108+3π【解析】由三视图可知,该几何体由两个长方体和一个圆柱组成.所以V=2×6×6×32+π×12×3=108+3π.57. 48【解析】由三视图可知,该几何体为四棱锥,所以V=13×62×4=48.58. 5359. 9π260. 13【解析】由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A−BCDE的高为1,四边形BCDE是边长为1的正方形,则V=13×1×1×1=13.61. 20π3【解析】三视图可得该几何体是组合体,上面是底面圆的半径为2m、高为2m的圆锥,下面是底面圆的半径为1m、高为4m的圆柱,所以该几何体的体积是13×4π×2+4π=20π3(m3).62. 8√3+4√3π3【解析】由三视图可知,该几何体是由半个圆锥和一个四棱锥组成,所以体积为12×13×π×22×2√3+13×3×4×2√3=8√3+4√33π.63. 16+8π【解析】由三视图可知,该几何体是由一个长方体和半个圆柱形成,所以体积为V=2×2×4+ 12π×22×4=16+8π.64. 9√3π【解析】如下图所示:PO=√62−32=3√3,所以体积为13⋅3√3⋅π⋅32=9√3π.65. 20π3【解析】该几何体的体积为π⋅4+13π⋅22⋅2=20π3m3.66. 3【解析】由三视图可知,该几何体为上面一个三棱柱,下方一个四棱柱.故V上=12×1×1×2=1,V下=2×1×1=2,所以V=1+2=3.67. 3【解析】由三视图可以看出,该几何体是由一个四棱锥和一个圆柱组成.体积为13×(2√2)2×√5+π×22x=12π+8√53,所以x=3.68. 9π【解析】由三视图可知,该几何体的侧面积为2π×1×3=6π,下底面面积为π×12=π,顶部为半个球的表面积12×4π×12=2π,所以该几何体的表面积为9π.69. 7π【解析】由三视图可知该几何体是由一个圆柱和半个球组成,所以表面积为π×12+2π×1×2+12×4π×12=7π.70. 33π【解析】上半部分为半个球,表面积为12×4πr2=18π.下半部分为圆锥,侧面积为12×2πr×母线=15π.所以表面积为33π.71. 18+9π【解析】由三视图可知,该几何体为两个相切的球上方加了一个长方体组成的组合体,所以其体积为V=3×6×1+2×43π×(32)3=18+9π(m3).72. 36π.73. 11274. 1375. 43π【解析】由俯视图可知,直角三角形的斜边中线等于斜边的一半,根据射影定理,球心为斜边中点,半径为1,所以球的体积为43πr3=43π.76. (18+2√3)cm2.77. 77π【解析】提示:依题意得20=13×12×5×6×ℎ,解出ℎ=4.可算出外接球半径为√772,所以外接球表面积为77π.78. 83π【解析】由三视图知该几何体由两个相同的圆锥和一个圆柱组成.其中,圆锥的底面半径和圆柱的底面半径均为1m,圆锥的高均为1m,圆柱的高为2m.因此该几何体的体积为V=2×13π×12×1+π×12×2=83πm3.79. 16π9+2√33【解析】由三视图可知,该几何体由23个圆锥和一个三棱锥组成,所以体积为23×13π×22×2+13×12×2√3×1×2=16π9+2√33.80. √63【解析】提示:设这个棱长为1的正四面体的四个顶点分别为A、B、C、D,可求得其高为ℎ=√63,设每个面面积为S,则V A−BCD =V P−ABC +V P−ACD +V P−ABD +V P−BCD ,所以13ℎS =13d 1S +13d 2S +13d 3S +13d 4S, 得 d 1+d 2+d 3+d 4=ℎ=√63. 第三部分81. (1) 交线围成的正方形 EHGF 如图.(2) 作 EM ⊥AB ,垂足为 M ,则 AM =A 1E =4,EB 1=12,EM =AA 1=8. 因为四边形 EHGF 为正方形,所以 EH =EF =BC =10. 于是 MH =√EH 2−EM 2=6,AH =10,HB =6.故 S 四边形A 1EHA =12×(4+10)×8=56,S 四边形EB 1BH =12×(12+6)×8=72. 因为长方体被平面 α 分为两个高为 10 的直棱柱,所以其体积的比值为 97(79 也正确). 82. ∵ D ,E 分别是 AB ,AC 中点, ∴ S △ADE =14S △ABC ,∴ V 三棱锥S−ADE =14V 三棱锥S−ABC ,∴ V 四棱锥S−BCED =V 三棱锥S−ABC −V 三棱锥S−ADE =34V 三棱锥S−ABC .∵ 三棱锥 S −ABC 的三条侧棱两两垂直,∴ V 三棱锥S−ABC =16⋅SA ⋅SB ⋅SC =16×5×4×3=10,∴ V 四棱锥S−BCED =34V 三棱锥S−ABC =34×10=152.83. (1) 因为点 E ,F 分别是棱 BC ,CD 的中点,所以AF ⊥DE又AF ⊥DD 1DE ∩DD 1=D}⇒AF ⊥面EDD 1⇒AF ⊥D 1E 又C 1D ∥B 1A C 1D ⊥面BCD 1}⇒D 1E ⊥B 1AB 1A ∩AF =A }}⇒D 1E ⊥面AB 1F.(2) V E−AB 1F =V B 1−AEF =13⋅1⋅38=18.(3) 由⑴可知:D 1E ⊥ 平面 AB 1F ,直线 B 1E ,B 1D 1 与平面 AB 1F 所成的角分别为 α,β,即 α+β=∠EB 1D 1,所以cos(α+β)=cos∠EB1D1=54+2−(14+1+1)2×√52×√2=√1010.84. (1)因为AB=5cm,BC=3cm,AC=4cm,所以∠ACB=90∘⇒AB为底面圆的直径⇒S侧=12⋅10⋅π⋅5=25π.圆锥的侧面展开图是一个扇形,设此扇形的中心角为θ,弧长为l,则l=10θ,所以2π×52=10θ,所以θ=π2.(2)沿着圆锥的侧棱SA展开,在展开图△ABS中,∠ASB=45∘,SA=SB=10,⇒AB2= SA2+SB2−2SA⋅SB⋅cos∠ASB⇒AB=10√2−√2.85. (1)在AC上取一点Q,使得AQQC=4,连接MQ,QN,则AMMD =AQQC=PNNC,所以QN∥AP,MQ∥CD,又CD∥AB,所以MQ∥AB.又因为AB⊂平面PAB,PA⊂平面PAB,MQ⊂平面MNQ,NQ⊂平面MNQ,所以平面PAB∥平面MNQ,又因为MN⊂平面MNQ,MN⊄平面PAB,所以MN∥平面PAB.(2)因为AB=3,BC=5,AC=4,所以AB⊥AC.过C作CH⊥AD,垂足为H,则CH=3×45=125,因为PA⊥平面ABCD,CH⊂平面ABCD,所以PA⊥CH,又CH⊥AD,PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,所以CH⊥平面PAD,因为PC=√PA2+AC2=√41,PNNC=4,所以N到平面PAD的距离ℎ=45CH=4825,所以V P−AMN=V N−PAM=13S△PAM⋅ℎ=13×12×5×4×4825=325.86. (1)在△BAD中,因为AB=2AD=2,∠BAD=60∘,所以由余弦定理可得BD=√3.AB2=AD2+BD2,所以AD⊥BD.又在直平行六面体中,GD⊥平面ABCD,BD⊂平面ABCD,所以GD⊥BD.又AD∩GD=D,所以BD⊥平面ADG.(2)由已知可得AG∥EF,AE∥GF,四边形AEFG是平行四边形.GD=AD=1,所以EF=AG=√2.EB=AB=2,所以GF=AE=2√2.过G作GM∥DC交CF于H,得FH=2,所以FC=3.过G作GM∥DB交BE于M,得GM=DB=√3,ME=1,所以GE=2.cos∠GAE=2×2√2×√2=34,所以sin∠GAE=√74.S AEFG=2×12×√2×2√2×√74=√7.该几何体的全面积S=√7+2×12×1×√3+12×1×1+12×2×2+12×(1+3)×2+12×(2+3)×1=√7+√3+9.87. (1)如果按方案一,仓库的底面直径变成16m,则仓库的体积V1=13Sℎ=13×π×(162)2×4=2563π(m3),如果按方案二,仓库的高变成8m,则仓库的体积V2=13Sℎ=13×π×(122)2×8=2883π(m3).(2)如果按方案一,仓库的底面直径变成16m,半径为8m.棱锥的母线长为l=√82+42=4√5,则仓库的表面积S1=π×8×4√5=32√5π(m2),如果按方案二,仓库的高变成8m.棱锥的母线长为l=√82+62=10,则仓库的表面积S2=π×6×10=60π(m2).(3)∵V2>V1,S2<S1,∴方案二比方案一更加经济.88. (1)因为EA=ED且EEʹ⊥平面ABCD,所以EʹD=EʹA,所以点Eʹ在线段AD的垂直平分线上,同理点Fʹ在线段BC的垂直平分线上.又ABCD是正方形,所以线段BC的垂直平分线也就是线段AD的垂直平分线即点EʹFʹ都居线段AD的垂直平分线上,所以直线E′F′垂直平分线段AD.(2)连接EB,EC,设AD中点为M,由题意知,AB=2,∠EAD=∠EAB=60∘,EF=2,所以ME=√3,BE=FC=2,则多面体ABCDEF可分割成正四棱锥E−ABCD和正四面体E−BCF两部分,在Rt△MEEʹ中,由于MEʹ=1,ME=√3,所以EEʹ=√2,所以V E−ABCD=13S正方形ABCD⋅EEʹ=13×4×√2=4√23.V E−BCF=V C−BEF=V C−BEA=V E−ABC=13S△ABC⋅EEʹ=13×12×4×√2=23√2,所以多面体ABCDEF的体积为V E−BCF+V E−ABCD=2√2.89. (1)在三棱锥A−BCD中,∵AB⊥平面BCD,又∵CD⊂平面BCD,∴AB⊥CD.又∵BD⊥CD,且BD∩AB=B,∴CD⊥平面ABD.(2)法一:由AB⊥平面BCD,得AB⊥BD,∵AB=BD=1,∴S△ABD=12.∵M是AD中点,∴S△ABM=12S△ABD=14.由(1)知,CD⊥平面ABD,∴三棱锥C−ABM的高ℎ=CD=1,因此三棱锥A−MBC的体积为V A−MBC=V C−ABM=13S△ABM⋅ℎ=112.法二:由AB⊥平面BCD知,平面ABD⊥平面BCD,又平面ABD∩平面BCD=BD,如图,过点M作MN⊥BD交BD于点N,则MN⊥平面BCD,且MN=12AB=12,又CD⊥BD,BD=CD=1,所以S△BCD=1 2 ,∴三棱锥A−MBC的体积V A−MBC=V A−BCD −V M−BCD =13AB ⋅S △BCD −13MN ⋅S △BCD=112.90. (1) 如图,因 ABCD 为菱形,O 为菱形中心,连接 OB ,则 AO ⊥OB ,因为 ∠BAD =π3,故OB =AB ⋅sin∠OAB =2sinπ6=1. 又因为 BM =12,且 ∠OBM =π3,在 △OBM 中OM 2=OB 2+BM 2−2OB ⋅BM ⋅cos∠OBM=12+(12)2−2×1×12×cos π3=34,所以OB 2=OM 2+BM 2,故 OM ⊥BM .又 PO ⊥ 底面 ABCD ,所以 PO ⊥BC ,从而 BC 与平面 POM 内两条相交直线 OM ,PO 都垂直, 所以 BC ⊥ 平面 POM .(2)由(1)可知,OA =AB ⋅cos∠OAB =2⋅cosπ6=√3, 设 PO =a ,由 PO ⊥ 底面 ABCD 知,△POA 为直角三角形,故PA 2=PO 2+OA 2=a 2+3,由 △POM 也是直角三角形,故PM 2=PO 2+OM 2=a 2+34,连接 AM ,在 △ABM 中,AM 2=AB 2+BM 2−2AB ⋅BM ⋅cos∠ABM=22+(12)2−2⋅2⋅12⋅cos 2π3=214,由已知MP⊥AP,故△APM为直角三角形,则PA2+PM2=AM2,即a2+3+a2+34=214,得a=√32,a=−√32(舍去),即PO=√32,此时S ABMO=S△AOB+S△OMB=12⋅AO⋅OB+12⋅BM⋅OM=12⋅√3⋅1+12⋅12⋅√32=5√3 8,所以四棱锥P−ABMO的体积V P−ABMO=13⋅S ABMO⋅PO=13⋅5√38⋅√32=5 16.91. (1)在△ABD中,因为AB=2,AD=4,∠DAB=60∘,所以BD=√AB2+AD2−2AB⋅ADcos∠DAB=2√3.所以AB2+BD2=AD2,所以AB⊥BD.又因为平面EBD⊥平面ABD.平面EBD∩平面ABD=BD,AB⊂平面ABD,所以AB⊥平面EBD.结合DE⊂平面EBD,可得AB⊥DE.(2)由(1)知AB⊥BD,因为CD∥AB,所以CD⊥BD,从而DE⊥BD.在Rt△DBE中,因为DB=2√3,DE=DC=AB=2,所以S△DBE=12DB⋅DE=2√3.又AB⊥平面EBD,BE⊂平面EBD,所以AB⊥BE.因为BE=BC=AD=4,所以S△ABE=12AB⋅BE=4.又DE⊥BD,平面EBD⊥平面ABD,故得到ED⊥平面ABD.而AD⊂平面ABD,所以ED⊥AD,因此S△ADE=12AD⋅DE=4.综上,三棱锥E−ABD的侧面积S=8+2√3.92. (1)如果按方案一,仓库的底面直径变成16m,则仓库的体积V1=13S⋅ℎ=13×π×(162)2×4=2563π(m3)如果按方案二,仓库的高变成8m,则仓库的体积V2=13S⋅ℎ=13×π×(122)2×8=2883π(m3)(2)如果按方案一,仓库的底面直径变成16m,半径为8m.圆锥的母线长为l1=√82+42=4√5(m),则仓库的侧面积S1=π×8×4√5=32√5π(m2);如果按方案二,仓库的高变成8m,圆锥的母线长为l2=√82+62=10(m),则仓库的侧面积S2=π×6×10=60π(m2).(3)因为V2>V1,S2<S1.所以方案二比方案一更加经济.93. (1)取AB的中点M,连接A1M.因为AF=14AB,所以F为AM的中点.。
高中数学8-3简单几何体的表体积第1课时柱体锥体台体的表面积与体积课后提能训练新人教A版必修第二册

第八章 8.3 第1课时A 级——基础过关练1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )A .4πB .3πC .2πD .π【答案】C【解析】底面圆半径为1,高为1,侧面积S =2πrh =2π×1×1=2π.故选C. 2.(2021年银川月考)已知正六棱柱的高为6,底面边长为4,则它的表面积为( ) A .48(3+3) B .48(3+23) C .24(6+2) D .144【答案】A【解析】由题意,知侧面积为6×6×4=144,两底面积之和为2×34×42×6=483,所以表面积S =48(3+3).3.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于( ) A .π B .2π C .4π D .8π【答案】B【解析】设圆柱的底面半径为r ,则圆柱的母线长为2r ,由题意得S 圆柱侧=2πr ×2r =4πr 2=4π,所以r =1,所以V 圆柱=πr 2×2r =2πr 3=2π.故选B.4.(2021年郑州模拟)如图,ABC -A ′B ′C ′是体积为1的三棱柱,则四棱锥C -AA ′B ′B 的体积是( )A .13B .12 C .23 D .34【答案】C【解析】∵V 三棱锥C -A ′B ′C ′=13V 三棱柱ABC -A ′B ′C ′=13,∴V 四棱锥C -AA ′B ′B =1-13=23.5.将一个正方体截去四个角后,得到一个四面体,这个四面体的体积是原正方体体积的( )A .23B .12 C .13 D .14【答案】C【解析】将正方体ABCD -A ′B ′C ′D ′截去四个角后得到一个四面体B -DA ′C ′.设正方体的棱长为a ,则V 三棱锥B -B ′A ′C ′=V 三棱锥A ′-ABD =V 三棱锥C ′-BCD =V 三棱锥D -A ′C ′D ′=13×12×a ×a ×a=a 36,∴四面体B -DA ′C ′的体积V =V 正方体ABCD -A ′B ′C ′D ′-4V 三棱锥B -B ′A ′C ′=a 3-2a 33=a33,∴这个四面体的体积是原正方体体积的13.故选C.6.表面积为3π的圆锥,它的侧面展开图是一个半圆面,则该圆锥的底面直径为________.【答案】2【解析】设圆锥的母线为l ,圆锥底面半径为r ,由题意可知,πrl +πr 2=3π,且πl =2πr ,解得r =1,即直径为2.7.已知棱长为1,各面均为等边三角形的四面体,则它的表面积是________,体积是________.【答案】 3212【解析】S 表=4×34×12=3,V 体=13×34×12×12-⎝ ⎛⎭⎪⎫332=212.8.圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为________.【答案】168π【解析】先画轴截面,再利用上、下底面半径和高的比求解.圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,则它的母线长为l =h 2+(R -r )2=(4r )2+(3r )2=5r =10,所以r =2,R =8.故S 侧=π(R +r )l =π(8+2)×10=100π,S 表=S 侧+πr 2+πR 2=100π+4π+64π=168π.9.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积. 解:设圆锥的底面半径为r ,母线为l , 则2πr =13πl ,得l =6r .又S 锥=πr 2+πr ·6r =7πr 2=15π,得r =157, 圆锥的高h =35×157, V =13πr 2h =13π×157×35×157=2537π. 10.在长方体ABCD -A 1B 1C 1D 1中,截下一个棱锥C -A 1DD 1,求棱锥C -A 1DD 1的体积与剩余部分的体积之比.解:已知长方体可以看成直四棱柱,设它的底面ADD 1A 1的面积为S ,高为h ,则它的体积为V =Sh .而棱锥C -A 1DD 1的底面积为12S ,高为h ,故三棱锥C -A 1DD 1的体积VC -A 1DD 1=13·⎝ ⎛⎭⎪⎫12S h =16Sh ,余下部分体积为Sh -16Sh =56Sh .所以棱锥C -A 1DD 1的体积与剩余部分的体积之比1∶5.B 级——能力提升练11.(2020年株洲期末)《九章算术》卷5《商功》记载一个问题“今有圆堡壔(d ǎo),周四丈八尺,高一丈-尺,文积几何?”意思是:今有圆柱形土筑小城堡,底面周长为4丈8尺,高1丈1尺,问它的体积是多少立方尺?这个问题的答案是(π≈3,1丈=10尺)( )A .2 112B .2 111C .4 224D .4 222【答案】A【解析】由已知,圆柱底面圆的周长为48尺,圆柱的高为11尺,∴底面半径r =482π=8(尺),∴它的体积V =11πr 2=2 112(立方尺).故选A.12.(2021年哈尔滨月考)鲁班锁起源于中国古代建筑的榫卯结构.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.图1是一个鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁玩具的表面积为( )A .8(6+62+3)B .6(8+82+3)C .8(6+63+2)D .6(8+83+2)【答案】A【解析】由题图,可知该鲁班锁玩具可以看成是由一个棱长为2(1+2)的正方体截去了8个正三棱锥而得到的,且被截去的正三棱锥的底面边长为2,侧棱长为2,则该鲁班锁玩具的表面积为6×4×(1+2)2-4×12×2×2+8×12×2×3=8(6+62+3).故选A.13.(2021年武汉模拟)已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是________,表面积是________.【答案】90 138【解析】该几何体的体积V =4×6×3+12×4×3×3=90,表面积S =2(4×6+4×3+6×3)-3×3+12×4×3×2+32+42×3+3×4=138.14.用一张正方形的纸把一个棱长为1的正方体礼品盒完全包住,不将纸撕开,则所需纸的最小面积是________.【答案】8【解析】如图1为棱长为1的正方体礼品盒,先把正方体的表面按图所示方式展开成平面图形,再把平面图形尽可能拼成面积较小的正方形,如图2所示,由图知正方形的边长为22,其面积为8.图1 图215.降水量是指水平平面上单位面积降水的深度,现用上口直径为38 cm 、底面直径为24 cm 、深度为35 cm 的圆台形水桶(轴截面如图所示)来测量降水量.如果在一次降雨过程中,此桶盛得的雨水正好是桶深的17,求本次降雨的降水量是多少毫米(精确到1 mm).解:因为这次降雨的雨水正好是桶深的17,所以水深为17×35=5(cm).如图,设水面半径为r cm ,在△ABC 中,AC A ′C ′=CB C ′B ,所以7r -12=7,r =13.所以V 水=13×(π×122+π×122×π×132+π×132)×5=2 3453π(cm 3).水桶的上口面积是S =π×192=361π(cm 2), 所以V 水S =2 3453π361π×10≈22(mm).故此次降雨的降水量约是22 mm.16.已知一个圆锥的底面半径为R ,高为H ,在其内部有一个高为x 的内接圆柱. (1)求圆柱的侧面积;(2)x 为何值时,圆柱的侧面积最大?解:(1)作圆锥的轴截面,如图所示.设圆柱底面半径为r ,因为r R =H -x H ,所以r =R -RHx .所以S 圆柱侧=2πrx =2πRx -2πRHx 2(0<x <H ).(2)因为-2πR H <0,所以当x =2πR 4πR H=H 2时,S圆柱侧最大.故当x =H2时,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.C 级——探索创新练17.一个封闭的正三棱柱容器,高为3,内装水若干(如图1,底面处于水平状态).将容器放倒(如图2,一个侧面处于水平状态),这时水面所在的平面与各棱交点E ,F ,F 1,E 1分别为所在棱的中点,则图1中水面的高度为( )A . 3B .2C .332D .94【答案】D【解析】设正三棱柱的底面积为S ,则VABC -A 1B 1C 1=3S . ∵E ,F ,F 1,E 1分别为所在棱的中点.∴S AEF S =14,即S AEF =14S .∴S BCEF =34S .∴VBCFE -B 1C 1F 1E 1=3×34S =94S .则图1中水面的高度为94.故选D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教A版必修第二册《8.3 简单几何体的表面积与体积》练习卷(2)一、选择题(本大题共5小题,共25.0分)1.若球的外切圆台的上、下底面半径分别为r,R,则球的表面积为()A. 4π(r+R)2B. 4πr2R2C. 4πrRD. π(R+r)22.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为()A. 43πa2 B. 73πa2 C. 83πa2 D. 163πa23.在封闭的直三棱柱ABC−A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A. 4πB. 9π2C. 6π D. 32π34.体积为64的正方体的顶点都在同一球面上,则该球面的表面积为()A. 12πB. 48πC. 8πD. 64π5.已知三棱锥P−ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,PB的中点,∠CEF=90°,则球O的体积为()A. 8√6πB. 4√6πC. 2√6πD. √6π二、填空题(本大题共7小题,共35.0分)6.已知正三棱柱底面边长是2,该三棱柱的体积为8√2,则该正三棱柱外接球的表面积是.7.已知正方体的棱长为2,则与正方体的各棱都相切的球的体积是_________.8.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为____.9.如图,正方体ABCD−A1B1C1D1中,AB=2,则三棱锥A−A1B1C的体积是______ .10.学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD−A1B1C1D1挖去四棱锥O−EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,AA1=4cm,3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,制作该模型所需原料的质量为___________g.11.若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为_______.12.如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则v1的值是_______.v2三、解答题(本大题共4小题,共48.0分)13.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2√2,AD=2,求四边形ABCD绕AD选择一周所成几何体的表面积及体积.14.一个正四棱台的上、下底面边长分别为4cm和10cm,高为4cm,求正四棱台的侧面积和体积.15.如图,底面ABCD是边长为4的正方形,ED⊥平面ABCD,ED=2,EF//BD,且2EF=BD.(1)求证:BF⊥AC:(2)求几何体ABCDEF的体积.16.三棱锥S−ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,求四棱锥S−BCED的体积.-------- 答案与解析 --------1.答案:C解析:本题考查球与圆台的组合体问题,属于中档题,解题关键要知道圆台是球的外切圆台,圆台的母线是R+r,则易计算出圆台的高为2√Rr,它就是球的直径,从而得球的表面积.解:由题意知,圆台的母线长为R+r,设圆台的高为h,由直角三角形的勾股定理知:ℎ=√(R+r)2−(R−r)2=2√Rr,∴球的半径为ℎ2=√Rr,则球的表面积为4πRr.故选C.2.答案:B解析:本题主要考查了三棱柱的结构特征,以及外接球表面积的求解,属于基础题..由题意作出图形,易知球心在三棱柱上、下底面的中心O,O1连线的中点O2处,利用几何关系即可求出答案.解:由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.设O,O1分别为下、上底面的中心,且球心O2为O1O的中点,又AD=√32a,AO=√33a,OO2=a2,设球的半径为R,则R2=|AO2|2=13a2+14a2=712a2,所以S球=4πR2=4π×712a2=73πa2.故选B.3.答案:B解析:本题考查的知识点是棱柱的几何特征,根据已知求出球的半径,是解答的关键.根据已知可得直三棱柱ABC −A 1B 1C 1的内切球半径为32,代入球的体积公式,可得答案. 解:∵AB ⊥BC ,AB =6,BC =8,∴AC =10.要使球的体积V 最大,则球与直三棱柱的部分面相切,若球与三个侧面相切,设底面△ABC 的内切圆的半径为r .则12×6×8=12×(6+8+10)·r ,所以r =2.2r =4>3,不合题意.球与三棱柱的上、下底面相切时,球的半径R 最大.由2R =3,即R =32.即直三棱柱ABC −A 1B 1C 1的内切球半径为32,此时V 的最大值43π⋅(32)3=9π2,故选B .4.答案:B解析:此题考查球的表面积公式的应用,先通过正方体的体积,求出正方体的棱长,然后求出球的半径,即可求出球的表面积.解:正方体体积为64,可知其边长为4,正方体的体对角线长为√42+42+42=4√3,即为外接球的直径,所以半径为2√3,所以球的表面积为4π(2√3)2=48π.故选B . 5.答案:D解析:本题考查多面体外接球体积的求法,考查空间想象能力与思维能力,考查计算能力,是中档题. 由题意画出图形,证明三棱锥P −ABC 为正三棱锥,且三条侧棱两两互相垂直,再由补形法求外接球球O 的体积.解:如图,由PA =PB =PC ,△ABC 是边长为2的正三角形可知,三棱锥P −ABC 为正三棱锥,则顶点P 在底面的射影O 为底面三角形的中心.连接BO 并延长,交AC 于G ,则AC ⊥BG ,又PO ⊥AC ,PO ∩BG =O ,可得AC ⊥平面PBG ,则PB ⊥AC .∵E ,F 分别是PA ,AB 的中点,∴EF//PB .又∠CEF =90°,即EF ⊥CE ,∴PB ⊥CE ,AC ∩CE =C ,得PB ⊥平面PAC ,∴正三棱锥P −ABC 的三条侧棱两两互相垂直.把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,其直径为D =√PA 2+PB 2+PC 2=√6,半径为√62,则球O 的体积为43π×(√62)3=√6π. 故选D .6.答案:48π解析:由底面边长和体积求得高,进而求得外接球半径,得解.此题考查了三棱柱外接球,难度不大.解:如图,M,N为上下底面中心,∵底面为正三角形,且边长为2,∴S△ABC=√3,AM=2√33,∴√3×MN=8√2,∴MN=8√63,∴外接圆半径OA=√AM2+OM2=2√3,∴外接球表面积为48π.故答案为:48π.7.答案:8√23π解析:本题考查球的体积,球的内接体的知识,是基础题.球的直径就是正方体的对角面长,以此求出球的半径,然后直接求出球的体积.解:由题设知球O的直径为2√2,R=√2,故其体积V=43πR3=8√23π.故答案为8√23π.8.答案:43解析:本题考查正方体的结构特征,及正四棱锥的体积计算.解:由正方体各面的中心围成的几何体为正八面体,是两个正四棱锥,底面为边长为√2,高为1,∴体积为2×13×(√2)2×1=43.故答案为43.9.答案:43解析:本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.由V A−A1B1C =V C−AA1B1,利用等积法能求出三棱锥A−A1B1C的体积.解:∵正方体ABCD−A1B1C1D1中,AB=2,∴BC⊥平面AA1B1,且BC=2,又S△AA1B1=12×2×2=2,∴V A−A1B1C=V C−AA1B1=13×S△A1B1C×BC=13×2×2=43.故答案为43.10.答案:118.8解析:本题考查制作该模型所需原料的质量的求法,考查长方体、四棱锥的体积等基础知识,考查推理能力与计算能力,考查数形结合思想,属于中档题.该模型体积为V ABCD−A1B1C1D1−V O−EFGH=6×6×4−13×(4×6−4×12×3×2)×3=132(cm3),再由3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,能求出制作该模型所需原料的质量.解:该模型为长方体ABCD−A1B1C1D1,挖去四棱锥O−EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,∴该模型体积为:V ABCD−A1B1C1D1−V O−EFGH=6×6×4−13×(4×6−4×12×3×2)×3=144−12=132(cm3),∵3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,∴制作该模型所需原料的质量为:132×0.9=118.8(g).故答案为:118.8.11.答案:解析:本题考查圆柱的体积,考查计算能力,正确认识圆柱的侧面展开图与几何体的关系,是解题的突破口,本题是基础题.通过侧面展开图是一个边长为2的正方形,求出底面半径,求出圆柱的高,然后求圆柱的体积.解:圆柱的侧面展开图是一个边长为2的正方形,所以底面半径为:1π,底面面积为:1π;所以圆柱的高为:2,所以圆柱的体积为:1π×2=2π故答案为2π.12.答案:32解析:本题考查球的体积以及圆柱的体积的求法,考查空间想象能力以及计算能力,设出球的半径,求出圆柱的体积以及球的体积即可得到结果.解:设球的半径为R,则球的体积为:43πR3,圆柱的体积为:πR2⋅2R=2πR3.则V1V2=2πR34πR33=32.故答案为32.13.答案:解:如图,∵∠ADC=135°,∴∠CDE=45°,又CD=2√2,∴DE=CE=2,又AB=5,AD=2,∴BC=5.则圆台上底面半径r1=2,下底面半径r2=5,高ℎ=4,母线长l=5,圆锥底面半径r1=2,高ℎ′=2,∴S表面=S圆台底面+S圆台侧面+S圆锥侧面,=π×52+π×(2+5)×5+π×2×2√2,=(4√2+60)π;V=V圆台−V圆锥=13π(25+10+4)×4−13π×4×2=1483π.解析:本题考查了旋转体的结构特征,面积和体积计算,属于中档题.画出四边形ABCD绕AD旋转一周所成几何体,然后求出圆台的底面积、圆台的侧面积及圆锥的侧面积作和得答案;由圆台的体积减去圆锥的体积求得几何体的体积.14.答案:解:由题意,斜高ℎ′=√32+42=5,则正四棱台的侧面积为12×4×(4+10)×5=140;体积为13×(42+102+√42×102)×4=208.解析:求出正四棱台的斜高,即可求正四棱台的侧面积和体积.本题考查求正四棱台的侧面积和体积,考查学生的计算能力,求出斜高是关键.15.答案:(1)证明:∵四边形ABCD为正方形,∴AC⊥BD,又ED⊥平面ABCD∴ED⊥AC而ED∩BD=D∴AC⊥平面EFBD;又BF⊂平面EFBD,∴AC⊥BF.(2)解:V ABCDEF=V A−BDEF+V C−BDEF=2V A−BDEF 又BD=4√2,EF=2√2V=13×12(4√2+2√2)×2×2√2×2=16.解析:(1)运用线面垂直的判定和性质,即可得证;(2)将多面体分割成棱锥A−BDEF和C−BDEF,则V ABCDEF=V A−BDEF+V C−BDEF=2V A−BDEF,运用三棱锥的条件公式即可得到体积.本题主要考查线面垂直的判定和性质,同时考查割补思想,以及棱锥的体积公式.16.答案:解:∵D、E分别是AB、AC中点,∴S△ADE=14S△ABC,∴S BCED=34S△ABC,∴V S−BCED=34V S−ABC,∵AS⊥BS,AS⊥CS,BS∩CS=S,∴AS⊥面BSC∴V S−ABC=V A−BSC=13AS⋅S△BSC=13×5×12×4×3=10,∴V S−BCED=34V S−ABC=34×10=152.解析:求四棱锥S−BCED的体积,转化为求V S−BCED=34V S−ABC,求三棱锥S−ABC的体积,即可求出结果.本题考查几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.。
