2013-01-2自然坐标系下的速度-加速度
2013-01-2自然坐标系下的速度-加速度解析

0
dv v 2 a n=a x i a y j a z k dt
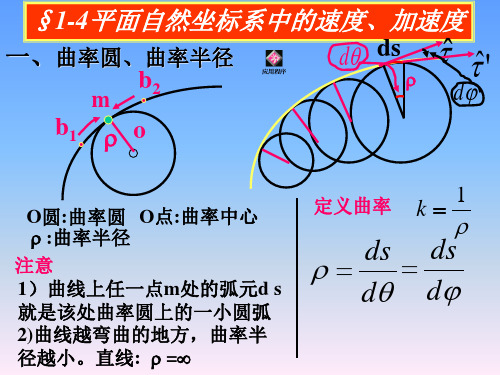
瞬时曲率半径
大学物理
三、推广:一般平面曲线运动 运动中的加速度
an
v
2
dv a dt
0
2
a
力学中利用加速度与曲率半径的关系求曲线轨迹上各点的曲率半径。
a
a
ds v v dt
ds v dt
1、 瞬时速率
v
:
n
S+
反映了质点任一时刻沿轨道运动的快 慢。
2、任何时刻质点的速度总沿轨道的 切线方向,速度只有切线分量而无法 向分量。
O
大学物理
二、 自然坐标系下的加速度
由加速度的定义有
d v a dt
由于质点速度的方向一定沿着轨迹的切向,因此, 自然坐标系中可将速度表示为:
2
=1
大学物理
自然坐标系下加速度表达式:
2 dv v a n dt R
o
n
a
即圆周运动的加速度可分解为两个正交分量:
an a P
a dv dt
2 v an R
a 切向加速度,其大小表示质点速率变化的快慢 an 法向加速度,其大小反映质点速度方向变化的快慢
大学物理
Key: c
大学物理
三、推广:一般平面曲线运动中的加速度
质点的轨迹可以看成是由无穷多个圆组合而成。 对圆周运动而言:曲率半径各点相同 R, 于是对曲线上任一点,研究该点的速度、加速度情况时, 仅需要将 R 换成 就得到一般曲线运动的加速度的正交分解式。
自然坐标系

r
t
t 0
AB .
t R
ern
v2 R
en
法向加速度
a
an
v2 R
vB
B vA
R
O
A
大小,方向,作用
2. 一般圆周运动的
切向加速度和法向加速度 分析方法
vB r
v vB vA vrn vr v
vrn 表示速度方向改变量 vr 表示速度大小改变量
lim lim vr
t 0
rr t
t 0
s t
er
ds dt
er
ds dt
三、 自然坐标系下的加速度
1. 匀速圆周运动, 法向加速度
v vB
vA
v vB
vA
Δv vB vA ,
AB R
lim lim ar
t 0
则:a an2 a 2 (1.88)2 (1.2)2 2.23(m / s2 )
tg an
a
12233'
总结解题策略:
(1)分析问题特点,建立恰当的坐标系 (2)由运动方程求解速度随时间变化的表达式 (3)分别计算出切向加速度与法向加速度,再 求解合加速度的大小和方向
解:根据加速度的定义:
ar
anern
a er
v2 R
ern
dv dt
er
a an2 a 2
v
ds dt
2
R
a
d
dt
1.2t
自然坐标系的加速度公式推导详解

自然坐标系的加速度公式推导详解在物理学中,加速度是描述物体速度变化率的物理量。
在自然坐标系中,我们可以通过推导得到加速度的计算公式。
假设一个物体在自然坐标系中运动,我们可以用矢量表示其位置、速度和加速度。
考虑一个时间间隔Δt内,物体的速度从v1变为v2,位移从r1变为r2。
根据定义,平均加速度a平均可以表示为:a平均 = (v2 - v1) / Δt为了得到瞬时加速度a,我们需要让时间间隔Δt趋近于0。
这样,我们可以写出加速度的定义:a = lim(Δt→0) [(v2 - v1) / Δt]接下来,我们将推导加速度的具体计算公式。
首先,我们将速度v 与位移r之间的关系进行分析。
根据定义,速度可以表示为位移对时间的导数:v = dr / dt其中,dr表示位移的微小变化,dt表示时间的微小变化。
我们可以将位移r表示为速度v对时间t的积分:r = ∫v dt现在,我们对上述等式两边进行微分,得到:dr = v dt将上式代入加速度的定义公式,得到:a = lim(Δt→0) [(v2 - v1) / Δt]= lim(Δt→0) [(dr2 / dt - dr1 / dt) / Δt]我们可以对上式进行化简。
首先,将分子展开得到:a = lim(Δt→0) [(∆r / ∆t - ∆r / ∆t)]= lim(Δt→0) [∆r / ∆t - ∆r / ∆t]然后,我们可以将上式中的分式展开:a = lim(Δt→0) [(∆r1 / ∆t - ∆r2 / ∆t)]= lim(Δt→0) [(r1 - r2) / ∆t]我们可以将分式中的∆t约去,得到最终的加速度公式:a = lim(Δt→0) [(r1 - r2) / ∆t]= d(r1 - r2) / dt我们得到了自然坐标系中加速度的计算公式:a = d(r1 - r2) / dt这个公式描述了物体在自然坐标系中的加速度,它表示了速度的变化率。
§2、速度、加速度的分量表达式

§2、速度、加速度的分量表达式上一次课,我们为了将运动的一些特征能直接的表示出来,而定义了速度和加速度,22;dt r d dt v d a dt r d v =≡≡ 。
在一般情况下它们往往都是时间t 的函数。
何谓定义呢?定义它本身不是可以用什么方法或者数学手段加以证明得到的,而是根据实际需要常常用到而定义下来的名称和概念。
例如过两点成一条直线……。
由于速度和加速度都是矢量,因此都可以将它们表示成分量的形式。
这次课将准备讨论速度、加速度在各种坐标系中的表达式。
一、 直角坐标系——直角坐标系又称笛卡儿坐标系在直角坐标系中,质点的位置矢径可以写成为:........z k y j x i r ++= (1)根据速度的定义可知dtr d v ≡将(1)代入,则有 1、速度: z y x v k v j v i dt dz k dt dy j dt dx i z k y j x i dt d dt r d v ++=++=++==...........................................)(于是,我们比较上面的等式,就可得到速度在直角坐标系中的分量表达式为:z dtdz v y dt dy v x dt dx v z y x ======;;可见速度沿三直角坐标轴的分量(即分速度)就等于其相应的坐标对时间t 的一阶导数。
速度的大小:222z y x v v v v v ++== 速度的方向就用方向余弦来表示:vv k v v v j v v v i v z y y ===),cos(;),cos(;),cos( 。
同理,我们由加速度的定义不难得到它的分量表达式。
2、加速度根据加速度的定义:zy x z y x a k a j a i dt dv k dt dv j dt dv i dt z d k y d j x d i dt dz k dy j dx i dt d dt v d a ++=++=++=++==2222)(比较这些恒等式可得加速度的直角坐标分量表达式:z dt z d v dv a y dt y d v dt dv a x dtx d v dt dv a z t z y y y x x x ============222222 于是可得加速度的大小为:222z y x a a a a a ++== 加速度的方向用方向余弦表示。
自然坐标系中的速度、加速度
a 0, 0 / 2, v
a 0, / 2, v const
a 0, / 2 , v
an 0 0,
直线运动
五、关于圆周运动 ( R)
an
v2 R
0
a
dv dt
a v2 nˆ dv ˆ
s
O’ oanR
a
a
R dt
若 v const
若 v const
M
S+
设M点在t=0时的初位置为 s0
则:运动方程:
s s0 a1t 2 / 2 v
ds dt
M s0
a1t O׳
an
v2 R
nˆ
a12t 2 R
nˆ
a
aM
a12t 2 R
nˆ a1ˆ
dv ˆ
dt
a1ˆ
注意:同一质点的加速度无论在直角坐标还是
a 自然坐标中总加速度
只能是一个值。
(匀速圆周运动)
dv 0 dt
a v2 nˆ R
则为变速圆周运动
例:一半径R的滑轮绕O轴运动,其上绕以绳索,绳索的
一沿端上挂一一点重M的物加,速已度知(重绳物不按伸h长,a与1t轮2 /之2 间规无律相下对降滑,动求)轮
a ? 已知:R,h a1t2 / 2 求:
解:如图建立自然坐标系O׳S+
切a向v单d位v矢v的dˆ增(量vˆ为) dˆ
O中 d
ˆ
'
dˆ
nˆ
O’
d
ads ˆ
dt dt
v dˆ ˆ dv
aan称称a为为nd切法t向向加a加速速度;dt
an
S
v
dˆ
dt
自然坐标系的加速度公式推导详解

自然坐标系的加速度公式推导详解在物理学中,加速度是描述物体运动状态的重要物理量。
加速度可以通过自然坐标系的公式进行推导和计算。
本文将详细解释自然坐标系的加速度公式的推导过程。
我们需要明确什么是自然坐标系。
自然坐标系是一种用来描述物体运动的参考系,它的基底与物体的运动方向一致。
在自然坐标系中,我们可以使用一组向量来表示物体的位置、速度和加速度。
假设一个物体在自然坐标系中的位置为P,其位置矢量为r。
我们可以将r表示为r = xi + yj + zk,其中i、j、k分别表示坐标轴x、y、z的单位向量。
当物体运动时,其位置会随时间发生变化。
假设物体在t时刻的位置为P(t),则其位置矢量r(t)也会随时间变化。
我们可以通过求导的方式来描述物体的速度和加速度。
首先我们求解速度。
速度是位置矢量对时间的导数,即v = dr/dt。
由于位置矢量r = xi + yj + zk,我们可以将速度v表示为v = (dx/dt)i + (dy/dt)j + (dz/dt)k。
这就是自然坐标系中的速度公式。
接下来,我们求解加速度。
加速度是速度对时间的导数,即 a = dv/dt。
我们已经知道速度v = (dx/dt)i + (dy/dt)j + (dz/dt)k,因此我们需要对速度进行求导。
对速度的各个分量进行求导,得到加速度的公式:ax = d²x/dt²ay = d²y/dt²az = d²z/dt²这就是自然坐标系中的加速度公式。
根据这个公式,我们可以计算物体在自然坐标系中的加速度。
需要注意的是,自然坐标系中的加速度公式是基于时间的二阶导数计算得到的。
因此,在实际应用中,我们需要通过测量物体的位置随时间的变化来计算加速度。
可以使用传感器或者运动学实验来获取位置和时间的数据,从而计算出加速度。
总结一下,自然坐标系的加速度公式是通过对速度进行求导得到的。
加速度是描述物体运动状态的重要物理量,可以通过测量物体的位置随时间的变化来计算。
自然坐标系

自然坐标系
作者:Michaelexe
自然坐标系中的速度和加速度
在质点的平面曲线运动中,当运动轨迹已知时,常用自然坐标系表述质点的位置、路程、速度和加速度。
如图所示,在某质点运动的轨迹线上任取一点O为自然坐标原点,以质点所在位置P点与O点间轨迹的长度s来确定质点的位置,则称s为质点的自然坐标,即
当质点经Δt从P点达Q点时,Δt内质点运动的路程为
设t时刻质点处于P点,在质点上做相互垂直的两个坐标轴,一个轴沿轨道切向指向质点前进方向,其单位矢量用表示;另一轴沿轨道法向指向轨道凹侧,其单位矢量用表示。
由于切向和法向坐标轴随
质点沿轨道的运动自然变换位置和方向,通常称这种坐标系为自然坐标系。
当质点沿平面曲线运动时,其速度矢量的大小(速率)可以写为
考虑其速度方向为轨道的切向,则速度矢量可表示为
下面我们讨论质点的加速度
为质点的切向加速度,它只改变速度的大小,所以
为质点的法向加速度,它只改变速度方向,所以
,其中为轨道曲线在该点的曲率半径(因为始终指向轨道内侧,故ρ始终大于0,所以ρ也可以定义为)
所以,
现在来求平面曲线y=f(x)的曲率和曲率半径
曲率的定义:
曲率半径的定义:
下面来求k和ρ的公式所以,。
用自然坐标表示平面曲线运动中的速度和加速度

解 ds
vx2
v
2 y
v z2dt
A 2 cos2 t A 2 sin2 t B2 dt
s
s
ds
t
A2 2 B2dt
0
0
v
vτ
dsτ
A2 2
B2
τ
dt
A2 2 B2t
例 将一根光滑的钢丝弯成一个竖直平面内的曲线,质点可沿
当 t 0 时
τ (t)
τ
τ (t)
θ θ
τ
//
n
θ
τ
τ
θ
n
τ (t t)
因而 dτ lim τ lim θ n lim θ s n 1vn dt t0 t t0 t t0 s t ρ
O 参考物
( lim
r
τ)
ds
dsτ
vτ
t0 s dt dt
速度矢量在切线上的投影
二. 加速度
v
dsτ
vτ
dt
a
dv dt
d dt
(dsτ) dt
d2s dt 2
τ
ds dt
dτ dt
第一项:d2s dt 2
τ
叫切向加速度
aτ
dy P ds
Ox
sin ds dy
v v0
vdv
y y0
gdy
v2
v
2 0
2g( y0
y)
径的圆弧所构成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
a
0,an
a
an
0
为匀速率曲线运动(圆 周运动)
dv dt
0
v2
n0
a an
a
a a a 2 an 2 dv dt2 v2 2
加速度总是指向曲线的凹侧
大学物理
自然坐标系中总加速度为:
a a an
改变速度大小
大小 a a 2 an2
加速度
方向 tan 1 an
下面三种情况分别代表那一类运动?
1. ,an=0, a 0, 2. =常量,an 0,a=0, 3. =常量,an 0,a 0,
1. 变速直线运动 2. 匀速率圆周运动 3. 变速率圆周运动
大学物理
讨论
质点沿固定的圆形轨道, 若速率 v 均匀增加,at 、an、
a以及加速度与速度间的夹角中哪些量随时间变化?
v lim r
t0 t
ds
dt
vr ds v v v
dt
z
v
p s
s
r q
r(t)
r(t t)
o
y x
自然坐标系下的 速度表达式
大学物理
讨论物理意义:
vr ds v v v
dt
ds v dt
1、 瞬时速率 v:
反映了质点任一时刻沿轨道运动的快 慢。
2、任何时刻质点的速度总沿轨道的 切线方向,速度只有切线分量而无法 向分量。
与切向加速度垂直
大学物理
例题
一质点沿半径为R的圆周按规律 s v0t b运t 2动/ 2,
v0、b 都是正的常量。求:
(1) t 时刻质点的总加速度的大小
(2) t 为何值时,总加速度的大小b
s
(3)当总加速度大小为b时,质点沿圆周运
行了多少圈。
o
P
R
大学物理
解:先作图如右,t = 0 时,质点位于s = 0 的 p 点处。
大学物理
上册
自然坐标系
在运动轨道上任一点建立正交坐 标系,其一根坐标轴沿轨道切线方 向,正方向为运动的前进方向;
另一根沿轨道法线方向,正方向 指向轨道内凹的一侧。
v,a
n
n
切向单位矢量
法向单位矢量 n
显然,轨迹上各点处,自然坐标轴的方位不断变化。
大学物理
一、自然坐标系下的速度
s s(t t) s(t)
大学物理
三、推广:一般平面曲线运动中的加速度
质点的轨迹可以看成是由无穷多个圆组合而成。
对圆周运动而言:曲率半径各点相同 R,
于是对曲线上任一点,研究该点的速度、加速度情况时,
仅需要将 R 换成 就得到一般曲线运动的加速度的正交分解式。
a n
v2
0
at
dv dt
a
dv dt
v2
n=a
x
i
解:(1)
x v0t y 1 gt 2
2
o
1 x2g
y 2
v02
y
v0
x
an
a
g
大学物理
(2) vx v0 , vy gt
o v0
x
v vx2 vy2 v02 g2t2
arctg gt
y
v0
an
a
g
dv
g2t
a dt v02 g2t 2
与速度同向
an
g2 a 2
v0 g v02 g2t2
ay
j
azk
瞬时曲率半径
大学物理
三、推广:一般平面曲线运动 运动中的加速度
v2
an
dv a dt
0
a
力学中利用加速度与曲率半径的关系求曲线轨迹上各点的曲率半径。
a
a 2 an2
v2
2
dv dt
2
v2
a2
dv
2
dt
1 yx2
3 2
yx
大学物理
四、讨论几种特殊情况:
R
即圆周运动的加速度可分解为两个正交分量:
o a
n
a n
P a
a
dv dt
a n
v2 R
aavn
切向加速度,其大小表示质点速率变化的快慢 法向加速度,其大小反映质点速度方向变化的快慢
大学物理
aan
aann00
切向加速度、反映速度大小变化, 法向加速度、反映速度方向变化,
an 0,a 0 变速直线运动;
S+
n
O
大学物理
二、 自然坐标系下的加速度
由加速度的定义有
a
dv dt
由于质点速度的方向一定沿着轨迹的切向,因此, 自然坐标系中可将速度表示为:
v
v
a
dv dt
d
v dt
大学物理
讨论物理意义:
以圆周运动为例讨论上式中两个分项的物理意义:
a
dv dt
dv
dt
难点:
d的大小如何?方向如何?
dt
大学物理
a dv d v(t)
以圆周运动为例:
dt dt
( dv ) v d
dt
dt
v dv
d B v
A
d 1 d n d ds n v n
dt dt
ds dt
d
dS d
d 1 ds
2d 1
a
dv
dt
v2
n0
=1
大学物理
自然坐标系下加速度表达式:
a dv v 2 n
dt
在t 时刻,质点运动到位置 s 处。其速度大小为:
v
ds dt
v0
bt
s
o
P
R
大学物理
(1)t 时刻切向加速度、法向加速度及加速度大小:
aτ
dv dt
d2s dt 2
b
an v 2
(v 0
bt)2
R
R
a
aτ2 an2
(v0 bt)2 (bR)2 R
(2)令a = b ,即
a (v0 bt)2 (bR)2 b R
t v0 b
大学物理
(3)当a = b 时,t = v0/b ,质点历经的弧长为
s v0t bt2/2
v02/2b
它与圆周长之比即为圈数:
n s v02
2R 4Rb
大学物理
选择=结果
汇报结束 谢谢观看! 欢迎提出您的宝贵意见!
大学物理
an at
an at
a
v2 an R
变化
a t 均匀=不变
a
a
a
2 t
a
2 n
变化
tg an
at
变化
大学物理
例、由楼窗口以水平初速度v0射出一发子弹,取枪 口为原点,沿v0为x轴,竖直向下为y轴,并取发射 时t=0.试求:
(1)子弹在任一时刻t的位置坐标及轨道方程;
(2)子弹在t时刻的速度,切向加速度和法向加速度。
a
? 两组单位矢量 i jk 与
n
的区别是什么?
a
a
an
o
大学物理
练习
1: 下列哪一种说法是正确的( ) (A)运动物体加速度越大,速度越快 (B)作直线运动的物体,加速度越来越小,速
度也越来越小 (C)切向加速度为正值时,质点运动加快 (D)法向加速度越大,质点运动的法向速度变
化越快
大学物
