2020年八年级上册期中考试卷 - 答案
[整合]人教版初中数学八年级上册期中试题(二)2020年秋部分附答案共3份
![[整合]人教版初中数学八年级上册期中试题(二)2020年秋部分附答案共3份](https://img.taocdn.com/s3/m/0b4be870da38376baf1faee2.png)
2020年秋绵阳外国语学校人教版初中八年级数学上册期中试题(附答案)一、选择题(每小题3分,共30分)1.(2020独家原创试题)2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油,武汉加油.在“中国加油”这4个汉字中,不可以看作轴对称图形的个数为 ()A.1B.2C.3D.42.(2019山东济宁邹城期中)如图,将△ABC的三个顶点坐标的横坐标都乘-1,并保持纵坐标不变,则所得图形与原图形的关系是 ()A.关于x轴对称B.关于y轴对称C.将原图形沿x轴的负方向平移了1个单位D.将原图形沿y轴的负方向平移了1个单位3.已知等腰三角形的周长为17 cm,一边长为4 cm,则它的腰长为 ()A.4 cmB.6.5 cmC.6.5 cm或9 cmD.4 cm或6.5 cm4.如图,已知∠1=∠2,下列添加的条件不能使△ADC≌△CBA的是 () A.AB∥DCB.AB=CDC.AD=BCD.∠B=∠D5.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是 ()A.AE=3CEB.AE=2CEC.AE=BDD.BC=2CE6.如图,在△ABC中,AB=AC,D为BC边上一点,E点在AC边上,AD=AE,若∠BAD=24°,则∠EDC= () A.24° B.20° C.15° D.12°7.如图,正五边形ABCDE中,直线l过点B,且l⊥ED,下列说法:①l是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.其中说法正确的是 ()A.①②B.①③C.②③D.①②③8.如图,等腰△ABC中,AB=AC,∠A=36°.用尺规作图作出线段BD,则下列结论错误的是 ()A.AD=BDB.∠DBC=36°C.S△ABD=S△BCDD.△BCD的周长=AB+BC9.如图,在四边形ABCD中,BC∥AD,CD⊥AD,P是CD边上的动点,要使PA+PB的值最小,则点P应满足的条件是 ()A.PB=PAB.PC=PDC.∠APB=90°D.∠BPC=∠APD10.如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD 与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②∠AOB=60°;③AP=BQ;④△PCQ是等边三角形;⑤PQ∥AE. 其中正确结论的个数是 ()A.5B.4C.3D.2二、填空题(每小题3分,共24分)11.(2019四川资阳中考)若正多边形的一个外角是60°,则这个正多边形的内角和是 .12.图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图9②,那么在Rt△ABC中,BC=6,则AB= .13.如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件: (填一个即可).14.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-4),AB的长是12,则△ABD的面积为 .15.我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为度.16.如图,已知△ABC关于直线y=1对称,C到AB的距离为2,AB的长为6,则点A、点B的坐标分别为 .17.(2019江苏南通中考)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=度.18.在△ABC中,AH是BC边上的高,若CH-BH=AB,∠ABH=70°,则∠BAC= .三、解答题(共66分)19.(6分)如图,学校要在两条小路OM和ON之间的S区域修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A、B的距离必须相等,到两条小路的距离也必须相等,则英语角C应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)20.(6分)如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).(1)在图中作出△ABC关于y轴对称的△A1B1C1;(2)写出点A1,B1,C1的坐标(直接写答案):A1 ;B1 ;C1 ;(3)△A1B1C1的面积为 ;(4)在y轴上画出点P,使PB+PC最小.21.(2019四川眉山中考)(7分)如图,在四边形ABCD中,AB∥DC,点E是CD 的中点,AE=BE.求证:∠D=∠C.22.(7分)如图,在△ABC中,AB=AC,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F,D是BC边上的中点,连接AD.(1)若∠BAD=55°,求∠C的度数;(2)猜想FB与FE的数量关系,并证明你的猜想.23.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD 于E,BF∥AC交CE的延长线于F.(1)求证:△ACD≌△CBF;(2)连接DF,求证:AB垂直平分DF.24.(10分)定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.(1)如图①,△ABC中,AB=AC,∠A=36°,求证:△ABC是倍角三角形;(2)如图②,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA 到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.25.(10分)数学课上,王老师出示了下面的题目:在△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系.小明与同桌小聪讨论后,进行了如下解答.(1)特殊情况,探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB的延长线上,且ED=EC,如图①,确定线段AE与DB的大小关系,请你直接写出结论 ;(2)特例启发,解答题目:王老师给出的题目中,AE与DB的大小关系是 .理由如下:如图②,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)26.(12分)如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP 是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以②的运动速度从点C出发,点P以原来的运动速度从点B 同时出发,都逆时针沿△ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇参考答案1.答案 C“中国加油”这4个汉字中,不可以看作轴对称图形的汉字有“国”“加”“油”,共三个,故选C.2.答案 B将△ABC的三个顶点坐标的横坐标都乘-1,纵坐标不变,则横坐标互为相反数,纵坐标相等,所得图形与原图形关于y轴对称,故选B.3.答案 B若4 cm是腰长,则底边长为20-4-4=12(cm),∵4+4<12,不能组成三角形,∴舍去;若4 cm是底边长,则腰长为17-42 =6.5(cm).故它的腰长为6.5 cm.故选 B.4.答案 B A.由AB∥CD,可得∠DCA=∠CAB,又因为∠1=∠2,AC=AC,故能判定△ADC≌△CBA,故选项A不符合题意;B.由AB=CD,∠1=∠2,AC=AC,不能判定△ADC≌△CBA,故选项B符合题意;C.由AD=BC,∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项C不符合题意;D.由∠D=∠B,∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项D不符合题意.故选B.5.答案 B连接BE,∵DE垂直平分AB,∴AE=BE,∴∠ABE=∠A=30°,∴∠CBE=∠ABC-∠ABE=30°.在Rt△BCE中,BE=2CE,∴AE=2CE,故选B.6.答案 D∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=∠B+24°,∵∠AED是△CDE的外角,∴∠AED=∠C+∠EDC,∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED,∴∠C+∠EDC=∠ADC-∠EDC=∠B+24°-∠EDC,解得∠EDC=12°.故选D7.答案 D∵正五边形ABCDE中,直线l过点B,且l⊥ED,∴l是线段AC的垂直平分线,∠BAC=36°,∴①②正确;正五边形ABCDE有五条对称轴,③正确.故选D.8.答案 C∵等腰△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°,由作图痕迹可知BD平分∠ABC,∴∠A=∠ABD=∠DBC=36°,∴AD=BD,故A,B结论正确;∵AD≠CD,∴S△ABD=S△BCD错误,故C结论错误;△BCD的周长=BC+CD+BD=BC+AC=BC+AB,故D结论正确.故选C.9.答案 D如图所示,作点A关于CD的对称点A',连接A'B,交CD于点P,连接AP,则PA+PB的最小值为A'B的长,点P即为所求.∵点A'与点A关于CD对称,∴∠APD=∠A'PD,∵∠BPC=∠A'PD,∴∠BPC=∠APD,故D符合题意.由图可知,选项A和选项B不成立,而C只有在PC=BC时才成立,故选项C不一定成立.故选D.10.答案 A①∵△ABC和△CDE为等边三角形,∴AC=BC,CD=CE,∠BCA=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,①正确.②∵∠ACB=∠DCE=60°,∴∠BCD=60°,∵△DCE是等边三角形,∴∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,②正确.④在△CDP和△CEQ中,∠ADC=∠BEC,CD=CE,∠DCP=∠ECQ,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,△PCQ是等边三角形,④正确.⑤∵∠CPQ=∠CQP=60°,∴∠QPC=∠BCA,∴PQ∥AE,⑤正确.③同④得△ACP≌△BCQ(ASA),∴AP=BQ,③正确.故选A.11.答案720°解析这个正多边形的边数为360°÷60°=6,则这个正多边形的内角和为(6-2)×180°=720°.12.答案 12解析由题意得AB=2BC=12.13.答案∠ABC=∠DBC或∠ACB=∠DCB解析∵∠A=∠D,BC=BC,∴当∠ABC=∠DBC或∠ACB=∠DCB时,△ABC≌△DBC(AAS),∴还需要补充一个条件为∠ABC=∠DBC或∠ACB=∠DCB.14.答案24解析如图,作DE⊥AB于E,∵点D的坐标是(0,-4),∴OD=4,∵AD是Rt△OAB的角平分线,∴DE=OD=4,∴S△ABD= 12×12×4=24.15.答案 90解析∵k=2,∴设该等腰三角形的顶角=2α,则底角=α,∴α+α+2α=180°,∴α=45°,∴该等腰三角形的顶角为90°.16.答案 (2,-2),(2,4)解析由题意可得点A、B的连线与直线y=1垂直,且两点到直线y=1的距离相等,∵AB=6,∴A、B两点的纵坐标分别为-2和4,又∵C到AB的距离为2,∴A、B两点的横坐标都为2.∴A、B两点的坐标分别为(2,-2),(2,4).17. 答案 70解析 在Rt △ABE 与Rt △CBF 中, ,,AE CF AB BC =⎧⎨=⎩∴Rt △ABE ≌Rt △CBF (HL).∴∠BAE =∠BCF =25°.∵AB =BC ,∠ABC =90°,∴∠ACB =45°,∴∠ACF =25°+45°=70°.18. 答案 75°或35°解析 当∠ABC 为锐角时,过点A 作AD =AB ,交BC 于点D ,如图1所示. ∵AB =AD ,∴∠ADB =∠ABH =70°,BH =DH . ∵CH -BH =AB ,∴AB +BH =CH , 又∵CH =CD +DH ,∴CD =AB =AD ,∴∠C = ∠ADB =35°, ∴∠BAC =180°-∠ABH -∠C =75°.当∠ABC 为钝角时,作AH ⊥BC ,交CB 的延长线于H , 如图2所示.∵CH -BH =AB ,∴AB +BH =CH ,又∵BH +BC =CH ,∴AB =BC ,∴∠BAC =∠ACB = 12 ∠ABH =35°. 故∠BAC =75°或35°.图1图219.解析如图所示,点C即为英语角应修建的位置.20.解析(1)△A1B1C1如图所示.(2)(3,2);(4,-3);(1,-1).(3)△A1B1C1的面积=3×5- 12×2×3- 12×1×5- 12×2×3=6.5.故填6.5.(4)如图所示,P点即为所求.21. 证明∵AE=BE,∴∠EAB=∠EBA, ∵AB∥DC,∴∠DEA=∠EAB,∠CEB=∠EBA,∴∠DEA=∠CEB,∵点E 是CD 的中点,∴DE =CE . 在△ADE 和△BCE 中, ,,,DE CE DEA CEB AE BE =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△BCE (SAS), ∴∠D =∠C .22. 解析 (1)∵AB =AC , ∴∠C =∠ABC , ∵BD =CD ,AB =AC , ∴AD ⊥BC , ∴∠ADB =90°, ∵∠BAD =55°,∴∠C =∠ABC =90°-55°=35°. (2)FB =FE .证明:∵BE 平分∠ABC ,∴∠ABE =∠CBE = 12∠ABC , ∵EF ∥BC , ∴∠FEB =∠CBE , ∴∠FBE =∠FEB , ∴FB =FE .23. 证明 (1)∵BF ∥AC ,∴∠ACB +∠CBF =180°, 又∵∠ACB =90°,∴∠CBF =90°,又∵CE ⊥AD ,∴∠CAE +∠ACF =∠ACF +∠ECD =90°, ∴∠CAE =∠ECD ,即∠DAC =∠FCB . 在Rt △ACD 和Rt △CBF 中, 90?,,,ACD CBF AC BC DAC FCB ∠=∠=⎧⎪=⎨⎪∠=∠⎩∴△ACD ≌△CBF . (2)由(1)得CD =BF ,∵D 为BC 的中点,∴CD =BD ,∴BF =BD . ∵△ABC 为等腰直角三角形, ∴∠CBA =45°,∵∠CBF =90°,∴∠FBA =45°,∴∠CBA =∠FBA , ∴BA 平分∠CBF .根据等腰三角形“三线合一”的性质得AB 垂直平分DF 24. 解析 (1)证明:∵AB=AC,∴∠B=∠C, ∵∠A+∠B+∠C=180°,∠A=36°, ∴∠B=∠C=72°,∴∠C=2∠A,即△ABC 是倍角三角形. (2)△ADC 是倍角三角形.证明:∵AD 平分∠BAE,∴∠BAD=∠EAD, ∵AB=AE,AD=AD,∴△ABD ≌△AED(SAS), ∴∠ADE=∠ADB,BD=DE. 又∵AB +AC =BD , ∴AE +AC =BD ,即CE =BD . ∴CE =DE .∴∠C =∠BDE =2∠ADC . ∴△ADC 是倍角三角形. 25. 解析 (1)AE =DB .(2)AE =DB .补充的过程如下: ∵△ABC 为等边三角形,∴∠AFE =∠ACB =∠ABC =60°,△AEF 为等边三角形, ∴∠EFC =∠EBD =120°,EF =AE ,∵ED =EC ,∴∠EDB =∠ECB ,∠ECB =∠FEC , ∴∠EDB =∠FEC .在△BDE 和△FEC 中, ,,,EBD EFC EDB FEC ED EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△FEC (AAS),∴BD =EF ,∴AE =BD 26. 解析 (1)①全等.理由如下:当点P 与点Q 运动1秒时,BP=CQ=3厘米. ∵AB=12厘米,D 为AB 的中点, ∴BD=6厘米.又∵PC=BC-BP=9-3=6(厘米),∴PC=BD. ∵AB=AC,∴∠B=∠C. 在△BPD 与△CQP 中,,,,BP CQ B C BD PC =⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP (SAS).②若点Q 与点P 的运动速度不相等, 要使△BPD ≌△CPQ ,只能BP =CP =4.5厘米, BD =CQ =6厘米.∴点P 的运动时间t = 3BP = 4.53=1.5(秒),此时v Q = CQt = 61.5=4(厘米/秒).(2)因为v Q >v P ,所以只能是点Q 追上点P ,即点Q 比点P 多走AB +AC 的路程.设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12,解得x=24.此时点P运动了24×3=72(厘米).又∵△ABC的周长为33厘米,72=33×2+6,∴点P、Q在BC边上相遇,故经过了24秒,点P与点Q第一次在BC边上相遇.期中综合检测题(附答案)一.选择题1.在3×3的方格中涂有阴影图形,下列阴影图形不是轴对称图形的是()A.B.C.D.2.若三角形的两边a、b的长分别为3和5,则其第三边c的取值范围是()A.2<c<5 B.3<c<8 C.2<c<8 D.2≤c≤83.下列图形中具有稳定性的是()A.等腰三角形B.长方形C.正方形D.平行四边形4.下列各图中,正确画出AC边上的高的是()A.B.C.D.5.已知一个等腰三角形一内角的度数为80°,则这个等腰三角形顶角的度数为()A.100°B.80°C.50°或80°D.20°或80°6.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是()A.AC=CE B.∠BAC=∠ECD C.∠ACB=∠ECD D.∠B=∠D7.如图,在△ABC和△A′B′C中,△ABC≌△A′B′C,AA′∥BC,∠ACB=α,∠BCB'=β,则α,β满足关系()A.α+β=90°B.α+2β=180°C.2α+β=180°D.α+β=180°8.点P(m,﹣2)与点P1(﹣4,n)关于x轴对称,则m,n的值分别为()A.m=4,n=﹣2 B.m=﹣4,n=2 C.m=﹣4,n=﹣2 D.m=4,n=29.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.角的内部到角的两边的距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形三条角平分线的交点到三条边的距离相等D.以上均不正确10.如图,以正方形ABCD的一边AD为边向外作等边三角形ADE,则∠BED等于()A.30°B.37.5°C.45°D.50°11.如图,在△ABC中,AD交边BC于点D.设△ABC的重心为M,若点M在线段AD上,则下列结论正确的是()A.∠BAD=∠CADB.AM=DMC.△ABD的周长等于△ACD的周长D.△ABD的面积等于△ACD的面积12.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕点P旋转时,下列结论错误的有()①EF=AP;②△EPF为等腰直角三角形;③AE=CF;④A.1个B.2个C.3个D.4个二.填空题13.一个多边形的每一个外角为30°,那么这个多边形的边数为.14.如图,直线l1⊥l2,在某平面直角坐标系中,x轴∥11,y轴∥l2,点A的坐标为(﹣1,2),点B的坐标为(2,﹣1),那么点C在第象限.15.如图,已知∠AOB=60°,点P在边OA上,OP=20,点M点N在边OB上,PM=PN.若MN =4,则OM等于.16.已知△ABC中,AH⊥BC,垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC=.17.如图,在△ABC中,BI、CI分别平分∠ABC、∠ACB,若∠BIC=125°,则∠A=°.18.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线.点P是EF上的动点,则|PA ﹣PB|的最大值为.三.解答题19.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.【问题解决】如图1,若点D在边BC上,求证:CE+CF=CD;【类比探究】如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.20.如图,一艘轮船以每小时40海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上.当轮船到达灯塔C的正东方向D处时,又航行了多少海里.21.已知:如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.(1)若∠DCB=40°,求∠CEF的度数;(2)求证:∠CEF=∠CFE.22.如图,△ABC为等边三角形,∠1=∠2=∠3,求证:△DEF是等边三角形.23.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD 交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE⊥CD;(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有(请写序号,少选、错选均不得分).24.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.25.如图,△ABD和△ACE都是等边三角形,BE和CD相交于点F.(1)若CD=6,求BE的长;(2)求证:AF平分∠DFE.参考答案一.选择题1.解:A、是轴对称图形,不合题意;B、是轴对称图形,不合题意;C、是轴对称图形,不合题意;D、不是轴对称图形,符合题意;故选:D.2.解:根据三角形的三边关系可得5﹣3<c<5+3,解得:2<c<8,故选:C.3.解:等腰三角形,长方形,正方形,平行四边形中只有等腰三角形具有稳定性.故选:A.4.解:根据三角形高线的定义,只有D选项中的BE是边AC上的高.故选:D.5.解:(1)若等腰三角形一个底角为80°,顶角为180°﹣80°﹣80°=20°;(2)等腰三角形的顶角为80°.因此这个等腰三角形的顶角的度数为20°或80°.故选:D.6.解:∵△ABC≌△CDE,AB=CD∴∠ACB=∠CED,AC=CE,∠BAC=∠ECD,∠B=∠D∴第三个选项∠ACB=∠ECD是错的.故选:C.7.解:当△ABC绕点C顺时针旋转到△A′B′C的位置,使AA′∥BC,∴∠CAA′=∠ACB=α,AC=A′C,∴∠AA′C=∠A′AC=α;∴∠ACA′=180°﹣∠CAA′﹣∠CA′A=180°﹣2α=β,∴2α+β=180°,故选:C.8.解:∵点P(m,﹣2)与点Q(﹣4,n)关于x轴对称,根据关于x轴对称的点,横坐标相同,纵坐标互为相反数,∴m=﹣4,n=2,故选:B.9.解:(1)如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,∵两把完全相同的长方形直尺,∴PE=PF,∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),故选:A.10.解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵△ADE是等边三角形,∴AD=AE,∠DAE=∠AED=60°,∴∠BAE=150°,AB=AE,∴∠AEB=15°,∴∠BED=45°,故选:C.11.解:∵△ABC的重心为M,∴AM=2DM,AD为△ABC的中线,∴BD=CD,∴S△ABD=S△ACD.故选:D.12.解:①、∵在△ABC中,AB=AC,∠BAC=90°,CP=BP,∴∠APC=∠EPF=90°,∠APF=90°﹣∠APE=∠BPE,又AP=BP,∠FAP=∠EBP=45°,∴△FAP≌△EBP,∴PE=PF,不能证明EF=AP,错误;②、由①可知△EPF为等腰直角三角形,正确;③、由△FAP≌△EBP,可知AF=BE,又AC=AB,故AE=CF,正确;④、∵△FAP≌△EBP,∴S四边形AEPF=S△FAP+S△APE=S△EBP+S△APE=S△APB=S△ABC,正确;故选:A.二.填空题13.解:多边形的边数:360°÷30°=12,则这个多边形的边数为12.故答案为:12.14.解:如图,∵点A的坐标为(﹣1,2),点B的坐标为(2,﹣1),∴点A位于第二象限,点B位于第四象限,∴点C位于第三象限.故答案是:三.15.解:过点P作PD⊥OB于点D,∵∠AOB=60°,PD⊥OB,OP=20,∴DO=10,∵PM=PN,MN=4,PD⊥OB,∴MD=ND=2,∴MO=8.故答案为:8.16.解:当∠ABC为锐角时,过点A作AD=AB,交BC于点D,如图1所示.∵AB=AD,∴∠ADB=∠ABH=80°,BH=DH.∵AB+BH=CH,CH=CD+DH,∴CD=AB=AD,∴∠C=∠ADB=40°,∴∠BAC=180°﹣∠ABH﹣∠C=60°.当∠ABC为钝角时,如图2所示.∵AB+BH=CH,∴AB=BC,∴∠BAC=∠ACB=∠ABH=40°.故答案为:60°或40°.17.解:依题意,在△BIC中,125°+∠IBC+∠ICB=180°.所以∠IBC+∠ICB=55°.在△ABC中,∠A+∠ABC+∠ACB=180°.又2∠IBC=∠ABC,2∠ICB=∠ACB,所以∠A=180°﹣55°×2=70°.故答案是:70°.18.解:如图,延长BA交EF于P′,此时|PA﹣PB|的值最大.∴|PA﹣PB|的最大值=AB=3.故答案为:3.三.解答题19.【问题解决】证明:在CD上截取CH=CE,如图1所示:∵△ABC是等边三角形,∴∠ECH=60°,∴△CEH是等边三角形,∴EH=EC=CH,∠CEH=60°,∵△DEF是等边三角形,∴DE=FE,∠DEF=60°,∴∠DEH+∠HEF=∠FEC+∠HEF=60°,∴∠DEH=∠FEC,在△DEH和△FEC中,,∴△DEH≌△FEC(SAS),∴DH=CF,∴CD=CH+DH=CE+CF,∴CE+CF=CD;【类比探究】解:线段CE,CF与CD之间的等量关系是FC=CD+CE;理由如下:∵△ABC是等边三角形,∴∠A=∠B=60°,过D作DG∥AB,交AC的延长线于点G,如图2所示:∵GD∥AB,∴∠GDC=∠B=60°,∠DGC=∠A=60°,∴∠GDC=∠DGC=60°,∴△GCD为等边三角形,∴DG=CD=CG,∠GDC=60°,∵△EDF为等边三角形,∴ED=DF,∠EDF=∠GDC=60°,∴∠EDG=∠FDC,在△EGD和△FCD中,,∴△EGD≌△FCD(SAS),∴EG=FC,∴FC=EG=CG+CE=CD+CE.20.解:∵CD⊥DB,∠CBD=60°,∴∠DCB=30°∴DB=BC,∴BC=2DB,又∵∠BCA=60°﹣30°=30°,∴BC=BA,∴BC=2×40=80(海里),∴DB=40海里,答:当轮船到达灯塔C的正东方向D处时,又航行了40海里21.解:(1)∵CD是高,∠DCB=40°,∴∠B=50°,又∵∠ACB=90°,∴∠BAC=40°,又∵AE是角平分线,∴∠BAE=∠BAC=20°,∴∠CEF=∠B+∠BAE=50°+20°=70°;(2)∵∠ACB=90°,CD⊥AB,∴∠ACD+∠BAC=∠B+∠BAC=90°,∴∠ACD=∠B,∵AE平分∠BAC,∴∠BAE=∠CAE,∵∠CFE是△ACF的外角,∠CEF是△ABE的外角,∴∠CFE=∠ACD+∠CAE,∠CEF=∠B+∠BAE,∴∠CFE=∠CEF.22.证明:∵△ABC是等边三角形,∴∠BAC=∠ABC.∵∠1=∠2,∴∠BAC﹣∠1=∠ABC﹣∠2,即∠CAF=∠ABD.在△ABD和△CAF中∴△ABD≌△CAF,∴∠ADB=∠CFA.∴∠FDE=∠DFE.同理可得∠DFE=∠FED.∴∠FDE=∠FED=∠DFE,∴△DEF是等边三角形.23.(1)证明:∵∠ABC=∠DBE,∴∠ABC+∠CBE=∠DBE+∠CBE,即∠ABE=∠CBD,在△ABE和△CBD中,,∴△ABE≌△CBD,∴AE=CD.(2)∵△ABE≌△CBD,∴∠BAE=∠BCD,∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,又∠CNM=∠ANB,∵∠ABC=90°,∴∠NMC=90°,∴AE⊥CD.(3)结论:②理由:作BK⊥AE于K,BJ⊥CD于J.∵△ABE≌△CBD,∴AE=CD,S△ABE=S△CDB,∴•AE•BK=•CD•BJ,∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,∴BM平分∠AMD.不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.故答案为②.24.证明:∵CE∥DF,∴∠ACE=∠D,在△ACE和△FDB中,,∴△ACE≌△FDB(SAS),∴AE=FB.25.解:(1)∵△ABD和△ACE都是等边三角形,∴∠DAB=60°,∠CAE=60°,∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,∵△ABD和△ACE都是等边三角形,∴AD=AB,AC=AE,∵在△ADC与△ABE中,∴△ADC≌△ABE(SAS),∴BE=CD=6.(2)在BE上截取EG=CF,连接AG,由(1)的证明,知△ADC≌△ABE,∴∠AEB=∠ACD,即∠AEG=∠ACF,∵AE=AC,在△AEG与△ACF中,∴△AEG≌△ACF(SAS),∴∠AGE=∠AFC,AG=AF,由∠AGE=∠AFC可得∠AGF=∠AFD,由AG=AF可得∠AGF=∠AFG,∴∠AFD=∠AFG,∴AF平分∠DFE.八年级数学期中试题(附答案)一.选择题(满分36分,每小题3分)1.一个正多边形的每一个外角都等于45°,则这个多边形的边数为()A.4 B.6 C.8 D.102.已知n是正整数,若一个三角形的三边长分别是n+2、n+4、n+8,则n的取值范围是()A.n>﹣1 B.n>0 C.n>2 D.n>33.在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是()A.B.C.D.4.下列说法不正确的是()A.一个三角形最多有一个直角B.一个三角形最多有一个钝角C.一个三角形的外角可以是锐角D.直角三角形的外角可以是锐角5.如图所示,已知△ABC中,∠A=80°,若沿图中虚线剪去∠A,则∠1+∠2等于()A.90°B.135°C.260°D.315°6.已知一个等腰三角形一内角的度数为80°,则这个等腰三角形顶角的度数为()A.100°B.80°C.50°或80°D.20°或80°7.如图,在△ABC中,AC=4,BC边上的垂直平分线DE分别交BC、AB于点D,若△AEC的周长是11,则AB=()A.28 B.18 C.10 D.78.如图,已知:AC=DF,AC∥FD,AE=DB,判断△ABC≌△DEF的依据是()A.SSS B.SAS C.ASA D.AAS9.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为()A.30°B.15°C.25°D.20°10.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,DE平分∠ADB,则∠B=()A.40°B.30°C.25°D.22.5°11.如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有()A.3个B.4个C.5个D.6个12.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是()A.22.5°B.45°C.67.5°D.135°二.填空题(满分40分,每小题5分)13.已知点P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2019的值为.14.如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,若∠ADC=60°,CD=2,则△ABC周长等于.15.若一个正多边形的内角和比四边形的内角和多360°,则这个正多边形的每个内角的度数为.16.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD于点E.若∠DBE=28°,则∠CAB=.17.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3,DE=5,则线段EC的长为.18.如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B的度数为.19.如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB 上的动点,则BM+MN的最小值是.20.如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“”.三.解答题21.(10分)如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.(1)由图观察易知点A(0,2)关于直线l的对称点A′坐标为(2,0),请在图中分别标明点B(5,3),C(﹣2,﹣5)关于直线l的对称点B′,C′的位置,并写出它们的坐标:B′、C′;(2)结合图形观察以上三组点的坐标,你发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′坐标为.22.(10分)如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H(1)求∠APB度数;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.23.(10分)如图,在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60cm和40cm 两部分,求边AC和AB的长.(提示:设CD=xcm)24.(10分)已知:在△ABC中,AB=AC,∠A=60°,求:∠B、∠C的度数,△ABC是什么三角形?25.(10分)如图,在△ABC中,∠ACB=110°,∠B>∠A,D,E为边AB上的两个点,且BD=BC,AE=AC.(1)若∠A=30°,求∠DCE的度数;(2)∠DCE的度数会随着∠A度数的变化而变化吗?请说明理由.26.(10分)已知:如图,△ABC的角平分线BE、CF相交于点P.求证:点P在∠A的平分线上.27.(14分)已知,如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.(1)求证:DB=DE;(2)若点F是BE的中点,连接DF,且CF=2,求等边三角形△ABC的边长.参考答案一.选择题1.解:多边形的边数为:360÷45=8.故选:C.2.解:∵三角形的三边长分别是n+2、n+4、n+8,∴n+2+n+4>n+8,解得n>2.故选:C.3.解:A、不是轴对称图形,故此选项不合题意;B、不是轴对称图形,故此选项不合题意;C、是轴对称图形,故此选项符合题意;D、不是轴对称图形,故此选项不合题意.故选:C.4.解:A、∵三角形的内角和等于180°,∴一个三角形最多有一个直角,故本选项说法正确,不符合题意;B、∵三角形的内角和等于180°,∴一个三角形最多有一个钝角,故本选项说法正确,不符合题意;C、∵钝角三角形有一个角是钝角,这个钝角的邻补角是锐角,∴一个三角形的外角可以是锐角,故本选项说法正确,不符合题意;D、∵直角三角形有一个直角,两个锐角,∴直角三角形的外角是直角或者钝角,不可以是锐角,故本选项说法错误,符合题意.故选:D.5.解:∵∠A=80°,∴∠B+∠C=100°,∵∠1+∠2+∠B+∠C=360°,∴∠1+∠2=260°.故选:C.6.解:(1)若等腰三角形一个底角为80°,顶角为180°﹣80°﹣80°=20°;(2)等腰三角形的顶角为80°.因此这个等腰三角形的顶角的度数为20°或80°.故选:D.7.解:∵DE是BC的中垂线,∴BE=EC,则AB=EB+AE=CE+EA,又∵△ACE的周长为11,故AB=11﹣4=7,故选:D.8.解:∵AC∥FD,∴∠CAD=∠ADF,∵AE=DB,∴ED=AB,∵AC=DF,∴△ABC≌△DEF(SAS),故选:B.9.解:证明:∵AD⊥BC,∴∠BDF=∠ADC,又∵∠BFD=∠AFE,∴∠CAD=∠FBD,在△BDF和△ADC中,∴△BDF≌△ADC(AAS)∴∠DBF=∠CAD=25°,∵DB=DA,∠ADB=90°,∴∠ABD=45°,∴∠ABE=∠ABD﹣∠DBF=20°故选:D.10.解:∵在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,∴CD=ED.在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴∠ADC=∠ADE(全等三角形的对应角相等).∵∠ADC+∠ADE+∠EDB=180°,DE平分∠ADB,∴∠ADC=∠ADE=∠EDB=60°.∴∠B+∠EDB=90°,∴∠B=30°.故选:B.11.解:∵在△ABC 中,∠A =36°,∠C =72°∴∠ABC =∠C ==72°,△ABC 是等腰三角形,∴∠DBC =36°,∴∠ABD =∠DBC =36°,∴BD 平分∠ABC ,∴∠ABD =∠DBC =36°,∵DE ∥BC ,∴∠EDB =∠DBC =36°,∴∠ABD =∠EDB =∠A ,∴AD =BD ,EB =ED ,即△ABD 和△EBD 是等腰三角形,∵∠BDC =180°﹣∠DBC ﹣∠C =72°,∴∠BDC =∠C ,∴BD =BC ,即△BCD 是等腰三角形,∵DE ∥BC ,∴∠AED =∠ABC ,∠ADE =∠C ,∴∠AED =∠ADE ,∴AE =AD ,即△AED 是等腰三角形.∴图中共有5个等腰三角形.故选:C .12.解:设∠B =x °,则∠A =3x °,由直角三角形的性质可得∠A +∠B =90°,∴x +3x =90,解得x =22.5,∴∠B =22.5°,故选:A .二.填空13.解:∵点P 1(a ﹣1,5)和P 2(2,b ﹣1)关于x 轴对称,∴a ﹣1=2,b ﹣1=﹣5,解得:a =3,b =﹣4,∴(a +b )2019=﹣1.故答案是:﹣1.14.解:∵∠C=90°,∠ADC=60°,∴∠CAD=30°,∵AD平分∠CAB,∴∠CAB=60°,∠B=30°,∵CD=2,∴AC=2,∴AB=2AC=2×2=4,∴BC==6,∴△ABC的周长为:AC+AB+BC=2+4+6=6+6,故答案为:6+6.15.解:设这个正多边形为n边形,根据题意,得(n﹣2)×180°=360°+360°.解得n=6.所以正六边形每个内角的度数为120°.故答案为120°16.解:∵BE⊥AE,∴∠E=∠C=90°,∵∠ADC=∠BDE,∴∠CAD=∠DBE=28°,∵AE平分∠CAB,∴∠CAB=2∠CAD=56°,故答案为56°.17.解:∵∠ABC和∠ACB的平分线相交于点F,∴∠DBF=∠FBC,∠ECF=∠BCF,∵DF∥BC,∴∠DFB=∠FBC,∠CFE=∠BCF,∴∠DFB=∠DBF,∠CFE=∠ECF,∴BD=DF=3,FE=CE,∴CE=DE﹣DF=5﹣3=2.故答案为:2.18.解:∵OA=OC,∴∠ACO=∠A=36°,∵BC∥AO,∴∠BCA=∠A=36°,∴∠BCO=72°,∵OB=OC,∴∠B=∠OCB=72°.故答案为:72°.19.解:如图,作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN为所求的最小值.∵AD是∠BAC的平分线,∴M′H=MN,∴BH是点B到直线AC的最短距离(垂线段最短),∵AB=5,∠BAC=45°,∴BH=AB•sin45°=5×=5.∴BM+MN的最小值是BM+MN=BM+MH=BH=5.故答案为:5.20.解:∵BE、CD是△ABC的高,∴∠CDB=∠BEC=90°,在Rt△BCD和Rt△CBE中,BD=EC,BC=CB,∴Rt△BCD≌Rt△CBE(HL),故答案为:HL.三.解答21.解:(1)如图,B′(3,5)、C′(﹣5,﹣2);(2)P′(b,a).故答案为(3,5),(﹣5,﹣2);P′(b,a).22.解:(1)∵AD平分∠BAC,BE平分∠ABC,∴∠PAB+∠PBA=(∠ABC+∠BAC)=45°,∴∠APB=180°﹣45°=135°;(2)∵∠APB=135°,∴∠DPB=45°,∵PF⊥AD,∴∠BPF=135°,在△ABP和△FBP中,,∴△ABP≌△FBP(ASA);(3)∵△ABP≌△FBP,∴∠F=∠BAD,AP=PF,AB=BF,∵∠BAD=∠CAD,∴∠F=∠CAD,在△APH和△FPD中,,∴△APH≌△FPD(ASA),∴AH=DF,∵BF=DF+BD,∴AB=AH+BD.23.解:∵AD是BC边上的中线,AC=2BC,∴BD=CD,设BD=CD=x,AB=y,则AC=4x,∵AC>AB,∴AC+CD=60,AB+BD=40,即4x+x=60,x+y=40,解得:x=12,y=28,即AC=4x=48cm,AB=28cm.24.解:∵在△ABC中,AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠B=∠C=60°.25.解:(1)设∠DCE=x,∠ACD=y,则∠ACE=x+y,∠BCE=110°﹣∠ACE=110°﹣x﹣y.∵AE=AC,∴∠ACE=∠AEC=x+y,∵BD=BC,∴∠BDC=∠BCD=∠BCE+∠DCE=110°﹣x﹣y+x=110°﹣y.在△DCE中,∵∠DCE+∠CDE+∠DEC=180°,∴x+(110°﹣y)+(x+y)=180°,解得x=35°,∴∠DCE=35°;(2)由(1)知,∠DCE的度数不会随着∠A度数的变化而变化.26.证明:如图,过点P作PD⊥AB、PM⊥BC、PN⊥AC垂足分别为D、M、N,∵BE平分∠ABC,点P在BE上,∴PD=PM,同理,PM=PN,∴PD=PN,∴点P在∠A的平分线上.27.(1)证明:∵△ABC是等边三角形∴∠ABC=∠ACB=60°又∵BD是中线∴BD平分∠ABC∴∠DBC=∠ABC=30°∵CE=CD∴∠E=∠CDE又∵∠ACB=∠E+∠CDE∴∠E=∠CDE=30°∴∠DBC=∠E∴DB=DE(2)解:由(1)可知DB=DE又∵点F是BE的中点∴DF⊥BE∵∠ACB=60°∴∠CDF=180°﹣90°﹣60°=30°又∵△CDF为直角三角形∴CF=CD,∴CD=4∵BD是中线∴AC=2CD=8即等边三角形△ABC的边长为8.。
四川2020-2022学年八年级上学期期中考试语文试题及答案分类汇编:古诗词默写 部编人教版八年级

四川2020-2022学年八年级上学期期中考试语文试题及答案分类汇编:古诗词默写部编人教版八年级上册四川省2020-2022学年八年级上学期期中考试语文试题分类汇编-古诗词默写+阅读四川省南充市营山县化育中学2020-2022学年八年级上学期期中考试语文试题11、按要求填写相应语句。
(共9分,每空1分)(1)晴川历历汉阳树,。
(《黄鹤楼》)(2)鸢飞戾天者,望峰息心;,。
(《与朱元思书》)(3),;烈士暮年,壮心不已。
(曹操《龟虽寿》)(4)《野望》中,点明时间、地点,表现诗人百无聊赖的彷徨心情的句子:,。
(5)《渡荆门送别》一诗中,化静为动,表现了雄浑开阔的意境的句子:,。
古诗文阅读欣赏(6分)【甲】使至塞上王维单车欲问边,属国过居延。
征蓬出汉塞,归雁入胡天。
大漠孤烟直,长河落日圆。
萧关逢候骑,都护在燕然。
【乙】战城南杨炯塞北途辽远,城南战苦辛。
幡旗如鸟翼,甲胄似鱼鳞。
冻水寒伤马,悲风愁杀人。
寸心明白日①,千里暗黄尘。
【注】白日:喻指君主。
典出宋玉《九辩》:“去白日之昭昭兮,袭长夜之悠悠。
”(1)下列对诗歌的赏析,不正确的一项是()(2分)A:甲诗通过描写出使塞上的所见所闻,表达了诗人的爱国之情。
同时“单车”“征蓬”“归雁”也传达内心的忧郁和激愤。
B:甲诗尾联是实写,又暗示了边塞将士紧张的战斗生活,表达了作者对将士们戍守边关、奋勇杀敌的敬意。
C:乙诗以征战者的口吻记述戍边生活,将战场上的血腥和残酷场面写得淋漓尽致,读者从诗句中感受到将士内心的低落与哀怨。
D:乙诗颔联通过典型景物“幡旗”“甲胄”来描绘战场景象。
战旗猎猎,盔甲似鱼鳞,不但写出了军队威严,而且写出了士兵斗志。
(2)请你发挥想象,用生动的语言描述“大漠孤烟直,长河落日圆”所展现的画面。
(2分)(3)甲乙两首诗颈联都描写了边塞景色,请分析景色的特点有何不同。
(2分)1芳草萋萋鹦鹉洲2经纶世务者,窥谷忘反3老骥伏枥,志在千里4东皋薄暮望,徙倚欲何依5山随平野尽,江入大荒流(1)C(2)广阔无垠的大漠上,烽火台上燃起一缕烽烟直上云霄;黄河如带,一轮落日孤悬于地平线上,显得又大又圆。
2020年人教版八年级语文上册期中试卷及参考答案(精品)

2020年人教版八年级语文上册期中试卷及参考答案(精品)满分:120分考试时间:120分钟一、语言的积累与运用。
(35分)1、下列词语中加点字注音全都正确的一项是()A.秀颀.(qí)烂熳.(màn)溃.退(kuì)深恶.痛疾(è)B.畸.形(qí)婆娑.(suō)甲胄.(zhóu)坦荡如砥.(dǐ)C.教诲.(huǐ)濒.临(pín)不逊.(xùn)惟妙惟肖.(xiào)D.嶙峋.(xún)黝.黑(yǒu)滞.留(zhì)触.目伤怀(chù)3、下列句子中加点成语使用不恰当的一项是()A.虽然她看见黄太太竟那样和颜悦色....地对待师母,但心里还是老大不痛快的。
B.我们读这首诗,尤其有一种入木三分....、痛快淋漓的感受。
C.清末革命军一起义,腐败的清廷毫无招架之力,瞬间就如摧枯拉朽....般地被推翻了。
D.这部小说情节跌宕起伏,抑扬顿挫....,具有很强的感染力。
4、下列句子没有语病的一项是()A.沪昆高铁开通后,从昆明到上海的时间大约需要12小时,比原来减少了三倍。
B.6月5日,中国选手马龙在2017世界乒乓球锦标赛男单决赛中,以4︰3的比分打败了对手樊振东,再次蝉联冠军。
C.通过全市上下的共同努力,让曲靖市交出了一份提升城乡人居环境满意的成绩单。
D.共享单车是指企业与政府合作,在校园、地铁站点、公交站点……提供自行车共享服务,是共享经济的一种新形态。
5、下列各项判断与分析中,不正确的一项是()A.咝溜溜的南风吹动了高粱叶子。
(这个句子的谓语是“吹动”。
)B.那树有一点佝偻,露出老态,但是坚固稳定,树顶像刚炸开的焰火一样繁密。
(这句话运用拟人和比喻的修辞手法,写出那树虽老但枝繁叶茂的状态。
)C.“狂澜”“沉湎”“鞠躬尽瘁”“呕心沥血”(这四个词感情色彩相同。
)D.防止校园欺凌事件不再发生,不让戾气弥漫整个校园,是一个系统工程,需要多方面、多领域齐心协力。
2020年部编版八年级语文上册期中试卷及答案(完整)

2020年部编版八年级语文上册期中试卷及答案(完整)2020年部编版八年级语文上册期中试卷及答案(完整)满分:120分考试时间:120分钟一、语言的积累与运用。
(35分)1、下列词语加点字注音完全正确的一项是()A.匿名(lì)遁形(dùn)溃退(kuì)油光可鉴(jiàn)B.咆哮(páo)揪紧(jiū)畸形(jī)正襟危坐(jīng)C.粗糙(cāo)滞留(zhì)骤雨(zhòu)杳无消息(yăo)D.湛蓝(zhàn)初衷(zōng)发髻(jì)广袤无垠(mào)3、下列句子中加点成语使用有误的一项是()A.这里风景优美,空气清新,只是重岩叠嶂走起来要小心。
B.“嫦娥一号”卫星的成功发射,无疑是为我国航天事业建起了一座巍峨的海市蜃楼。
C.只见落梅山庄坐落在群山万壑之间,风景秀丽,宁静而又祥和的气氛让人望峰息心。
D.西南方有一片竹林,林子遮天蔽日,棵棵翠绿挺拔。
一阵秋风吹过,林子“沙沙”作响。
4、下列句子中有语病的一项是()A.我们将通过植树造林,使有着“山水洲城”美誉的长沙山更青、水更碧。
B.随着城市街头共享单车的出现,不仅给人们的出行带来便利,而且环保、经济。
XXX是这笔资金的合法拥有者,并管理这笔资金的投资,但与诺贝尔奖的评定无关。
D.他留下来的资金每年的利息将领取这5种诺贝尔奖金。
5、以下句子没有使用修辞手法的一项是()A.其岸势犬牙差互,不可知其源。
B.母亲自得地说了一遍又一遍,兴奋得两颊红红的,跟喝过酒似的。
C.啊!黄河!你一泻万丈,声势赫赫,向南北两岸伸出万万条铁的臂膀。
D.容不得束缚,容不得羁绊,容不得闭塞。
6、请选出下列选项中排序正确的一项()①关于它的起源,最初是祛除暑热疫病、禳灾止恶的活动。
②逐渐形成了缅怀先贤、忠君爱国的传统。
③经过几千年的文化积累和节俗传承,吃粽子、赛龙舟、纪念XXX已经成为当今流传范围最广的端午节俗活动,融进了世代中华儿女的生活记忆。
2020-2021学年八年级上学期数学期中考试卷附答案
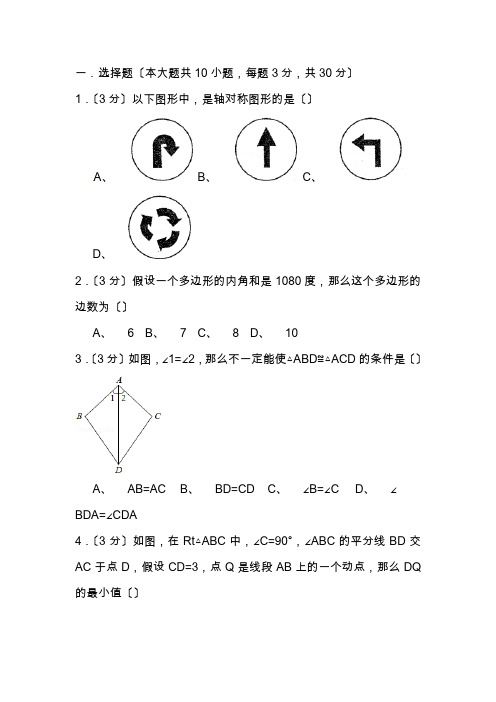
一.选择题〔本大题共10小题,每题3分,共30分〕1.〔3分〕以下图形中,是轴对称图形的是〔〕A、 B、C、D、2.〔3分〕假设一个多边形的内角和是1080度,那么这个多边形的边数为〔〕A、 6B、7C、8D、103.〔3分〕如图,∠1=∠2,那么不一定能使△ABD≌△ACD的条件是〔〕A、AB=ACB、BD=CDC、∠B=∠CD、∠BDA=∠CDA4.〔3分〕如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,假设CD=3,点Q是线段AB上的一个动点,那么DQ 的最小值〔〕A、 5B、 4C、 3D、 25.〔3分〕为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是〔〕A、5mB、15mC、20mD、28m6.〔3分〕如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处.假设∠1=129°,那么∠2的度数为〔〕A、49°B、50°C、51°D、52°7.〔3分〕如下图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是〔〕A、SSSB、SASC、AASD、ASA8.〔3分〕如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,那么以下结论不正确是〔〕A、AE平分∠DAEB、AB∥CDC、△EBA≌△DCED、AB+CD=AD9.〔3分〕如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,那么这样的三角形〔不包含△ABC本身〕共有〔〕A、1个B、2个C、3个D、4个10.〔3分〕如下图的正方形网格中,网格线的交点称为格点.A、B 是两格点,如果C也是图中的格点,且使得△ABC为等腰直角三角形,那么点C的个数是〔〕A、 2B、 4C、 6D、8【二】填空题〔此题共6小题,每题3分,共18分〕11.〔3分〕等腰三角形一边长等于4,一边长等于9,它的周长是.12.〔3分〕如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于点D,如果BC=10cm,那么△BCD的周长是cm.13.〔3分〕如图△ABC中,AB=AD=DC,∠BAD=40°,那么∠C=.14.〔3分〕如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=4,那么AD=.15.〔3分〕如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E、假设AB=5,AC=4,那么△ADE的周长是.16.〔3分〕如图,图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板〔即其边长为前一块被剪掉正三角形纸板边长的后,得图③、④,…,记第n〔n≥3〕块纸板的周长为Pn,那么周长Pn=.三.解答题〔此题共10题,共102分,解答应写文字说明,证明过程或演算步骤〕17.〔10分〕△ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF ⊥AC于F,求证:DE=DF.18.〔10分〕如图,边长为1的正方形网格中,△ABC的顶点均在格点上,在所给的直角坐标系中解答以下问题〔1〕画出△ABC关于x轴对称的△A′B′C′,并写出A′、B′、C′三点的坐标;〔2〕在y轴上作出点P,使PA+PB的长最小.〔保留痕迹找出点P 即可〕〔3〕假设△ABC内有一点Q〔2m+n,3.5〕关于x轴对称后Q′〔2.5,n﹣m〕,求m,n的值.19.〔10分〕等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.20.〔10分〕如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于D,求:〔1〕∠CBD的度数;〔2〕假设△BCD的周长是m,求BC的长.21.〔10分〕如图,在平面直角坐标系中,在第一象限内,OM与OB是两坐标轴的夹角的三等分线点E是OM上一点,EC⊥X轴于C 点,ED⊥OB于D点,OD=8,OE=10〔1〕求证:∠ECD=∠EDC;〔2〕求证:OE垂直平分CD、22.〔10分〕如图,△ABC为等边三角形,点D,E分别在BC,AC 边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.〔1〕求证:△ABE≌△CAD;〔2〕求AD的长.23.〔10分〕如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE、〔1〕求证:△DEF是等腰三角形;〔2〕当DE⊥EF,E是BC的中点时,试比较BD+CF与DF的大小.24.〔10分〕四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC= 120°,∠MBN=60°,∠MBN的两边分别交AD、CD于E、F.〔1〕当AE=CF时,如图1试猜想AE+CF与EF之间存在怎样的数量关系?请给予证明.〔2〕当AE≠CF,如图2的情况下,上问的结论分别是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.25.〔12分〕:在平面直角坐标系中,等腰Rt△ABC的顶点A、C在坐标轴上运动,且∠ACB=90°,AC=BC、〔1〕如图1,当A〔0,﹣2〕,C〔1,0〕,点B在第四象限时,那么点B的坐标为;〔2〕如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.〔3〕如图3,当点C在y轴正半轴上运动,点A在x轴正半轴上运动,使点D恰为BC的中点,连接DE,求证:∠ADC=∠BDE、参考答案与试题解析一.选择题〔本大题共10小题,每题3分,共30分〕1.〔3分〕以下图形中,是轴对称图形的是〔〕A、 B、C、D、考点:轴对称图形.分析:根据轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线〔成轴〕对称,进而得出答案.解答:解:A、不是轴对称图形,故A错误;B、是轴对称图形,故B正确;C、不是轴对称图形,故C错误;D、不是轴对称图形,故D错误.应选:B、点评:此题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.2.〔3分〕假设一个多边形的内角和是1080度,那么这个多边形的边数为〔〕A、 6B、7C、8D、10考点:多边形内角与外角.分析:n边形的内角和是〔n﹣2〕•180°,如果多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.解答:解:根据n边形的内角和公式,得〔n﹣2〕•180=1080,解得n=8.∴这个多边形的边数是8.应选:C、点评:此题考查了多边形的内角与外角,熟记内角和公式和外角和定理并列出方程是解题的关键.根据多边形的内角和定理,求边数的问题就可以转化为解方程的问题来解决.3.〔3分〕如图,∠1=∠2,那么不一定能使△ABD≌△ACD的条件是〔〕A、AB=ACB、BD=CDC、∠B=∠CD、∠BDA=∠CDA考点:全等三角形的判定.专题:压轴题.分析:利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.解答:解:A、∵∠1=∠2,AD为公共边,假设AB=AC,那么△ABD ≌△ACD〔SAS〕;故A不符合题意;B、∵∠1=∠2,AD为公共边,假设BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;C、∵∠1=∠2,AD为公共边,假设∠B=∠C,那么△ABD≌△ACD〔AAS〕;故C不符合题意;D、∵∠1=∠2,AD为公共边,假设∠BDA=∠CDA,那么△ABD≌△ACD 〔ASA〕;故D不符合题意.应选:B、点评:此题主要考查学生对全等三角形判定定理的理解和掌握,此题难度不大,属于基础题.4.〔3分〕如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,假设CD=3,点Q是线段AB上的一个动点,那么DQ 的最小值〔〕A、 5B、 4C、 3D、 2考点:角平分线的性质;垂线段最短.分析:根据垂线段最短,过点D作DQ⊥AB于Q,此时DQ的值最小,再根据角平分线上的点到角的两边距离相等可得DQ=CD、解答:解:如图,过点D作DQ⊥AB于Q,由垂线段最短可得,此时DQ的值最小,∵∠C=90°,BD是∠ABC的平分线,∴DQ=CD=3.应选C、点评:此题考查了角平分线上的点到角的两边距离相等的性质,垂线段最短的性质,熟记性质并确定出DQ最短的情况是解题的关键.5.〔3分〕为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是〔〕A、5mB、15mC、20mD、28m考点:三角形三边关系.专题:应用题.分析:首先根据三角形的三边关系定理求出AB的取值范围,然后再判断各选项是否正确.解答:解:∵PA、PB、AB能构成三角形,∴PA﹣PB<AB<PA+PB,即4m<AB<28m.应选D、点评:三角形的两边,那么第三边的范围是:大于的两边的差,而小于两边的和.6.〔3分〕如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处.假设∠1=129°,那么∠2的度数为〔〕A、49°B、50°C、51°D、52°考点:翻折变换〔折叠问题〕;三角形内角和定理.专题:计算题.分析:根据翻折的性质可知,∠DOE=∠A,∠HOG=∠B,∠EOF=∠C,又∠A+∠B+∠C=180°,可知∠1+∠2=180°,又∠1=129°,继而即可求出答案.解答:解:根据翻折的性质可知,∠DOE=∠A,∠HOG=∠B,∠EOF=∠C,又∵∠A+∠B+∠C=180°,∴∠DOE+∠HOG+∠EOF=180°,∴∠1+∠2=180°,又∵∠1=129°,∴∠2=51°.应选C、点评:此题考查翻折变换的知识,解答此题的关键是三角形折叠以后的图形和原图形全等,对应的角相等,同时注意三角形内角和定理的灵活运用.7.〔3分〕如下图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是〔〕A、SSSB、SASC、AASD、ASA考点:全等三角形的应用.分析:根据图象,三角形有两角和它们的夹边是完整的,所以可以根据〝角边角〞画出.解答:解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用〝角边角〞定理作出完全一样的三角形.应选D、点评:此题考查了三角形全等的判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.8.〔3分〕如图,∠B=∠C=90°,E是BC的中点,DE平分线∠ADC,那么以下结论不正确是〔〕A、AE平分∠DAEB、AB∥CDC、△EBA≌△DCED、AB+CD=AD考点:全等三角形的判定与性质;平行线的判定.分析:由∠B=∠C=90°,直接得出选项B成立;作EF⊥AD垂足为点F,证得△DEF≌△DCE和△AFE≌△ABE,得出选项A、选项D成立;因为AB≠CD,AE≠DE,不可能得出选项C成立;由此得出结论即可.解答:解:∵∠B=∠C=90°,∴∠B+∠C=180°,∴AB∥CD,故B正确;如图,作EF⊥AD垂足为点F,∴∠DFE=90°,∴∠DFE=∠C,∵DE平分∠ADC,∴∠FDE=∠CDE,在△DEF和△DCE中;,∴△DEF≌△DCE〔AAS〕;∴CE=EF,DC=DF,∠CED=∠FED,又∵∠B=∠C=∠DFE=90°,AE=AE,在Rt△AFE和Rt△ABE中,,∴Rt△AFE≌Rt△ABE〔HL〕;∴AF=AB,∠FAE=∠BAE,∠AEF=∠AEB,∴AE平分∠DAB,故A正确;AD=AF+DF=AB+CD,故D正确;∠AED=∠FED+AEF=∠FEC+∠BEF=90°,即AE⊥DE、∵AB≠CD,AE≠DE,∴△EBA≌△DCE不可能成立.即C不正确;应选:C、点评:此题题综合考查了角平分线的性质、三角形全等的判定与性质等知识点.9.〔3分〕如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,那么这样的三角形〔不包含△ABC本身〕共有〔〕A、1个B、2个C、3个D、4个考点:轴对称的性质.分析:先把田字格图标上字母如图,确定对称轴找出符合条件的三角形,再计算个数.解答:解:△HEC关于CD对称;△FDB关于BE对称;△GED关于HF对称;关于AG对称的是它本身.所以共3个.应选C、点评:此题考查了轴对称的性质;确定对称轴然后找出成轴对称的三角形是解题的关键.10.〔3分〕如下图的正方形网格中,网格线的交点称为格点.A、B 是两格点,如果C也是图中的格点,且使得△ABC为等腰直角三角形,那么点C的个数是〔〕A、 2B、 4C、 6D、8考点:等腰直角三角形;勾股定理.专题:网格型.分析:根据题意,结合图形,分两种情况讨论:①AB为等腰△ABC 底边;②AB为等腰△ABC其中的一条腰.解答:解:如上图:分情况讨论①AB为等腰直角△ABC底边时,符合条件的C点有2个;②AB为等腰直角△ABC其中的一条腰时,符合条件的C点有4个.应选:C、点评:此题考查了等腰三角形的判定;解答此题关键是根据题意,画出符合实际条件的图形,再利用数学知识来求解.数形结合的思想是数学解题中很重要的解题思想.【二】填空题〔此题共6小题,每题3分,共18分〕11.〔3分〕等腰三角形一边长等于4,一边长等于9,它的周长是22.考点:等腰三角形的性质.分析:题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.解答:解:∵4+4=8<9,0<4<9+9=18∴腰的不应为4,而应为9∴等腰三角形的周长=4+9+9=22故填:22.点评:此题考查了等腰三角形的性质和三角形的三边关系;没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.12.〔3分〕如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于点D,如果BC=10cm,那么△BCD的周长是26 cm.考点:线段垂直平分线的性质;等腰三角形的性质.分析:连接BD,根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,然后求出△BCD的周长=BC+AC,代入数据计算即可得解.解答:解:如图,连接BD、∵DE是AB的垂直平分线,∴AD=BD,∴△BCD的周长=BC+BD+CD=BC+AD+CD=BC+AC,∵AC=16cm,BC=10cm,∴△BCD的周长=10+16=26cm.故答案为:26.点评:此题考查了线段垂直平分线上的点到两端点的距离相等的性质,熟记性质是解题的关键.13.〔3分〕如图△ABC中,AB=AD=DC,∠BAD=40°,那么∠C=35°.考点:等腰三角形的性质.分析:根据等腰三角形两底角相等求出∠B,根据等边对等角可得∠C=∠CAD,然后利用三角形的内角和定理列式进行计算即可得解.解答:解:∵AB=AD,∠BAD=40°,∴∠B=〔180°﹣∠BAD〕=〔180°﹣40°〕=70°,∵AD=DC,∴∠C=∠CAD,在△A BC中,∠BAC+∠B+∠C=180°,即40°+∠C+∠C+70°=180°,解得∠C=35°.故答案为:35°.点评:此题考查了等腰三角形两底角相等的性质,等边对等角的性质,熟记性质是解题的关键.14.〔3分〕如图,在△ABC中,∠C=90°,∠A=15°,∠DBC=60°,BC=4,那么AD=8.考点:含30度角的直角三角形;等腰三角形的判定与性质.分析:根据直角三角形两锐角互余求出∠BDC=30°,然后根据30°角所对的直角边等于斜边的一半求出BD,再求出∠ABC,然后求出∠ABD=15°,从而得到∠ABD=∠A,根据等角对等边可得AD=BD,从而得解.解答:解:∵∠DBC=60°,∠C=90°,∴∠BDC=90°﹣60°=30°,∴BD=2BC=2×4=8,∵∠C=90°,∠A=15°,∴∠ABC=90°﹣15°=75°,∴∠ABD=∠ABC﹣∠DBC=75°﹣60°=15°,∴∠ABD=∠A,∴AD=BD=8.故答案为:8.点评:此题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余的性质,等角对等边的性质,熟记性质是解题的关键.15.〔3分〕如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E、假设AB=5,AC=4,那么△ADE的周长是9.考点:等腰三角形的判定与性质;平行线的性质.专题:压轴题.分析:由在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,易证得△DOB与△EOC是等腰三角形,即DO=DB,EO=EC,继而可得△ADE的周长等于AB+AC,即可求得答案.解答:解:∵在△ABC中,∠B与∠C的平分线交于点O,∴∠DBO=∠CBO,∠ECO=∠BCO,∵DE∥BC,∴∠DOB=∠CBO,∠EOC=∠BCO,∴∠DBO=∠DOB,∠ECO=∠EOC,∴OD=BD,OE=CE,∵AB=5,AC=4,∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.故答案为:9.点评:此题考查了等腰三角形的判定与性质、角平分线的定义以及平行线的性质.此题难度适中,注意证得△DOB与△EOC是等腰三角形是解此题的关键,注意掌握数形结合思想与转化思想的应用.16.〔3分〕如图,图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板〔即其边长为前一块被剪掉正三角形纸板边长的后,得图③、④,…,记第n〔n≥3〕块纸板的周长为Pn,那么周长Pn=3﹣.考点:规律型:图形的变化类;等边三角形的性质.分析:根据等边三角形的性质〔三边相等〕求出等边三角形的周长P1,P2,P3,P4,然后即可得到规律.解答:解:P1=1+1+1=3,P2=1+1+==3﹣,P3=1+1+×3==3﹣,P4=1+1+×2+×3==3﹣,…Pn=3﹣,故答案为:3﹣.点评:此题主要考查对等边三角形的性质的理解和掌握,此题是一个规律型的题目,题型较好.三.解答题〔此题共10题,共102分,解答应写文字说明,证明过程或演算步骤〕17.〔10分〕△ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF ⊥AC于F,求证:DE=DF.考点:全等三角形的判定与性质;等腰三角形的性质.专题:证明题.分析:根据AB=AC,D是BC中点,DE⊥AB于E,DF⊥AC于F,利用角角边定理可证此题,解答:证明:∵AB=AC,D是BC中点,∴∠ABC=∠ACB,BD=DC、∵DE⊥AB于E,DF⊥AC于F,∴∠DEB=∠DFC=90°在△DEB和△DFC中,,∴△DEB≌△DFC〔AAS〕,∴DE=DF.点评:此题主要考查学生对全等三角形的判定与性质和等腰三角形的性质的理解和掌握,难度不大,是一道基础题.18.〔10分〕如图,边长为1的正方形网格中,△ABC的顶点均在格点上,在所给的直角坐标系中解答以下问题〔1〕画出△ABC关于x轴对称的△A′B′C′,并写出A′、B′、C′三点的坐标;〔2〕在y轴上作出点P,使PA+PB的长最小.〔保留痕迹找出点P 即可〕〔3〕假设△ABC内有一点Q〔2m+n,3.5〕关于x轴对称后Q′〔2.5,n﹣m〕,求m,n的值.考点:作图-轴对称变换;轴对称-最短路线问题.分析:〔1〕直接利用关于x轴对称点的性质得出各点坐标画出图形即可;〔2〕利用轴对称求最短路线的方法得出即可;〔3〕利用关于x轴对称点的性质得出横纵坐标关系得出答案.解答:解:〔1〕如下图:A′〔4,﹣4〕、B′〔1,﹣2〕、C′〔3,﹣2〕;〔2〕如下图:P点即为所求;〔3〕∵△ABC内有一点Q〔2m+n,3.5〕关于x轴对称后Q′〔2.5,n﹣m〕,∴,解得:.点评:此题主要考查了轴对称变换以及利用轴对称求最短路径问题,得出对应点位置是解题关键.19.〔10分〕等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.考点:等边三角形的判定;全等三角形的判定与性质.专题:探究型.分析:先证△ABP≌△ACQ得AP=AQ,再证∠PAQ=60°,从而得出△APQ是等边三角形.解答:解:△APQ为等边三角形.证明:∵△ABC为等边三角形,∴AB=AC、在△ABP与△ACQ中,∵,∴△ABP≌△ACQ〔SAS〕.∴AP=AQ,∠BAP=∠CAQ.∵∠BAC=∠BAP+∠PAC=60°,∴∠PAQ=∠CAQ+∠PAC=60°,∴△APQ是等边三角形.点评:考查了等边三角形的判定及全等三角形的判定方法.20.〔10分〕如图,AB=AC=10,∠A=40°,AB的垂直平分线MN交AC于D,求:〔1〕∠CBD的度数;〔2〕假设△BCD的周长是m,求BC的长.考点:线段垂直平分线的性质;等腰三角形的性质.分析:〔1〕由垂直平分线的性质可知DA=DB,可求得∠ABD=40°,再由AB=AC,可求得∠ABC,再利用角的和差可求得∠CBD;〔2〕由〔1〕可知AD=BD,可得BD+CD=AC=10,结合△BCD的周长可求得BC、解答:解:〔1〕∵AB的垂直平分线MN交AC于D,∴DA=DB,∴∠ABD=∠A=40°,∵AB=AC,∴∠ABC=∠ACB==70°,∴∠CBD=∠ABC﹣∠ABD=70°﹣40°=30°;〔2〕由〔1〕可知DA=DB,∴BD+DC=AD+DC=AC=10,∵△BCD的周长是m,∴BC=m﹣10.点评:此题主要考查线段垂直平分线的性质,掌握线段垂直平分线的点到线段两端点的距离相等是解题的关键.21.〔10分〕如图,在平面直角坐标系中,在第一象限内,OM与OB是两坐标轴的夹角的三等分线点E是OM上一点,EC⊥X轴于C 点,ED⊥OB于D点,OD=8,OE=10〔1〕求证:∠ECD=∠EDC;〔2〕求证:OE垂直平分CD、考点:角平分线的性质;全等三角形的判定与性质;等腰三角形的判定与性质.分析:〔1〕由角平分线的性质可得ED=EC,那么可得∠ECD=∠EDC;〔2〕由角平分线的性质可知ED=EC,在Rt△ODE中可求得DE=6,那么EC=6,在Rt△OEC中可求得OC=8=OD,可得点E、O都在线段CD的垂直平分线上,可知OE垂直平分CD、解答:证明:〔1〕∵OM与OB是两坐标轴的夹角的三等分线,∴OM平分∠BOC,∵EC⊥X轴于C点,ED⊥OB于D点,∴DE=CE,∴∠ECD=∠EDC;〔2〕在Rt△ODE中,OD=8,OE=10,由勾股定理可求得DE=6,由〔1〕可得EC=ED=6,在Rt△OCE中,OE=10,EC=6,由勾股定理可求得OC=8,∴OC=OD,∴点O、E都在线段CD的垂直平分线上,∴OE垂直平分CD、点评:此题主要考查角平分线的性质及等腰三角形的性质、线段垂直平分线的判定,由条件得到DE=CE且求得OC=OD=8是解题的关键,注意勾股定理的应用.22.〔10分〕如图,△ABC为等边三角形,点D,E分别在BC,AC 边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.〔1〕求证:△ABE≌△CAD;〔2〕求AD的长.考点:全等三角形的判定与性质;等边三角形的性质.分析:〔1〕根据AE=CD,AB=AC,∠BAC=∠C即可求得△ABE≌△CAD;〔2〕由〔1〕得∠AEB=∠ADC,即可求得∠BPQ=∠C,即可求得BP 的长,即可解题.解答:解:〔1〕∵在△ABE和△CAD中,,∴△ABE≌△CAD,〔SAS〕〔2〕∵△ABE≌△CAD,∴AD=BE,∠AEB=∠ADC∵∠DAC+∠ADC+∠ACB=180°,∠DAC+∠AEB+∠APE=180°,∴∠ACB=∠APE=60°,∴∠BPQ=60°,∴∠PBQ=30°,∴BP=2PQ=6,∴AD=BE=BP+PE=6+1=7.点评:此题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,此题中求证△ABE≌△CAD是解题的关键.23.〔10分〕如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE、〔1〕求证:△DEF是等腰三角形;〔2〕当DE⊥EF,E是BC的中点时,试比较BD+CF与DF的大小.考点:全等三角形的判定与性质;等腰三角形的判定与性质.分析:〔1〕根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;〔2〕根据E是BC的中点BD=CF=BE=CE,即可求得DF∥BC,即可解题.解答:〔1〕证明:∵AB=AC,[来源:]∴∠B=∠C,∵在△BDE和△CEF中,,∴△BDE≌△CEF,〔SAS〕∴DE=EF,∴△DEF是等腰三角形;〔2〕解:∵E是BC的中点,BE=CF,BD=CE、∴BD=CF=BE=CE,∴BD+CF=BC,∴∠BDE=∠CFE,∴∠ADF=∠AFD,∴DF∥BC,∵BC>DF,∴BD+CF>DF.点评:此题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,此题中求证△BDE≌△CEF是解题的关键.24.〔10分〕四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC= 120°,∠MBN=60°,∠MBN的两边分别交AD、CD于E、F.〔1〕当AE=CF时,如图1试猜想AE+CF与EF之间存在怎样的数量关系?请给予证明.〔2〕当AE≠CF,如图2的情况下,上问的结论分别是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.考点:全等三角形的判定与性质;等边三角形的判定与性质.分析:〔1〕作BQ⊥EF,易证△ABE≌△CBF和△BEF为等边三角形,可得∠ABE=30°和EF=BF,即可解题;〔2〕延长DA,使得AQ=CF,可证RT△BCF≌RT△BAQ,可得∠ABQ=∠CBF,CF=AQ,进而可以求证△BEF≌△BEQ得到QE=EF,即可解题.解答:解:〔1〕作BQ⊥EF,∵AE=CF,AB=BC,∴根据勾股定理可得:BF=BE,∵∠MBN=60°∴△BEF为等边三角形,∴EF=BF=BE,在RT△ABE和RT△CBF中,,∴RT△ABE≌RT△CBF〔HL〕,∴∠ABE=∠CBF,∵∠MBN=60°,∠ABC=120°,∴∠ABE=∠CBF=30°,∴BF=2CF,∴AE+CF=EF;〔2〕延长DA,使得AQ=CF,∵AQ=CF,AB=AC,∴根据勾股定理可得:BQ=BF,在RT△BCF和RT△BAQ中,,∴RT△BCF≌RT△BAQ〔HL〕,∴∠ABQ=∠CBF,CF=AQ,∴∠FBQ=∠ABC=120°,∴∠QBE=60°,在△BEF和△BEQ中,,∴△BEF≌△BEQ〔SAS〕,∴QE=EF,∴EF=QE=AE+AQ=AE+CF.点评:此题考查了全等三角形的判定,考查了全等三角形对应边相等、对应角相等的性质,此题中,〔1〕中求证RT△ABE≌RT△CBF,〔2〕中求证△BEF≌△BEQ是解题的关键.25.〔12分〕:在平面直角坐标系中,等腰Rt△ABC的顶点A、C在坐标轴上运动,且∠ACB=90°,AC=BC、〔1〕如图1,当A〔0,﹣2〕,C〔1,0〕,点B在第四象限时,那么点B的坐标为〔3,﹣1〕;〔2〕如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断与哪一个是定值,并说明定值是多少?请证明你的结论.〔3〕如图3,当点C在y轴正半轴上运动,点A在x轴正半轴上运动,使点D恰为BC的中点,连接DE,求证:∠ADC=∠BDE、考点:全等三角形的判定与性质;坐标与图形性质;等腰直角三角形.分析:〔1〕作BD⊥CD,易证△OAC≌△DCB,即可解题;〔2〕作BE⊥OC,易证OAC≌△ECB,可求得OC=AO+BD,即可解题;〔3〕过点B作BG⊥BC交y轴于点G,易证△BCG≌△CAD,可得BG=BD,进而可以求证△DBE≌△GBE,可得∠BDE=∠BGE,即可解题.解答:解:〔1〕作BD⊥CD,∵∠OCA+∠DCB=90°,∠OAC+∠DCB=90°,∴∠OAC=∠DCB,∵在△OAC和△DCB中,,∴△OAC≌△DCB,〔AAS〕∴CD=OA=2,BD=OC=1,OD=3,∴B点坐标为〔3,﹣1〕;〔2〕作BE⊥OC,那么四边形ODBE为矩形,∵∠ACO+∠BC O=90°,∠ACO+∠OAC=90°,∴∠BCO=∠CAO,∵△OAC和△ECB中,,∴△OAC≌△ECB,〔AAS〕∴EC=OA,∵四边形ODBE为矩形,∴OE=BD,∵OC=OE+EC,∴OC=AO+BD,∴存在定值,且为1;〔3〕过点B作BG⊥BC交y轴于点G,∴∠CBG=∠ACD=90°,∵∠BCG+∠ACG=90°,∠ACO+∠DCO=90°,∴∠DCO=∠CAO.在△BCG和△CAD中,,∴△BCG≌△CAD〔ASA〕,∴BG=CD=BD、∵∠ABC=∠BAC=45°,∴∠EBG=∠DBE=45°,在△DBE和△GBE中,,∴△DBE≌△GBE〔SAS〕,∴∠BDE=∠BGE,∵∠BCG+∠BGE=90°,∠BCG+∠ADC=90°,∴∠BGE=∠ADC,∴∠ADB=∠CDE、点评:此题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,此题中每一问都找出全等三角形并求证是解题的关键.。
【2020】最新八年级上数学期中试卷及答案新版

(1)如图1,如果∠BAD=30°AD是BC上的高,AD=AE,则∠EDC=__________
(2)如图2,如果∠BAD=40°AD是BC上的高,AD=AE,则∠EDC=__________
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由
(1)(2)(3)
3.如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB.B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1.C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过20xx次操作后△A20xxB20xxC20xx的面积为_____________
19.如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯至少要
米长。
20.有一块田地的形状和尺寸如图所示,则它的面积为。
三.耐心做一做(本题有6小题,共50分,各小题都必须写出解答过程)
21.(本题6分)如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹。
(3)∵∠DBC=∠A+∠ACB,
∵P为△ABC两外角平分线的交点,
∴ ∠DBC= ∠A+ ∠ACB,同理可得:∴ ∠BCE= ∠A+ ∠ABC,
2020年八年级数学上期中试卷含答案

2020年八年级数学上期中试卷含答案一、选择题1.下列四个图形中,既是轴对称图形又是中心对称图形的有()A.4个 B.3个 C.2个 D.1个2.华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A.7710⨯﹣B.80.710⨯﹣C.8710⨯﹣D.9710⨯﹣3.从甲地到乙地有两条路:一条是全长750km的普通公路,另一条是全长600km高速公路.某客车从甲地出发去乙地,若走高速公路,则平均速度是走普通公路的平均速度的2倍,所需时间比走普通公路所需时间少5小时.设客车在普通公路上行驶的平均速度是x km/h,则下列等式正确的是()A.600x+5=7502xB.600x-5=7502xC.6002x+5=750xD.6002x-5=750x4.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114°D.124°5.如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )A.△ABC≌△CDE B.CE=AC C.AB⊥CD D.E为BC的中点6.如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于()A .132°B .134°C .136°D .138° 7.具备下列条件的△ABC 中,不是直角三角形的是( ) A .∠A+∠B=∠CB .∠A=12∠B=13∠C C .∠A :∠B :∠C=1:2:3D .∠A=2∠B=3∠C8.如图,直线123l l l 、、表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .二处C .三处D .四处9.如图,在ABC ∆中,64A ∠=︒,ABC ∠与ACD ∠的平分线交于点1A ,得1A ∠;1A BC ∠与1A CD ∠的平分线相交于点2A ,得2A ∠;……;1n A BC -∠与1n A CD -∠的平分线交于点n A ,要使n A ∠的度数为整数,则n 的最大值为( )A .4B .5C .6D .710.已知A =﹣4x 2,B 是多项式,在计算B+A 时,小马虎同学把B+A 看成了B•A ,结果得32x 5﹣16x 4,则B+A 为( )A .﹣8x 3+4x 2B .﹣8x 3+8x 2C .﹣8x 3D .8x 3 11.下列各式中,从左到右的变形是因式分解的是( ) A .()()2224a a a +-=-B .()ab ac d a b c d ++=++C .()2293x x -=-D .22()a b ab ab a b -=-12.如图所示,在平行四边形ABCD 中,分别以AB 、AD 为边作等边△ABE 和等边△ADF,分别连接CE ,CF 和EF ,则下列结论,一定成立的个数是( )①△CDF≌△EBC;②△CEF 是等边三角形;③∠CDF=∠EAF;④CE∥DFA .1B .2C .3D .4二、填空题13.如果等腰三角形两边长是6cm 和3cm ,那么它的周长是_____cm .14.使1 2x +有意义的x 取值范围是_____;若分式3 3x x --的值为零,则x =_____;分式2211 x x x x-+,的最简公分母是_____. 15.使分式的值为0,这时x=_____.16.分解因式:2x 2﹣8=_____________17.某工厂储存350吨煤,按原计划用了3天后,由于改进了炉灶和烧煤技术,每天能节约2吨煤,使储存的煤比原计划多用15天.若设改进技术前每天烧x 吨煤,则可列出方程________.18.如图所示,已知△ABC 的周长是20,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD=3,则△ABC 的面积是 .19.如图,AD 是ABC ∆的角平分线,DF AB ⊥,垂足为F ,DE DG =,ADG ∆和EFD ∆的面积分别为50和4.5,则AED ∆的面积为_________.20.已知13a a +=,则221+=a a_____________________; 三、解答题21.解分式方程:23211x x x +=+- 22.已知等腰三角形一腰上的中线将三角形的周长分为9cm 和15cm 两部分,求这个等腰三角形的底边长和腰长.23.已知:如图,AB =AC ,点D 是BC 的中点,AB 平分∠DAE ,AE ⊥BE ,垂足为E . 求证:AD =AE .24.解分式方程(1)2101x x -=+. (2)2216124x x x --=+- 25.解分式方程:22111x x x +=--【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】试题分析:A 选项既是轴对称图形,也是中心对称图形;B 选项中该图形是轴对称图形不是中心对称图形;C 选项中既是中心对称图形又是轴对称图形;D 选项中是中心对称图形又是轴对称图形.故选B .考点: 1.轴对称图形;2.中心对称图形.2.D解析:D【解析】【分析】由科学记数法知90.000000007710-=⨯;解:90.000000007710-=⨯;故选:D .【点睛】本题考查科学记数法;熟练掌握科学记数法10n a ⨯中a 与n 的意义是解题的关键.3.C解析:C【解析】【分析】分别表示出客车在普通公路和高速公路上行驶的时间,即可得到方程.【详解】 根据题意:客车在普通公路上行驶的时间是750x 小时,在高速公路上行驶的时间是6002x 小时,由所需时间比走普通公路所需时间少5小时可列方程:6002x +5=750x, 故选:C.【点睛】 此题考查分式方程的实际应用,正确理解题意找到等量关系是解题的关键.4.C解析:C【解析】【分析】根据平行四边形性质和折叠性质得∠BAC =∠ACD =∠B′AC =12∠1,再根据三角形内角和定理可得.【详解】∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ACD =∠BAC ,由折叠的性质得:∠BAC =∠B′AC ,∴∠BAC =∠ACD =∠B′AC =12∠1=22° ∴∠B =180°-∠2-∠BAC =180°-44°-22°=114°;故选C .【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质,求出∠BAC 的度数是解决问题的关键.5.D解析:D【分析】首先证明△ABC ≌△CDE ,推出CE=AC ,∠D=∠B ,由∠D+∠DCE=90°,推出∠B+∠DCE=90°,推出CD ⊥AB ,即可一一判断.【详解】在Rt △ABC 和Rt △CDE 中,AB CD BC DE =⎧⎨=⎩, ∴△ABC ≌△CDE ,∴CE =AC ,∠D =∠B ,90D DCE ∠+∠=o Q ,90B DCE ∴∠+∠=o ,∴CD ⊥AB ,D :E 为BC 的中点无法证明故A 、B 、C.正确,故选. D【点睛】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质,属于基础题.6.B解析:B【解析】过E 作EF ∥AB ,求出AB ∥CD ∥EF ,根据平行线的性质得出∠C=∠FEC ,∠BAE=∠FEA ,求出∠BAE ,即可求出答案.解:过E 作EF ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥EF ,∴∠C=∠FEC ,∠BAE=∠FEA ,∵∠C=44°,∠AEC 为直角,∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,∴∠1=180°﹣∠BAE=180°﹣46°=134°,故选B .“点睛”本题考查了平行线的性质的应用,能正确作出辅助线是解此题的关键.7.D解析:D【解析】【分析】根据三角形内角和为180°,直接进行解答.【详解】解:A中∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,同理,B,C均为直角三角形, D选项中∠A=2∠B=3∠C,即3∠C +32∠C +∠C =180°,∠C =36011,三个角没有90°角,故不是直角三角形.“点睛”本题考查三角形内角和定理以及直角的判定条件,熟知三角形内角和是180°是解答此题的关键.8.D解析:D【解析】【分析】由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.【详解】解:∵△ABC内角平分线的交点到三角形三边的距离相等,∴△ABC内角平分线的交点满足条件;如图:点P是△ABC两条外角平分线的交点,过点P作PE⊥AB,PD⊥BC,PF⊥AC,∴PE=PF,PF=PD,∴PE=PF=PD,∴点P到△ABC的三边的距离相等,∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;综上,到三条公路的距离相等的点有4处,∴可供选择的地址有4处.故选:D【点睛】考查了角平分线的性质.注意掌握角平分线上的点到角两边的距离相等,注意数形结合思想的应用,小心别漏解.9.C解析:C【解析】【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=12∠ABC,∠A1CD=12∠ACD,然后整理得到∠A1=12∠A,由∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,而A1B、A1C分别平分∠ABC和∠ACD,得到∠ACD=2∠A1CD,∠ABC=2∠A1BC,于是有∠A=2∠A1,同理可得∠A1=2∠A2,即∠A=22∠A2,因此找出规律.【详解】由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,∵∠ABC的平分线与∠ACD的平分线交于点A1,∴∠A1BC=12∠ABC,∠A1CD=12∠ACD,∴∠A1+∠A1BC=12(∠A+∠ABC)=12∠A+∠A1BC,∴∠A1=12∠A=12×64°=32°;∵A1B、A1C分别平分∠ABC和∠ACD,∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,∴∠A=2∠A1,∴∠A1=12∠A,同理可得∠A1=2∠A2,∴∠A2=14∠A,∴∠A=2n∠A n,∴∠A n=(12)n∠A=642n,∵∠A n的度数为整数,∵n=6.故选C.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的12是解题的关键.10.C解析:C【解析】【分析】根据整式的运算法则即可求出答案.【详解】由题意可知:-4x2•B=32x5-16x4,∴B=-8x3+4x2∴A+B=-8x3+4x2+(-4x2)=-8x3故选C.【点睛】本题考查整式的运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.11.D解析:D【解析】【分析】根据因式分解的意义对四个选项进行逐一分析即可.【详解】解:A、等式右边不是几个因式积的形式,故不是分解因式,故本选项错误;B、等式右边不是几个因式积的形式,故不是分解因式,故本选项错误;C、等式右边应该是(x+3)(x-3),故不符合题意,故本选项错误.D 、等式右边是几个因式积的形式,故是分解因式,故本选项正确;故选D.【点睛】本题考查了因式分解的意义,解题的关键是掌握把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.12.C解析:C【解析】【分析】利用“边角边”证明△CDF 和△EBC 全等,判定①正确;同理求出△CDF 和△EAF 全等,根据全等三角形对应边相等可得CE CF EF ==,判定△ECF 是等边三角形,判定②正确;利用“8字型”判定③正确;若CE DF P ,则C 、F 、A 三点共线,故④错误;即可得出答案.【详解】在ABCD Y 中,ADC ABC ∠∠=,AD BC =,CD AB =,∵ABE ADF V V 、都是等边三角形,∴AD DF =,AB EB =,60DFAADF ABE ∠∠∠︒===, ∴DF BC =,=CD BE ,∴60CDF ADC ∠∠︒=﹣,60EBC ABC ∠∠︒=﹣,∴CDF EBC ∠∠=,在CDF V 和EBC V 中,DF BC CDF EBC CD EB =⎧⎪∠=∠⎨⎪=⎩,∴CDF EBC SAS V V ≌(),故①正确; 在ABCD Y 中,设AE 交CD 于O ,AE 交DF 于K ,如图:∵AB CD ∥,∴60DOA OAB ∠∠︒==,∴DOA DFO ∠∠=,∵OKD AKF ∠∠=,∴ODF OAF ∠∠=,故③正确;在CDF V 和EAF △中,CD EA CDF EAF DF AF =⎧⎪∠=∠⎨⎪=⎩,∴CDF EAF SAS V V ≌(), ∴EF CF =,∵CDF EBC ≌△△,∴CE CF =,∴EC CF EF ==,∴ECF △是等边三角形,故②正确;则60CFE ∠︒=,若CE DF P 时,则60DFE CEF ∠∠︒==,∵60DFA CFE ∠︒∠==,∴180CFE DFE DFA ∠+∠+∠︒=,则C 、F 、A 三点共线已知中没有给出C 、F 、A 三点共线,故④错误;综上所述,正确的结论有①②③.故选:C .【点睛】本题主要考查三角形全等的判定与性质,解题的关键是能通过题目所给的条件以及选用合适的判定三角形全等的方法证明.二、填空题13.15【解析】【分析】题目给出等腰三角形有两条边长为6cm 和3cm 而没有明确腰底分别是多少所以要进行讨论还要应用三角形的三边关系验证能否组成三角形【详解】当腰为3cm 时3+3=6不能构成三角形因此这种解析:15【解析】【分析】题目给出等腰三角形有两条边长为6cm 和3cm ,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【详解】当腰为3cm 时,3+3=6,不能构成三角形,因此这种情况不成立.当腰为6cm 时,6-3<6<6+3,能构成三角形;此时等腰三角形的周长为6+6+3=15cm .故填15.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.14.【解析】【分析】(1)令分母不为0即可;(2)令分子为0且分母不为0可得;(3)先对两个分式分母进行因式分解然后观察得出最简公分母【详解】(1)要使有意义则x+2≠0解得:x=2(2)分式的值为零则解析:x -2≠ x -3= 3x -x【解析】【分析】(1)令分母不为0即可;(2)令分子为0,且分母不为0可得;(3)先对两个分式分母进行因式分解,然后观察得出最简公分母.【详解】(1)要使1 2x +有意义 则x+2≠0解得:x=2(2)分式33x x --的值为零则3=0x -,且x -3≠0解得:x=-3(3)∵221111 =(1)(1)x x x x x x x x =--++, ∴两个分式的最简公分母为:x(x-1)(x+1)=3x -x故答案分别为:x=2;x=-3;3x -x【点睛】本题考查分式有意义的条件、分式为0的条件以及最简公分母的求解,注意分式有意义的条件和为0的情况是有所区别的.15.1【解析】试题分析:根据题意可知这是分式方程x2-1x+1=0然后根据分式方程的解法分解因式后约分可得x-1=0解之得x=1经检验可知x=1是分式方程的解答案为1考点:分式方程的解法解析:1【解析】试题分析:根据题意可知这是分式方程,=0,然后根据分式方程的解法分解因式后约分可得x-1=0,解之得x=1,经检验可知x=1是分式方程的解.答案为1.考点:分式方程的解法16.2(x+2)(x﹣2)【解析】【分析】先提公因式再运用平方差公式【详解】2x2﹣8=2(x2﹣4)=2(x+2)(x﹣2)【点睛】考核知识点:因式分解掌握基本方法是关键解析:2(x+2)(x﹣2)【解析】【分析】先提公因式,再运用平方差公式.【详解】2x2﹣8,=2(x2﹣4),=2(x+2)(x﹣2).【点睛】考核知识点:因式分解.掌握基本方法是关键.17.【解析】【分析】设改进技术前每天烧吨煤则改进技术后每天烧(x-2)吨根据储存的煤比原计划多用15天即可列方程求解【详解】解:设改进技术前每天烧吨煤则改进技术后每天烧(x-2)吨根据题意得:故答案为:解析:3503350315 2x xx x---=-【解析】【分析】设改进技术前每天烧x吨煤,则改进技术后每天烧(x-2)吨,根据储存的煤比原计划多用15天,即可列方程求解.【详解】解:设改进技术前每天烧x吨煤,则改进技术后每天烧(x-2)吨,根据题意得:35033503152x xx x---=-,故答案为:35033503152x xx x---=-.【点睛】本题考查了分式方程的应用,利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.18.【解析】试题分析:如图连接OA∵OBOC分别平分∠ABC和∠ACB∴点O到ABACBC的距离都相等∵△ABC的周长是20OD⊥BC于D且OD=3∴S△ABC=×20×3=30考点:角平分线的性质解析:【解析】试题分析:如图,连接OA,∵OB 、OC 分别平分∠ABC 和∠ACB ,∴点O 到AB 、AC 、BC 的距离都相等,∵△ABC 的周长是20,OD ⊥BC 于D ,且OD=3,∴S △ABC =12×20×3=30. 考点:角平分线的性质.19.41【解析】【分析】作垂足为M 可得出由此推出从而得出【详解】解:作垂足为M ∵是的角平分线∴∴∴故答案为:41【点睛】本题考查的知识点是与角平分线有关的计算根据角平分线的性质得出是解此题的关键解析:41【解析】【分析】作DM AC ⊥,垂足为M ,可得出,ADF ADM DFE DMG ≅≅V V V V ,由此推出50 4.545.5ADM ADF ADG EFD S S S S ==-=-=V V V V ,从而得出45.5 4.541AED ADF EFD S S S=-=-=V V V . 【详解】解:作DM AC ⊥,垂足为M ,∵AD 是ABC ∆的角平分线,DF AB ⊥,∴,ADF ADM DFE DMG ≅≅V V V V ,∴50 4.545.5ADM ADF ADG EFD S S S S ==-=-=V V V V ,∴45.5 4.541AED ADF EFD S S S=-=-=V V V .故答案为:41.【点睛】本题考查的知识点是与角平分线有关的计算,根据角平分线的性质得出,ADF ADM DFE DMG ≅≅V V V V 是解此题的关键.20.7【解析】【分析】把已知条件平方然后求出所要求式子的值【详解】∵∴∴=9∴=7故答案为7【点睛】此题考查分式的加减法解题关键在于先平方 解析:7【解析】【分析】把已知条件平方,然后求出所要求式子的值.【详解】 ∵13a a+=, ∴219a a ⎛⎫+= ⎪⎝⎭, ∴2212+a a + =9, ∴221+=a a =7. 故答案为7.【点睛】此题考查分式的加减法,解题关键在于先平方.三、解答题21.x =-5【解析】【分析】本题考查了分式方程的解法,把方程的两边都乘以最简公分母(x +1)( x -1),化为整式方程求解,求出x 的值后不要忘记检验.【详解】解:方程两边同时乘以(x +1)( x -1)得: 2x (x -1)+3(x +1)=2(x +1)( x -1)整理化简,得 x =-5经检验,x =-5是原方程的根∴原方程的解为:x =-5.22.底边长为4cm ,腰长为10cm.【解析】【分析】根据题意画出图形,设△ABC 的腰长为xcm ,则AD =DC =12xcm ,然后根据AB+AD=9和AB+AD=15两种情况分别求出底边和腰长,最后根据三角形的三边关系进行判定是否能够构成三角形,从而得出答案.【详解】如图,△ABC 是等腰三角形,AB =AC ,BD 是AC 边上的中线.设△ABC 的腰长为xcm ,则AD =DC =12xcm. 分下面两种情况解:①AB +AD =x +12x =9, ∴x =6. ∵三角形的周长为9+15=24(cm), ∴三边长分别为6cm ,6cm ,12cm. 6+6=12, 不符合三角形的三边关系,舍去;②AB +AD =x +12x =15, ∴x =10. ∵三角形的周长为24cm , ∴三边长分别为10cm ,10cm ,4cm ,符合三边关系.综上所述,这个等腰三角形的底边长为4cm ,腰长为10cm.【点睛】本题主要考查的是等腰三角形的性质以及分类讨论思想的应用,属于中等难度的题型.学会分类讨论是解决这个问题的关键.23.见解析【解析】试题分析:证明简单的线段相等,可证线段所在的三角形全等,结合本题,证△ADB≌△AEB 即可.试题解析:∵AB=AC,点D 是BC 的中点,∴AD⊥BC,∴∠ADB=90°.∵AE⊥EB,∴∠E=∠ADB=90°.∵AB 平分∠DAE,∴∠BAD=∠BAE.在△ADB 和△AEB 中,∠E=∠ADB,∠BAD=∠BAE,AB=AB,∴△ADB≌△AEB(AAS),∴AD=AE.24.(1)x=-2;(2)无解【解析】【分析】【详解】(1)去分母得:2(1)0x x +-=,解此整式方程得:2x =-,检验:当2x =-时,(1)0x x +≠,∴原方程的解为:2x =-.(2)去分母得:22(2)164x x --=-,解此整式方程得:2x =-,检验:当2x =-时,(2)(2)0x x +-=,∴2x =-是原方程的增根,∴原方程无解.【点睛】解分式方程时需注意两点:(1)解分式方程的基本思路是“去分母,化分式方程为整式方程”;(2)求得对应的整式方程的解后,需检验,再作结论.25.x=-3【解析】分析:分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.详解:方程左右两边同时乘以(x-1)²得:2+2x=x-1,解得:x=-3,经检验x=-3是原分式方程的解.点睛:此题考查了解分式方程,熟练掌握运算法则是解本题的关键.。
2020年八年级上学期物理期中测试试卷(附答案)

2020年八年级上学期物理期中测试试卷(附答案)一、单选题(共15题;共30分)1.泡沫混凝土是一种新型的建筑材料,具有轻质、多孔、保温、隔热、隔音、减震等优点,同学们对此很好奇,围绕其保温、隔热的性能,提出了以下的问题,你认为较有价值且可探究的问题是:()A. “它为什么能防火、保温?” B. “它的轻质特点对减震有什么影响?”C. “厚度的变化对保温、隔热性能有什么影响?”D. “多孔结构对隔音性能有什么影响?”2.一位随州籍留美学子,在家乡的一次聚会上动情地说:“我珍藏着一首乐曲《我的祖国》,前半部分是编钟演奏的,后半部分是交响乐.编钟曲让我自豪,交响乐让我振奋!”从“声音的特性”看不同乐器演奏同一支曲子的主要区别在于()A. 音调B. 音色C. 响度D. 声速3.用大小不同的力击打同一鼓面,鼓面发出的声音的不同点是()A. 响度B. 音调C. 音色D. 频率4.关于老牛叫的声音和蚊子发出的声音相比较,说法正确的是()A. 老牛的音调高,响度大B. 老牛的音调低,响度大C. 老牛的音调低,响度小D. 老牛的音调高,响度小5.关于声现象,下列说法中正确的是()A. 敲锣时用力越大,声音的音调越高B. “闻其声而知其人”主要是根据声音的响度来判断的C. 市区内某些路段“禁鸣喇叭”,这是在声源处减弱噪声D. 用超声波能粉碎人体内的“小石头”,说明声波能传递信息6.在一个同学的物理笔记上,有如下的四句话。
其中错误的是()A. 光反射时,反射光与入射光的速度相等B. 紫外线最显著的性质是能使荧光物质发光C. 平面镜中所成像的大小与平面镜的大小有关D. 光在真空的传播速度为3×108m/s7.下列对有关物理学家及其所做的实验表述不正确的是()A. 托里拆利通过实验精确地测量了大气压的值B. 奥斯特通过实验证明了电流周围存在磁场C. 法拉第通过实验研究了磁场对通电导线的作用D. 焦耳最先确定了电流产生的热量与电流、电阻和通电时间的关系8.寒冷冬季的早晨,往往能在屋顶和地面上看见晶莹的霜花,它是属于下列哪种物态变化()A. 熔化B. 凝华C. 液化D. 蒸发9.关于液体蒸发和沸腾的比较,下列哪句话是错误的?()A. 蒸发和沸腾都属汽化现象B. 蒸发和沸腾都要吸收热量C. 蒸发和沸腾在任何温度下都可以发生D. 蒸发能在任何温度下发生,沸腾只在一定温度下发生10.我国是一个缺水的国家,因而污水净化具有重要的意义.如图是江涛发明的太阳能净水器,该净水器在污水净化过程中发生的物态变化是()A.先熔化,后液化B. 先升华,后凝华C. 先汽化,后液化D. 先汽化,后凝固11.课本中想想做做的小实验﹣﹣纸锅烧水,把盛有水的纸锅放在火焰上烧,水烧开了纸锅仍不会燃烧,这是因为()A. 纸的比热容大于水的比热容,所以纸锅不会燃烧B. 火焰的温度较低,低于纸的着火点C. 水烧开后温度保持不变且低于纸的着火点D. 纸不吸收热量,所以纸锅不会燃烧12.红外线和紫外线的应用非常广泛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年八年级(上)期中考试题卷语文考生注意:1、本学科试卷分试题卷和答题卡两部分,考试时量150分钟,满分120分。
2、请将姓名、班级、考号填在答题卡上。
3、请在答题卡...上作答,答在试卷上无效。
一、语言的积累与运用(30分)1.下列词语中字形和加点字的注音完全正确的一项是()(2分)A. 溃退(kuì) 锐不可当(dànɡ)狼籍迂腐B. 要塞(sāi)尴尬(ɡān)张惶失措荡然无存C.炽热(zhì)瞥见(piē)粗制滥造抑扬顿挫D.踌躇(chóu)屏息(bǐng)藏污纳垢器宇轩昂2.下列句子中,加点成语使用不恰当的一项是()(2分)A、成都草堂是四川人民心中的文化圣殿,这是无可置疑....的。
B、枣儿的父母三年前走出大山,前往广东,除了节假日偶尔和枣儿通电话,至今杳无音信....。
C、我们的语文老师读起课文来声音清脆,声调抑扬顿挫....,我们都为之着迷。
D、假冒伪劣产品一度肆虐,老百姓对只追求利益的商家深恶痛疾....。
3、下列句子中,没有..病句的一项是()(2分)A、有关领导在会议上明确要求,各部门必须尽快提高传染病防控工作。
B、曹文轩获“国际安徒生奖”,实现了中国作家在该奖项上零的突破。
C、随着部分地区高大树木的减少,使某珍稀鸟类只能选择在高压电塔上筑巢。
D、在巡检排查过程中,我市电部门解决并发现了居民用电方面的问题。
4.下列关于文学文化常识的表述不正确的一项是( )(2分)A.《“飞天”凌空———跳水姑娘吕伟夺魁记》———新闻特写———记叙中国跳水姑娘夺取桂冠的1.7秒,赞美了中国健儿的拼搏精神。
B.《藤野先生》———回忆性散文———以作者与藤野先生的交往为叙事线索,围绕表现藤野先生的崇高品质这一中心组织材料。
C.《回忆我的母亲》———回忆性散文———回忆了母亲勤劳的一生,追述了母亲对作者的深刻影响。
D.《与朱元思书》———写景小品文——富春江的奇山异水,主要表达希望与朋友共赏美景之情。
5、下面句子中的标点符号,使用不正确的一项是()(2分)A.没有实力,信心不过是无源之水;没有信心,拼搏只能是无本之木。
B.雨果说:“一个有坚强心志的人,财产可以被人掠夺,勇气却不会被人剥夺。
”C.转基因技术的迅猛发展,是给人类带来了福祉,还是给人类埋下了隐患?D.上海迪士尼乐园的设计方案,融入了海洋、森林、高山、沙漠……等六大元素。
6、下列句子的排列顺序准确的一项是()(2分)①百般不能排解思情, 不妨往诗文中寻个消遣处。
②王维的乡思亦有画意: 来日绮窗前, 寒梅著花未?③从古自今, 乡愁是诗人的惆怅。
④没有什么像乡愁一样令我悲伤, 这么美丽的文字, 这么伤感的情怀, 只有诗人才能表达。
⑤诗云: 今夜月明人尽望, 不知秋思落谁家。
A. ①③④⑤②B. ③⑤①②④C. ③①⑤②④D. ⑤①③④②7.填空(每空1分,共10分)(1)晓雾将歇,______________;夕日欲颓,_____________。
(陶弘景《答谢中书书》)(2)孤山寺北贾亭西,水面初平云脚低。
______________, ________________。
(白居易《钱塘湖春行》)(3)______________,志在千里;______________壮心不已。
(曹操《龟虽寿》)(4)《使至塞上》中描绘塞外荒漠的壮美风光的诗句:_____________,_____________。
(王维《使至塞上》)(5)请写出连续两句描写鸟的古诗句______________, ________________。
8、生活语文题(4分)(1)一位同学用成语给自己“画像”:突出优点——知过必改;明显缺点——粗枝大叶;待人接物——与人为善;理想——品学兼优请你也用成语给自己“画像”,让大家对你有一个初步印象。
(请任选两项作答,不得照搬上面那位同学使用过的成语)(2分)突出的优点:明显的缺点:待人接物:理想:9、阅读下面表格,按要求回答问题。
(4分)(1)用文字概括世界能源的发展趋势。
(2分)____________________________________________________________(2)读此表后你有什么感受?(2分)__________________________________________________________________二、阅读理解(40分)(一)阅读下面两篇文言文,完成下列题目。
(17分)(甲)答谢中书书山川之美,古来共谈。
高峰入云,清流见底。
两岸石壁,五色交辉;青林翠竹,四时俱备。
晓雾将歇,猿鸟乱鸣;夕日欲颓,沉鳞竞跃。
实是欲界之仙都。
自康乐以来,未复有能与其奇者。
(乙)记承天寺夜游元丰六年十月十二日夜。
解衣欲睡。
月色入户,欣然起行。
念无与为乐者,遂至承天寺,寻张怀民。
怀民亦未寝,相与步于中庭。
庭下如积水空明,水中藻荇交横,盖竹柏影也。
何夜无月?何处无竹柏?但少闲人如吾两人耳。
10、下列句子朗读节奏划分,不正确的一项是()(2分)A、念/无与为乐者B、遂/至承天寺/寻张怀民C.未复/有能与其奇者D.实是/欲界之仙都11. 下列句子中,加点词的意义相同的一组是()(2分)A.夕日欲.颓实是欲.界之仙都B.自.康乐以来自.三峡七百里中C.念无与.为乐者未复有能与.其奇D.但.少闲人如无两人者耳无他,但.手熟尔12.下列对语段内容说法错误的一项是()(2分)A.《答谢中书书》一文中结尾以赞美和感慨收束。
“实是欲界之仙都”,将此地山水比作人间天堂,应是最大的褒奖和赞美!“自康乐以来,未复有能与其奇者”,但遗憾的是,没有人能够欣赏它的妙处。
这既是对前贤的钦佩和追慕,有惋惜世人对秀美山水的无动于衷。
B.“怀民亦未寝,相与步于中庭”相同遭际,相似处境,想来也是一样无眠,于是,一起到院中散步赏月。
C.《答谢中书书》表达了作者沉醉山水的愉悦和与古今知音共赏美景的闲适自得之情;《记承天诗夜游》表达的感情是微妙而复杂的,贬谪的悲凉,人生的感慨,赏月的欣喜,漫步的悠闲都包含其中。
D.《记承天诗夜游》中,作者写景只用了18个字,就点染出一个空明澄澈、疏影摇曳、是真实幻的美妙境界。
这空灵的境界,也许正是作者彼时的写照。
13. 用现代汉语写出下面句子的意思。
(6分)①晓雾将歇,猿鸟乱鸣。
_____________________________________________________________________ ②庭下如积水空明,水中藻荇交横,盖竹柏影也。
_____________________________________________________________________ 14.细读《记承天寺夜游》,结合写作背景和你对苏轼生平、思想的认识,谈谈对“闲人”的理解。
(5分)_____________________________________________________________________ _____________________________________________________________________ (二)阅读《题奉晚》,回答问题。
(6分)《题奉晚》(周敦颐)花落柴门拾夕晖,昏鸦数点傍林飞。
吟余小立阑干外,遥见樵渔一路归。
15、这首诗中哪一句话交代了诗人观景的立足点?诗人观察到了哪些景象?(4分)答:16、诗人描写昏鸦时为什么用“点”而不用“只”?说说你的理解。
(2分)答:(三)“朋友圈”的前世今生(6分)①近年来,微信风头正健,男女老幼皆会在“朋友圈”里晒晒个人私事,传传八卦新闻。
实际上,“朋友圈”并不是21世纪的专属产物,早在几个世纪前,甚至更久以前就已经存在了。
②“朋友圈”的雏形其实是名为albaamicorum的纸书(拉丁文直译为“朋友书”,英文可译为Friends’Books,即“友人之书”),它堪称当今各类社会媒体的老祖宗,寿龄已高达几个世纪。
③荷兰历史学家苏菲研究了这段有趣的历史细节,发现从1560年起,一些北欧年轻人就开始用这种纸书记录朋友圈的种种,不过鉴于17世纪的社会风俗,男孩和女孩运用这些书刷“朋友圈”的目的各不相同。
在当时,男孩通常会被送去欧洲著名的大学机构镀金,拜谒当时的思想巨头、学术大家,“朋友圈”对他们来说更像是今天的职业社交网站,其目的是求教方家。
一位名叫迈克尔的少年在周游欧罗巴大陆的过程中,就留下了一册极为典型的“朋友圈”纸书。
除了记录在各处的旅行见闻外,还包括与贵族会面的图片。
这样的插图不仅博人眼球,且彰显身份。
另外,他还在纸书上面形象地诠释了他对一些古老问题的见解,就像我们在朋友圈上发表观点一样。
④女孩则往往被送去修道院,或者去宫廷做仕女,这有助于她们将来成功成为名媛淑女。
虽然不能像男孩那样到处去旅游,但她们也有自己的友谊书。
如果说男孩版朋友圈填满了科学家和艺术家笔录,那么女孩版的则更像脸书和微信,晒晒与朋友、钦慕者的通信往来,记点圈内笑话,描绘社交事件的细节等。
当然,它不会像日记那样被锁在抽屉里默默珍藏,而是要与大家一起分享的,这给当时社交圈子非常狭窄的女孩们带来了莫大的乐趣。
⑤这些装饰精美的“朋友圈”记录册和我们熟悉的微信非常相似,区别只在技术层面。
“照片”是被画出来的——这比拍照难度大多了,各账号不是转发阅读文章,而是在留言页上写下自己喜欢的格言、警句、诗歌等。
这样的“朋友圈”可以帮助历史学家逼真地还原当时的风土人情,甚至还能拼凑出长达400年的关系网络。
若再把视线放远一些,我们可以看到中国古人在一千多年以前就热衷于用纸笔搜集好友、同僚的图文信息,并广为分享了。
且不说皇亲贵胄、达官名士游历名山大川,即使平民百姓近处郊游、赶集等,也会把这一天感受最深的事情涂鸦记录下来,然后供街坊邻居传看,兴味十足。
⑥古人旅游途中还喜欢在崖壁山石、亭台楼阁等地方题诗刻字,这也是发朋友圈的一种方式,既能体现自己的文化品位,又能获得许多陌生朋友点赞,是颇为风雅的一件事,许多诗词碑刻就是这么成为经典的。
传说1400多年前,李白登黄鹤楼,目睹眼前之景,再看崔颢的《黄鹤楼》一诗,大为折服。
于是提笔在黄鹤楼上怅然题写了“眼前有景道不得,崔颢题诗在上头”,这应该算是历代文人墨客朋友圈里最有面子的“点赞”了吧?⑦正如《圣经》中所言,太阳底下没有新鲜事。
现代人自以为时髦的“朋友圈”,在几百年甚至千年前就已经被中外古人们抢先体验了。
(选自《知识窗》2016年第1期)17.阅读全文,说说文章以“‘朋友圈’的前世今生”为题有何好处。
(3分)答:18.第⑥段画线句运用、的说明方法,选择一种,简要分析表达作用。
(3分)(四)清澈的声音(11分)①有一些声音就似遗落在人间的精灵,偶入耳中,便入心底,濯洗着那些漫...漫尘埃...........。
