复变函数一复数的乘幂与方根
合集下载
复变函数入门 1ppt课件
3. 两复数的商:
z1 z2
x1 x2 x22
y1 y2 y22
i
x2 y1 x22
x1 y2 y22
ቤተ መጻሕፍቲ ባይዱ
.
注解：
➢ 复数的减法运算是加法运算的逆运算
➢ 复数的除法运算是乘法运算的逆运算
➢ 复数的四则运算与实数的四则运算保持一致
7
定理: 全体复数关于上述运算做成一个数域.
称为复数域，用C表示.即
复数的四则运算满足以下运算律 ①加法交换律 z1 z2 z2 z1 ②加法结合律 z1 (z2 z3) (z1 z2 ) z3 ③乘法交换律 z1 z2 z2 z1 ④乘法结合律 z1 (z2 z3) (z1 z2 ) z3 ⑤乘法对加法的分配律
面上的点向量oz 表示.
o
x
x
18
结论:
两个复数的加减法运算与相应的向量的 加减法运算一致.
y
z2
z1 z2
y
z2
z1
o
z1
x
o
x
z1 z2
z2
19
附录： 向Hamilton 学习
Hamilton.William Rowan（威廉.罗万.哈 密儿顿，1805——1865）爵士，无 疑是使爱尔兰人在数学领域中享有 盛益的最伟大的人物，同时也是有 名望的物理学家和天文学家。他 1805年生于都柏林，除了短时间外 出访问外，一生都是在这里度过 的。他才一岁时，被委托给一位叔 叔教育，这位叔叔的热心在于给他 侧重语言上的教育，不久之后，他 就成了孤儿。Hamilton是个神童，3 岁时能阅读英文，5岁时能阅读、
以上各式证明略.
10
例3 将下列复数表示为 x iy 的形式.
复变函数(全)解析
1
2
1
2
1
2
乘法
z z (x x y y ) i(x y x y ),
12
12
12
21
12
商
z 1
xx 12
yy 12
i
xy 21
xy 12
z
x2 y2
x2 y2
2
2
2
2
2
第一节 复数及其代数运算
(2)性质
z z z z , zz zz;
1
2
2
1
12
21
z (z z ) (z z ) z ,z (z z ) (z z )z
1
2
3
1
2
3 1 23
12 3
z (z z ) z z z z
12
3
12
13
第二节 复数的几何表示
1.复平面 （ 1 ） 定 义 复 数 z x iy 与 有 序 实 数
(x, y) 一一对应，对于平面上给定的直角 坐标系，复数的全体与该平面上的点的全
体成一一对应关系，从而复数 z x iy 可
对复平面内任一点z ,用一条直线将N 与z 连结起来,该直线与球面交于异于N 的 唯一点P ,这样除了N 之外,复平面内点与 球面上的点存在一一对应的关系.这样的 球面称为复球面.
第三节 复数的乘幂与方根
1. 乘积与商
设有两个复数
（1）乘积
z1
r1 (cos 1
sin1 )
r e i1 1
,
z2
r2 (cos2
z2 r2
第二节 复数的几何表示
2.幂与根 (1) 幂 n个相同复数z 的乘积称为z 的n次幂,记作zn ,即
第一章3复数的乘幂与方根
复变函数与积分变换
第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ，为正整数．
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心，半径为 2的圆的正方形的顶点
8
谢谢观看！
当 = , + 1, ⋯ 时，这些根又重复出现.
=
=
1
[cos
2 在几何上，
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心， 为
半径的圆的内接正边形的个顶点.
例3．求 1 + .
4
解： 1 + = 2(cos + sin )
特别地，当 = 1时，得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ，即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ，为正整数．
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心，半径为 2的圆的正方形的顶点
8
谢谢观看！
当 = , + 1, ⋯ 时，这些根又重复出现.
=
=
1
[cos
2 在几何上，
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心， 为
半径的圆的内接正边形的个顶点.
例3．求 1 + .
4
解： 1 + = 2(cos + sin )
特别地，当 = 1时，得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ，即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
复变函数1-3
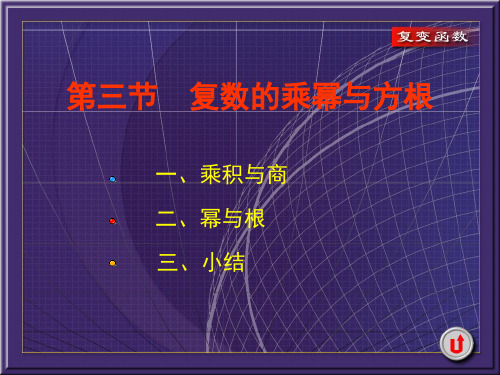
i,
z1 z2
cos
3
6
i
sin
3
6
3 1i. 22
7
二、幂与根
1. n次幂: n 个相同复数 z 的乘积称为z 的 n 次幂,
记作 zn , zn z z z .
n个
对于任何正整数n, 有 zn rn(cosn i sin n ).
如果我们定义
zn
1 zn
,
那么当
幂为负整数时,
求出z的幂.
8
2.棣莫佛公式
当 z 的模 r 1,即 z cos i sin ,
(cos i sin )n cosn i sin n .
棣莫佛公式
3. 方程 wn z 的根 w, 其中 z 为已知复数.
w
n
z
r
1 n
cos
2kπ n
i sin
2kπ n
(k 0,1,2, ,n 1)
w2
o
w0 x
w3
15
三、小结
应熟练掌握复数乘积与商，幂与根的运算. 在各种形式中以三角形式、指数形式最为方便:
z1
z2
r1
r ei(12 ) 2
z2 r e2 i(2 1 )
z1 r1
对于任何正整数n, 有 zn rn(cosn i sin n ).
w
n
z
r
1 n
cos
2kπ
i sin
2kπ
n
n
(k 0,1,2, ,n 1)
放映结束，按Esc退出.
16
i sin(1 2 n )]
r1 r2 rnei(12 n ) .
5
定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差.
复数的乘幂与方根
复数的乘幂与方根教学目的：掌握复数的乘幂与方根的计算方法，了解乘幂、方根的几何意义教学重点：掌握利用复数的三角表示式求解复数的乘幂与方根教学难点：理解乘幂与方根的几何解释，方根的计算方法教学类型：板书教学时数：1学时教学过程：1、乘幂的计算定义1 n 个相同的复数 z 的乘积称为 z 的 n 次幂，记为 z n.显然由定理1 及其推广可知,|z n|=|z|n; Arg z n=nArg z,即若 z=r(cosθ+i sinθ),则有z n=r n(cos nθ+i sin nθ).思考：若是用代数形式 z=x+iy 计算 z n难度有多大？例：计算 (1+i)100.,解：|1+i|=2+12=√2,θ=π4因此，(1+i)100=(√2)100(cos25π+i sin25π)=250(−1+i∙0)=−250.2、方根的计算n.定义2 若 w=z n,称 z 为 w 的 n 次方根,记为 z=√w分析：已知复数 w =r (cos θ+i sin θ)，求复数z =ρ(cos φ+i sin φ),使得 w =z n 成立，即有r (cos θ+i sin θ)= ρn (cos nφ+i sin nφ).从上式中可以得到r = ρn ,θ+2kπ=nφ,k ∈Z .因此，ρ= r 1n , φ=θ+2kπn ⁄, k ∈Z ,z =√w n =r 1n (cos θ+2kπ+i sin θ+2kπ) 究竟有几个？k =0,1,2,⋯,n −1时，得到 n 个互异的值z 0=r 1n (cos θn +i sin θn )； z 1=r 1n (cos θ+2πn +i sin θ+2πn)； ⋯⋯z n−1=r 1n (cos θ+2(n −1)πn +i sin θ+2(n −1)πn) 由三角函数的周期性，可知当 k 取其他整数值时，方根的值重复出现，因此可知 n 次方根有且仅有 n 个！综上所述，n 次方根的计算方法为（1） 将复数w =x +iy 表示成三角表示式w =r (cos θ+i sin θ)（2） √w n =r 1n (cos θ+2kπn +i sin θ+2kπn )（3） k =0,1,2,⋯,n −1例：计算√i 3.解：（1）r =|i |=1,θ=π2, w =i =r (cos θ+i sin θ);（2）√w 3=r 1(cosθ+2kπ3+i sin θ+2kπ3) =cos (1+4k)π6+i sin (1+4k)π6;（3）k =0,1,2.即√i 3 分别为z 0=cos π6+i sin π6；z 1=cos 5π+i sin 5π; z 2=cos 9π6+i sin 9π6. 注解 n 次方根的几何解释上述例子中的3个3次方根正好是以原点为中心以1为半径的圆的内接正三角形的三个顶点。
1.3 复数的乘幂与方根
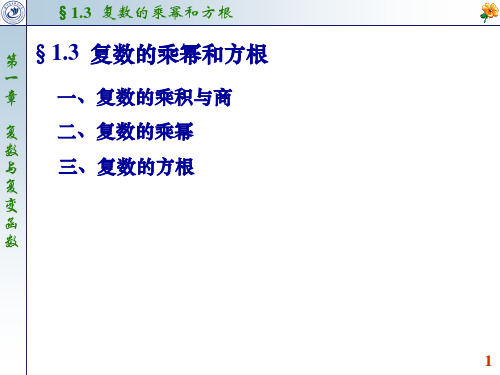
)3
eπi
1.
变
2 2
函
数
此外，显然有 (1)3 1.
由此引出方根的概念。
8
§1.3 复数的乘幂与方根
§1.3 复数的乘幂与方根
第 一 三、 复数的方根 P15
章
复数求方根是复数乘幂的逆运算。
复 数
定义
设 z 是给定的复数，n 是正整数，求所有满足wn z 的
与 复
复数 w ，称为把复数 z 开 n 次方，或者称为求复数 z 的
2e 3 .
1
12
§1.2 复数的几种表示
附：关于 Arg (z1 z2 ) Arg z1 Arg z2(在集合意义下)
第
一
所谓“在集合意义下”是指：
章 分别从集合 Arg z1 中与集合 Arg z2 中任取一个
复 数
元素(即辐角)，相加后，得到集合Arg (z1 z2 ) 中的
与
一个元素(即辐角)。
2e 6
有
复 数
πi
5π i
( π 5π )i
(1 3 i)( 3 i) 2e 3 2e 6 4e 3 6
与
复
πi
变
4e 2 4 i .
函 数
1 3i 3i
πi
2e 3
5π i
( π 5π )i
7π i
e 3 6 e 6
2e 6
cos 7π i sin 7π 3 1 i .
章 复
wk
n
z
n
r
i(
en
2k n
)
,
(k 0,1, , n 1) .
数 与
描述 在复平面上， 这 n 个根均匀地
复变函数课件
10
2.棣莫佛公式
当 z 的模 r 1, 即 z cos i sin ,
棣莫佛介绍
(cos i sin )n cos n i sin n . 棣莫佛公式
3. 方程 w n z 的根 w , 其中 z 为已知复数.
2kπ 2kπ w z r cos i sin n n ( k 0,1,2,, n 1)
r 为半径的圆的内接正n 边形的 n 个顶点.
14
例3
解
化简 (1 i )n (1 i )n .
1 1 1 i 2 i 2 2 2 cos i sin 4 4 1 1 1 i 2 i 2 2
因为复数 e 的模为1, 转角为 , 3
8
i 3
z3 z1 e ( z2 z1 )
i 3
3 1 i (1 i ) 2 2 3 1 3 1 i 2 2 2 2
o
y
z3
z2 2 i
3
z1 1
4
设复数z1和z2的指数形式分别为
z1 r1e ,
i 1
z2 r2e i 2 , 则 z1 z2 r1 r2e i (1 2 ) .
由此可将结论推广到 n 个复数相乘的情况:
设 zk rk (cos k i sin k ) rk e
i k
, ( k 1,2,, n)
4 i 5
,
,
w4 e
21
w 1 e i 1 cos i sin 1 因为 z i w 1 e 1 cos i sin 1
2.棣莫佛公式
当 z 的模 r 1, 即 z cos i sin ,
棣莫佛介绍
(cos i sin )n cos n i sin n . 棣莫佛公式
3. 方程 w n z 的根 w , 其中 z 为已知复数.
2kπ 2kπ w z r cos i sin n n ( k 0,1,2,, n 1)
r 为半径的圆的内接正n 边形的 n 个顶点.
14
例3
解
化简 (1 i )n (1 i )n .
1 1 1 i 2 i 2 2 2 cos i sin 4 4 1 1 1 i 2 i 2 2
因为复数 e 的模为1, 转角为 , 3
8
i 3
z3 z1 e ( z2 z1 )
i 3
3 1 i (1 i ) 2 2 3 1 3 1 i 2 2 2 2
o
y
z3
z2 2 i
3
z1 1
4
设复数z1和z2的指数形式分别为
z1 r1e ,
i 1
z2 r2e i 2 , 则 z1 z2 r1 r2e i (1 2 ) .
由此可将结论推广到 n 个复数相乘的情况:
设 zk rk (cos k i sin k ) rk e
i k
, ( k 1,2,, n)
4 i 5
,
,
w4 e
21
w 1 e i 1 cos i sin 1 因为 z i w 1 e 1 cos i sin 1
复变函数论
arg
z
arctg
3 1
3
2 3
，
Argz arg z 2k 2 2k ,
3
(k 0,1,2,3)
z
2(cos(
2
)
sin(
2
))
i(
2e
2 3
)
3
3
二、复数的运算：
1．相等： x1 iy1 x2 iy2 x1 x2, y1 y2 2.四则运算：运算规律
复数形式的方程表示时更简明。
2
2i
实数形式复数形式
z xiy
例 6: 连接 z1及 z2两点的线段的参数方程为：
z z1 t(z2 z1) (o t 1)
过 z1及z2两点直线的参数方程为：
z z1 t(z2 z1) ( t )
例 7: 求下列方程所表示的曲线
2
2
当 x 0, y 0 时，
x 0, y 0, arg z 0
x
0,
y
0, arg
z
当 x 0 时，
一象限 二象限
arg z( (0, )) arctan y ( (0, ))
2
x
2
arg
z (
(
,
))
arctan
y
(
(
,0))
(x 2)2 y2 9 .
2）几何上，该方程表示到复平面上点 2 和点 4
距离相等的点的轨迹，所以方程表示的曲线就是连接
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单连通域 (一个整体)
多连通域 (带有裂痕,漏洞)
9 )
16
w2
8
17
2 (c os 16
i sin 17
16
)
w2
w3
8
2 (c os 25
16
i sin
25
16
)
四个根是内接于中心在原点,半 径为21/8的圆的正方形的四个 顶点.
y
w1
1i
8 2 w0
x
w3
1.3 平面点集
1.3.1 区域
平面上以 z0为中心, d (任意的正数)为半径的圆: |zz0|<d 内部的点的集合称为z0的邻域, 而称由不等式 0<|zz0|<d
1.2 复数的乘幂与方根
1.2.1 复数的乘幂
复数乘积的指数表达式
z1
z2
r r ei(1 2 ) 12
z1 r1ei1 , z2 r2ei2
特殊情况：z1 z2 z rei ,则z 2 z1 z2 r 2ei2
推广(幂运算）：若z rei ,则zn r nein
注: (1)此公式对于任意整数n都成立。
由几段光滑曲线衔接而成的曲线称为分段光滑曲线.
假设x'(t), y'(t)同时为零，则
导数（斜率）dy y' (t) 不存在 dx x' (t)
1.3.3 单连通区域,多连通区域
定义：设D是平面上一区域，若在D内任作一条简单 闭曲线，而曲线所围成的部分总属于D，则称区域 D为单连通区域；
不是单连通的区域称为多连通区域（复连通区域）。
(c
os
)k
(i
sin
)3
k
cos3 3 cos sin2 i(3 cos2 sin sin3 )
cos3 cos3 3cos sin2
例2： 计算（1 i）5
( 3 i)6
解: 1 i 2 Arg(1 i) 2k
i
1 i 2e 4
4
(1 i)5 (
2)5
i 5
e4
3 i 2 Arg( 3 i) 2k
i
3 i 2e 6
(3ຫໍສະໝຸດ 6i)626
i
e
6
6
（1 i）5
(
2
)5
i
e
5 4
( 3 i)6
26
e
i
6 6
( 2)5 26
ei( 5 6 )
4 6
1
i
e4
82
1.2.3 复数的方根(乘幂的逆运算)
称满足方程 wn z (w 0, n 2)的复数w为z的n次方根， 1
记作n z 或 z n。
设z rcos i sin , w cos i sin
则 wn n (cos n i sin n)
n cos n r cos , n sin n r sin
n r , cos n cos , sin n sin
n 2k , k 0,1,2,
n r为半径的圆内接正n边形的n个顶点。
例3：计算4 1 i
解:
因为
1i
2(cos i sin )
4
4
2k
2k
所以 4 1 i 8 2 (cos 4
i sin 4
)
4
4
(k 0,1,2,3)
即
w0
8
2(cos i sin )
16
16
w1
8
2 (c os 9
16
i sin
(2)特别地，当r 1时， (ei )n ein
cos i sin n cos n i sin n 棣莫弗公式.
例1：将cos 3利用cos ,sin表示
解: cos3 Re[cos3 i sin 3 ]
cos 3 i sin 3 (cos i sin )3
3 k0
c3k
所确定的点集为z0的去心邻域.
设G为一平面点集, z0为G中任意一点. 如果存在z0的一 个邻域, 该邻域内的所有点都属于G, 则称z0为G的内点.
如果G内的每个点都是它的内点, 则称G为开集
平面点集D称为一个区域, 如果它满足下列两个条件: 1) D是一个开集; 2) D是连通的。就是说D中任何两点都可以用完全属于D
z=z(t) (atb) 来代表. 这就是平面曲线的复数表示式.
设C: z=z(t) (atb)为一条连续曲线, z(a)与z(b)分别为C
的起点与终点. 对于满足 a<t1<b, at2b 的 t1与 t2, 当 t1t2 而有 z(t1)=z(t2) 时, 点 z(t1)称为曲线 C的重点. 没有重点的 连续曲线 C, 称为简单曲线或若尔当(Jardan)曲线. 如果简
k
n
1,
wn1
n
r (cos
2(n 1)
n
i sin
2(n 1)
n
)
k n,
wn
n
r (cos
2n
n
i sin
2n
n
)
w0
n z n r (cos 2k i sin 2k ), k o,1, , n 1
n
n
注: （1）复数z的n次方根共有n个。
(2)几何意义：n z的n个值就在以原点为圆心，
的一条折线连接起来.
例4: 圆环：r1 z z0 r2
r
z0
z z0 r
不是区域 (不是开集)
z1
点集S {z | z 1}{z | z 2 1}
不是区域(不连通)
r2 z0 r1
区域
z2
如果一个区域可以被包含在一个以原点为中心的圆里面, 即存在正数 M,使区域 D的每个点z都满足 |z|<M, 则称 D为 有界的, 否则称为无界的.
|z|>M M
0
1.3.2 曲线
1.简单曲线,简单闭曲线
在数学上, 经常用参数方程来表示各种平面曲线. 如果 x(t)和y(t)是两个连续的实变函数, 则方程组
x=x(t), y=y(t), (atb) 代表一条平面曲线, 称为连续曲线. 如果令
z(t)=x(t)+iy(t) 则此曲线可用一个方程
2k , k 0,1,
n
w
n
z
n
r (cos
2k
i sin
2k
)
n
n
k 0
k 1,
w0
w1 n
n r (cos
n
r (cos 2 n
i sin )
n
isin 2 ) n
w1 wn1
(cos 2
n
(cos 2
n
2
i sin n )w0
2
i sin n )wn2
单曲线 C的起点与终点闭合, 即 z(a)=z(b) , 则曲线 C 称为
简单闭曲线.
z(b)
z(b)
z(a) z(b)
简单,闭
z(a)
简单,不闭
z(a)
非简单,不闭
z(a) z(b)
非简单,闭
2.光滑曲线,逐段光滑曲线
设曲线C的方程为
z(t) x(t) iy(t), (a t b)
若在区间[a,b]上，x'(t), y'(t)连续且不全为零，则称 曲线C为光滑曲线。