二年级奥数:数图形
小学二年级奥数 第13讲:图形数一数
图形数一数
【例1】(★★)
数一数,下图中有多少条线段?同学们,你们能一眼找到下图中的10个人头吗?
【拓展】(★★)
数一数,下图中有多少个角?
【例2】(★★★) 【例3】(★★★)
数一数,下图中共有多少个三角形?
数一数,下图中共有多少个长方形?
【拓展】(★★)
数一数,下图中共有多少个长方形?
【拓展】(★★)
1
【例4】(★★★★) 【例5】(★★★★)
下图中一共有多少个三角形?数一数,图中共有多少个正方形?
【例6】(★★★★)
下图中有多少个正方形?
一、核心点:先观察
【本讲总结】
二、要求:有序、全面
三、基本方法:
【拓展】(★★★★)
(2008 年第八届“春蕾杯”小学数学邀请赛初赛)
数一数图中有多少个正方形。
转化
不规则图形规则图形
(分类、拆分)
2。
小学二年级奥数题图形及答案
一、计算题。
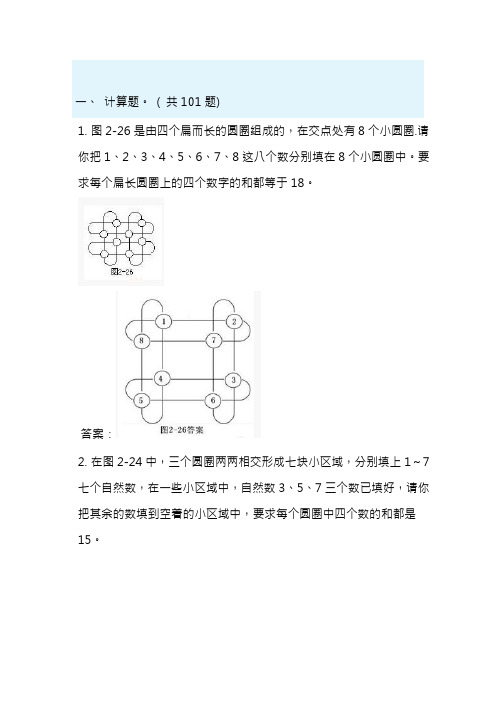
( 共101题)1. 图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2. 在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3. 图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4. 将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5. 仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图答案:6. 请看下图,共有多少个正方形答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共9 个,9 个小方格为一个正方形共4 个,最大的(16 个小方格)是1 个。
16+9+4+1=30(个)共计30 个正方形。
7. 仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么答案:8. 把上面一排的立体图形剪开,可以剪成下面哪种图形的样子动手试一试。
二年级奥数:巧数图形

二年级奥数:巧数图形体系所属体系板块:第三级上能力培养:分类思考、数形结合思想体系对接:第一级下《有趣的平面图形》第三级下《飞速图形计数》预热知识一、分类法1、打枪法2、恰含法3、分大小【例】下图你能数出多少条线段?【例】下图共有多少个长方形?【解析】分类法(打枪法)【解析】分类数(恰含法)总:4+3+2+1=10(个)总:3+2+1=6(个)答:共10个。
答:共6个。
【例】下图你能数出多少个正方形?【解析】分类数(大小)1个小正方形:4个4个小正方形:1个总:4+1=5(个)答:共5个。
二、巧数图形(分层数)1、总数=每层个数相加每层个数=上层个数+看得见【例】下图中的小方块有几个?【解析】巧数图形(分层数)总:1+4+5=10(个)答:有10个。
课前思考1、正方形如何计数呢?2、小方块如何计数呢?3、如何利用学过的乘法来进行计数?4、一年级秋季要求背的1-10的三角形数还记得吗?数数中的枚举知识点精讲知识点总结一、数字:0、1、2、3、4、5、6、7、8、9(共10个)数:由数字组成的(无数个)二、组数(最高位不为0)1.确定几位数2.确定从哪位开始写注:①“比”后为目标②“相差”:2种情况3.确定顺序(从小到大/从大到小)4.有无特殊要求反序数下降数(上升数)例题精讲1.根据条件组数——有序的排列(例2)你能根据下面的要求,写出所有符合条件的两位数吗?(1)十位上的数字比个位上的数字大2;(2)十位上的数字与个位上的数字相差2。
解析:(1)先确定要题目要求我们写的是两位数,再确定从哪一位开始写——通过比较,发现先写出“比”字后面的,再写前面的思考起来更容易,所以一般我们把“比”字后面的当做是目标。
在这里也就是“个位上的数字”为目标,先写出来个位可能是几,再寻找十位上比个位上大2的数字即可组成我们需要的两位数。
个位上可能是:0、1、2、3、4、5、6、7、8、9。
而十位上最大是9,十位上的数字比个位上的数字大2,所以个位上最大是7。
二年级奥数:有趣的图形计数

二年级奥数:有趣的图形计数知识点总结一、平面图形计数1.规则图形——跑火车基本图形数依次加到12.不规则图形——分层数分类(大小分类,方向分类)3.方法:观察规律,变加为乘二、立体图形计数——分层数每层个数=上层个数+本层露出头顶的个数二、染色问题1重合2不染知识点精讲一、平面图形1、规则图形公式法(跑火车)(适用于数线段、数角、数三角形等)例数线段分析:有3条基本线段(火车头是3),所以一共有3+2+1=6(条)线段例数角分析:有3个基本角,共有3+2+1=6(个)角例数三角形分析:有4个基本三角形,共有4+3+2+1=10(个)三角形(2)不规则图形①分层数例数多层长方形(分层数)分析:每层有3+2+1=6(个),有3层,所以共有6╳3=18(个)也可以,长边上线段总数3+2+1=6(个)宽边上线段总数2+1=3(个)总共有:3×6=18(个)例图中有多少个三角形?解析:观察本图不是规则图形,不能直接用公式.但可以将它分成2层(中间横线以上是一层,去掉横线是一层),且每层都是一个规则的数三角的图形.每层个数:3+2+1=6(个)层数:2层总个数6×2=12(个)②分类数:大小、方向例数三角形方法:标号法(适用于任何基本的平面图形,建议重点掌握)分析:用标号法如图小三角形有6个,两个小三角形拼成的有(2,3)(4,5)(6,1)3个三个小三角形拼成的有(1,2,3)(2,3,4)(3,4,5)(4,5,6)(5,6,1)(6,1,2)6个六小三角形拼成的有1个共6+3+6+1=16(个)二、其它平面图形计数1、数棋盘:细观察,找规律,变加为乘2、数方块: 补、拆三、立体图形计数1、数立方体推荐方法:从上往下一层一层的数每层个数=上层个数+本层露出头顶的个数例数一数下图有多少块立方体?分析:如图,从上往下,一层一层的数即1+3+6+10=20(块)2、补成大正方体/长方体推荐方法:要补的块数=总数-现有的块数例至少添加多少个小正方体可以组成一个较大的正方体?分析:先观察发现这幅图有4层,那么要想拼出一个大正方体,那么每层应该有4行4列,所以拼成的大正方体至少得4╳4╳4=64块,现在有3+4+5+7=19块,所以至少得补64-19=45块3、染色问题简单情况可使用观察法没被染色的面即为粘在一起的面(重合面),粘一处少两个面,(两个方块各少一个面)例下面是用小正方体堆成的图形,现在把这个图形的表面涂上红色,数一数有多少个小正方形没有被涂色?分析:“横着”粘的:第一层+第二层的块数1+2=3处。
小学二年级奥数题图形及答案

⼩学⼆年级奥数题图形及答案⼀、计算题。
( 共101题)1.图2-26是由四个扁⽽长的圆圈组成的,在交点处有8个⼩圆圈.请你把1、2、3、4、5、6、7、8这⼋个数分别填在8个⼩圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块⼩区域,分别填上1~7七个⾃然数,在⼀些⼩区域中,⾃然数3、5、7三个数已填好,请你把其余的数填到空着的⼩区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3⽤的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在⾥⾯。
但题⽬总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个⼤圆,在⼤圆的交点上有六个⼩圆圈。
请你把1、2、3、4、5、6六个数分别填在六个⼩圆圈⾥,要求每个⼤圆上的四个⼩圆圈中的数之和都是14。
答案:案把14拆成4个⾃然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把⼀个数填⼊,然后试⼀下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下⾯图表,使每⼀横⾏、竖⾏、斜⾏的三个数相加的和都相等。
答案:案九宫格填九数的⽅法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下⾯的图形,找出变化规律,猜猜在第3组的右框空⽩格内填⼀个什么样的图?答案:6.请看下图,共有多少个正⽅形?答案:30 个正⽅形。
⼩结⼩⽅格16 个,4 个⼩⽅格为⼀个正⽅形共 9 个,9 个⼩⽅格为⼀个正⽅形共 4 个,最⼤的(16 个⼩⽅格)是 1 个。
16+9+4+1=30(个)共计 30 个正⽅形。
7.仔细观察这些图案可以发现,他们是按照下⾯这5个图案为⼀组,循环往复排列的,请问第52个图形是什么?答案:8.把上⾯⼀排的⽴体图形剪开,可以剪成下⾯哪种图形的样⼦?动⼿试⼀试。
小学二年级奥数题图形及答案

1.图2-26是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3用的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在里面。
但题目总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个大圆,在大圆的交点上有六个小圆圈。
请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14。
答案:案把14拆成4个自然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把一个数填入,然后试一下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下面图表,使每一横行、竖行、斜行的三个数相加的和都相等。
答案:案九宫格填九数的方法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?答案:6.请看下图,共有多少个正方形?答案:30 个正方形。
小结小方格16 个,4 个小方格为一个正方形共 9 个,9 个小方格为一个正方形共 4 个,最大的(16 个小方格)是 1 个。
16+9+4+1=30(个)共计 30 个正方形。
7.仔细观察这些图案可以发现,他们是按照下面这5个图案为一组,循环往复排列的,请问第52个图形是什么?答案:8.把上面一排的立体图形剪开,可以剪成下面哪种图形的样子?动手试一试。
小学二年级奥数题图形及答案(DOC)

⼩学⼆年级奥数题图形及答案(DOC)⼀、计算题。
( 共101题)1.图2-26是由四个扁⽽长的圆圈组成的,在交点处有8个⼩圆圈.请你把1、2、3、4、5、6、7、8这⼋个数分别填在8个⼩圆圈中。
要求每个扁长圆圈上的四个数字的和都等于18。
答案:2.在图2-24中,三个圆圈两两相交形成七块⼩区域,分别填上1~7七个⾃然数,在⼀些⼩区域中,⾃然数3、5、7三个数已填好,请你把其余的数填到空着的⼩区域中,要求每个圆圈中四个数的和都是15。
答案:15=1+2+5+7,15=1+3+4+7,15=1+3+5+6,15=2+3+4+6 其中1和3⽤的次数最多,图中最中间的部分被三个圆包围,所以1和3应该填在⾥⾯。
但题⽬总3已填好,所以只能填1。
1填好后其他的也就好确定了。
答案见下图3.图2-23中有三个⼤圆,在⼤圆的交点上有六个⼩圆圈。
请你把1、2、3、4、5、6六个数分别填在六个⼩圆圈⾥,要求每个⼤圆上的四个⼩圆圈中的数之和都是14。
答案:案把14拆成4个⾃然数的和,如下14=1+2+5+6;14=1+3+4+6;14=2+3+4+5。
先把⼀个数填⼊,然后试⼀下确定其他数的位置。
答案如下图4.将2、4、6、8、10、12、14、16、18填在下⾯图表,使每⼀横⾏、竖⾏、斜⾏的三个数相加的和都相等。
答案:案九宫格填九数的⽅法,确定中间是10最关键了,然后我们对这些数加和除以3,就有了相等的和应该是30,图形如下(有很多种,但是中间那个肯定是10)5.仔细观察下⾯的图形,找出变化规律,猜猜在第3组的右框空⽩格内填⼀个什么样的图?答案:6.请看下图,共有多少个正⽅形?答案:30 个正⽅形。
⼩结⼩⽅格16 个,4 个⼩⽅格为⼀个正⽅形共 9 个,9 个⼩⽅格为⼀个正⽅形共 4 个,最⼤的(16 个⼩⽅格)是 1 个。
16+9+4+1=30(个)共计 30 个正⽅形。
7.仔细观察这些图案可以发现,他们是按照下⾯这5个图案为⼀组,循环往复排列的,请问第52个图形是什么?8.把上⾯⼀排的⽴体图形剪开,可以剪成下⾯哪种图形的样⼦?动⼿试⼀试。
二年级下册数学试题-奥数思维拓展:第一讲 图形的计数(解析版)全国通用

第一讲图形计数【精品】课前复习数一数下面的图形.( 10 )条线段( 18 )个长方形( 10 )个正方形( 16 )个三角形( 8 )个圆同学们,我们已经会数平面图形的个数了(如三角形、正方形、长方形、圆形等).这一节我们要一起来学习数立体图形,比如数小方块等,在数这一类图形中,一定要认真仔细观察图形特点及摆布特点,有次序地去数,不能遗漏也不能重复,只有这样我们才能又快又准的数出这些图形的个数.同学们,加油吧!实践应用【例1】下面的这堆木方块共有多少块?【分析】引导学生按顺序来数,可以一层一层的数;也可以一排一排的数;还可以先数看得见的,再数看不见的,我们一般根据图形的特点来选择合适的方法.(1)3+1=4(块)(2)5+2=7(块)(3)7+4=11(块)(4)4×2=8(块)拓展训练数一数,下面的方块各有多少?( 9 )块( 10 )块( 9 )块列式:5+4=9(块)列式:6+3+1=10(个)列式:6+3=9(块)或:4+3+2=9(块)或:5+4=9(块)( 12 )块( 16 )块( 12 )块列式:6×2=12(块)列式:9+5+2=16(块)列式:9+3=12(块)【例2】下面的图形中一共有几个小方块?【分析】这个图形的数法非常多,在众多的方法中要经过比较,找到最简便的方法:拓展训练这堆方木块共有多少块?方法一:分层数:一共有木方块6+12+18=36(块)或6×6=36(块).方法二:分列数:6×6=36(块)【例3】下面这堆木方块共有多少块?(中间打阴影部分是空心)【分析】因为中间是空心的,所以一层只有8块,一共8×4=32(块).延伸:想一想还可以怎样数?方法二:第一列有12个,第二列有8个,第三列有12个,一共有:12+8+12=32(块)方法三:不看阴影部分一共有:12×3=36(块),中间缺得部分是4个,一共有方块:36-4=32(块)拓展训练下图由多少块正方体组成?(中间阴影部分是空心的)【分析】虽然部分方块被遮住了,但是我们还是可以发现,如果不看中间空心的部分,每边是3个方块,共3层.方法一:9+6+9=24(块)或3×8=24(块)方法二:一层8个,共8×3=24(块)方法三:3×9-3=24(块)【例4】数一数,图1和图2中各有多少黑方块和白方块?【分析】图1:仔细观察图1,可发现黑方块和白方块同样多.因为每一行中有4个黑方块和4个白方块,共有8行,所以黑方块是:4×8=32(个);白方块是:4×8=32(个).图2:再仔细观察图2,从上往下看:第一行.白方块5个,黑方块4个;,第二行白方块4个,黑方块5个;第三、五、七行同第一行,第四、六、八行同第二行;但最后的第九行是白方块5个,黑方块4个.可见白方块总数比黑方块总数多1个.白方块总数:5+4+5+4+5+4+5+4+5=41(个)黑方块总数:4+5+4-5+4+5+4+5+4=40(个)再一种方法是:每一行的白方块和黑方块共9个.共有9行,所以,白、黑方块的总数是:9×9=81(个).由于白方块比黑方块多1个,所以白方块是41个,黑方块是40个.【例5】书库里把书如图所示的那样沿墙堆放起来.请你数一数这些书共有多少本?【分析】方法1:从左往右一摞一摞地数:10+11+12+13+14+15+14+13+12+11+10=135(本).方法2:把这摞书形成的图形看成是由一个长方形和一个三角形“尖顶”组成.长方形中的书 10×11=110 三角形中的书 1+2+3+4+5+4+3+2+1=25 总数:110+25=135(本).【例6】请你数一数,这个跳棋盘上可以放多少个棋子?【分析】要知道可以放多少个棋子,就要数有多少个棋孔.因为棋孔较多,应找出排列规律,以便于计数.仔细观察可知,图中大三角形ABC上的棋孔的排列规律是(从上往下数):1,2,3,4,5,6,7,8,9,10,11,另外还有三个小三角形中的棋孔的排列规律是1,2,3,所以棋孔总数是:(1+2+3+4+5+6+7+8+9+10+11)+(1+2+3)×3=66+6×3=84(个).拓展训练如图所示砖墙是由正六边形的特型砖砌成,问需要几块正六边形的砖才能把它补好?【分析】仔细观察,并发挥想象力可得出答案,用七块正六边形的砖可把这个墙洞补好.如果动手画一画,就会看得更清楚了.【例7】将10个小长方体组成一个“工"字形,再将表面涂成蓝色,然后把小正方体分开,(1)3面涂成蓝色的小长方体有几个?(2)4面涂成蓝色的小长方体有几个?(3)5面涂成蓝色的小长方体有几个?【分析】整个图形表面涂成蓝色,只有那些“黏在一起”的面没有被涂色.左、右两端中间各有1个小正方体3面涂色,中间的4个小正方体4面涂色,剩下的4个小正方体都是5面涂色.3面涂成蓝色的小正方体有2个;4面涂成蓝色的有4个;5面涂成蓝色的有4个.【例8】一个大长方体的表面上都涂上红色,然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:(1)1面涂成红色的有几个?(2)2面涂成红色的有几个?(3)3面涂成红色的有几个?【分析】仔细观察图形,并发挥想象力,可知:(1)上下两层中间的2块只有一面涂色;(2)每层四边中间的1块有两面涂色,上下两层共8块;(3)每层四角的4块有三面涂色,上下两层共有8块.最后检验一下小立体总块数:2+8+8=18(个).【例9】如图所示,一个木制的正方体,棱长为3厘米,它的六个面都被涂成了红色.如果沿着图中画出的线切成棱长为1厘米的小正方体.求:(1)3面涂成红色的有多少块?(2)2面涂成红色的有多少块?(3)1面涂成红色的有多少块?(4)各面都没有涂色的有多少块?(5)切成的小正方体共有多少块?【分析】(1)3面涂色的有8块:它们是最上层四个角上的4块和最下层四个角上的4块.(2)2面涂色的有12块:它们是上、下两层每边中间的那块共8块和中层四角的4块.(3)1面涂色的有6块:它们是各面(共有6个面)中心的那块.(4)各面都没有涂色的有一块:它是正方体中心的那块.(5)共切成了3×3×3=27(块). 或是如下计算:8+12+6+1=27(块).【例10】一个由小正方体堆成的“塔”.如果把它的外表面(包括底面)全部涂成绿色,那么当把“塔”完全拆开时,3面被涂成绿色的小正方体有多少块?【分析】3面被涂成绿色的小正方体共有16块,就是图中有“点”的那些块(注意最下层有2块看不见).附加题(以下提供的内容,供老师参考使用)1.如图所示为一块地板,它是由1号、2号和3号三种不同图案的瓷砖拼成.问这三种瓷砖各用了多少块?【分析】因为图形复杂,要特别仔细,最好是有次序地按行分类数,再进行统计:1号瓷砖共12块统计: 2号瓷砖共16块总数:36块.3号瓷砖共8块2.下图中还差多少个小正方体可以组成一个较大的正方体?【分析】先从整体上考虑组成一个较大的正方体需要多少个小正方体,再数出已有的小正方体的个数,便能得出相差的个数.组成较大的正方体需要的小正方体个数:3×3×3=27(个)已有小正方体个数:9+6+3=18(个)还差正方体个数:27-18=9(个)答:还差9个小正方体可以组成一个较大的正方体.3.染色问题补充:右图是一个正方体木块,在它的表面涂上颜色,然后沿图中虚线竖直切开.没有涂颜色的面共有几个?【分析】先分析能切成多少块,再考虑每块上有几个面没涂颜色.解:2×8=16(个)答:没有涂颜色的面共有16个.4. 下图所示为棱长4厘米的正方体,将它的表面全染成蓝色,然后锯成棱长1厘米的小正方体.问:(1)有3面被染成蓝色的多少块? 8块;(2)有2面被染成蓝色的多少块? 24块;(3)有1面被染成蓝色的多少块? 24块;(4)各面都没有被染色的多少块? 8块;(5)锯成的小正方体木块共有多少块? 64块.练习一1.图中有多少个小正方体?【答案】 7+2=9(个).2.这堆木方块共有多少块?你能用几种不同的方法数出来和算出来吗?【答案】6+4+2=12(块)或6×2=12(块).3.这堆木方块共有多少块?(中间打阴影部分是空心)【答案】3×3×5-2×3=39(块)或3×3×3+6×2=39(块)4. 用不同的方法数这两个图形各有多少个方块?【答案】(1)4+3+1=8(个);(2)3×2+4=10(个).5.小狗与小猫的外形是用绳子围成的,你知道哪一条绳子长吗?(仔细观察,想办法比较出来).【答案】分类数一数可知,围成小猫的那条绳子比较长.因为小狗身体的外形是由32条直线段和6条斜线段组成;小猫身体的外形是由32条直线段和8条斜线段组成.6.将8个小立方块组成“丁”字型,再将表面都涂成红色,然后就把小立方块分开,(1)3面被涂成红色的小立方块有多少个?(2)4面被涂成红色的小立方块有多少个?(3)5面被涂成红色的小立方块有多少个?【答案】看着图,想象涂色情况.当把整个表面都涂成红色后,只有那些“粘在一起”的面(又叫互相接触的面),没有被涂色.每个小立方体都有6个面,减去没涂色的面数,就得涂色的面数.每个小立方体涂色面数都写在了它的上面.3面涂色的小立方体共有1个;4面涂色的小立方体共有4个;5面涂色的小立方体共有3个.数学故事从一加到一百高斯有许多有趣的故事,故事的第一手资料常来自高斯本人,因为他在晚年时总喜欢谈他小时候的事,我们也许会怀疑故事的真实性,但许多人都证实了他所谈的故事. 高斯的父亲作泥瓦厂的工头,每星期六他总是要发薪水给工人.在高斯三岁夏天时,有一次当他正要发薪水的时候,小高斯站了起来说:“爸爸,你弄错了.”然后他说了另外一个数目.原来三岁的小高斯趴在地板上,一直暗地里跟着他爸爸计算该给谁多少工钱.重算的结果证明小高斯是对的,这把站在那里的大人都吓的目瞪口呆.高斯常常带笑说,他在学讲话之前就已经学会计算了,还常说他问了大人字母如何发音后,就自己学着读起书来.七岁时高斯进了小学.大约在十岁时,老师在算数课上出了一道难题:“把1到100的整数写下来,然后把它们加起来!”每当有考试时他们有如下的习惯:第一个做完的就把石板﹝当时通行,写字用﹞面朝下地放在老师的桌子上,第二个做完的就把石板摆在第一张石板上,就这样一个一个落起来.这个难题当然难不倒学过算数级数的人,但这些孩子才刚开始学算数呢!老师心想他可以休息一下了.但他错了,因为还不到几秒钟,高斯已经把石板放在讲桌上了,同时说道:“答案在这儿!”其他的学生把数字一个个加起来,额头都出了汗水,但高斯却静静坐着,对老师投来的,轻蔑的、怀疑的眼光毫不在意.考完后,老师一张张地检查着石板.大部分都做错了,学生就吃了一顿鞭打.最后,高斯的石板被翻了过来,只见上面只有一个数字:5050(用不着说,这是正确的答案.)老师吃了一惊,高斯就解释他如何找到答案:1+100=101,2+99=101,3+98=101,……,49+52=101,50+51=101,一共有50对和为101的数目,所以答案是50×101=5050.由此可见高斯找到了算术级数的对称性,然后就像求得一般算术级数合的过程一样,把数目一对对地凑在一起.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二年级奥数:数图形
1、数一数下面的图形中各有几个角?其中直角有几个?2、数一数,填一填。
()个角()个直角
1、下面的图形中各有几个角?
2、下面的图形中各有几条线段?
3、数一数,下面图中有多少个正方形?
通过本次学习,我的收获是
第一部分必做题
1、填空。
⑴(☆)一条红领巾有()个角。
⑵(☆)数学书的封面有()个角,()个直角。
2、数一数,下面的图形中各有几个角,其中直角有几个?
⑴(☆) ⑵(☆)
3、下图中各有多少个角?
⑴(☆☆) ⑵(☆☆)
4、下图中各有多少条线段?
⑴(☆☆) ⑵(☆☆)
5、下图中各有多少个角?
⑴(☆) ⑵(☆)
6、下图中各有多少个直角?
⑴(☆) ⑵(☆)
⑶(☆) ⑷(☆)
7、(☆☆)数一数下图中有()个三角形,()个正方形,()个长方形。
8、画一画。
⑴(☆)用直尺或三角尺画三个角,要使其中有一个角是直角。
⑵(☆)用直尺或三角尺画一个有四个直角的图形。
第二部分选做题
9、(☆☆)画一个四边形,其中有两个角是直角,另外两个角不是直角。
10、(☆☆)画一个有8个角的图形。
11、(☆☆)下图中有多少个正方形?
12、(☆☆)给下面的三个图形各加1条直线,使这些图形分别有4个直角、5个
直角、6个直角。
13、(☆☆☆)数一数,填一填。
⑴
比直角小的角有()个,比直角大的角有()个。
⑵⑶
()个角()个直角,()个钝角
14、(☆☆☆)下列图形中有多少三角形?。
