电磁场与电磁波 第二版 冯恩信 第三章课后习题答案
电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)第3章

可见,空间某点r对于任一参考点r0的电位为
对于本题,若取坐标原点作为电位参考点,因为原线电荷 离坐标原点的距离为2h,离场点P的距离为r0,那么该线电荷在P点产生的电位为
因为全部镜像电荷离坐标原点的距离均为2h,那么,劈间任一点P以坐标原点作为电位参考点的电位为
即
要使点电荷受力为零,则 应满足下列方程
求解此高次方程可用作图法。为此,先将上式化简为
再化为关于 的方程即
若 ,则上面的方程又可写为
令 , ,分别作图求得y1和y2的交点,即是所要求的解。根据题意可知 ,由下图可见 的解位于 =1.5~2之间。其值近似为 ,即 时,点电荷q受力为零。
3-14试证位于内半径为a的导体球形空腔中的点电荷q受到的电场力大小为
答根据镜像法,如果劈形导体的夹角不为 的整数分之一时,则镜像电荷不能最终和原电荷重合,这样将会产生无限多个镜像电荷,每个镜像电荷都会产生一定的电位,导致合成电位无限大,因而无解。
当点电荷位于两块无限大导体板之间时,可采用镜像法求解。此时虽然也会产生无限多个镜像电荷,但是远处的镜像电荷对于两板之间的场点贡献越来越小,因
当球壳的电位为时,由上题获知位于球心的镜像电荷q应为
壳外的场强将由点电荷 及其镜像电荷 和q共同产生,壳外的合成电位为
式中镜像电荷 ,离球心的距离为 ,则壳外的电场强度为
2球壳表面的电荷密度为
其最大值为
③系统能量的改变来自外力作的功。已知点电荷 受到的电场力为
由此可见,若q>0q<0,又因<0,故电场力的实际方向为(-er)。在外力作用下,当点电荷q离开球心的距离增加一倍时,外力F作的功为
因为 ,即 ,代入上式,考虑到 ,即当 时,取上式极限,求得
电磁场与电磁波:第三章作业答案
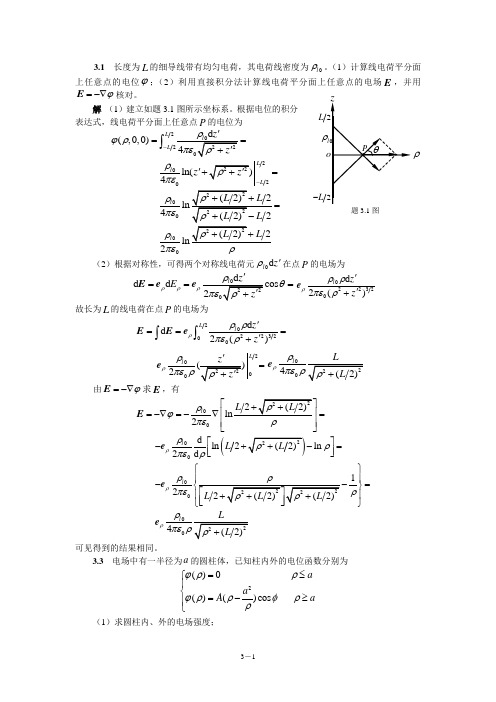
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
《电磁场与电磁波》习题参考答案

《电磁场与电磁波》知识点及参考答案第1章 矢量分析1、如果矢量场F 的散度处处为0,即0F∇⋅≡,则矢量场是无散场,由旋涡源所产生,通过任何闭合曲面S 的通量等于0。
2、如果矢量场F 的旋度处处为0,即0F ∇⨯≡,则矢量场是无旋场,由散度源所产生,沿任何闭合路径C 的环流等于0。
3、矢量分析中的两个重要定理分别是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分别是:散度(高斯)定理:SVFdV F dS ∇⋅=⋅⎰⎰和斯托克斯定理:sCF dS F dl∇⨯⋅=⋅⎰⎰。
4、在有限空间V 中,矢量场的性质由其散度、旋度和V 边界上所满足的条件唯一的确定。
( √ )5、描绘物理状态空间分布的标量函数和矢量函数,在时间为一定值的情况下,它们是唯一的。
( √ )6、标量场的梯度运算和矢量场的旋度运算都是矢量。
( √ )7、梯度的方向是等值面的切线方向。
(× )8、标量场梯度的旋度恒等于0。
( √ ) 9、习题1.12, 1.16。
第2章 电磁场的基本规律(电场部分)1、静止电荷所产生的电场,称之为静电场;电场强度的方向与正电荷在电场中受力的方向相同。
2、在国际单位制中,电场强度的单位是V/m(伏特/米)。
3、静电系统在真空中的基本方程的积分形式是:V V sD d S d V Q ρ⋅==⎰⎰和0lE dl ⋅=⎰。
4、静电系统在真空中的基本方程的微分形式是:V D ρ∇⋅=和0E∇⨯=。
5、电荷之间的相互作用力是通过电场发生的,电流与电流之间的相互作用力是通过磁场发生的。
6、在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量B 1n -B 2n =0。
7、在介电常数为e 的均匀各向同性介质中,电位函数为 2211522x y z ϕ=+-,则电场强度E=5x y zxe ye e --+。
8、静电平衡状态下,导体内部电场强度、磁场强度等于零,导体表面为等位面;在导体表面只有电场的法向分量。
电磁场与电磁波基础教程(第2版)习题解答

《电磁场与电磁波基础教程》(第2版)习题解答第1章1.1 解:(1)==A B=C(2))))23452A x y zB y zC x z ==+-=+=-,,;A a a a a a -a a a a a A(3)()()+2431223x y z x y z =+-+-+=--=+;A B a a a a a a A B (4)()()23411x y z y z ⋅=+-⋅-+=-;A B a a a a a (5)()()234104x y z y z x y z ⨯=+-⋅-+=---;A B a a a a a a a a (6)()()()1045242x y z x z ⨯⋅=-++⋅-=-;A B C a a a a a(7)()()()x 2104522405x y z x z y ⨯⨯=-++⨯-=-+A B C a a a a a a a a 。
1.2解:cos 68.56θθ⋅===︒;A B A BA 在B 上的投影cos 1.37B A θ===A ;B 在A 上的投影cos 3.21A B θ===B 。
1.3 解:()()()()()()()4264280⋅=-++-=正交A B 。
1.4 解:1110x x y y z z x y y z z y ⋅=⋅=⋅=⋅=⋅=⋅=,,;;a a a a a a a a a a a a 0x x y y z z ⨯=⨯=⨯=;a a a a a a x y z y z x z x y ⨯=⨯=⨯=;,a a a a a a a a a 。
1.5 解:(1)111000z z z z ρρϕϕρϕϕρ⋅=⋅=⋅=⋅=⋅=⋅=,,;,,a a a a a a a a a a a a ;000z z z z z ρρϕϕρϕϕρρϕ⨯=⨯=⨯=⨯=⨯=⨯=,,;,,a a a a a a a a a a a a a a a 。
电磁场与电磁波_部分课后习题解答

电磁场与电磁波部分课后习题解答CH11.2给定三个矢量A ,B ,C:A =x a+2y a -3z a B= -4y a +z aC =5x a-2z a求:⑴矢量A的单位矢量A a ;⑵矢量A 和B的夹角AB θ; ⑶A ·B 和A ⨯B⑷A ·(B ⨯C )和(A ⨯B)·C ;⑸A ⨯(B ⨯C )和(A ⨯B )⨯C解:⑴A a =A A=(x a +2y a -3z a )⑵cos ABθ=A ·B /A BAB θ=135.5o⑶A ·B =-11, A ⨯B=-10x a -y a -4z a⑷A ·(B ⨯C )=-42(A ⨯B)·C =-42⑸A ⨯(B ⨯C)=55x a -44y a -11z a(A ⨯B)⨯C =2x a -40y a +5z a1.3有一个二维矢量场F(r) =x a(-y )+y a (x),求其矢量线方程,并定性画出该矢量场图形。
解:由dx/(-y)=dy/x,得2x +2y =c1.6求数量场ψ=ln (2x +2y +2z )通过点P (1,2,3)的等值面方程。
解:等值面方程为ln (2x +2y +2z )=c 则c=ln(1+4+9)=ln14 那么2x +2y +2z =141.9求标量场ψ(x,y,z )=62x 3y +ze 在点P (2,-1,0)的梯度。
解:由ψ∇=x a x ψ∂∂+y a y ψ∂∂+z a zψ∂∂=12x 3y x a +182x 2y y a +z e z a 得ψ∇=-24x a +72y a +z a1.10 在圆柱体2x +2y =9和平面x=0,y=0,z=0及z=2所包围的区域,设此区域的表面为S: ⑴求矢量场A沿闭合曲面S 的通量,其中矢量场的表达式为A =x a32x +y a (3y+z )+z a (3z -x)⑵验证散度定理。
电磁场与电磁波第二版课后答案

电磁场与电磁波第二版课后答案本文档为《电磁场与电磁波》第二版的课后答案,包含了所有章节的练习题的答案和解析。
《电磁场与电磁波》是电磁学领域的经典教材,它讲述了电磁场和电磁波的基本原理和应用。
通过学习本书,读者可以深入了解电磁学的基本概念和原理,并且能够解决一些相关问题。
第一章绪论练习题答案1.电磁场是由电荷和电流产生的一种物质性质,具有电场和磁场两种形式。
电磁波是电磁场的振动。
电磁辐射是指电磁波传播的过程。
2.对于一点电荷,其电场是以该点为中心的球对称分布,其强度与距离成反比。
对于无限长直导线产生的电场,其强度与距离呈线性关系,方向垂直于导线轴线。
3.电磁场的本质是相互作用力。
电场力是由于电荷之间的作用产生的,磁场力是由于电流之间的作用产生的。
解析1.电磁场是由电荷和电流产生的物质性质。
当电荷存在时,它会产生一个电场,该电荷周围的空间中存在电场强度。
同时,当电流存在时,它会产生一个磁场,该电流所在的区域存在磁场。
电磁波是电磁场的振动传播。
电磁波是由电磁场的变化引起的,相邻电磁场的振动会相互影响,从而形成了电磁波的传播。
电磁辐射是指电磁波在空间中的传播过程。
当电磁波从一个介质传播到另一个介质时,会发生折射和反射现象。
2.在一点电荷产生的电场中,电场强度与该点到电荷的距离成反比,即\(E = \frac{{k \cdot q}}{{r^2}}\),其中\(E\)为电场强度,\(k\)为电场常数,\(q\)为电荷量,\(r\)为距离。
对于无限长直导线产生的电场,其电场强度与离导线的距离呈线性关系。
当离无限长直导线的距离为\(r\)时,其电场强度可表示为\(E = \frac{{\mu_0 \cdot I}}{{2 \pi \cdot r}}\),其中\(E\)为电场强度,\(\mu_0\)为真空中的磁导率,\(I\)为电流强度。
3.电磁场的本质是相互作用力。
当两个电荷之间有作用力时,这个作用力是由于它们之间的电场力产生的。
电磁场与电磁波》冯恩信第二版西安交通大学课后答案

1.6
将圆柱坐标系中的矢量场
r F1
(
ρ
,
ϕ
,
z)
=
2ρ$ ,
r F2
(ρ,ϕ,
z)
=
3ϕ$
用直角坐标系中的坐标
分量表示。
解:由(1.2-9)式,
r F1
=
2ρˆ
=
2 cosϕxˆ
+
2sin ϕyˆ
=
2 (xxˆ + yyˆ) x2 + y2
r F2
=
3ϕˆ
=
−3sin ϕxˆ + 3cosϕyˆ
⋅
∇e
kr
=
r k
⋅
rˆke
kr
1.17
(c) ∇r 已知rA
× =
ρyrx$=−r0x;y∇$ ,× r计r r=算0;A∇r ⋅×(∇(z×ρˆ
)r= A)
ϕˆ
解: ∇ × A = 1.18 已知 ∇ ⋅
−Fr2=zˆ;δA(⋅x()∇δ (×yA)δ)(=z)0,∇
×
r Fr
=
0,
计算
r F
r
+ ϕˆ + zzˆ
1 4π
(∇
1 r
×
zˆ
+
1 r
∇×
zˆ)
=
zˆ × rˆ 4πr 2
穿过由 ρ ≤ 1,0 ≤ ϕ ≤ π ,0 ≤ z ≤
1
确定的区域的封闭面的
通量。 解:根据高斯定理,矢量场
r F
=
ρρˆ
+
ϕˆ
+
zzˆ
穿过由
ρ
≤
电磁场与电磁波实际(第二版)(徐立勤-曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+ 0202εερA -=Φ∇-= (2) ()x y z E A e yz e xz e xy Φ=-∇=-++ 020=Φ∇-=ερ (3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦20004sin sin 3sin BzBz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭ (4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为0011100)()22S S d R d ρρΦεε==- 下顶面在球心产生的电位为0022200)()22S S d R d ρρΦεε==- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
