载常数和形常数表 单跨超静定梁PPT演示文稿
形常数和载常数表

形常数和载常数表在结构力学中,形常数和载常数是非常重要的概念。
它们对于分析和计算结构的内力、位移等起着关键作用。
接下来,让我们一起深入了解一下形常数和载常数表。
首先,我们来谈谈形常数。
形常数是指由杆件的单位杆端位移引起的杆端内力。
简单来说,就是当杆件的一端发生了某种特定的位移,比如转角或者线位移时,在这一端产生的内力大小。
为了方便计算和分析,这些内力的大小被整理成了形常数表。
比如说,对于等截面的梁,当一端发生单位转角时,在这一端产生的弯矩就是一个固定的值。
同样,当一端发生单位线位移时,产生的剪力也有一个确定的值。
这些固定的值就构成了形常数。
形常数的确定通常基于结构的几何形状和材料特性。
不同类型的杆件,如梁、柱、桁架中的杆件等,其形常数是不同的。
而且,对于同一类型的杆件,在不同的约束条件下,形常数也会有所变化。
接下来,再说说载常数。
载常数是指由单位荷载作用在杆件上引起的杆端内力。
单位荷载可以是集中力、均布荷载、力偶等。
与形常数类似,载常数也是为了方便计算和分析而整理成表的。
例如,在一个简支梁上,作用一个单位集中力时,在梁的两端产生的弯矩和剪力就有特定的值。
这些值就是载常数。
形常数和载常数表在结构力学的计算中有着广泛的应用。
比如,在使用力法、位移法等求解超静定结构时,就需要用到这些常数表。
通过形常数和载常数表,我们可以快速准确地确定杆件在各种位移和荷载作用下的内力。
这大大简化了计算过程,提高了工作效率。
在实际工程中,准确地确定形常数和载常数是非常重要的。
如果这些常数出现误差,可能会导致结构设计的不合理,影响结构的安全性和可靠性。
为了更清楚地理解形常数和载常数,我们来看一个具体的例子。
假设我们有一个悬臂梁,固定端在左端,自由端在右端。
当右端发生单位转角时,固定端的弯矩就是一个确定的形常数。
如果在梁的自由端作用一个单位集中力,那么固定端的弯矩和剪力就是相应的载常数。
在实际计算中,我们可以根据具体的结构形式和受力情况,从形常数和载常数表中查找到相应的数值,然后进行后续的计算和分析。
形常数和载常数表

形常数和载常数表在结构力学的领域中,形常数和载常数表是非常重要的工具。
它们帮助工程师和学者们更有效地分析和设计各种结构。
首先,让我们来理解一下什么是形常数。
形常数是指在杆件结构中,由于杆件的位移引起的内力与变形之间的关系所确定的常数。
简单来说,就是当杆件发生某种特定的变形时,所产生的内力的大小是由形常数决定的。
比如说,对于一个两端固定的梁,当它在中间受到一个集中力作用时,梁的弯曲变形就与某些特定的形常数相关。
形常数的确定通常需要通过对结构的力学分析和计算来得到。
不同的杆件结构和边界条件,其形常数也会有所不同。
常见的形常数包括弯曲形常数、拉伸形常数、扭转形常数等等。
接下来再谈谈载常数。
载常数则是指在杆件结构中,由于外部荷载作用引起的内力与荷载之间的关系所确定的常数。
比如,在一个简支梁上作用一个均布荷载,梁内产生的弯矩、剪力等内力与这个均布荷载之间的关系就由载常数来描述。
载常数的确定也需要基于结构力学的原理和计算方法。
它与荷载的类型、大小、作用位置以及结构的形式和边界条件等因素密切相关。
为了更直观地应用形常数和载常数,人们通常会将它们整理成表格的形式,这就是形常数和载常数表。
这些表格中详细列出了各种常见结构形式和荷载情况下的形常数和载常数的值。
在实际工程应用中,形常数和载常数表具有很大的价值。
比如在设计桥梁时,工程师可以通过查阅形常数和载常数表,快速地确定在不同的荷载作用下桥梁各个部位的内力和变形情况,从而评估桥梁的安全性和稳定性。
在对建筑物进行结构分析时,也能利用这些表格来简化计算过程,提高设计效率。
而且,形常数和载常数表不仅仅在传统的土木工程领域有用,在机械工程、航空航天工程等领域也有着广泛的应用。
比如在设计飞机机翼的结构时,就需要考虑各种载荷情况下的形变量和内力分布,这时形常数和载常数表就能提供重要的参考。
然而,需要注意的是,在使用形常数和载常数表时,必须要确保所选用的表格与实际的结构形式和荷载情况相匹配。
超静定问题PPT课件
FN1 cos FN2 cos FN3 F 0
FN1
FN 3
EA cos2
E3 A3
FN3 1 2
F EA
cos2
E3 A3
FN1
FN 2
1 2cos
F
E
E3 A3
A cos2
第13页/共59页
B 1
1
Δl3
D
3
C 2
A
3 F2
A
Δl1A' NhomakorabeaFA A C
F
B FB
14
b
a
l
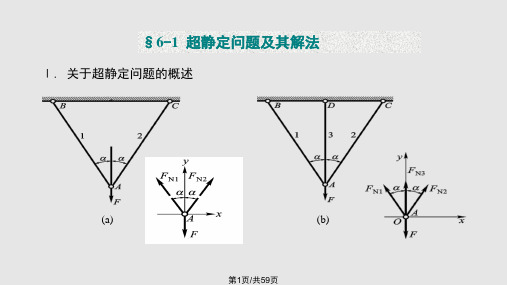
第六章 简单的超静定问题
例题2 求图a所示等直杆AB上,下端的约束力, 并求C截面的位移。杆的拉压刚度为EA。
解: 1. 列平衡方程 有两个未知约束力FA , FB(见图a),但只有一个独 立的平衡方程
FA+FB-F=0 为一次超静定问题。
第14页/共59页
2. 取固定端B为“多余”约束。相应 的相当系统如图b,它应满足相容条件 ΔBF+ΔBB=0,参见图c,d。
MA 0
F a F 2a 0
A
B
P
FN1 a
A
FN2 a
FN3 B
P
第17页/共59页
变形协调方程:
ΔL 1
L1 L3 2(L2 L3 ) (2)
物理方程:
l1
FN 1l EA
l2
FN 2l EA
l3
FN 3l EA
(3)
联解(1)(2)(3)式得:
F 5P 6
F
2
1 3
P
F
3
1 6
D
由位移相容条
载常数和形常数表 单跨超静定梁PPT演示文稿

AB
A
B
l
AB
M 2i 4i 6i M F
BA
A
B
l
BA
↓↓↓↓↓↓↓↓
Δ
MAB QAB
β θA
θB
转角位移方程
QBA MBA
4、已知杆端弯矩求剪力:取杆 件为分离体建立矩平衡方程:
QABMAB l MBAQA FB
MAB QAB
MAB
Q’‘ AB
P
MBA
+
P
QBA MBA
Q’‘ BA
Q0 AB
A B
i, l B
1
3FPl 16
11FP
3i
5FP l
16
3i
3i l2
16
l2
4
一端固定一端定向滑动的单跨超静定梁的载常数和形常数
q
A i, l
i, l
B
A
1
ql 2
3
ql 2
ql
6 0
i
0
B
i
0
A
FPl 2
FP
Hale Waihona Puke FPi, lB
FPl 2 0
5
3、转角位移方程:杆端弯矩的一般公式:
M 4i 2i 6i M F
q
i, l
B
A 1
B
i, l
6i
ql 2
l
2i
ql 12 4i
6i
l 2
FP i, l
A B
FPl 6i
FP
8l
12i
2
l2
i, l B
1
12i
l2
6i
l
《超静定梁》PPT课件

B
8 Fa 9 - 2021/4/23
FN' wBB2
1F 9 B
wB1 wB2
C
查表得:
wB1
(F
FN 3EI
)a3
C
wB 2
FN (2a)3 3EI
代入上式得:FN
FN
1 9
F
C
弯矩图为:
2
-
Fa 9
21
四、超静定结构(梁)的其它解法及研究现状
将未知问题转化为 已知问题,通过消除已 知问题和原问题的差别, 使未知问题得以解决。
2021/4/23
16
么么么么方面
• Sds绝对是假的
方法二 取支座 A 处阻止梁转动的约束 为多余约束。 代之以与其相应的多余反力偶 MA 得基本静定系。
变形相容条件为:
A 0
2021/4/23
q
B
A l
MA
q
B A
l
基本静定系
18
MAqΒιβλιοθήκη 变形相容条件为: A 0 B
几何方程
A
Aq AMA 0
郑州大学的李会知教授分析了集中荷载或均布荷载作用下 两端固支梁和一次超静定梁的弹塑性加载及变形过程,并 给出了加载各阶段的弯矩和位移计算公式。
中南大学的陈玉骥副教授采用半逆解法,求出了一端固定 一端铰支单跨超静定梁在均布荷载作用下的应力和位移, 并由此说明了材料力学解的精度和适用性。
燕山大学的韩晓娟副教授在三弯矩方程应用中引入刚度系 数和载荷分布系数,使应用这一定理解决工程实际问题时 更简捷、方便和实用.
2021/4/23
9
三 、变形比较法解超静定梁
图示为抗弯刚度为 EI 的一次超静定梁。 变形比较法: (1)将可动铰链支座B
载常数

t0
+
t/
t 0 ( t1 t 2 ) / 2, t / ( t1 t 2 ) / 2
R1t R1/t R1//t / R1t 9it 0 同上例 t / l 3i / t / l // R1t 3i t l 2i h l h r11 Z1 R1t 0 M MZ1 M t
例8. M图,
EI=常数, t1〉t2 r11 8i 同上例
R1t的算:
t
o 2
o t2 o t1 o t1
Z1
o t2 o t2 o t1
// R1t
l h
t0
o t1
l
l
t0
/ R1t
R1t o
t2 t1o
t
/
t/ t/
t1o
=
t0
P
EI=C
=
P/2
P/2
+
P/2
P/2
力法:6个未知量 P/2 位移法:6个未知量 P/2
部分力法,部分位移法:4个未知量
2.混合法
• 基本思路
联合法是一个计算简图用同一种方法, 联合应用力法、位移法。
混合法则是同一个计算简图一部分用 力法、另一部分用位移法。超静定次数 少,独立位移多的部分取力为未知量。 超静定次数多,独立位移少的部分取位 移作未知量。
• 位移法
基本未知量:结点独立位 移 基本结构:单跨梁系 作单位和外因内力图 由内力图的结点、隔离体 平衡求系数,主系数恒正。 建立位移法方程(平衡) K F 0 解方程求独立结点位移 迭加作内力图 用平衡条件进行校核 可以解静定结构
X
超静定结构内力计算不错讲义.pptx

超静定结构的力法计算的基本思想是利用静定的基本体系来计算多余未知力, 基本体系的内力、变形与原来超静定结构完全相同。因此,在求解超静定结构的位移
时,仍可以借助于基本体系,把已求出的多余力当作主动力来看待,采用前面的静定
结构求位移的方法即可以求出基本体系的位移,该位移也就是原来超静定结构中相应
X1
3EI l2
(
a) l
(3) 求内力。原超静定结构内力与基本体系相同,而支座移动在基本体系(静定结
构)中不引起内力,所以最后弯矩为:
M= M i X i
i
第15页/共52页
力法
原结构的弯矩图如图6.13(e)所示。 由此可以看出,计算超静定结构由于支座移动引起的内力时,其力法方程右端 项应等于原结构相应处的位移,而自由项为基本结构由于支座移动产生的与多余未知 力相应的位移。该两项可直接由基本结构中变形关系求出。结构的最后内力全部由多
力法
下面结合具体例子说明力法的运用。 【例6.2】 用力法计算如图6.10(a)所示的刚架,各杆的EI 相等且为常数,绘制内力图。
图6.10 超静定刚架
解 (1) 由几何组成分析知,该结构是二次超静定结构,去掉处的两个多余约束, 得到基本结构,如图6.10(b)所示。
第10页/共52页
力法
(2) 由已知点的位移条件,列出力法的典型方程:
第5页/共52页
力法
△1 =0 ,
△2=0
图6.9 力法解二次超静定刚架
第6页/共52页
力法
设各单位未知力X1=1、X2=1 和荷载分别作用于基本结构上,A点沿X1 方向的位 移分别为δ11、 δ12、 △1P ;沿X2 方向的位移分别为δ21、 δ22、 △2P (如图6.9(c)、(d)、 (e))所示。根据叠加原理,上述位移条件可表示为:
形常数和载常数表

形常数和载常数表在结构力学中,形常数和载常数表是非常重要的工具,它们对于分析和计算结构的内力与变形起着关键作用。
首先,让我们来了解一下什么是形常数。
形常数指的是在杆件仅发生单位位移(例如单位转角或单位线位移)时,杆件内部所产生的内力(例如弯矩、剪力等)。
这些内力的大小和分布规律是固定的,只与杆件的几何形状和约束条件有关。
比如说,对于两端固定的梁,当在其中一端发生单位转角时,所产生的弯矩分布就是一种形常数。
通过对各种常见杆件结构的分析和计算,可以得到相应的形常数表。
这些形常数表通常以表格的形式呈现,清晰地列出了不同杆件结构在不同单位位移下的内力值。
接下来,我们再看看载常数。
载常数是指在杆件上作用单位荷载(集中力、均布力等)时,杆件内部所产生的内力。
与形常数类似,载常数也只与杆件的几何形状和约束条件有关。
以简支梁为例,当在梁上作用单位集中力时,梁内产生的弯矩和剪力就是载常数。
同样,各种不同类型的杆件结构在不同单位荷载作用下的载常数也可以整理成表格形式,方便我们在结构分析和计算中直接查阅和使用。
那么,形常数和载常数表有什么实际用途呢?在结构力学的计算中,我们常常需要求解复杂结构在各种荷载作用下的内力和变形。
通过利用形常数和载常数表,可以将复杂的结构分解为简单的杆件单元,然后根据各杆件单元的连接方式和荷载情况,运用叠加原理,快速准确地计算出整个结构的内力和变形。
比如说,对于一个由多个梁和柱组成的框架结构,我们可以先分别确定每个梁和柱的形常数和载常数,然后根据它们在框架中的位置和连接关系,将各个杆件单元的内力和变形进行叠加,从而得到整个框架结构的内力和变形。
在实际工程中,形常数和载常数表的应用非常广泛。
无论是建筑结构的设计、桥梁的建造,还是机械结构的分析,都离不开对形常数和载常数的准确掌握和运用。
然而,需要注意的是,在使用形常数和载常数表时,必须要确保所分析的结构与表中所列的杆件结构类型和约束条件相符。
如果结构存在特殊的情况或者与标准的杆件结构有较大的差异,就不能简单地直接套用形常数和载常数表,而需要进行专门的分析和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BA
A
B
l
BA
↓↓↓↓↓↓↓↓
Δ
MAB QAB
β θA
θB
转角位移方程
QBA MBA
4、已知杆端弯矩求剪力:取杆 件为分离体建立矩平衡方程:
QABMAB l MBAQA FB
MAB QAB
MAB
Q’‘ AB
P
MBA
+
P
QBA MBA
Q’‘ BA
Q0 AB
Q0 BA
单跨超静定梁 载常数和形常数表
1、形常数:由单位杆端位移引起的杆端力 (只 与截面尺寸和材料性质有关的常数)。 2、载常数:由荷载引起的杆端力 (只与荷载形 式有关的常数)
1
2
A
ql 2 12
ql 2
A
FPl 8
FP 2
两端固定的单跨超静定梁的载常数和形常数
q
i, l
B
A 1
B
i, l
6i
ql 2
3i
5FP l
16
3i
3i l2
16
l2
4
一端固定一端定向滑动的单跨超静定梁的载常数和形常数
q
A i, l
i, l
B
A
1
ql 2
3
ql 2
ql
6 0
i
0
B
i
0
A
FPl 2
FP
FP
i, l
B
FPl 2 0
5
3、转角位移方程:杆端弯矩的一般公式:
M 4i 2i 6i M F
AB
A
B
lHale Waihona Puke ABM 2i 4i 6i M F
l
2i
ql 12 4i
6i
l 2
FP i, l
A B
FPl 6i
FP
8l
12i
2
l2
i, l B
1
12i
l2
6i
l
3
一端固定一端铰支的单跨超静定梁的载常数和形常数
q
i, l
A
B
A 1
B
i, l
3i
ql 2
l
3i
8 5ql
3ql 3i
l
8
8
FP A
i, l
A B
i, l B
1
3FPl 16
11FP
