第四章 控制系统的传递函数(1)
合集下载
自动控制原理 孟华 第4章习题解答
4-1如果单位反馈控制系统的开环传递函数1)(+=s K s G 试用解析法绘出K 从零向无穷大变化时的闭环根轨迹图，并判断下列点是否在根轨迹上： (2，j 0)，(0+j 1)，(3+j 2)。
解：根轨迹如习题4-1答案图所示。
（-2，+j 0）在根轨迹上；(0,+j 1), (-3, +j 2) 不在根轨迹上。
习题4-1答案图4-2设单位反馈控制系统的开环传递函数。
)12()13()(++=s s s K s G试用解析法给出开环增益K 从零增加到无穷时的闭环根轨迹图。
解： 解析法：K =0时：s=-1/2，0；K =1：s=-122；K =-∞：s=-∞，-1/3。
根轨迹如习题4-2答案图所示。
习题4-2答案图4-3 已知系统的开环传递函数)1()1()()(-+=s s s K s H s G ，试按根轨迹规则画出该系统的根轨迹图，并确定使系统处于稳定时的K 值范围。
解：分离点：；会合点： ；与虚轴交点：±j 。
稳定的K 值范围：K >1。
根轨迹如习题4-3答案图所示。
习题4-3答案图4-4已知一单位反馈系统的开环传递函数为2*)4)(1)(1()(+-+=s s s K s G （1）试粗略画出K *由0到∞的根轨迹图；（2）分析该系统的稳定性。
解：稳定性分析：系统不稳定。
根轨迹如习题4-4答案图所示。
-10-505-8-6-4-22468Root LocusReal AxisI m a g i n a r y A x i s习题4-4答案图4-5 设控制系统的开环传递函数为)164)(1()1()()(2*++-+=s s s s s K s H s G ，试绘制系统根轨迹图，并确定使系统稳定的开环增益范围。
解：渐近线：=60°，180°；=-2/3；复数极点出射角55°；分离会合点和；与虚轴交点和；使系统稳定的开环增益为 ＜K ＜ (即 ＜K *＜。
现代控制理论-4-控制系统的稳定性分析
2、内部稳定性：指系统在零输入条件下通过其内部状态变化 所定义的内部稳定性。状态稳定。
外部稳定性只适用于线性系统，内部稳定性不但适用于线性系 统，而且也适用于非线性系统。对于同一个线性系统，只有在 满足一定的条件下两种定义才具有等价性。
不管哪一种稳定性，稳定性是系统本身的一种特性，只和系统 本身的结构和参数有关，与输入－输出无关。
V ( x)半负定
同时有
& V
(
x
)
-
2
x22
不可能恒为零。
由判据2可知，系统在原点处的平衡状态是渐近稳定的。
27
4.5 李雅普诺夫方法 在线性系统中的应用
28
一、线性定常连续系统的稳定性分析
目的：将李氏第二法定理来分析线性定常系统 x& Ax 的稳定性
讨论：V选&(x择) 二(x次T P型x)函 x&数T PVx +(xx)TPxx& TP(xAx为)T P李x +氏x函T PA数x。
如果d 与初始时刻 t0无关，则称平衡状态xe为一致渐近稳定。
渐近稳定几何表示法：
10
3、大范围渐近稳定
如果对状态空间的任意点，不管初始偏差有多大，都有渐
近稳定特性，即：lim x t
- xe
0
对所有点都成立，称平衡状态xe为大范围渐近稳定的。其
渐近稳定的最大范围是整个状态空间。
必要性：整个状态空间中，只有一个平衡状态。 （假设有2个平衡状态，则每个都有自己的稳定范 围，其稳定范围不可能是整个状态空间。）
（2） 求系统的特征方程：
det(lI
-
A)
l
- 1
求得： l1 2，l2 -3
外部稳定性只适用于线性系统，内部稳定性不但适用于线性系 统，而且也适用于非线性系统。对于同一个线性系统，只有在 满足一定的条件下两种定义才具有等价性。
不管哪一种稳定性，稳定性是系统本身的一种特性，只和系统 本身的结构和参数有关，与输入－输出无关。
V ( x)半负定
同时有
& V
(
x
)
-
2
x22
不可能恒为零。
由判据2可知，系统在原点处的平衡状态是渐近稳定的。
27
4.5 李雅普诺夫方法 在线性系统中的应用
28
一、线性定常连续系统的稳定性分析
目的：将李氏第二法定理来分析线性定常系统 x& Ax 的稳定性
讨论：V选&(x择) 二(x次T P型x)函 x&数T PVx +(xx)TPxx& TP(xAx为)T P李x +氏x函T PA数x。
如果d 与初始时刻 t0无关，则称平衡状态xe为一致渐近稳定。
渐近稳定几何表示法：
10
3、大范围渐近稳定
如果对状态空间的任意点，不管初始偏差有多大，都有渐
近稳定特性，即：lim x t
- xe
0
对所有点都成立，称平衡状态xe为大范围渐近稳定的。其
渐近稳定的最大范围是整个状态空间。
必要性：整个状态空间中，只有一个平衡状态。 （假设有2个平衡状态，则每个都有自己的稳定范 围，其稳定范围不可能是整个状态空间。）
（2） 求系统的特征方程：
det(lI
-
A)
l
- 1
求得： l1 2，l2 -3
自动控制原理与系统控制系统的频率特性
如图4-6所示。
12
四、惯性环节 传递函数 ： G(s) C(s) 1
R(s) Ts 1
频率特性 ： G( j) C( j) 1
R( j) jT 1
对数频率特性 ： L() 20lg
1
20lg
(T)2 1
(T)2 1
Bode图 ： arctanT
▪对数幅频特性L(ω)是一条曲线,逐点描绘很烦琐,通常采用近似的 绘制方法,用两条渐进线近似表示.
（极坐标表示法）
U () jV ()
（直角坐标表示法）
（A指(数表)e示j法 (）)
图4-2
A() G(j) U 2 () V 2 ()
() G( j) arctan 1 V () U ()
6
例4-1 写出惯性环节的幅频特性、相频特性和频率特性。
解：惯性环节的传递函数为
G(s) 1 Ts 1
2
• 系统（或环节）输出量与输入量幅值之比为幅值频率特性， 简称幅频特性，它随角频率ω变化，常用M(ω)表示。
A()
A c
A r
• 输出量与输入量的相位差为相位频率特性，简称相频特性，它 也随角频率ω变化，常用φ(ω)表示，
c r
幅频特性和相频特性统称为频率特性，用G( jω)表示
3
频率特性就是线性系统(或环节)在正弦输入信号 作用下稳态时输出相量与输入相量之比。
G (j) G(j) G(j)
A() G(j)
() G(j)
幅频特性是输出量与输入量幅值之比M(ω),描述系统 对不同频率正弦输入信号在稳态时的放大（或衰减） 特性。
相频特性是输出稳态相对于正弦输入信号的相位差 φ(ω),描述系统稳态输出时对不同频率正弦输入信号 在相位上产生的相角迟后（或超前）的特性。
2.5反馈控制系统的传递函数
第五节 反馈控制系统的传递函数
一、系统的开环传递函数
闭环控制 R(s) 系统的典型
结构：
开环传递函数：
E(s)
_ G1(s)
B(s)
D(s)
+
C(s) G2(s)
H(s)
系统反馈量与误差信号的比值
Gk(s)=
B(s) E(s)
=G1(s)G2(s)H
(s)=G(s)H(s)
第五节 反馈控制系统的传递函数
求
DR(s()s) +_
_G3 G1
C(s)
H1
D(s) G1G2
G2G1 - H1
1+G1G2H1
D(s)
_
G2
C(s+)
C(s) G3
- -1
H-(21+H2/G1)
H2 /G1
解:
D(s) 系+统传G递3 函数为：
C(s)
R(s) = 0
H1
结 变构换图为CD((ss))= 1+G1GGG22H3(11++G-G21GGG32H1H21+- )GH21G2-1G3
解1+: 1RERG+1(G+(G(s1sDs)GG1)1)G(G=21s-GG21)2GH+32=GH3G13H0111HG2+2/2GGG结H121=1G构+1G2-+H图HG21G1变1+GG3GHG换122GH12G+为21G3G+H-：G13G2E2G(2sG)3H3 2
第五节 反馈控制系统的传递函数
B(s) H(s)
第五节 反馈控制系统的传递函数
2．扰动信号D(s)作用
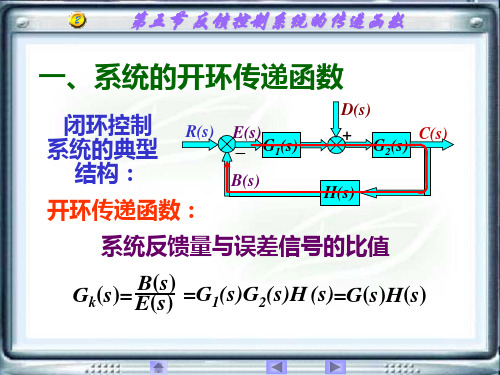
一、系统的开环传递函数
闭环控制 R(s) 系统的典型
结构：
开环传递函数：
E(s)
_ G1(s)
B(s)
D(s)
+
C(s) G2(s)
H(s)
系统反馈量与误差信号的比值
Gk(s)=
B(s) E(s)
=G1(s)G2(s)H
(s)=G(s)H(s)
第五节 反馈控制系统的传递函数
求
DR(s()s) +_
_G3 G1
C(s)
H1
D(s) G1G2
G2G1 - H1
1+G1G2H1
D(s)
_
G2
C(s+)
C(s) G3
- -1
H-(21+H2/G1)
H2 /G1
解:
D(s) 系+统传G递3 函数为：
C(s)
R(s) = 0
H1
结 变构换图为CD((ss))= 1+G1GGG22H3(11++G-G21GGG32H1H21+- )GH21G2-1G3
解1+: 1RERG+1(G+(G(s1sDs)GG1)1)G(G=21s-GG21)2GH+32=GH3G13H0111HG2+2/2GGG结H121=1G构+1G2-+H图HG21G1变1+GG3GHG换122GH12G+为21G3G+H-：G13G2E2G(2sG)3H3 2
第五节 反馈控制系统的传递函数
B(s) H(s)
第五节 反馈控制系统的传递函数
2．扰动信号D(s)作用
自动控制原理第四章习题解答
根轨迹如图中红线所示。
4
胡寿松自动控制原理习题解答第四章
（２） G(s) =
K ∗ (s + 20)
。
s(s + 10 + j10)(s + 10 − j10)
解：
系统开环传递函数为 G(s) =
K ∗ (s + 20)
s(s + 10 + j10)(s + 10 − j10)
有三个极点：p1 =（0，j0），p2 =（-10＋ｊ10），p3 =（－10-ｊ10），有一个零点 z1 =（－
(2) 确定 G(s) = K ∗ (s + z)
产生纯虚根为±ｊ1 的ｚ值和 K ∗ 值。
s 2 (s + 10)(s + 20)
解：系统特征方程为 s4 + 30s3 + 200s2 + K *s + K *z = 0 令 s = j1代入特征方程中得：
20，ｊ０）。 起始角：
∑ ∑ θ pi
= (2k
+ 1)π
+
m
ϕ z j pi
j =1
n
−
θ pi pi
j =1
( j≠i)
k = 0,±1,±2,L
θ p1 = 1800
θ p2 = 1800 ϕ + z1p2 θ − p1p2 θ − p3p2 = 1800 + 450 − 1350 − 900 = 00
有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。
分离点坐标计算如下：
1+ 1 = 1 d d + 0.5 d + 1
d 2 + 2d + 0.5 = 0 解方程的 d1 = −1.7 ， d2 = −0.29
4
胡寿松自动控制原理习题解答第四章
（２） G(s) =
K ∗ (s + 20)
。
s(s + 10 + j10)(s + 10 − j10)
解：
系统开环传递函数为 G(s) =
K ∗ (s + 20)
s(s + 10 + j10)(s + 10 − j10)
有三个极点：p1 =（0，j0），p2 =（-10＋ｊ10），p3 =（－10-ｊ10），有一个零点 z1 =（－
(2) 确定 G(s) = K ∗ (s + z)
产生纯虚根为±ｊ1 的ｚ值和 K ∗ 值。
s 2 (s + 10)(s + 20)
解：系统特征方程为 s4 + 30s3 + 200s2 + K *s + K *z = 0 令 s = j1代入特征方程中得：
20，ｊ０）。 起始角：
∑ ∑ θ pi
= (2k
+ 1)π
+
m
ϕ z j pi
j =1
n
−
θ pi pi
j =1
( j≠i)
k = 0,±1,±2,L
θ p1 = 1800
θ p2 = 1800 ϕ + z1p2 θ − p1p2 θ − p3p2 = 1800 + 450 − 1350 − 900 = 00
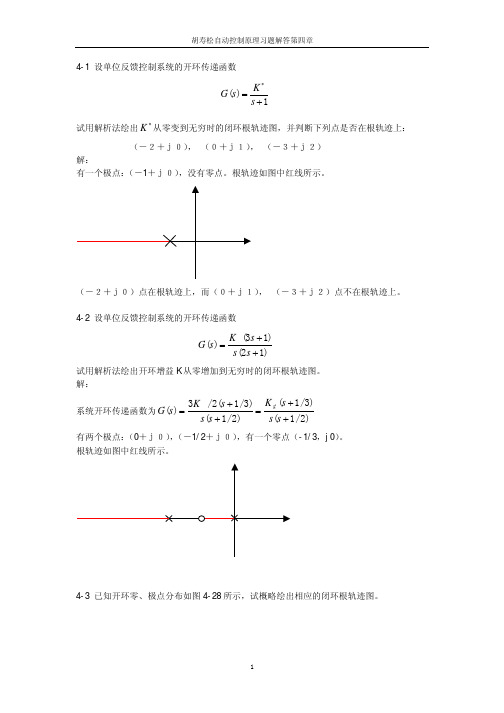
有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。
分离点坐标计算如下：
1+ 1 = 1 d d + 0.5 d + 1
d 2 + 2d + 0.5 = 0 解方程的 d1 = −1.7 ， d2 = −0.29
自动控制原理第二版第四章课后答案
自动控制原理第二版第四章课后答案【篇一：《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上，并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上，则点s1应满足相角条件?g(s)h(s)??(2k?1)?，如图解4-1所示。
对于s1= -1+j3，由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件，因此s1= -1+j3在根轨迹上。
将s1代入幅值条件： g(s1)h（s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出： k=12 ，k=*?324-2 已知开环零、极点如图4-2 所示，试绘制相应的根轨迹。
解根轨如图解4-2所示：4-3 单位反馈系统的开环传递函数如下，试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点：p1?0,p2= -2,p3 = -5①实轴上的根轨迹：???,?5?, ??2,0?0?2?57?????a??33②渐近线： ????(2k?1)????,?a?33?③分离点：1d?1d?5?1d?2?0解之得：d1??0.88，d2?3.7863(舍去)。
④与虚轴的交点：特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j）与虚轴的交点（0，?示。
⑵根轨迹绘制如下：①实轴上的根轨迹：??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线： ????(2k?1)????a?22?③分离点： 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
第四章 控制系统的传递函数(2)
Rcs 1 Ts 1
例2
ui
Ri
a
R1 if
ub R2
C i Ui(s) Ri a
Zm If (s) Uo (s)
uo
U b ( s) I f ( s) R1
1 R1 R1 cs U b ( s) I ( s) I ( s) 1 R1cs 1 R1 cs U ( s) Ub ( s) I ( s) o R2
设 X1(s)=Xi(s)· G1(s), Xo(s)=X1(s) · G2(s)
则用框图表示如下 Xi(s)
G1(s)
X1(s)
G2(s)
Xo(s)
对于串连的传递函数
Xo(s)=X1(s) · G2(s) = G1(s) · G2(s) · Xi(s)
∴G(s)= G1(s) · G2(s)
如一个系统由n各环节串联而成，则系统的传递函数为
G( s ) Gi ( s)
i 1
n
② 并联
设 X1(s)=Xi(s)· G1(s), X2(s)=Xi(s)· G2(s), Xo(s)=X1(s)± X2(s) 对于并连的传递函数 Xo(s) ± Xo(s) = X1(s)± X2(s) = Xi(s)· G1(s) ± Xi(s)· G2(s) = [G1(s) ± G2(s)] Xi(s) 则用框图表示如下
Xi(s) + A
E(s)
±
B(s)
G(s)
Xo(s)
H(s)
如果在点 A 处将反馈回路切断，则得到以E(s)为输入，B(s) 为输出的传递函数Gk(s)，称之为闭环系统的开环传递函数。 Gk(s) = H(s)G(s) Xi(s)
第四章 控制系统的传递函数(2)
Ub(s) R2
ቤተ መጻሕፍቲ ባይዱ
Uo(s) I(s)
C1
C2
I f ( s)
U b ( s) 1 R1 c1s
R c s 1 1 1 1 1 I ( s ) U ( s ) I ( s ) R // b 1 2 c c s c s c s c s s 1 1 2 2 1 1 2 c R
2 d dx o o ⑤ 二阶环节和振荡环节 T x T x Kx o o i 2 dt dt
G(s)
2 K n 2 2 s 2 s n n
⑥ 延时环节
xo (t) = xi (t-τ)
G (s) es
求右图油缸-阻尼-弹簧 系统的传递函数.其中， p为输入，xo为输出。
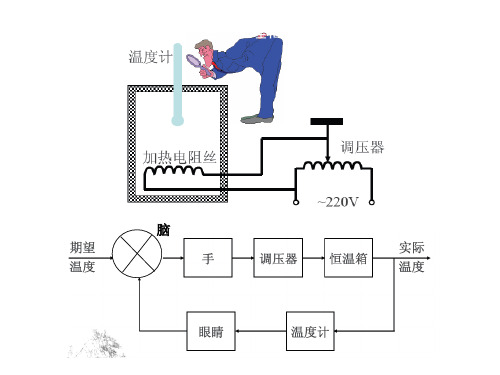
试画出人工控制的恒温箱原理框图
脑
① 比例环节
xo(t)=kxi(t)
G(s)
Xo (s) Xi (s)
k
小 节
② 微分环节
③ 积分环节
dx i (t) xo(t) T G(s)=TS dt
x ( t) T t) dt G(s)=T/S o i( x
dx K G ( s ) ④ 惯性环节 T o xo Kx i Ts1 dt
第四章 控制系统的传递函数
第二节 复合环节传递函数
一般来说，采用调节器的控制系统，既能获得较高的 静态精度，又具有较快的动态响应。
2014.10.13
1. 复合环节概念
在自动控制技术中，常用到一些被称为调节器（校正器）的 动态元件。他们就是由一些典型环节组成的复合环节。不同 环节的组合，构成各种性能不同的调节器。了解这些调节器 的传递函数，会方便以后的设计。 单一典型环节组合 复合环节，如PI调节器、PD调节器
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：根据传动关系有
dxo Dn dt
sX o ( s) DN ( s)
G( s)
D
s
但如以vo(t)表示齿条的移动速度，则
vo (t ) Dn
Vo ( s) DN ( s)
G ( s ) D
例5
ui
下图是一个由运算放大器组成的积分器，求G(s)。 Zc C 对各变量取 I 拉氏变换 uc i R R Ui(s) uo + +
凡能用二阶线性微分方程来描述的环节都称为二阶环节。
d 2 xo dxo 运动方程为 T To xo Kxi 2 dt dt
两边取拉氏变换得 Ts2 X o ( s) To sX o ( s) X o ( s) KX i ( s)
2 K Kn 2 G( s) 2 2 Ts To s 1 s 2n s n
K—惯性环节的增益；T—惯性环节的时间常数
例6
求右图电路的G(s)。
ui
R i C uo
解： Z c 1 cs
zc uo ui R zc
G( s)
Zc U o ( s ) Ui ( s) R Zc
I
Ui Uo
Zc 1 R Z c Rcs 1
如果Rcs » 1，则G(s)=1/Rcs=1/Ts
X i1 X i2
② 传递函数以简明的数学形式表达了系统的动态模型组 成，只要动态性能相似，就可以用相似的传递函数； ③ 传递函数可以有量纲，也可以无量纲；
④ 传递函数是s的有理分式； ⑤若传递函数分母s的最高阶次为m，则该系统为m阶系统
3. 典型环节传递函数
系统总是由各种元件组成，这些元件可能是机械
的、液压的、热力学的，也可能是电气的、光学的， 或者几者兼而有之。不管这些元件的属性如何，只要 其动态性能相似，就可以用相同的传递函数来表达。 如果把系统Leabharlann 元件按其运动方程(微分方程)的形式来
分类，就得到各种不同的动态环节,简称环节。
这样，就可以把一个复杂的系统分解为由简单的 环节组成，从而方便地建立整个系统的数学模型。
Ts
Ts« 1
求图示液压阻尼器的 传递函数,并判断属于 什么环节
q
R
xo(t)
K
解
A( p2 p1 ) Kxo (t )
dxi dxo q A dt dt
p 2 p1 q R
G( s) s K s 2 A R
p1
A
p2
xi(t)
K X o ( s) s 2 sX i ( s) A R
已知
3s 2 2s 8 F ( s) s( s 2)(s 2 2s 4)
求 f ( t)
函数有两个单极点0、-2和一对共轭复根，故将函 解： 若出现共轭复数极点应怎样办？ 数展开为
可当作两个单极点，也可作一些特殊处理
2 2. L k p 4q 0 1 k k s k q ) 假设F(s)分母含有 ( s 的项，其中 2 ps 21 22 F ( s) 2 K 31 s K 32 ss K4 s s2 s K 21 2 22 ...
1 K1 Y (s)(s 3) s3 8
3 K 2 Y (s)(s 1) s1 8
K3
1 Y (s)(s 1) s1 4
把K1、K2、K3的值代回（1）式得
1 1 3 1 1 1 Y ( s) 8 s 3 8 s 1 4 s 1
求方程
y"2 y'3 y e
t
满足初始条件
y(0) 0, y' (0) 1 的解
根据微分定理对两边取拉氏变换
解 设 [ y (t )] Y ( s)
2
1 [ s Y ( s ) sy (0) y ' (0)] 2[ sY ( s) y (0)] 3Y ( s) s 1
dxi (t ) 运动方程为 xo (t ) T dt
例3
解
求图示微分电路的G(s)
Ui
Uo
1 U o ( s) U o ( s) U i ( s) Rcs
{
1 idt uo ui c u i o R
G( s)
1 uo dt uo ui Rc
Ts Rcs Rcs 1 Ts 1
那么展开时增加下列各项：
( s 2 ps q) L
( s 2 ps q) L1
首先用留数法求k1、k2
k1 F ( s)s s0
3s 2 2s 8 ( s 2)(s 2 2s 4)
s 0
1
k2 F (s)(s 2) s2
将k1、k2代回F(s)得
2 3 2
得联立方程 k 21 1 0
{
2k21 k 22 3 2k 22 2
{k
k 21 1
22
1
1 2 s 1 1 2 s 1 F ( s) 2 2 2 s s 2 s 1 3 s s 2 s 2s 4
① 比例环节
凡输出量xo(t)与输入量xi(t)成比例，不失真也不延时的环节，
又称P调节器。
比例环节运动方程为 xo(t)=kxi(t)，所以比例环节传递函数为
G( s) X o ( s) X i ( s)
k
k为比例环节的增益或称为放大系数
例1
解
求一对齿轮传动的传递函数 忽略传动间隙
ni(t)
• 直接导出系统的某些动态特性；
• 频域法是在传递函数的基础上直接推导出来的。
定义：初始条件为零时，系统的输出量的拉氏变换与 输入量的拉氏变换之比，称为该系统的传递函数。
X o ( s) 特别地，当xi(t)=δ(t)，亦即 即 G( s) ， X i ( s) Xi(s)=1时，G(s)=Xo(s)
③ 积分环节
凡输出量xo(t)与输入量xi(t)的一次积分成比例的环节，又称为 I调节器。
运动方程为
xo (t ) T xi (t )dt 因此传递函数为： G(s)=T/S
n(t) D xo(t)
例4
右图为一齿轮齿条传动机构。n(t) 为输入转速， xo(t)为线位移。求 该传动机构的传递函数。
z1
no z1 k ni z2
∴G(s)=k
no(t)
z2
例2
i 1= i 2
求右图运算放大器的传递函数
ei ea ea eo R1 R2
ei eo R1 R2
ei
eo 数伏 ~ 10多 伏 ea 4 6 10 ~ 10 Ko
R2 R1 e i2 a Ko a i3 i1 +
例7 下图是运算放大器组成的惯性环节，求该环节的K和T。
R2
Z
Ui(s) uo R1 I -
ui
R1
+
C
+
Uo(s)
解： Z=R2∥Zc=R2∥1/cs = R2 / (R2cs+1)
Z R2 1 G( s) R1 R1 R2cs 1
R2 K R1
T R2c
⑤ 二阶环节和振荡环节
系数的求法:①系数比较法 ②留数法 k i F ( s )( s si ) s si
k11 F ( s )( s sk ) n
k1 p
s sk
1 d p 1 n F ( s )(s sk ) p 1 ( p 1)! ds ss
k
例 6
其中，
n
1 T
——环节的 固有频率
To 1 2 T
——环节的 阻尼比
如果0≤ξ<1，二阶环节称为振荡环节
阻尼（英语：damping）是指任何振动系统在振动中，由于外
界作用和/或系统本身固有的原因引起的振动幅度逐渐下降的
特性，以及此一特性的量化表征 在物理学和工程学上，阻尼的力学模型一般是一个与振动速
3s 2 2s 8 s ( s 2 2 s 4)
s 2
2
1 2 k 21 s k 22 F ( s) 2 s s 2 s 2s 4
再用比较系数法求k21、k22，对上式去分母并整理得
3s 2s 8 (k21 1)s (2k21 k22 )s 2k22 s 8
度大小成正比，与振动速度方向相反的力，该模型称为粘性
因此，系统的传递函数就是系统单位脉冲响应的
拉氏变换。
关于传递函数的几点说明
(1)传递函数是在拉氏变换的基础上导出的,拉氏变换是一种线 性积分变换,因此,传递函数的概念只适用于线性定常系统. (2)传递函数是描述系统动态特性的一种数学模型,但它是在系 统工作在某个相对静止状态时得出的.因为传递函数是在零 初始条件下定义的,因此,传递函数原则上不能反应系统在 非零初始条件下的全部运动规律. (3)传递函数只表示输出量与输入量的关系,是一种函数关系. 这种函数关系由系统的结构和参数所决定,与输入信号和输 出信号无关.这种函数是在信号传递的过程中得以实现的, 所以称为传递函数. (4)传递函数只能表示一个输入对一个输出的关系,所以只适用 于单输入单输出系统的描述,而且系统内部中间变量的变化 情况,
对上式求拉氏反变换得
1 3t 3 t 1 t y (t ) e e e 8 8 4
第四章 控制系统的传递函数
第一节 典型环节传递函数
1. 传递函数的概念
传递函数是在拉氏变换的基础上建立起来的一种数 学模型，是经典控制论中对线性系统进行研究、分 析与综合的重要数学工具。 • 更直观，物理意义更明确； • 实数域里的微积分变为复数域里的代数运算；