【精品课件】2020(新增4页)教版中考数学复习解题指导:第1讲 实数的有关概念_6-10
合集下载
中考数学一轮教材梳理复习课件:第1课实数

四大卫星导航系统之一的中国北斗卫星导航系统
全面建成.该卫星距离地面约 36 000 千米,将数
据 36 000 用科学记数法表示为( B )
A.3.6×103
B.3.6×104
C.3.6×105
D.36×104
首页
下一页
实数运算(7 年 5 考)
【例 4】(2018·广东)计算:|-2|-2 0180+12 -1 .
三、计算题
10.(2019·深圳改编)计算: 16 -4cos 60°+
1 6
-1+(π-3.14)0.
解:原式=4-4×12 +6+1=4-2+6+1=9.
首页
下一页
11.(2019·北京)计算:|- 3 |-(4-π)0+2sin
60°+14 -1.
解:原式=
3
-1+2×
3 2
+4=
3 -1+
首页
下一页
6.(2019·包头)实数 a,b 在数轴上的对应点的位 置如图所示.下列结论正确的是( C )
A. a>b C.-a>b
B.a>-b D.-a<b
首页
下一页
二、填空题 7.(2019·陕西)已知实数-12 ,0.16, 3 ,π,
25 , 3 4 ,其中为无理数的是__3__,_π__,__3__4.
0
-
9
+2sin
30°.
解:原式=2+1-3+2×12
=2+1-3+1 =1.
首页
下一页
15.如图,已知 A,B 两点在数轴上,点 A 表示 的数为-10,OB=3OA,点 M 以每秒 3 个单位 长度的速度从点 A 向右运动.点 N 以每秒 2 个单 位长度的速度从点 O 向右运动(点 M、点 N 同时 出发),经过几秒,点 M、点 N 分别到原点 O 的 距离相等?
中考数学 第一部分 教材知识梳理 第一单元 第1课时 实数的有关概念课件

科学记数法(高频考点)
1.大数的科学记数法:一个大于10的数可以表示成
23
a 10 的形式,其中1≤a<10,n是正整数 ______
n
(n 等于原数的整数位数减去1),这种记数法叫做 科学记数法.有计数单位的数,先把计数单位转化 为数字,再用科学记数法表示.常用的计数单位:
4 8 1亿= 24 ____ , 1 万 = 10 10
1 6
混淆算术平方根与平方根 (√ )
0的平方根为0
-4的平方根为-2
2的算术平方根为 2
( ×)
( ×)
【名师提醒】一个正数的算术平方根为一个 正数,而其平方根为正、负两个数
最新中小学教案、试题、试卷、课 件
18
Hale Waihona Puke 2. 立方根如果一个数b,使得 b 3 a ,那么把b叫做a的
a 正数 一个立方根,也叫三次方根,记作 29_____.
简结果;而带负号的数仅看所给数中是否含“-”号.
最新中小学教案、试题、试卷、课 件
4
(2)意义:正负数可用来表示具有相
反意义的量.常用来表示具有相反意义的量
有:“升高”与“降低”,“零上”与
“④_____ 零下 ”,“前进”与“后退”等.
最新中小学教案、试题、试卷、课 件
5
2.数轴 规定了原点、正方向和单位长度的直线叫 做数轴.任何⑤_____ 实数 都可以用数轴上唯一的一 个点来表示,即实数与数轴上的点是一一对应 的.
3
有一个正的立方根;负数有一个负的立方根;0的
立方根是 30 ___. 0
最新中小学教案、试题、试卷、课 件
19
常考类型剖析
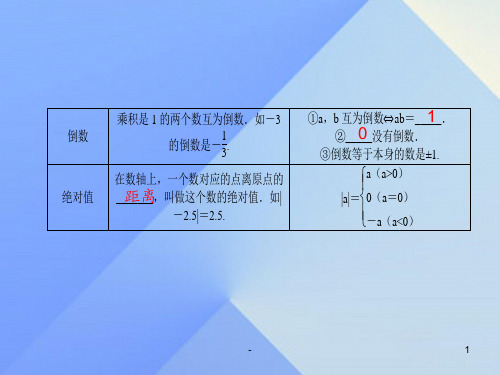
类型一 相反数、绝对值、倒数 例1
2024年中考数学复习课件 第1讲 实数的有关概念

1
0
1
2.实数的分类和性质
(1)分类
①按定义分
无限循环
无限不循环
②按大小分
正实数___负实数
0
实数
(2)性质大于或等于___的数称为非负数.若几个非负数的和为0,则这几个非负数都为___.
0
0
3.科学记数法
(1)科学记数法的表示
类型
形式
的取值
的值
绝对值大于10的数
等于原数的整数位数减___或原数变为 时小数点向左移动的位数
例4 下列说法中,正确的是( ) .
D
A. 的立方根是 B. C. 的平方根是 D.算术平方根等于本身的数有0和1
思路点拨
选项
分析
A
B
表示0.25的算术平方根,
C
,4的平方根是
D
0的算术平方根是0,1的算术平方根是1
考点专练
7.(2023·嘉兴) 的立方根是( ) .
(3)绝对值
定义
数轴上表示数 的点到______的距离叫作数 的绝对值,记作____
性质
___ )___ ____ ②在数轴上,离原点越远的数的绝对值越____
原点
0
大
①
(4)倒数
定义
乘积是___的两个数互为倒数
性质
的倒数是_ _②___没有倒数③ 与 互为倒数 ___
C
A. B.2 C. D.不存在
8. 的算术平方根是__.9.(2023·广安) 的平方根是____.
考点五 实数的分类
名师指导 1.有理数的几种常见形式:(1)整数,如 ;(2)分数,如 ;(3)有限小数,如0.1;(4)无限循环小数,如 . 2.无理数的几种常见形式:(1)开平方或开立方等开不尽的数,如 , ;(2) 及含 的数,如 , ;(3)有规律的无限不循环小数,如 (相邻两个3之间0的个数逐次增加1).
0
1
2.实数的分类和性质
(1)分类
①按定义分
无限循环
无限不循环
②按大小分
正实数___负实数
0
实数
(2)性质大于或等于___的数称为非负数.若几个非负数的和为0,则这几个非负数都为___.
0
0
3.科学记数法
(1)科学记数法的表示
类型
形式
的取值
的值
绝对值大于10的数
等于原数的整数位数减___或原数变为 时小数点向左移动的位数
例4 下列说法中,正确的是( ) .
D
A. 的立方根是 B. C. 的平方根是 D.算术平方根等于本身的数有0和1
思路点拨
选项
分析
A
B
表示0.25的算术平方根,
C
,4的平方根是
D
0的算术平方根是0,1的算术平方根是1
考点专练
7.(2023·嘉兴) 的立方根是( ) .
(3)绝对值
定义
数轴上表示数 的点到______的距离叫作数 的绝对值,记作____
性质
___ )___ ____ ②在数轴上,离原点越远的数的绝对值越____
原点
0
大
①
(4)倒数
定义
乘积是___的两个数互为倒数
性质
的倒数是_ _②___没有倒数③ 与 互为倒数 ___
C
A. B.2 C. D.不存在
8. 的算术平方根是__.9.(2023·广安) 的平方根是____.
考点五 实数的分类
名师指导 1.有理数的几种常见形式:(1)整数,如 ;(2)分数,如 ;(3)有限小数,如0.1;(4)无限循环小数,如 . 2.无理数的几种常见形式:(1)开平方或开立方等开不尽的数,如 , ;(2) 及含 的数,如 , ;(3)有规律的无限不循环小数,如 (相邻两个3之间0的个数逐次增加1).
2020年人教版九年级数学中考总复习课件:第1章 数与式 1.1实数(共37张PPT)

第一章 数与式
1.1 实 数
一 实数的有关概念
1.实数的分类
(1)按定义分类
正整数
整数 零
负整数
有理数
正分数
实数
分数 负分数 有限小数或无限循环小数
正无理数 无理数 负无理数 无限不循环小数
第2页
(2)按性质分类:正实数、①__0___、负实数. (3)正负数的意义 一般地,对于具有相反意义的量,可以把其中的一个量规定为正,另一个规定 为负,如规定正东为“+”,则正西为“-”.
第 13 页
三 实数的大小比较
1.利用数轴比较——几何方法
数轴上的点表示的实数,右边的数总比左边的数○26 __大____.
2.根据性质比较——代数方法 (1)正数>0>负数;
(2)两个负数相比较,○27 ___绝__对__值__大___的反而小.
3.作差比较法
对于任意实数 a、b,若 a-b>0,则 a○28 ___>___b;若 a-b=0,则 a○29 __=____b; 若 a-b<0,则 a○30 ___<___b.
第6页
4.倒数 1
(1)实数a(a≠0)的倒数可表示为⑩___a___;⑪___0__没有倒数. (2)性质:实数a与b互为倒数⇔ab=⑫__1___. (3)倒数是它本身的数是⑬__±__1___.
第7页
5.绝对值 (1)几何意义:在数轴上表示实数 a 的点到⑭___原__点___的距离. (2) 代 数 意 义 : 一 个 正 数 的 绝 对 值 是 它 本 身 ; 一 个 负 数 的 绝 对 值 是 它 的 ⑮ __相__反__数____;0 的绝对值是⑯__0___.即数 a 的绝对值记作|a|,用式子表示为 a = aa≥0, -aa<0. (3)绝对值的非负性:不论实数 a 取何值,总有|a|⑰___≥___0.
1.1 实 数
一 实数的有关概念
1.实数的分类
(1)按定义分类
正整数
整数 零
负整数
有理数
正分数
实数
分数 负分数 有限小数或无限循环小数
正无理数 无理数 负无理数 无限不循环小数
第2页
(2)按性质分类:正实数、①__0___、负实数. (3)正负数的意义 一般地,对于具有相反意义的量,可以把其中的一个量规定为正,另一个规定 为负,如规定正东为“+”,则正西为“-”.
第 13 页
三 实数的大小比较
1.利用数轴比较——几何方法
数轴上的点表示的实数,右边的数总比左边的数○26 __大____.
2.根据性质比较——代数方法 (1)正数>0>负数;
(2)两个负数相比较,○27 ___绝__对__值__大___的反而小.
3.作差比较法
对于任意实数 a、b,若 a-b>0,则 a○28 ___>___b;若 a-b=0,则 a○29 __=____b; 若 a-b<0,则 a○30 ___<___b.
第6页
4.倒数 1
(1)实数a(a≠0)的倒数可表示为⑩___a___;⑪___0__没有倒数. (2)性质:实数a与b互为倒数⇔ab=⑫__1___. (3)倒数是它本身的数是⑬__±__1___.
第7页
5.绝对值 (1)几何意义:在数轴上表示实数 a 的点到⑭___原__点___的距离. (2) 代 数 意 义 : 一 个 正 数 的 绝 对 值 是 它 本 身 ; 一 个 负 数 的 绝 对 值 是 它 的 ⑮ __相__反__数____;0 的绝对值是⑯__0___.即数 a 的绝对值记作|a|,用式子表示为 a = aa≥0, -aa<0. (3)绝对值的非负性:不论实数 a 取何值,总有|a|⑰___≥___0.
中考数学总复习第1讲实数及其有关概念课件

实数的有关概念 1 C. 4 1 D.- 4
1.(2016· 葫芦岛 1 题 3 分)4 的相反数是( B ) A .4 B.-4
2.(2016· 丹东 1 题 3 分)-3 的倒数是( C ) A .3 1 B. 3 1 C.- 3 D.-3
3.(2015· 丹东 1 题 3 分)-2015 的绝对值是( B ) A.-2015 B.2015 1 1 C. D.- 2015 2015
2 解:原式= 2-1+2× -4-2 2 =2 2-7.
1.实数的运算
试题 (2016· 泸州)计算:( 2-1)0- 12×sin60°+(-2)2. 本题考查实数的运算,先分别计算出每一项的值,再根据实
审题视角
数混合运算的顺序进行计算,即先乘除,再加减,同级运算,按从左向 右进行计算. 规范答题
1.实数运算中的常见错误
试题 错解 1- 3 计算:|1- 2|+2×cos45°-( ) 2+ -8. 2 解:原式=1- 2+2× 2 -(-4)+2 2
=1+4+2 =7. 剖析 (1)去绝对值符号时,要考虑是否变号,即要判断绝对值符号内数 据的正负;(2)负整数指数幂,指数是偶数则结果为正;(3)立方根的运算 中,正数的立方根为正数,负数的立方根为负数. 正解
4.实数的大小比较 (1)数轴比较法:数轴上的两个数,右边的数总大于左边的数; (2)代数比较法:正数>0>负数,两个负数比较大小,绝对值大的反而小; (3)差值比较法:①a-b>0⇔a>b;②a-b=0⇔a=b; ③a-b<0⇔a<b; a a a (4)求商比较法:若 b>0,则① >1⇔a>b;② =1⇔a=b;③ <1⇔a< b b b b; 1 1 (5)倒数比较法:若 > 且 a 与 b 同号时,a<b; a b (6)平方比较法:对于任意正实数 a, b有 a2>b⇔a> b.
(中考复习)第1讲 实数的有关概念 公开课获奖课件

对接点一:有理数与无理数
常考角度:1.实数的分类,无理数的定义; 2.算术平方根、零指数、负整数指数的直接计算; 3.特殊角的三角函数值.
【例题 1】 (2013·湖州)实数π ,15,0,-1 中,无理数
是
()
A.π
1 B.5
Hale Waihona Puke C.0D.-1解析 根据常见的无理数的三种形式判断,只有π
是无理数.
-1,∴a2 013=(-1)2 013=-1.
答案 B
对接点三:科学记数法、近似数与有效数字
常考角度:1.用科学记数法表示一个数及单位换算;
2.根据要求取近似数和保留有效数字;
3.近似数精确到的位数.
【例题3】 (2013·嘉兴)据统计,1959年南湖革命纪念馆成
立以来,约有2 500万人次参观了南湖红船(中共一大会
-1 在 3 和 4 之间.
答案 C
【名师课堂】
1.两边逼近法:用能开的尽方的两个正数的算术平方根逼 近:如(1) 9< 13< 16,即 3< 13<4;(2) 2.42< 6<
2.52,2.4< 6<2.5. 2.要特别注意算术平方根和平方根的区别和联系.
【预测4】 实数-27的立方根是____________. 解析 ∵(-3)3=-27,∴-27的立方根是-3. 答案 -3
第一板块 基础知识梳理
第一部分 数与式 第一讲 实数的有关概念
考纲要求
1.理解有理数的意义,能用数轴上的点表示有理数; b 2.理解相反数和绝对值的意义,会求有理数的相反数、 b
倒数和绝对值(绝对值符号内不含字母); 3.了解无理数和实数的概念,知道实数与数轴上的点的 a
一一对应关系; 4.了解平方根、算术平方根、立方根的概念;知道开方 a
中考数学第1讲实数及其运算PPT课件
1≤|a|<10,n 是整数),这种记数法叫做科学记数法;一个近似数,_四___舍__五___入到哪
一位,就说这个数精确到哪一位.如:3.14549 精确到 0.01 为___3__.1__5__,精确到
0.001 为___3_._1_4__5_.
4.零指数幂,负整数指数幂
任何一个不等于零的数的零次幂都等于 1,即__a_0_=__1__(_a_≠_0;)任何不等于零的
-
9
1.(2016·金华)如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其
中不合格的是( B)
A.Φ45.02 B.Φ44.9 C.Φ44.98 D.Φ45.01
2.(2016·河南)-13的相反数是( B)
A.-13
1 B.3
C.-3
D.3
-
10
3.(2015·河南)下列各数中最大的数是( A)
A.5 B. 3 C.π D.-8
4.(2016·盐城)下列实数中,是无理数的为( D)
A.-4 B.0.101 001
1 C.3 D. 2
5.(2016·河南)某种细胞的直径是 0.000 000 95 米,将 0.000 000 95 米用科学记数法表示
为( A)
A.9.5×10-7 B.9.5×10-8
(5)平方比较法:∵由 a>b>0,可得 a> b,∴可以把 a与 b的大小问题转化成比较 a 和 b 的大小问题。
-
8
4.三个非负数 初中阶段所涉及的三个非负数:|a|,a2, a(a≥0).若几个非负数的和为 0,则这几个 非负数都同时为 0.如:若|a|+b2+ c=0,则 a=b=c=0.
示为( B)
A.7.6×10-9 B.7.6×10-8 C.7.6×109 D.7.6×108
2020届江西中考数学一轮复习课件 第1讲 实数的相关概念 (共43张PPT)

温馨提示
基础点对点
5.(近似数)899.49精确到个位是 899 精确到 千 位. 6.(科学记数法)用科学记数法表示: 123000000= 1.23×108 . 235万= 2.35×106 . 36亿= 3.6×109 . 0.0000175= 1.75×10-5 . 920nm= 9.2×10-7 m.
(GBT16127-1995)规定:居室内空气中甲醛的最高容许浓度
为0.00008g/m3,将0.00008用科学记数法可表示为(
)D
A.0.8×10-4
B.8×10-4
C.0.8×10-5
D.8×10-5
焦点3
实数的大小比较
变式训练
方法指导
在实数比较大小中,一组数里有正数、 0、负数,求最大或最小的数时,最大 的数直接在正数里面选,最小的数直接 在负数里面选,然后再比较正数或负数 的大小.
了“万物皆数”的局限认识,迎来了数学的一次飞跃发展.下
B 面关于无理数的说法错误的是(
)
A.面积为2的正方形的边长是无理数
B.无限小数是无理数
C.无理数可以用数轴上的点来表示
D.半径为1的圆的周长是无理数
温馨提示
1.互为相反数的两个数表示的点分别位于数轴 上原点的两侧,且到原点的距离 相等 , 即互为相反数的两个数表示的点关于原点 对称 .
温馨提示
2.相反数等于它本身的数只有 0 .绝 对值等于其本身的数是 正数和0 ,绝 对值等于它相反数的数是 负数和0 . 绝对值最小的数是 0 .倒数等于它本 身的数是 ±1 .
(填“>”“<”或“=”)
课堂讲义
焦点1
数轴、相反数、绝对值、倒数
变式训练
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
互为倒数
本身的数是1或-1
精品课件
1
第1讲┃ 考点聚焦
名称 定义
性质
绝对 值
数法
数轴上表示数a的点与原点的________, 记作距|a离|
a(a>0) |a|=0(a=0)
-a(a<0)
设这个数为m,①当
|m|≥10时,n等于
把一个数写成__a_×__1_0_n_的形式.(其中
1≤|a|<10.n为整数),这种记数法
第1讲┃ 考点聚焦 考点2 实数的有关概念
名称 数轴 相反数 倒数
定义
性质
规定了__原__点___、 __正__方__向_、_单__位__长__度_的
直线
只有__符__号__不同的两个 数互为相反数
数轴上的点与实数一 一对应
若a、b互为相反数, 则有a+b=0,|a|= |b|.0的相反数是0
___乘__积___为1的两个数 0没有倒数,倒数等于
有( C ) A.1 个 B.2 个 C.3 个 D.4 个
[解析] 3 8 =2是有理数,cos45°=是无理数.故无理数有 3 8 ,π, cos45°共三个.
精品课件
4
第1讲┃ 归类示例
对无理数的判定,不能只被表面形式迷惑,
而应从最后结果去判断.一般来说,用根号表示
的数不一定就是无理数,如
是有理数,
用三角函数符号表示的数也不一定就是无理数,
如sin30°、tan45°也不是无理数,一个数是不
是无理数关键在于不同形式表示的数的最终结果
是不是无限不循环小数.
精品课件
5
每天它都哆哆嗦嗦地躲过去了,得到了胜利,每天它都欢呼道:“谢天谢地,我还活着!” 这还不算——它没有结婚,没有子女,虽然它父亲曾经有个颇大的家庭。狐狸正洋洋得意,一点也没有发现老虎就在身后。他唯一感兴趣的事情,就是偏不照妈妈的话去做数法
等于原数左起第一
个非零数字前所有
零的个数
近似 数
一个近似数四舍五入到哪一位,那么就说这个近似数精确到哪 一位.对于带计数单位的近似数,由近似数的位数和后面的 单位共同确定.如3.618万,数字8实际上是十位上的数字, 即精确到十位
精品课件
2
第1讲┃ 考点聚焦 考点3 非负数
非负数 的概念
常见的 非负数
非负数的 性质
正数和零叫做非负数
/a/,a2,√a(a≥0,a可代表一个数或一个
式)
若几个非负数的和等于零,则这几个数都为0
精品课件
3
第1讲┃ 归类示例
归类示例
► 类型之一 实数的概念及分类
命题角度: 1.有理数与无理数的概念; 2.实数的分类.
例1 [2012·六盘水] 数字 2,13,π,3 8,cos45°,0.3·2·中是无理数的
足球比分网:/ 一瞬间,所有的豪门与贵族烟消云散,由于小青的家在梯田的边缘而且她的麦穗小的可怜,收割机根本够不着。
虎妈妈对狮妈妈说:“让孩子多摔打、多锻炼是真正的爱孩子,溺爱孩子有害而无益啊!” 虎王要做一条褥子,还缺小小的皮儿一张。, 有一天,狼和老虎聊天
6
