第十章习题解答
第十章(含耦合电感的电路)习题解答

第十章(含耦合电感的电路)习题解答一、选择题1.图10—1所示电路的等效电感=eq L A 。
A.8H ; B.7H ; C.15H ; D.11H解:由图示电路可得 121 d d 2d d )63(u t i t i =++, 0d d 4d 221=+tit i d从以上两式中消去ti d d 2得t iu d d 811=,由此可见8=eq L H2.图10—2所示电路中,V )cos(18t u s ω=,则=2i B A 。
A.)cos(2t ω; B.)cos(6t ω; C.)cos(6t ω-; D.0解:图中理想变压器的副边处于短路,副边电压为0。
根据理想变压器原副边电压的关系可知原边的电压也为0,因此,有A )cos(29)cos(18 1t t i ω=ω=再由理想变压器原副边电流的关系ni i121= (注意此处电流2i 的参考方向)得A )cos(612t ni i ω==因此,该题应选B 。
3.将图10─3(a )所示电路化为图10—3(b )所示的等效去耦电路,取哪一组符号取决于 C 。
A.1L 、2L 中电流同时流入还是流出节点0;B.1L 、2L 中一个电流流入0,另一个电流流出节点0 ;C.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向无关;D.1L 、2L 的同名端相对于0点是在同侧还是在异侧,且与电流参考方向有关。
解:耦合电感去耦后电路中的M 前面是取“+”还是取“–”,完全取决于耦合电感的同名端是在同侧还是在异侧,而与两个电感中电流的参考方向没有任何关系。
因此,此题选C 。
4.图10—4所示电路中,=i Z B 。
A .Ω2j ; B.Ωj1; C.Ωj3; D.Ωj8解:将图10—4去耦后的等效电路如图10—4(a ),由图10—4(a )得j1 j6j6j6j6j2Ω=+⨯+-=i Z因此,该题选B。
5.在图10—5所示电路中,=i Z D 。
第十章_电荷和静电场课后习题答案

证:由库仑定律得 :
而:
∵ 角很小
∴
故:
即得: 证毕
10-4 在上题中, 如果l = 120 cm,m = 0.010 kg,x = 5.0 cm,问每个小
球所带的电量q为多大?
解:由上题得:
10-5 氢原子由一个质子和一个电子组成。根据经典模型,在正常状态
下,电子绕核作圆周运动,轨道半径是。质子的质量,电子的质量,
∴
10-16 一个半径为R的半球面均匀带电,面电荷密度为s。求球心的电 场强度。
解:由题9-14知:圆环的电场强度为: 10-17 回答下列问题: (1)处于高斯面内的任何位置上的电荷对该高斯面的电通量是否都有贡 献?是否只要电量相同,贡献就相等? (2)处于高斯面外的任何位置上的电荷对该高斯面的电通量是否都无贡 献? (3)假设一个点电荷正好处于高斯面上,那么这个点电荷对该高斯面的 电通量是否有贡献? 答:(1)是的。高斯面内的任何位置上电荷对高斯面的电通量都有贡 献。只要电量相同,电性相同,贡献就相同。
∴ 方向沿轴线方向
故:
∴
(2) ∴
∴
∴ 10-14 一个半径为R的圆环均匀带电,线电荷密度为l。求过环心并垂 直于环面的轴线上与环心相距a的一点的电场强度。 解:如图:圆环上一线元上产生的电场强度为:
与其对称的一线元产生的电场强度为 : ,
两个电场强度的合成为: ∴ 故:
10-15 一个半径为R的圆盘均匀带电,面电荷密度为。求过盘心并垂直 于盘面的轴线上与盘心相距的P点电场强度。 解:由上题知,圆环上电场强度
∴ 10-11 有两个点电荷,电量分别为5.0´10-7C和2.8´10-8C,相距15 cm。求:
(1)一个电荷在另一个电荷处产生的电场强度; (2)作用在每个电荷上的力 已知:点电荷 求: 解: (方向沿两电荷联线向外)
第十章 静电场中的导体和电介质习题解答
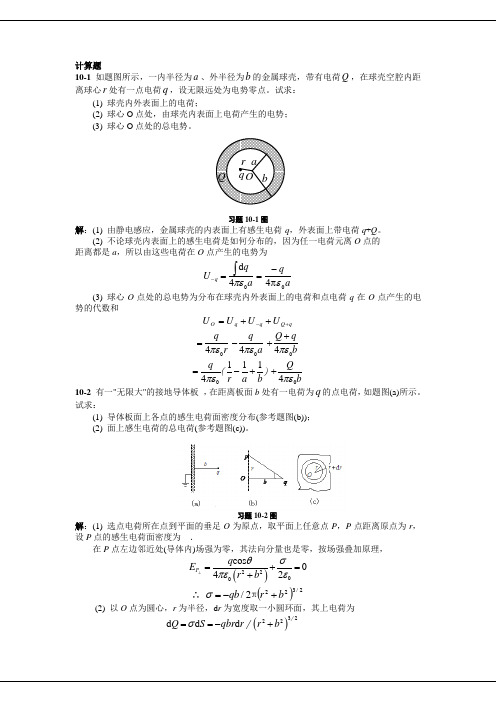
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
第10章 波动习题解答

2
2
15 15 . 5
5 5 . 5
(2)距波源为16.0m和17.0m的两质点间相位差
16 ,17 (100 t 16 or : 2
2
) (100 t 17
2
)
x,
x 17 16 1 m ,
则( C )
(A)波长为100m; (C)周期为 解:y
1 3 s
(B)波速为10m/s; (D)波沿x轴正方向传播
x u )]
;
A cos[ ( t
6
T 2
y 0 . 05 cos[ 6 ( t
x 100
)]
1 3
s
u 100 m / s
uT 33 . 3 m
第十章
波动
习题解答
1
第十章 习题
10-1 图(a)表示t=0 时的简谐波的波形图,波沿x轴正
方向传播,图(b)为一质点的振动曲线. 则图(a)中所
表示的x=0处质点振动的初相位与图(b)所表示的振动
的初相位分别为(D )
y A cos(t ) v A sin( t )
(A)均为零
(D) 2 与
y 0
y
2
(B) 均为 2
u
x
y 0
(C) 均为
(E) 2 与
y
2
2
v 0 2
O
(a)
v 0 2
O
(b)
t
2
10-2 机械波的表达式为
大学物理第十章课后答案

题图10-1题10-1解图d第十章习题解答10-1 如题图10-1所示,三块平行的金属板A ,B 和C ,面积均为200cm 2,A 与B 相距4mm ,A 与C 相距2mm ,B 和C 两板均接地,若A 板所带电量Q =3.0×10-7C ,忽略边缘效应,求:(1)B 和C 上的感应电荷?(2)A 板的电势(设地面电势为零)。
分析:当导体处于静电平衡时,根据静电平衡条件和电荷守恒定律,可以求得导体的电荷分布,又因为B 、C 两板都接地,所以有ACAB U U =。
解:(1)设B 、C 板上的电荷分别为B q 、C q 。
因3块导体板靠的较近,可将6个导体面视为6个无限大带电平面。
导体表面电荷分布均匀,且其间的场强方向垂直于导体表面。
作如图中虚线所示的圆柱形高斯面。
因导体达到静电平衡后,内部场强为零,故由高斯定理得:1A C q q =-2A B q q =-即 ()A B C q q q =-+ ①又因为: ACAB U U =而: 2AC ACdU E =⋅ AB AB U E d =⋅∴ 2AC AB E E =于是:002C B σσεε =⋅ 两边乘以面积S 可得: 002C B S S σσεε =⋅即: 2C B q q = ②联立①②求得: 77210,110C B q C q C --=-⨯=-⨯题图10-2(2) 00222C C A AC C AC AC q d d d U U U U E S σεε =+==⋅=⋅=⋅ 733412210210 2.2610()200108.8510V ----⨯=⨯⨯=⨯⨯⨯⨯10-2 如题图10-2所示,平行板电容器充电后,A 和B 极板上的面电荷密度分别为+б和-б,设P 为两极板间任意一点,略去边缘效应,求:(1)A,B 板上的电荷分别在P 点产生的场强E A ,E B ;(2)A,B 板上的电荷在P 点产生的合场强E ; (3)拿走B 板后P 点处的场强E ′。
第十章 物流成本管理习题与答案

第十章物流成本管理一、名词解释1.物流成本2.物流成本管理系统3.成本性态4.本量利分析5.边际贡献6.盈亏平衡分析二、填空题1.物流成本是指________________________________________,是物流活动中所消耗的_____________________的货币表现。
2.企业物流成本管理是通过___________、物流预算编制、物流预算管理以及___________等工作来完成的。
3.______________是通过编制成本预算来控制物流活动。
4.物流成本的管理与控制由两个部分组成,一是______________,一是_______________。
5.______________是指在物流成本核算的基础上,采用各种成本管理与管理会计方法,进行物流成本的管理与控制。
6._______________是指在日常物流运营的每个作业环节,依据现代物流运营理论,采用先进的物流技术与方法,降低整个物流成本的一系列措施。
7.___________是物流成本管理的中心环节。
8.物流成本的核算对象应根据__________________及企业物流活动的特点予以确定。
以_____________为对象的核算方式有助于加强每个物流功能环节的管理、提高每个环节作业水平。
9.___________也称为成本习性,是指成本总额与业务总量之间的依存关系。
10.___________是指随着业务量的变化而变化的成本;___________是在一定的业务量范围内,与业务量的增减变化无关的成本。
11.___________是成本-业务量-利润关系分析的简称。
12.边际贡献是指_______________________________________________________。
13.___________,又称为保本点,是指企业或物流系统的经营规模(业务量)刚好使利润等于零,即出现不盈不亏的状况。
第十章中级无机化学课后习题答案

第10章习题1 简要回答问题(1) 什么叫稀土元素? 什么叫镧系元素?答:参见本书10.1节《概述》。
(2) 镧系收缩的原因是什么? 简述镧系收缩造成的影响。
答:关于镧系收缩的原因参见本书10.1.2节《原子半径和离子半径》。
由于镧系收缩的影响,使第二、三过渡系的Zr和Hf、Nb与Ta、Mo与W三对元素的半径相近,化学性质相似,分离困难。
(3) 为什么Eu、Yb原子半径比相邻元素大? 而Ce又小?答:① Eu、Yb元素参与形成金属键的电子数为2,Ce为3.1,其余为3.0;② Eu、Yb具碱土性;③ Eu、Yb的f7、f14的半充满和全充满的结构能量低、稳定、屏蔽大,核对外面的6s电子吸引较弱。
(4) 为什么镧系元素的电子结构在固态和气态不同?解:参见本书10.1.1节《镧系元素的价电子层结构》。
(5) 镧系离子的电子光谱同d区过渡金属离子相比有何不同? 为什么?解:除La3+、Lu3+离子的4f电子层是全空(4f0)和全满(4f14)之外,其余Ln3+离子4f轨道上的电子数由1到14,这些电子可以在7条4f简并轨道上任意排布,这样就会产生各种光谱项和能级。
4f 电子在不同能级间跃迁可以吸收或发射从紫外经可见直至红外区的各种波长的电磁辐射。
通常具有未充满的4f电子壳层的原子或离子,可以观察到的光谱线大约有30 000条,而具有未充满d电子壳层的过渡金属元素的谱线约有7 000条。
在理论上,f→f跃迁产生的谱线强度不大。
但是某些f→f跃迁的吸收带的强度,随镧系离子周围环境的变化而明显增大(这种跃迁称为超灵敏跃迁)。
这可能是由于配体的碱性、溶剂的极性、配合物的对称性以及配位数等多种因素的影响,亦即离子周围环境的变化,再加上镧系离子本身的性质等诸因素的综合作用所引起的。
镧系离子的吸收谱带范围较广且镧系离子光谱谱带狭窄,表明电子跃迁时并不显示激发分子振动,狭窄的谱带意味着电子受激发时分子势能面几乎没有变化,这与f 电子与配体只存在弱相互作用相一致。
第10章 习题解答
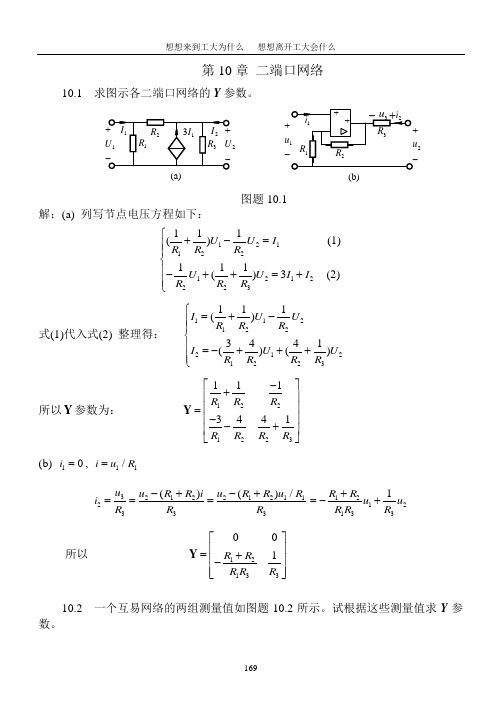
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。
22u (b)图题10.1解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题10.2解:图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。
(b)图题10.3解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 信号产生电路
10.1 证明:题10.1图所示RC 振荡电路的振荡频率为2
121R R C
f o
π=
F
= 因此,对应的关系式为
即 0ω=因此振荡频率为
C
R R f 210
0212π
π
ω=
=
10.2 题10.1图中,R 1=2k Ω,R 2=1k Ω,R 3=5.1k Ω,R F =10k Ω,R 3大致调到多大时,电路才能起振?估算R 3=4k Ω时输出电压的幅值。
设二极管的正向压降为0.6V 。
解:20
12
11()222
4
R F j R R ω==
=
++
3
1R R A F +=
由起振条件:AF ≥1 得 Ω=≤
k R R F 3.33
3
即R 3大致调到3.3k Ω时电路就能起振。
设R 3=4k Ω时,电路有稳定的正弦电压输出,则根据平衡条件,有
1)1(413
=++
⋅R R R D
F ,
为R 和R 1的阻值。
系数电阻应是R F 。
由振荡频率公式RC
f π210=
得
Ω=⨯⨯⨯⨯⨯=
=
-k C
f R 27.110
1.01025.114.321
216
3
0π
由平衡条件311
=+=R R A F 得
Ω==
k R R F 22
1
10.4 试用相位平衡条件判断题10.4图所示电路能否产生自激振荡,并说明理由。
解:三个电路均不能产生自激振荡。
a 电路中,对并联谐振频率2
1210C LC C C +=
ω,A ϕ=180°,而
(a)
题10.4(a)
(c)
(b)
题10.5图
01212
002
1
11j C C F
C C j C
j C ωωω==
++
即 =F ϕ0
因此,要使电路能自激振荡,需再接入一级反相放大电路,使A ϕ=360°。
b 图电路中,u B =0。
电路不可能有交流输出,要产生自激振荡,应重新连线,改成电容三点式振荡电路,振荡频率2
1210C LC C C +=
ω
c 图电路中,集电极交流接地,故无交流输出,加入放集电极电阻R C 并改变L 2的同名端,则对并联谐振频率
有 A ϕF
10.6 ,U Z =7V 。
T 2=Z H T
f 3
103.21⨯==
电容电压的幅值V U R R R U U Z cm 5.372
12
11=⨯=
+=
=+
10.7 在图10.4.4(a)所示电路的方波—三角波产生电路中,已知U Z =7V ,R 1=20 k Ω,C=0.1uF ,三角波的峰峰值为14V ,频率为500H Z ,试确定R 2、R 4的阻值。
解:三角波峰值V U R R U Z m 72
142
10==
=,故R 2=R 1=20k Ω
由频率公式C
R R R f 4124=
得
Ω⨯=⨯⨯=
=
-3
7
410510
5004141fC
R
t 11
2
t p
p
故 112
2P
R R C T R ''=
从t 2到t 3,电容充电,输出电压的变量为
32
1022
212t Z Z om Z t p
P
U R u U dt T U U R C R C R ∆=-
=
=-=-
''⎰
122
2P
R R C T R '=
故 11122
2
2()2P
P P R R R C R R C T T T R R '''+=+=
=
10.9 在题10.9图所示电路中,U Z =6V ,u I 为小于6V 的正电压,D 为理想二极管。
(1)分析电路的工作原理;(2)画出u o1和u o2的波形,标明电压幅值;(3)计算u I =5V 时的振荡频率。
因此,u 016V ,解得
4
由电压控振荡器的频率公式(10.4.10)得
4
3112
55022101000.1
6
I
Z Z Z
R u f kH H R R C U =
=
⨯=⨯⨯⨯
10.10 在图10.4.6(a)所示的压控振荡电路中,若u I <0,电路应如何改动才能正常工作?当u I 变化时,三角波和矩形波的幅值是否变化,为什么?
解:u I<0,|u I|<U Z,时,为使电路能正常工作,二极管D应反接,如图所示。
这样,设通电后,u O1=+U z,则D导通,电容快速充电,u O由零快速下降至-U O m,U O1跳变为-U z,二极管截止;电容再通过R4放电,u O线性上升,至U O m后u O1再跳度为+U Z,D导通,电容快速充电。
如此反复,产生周期信号。
由于u O的幅值由R1、R2和U Z决定,因此,u I
变化时,三角波和矩形波的幅值不会变化。
