二点群单形及空间群
点群空间群
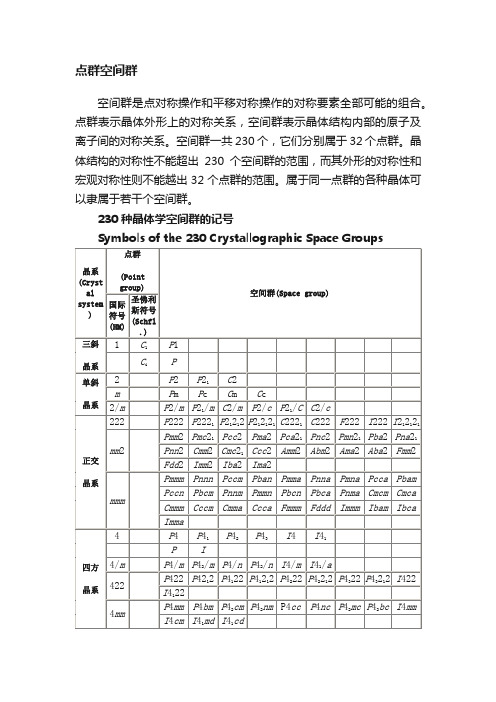
Symbols of the 230 Crystallographic Space Groups
晶系(Crystal system)
点群
(Point group)
空间群(Space group)
国际符号(HM)
圣佛利斯符号(Schfl.)
三斜
晶系
1
C1
P1
Ci
P
单斜
晶系
2
P2
Imma
四方
晶系
4
P4
P41
P42
P43
I4
I41
P
I
4/m
P4/m
P42/m
P4/n
P42/n
I4/m
I41/a
422
P422
P4212
P4122
P41212
P4222
P42212
P4322
P43212
I422
I4122
4mm
P4mm
P4bm
P42cm
P42nm
P4cc
P4nc
P42mc
P42bc
I4mm
I4cm
I41md
I41cd
2m
P2m
P2c
P21m
P21c
Pm2
Pc2
Pb2
Pn2
Im2
Ic2
I2m
I2d
4/mmm
P4/mmm
P4/mcc
P4/nbm
P4/nnc
P4/mbm
P4/mnc
P4/nmm
P4/ncc
P42/mmc
P42/mcm
P42/nbc
P42/nnm
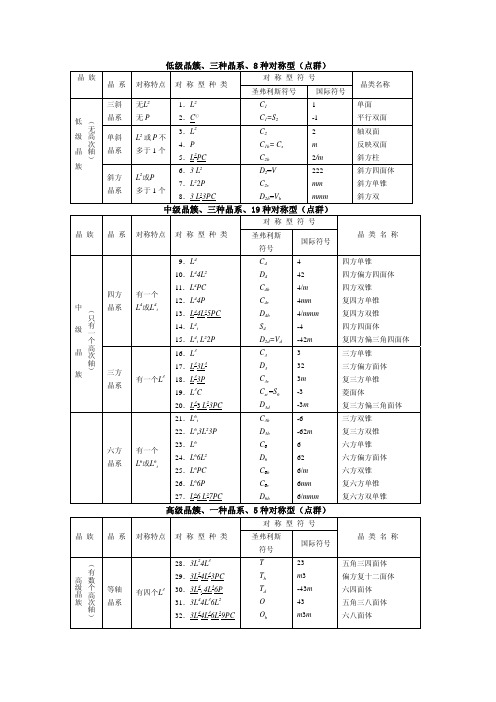
点群格子及空间群
单面 平行双面 轴双面 反映双面 斜方柱 斜方四面体 斜方单锥 斜方双
对称型符号
对称特点 对 称 型 种 类
圣弗利斯 符号
国际符号
晶类名称
9.L4
C4
4
10.L44L2
D4
42
有一个 L4或L4i
11.L4PC 12.L44P 13.L44L25PC
C4h
4/m
C4v
4mm
D4h
4/mmm
14.L4i
Oh5
226
228
Oh8
229
Oh9
230
Oh10
P31 m P3 c 1 P31 c R3 m R3 c
P23 F23 I23 P213 I213 Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3 P432 P4232 F 432 F4132 I 432 P4332 P4132 I 4132 P-43m F-43m I-43m P-43n F-43c I-43d Pm3m Pn3n Pm3n Pn3m Fm3m Fm3c Fd3m Fd3c Im3m Ia3d
对称型符号
对称特点 对 称 型 种 类
圣弗利斯 符号
国际符号
晶类名称
28.3L24L3
T
29.3L24L33PC
Th
有四个L3 30.3L4i 4L36P
Td
31.3L44L36L2
O
32.3L44L36L29PC
Oh
23 m3 -43m 43 m3m
五角三四面体 偏方复十二面体 六四面体 五角三八面体 六八面体
C6
6
D6
62
C6h
6/m
26.L66P
2.2.3点群和空间群

该图形显然具有一个对称中心
因此 3 次倒转轴相当于 1 条 3 次旋转轴加上一个对称中心
3 3i
4 次倒转轴
相当于旋转90后再对中 心反演而图形不变。
这是一个独立的对称操 作。它既没有 4 次旋转 轴也没有对称中心,不 能分解成其他基本对称 要素的组合。
注意这里的 2、6、4、 8 这四个点是不存在的, 也是过渡点。
对称面
对称面是一个假想的平面,相应 的对称操作为对此平面的反映。对 称面就像一面镜子,把物体的两个 相同的部分以互成镜像反映的关系 联系起来。 垂直于对称面作任意直线,位于 直线两侧等距离的两点是性质完全 相同的对应点 晶体中如果存在有对称面,则必 定通过晶体的几何中心并将晶体分 为互成镜像反映的两个相同部分 在结晶学中,对称面一般用符号 “m” 表示。
倒转轴
倒转轴是一种复合对称 要素,由一根假想的直线 和在此直线上的一个定点 组成。相应的对称操作是 绕此直线旋转一定角度以 及对此定点的倒反。 根据晶体对称轴定律,倒 转轴也只有 1 次、2 次、 3 次、4 次和 6 次 5 种
倒反类倒转轴 中,只有 4 次倒转轴是一个独立的基本对称操
点群:在宏观晶体中存在的所有对称要素都必定 通过晶体的中心,因此不论如何进行对称操作,晶
体中至少有一个点是不变的,因此对称型也称为点
群。32点群
特征对称元素与7 大晶系
在32晶体学点群中,某些点群均含有一种相同的对称元素, 这样的对称元素叫做特征对称元素。
根据相应的对称性特征,晶体结构可以分为 7 类, 称为 7 大晶系。这 7 大晶系按对称程度增加的次序
在旋转操作中,使物体复原所需的最小旋转角 称为基转角。轴次 n 可以写成
点群空间群和晶体结构

点群空间群和晶体结构晶体是由原子、分子或离子组成的固态物质。
在结晶过程中,这些粒子以一种有序的方式排列,形成了晶体的特定结构。
晶体结构的研究是固体科学的重要分支之一,可以帮助我们理解固体的物理、化学性质以及它们在各种应用中的作用。
点群是空间中对称性的一种表示方式。
点群描述了一个结构中的元素在一组操作下保持不变的方式。
这些操作可以是旋转、翻转或镜像。
常见的点群包括旋转群、镜面群和反演群。
每个点群由一组操作组成,这些操作在结构中的每个点上施加时,都可以保持结构的不变性。
点群对于确定晶体结构的对称性非常重要,因为它可以帮助我们预测晶体的物理性质,例如电学性、磁学性、光学性等。
空间群是点群在三维空间中的扩展。
它描述了一个晶体结构在所有操作下的对称性。
空间群由点群以及平移操作组成。
平移操作使得结构在空间中移动,形成了无穷多的平行结构。
这些平行结构可以通过空间群中的平移操作进行描述。
空间群的数量非常庞大,目前已知有230个不同的空间群。
每个空间群都有一个唯一的编号和名称,用于标识它的对称性。
晶体结构是晶体中离子、原子或分子的排列方式。
不同的晶体结构由不同的元素组成,以及不同的点群和空间群类型。
它们可以由晶体学的X射线衍射实验来确定。
X射线衍射会产生一种特殊的模式,称为衍射图样。
通过对衍射图样进行分析,可以确定出晶体中的原子或离子的位置,从而推断出晶体的结构。
晶体结构是固体科学的基础,它们在材料科学、化学、凝聚态物理学等领域中有着广泛的应用。
通过对晶体结构的研究,可以优化材料的性能,设计新型材料,解释物质的性质,并探索新的应用领域。
总而言之,点群、空间群和晶体结构是固体晶体学中的重要概念。
它们描述了晶体的对称性以及晶体中原子、离子或分子的排列方式。
通过对晶体结构的研究,我们可以了解晶体物质的性质和行为,并为材料科学和应用领域提供基础性的知识。
晶体点群、空间群简要归纳

晶体点群、空间群简要归纳本⽂只是很简要的归纳,具体内容还请见李新征⽼师群论书和其在蔻享的群论课。
另外推荐肖瑞春⽼师科学⽹博客的这篇博⽂,介绍了群论及后续的学习:若研究中涉及群论和物理性质相关,其中陈纲的《晶体物理学基础》书特别好,易懂,将主动变换和被动变换等分析得特别清晰,不过此书太厚,注意⽤到什么学什么,⽤minimized的知识来科研,否则被导师批评...1.对称操作、对称元素对称操作:保持系统不变的操作。
对称元素:它是⼀个⼏何实体,对称操作可以依据对称元素施⾏对称操作。
对称元素可以是点、直线、⾯等。
2.点群:1)定义:三维实正交群O(3)群的有限⼦群物理理解:实际上点群是实际的物理系统在三维空间的⼀些对称操作的集合。
这些对称操作会保持⼀个点不动。
2)点群分类第⼀类点群:只包含纯转动元素的点群。
第⼆类点群:点群中,除了纯转动元素,还包含转动反演元素的点群。
因为点群是O(3)群的⼦群,⽽O(3)群中有固有转动和⾮固有转动。
3)点群的性质{()}性质1:点群这个集合可以写成C k(2π/n)、IC k′2π/n′的形式,其中n,→k′,n′取有限个⽅向和值;C k(2π/n)是绕→k轴转2π/n⾓的操作。
性质2:设G是点群,K是G的纯转动部分,由于纯转动部分的乘积以及逆元必属于这个纯转动部分,所以K也是G的纯转动⼦群,即K=G∩SO(3)∘.点群G与其有限⼦群K的关系有以下三种可能的情况:1.G=K, 即点群只包含纯转动操作;称为第⼀类点群。
2.若点群G中除了纯转动操作,还包含纯空间反演操作I, 则可以通过G=K∪IK得到这种情况对应的第⼆类点群。
3.若点群G中除了纯转动操作,且G中不包含纯反演操作I时 , 此第⼆类点群G⼀定与⼀个第⼀类G+同构,其中,G+=K∪K+, ⽽K+定义为:K+={Ig∣g∈G,但g∉K}根据这⾥的第3点,可以知道构造这种情况对应的第⼆类点群的⽅法:根据⼀个已知的第⼀类点群K∪K+,即可以构造⼀个第⼆类点群K∪I K+.还可以证明K必须是K∪K+的不变⼦群,其阶数是K∪K+的⼀半。
晶体结构空间群点群

(二)点群、单形及空间群点群:晶体可能存在的对称类型。
通过宏观对称要素在一点上组合运用而得到。
只能有32种对称类型,称32种点群表1- 3 32种点群及所属晶系*2/m表示其对称面与二次轴相垂直,/表示垂直的意思。
其余类推同一晶系晶体可为不同点群的原因:阵点上原子组合情况不同。
如错误!未找到引用源。
,对称性降低,平行于六面体面的对称面不存在,4次对称轴也不存在。
理想晶体的形态―单形和聚形:单形:由对称要素联系起来的一组同形等大晶面的组合。
32种对称型总共可以导出47种单形,如错误!书签自引用无效。
,错误!书签自引用无效。
,错误!书签自引用无效。
所示聚形:属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。
大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体,如单形四方柱与平行双面形成了四方柱体的真实晶体形态空间群:描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。
属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群,空间群有230种,见教材中表1- 4国际通用的空间群符号及其所代表的意义为:P:代表原始格子以及六方底心格子(六方底心格子为三方晶系和六方晶系所共有)。
F:代表面心格子。
I:代表体心格子。
C:代表(001)底心格子(即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
A:代表(100)底心格子(即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
R:代表三方原始格子。
其它符号:意义与前述相同表1- 4 晶体的空间群、点群、晶系、晶族一览表续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4续表1- 4点群符号m 43m2晶 系 等轴晶系 晶 族高级晶族/k/174/stu/content/1.1.3.2.htm。
第四章 点群 2014汇总

一、定义
若一个物质体系的某些对称操作构成群,且在该
群所有群元操作下,体系中至少有一个点的空间坐
标保持不变,则该群为该体系的一个点群。
(1)点群的所有群元都是点操作;
(旋转,反射,或它们的组合)
(2)两次反射的平面必须相交。旋转轴与反射面
必须有公共点。两个转轴必须相交(共点);
1. 单轴旋转群Cn (5种):C1 , C2 , C3 , C4 , C6(g = n)
2. Cnh 群(5种):C1h , C2h , C3h , C4h , C6h (g = 2n)
Cn , Cnh 是Abel群
3. Cnv 群(4种): C2v , C3v , C4v , C6v (g = 2n)
C
c
( )
c
,c
,...,c
e
P2 P1
m
m
m
m
m
m
P3
Rj
点群的一个循环子群
• P1 P1 轴是 cm 的转轴, m重轴;
O
.
P3'
• 点P1和P1' 称为极点,m重极点,
对应 m 个旋转;
P1'
P2'
• 单位元无极点,因其极点任意;
• 除了单位元,每个群元有两个极点,
分别重合。
d c '
2
n
2 2n
利用 c
(c2*)
*
σ
c
c
c
α
d
2 d
2 2 h c z 2 h
O
d
φ
第5讲、点群、空间群和表面几何结构

单位元素 —— 不动操作
第一章 晶体结构
任意元素的逆元素 ——绕转轴角度,其逆操作 为绕转轴角度- ; 中心反演的逆操作仍是中心反演; A 操作 —— 绕OA轴转动/2 —— S点转到T'点
B 操作 —— 绕OC轴转动/2 —— T'点转到S点 —— T点转到T'点
连续进行A和B操作 —— 相当于C操作
t 为一非完整格矢。
10
n度螺旋及其轴
绕轴每转2π/n角度后,再沿该轴的方向平移 T/n的l 倍,则晶体中的
原子与相同的原子重合。
第一章 晶体结构
(l为小于 n 的整数, 为沿轴方向上的周期矢量) T
晶体只能有1、2、3、4和6度螺旋轴。
例1:4度螺旋轴
A4
例2: 金刚石结构
上下底心的连线就是4度螺旋轴
可以证明8个基本的点对称操作可组合成32个点群。
空间群 (space group) ——包含点群的对称操作和平移对称操作的所 有组合方式。 (布喇菲格子和复式格子)
可以证明有230个空间群。
6
第一章 晶体结构
(一)、点群 —由点对称操作作为元素构成的群。
从宏观上看晶体是有限的,有限物体的对称群不能包含 平移操作,所以晶体的宏观对称性质用点群描写。
n12346由6种对称素可以组成10种二维点群按照点群对基矢的要求划分二维格子有4个晶系5种布拉伐格子25晶系轴和角度布拉伐格子简单斜方长方简单长方中心长方正方简单正方六角简单六方二维晶格的晶系和布拉伐格子26晶体表面相对于晶体表面结构的研究表明晶体表面的结构不完全是晶体内部相应结构的面的延续晶体表面是晶体三维周期性结构和真空之间的过渡层可以将它看作是特殊的相表面相晶体内部与表面平行的平面基矢晶体表面二维晶格基矢这两族基矢有可能是不同的表面的再构27典型表面再构之一晶体表面平面的密勒指数例如111si面原子排列的周期为体内相应平面的7倍28典型表面再构之二不同的方法可以获得不同的再构表面表面的再构现象与表面原子的驰豫原子的吸附有关通常可由低能电子衍射leed获得表面再构的几何规其中s为表面吸附原子29预告
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
滑动面表示符号:平移为a/2、b/2或c/2时,写作a、b或c;沿体对角线平移1/2距离,写作n;沿面对角线平移1/4距离,写作d。
(2)螺旋轴:由回转轴和平行于轴的平移构成。
图1-24为3
次螺旋轴,绕轴回转120º并沿轴平移c/3。
螺旋轴按其回
转方向有右旋和左旋之分
螺旋轴表示符号:21(表示2次、c/2),31(表示3次、c/3、右旋),32(表示3次、c/3、左旋),41(表示4次、c/4、右旋),42(4次、c/2),43(表示4次、c/4、左旋),61(6次、c/6、右旋),62(6次、c/3、右旋),63(6次、c/2),64(6次、c/6、左旋),65(6次、c/3、左旋)
所有对称要素归纳:
回转对称轴:1、2、3、4、6
对称面:m(2)
对称中心:1(z)
回转-反演轴:3、4、6
滑动面:a、b、c、n、d
螺旋轴:21、31、32、41、42、43、61、62、63、64、65
(二)点群、单形及空间群
点群:晶体可能存在的对称类型。
通过宏观对称要素在一点上组合运用而得到。
只能有32种对称类型,称32种点群
表1- 3 32种点群及所属晶系
*2/m表示其对称面与二次轴相垂直,/表示垂直的意思。
其余类推
同一晶系晶体可为不同点群的原因:阵点上原子组合情况不同。
如错误!未找到引用源。
,对称性降低,平行于六面体面的对称面不存在,4次对称轴也不存在。
理想晶体的形态―单形和聚形:
单形:由对称要素联系起来的一组同形等大晶面的组合。
32种对称
型总共可以导出47种单形,如错误!书签自引用无效。
,错误!
书签自引用无效。
,错误!书签自引用无效。
所示
聚形:属于同一晶类的两个或两个以上的单形聚合而成的几何多面体。
大量的晶体形态是由属于同一晶类的单形聚合而成的封闭一定空间的几何多面体,如单形四方柱与平行双面形成了四方柱体的真实晶体形态
空间群:描述晶体中原子通过宏观和微观对称要素组合的所有可能方式。
属于同一点群的晶体可因其微观对称要素的不同而分属不同的空间群,空间群有230种,见教材中表1- 4
国际通用的空间群符号及其所代表的意义为:
P:代表原始格子以及六方底心格子(六方底心格子为三方晶系和六方晶系所共有)。
F:代表面心格子。
I:代表体心格子。
C:代表(001)底心格子(即与z轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
A:代表(100)底心格子(即与x轴相交的平行六面体两个面中心与八个角顶有相当的构造单位配布)。
R:代表三方原始格子。
其它符号:意义与前述相同
表1- 4 晶体的空间群、点群、晶系、晶族一览表
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
续表1- 4
§1-2晶体化学基本原理
前面了解了晶体构造方面的内容,为后面掌握实际晶体打下了基础。
而实际晶体的形成及性质还与原子的成键及相互作用力相关。
一、电负性
电负性:形成负离子倾向大小的量度。
分子中一个原子向它本身吸引电子的能力。
电负性与分子内一个原子的电离能和电子亲和力相关
电负性↑→得电子能力↑→非金属元素
电负性↓→得电子能力↓→金属元素
大致可用X=2将两类元素分开。
表1- 5,元素电负性值。
