6-2二组分系统理想液态混合物的气—液平衡相图
合集下载
第六章 相平衡.(2)

* * p A , p B , A 或 x B ,就可把各液相组成对应的气 x 已知
相组成求出,画在 p-x 图上就得 p-x-y 图。
理想的完全互溶双液系
如果 pA pB ,则 y A xA ,即易挥发的组分在气 相中的成分大于液相中的组分,反之亦然。
* *
在等温条件下,p-x-y 图分为三个区域。在液相 线之上,体系压力高于任一混合物的饱和蒸气压,气 相无法存在,是液相区。
理想的完全互溶双液系
T-p-x图
把p-x图和T-x图合在一起,就得到T-p-x三维图。
三个坐标分别代表p,T,和x; 在右边的垂直面 xA 1, xB 0 , 则压力和温度坐标分别代表纯A * p A和沸点 T * ; 组分的饱和蒸气压 A
* p B 和 TB* 。 同理左边垂直面上是 * * pA TA* 和 p B TB* 分别代 连线
水的相图
水的相图(静分析)
水的相图是根据实验绘制的。图上有: 三个单相区 在气、液、固三个 单相区内, p=1,f=2. 温度和压力 独立地有限度地变化不会引起相的 改变。 三条两相平衡线 P=2,f=1,压力与温度只能改变一 个,指定了压力,则温度由体系自定。
水的相图
OA 是气-液两相平衡线,即水的蒸气压曲线。它 不能任意延长,终止于临界点。临界点 T 647 K , p 2.2 107 Pa ,这时气-液界面消失。高于临界温 度,不能用加压的方法使气体液化。
本章基本要求
• 理解相律的意义、推导,掌握其应用。 • 掌握单组分系统、二组分气——液平衡系 统和二组分凝聚系统典型相图的分析和应 用。 • 掌握用杠杆规则进行分析与计算。 • 了解由实验数据绘制简单相图的方法。
6-4相平衡-二组分理想液态混合物气液平衡相图

p* A3
p* As
p* B3
p* Bs
x B3 1.0
y B 3 1.0
3.绘图: T—XB线(紫)T—YB线(红)
§6-3二组分理想液态混合物气液平衡相图
四、温度——组成图(T—X图)分析 1.相图静分析:坐标、区、线、点 坐标:T,XB(YB) 区: 下线下边(浅蓝色区)
P=1、液相、F=2 上线上边(灰色区)
第六章 相平衡
§6-!本章基本要求 §6-1 相平衡系统基本概念 §6-2 单组分相平衡 §6-3二组分理想液态混合物气液平衡相图 §6-4二组分真实液态混合物液态完全互溶系统气液平衡相图 *§6-5 精镏原理 §6-6二组分液态部分互溶及完全不互溶系统气液平衡相图 §6-7二组分无中间化合物的凝聚系统相图 §6-8二组分有中间化合物的凝聚系统相图 *§6-9三组分系统相图简介 §6-$本章小结与学习指导
(上册)
第六章就先讲到这里 下节课再见!
LM G
§6-3二组分理想液态混合物气液平衡相图
二、压力——组成图(p—x图)分析 2.相图动分析: 压力不变往液体A中
加入B气体 组成不变改变压力
§6-3二组分理想液态混合物气液平衡相图
三、杠杆规则(物料衡算)
对二组分2相系统(如左下图气液2相):
中间M点称为系统点
L
M点组成XM,B称为系统组成
§6-3二组分理想液态混合物气液平衡相图
前面课程我们讲述了二组份系统的特征 1.描述二组分系统需要的三个独立变量,可以用三维坐标系表
示二组分系统相平衡 。 2.二组分系统若固定一个变量,就可以用二维坐标系表示相平
衡。 3主要讨论:确定温条件下的压力—组成图,确定压条件下的温
二组分凝聚系统相图.

473
T
' c
等压
c'
两相
T/K
453
413
373
Tc
c
0.2 0.4 0.6
单相
0.8 1.0
0
水
质量分数 水-烟碱的溶解度图
烟碱
6.4 二组分凝聚系统相图 一、二组分固态完全不互溶系统液固平衡相图
1. 热分析法
基本原理:二组分系统 C=2,指定压力不变,
f * = C +1 -F =3 -F
F = 1
f f 1 ** f f 2
*
相点 表示某个相状态(如相态、组成、温度等)的 点称为相点。 物系点 相图中表示系统总状态的点称为物系点。在T-x 图上,物系点可以沿着与温度坐标平行的垂线上、 下移动;在水盐相图上,随着含水量的变化,物系 点可沿着与组成坐标平行的直线左右移动。
单相区,物系点与相点重合;两相区中,只有 物系点,它对应的两个相的组成由对应的相点表示
B
3. 全部变为固体Bi后
f * C 1 Φ 1
t /s
温度又可以下降 纯Cd步冷曲线与之相同
Cd-Bi二元相图的绘制
w(Cd) 0.2
的步冷曲线
b
T /K
f* 2
C
D
f * 1
1. 加热到b点,Bi-Cd全部熔化 Φ 1 f * 2 1 Φ 2 温度可以下降,组成也可变 2. 冷至C点,固体Bi开始析出 Φ 2 f * 2 1 Φ 1 温度可以下降 3.D点固体Bi、Cd同时析出
Φ 3
f* 0 温度不能改变 f * 1 4.熔液消失,Bi和Cd共存
f 2 1 Φ 0
*
T
' c
等压
c'
两相
T/K
453
413
373
Tc
c
0.2 0.4 0.6
单相
0.8 1.0
0
水
质量分数 水-烟碱的溶解度图
烟碱
6.4 二组分凝聚系统相图 一、二组分固态完全不互溶系统液固平衡相图
1. 热分析法
基本原理:二组分系统 C=2,指定压力不变,
f * = C +1 -F =3 -F
F = 1
f f 1 ** f f 2
*
相点 表示某个相状态(如相态、组成、温度等)的 点称为相点。 物系点 相图中表示系统总状态的点称为物系点。在T-x 图上,物系点可以沿着与温度坐标平行的垂线上、 下移动;在水盐相图上,随着含水量的变化,物系 点可沿着与组成坐标平行的直线左右移动。
单相区,物系点与相点重合;两相区中,只有 物系点,它对应的两个相的组成由对应的相点表示
B
3. 全部变为固体Bi后
f * C 1 Φ 1
t /s
温度又可以下降 纯Cd步冷曲线与之相同
Cd-Bi二元相图的绘制
w(Cd) 0.2
的步冷曲线
b
T /K
f* 2
C
D
f * 1
1. 加热到b点,Bi-Cd全部熔化 Φ 1 f * 2 1 Φ 2 温度可以下降,组成也可变 2. 冷至C点,固体Bi开始析出 Φ 2 f * 2 1 Φ 1 温度可以下降 3.D点固体Bi、Cd同时析出
Φ 3
f* 0 温度不能改变 f * 1 4.熔液消失,Bi和Cd共存
f 2 1 Φ 0
*
物理化学 06-04

11
§6.6 精馏原理
1.简单蒸馏原理
将液态混合物同 时经多次部分气化和 部分冷凝而使之分离 的操作称为精馏
g
t 3 : x3 < x2
t2 : y2 >x>x2 t1 : y1 > y2
l
精馏原理:气液
平衡时气相组成与 液相组成不同
13
2.精馏原理 2.精馏原理
t/℃
G3 M2 L1 G2 M1 M2 ´ L2´ t0 G1 p=const.
g
(4)
p = [2.97 x B + 9.96(1 − x B )]kPa = 9.00kPa
9.00 − 9.96 xB = = 0.137 2.97 − 9.96 x A = 0.863 Nhomakorabea24
(5)
pB = p x B = p (1 − x B ) = p A
p 2.97 xB = ∗ = = 0.230 ∗ p A + pB 2.97 + 9.96 x A = 0.770
g
L3 t2 t1
M3 L2
G2´
a l
A
x3
x2
y3
x1 y2 x0
y1
B
14
精馏塔
在精馏塔中, 在精馏塔中, 部分气化与部分 冷凝同时连续进 行,即可将 A、B 分开
15
从相图看精馏分离的难易
易挥发组分从塔顶出来; 挥发组分从塔釜出来。 易挥发组分从塔顶出来;不易 挥发组分从塔釜出来。
16
对于最大正负偏差系统
1) 将p-x图与 -x图相比 图与t 图与 图相比 液相线和气相线的位置;相区位置; 液相线和气相线的位置;相区位置; 饱和蒸气压大的组分沸点低,饱和蒸气压小的沸点高。 饱和蒸气压大的组分沸点低,饱和蒸气压小的沸点高。 2)比较理想液态混合物与一般正负偏差的p-x与t-x图 )比较理想液态混合物与一般正负偏差的 与 图 除理想液态混合物的p 图中液相线为直线外, 除理想液态混合物的 -x图中液相线为直线外,它们 图中液相线为直线外 具有以下共同特征 共同特征: 具有以下共同特征: ①
§6.6 精馏原理
1.简单蒸馏原理
将液态混合物同 时经多次部分气化和 部分冷凝而使之分离 的操作称为精馏
g
t 3 : x3 < x2
t2 : y2 >x>x2 t1 : y1 > y2
l
精馏原理:气液
平衡时气相组成与 液相组成不同
13
2.精馏原理 2.精馏原理
t/℃
G3 M2 L1 G2 M1 M2 ´ L2´ t0 G1 p=const.
g
(4)
p = [2.97 x B + 9.96(1 − x B )]kPa = 9.00kPa
9.00 − 9.96 xB = = 0.137 2.97 − 9.96 x A = 0.863 Nhomakorabea24
(5)
pB = p x B = p (1 − x B ) = p A
p 2.97 xB = ∗ = = 0.230 ∗ p A + pB 2.97 + 9.96 x A = 0.770
g
L3 t2 t1
M3 L2
G2´
a l
A
x3
x2
y3
x1 y2 x0
y1
B
14
精馏塔
在精馏塔中, 在精馏塔中, 部分气化与部分 冷凝同时连续进 行,即可将 A、B 分开
15
从相图看精馏分离的难易
易挥发组分从塔顶出来; 挥发组分从塔釜出来。 易挥发组分从塔顶出来;不易 挥发组分从塔釜出来。
16
对于最大正负偏差系统
1) 将p-x图与 -x图相比 图与t 图与 图相比 液相线和气相线的位置;相区位置; 液相线和气相线的位置;相区位置; 饱和蒸气压大的组分沸点低,饱和蒸气压小的沸点高。 饱和蒸气压大的组分沸点低,饱和蒸气压小的沸点高。 2)比较理想液态混合物与一般正负偏差的p-x与t-x图 )比较理想液态混合物与一般正负偏差的 与 图 除理想液态混合物的p 图中液相线为直线外, 除理想液态混合物的 -x图中液相线为直线外,它们 图中液相线为直线外 具有以下共同特征 共同特征: 具有以下共同特征: ①
物理化学6-2ppt
l1+l2
C´ wB/%
l 100 B
苯 (A) - 硫 (B)系统 3) 苯 - 硫系统在 163°C 以下部分互溶,在 226°C以 上也部分互溶,但在这两个 温度之间却完全互溶。此类 系统的低会溶点位于高会溶 点的上方。 t p=const. l1+l2 C´ tC C l1+l2 l
0 A
g+l
g
l
0.0 A
xB
氯仿 - 丙酮系统的 温度 - 组成图(具有最大负偏差)
1.0 B
对恒沸混合物,下列说法错误的是 A. 不具有确定的组成 B. 平衡时气、液相组 成相同 C. 其沸点虽外压改变而改变 D. 与化合物一 样具有确定的组成
小结
(1)正偏差不是很大的体系 等温
p
pB
等温
pB*
wB/%
c
N
100 B(苯酚)
液相的相点分别沿 L1 L1´ 和 L2 L2´ 变化, 两液相的质量也不断变化,水层减少,苯 酚层逐渐增加。在 L2´ 水层状态为L1´ , 然后水层消失,只剩一个苯酚层。此为第 一种类型。
当系统由a 升温到L2´时,两个共轭
t
p=const. e b C L’ L11´ L2 ’ l ´
0 A
xB
p/kPa
1 B
氯仿
乙醚
t=25°C 蒸气总压对理想情况为正偏 差,但在某一组成范围内,混合 物的蒸气总压比易挥发组分的饱 和蒸气压还大,因而蒸气总压出 现最大值。 例子: 甲醇(A) - 氯仿(B)系统。 p/kPa 0 A 甲醇
3) 具有最大正偏差的系统:
xB
1 B 氯仿
特点: p实 > p理 在 p-x 图上有最高点,即p实 >pB*>pA* ,
ch6.3二组分理想液态混合物的气液平衡相图

l+g
L2
M
G3
G1
G2
pA
b
g
0 A
xL
xM
xG
xB 2) 到达L1后,液相开始蒸发, 最初形成的蒸气相的状态为G1 C6H5CH3(A) - C6H6(B) 所示,系统进入气-液平衡两相区。
1 B
当系统点为M点时,两相平衡 的液相点为L2,气相点为G2, 这两点均为相点。 两个平衡相点的连接线称为结线。
pB pB xB
* pB
p
* A
pA pA (1 xB )
A
xB
B
∵T=常数,且系统达到气液平衡时,自由度数F= 1, 表明压力和组成中只有一个为变量,若选液相组成xB 为独立变量,即 p = f(xB),且yB = f(xB)
(2) p-x-y图
这是 p-x 图的一种,把液相组成 x 和气相组成 y 画在同一张图上。 • yA 和 yB的求法如下:
y=f(p)
0 A
xL
xM xB
xG
1 B
C6H5CH3(A) - C6H6(B)
•问题 有F = 0的点么? 端点 纯物 F = 0
(4)几点说明
①相点与系统点
p
l
a L1 L3
t=const.
pB
•相点:表示某一相组成的点, 可以随 T、p 变。
•系统点:表示系统总组成的 点,不随 T、p 变。
1 B
强调一点:在结线上不同的任意两个物系点
1) 2) 3) 两个物系总组成不同; 两个物系,气液两相的相对数量不同; 但两个物系,平衡压力,两相组成均相同。
2. 温度-组成图
亦为沸点-组成图,恒定压力下表示二组分系统气 -液平衡时的温度与组成关系的相图,叫做温度-组成 图。 外压为大气压力,当溶液的蒸气压等于外压时, 溶液沸腾,这时的温度称为沸点。 某组成的蒸气压越高,其沸点越低,反之亦然。 T-x图在讨论蒸馏时十分有用,因为蒸馏通常在等 压下进行。
二组分理想液态混合物的气-液平衡相图.

精馏是多次蒸馏过程
x1>x2>x3 ---→纯A y1< y2/<y3 / --→纯B • 6.3 精馏操作的条件
蒸气总压介于两纯组分饱和 蒸气压之间
恒沸点:沸腾时温度不变
特点—该点气相组成始终等于液 相组成
相律解释—C=S-R-R/=2-0-1=1, F=1-2+1=0
恒沸混合物不是化合物
§6.6 精馏原理
• 6.1 精馏操作的理论基 础
易挥发组分在气相中的含量 大于液相中的含量,难挥发组 分在液相中的含量大于气相中 的含量
• 6.2 精馏操作过程分析
• 5.1 真实液态混合物与理想 液态混合物的差别 • 5.2 蒸气压-组成图
(1)一般正、负偏差
在一定温度下,混合物中任一组分是否在 全部组成范围内都符合拉乌尔定律
§6.5 二组分真实液态混合物的气-
液平衡相图• 5.1 真实液态 Nhomakorabea合物与理想 液态混合物的差别 • 5.2 蒸气压-组成图
(1)一般正、负偏差 (2)最大正、负偏差
液相线—泡点,泡点线
(2)对比T-x图与p-x图
① p-x图中液相区在上,气相区在
下; T-x图则相反
② p-x图中液相线为直线,气相线
为曲线;T-x图中液相线和气相
线都为曲线
(3)a→b系统加热过程状态变化分析
易挥发组分在气相中的含量大于 液相中的含量
§6.5 二组分真实液态混合物的气-
液平衡相图
§6.4 二组分理想液态混合物的气-
液平衡相图 复 习
• 4.1 二组分系统相律分析
温度-组成图:恒定压力下研究
• 4.2 压力-组成图
T、x、y之间关系
• 4.3 温度-组成图
x1>x2>x3 ---→纯A y1< y2/<y3 / --→纯B • 6.3 精馏操作的条件
蒸气总压介于两纯组分饱和 蒸气压之间
恒沸点:沸腾时温度不变
特点—该点气相组成始终等于液 相组成
相律解释—C=S-R-R/=2-0-1=1, F=1-2+1=0
恒沸混合物不是化合物
§6.6 精馏原理
• 6.1 精馏操作的理论基 础
易挥发组分在气相中的含量 大于液相中的含量,难挥发组 分在液相中的含量大于气相中 的含量
• 6.2 精馏操作过程分析
• 5.1 真实液态混合物与理想 液态混合物的差别 • 5.2 蒸气压-组成图
(1)一般正、负偏差
在一定温度下,混合物中任一组分是否在 全部组成范围内都符合拉乌尔定律
§6.5 二组分真实液态混合物的气-
液平衡相图• 5.1 真实液态 Nhomakorabea合物与理想 液态混合物的差别 • 5.2 蒸气压-组成图
(1)一般正、负偏差 (2)最大正、负偏差
液相线—泡点,泡点线
(2)对比T-x图与p-x图
① p-x图中液相区在上,气相区在
下; T-x图则相反
② p-x图中液相线为直线,气相线
为曲线;T-x图中液相线和气相
线都为曲线
(3)a→b系统加热过程状态变化分析
易挥发组分在气相中的含量大于 液相中的含量
§6.5 二组分真实液态混合物的气-
液平衡相图
§6.4 二组分理想液态混合物的气-
液平衡相图 复 习
• 4.1 二组分系统相律分析
温度-组成图:恒定压力下研究
• 4.2 压力-组成图
T、x、y之间关系
• 4.3 温度-组成图
6.3理想液态混合物气液平衡相图6.4真实液态混合物

a G1 G2
∗ pB
L3
L2
M G3 b
0 A
xM
1 B
0 A
xL
xM xG xB
1 B
4. 杠杆规则 物系点、相点、 物系点、相点、结线 当系统的物系点落 在两相平衡区时, 在两相平衡区时,系统 呈两相平衡, 呈两相平衡,可以根据 物系点及两个相点在相 图上的位置, 图上的位置,确定平衡 两相的数量比。 两相的数量比。 p t=const.
基本要求
(1)掌握各相图的特征 掌握各相图的特征 (2)指出各区、线、点的意义和稳定相态,存在的相平衡, 指出各区、 指出各区 点的意义和稳定相态,存在的相平衡, 会用相律进行分析(会计算 。 会用相律进行分析 会计算 F )。 (3)用相图分析:状态为 a 的系统在冷却或加热过程中系统 用相图分析: 用相图分析 的相变情况 液平衡-----文字描述 气-液平衡 液平衡 文字描述 固平衡——冷却曲线 液-固平衡 固平衡 冷却曲线 (4)应用 应用
xB
1.0 B
(2) p - y 线——气相线 气相线
∗ pA pA x A yA = = p p
∗ pB pB x B yB = = p p
甲苯-苯系统: 甲苯 苯系统: pA∗ < p <pB ∗ 苯系统 yB> xB 易挥发组分在气相中的相对含量大于它在液相中的含量。 易挥发组分在气相中的相对含量大于它在液相中的含量。
三相
g ⇔ l ⇔ s g ⇔ l ⇔ l 1 2 l ⇔ s1 ⇔ s 2 g ⇔ s1 ⇔ s 2
P=3 F=0
在恒压图中, 在恒压图中, 三相平衡 的温度与组成都不能变。 的温度与组成都不能变。
两组分系统相图分类
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二组分系统液态互溶情况:
(a)完全互溶
(b)完全不互溶 (c)部分互溶
液态完全互溶系统 p-x、t-x图
理想系统 真实系统
一般正偏差 最大正偏差
一般负偏差 最大负偏差
液态部分互溶系统 t-x图
气相组成介于两液相之间 气相组成位于两液相同侧
液态完全不互溶系统 t-x图
完全互溶系统:理想液态混合物系统气-液平衡相图
1. 压力—组成图
A、B形成理想液态混合物:均符合拉乌尔定律
A组分分压: pA pA* xA pA* 1 xB
B组分分压: pB pB* xB
pA,pB,p和xB均成
气相总压: p pA pB
直线关系
pA* 1 xB pB* xB
pA* pB* pA* xB
液相线:气相总压 p 与液相组成 xB 之间的关系曲线
nL
解: (1) 先确定系统点的总组成
xM
nB nA nB
6 46
0.6
利用
nG (xM yB ) nL (xB xM ) 即 nG (0.6 0.2) nL (0.7 0.6) (1)
nG nL n总 =4+6=10mol (2)
解得
nG =2mol
nL =8mol
(2) 气相中: 甲苯 nB nG yB 2 0.2 0.4mol 苯 nA nG yA 2 0.8 1.6mol
(4)最大负偏差系统
p实际 p理想
且在某一组成范围内比 难挥发组分的饱和蒸气 压还小,实际蒸气总压 出现最小值
液相线
氯仿(A)—丙酮(B)系统
加上气相线:
一般正偏差系统
一般负偏差系统
最大正偏差系统
液相线 气相线
甲醇(A)—氯仿(B)系统
最高点:液相线和 气相线相切
在 p–x图 中 的 最 高 点处, yB = xB
nA ----A组分的物质的量
nB ---B组分的物质的量
xM----B组分在系统的总组成
nG ----气相总的物质的量
xG---B组分在气相中的组成
nL ----液相总的物质的量
xL---B组分在液相中的组成
xM
nB nA nB
n nA nB nL nG
xM nL nG nG xG nL xL
若液态混合物中 增加某组分B后, 蒸气总压增加, 则yB>xB
--柯诺瓦洛夫--吉布斯定律
最大负偏差系统
液相线 气相线
氯仿(A)—丙酮(B)系统
最低点:液相线和 气相线相切
在 p–x图 中 的 最 低 点处, yB = xB
若液态混合物中 增加某组分B后, 蒸气总压增加, 则yB>xB
--柯诺瓦洛夫--吉布斯定律
气相线:气相总压 p 与气相组成 yB 之间的关系曲线
yA
pA p
pA* 1 xB pA* pB* pA*
xB
F=1
F=2
yB
pB p
pA*
pB* xB pB* pA*
xB
F=2
温度恒定 F = C-P+1
甲苯(A)—苯(B)系统
2、杠杆规则: ----确定平衡两相的物质的量或质量
液相线
苯(A)—丙酮(B)系统
(2)一般负偏差易挥发
(0 x 1)
液相线
氯仿(A)—乙醚(B)系统
(3)最大正偏差系统
p实际 p理想
且在某一组成范围内比 易挥发组分的饱和蒸气 压还大,实际蒸气总压 出现最大值
液相线 甲醇(A)—氯仿(B)系统
液相中: 甲苯 nB nL xB 8 0.7 5.6mol 苯 nA nL xA 8 0.3 2.4mol
3. 理想液态混合物系统温度—组成图
T-x亦称为沸点-组成图
在 T-x 图 上 , 气 相 线 在上,液相线在下,上 面是气相区,下面是液 相区,梭形区是气-液 两相区。
压力恒定 F = C-P+1
2. 温度—组成图
甲醇(A)—氯仿(B)系统
最大正偏差系统
p–x图上最高点 T–x图上最低点( yB = xB ) 最低恒沸点→恒沸混合物
恒沸混合物不是一种化合物 改变压力:可改变恒沸混合物组 成,或使恒沸点消失。恒沸混合 物的组成取决于压力。
氯仿(A)—丙酮(B)系统
最大负偏差系统
p–x图上最低点 T–x图上最高点( yB = xB ) 最高恒沸点→恒沸混合物
两相平衡,相应的组成为xB = 0.7, yB = 0.2,求系统中气液两相的 物质的量各为多少?气、液二相中,甲苯和苯的量各为多少?
分析:
通过题目中的xB ,yB,知道是甲苯(B)的组成变化作为
横坐标,确定系统的总组成xM 再利用杠杆规则
xM
nB nA nB
yB 0.2
nG
xM 0.6
xB 0.7
恒沸混合物不是一种化合物 改变压力:可改变恒沸混合物组 成,或使恒沸点消失。恒沸混合 物的组成取决于压力。
1) 若恒沸混合物的恒沸点在沸点----组成图上为最低点, 则在压力----组成图上为最高点。( ) 2) 恒沸混合物不是化合物。( ) 3) 二元恒沸混合物的组成随温度而变。( )
1) √ 2) √ 3) ×
解得 nL, nG ——液相、气相物质的量。
关于杠杆规则的适用对象, 下面的说法中不正确的是 B (A) 不适用于单组分系统 (B) 适用于二组分系统的任何相区 (C) 适用于二组分系统的两相平衡区 (D) 适用于三组分系统的两相平衡区
例 将4mol苯(A)和6mol甲苯(B)混合,在95℃、pӨ下,气液
§6-3 二组分系统理想液态混合物的气—液平 衡相图
将相律应用于二组分系统: F =2-P+2=4-P ≥0
P=1, P=4,
F=3 F=0
即:最多有3个独立变量,即温度、压力、组成
平面图:
固定温度T 固定压力p
: p x (压力 组成图) : t x (温度 组成图)
二组分系统相图:气—液平衡相图
甲苯(A)—苯(B)系统
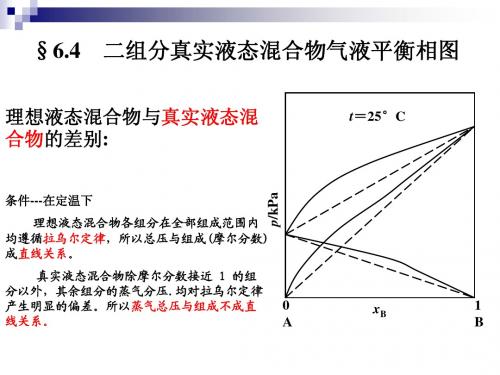
§6-4 二组分真实液态混合物的气—液 平衡相图
完全互溶系统:真实液态混合物对拉乌尔定律产生偏差 可将偏差分为四类:
• 一般正偏差 • 一般负偏差 • 最大正偏差 • 最大负偏差
1. 压力—组成图
(1) 一般正偏差系统
p实际 p理想
p* 难挥发
p实际
p* 易挥发
(0 x 1)
整理可得:
nL xM xL nG xG xM
即: nL L2M nG MG2
杠杆规则
若横坐标为wB
mL L2M mG MG2
注意:
(1)杠杆规则适用于任意两相平衡共存区
(2)若已知系统的总的物质的量 n(总), 则如下联立方程:
nL + nG = n(总)
(1)
nL xM xL nG xG xM (2)
(a)完全互溶
(b)完全不互溶 (c)部分互溶
液态完全互溶系统 p-x、t-x图
理想系统 真实系统
一般正偏差 最大正偏差
一般负偏差 最大负偏差
液态部分互溶系统 t-x图
气相组成介于两液相之间 气相组成位于两液相同侧
液态完全不互溶系统 t-x图
完全互溶系统:理想液态混合物系统气-液平衡相图
1. 压力—组成图
A、B形成理想液态混合物:均符合拉乌尔定律
A组分分压: pA pA* xA pA* 1 xB
B组分分压: pB pB* xB
pA,pB,p和xB均成
气相总压: p pA pB
直线关系
pA* 1 xB pB* xB
pA* pB* pA* xB
液相线:气相总压 p 与液相组成 xB 之间的关系曲线
nL
解: (1) 先确定系统点的总组成
xM
nB nA nB
6 46
0.6
利用
nG (xM yB ) nL (xB xM ) 即 nG (0.6 0.2) nL (0.7 0.6) (1)
nG nL n总 =4+6=10mol (2)
解得
nG =2mol
nL =8mol
(2) 气相中: 甲苯 nB nG yB 2 0.2 0.4mol 苯 nA nG yA 2 0.8 1.6mol
(4)最大负偏差系统
p实际 p理想
且在某一组成范围内比 难挥发组分的饱和蒸气 压还小,实际蒸气总压 出现最小值
液相线
氯仿(A)—丙酮(B)系统
加上气相线:
一般正偏差系统
一般负偏差系统
最大正偏差系统
液相线 气相线
甲醇(A)—氯仿(B)系统
最高点:液相线和 气相线相切
在 p–x图 中 的 最 高 点处, yB = xB
nA ----A组分的物质的量
nB ---B组分的物质的量
xM----B组分在系统的总组成
nG ----气相总的物质的量
xG---B组分在气相中的组成
nL ----液相总的物质的量
xL---B组分在液相中的组成
xM
nB nA nB
n nA nB nL nG
xM nL nG nG xG nL xL
若液态混合物中 增加某组分B后, 蒸气总压增加, 则yB>xB
--柯诺瓦洛夫--吉布斯定律
最大负偏差系统
液相线 气相线
氯仿(A)—丙酮(B)系统
最低点:液相线和 气相线相切
在 p–x图 中 的 最 低 点处, yB = xB
若液态混合物中 增加某组分B后, 蒸气总压增加, 则yB>xB
--柯诺瓦洛夫--吉布斯定律
气相线:气相总压 p 与气相组成 yB 之间的关系曲线
yA
pA p
pA* 1 xB pA* pB* pA*
xB
F=1
F=2
yB
pB p
pA*
pB* xB pB* pA*
xB
F=2
温度恒定 F = C-P+1
甲苯(A)—苯(B)系统
2、杠杆规则: ----确定平衡两相的物质的量或质量
液相线
苯(A)—丙酮(B)系统
(2)一般负偏差易挥发
(0 x 1)
液相线
氯仿(A)—乙醚(B)系统
(3)最大正偏差系统
p实际 p理想
且在某一组成范围内比 易挥发组分的饱和蒸气 压还大,实际蒸气总压 出现最大值
液相线 甲醇(A)—氯仿(B)系统
液相中: 甲苯 nB nL xB 8 0.7 5.6mol 苯 nA nL xA 8 0.3 2.4mol
3. 理想液态混合物系统温度—组成图
T-x亦称为沸点-组成图
在 T-x 图 上 , 气 相 线 在上,液相线在下,上 面是气相区,下面是液 相区,梭形区是气-液 两相区。
压力恒定 F = C-P+1
2. 温度—组成图
甲醇(A)—氯仿(B)系统
最大正偏差系统
p–x图上最高点 T–x图上最低点( yB = xB ) 最低恒沸点→恒沸混合物
恒沸混合物不是一种化合物 改变压力:可改变恒沸混合物组 成,或使恒沸点消失。恒沸混合 物的组成取决于压力。
氯仿(A)—丙酮(B)系统
最大负偏差系统
p–x图上最低点 T–x图上最高点( yB = xB ) 最高恒沸点→恒沸混合物
两相平衡,相应的组成为xB = 0.7, yB = 0.2,求系统中气液两相的 物质的量各为多少?气、液二相中,甲苯和苯的量各为多少?
分析:
通过题目中的xB ,yB,知道是甲苯(B)的组成变化作为
横坐标,确定系统的总组成xM 再利用杠杆规则
xM
nB nA nB
yB 0.2
nG
xM 0.6
xB 0.7
恒沸混合物不是一种化合物 改变压力:可改变恒沸混合物组 成,或使恒沸点消失。恒沸混合 物的组成取决于压力。
1) 若恒沸混合物的恒沸点在沸点----组成图上为最低点, 则在压力----组成图上为最高点。( ) 2) 恒沸混合物不是化合物。( ) 3) 二元恒沸混合物的组成随温度而变。( )
1) √ 2) √ 3) ×
解得 nL, nG ——液相、气相物质的量。
关于杠杆规则的适用对象, 下面的说法中不正确的是 B (A) 不适用于单组分系统 (B) 适用于二组分系统的任何相区 (C) 适用于二组分系统的两相平衡区 (D) 适用于三组分系统的两相平衡区
例 将4mol苯(A)和6mol甲苯(B)混合,在95℃、pӨ下,气液
§6-3 二组分系统理想液态混合物的气—液平 衡相图
将相律应用于二组分系统: F =2-P+2=4-P ≥0
P=1, P=4,
F=3 F=0
即:最多有3个独立变量,即温度、压力、组成
平面图:
固定温度T 固定压力p
: p x (压力 组成图) : t x (温度 组成图)
二组分系统相图:气—液平衡相图
甲苯(A)—苯(B)系统
§6-4 二组分真实液态混合物的气—液 平衡相图
完全互溶系统:真实液态混合物对拉乌尔定律产生偏差 可将偏差分为四类:
• 一般正偏差 • 一般负偏差 • 最大正偏差 • 最大负偏差
1. 压力—组成图
(1) 一般正偏差系统
p实际 p理想
p* 难挥发
p实际
p* 易挥发
(0 x 1)
整理可得:
nL xM xL nG xG xM
即: nL L2M nG MG2
杠杆规则
若横坐标为wB
mL L2M mG MG2
注意:
(1)杠杆规则适用于任意两相平衡共存区
(2)若已知系统的总的物质的量 n(总), 则如下联立方程:
nL + nG = n(总)
(1)
nL xM xL nG xG xM (2)
