第2章多元回归分析
合集下载
古扎拉蒂《计量经济学基础》第2章

国内外经典教材名师讲堂
古扎拉蒂 《计量经济学基础》
第二章 双变量回归分析: 一些基本思想
主讲老师:李庆海
2.1 本章要点
●一些基本概念 ●总体回归函数 ●“线性”函数的定义 ●PRF的随机设定 ●随机干扰项的意义
●样本回归函数
2.2 重难点导学
一、一些基本概念
条件概率:给定X的Y的概率,记为P(Y|X)。
条件均值(如图2-1所示)
Y
条件均值
149 101 65
E(Y|Xi)
80
140 220
X
图2-1 总体回归线
总体回归曲线
思考:给定一个X,就对应一个(惟一 的)E(Y|X)。因此,(X,E(Y|X))可以 表示成平面上的一个点。 总体回归曲线(Popular Regression Curve):Y的条件均值的轨迹。即Y对X的回 归。 总体回归曲线的几何意义:当解释变量给 定值时因变量的条件期望值的轨迹。
已知给定X=1,Y取5个不同的值:1、2、3、4、
5。 问:Y取每个值的概率有多大?
古典概率模型:取每个值的概率相等。因此有:
P(Y=1|X=1)=1/5; P(Y=2|X=1)=1/5;
P(Y=3|X=1)=1/5;
P(Y=4|X=1)=1/5; P(Y=5|X=1)=1/5;
词总是指对参数为线性的一种回归(即参数
只以它的1次方出现)。
Y= 1+2X+u, lnY= 1+2lnX+u 是线性的!
Y= 1ln(2X+u)不是线性的!
模型对参数为线性?
模型对变量为线性?
是
不是
是
LRM
LRM
不是
NLRM
古扎拉蒂 《计量经济学基础》
第二章 双变量回归分析: 一些基本思想
主讲老师:李庆海
2.1 本章要点
●一些基本概念 ●总体回归函数 ●“线性”函数的定义 ●PRF的随机设定 ●随机干扰项的意义
●样本回归函数
2.2 重难点导学
一、一些基本概念
条件概率:给定X的Y的概率,记为P(Y|X)。
条件均值(如图2-1所示)
Y
条件均值
149 101 65
E(Y|Xi)
80
140 220
X
图2-1 总体回归线
总体回归曲线
思考:给定一个X,就对应一个(惟一 的)E(Y|X)。因此,(X,E(Y|X))可以 表示成平面上的一个点。 总体回归曲线(Popular Regression Curve):Y的条件均值的轨迹。即Y对X的回 归。 总体回归曲线的几何意义:当解释变量给 定值时因变量的条件期望值的轨迹。
已知给定X=1,Y取5个不同的值:1、2、3、4、
5。 问:Y取每个值的概率有多大?
古典概率模型:取每个值的概率相等。因此有:
P(Y=1|X=1)=1/5; P(Y=2|X=1)=1/5;
P(Y=3|X=1)=1/5;
P(Y=4|X=1)=1/5; P(Y=5|X=1)=1/5;
词总是指对参数为线性的一种回归(即参数
只以它的1次方出现)。
Y= 1+2X+u, lnY= 1+2lnX+u 是线性的!
Y= 1ln(2X+u)不是线性的!
模型对参数为线性?
模型对变量为线性?
是
不是
是
LRM
LRM
不是
NLRM
气象统计分析与预报方法:08-第二章-回归分析4

▪ 感谢阅读
End Of Curve Estimation
➢非线性回归 2
多项式回归
yi 0 1xi 2 xi2 ... p xip ei
可化为线性的曲线回归 初等函数变换
一般的非线性回归
yi f ( xi , ) ei
用Gauss-Newton 法确定系数向量
感谢阅读
▪ 感谢阅读
▪ 感谢阅读
2.20 162.00 5.09
.79
10.00 12.00 2.48 2.30
8.10 19.00 2.94 2.09
Let Y2=ln(Y), X2=ln(X) Then Y2=ln(b)+b1* ln(X)
14.80 7.90 2.07 2.69
5.5
2.80 178.00 5.18 1.03
参数设置 因变量 自变量
Models (Selection)
中文含义
线性 二次曲线 复合函数 生长曲线 对数函数 三次曲线 S--曲线 指数函数 倒数函数 幂函数 逻辑斯谛函数
其它例子: 1)Y=b0+b1t+b2t2 令:X1=t; X2=t2 则化为线性二元回归方程: Y= b0+b1X1+b2X2 2)Y=a X-b exp(-cX) 取对数:ln(Y)=ln(a)-b*ln(X)-c*X
3.00 135.00
200
11.40
8.90
4.80 6.80 10.20
61.60 39.80 10.00
Example 2:power
100
Observed
Cu b i c
0
P ow er
2
4
6
8
第2章计量经济学回归分析的性质ppt课件

§2.4 数据
一、数据的分类 按照数据与时间的关系,可以分为: ❖ 时间序列数据(time series data) ❖ 横截面数据(cross-section data) ❖ 面板数据(panel data/ pooling data)
实例:我国地区的生产总值
二、数据的来源和质量
❖ 社会科学数据都是非实验所得,存在测量误 差,或出于疏漏或差错 ;
cov(Xt,Yt)
Var(Xt) Var(Yt)
样本相关系数r
rXYˆ
1 T1
(Xt X)(Yt Y)
1 T1
(Xt X)2
1 T1
(Yt Y)2
(Xt X)(Yt Y)
(Xt X)2 (Yt Y)2
性质: (1)r具有对称性 (2)r与原点和尺度都无关
400
200
0 0
X
10
20
30
40
50
完全相关
Y 2
1
X
0
10
20
30
40
50
高度相关
3.0
2.5
Y
2.0
1.5
1.0
0.5
2.0
2.5
3.0
3.5
弱相关
X
4.0
4.5
4
Y 2
0
-2
X -4
-4
-2
0
2
4
零相关
2、按变量个数
200 150 100
50 0 0
Y
X
50
100
150
200
250
非线性相关/负相关
Y 2
1
第2章多元回归分析

第二章 多元回归分析:估计
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1
Multiple Regression Analysis
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1. Estimation
2
Parallels with Simple Regression
fIrno mthethgeefniersrtalocrdaeser cwointhd iktioinnd, ewpeencdanengtevt akriab1 les,
lwineeasreeeqkueasttiiomnastienskbˆ0,1bˆu1,n k n,obˆwk
tynˆheryebiˆf0orbeˆb,0ˆ1mx1ibnˆ1ixmi1 izebˆtkhxekbˆskuxmik of
The STATA command
Use [path]wage1.dta (insheet using [path]wage1.raw/wage1.txt) Reg wage educ exper tenure Reg lwage educ exper tenure
7
A “Partialling Out” Interpretation
8
“Partialling Out” continued
Previous equation implies that regressing y on x1 and x2 gives same effect of x1 as regressing y on residuals from a regression of x1 on x2
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1
Multiple Regression Analysis
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1. Estimation
2
Parallels with Simple Regression
fIrno mthethgeefniersrtalocrdaeser cwointhd iktioinnd, ewpeencdanengtevt akriab1 les,
lwineeasreeeqkueasttiiomnastienskbˆ0,1bˆu1,n k n,obˆwk
tynˆheryebiˆf0orbeˆb,0ˆ1mx1ibnˆ1ixmi1 izebˆtkhxekbˆskuxmik of
The STATA command
Use [path]wage1.dta (insheet using [path]wage1.raw/wage1.txt) Reg wage educ exper tenure Reg lwage educ exper tenure
7
A “Partialling Out” Interpretation
8
“Partialling Out” continued
Previous equation implies that regressing y on x1 and x2 gives same effect of x1 as regressing y on residuals from a regression of x1 on x2
第二章 双变量回归分析(计量经济学,南开大学)
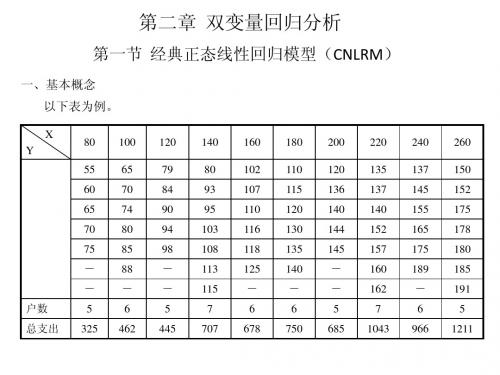
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
6、样本回归函数(SRF) 由于在大多数情况下,我们只知道变量值得一个样本,要用样本信息的基础 上估计PRF。(表) 样本1
X(收入) Y(支出) 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ: 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差:VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量(Estimator):一个估计量又称统计量(statistic),是指一个规则、公式 或方法,以用来根据已知的样本所提供的信息去估计总体参数。在应用中,由估 计量算出的数值称为估计(值)(estimate)。 样本回归函数SRF的随机形式为:
第2章(回归分析)

《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型 对应不同收入水平的60户家庭的每周消费 户家庭的每周消费Y 对应不同收入水平的 户家庭的每周消费
200 160
120
80
40 60 80 100 120 140 160 180 200 220 240 260 280
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
二.总体回归模型中的 Ui 所包含的内容 2.从实际经济行为看 从实际经济行为看Ui 从实际经济行为看
Yi = E (Y X i ) + U i = β 0 + β1 X i + U i
从经济学理论可知, 除收入X外 家庭财富、 从经济学理论可知 除收入 外,家庭财富、 通胀、利率, 通胀、利率,预期等对消费支出产生影响的因 包含在U之中 素,包含在 之中
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1. 总体 2. 总体回归模型 二、总体回归模型中 ui所包含的内容 1.从数量上看 ui 从数量上看 2.从实际经济行为看 ui 从实际经济行为看 3.从回归关系看 ui 从回归关系看
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
家庭每周收入X 家庭每周收入
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型
上图说明,收入 从 变化至 变化至280,这一变化 上图说明,收入X从80变化至 说明 , 解释了消费Y的总体的条件期望 均值) 的总体的条件期望( 解释了消费 的总体的条件期望(均值)从65、 、 89等变化至 等变化至173。也就是说,X的变化解释了 等变化至 。也就是说, 的变化解释了 Y的总体的条件期望的变化(总体的平均变 的总体的条件期望的变化( 的总体的条件期望的变化 )。或者说 或者说, 的变化 决定了Y的总体的 的变化, 化)。或者说,X的变化,决定了 的总体的 平均变化。 的变化解释( 平均变化。而X的变化解释(或决定)了Y 的 的变化解释 或决定) 总体的平均变化,这正是回归分析的意义所在。 总体的平均变化,这正是回归分析的意义所在。 因此,称这条线为总体回归模型。 因此,称这条线为总体回归模型。 由于它是一条直线, 由于它是一条直线,故也称为总体回归直线
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型 对应不同收入水平的60户家庭的每周消费 户家庭的每周消费Y 对应不同收入水平的 户家庭的每周消费
200 160
120
80
40 60 80 100 120 140 160 180 200 220 240 260 280
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
二.总体回归模型中的 Ui 所包含的内容 2.从实际经济行为看 从实际经济行为看Ui 从实际经济行为看
Yi = E (Y X i ) + U i = β 0 + β1 X i + U i
从经济学理论可知, 除收入X外 家庭财富、 从经济学理论可知 除收入 外,家庭财富、 通胀、利率, 通胀、利率,预期等对消费支出产生影响的因 包含在U之中 素,包含在 之中
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1. 总体 2. 总体回归模型 二、总体回归模型中 ui所包含的内容 1.从数量上看 ui 从数量上看 2.从实际经济行为看 ui 从实际经济行为看 3.从回归关系看 ui 从回归关系看
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
家庭每周收入X 家庭每周收入
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型
上图说明,收入 从 变化至 变化至280,这一变化 上图说明,收入X从80变化至 说明 , 解释了消费Y的总体的条件期望 均值) 的总体的条件期望( 解释了消费 的总体的条件期望(均值)从65、 、 89等变化至 等变化至173。也就是说,X的变化解释了 等变化至 。也就是说, 的变化解释了 Y的总体的条件期望的变化(总体的平均变 的总体的条件期望的变化( 的总体的条件期望的变化 )。或者说 或者说, 的变化 决定了Y的总体的 的变化, 化)。或者说,X的变化,决定了 的总体的 平均变化。 的变化解释( 平均变化。而X的变化解释(或决定)了Y 的 的变化解释 或决定) 总体的平均变化,这正是回归分析的意义所在。 总体的平均变化,这正是回归分析的意义所在。 因此,称这条线为总体回归模型。 因此,称这条线为总体回归模型。 由于它是一条直线, 由于它是一条直线,故也称为总体回归直线
第2章人工智能技术基本原理2.2回归算法-高中教学同步《信息技术-人工智能初步》(教案
《信息技术-人工智能初步》教案
课题
第2章人工智能技术基本原理2.2回归算法
课型
班课
课时
1
授课班级
高一1班
学习目标
理解回归算法的基本概念及其在学习中的应用,包括一元回归和多元回归、线性回归和非线性回归的区别。
掌握回归分析的适用场景,能够区分连续值预测问题与离散值分类问题。
学习回归算法的一般流程,包括数据收集、算法训练、测试和应用。
培养技能:训练学生的数据处理和软件操作能力。
活动四:
巩固练习
素质提升
布置练习题:给出一些与回归分析相关的练习题,如使用其他数据集来练习回归分析。
讨论与反馈:组织课堂讨论,回顾学到的知识,并给予学生反馈。
独立练习:独立完成教师布置的练习题,应用所学知识。
知识回顾:参与讨论,回顾本节课的重点和难点。
巩固知识:通过练习加深对回归算法流程和类型的理解。
文本材料:包括教材、PPT课件和打印的讲义,这些材料中包含有关回归算法的详细说明、公式、实例和应用案例,是传递理论知识的主要媒介。
数据分析工具:如果课程中包含实践操作,可能会使用到数据分析软件(如Excel、Python等),通过实际操作来训练算法并测试结果。
实例数据表:表2.2.2作为一个具体的数据集例子,用于在课堂上展示如何从实际数据中探索变量间的关系。
观察数据:学生先观察表格数据,尝试找出尺寸与价格之间可能存在的关系。
讨论可能的方法:分小组讨论如何使用这些数据来预测未知尺寸的蛋糕价格。
激发兴趣:通过实际问题引起学生的兴趣和好奇心。
引导思考:促使学生从生活实例出发,思考变量间的关系,培养数据分析意识。
活动二:
调动思维
探究新知
课题
第2章人工智能技术基本原理2.2回归算法
课型
班课
课时
1
授课班级
高一1班
学习目标
理解回归算法的基本概念及其在学习中的应用,包括一元回归和多元回归、线性回归和非线性回归的区别。
掌握回归分析的适用场景,能够区分连续值预测问题与离散值分类问题。
学习回归算法的一般流程,包括数据收集、算法训练、测试和应用。
培养技能:训练学生的数据处理和软件操作能力。
活动四:
巩固练习
素质提升
布置练习题:给出一些与回归分析相关的练习题,如使用其他数据集来练习回归分析。
讨论与反馈:组织课堂讨论,回顾学到的知识,并给予学生反馈。
独立练习:独立完成教师布置的练习题,应用所学知识。
知识回顾:参与讨论,回顾本节课的重点和难点。
巩固知识:通过练习加深对回归算法流程和类型的理解。
文本材料:包括教材、PPT课件和打印的讲义,这些材料中包含有关回归算法的详细说明、公式、实例和应用案例,是传递理论知识的主要媒介。
数据分析工具:如果课程中包含实践操作,可能会使用到数据分析软件(如Excel、Python等),通过实际操作来训练算法并测试结果。
实例数据表:表2.2.2作为一个具体的数据集例子,用于在课堂上展示如何从实际数据中探索变量间的关系。
观察数据:学生先观察表格数据,尝试找出尺寸与价格之间可能存在的关系。
讨论可能的方法:分小组讨论如何使用这些数据来预测未知尺寸的蛋糕价格。
激发兴趣:通过实际问题引起学生的兴趣和好奇心。
引导思考:促使学生从生活实例出发,思考变量间的关系,培养数据分析意识。
活动二:
调动思维
探究新知
医用数据挖掘案例与实践 第2章 多元线性回归分析

11
在实际应用中,自变量之间可能会存在多重共线性,从而影 响多元线性回归的结果。为此,可以选择对自变量进行筛选 实施多元逐步线性回归,即从多个自变量中找出对因变量真 正有影响的自变量。筛选的方法有前进法(Forward)、后退 法(Backward)和逐步法(Stepwise)等。
12
仍然选用上面的例子,作多元逐步线性回归分析。这里选择逐步筛选法 (Stepwise),如果选择前进法,可以选择“Forward”,如果选择后退法,可 以选择“Backward”。 点开【Option...】按钮,默认筛选变量时入选标准“Entry”为“0.05”,剔除 标准“Removal”为“0.1”。具体操作如见图2.5所示。
图2.5 多元逐步线性回归分析中筛选变量的主对话框和Options子对话框
13
主要输出结果如图2.6~图2.9所示
Model Sum m ary
Model 1
2
R
R Square
.610a
.372
.696b
.484
A djuste d R Square
.347
.441
Std. Error of the Estimate
第二章 多元线性回归分析
1
在医学研究中,常常需要分析变量之间的关系。 比如人的体重与身高和胸围的关系;血压值与年龄、 性别、饮食习惯、吸烟状况和家族史的关系;血糖 水平与年龄、胰岛素、体重指数的关系;肿瘤预后 与患者的肿瘤亚型、肿瘤大小、治疗方式的关系等 等。
此时应采用回归分析的方法来研究变量之间的依存 关系,并对各个因素做出评价,也可用于预测和判 别。
14
如图2.7所示的输出表是对回归模型作的方差分析,同样分为两步,第一步
在实际应用中,自变量之间可能会存在多重共线性,从而影 响多元线性回归的结果。为此,可以选择对自变量进行筛选 实施多元逐步线性回归,即从多个自变量中找出对因变量真 正有影响的自变量。筛选的方法有前进法(Forward)、后退 法(Backward)和逐步法(Stepwise)等。
12
仍然选用上面的例子,作多元逐步线性回归分析。这里选择逐步筛选法 (Stepwise),如果选择前进法,可以选择“Forward”,如果选择后退法,可 以选择“Backward”。 点开【Option...】按钮,默认筛选变量时入选标准“Entry”为“0.05”,剔除 标准“Removal”为“0.1”。具体操作如见图2.5所示。
图2.5 多元逐步线性回归分析中筛选变量的主对话框和Options子对话框
13
主要输出结果如图2.6~图2.9所示
Model Sum m ary
Model 1
2
R
R Square
.610a
.372
.696b
.484
A djuste d R Square
.347
.441
Std. Error of the Estimate
第二章 多元线性回归分析
1
在医学研究中,常常需要分析变量之间的关系。 比如人的体重与身高和胸围的关系;血压值与年龄、 性别、饮食习惯、吸烟状况和家族史的关系;血糖 水平与年龄、胰岛素、体重指数的关系;肿瘤预后 与患者的肿瘤亚型、肿瘤大小、治疗方式的关系等 等。
此时应采用回归分析的方法来研究变量之间的依存 关系,并对各个因素做出评价,也可用于预测和判 别。
14
如图2.7所示的输出表是对回归模型作的方差分析,同样分为两步,第一步
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Consider the case wherek 2, i.e.
yˆ bˆ0 bˆ1x1 bˆ2 x2 , then
bˆ1 rˆi1yi
rˆi12 , w hererˆi1 are
the residuals from the estimated
regression xˆ1 ˆ0 ˆ2 xˆ2
yi y2 is the totalsum of squares(SST) yˆi y2 is the explained sum of squares(SSE) uˆi2 is the residualsum of squares(SSR)
Then SST SSE SSR
13
Goodness-of-Fit (continued)
What determines the person to commit crime? (the dependent variable is the number of times the man was arrested during 1986, narr86)
第二章 多元回归分析:估计
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1
Multiple Regression Analysis
y = b0 + b1x1 + b2x2 + . . . bkxk + u
1. Estimation
2
Parallels with Simple Regression
This means only the part of xi1 that is uncorrelated with xi2 are being related to yi so we’re estimating the effect of x1 on y after x2 has been “partialled out”
line. The population regression line is
E( y | x) b0 b1x1 b2 x2 L bk xk
5
Interpreting Multiple Regression
yˆ bˆ0 bˆ1x1 bˆ2 x2 ... bˆk xk , so yˆ bˆ1x1 bˆ2x2 ... bˆk xk ,
How do we think about how well our sample regression line fits our sample data?
Can compute the fraction of the total sum of squares (SST) that is explained by the model, call this the R-squared of regression
The STATA command
Use [path]wage1.dta (insheet using [path]wage1.raw/wage1.txt) Reg wage educ exper tenure Reg lwage educ exper tenure
7
A “Partialling Out” Interpretation
yˆ bˆ0 bˆ1x1 bˆ2x2 L bˆk xk
The above estimated equation is called the OLS regression line or the sample regression function (SRF)
the above equation is the estimated equation, is
Now, we first regress educ on exper and tenure to patial out the exper and tenure’s effects. Then we regress wage on the residuals of educ on exper and tenure. Whether we get the same result.?
The estimated equations without tenure
wage=3.3910.644educ+0.070exper log(wage)=0.2170.098educ+0.0103exper
wage=0.9050.541educ log(wage)=0.5840.083educ
so holding x2,...,xk fixed implies that
yˆ bˆ1x1, that is each b has
a ceteris paribus interpretation
6
An Example (Wooldridge, p76)
The determination of wage (dollars per hour), wage:
educ=13.575-0.0738exper+0.048tenure wage=5.896+0.599resid log(wage)=1.623+0.092resid
We can see that the coefficient of resid is the same of the coefficien of the variable educ in the first estimated equation. And the same to log(wage) in the second equation.
wage=b0b1educ+b2exper+b3tenure+u log(wage)=b0b1educ+b2exper+b3tenure+u
The estimated equation as below:
wage=2.8730.599educ+0.022exper+0.169tenure log(wage)=0.2840.092educ+0.0041exper+0.022tenure
R2 = SSE/SST = 1 – SSR/SST
14
Goodness-of-Fit (continued)
We can also think of R2 as being equal to
the squaredcorrelation coefficient between
the actual yi and the values yˆi
8
“Partialling Out” continued
Previous equation implies that regressing y on x1 and x2 gives same effect of x1 as regressing y on residuals from a regression of x1 on x2
assumption, so now assume that E(u|x1,x2, …,xk) = 0 Still minimizing the sum of squared residuals,
so have k+1 first order conditions
3
Obtaining OLS Estimates
12
Goodness-of-Fit
We can thinkof each observation as being made up of an explained part, and an unexplained part, yi yˆi uˆi Wethen define the following :
10
Simple vs Multiple Reg Estimate
Compare thesimple regression ~y b~0 b~1x1 with themultiple regression yˆ bˆ0 bˆ1x1 bˆ2x2 Generally, b~1 bˆ1 unless : bˆ2 0 (i.e. no partial effectof x2 ) OR
fIrnomthethgeefniersrtalocrdaeser cwointhdiktioinnd, ewpeencdanengtevtakriab1les,
lwtiynˆhneeerasyebreiˆf0eeoqkrbeuˆeb,0aˆs1mttxiio1mibnnˆ1aisxLmtiie1niszkbeLˆb0ˆtk,h1xbeˆkb1uˆs,nkKuxkmink,oboˆwkf ns0inqsubtˆha0re,ebedˆ1q,ruKeistii,dobˆunka:ls:
x y inn1
ii11 i1 i
yi
bˆ0bˆ0
bˆ1bxˆi11xi1 L L
bˆkbxˆkikxik2
0
n xi2 yi bˆ0 bˆ1xi1 L bˆk xik 0
i 1
M
n 0.
i 1
4
Obtaining OLS Estimates, cont.
9
The wage determinations
The estimated equation as below:
wage=2.8730.599educ+0.022exper+0.169tenure log(wage)=0.2840.092educ+0.0041exper+0.022tenure
not the really equation. The really equation is
population regression line which we don’t know.
