解一元一次方程的算法 (1)
5.2 解一元一次方程第4课时 利用去分母解一元一次方程(共31张PPT)【人教2024版七上数学】

答:该单位参加旅游的职工有360人.
5.清人徐子云《算法大成》中有一首诗: 巍巍古寺在山林,不知寺中几多僧. 三百六十四只碗,众僧刚好都用尽. 三人共食一碗饭,四人共吃一碗羹. 请问先生名算者,算来寺内几多增?
诗的意思: 3个僧人吃一碗饭,四个僧人吃一碗羹,刚好用了 364只碗,请问寺内有多少僧人?
移项 合并同类项
移项法则
合并同类项法 则
两边同除以未知 等式性质2 数的系数
移项要变号 系数相加,不漏项 不要把分子、分母搞颠倒
3
6
2
A.x=1 B.x=2 C.x=4
D.x=6
2
解方程
5 6
6 5
x-1
=2.
下面几种解法中,较简便
的是( C )
A.先两边同乘6
B.先两边同乘5
C.先去括号再移项
D.括号内先通分
3. 解下列方程:
(1) x 3 3x 4; 5 15
(2) 5y 4 y 1 2 5y 5 .
解:设寺内有x个僧人,依题意得 1 x 1 x 364. 34
解得x=624.
答:寺内有624个僧人.
课堂小结
✓ 归纳总结 ✓ 构建脉络
课堂小结
步骤 去分母
根据
等式性质2
注意事项
1.不要漏乘不含分母的项 2. 分子是多项式应添括号
去括号
分配率 去括号法则
1.不要漏乘括号中的每一项 2.括号前是“—”号,要变号
去括号,得
18x+3x-3 =18-4x +2. 移项,得
18x+3x+4x =18 +2+3. 合并同类项,得
25x = 23. 系数化为1,得
一元一次方程-中考数学一轮复习考点专题复习大全(全国通用)

考向09 一元一次方程【考点梳理】1.一元一次方程的一般式:ax+b=0(x 是未知数,a 、b 是常数,且a ≠0).2.一元一次方程解法的一般步骤:整理方程 …… 去分母 …… 去括号 …… 移项 …… 合并同类项 …… 系数化为1 …… 得到方程的解.3.列方程解应用题的常用公式:(1)行程问题: 距离=速度·时间 时间距离速度= 速度距离时间=; (2)工程问题: 工作量=工效·工时 工时工作量工效= 工效工作量工时=; (3)比率问题: 部分=全体·比率 全体部分比率= 比率部分全体=; (4)顺逆流问题: 顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;(5)商品价格问题: 售价=定价·折·101 ,利润=售价-成本, %100⨯-=成本成本售价利润率; (6)周长、面积、体积问题:C 圆=2πR ,S 圆=πR 2,C 长方形=2(a+b),S 长方形=ab , C 正方形=4a ,S 正方形=a 2,S 环形=π(R 2-r 2),V 长方体=abc ,V 正方体=a 3,V 圆柱=πR 2h ,V 圆锥=31πR 2h.【题型探究】题型一:一元一次方程定义1.(2021·全国·九年级专题练习)关于x 的一元一次方程2224a x m --+=的解为1x =,则a m +的值为( )A .9B .8C .7D .52.(2022·广东·九年级专题练习)已知关于x 的方程()()22426k x k x k -+-=+是一元一次方程,则方程的解为( )A .-2B .2C .-6D .-13.(2019·福建漳州·校联考中考模拟)若x =2是关于x 的一元一次方程ax -2=b 的解,则3b -6a +2的值是( ).A .-8B .-4C .8D .4题型二:一元一次方程方程的解法4.(2022·贵州黔西·统考中考真题)小明解方程12123x x +--=的步骤如下:解:方程两边同乘6,得()()31122x x +-=-①去括号,得33122x x +-=-②移项,得32231x x -=--+③合并同类项,得4x =-④以上解题步骤中,开始出错的一步是( )A .①B .②C .③D .④5.(2023·河北·九年级专题练习)解方程221123x x --=-,嘉琪写出了以下过程:①去分母,得3(2)62(21)x x -=--;②去括号,得36642x x -=--;③移项、合并同类项,得710x =;④系数化为1,得107x =,开始出错的一步是( ) A .① B .② C .③ D .④6.(2022·重庆南岸·统考一模)解一元一次方程()()11151753x x +=--的过程如下. 解:去分母,得()()3151557x x +=--. ①去括号,得3451557x x +=-+. ②移项、合并同类项,得823x =-. ③化未知数系数为1,得823x =-. ④ 以上步骤中,开始出错的一步是( )A .①B .②C .③D .④题型三:配套 工程和销售问题7.(2022·广西南宁·南宁二中校考三模)用200张彩纸制作圆柱,每张彩纸可制作圆柱侧面20个或底面60个,一个圆柱侧面与两个底面组成一个圆柱.为使制作的圆柱侧面和底面正好配套,设把x 张彩纸制作圆柱侧面,则方程可列为( )A .6020(200)x x =-B .20260(200)x x =⨯-C .26020(200)x x ⨯=-D .22060(200)x x ⨯=-8.(2021·新疆乌鲁木齐·乌鲁木齐市第六十八中学校考三模)某工程甲单独完成要25天,乙单独完成要20天.若乙先单独干10天,剩下的由甲单独完成,设甲、乙一共用x 天完成,则可列方程为( )A .101012025x ++=B .101012520x ++=C .101012520x -+=D .101012520x -+= 9.(2022·贵州遵义·统考二模)如图为某披萨店的公告.某会员购买一个榴莲披萨付款83.6元,则一个榴莲披萨调价前的原价为()A .72.2元B .78元C .80元D .96.8元题型四:比赛 积分和数字问题10.(2022·贵州铜仁·统考中考真题)为了增强学生的安全防范意识,某校初三(1)班班委举行了一次安全知识抢答赛,抢答题一共20个,记分规则如下:每答对一个得5分,每答错或不答一个扣1分.小红一共得70分,则小红答对的个数为( )A .14B .15C .16D .1711.(2022·福建·模拟预测)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房住;如果每一间客房住9人,那么就空出一间房.设该店有x 间客房,则所列方程为( )A .7x-7=9x+9B .7x +9=9x+7C .7x +7=9x ﹣9D .7x-7=9x ﹣912.(2022·湖南长沙·模拟预测)《九章算术》一书中记载了一道题:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、物价各几何?题意是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.则买鸡的人数和鸡的价钱各是( )A .8人,61文B .9人,70文C .10人,79文D .11人,110文题型五:几何 和差倍和水电问题13.(2022·江苏南通·统考模拟预测)如图,矩形ABCD 中,8cm AB =,4cm BC =,动点E 和F 同时从点A 出发,点E 以每秒2cm 的速度沿A D →的方向运动,到达点D 时停止,点F 以每秒4cm 的速度沿A B C D →→→的方向运动,到达点D 时停止.设点F 运动x (秒)时,AEF △的面积为()2cm y ,则y 关于x 的函数的图象大致为( )A .B .C .D .14.(2022·福建南平·统考模拟预测)中国一本著名数学文献《九章算术》,书中出现了一个“共买鸡问题”,原文是:今有共买鸡,人出九,盈十一;人出六,不足十六,问人数、物价各几何?其题意是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.问买鸡的人数、鸡的价钱各是多少?设买鸡的人数为x ,则下面符合题意的方程是( )A .9+11616x x =-B .9+61611x x =+C .9+11616x x =+D .911616x x =+-15.(2018·四川绵阳·校联考中考模拟)滴滴快车是一种便捷的出行工具,计价规则如下表: 计费项目里程费 时长费 远途费 单价 1.8元/公里 0.3元/分钟 0.8元/公里注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差( )A .10分钟B .13分钟C .15分钟D .19分钟题型六:行程 比例和行程问题16.(2022·重庆璧山·统考一模)小明和爸爸从家里出发,沿同一路线到图书馆,小明匀速跑步先出发,2分钟后,爸爸骑自行车出发,匀速骑行一段时间后,在途中商店买水花费了5分钟,从商店出来后,爸爸的骑车速度比他之前的骑车速度增加60米/分钟,结果与小明同时到达图书馆.小明和爸爸两人离开家的路程s (米)与小明出发的时间t (分钟)之间的函数图像如图所示,则下列说法错误的是( )A .17a =B .小明的速度是150米/分钟C .爸爸从家到商店的速度是200米/分钟D .9t =时,爸爸追上小明17.(2023·福建泉州·泉州五中校考三模)明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两,如果每人分九两,则还差半斤(注: 明代时 1 斤=16 两,故有“半斤八两”这个成语).设总共有 x 个人,根据题意所列方程正确的是( )A .7x - 4 = 9x +8B .7x +4 = 9x -8C .4879x x +-=D .4879x x -+= 18.(2019·湖北荆州·统考一模)在如图所示的2018年1月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和可能是( )A .23B .51C .65D .75题型七:一元一次方程的综合19.(2019·重庆·统考中考真题)若关于x 的一元一次不等式组11(42)423122x a x x ⎧--≤⎪⎪⎨-⎪<+⎪⎩的解集是x ≤a ,且关于y 的分式方程24111y a y y y ---=--有非负整数解,则符合条件的所有整数a 的和为( )A .0B .1C .4D .6 20.(2020·江苏盐城·统考中考真题)把19-这9个数填入33⨯方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图①),是世界上最早的“幻方”.图②是仅可以看到部分数值的“九宫格”,则其中x 的值为:( )A .1B .3C .4D .621.(2022·湖北宜昌·统考中考真题)某造纸厂为节约木材,实现企业绿色低碳发展,通过技术改造升级,使再生纸项目的生产规模不断扩大.该厂3,4月份共生产再生纸800吨,其中4月份再生纸产量是3月份的2倍少100吨.(1)求4月份再生纸的产量;(2)若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加%m .5月份每吨再生纸的利润比上月增加%2m ,则5月份再生纸项目月利润达到66万元.求m 的值; (3)若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了25%.求6月份每吨再生纸的利润是多少元?【必刷基础】一、 单选题22.(2022·重庆沙坪坝·统考一模)若关于x 的方程25x a +=的解是2x =,则a 的值为( )A .9-B .9C .1-D .123.(2022·辽宁营口·统考中考真题)我国元朝朱世杰所著的《算学启蒙》一书是中国较早的数学著作之一,书中记载一道问题:“良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天可以追上慢马?若设快马x 天可以追上慢马,则下列方程正确的是( )A .24015015012x x +=⨯B .24015024012x x -=⨯C .24015024012x x +=⨯D .24015015012x x -=⨯24.(2022·江苏苏州·统考中考真题)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术,其中方程术是其最高的代数成就.《九章算术》中有这样一个问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)”设走路快的人要走x步才能追上,根据题意可列出的方程是()A.60100100x x=-B.60100100x x=+C.10010060x x=+D.10010060x x=-25.(2022·云南昆明·云南师范大学实验中学校考三模)若整数a使关于x的方程21x a+=的解为负数,且使关于的不等式组()122113x axx⎧-->⎪⎪⎨+⎪-≥⎪⎩无解,则所有满足条件的整数a的值之和是()A.6 B.7 C.9 D.1026.(2022·湖南长沙·长沙市湘郡培粹实验中学校考三模)周末晚会上,师生共有20人参加跳舞,其中方老师和7个学生跳舞,张老师和8个学生跳舞……依次下去,一直到何老师,他和参加跳舞的所有学生跳过舞,这个晚会上参加跳舞的学生人数是()A.15 B.14 C.13 D.1227.(2022·山东济宁·济宁市第十三中学校考一模)由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只;(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本).28.(2022·宁夏吴忠·校考一模)2020年,一场突如其来的疫情席卷全国,给人民生命、财产造成巨大损失,但英勇的中国人民不畏艰难,众志成城,最终取得了抗击疫情的阶段性胜利,疫情防控初期,某药店库存医用外科口罩10000副,进价2元/副,由于市民疯狂抢购,量价齐升,5天销售一空,通过5天的销售情况进行统计,得到数据如下:(1)求该药店这5天销售口罩的平均利润.(2)通过对上面表格分析,发现销售量y (副)与单价x (元/副)存在函数关系,求y 与x 的函数关系式.(3)该药店购进第二批口罩20000副,进价2.5元/副,虽然畅销,但被物价部门限价,每副口罩销售价为m 元,销售一半后,该药店响应国家号召,将剩余口罩全部捐献给了抗疫定点医院,若在两批口罩销售中,药店不亏也不赚,则m 的值是多少?【必刷培优】一、单选题29.(2022·云南德宏·统考模拟预测)若关于x 的方程()6324x k -=-的解为非负整数,且关于x 的不等式组()23432x x k x x ⎧-+≤-⎪⎨-≤⎪⎩无解,则符合条件的整数k 的值可以为( ) A .0 B .3 C .4 D .630.(2023·全国·九年级专题练习)解方程2233522x x x x x--+=--,以下去分母正确的是( ) A .22335x x x ---=B .22335x x x --+=C .()223352x x x x ---=-D .()223352x x x x --+=-31.(2022·广西钦州·统考模拟预测)《九章算术》是我国古代第一部数学专著,此专著中有这样一道题:今有人共买鹅,人出九,盈十一;人出六,不足十六,人数、鹅价几何?这道题的意思是:今有若干人共买一只鹅,若每人出9文钱,则多出11文钱;若每人出6文钱,则相差16文钱,求买鹅的人数和这只鹅的价格.设买鹅的人数有x 人,可列方程为( )A .911616x x -=-B .911616x x -=+C .911616x x +=+D .911616x x +=-32.(2022·河北·统考二模)数学实践活动课上,陈老师准备了一张边长为a 和两张边长为()b a b >的正方形纸片如图1、图2所示,将它们无重叠的摆放在矩形ABCD 内,矩形未被覆盖的部分用阴影表示,设左下阴影矩形的周长为1l ,右上阴影矩形的周长为2l .陈老师说,如果126l l -=,求a 或b 的值.下面是四位同学得出的结果,其中正确的是( )A .甲:6a =,4b =B .乙:6a =,b 的值不确定C .丙:a 的值不确定,3b =D .丁:a ,b 的值都不确二、填空题33.(2022·山东济南·山东师范大学第二附属中学校考模拟预测)已知224x x +=,且224120ax ax +-=,则22a a +的值为______.34.(2022·江苏扬州·校考二模)我国古代名著《九章算术》中有一问题:“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”假设经过x 天相逢,则可列方程为_____.35.(2022·重庆大渡口·重庆市第三十七中学校校考二模)青团是清明节的一道极具特色的美食,据调查,广受消费者喜欢的口味分别是:红豆青团、肉松青团、水果青团,故批发商大量采购红豆青团、肉松青团、水果青团,为了获得最大利润,批发商需要统计数据,更好地进货.3月份批发商统计销量后发现,红豆青团、肉松青团、水果青团销量之比为2:3:4,随着市场的扩大,预计4月份青团总销量将在3月份基础上有所增加,其中水果青团增加的销量占总增加的销量的15,则水果青团销量将达到4月份总销量的13,为使红豆青团、肉松青团4月份的销量相等,则4月份肉松青团还需要增加的销量与4月份总销量之比为_____________.36.(2022·四川攀枝花·统考中考真题)如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程1103x -=是关于x 的不等式组2220x n n x -≤⎧⎨-<⎩的关联方程,则n 的取值范围是 ___________.37.(2022·北京西城·校考模拟预测)我校学生会正在策划一次儿童福利院的慰问活动.为了筹集到600元活动资金,学生会计划定制一批穿校服的毛绒小熊和带有校徽图案的钥匙扣,表格中有这两种商品的进价和售价.另外,若将一个小熊和一个钥匙扣组成一份套装出售,则将售价打九折.为了更好的制定进货方案,学生会利用抽样调查的方式统计了校内学生对商品购买意向的百分比情况(见表格),若按照这个百分比情况定制商品,至少定制小熊______个和钥匙扣______个,才能筹集到600元资金(即获得600元利润).38.(2022·广西·统考中考真题)阅读材料:整体代值是数学中常用的方法.例如“已知32a b -=,求代数式621a b --的值.”可以这样解:()6212312213a b a b --=--=⨯-=.根据阅读材料,解决问题:若2x =是关于x 的一元一次方程3ax b +=的解,则代数式2244421a ab b a b ++++-的值是________.三、解答题39.(2022·福建泉州·校考三模)国庆黄金周,某商场促销方案规定:商场内所有商品按标价的80%出售,同时当顾客在商场内一次性消费满一定金额后,按下表获得相应的返还金额.注:500~1000表示消费金额大于500元且小于或等于1000元,其他类同.根据上述促销方案,顾客在该商场购物可以获得双重优惠.例如,若购买标价为1000元的商品,则消费金额为800元,获得的优惠额为1000(180%)60260⨯-+=(元).(1)购买一件标价为1600元的商品,顾客获得的优惠额是多少?(2)若顾客在该商场购买一件标价x 元(1250)x >的商品,那么该顾客获得的优惠额为多少?(用含有x 的代数式表示)(3)若顾客在该商场第一次购买一件标价x 元(1250)x >的商品后,第二次又购买了一件标价为500元的商品,两件商品的优惠额共为650元,则这名顾客第一次购买商品的标价为______元.40.(2022·河北邯郸·校考三模)如图,数轴上a 、b 、c 三个数所对应的点分别为A 、B 、C ,已知b 是最小的正整数,且a 、c 满足2(6)20c a -++=.(1)①直接写出数a、c的值,;②求代数式222+-的值;a c ac(2)若将数轴折叠,使得点A与点C重合,求与点B重合的点表示的数;(3)请在数轴上确定一点D,使得AD=2BD,则D表示的数是.41.(2022·江苏镇江·统考中考真题)某地交警在一个路口对某个时段来往的车辆的车速进行监测,统计数据如下表:车速(km/h)40 41 42 43 44 45频数 6 8 15 a 3 2其中车速为40、43(单位:km/h)的车辆数分别占监测的车辆总数的12%、32%.(1)求出表格中a的值;(2)如果一辆汽车行驶的车速不超过40km/h的10%,就认定这辆车是安全行驶.若一年内在该时段通过此路口的车辆有20000辆,试估计其中安全行驶的车辆数.42.(2022·广西玉林·统考二模)疫情期间,消毒液、口罩成为了咱们的生活必需品.淘宝某医用器械药房推出2种口罩进行销售,医用一次性口罩2.5元/个,医用外科口翠3元/个.(1)某地某学校购进两种口罩25000个,共花费70000元,请问学校购买医用外科口罩多少个?(2)因为4月份疫情逐渐过去,但口罩的市场需求盘依旧旺盛,该药房决定用320000元再次购进一批口罩进行销售.医用一次性口罩100个/盒,每盒120元,医用外科口罩50个/盒,每盒100元.要求购进的医用外科口罩个数不超过医用一次性口罩的2.6倍,但不低于医用一次性口罩的1.9倍.若这批口罩全部销售完毕,为使获利最大,该药房应如何进货?最大获利为多少元?43.(2021·贵州遵义·校考模拟预测)甲、乙两地间的直线公路长为400千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发1小时,途中轿车出现了故障,停下维修,货车仍继续行驶.1小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离y(千米)与轿车所用的时间x(小时)的关系如图所示,请结合图象解答下列问题:(1)货车的速度是______千米/小时;轿车的速度是______千米/小时.(2)求轿车距其出发地的距离y(千米)与所用时间x(小时)之间的函数关系式,并写出自变量x的取值范围;(3)求货车出发多长时间两车相距90千米.参考答案:1.C【分析】先根据一元一次方程的定义可得出a 的值,再根据一元一次方程的解定义可求出m 的值,然后代入求值即可. 【详解】方程2224a x m --+=是关于x 的一元一次方程,21a ∴-=,解得3a =,∴方程为224x m -+=,又1x =是方程224x m -+=的解,2124m ∴⨯-+=,解得4m =,则347a m +=+=,故选:C .【点睛】本题考查了一元一次方程的定义、以及解定义,掌握理解一元一次方程的定义是解题关键.2.D【分析】利用一元一次方程的定义确定出k 的值,进而求出k 的值即可.【详解】解:∵方程()()22426k x k x k -+-=+是关于x 的一元一次方程,∴24020k k ⎧-=⎨-≠⎩, 解得:k =-2,方程为-4x =-2+6,解得:x =-1,故选:D .【点睛】此题考查了解一元一次方程,以及一元一次方程的定义,熟练掌握一元一次方程的定义是解本题的关键.3.B【分析】根据已知条件与两个方程的关系,可知2a- 2= b ,即可求出3b-6a 的值,整体代入求值即可.【详解】把x=2代入ax -2=b ,得2a- 2= b .所以3b-6a=-6.所以,3b -6a +2=-6+2=-4.故选B .【点睛】本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.4.A【分析】按照解一元一次方程的一般步骤进行检查,即可得出答案.【详解】解:方程两边同乘6,得()()31622x x +-=-①∴开始出错的一步是①,故选:A .【点睛】本题考查了解一元一次方程,熟练掌握解一元一次方程的一般步骤以及注意事项是解决问题的关键.5.B【分析】解决此题应先去括号,再移项,移项时要注意符号的变化.【详解】在第②步,去括号得36642x x -=--,等式右边去括号时忘记变号,故选B .【点睛】解一元一次方程的一般步骤是去分母、去括号、移项、合并同类项和系数化为1;在移项时要注意符号的变化,此题是形式较简单的一元一次方程.6.B【分析】检查解一元一次方程的解题过程,根据去分母,去括号,移项,合并同类项,系数华为1,找出出错的步骤,以及出错的原因.【详解】第②步出现错误,3451557x x +=-+. ②错误的原因是去括号时出现错误,应该改为:34515535x x +=-+.故选:B【点睛】此题考查了解一元一次方程,解方程去括号时,要注意不要漏乘括号里的每一项.7.D【分析】根据题意列出一元一次方程求解即可.【详解】解:设把x 张彩纸制作圆柱侧面,则有(200-x )张纸作圆柱底面,根据题意可得:22060(200)x x ⨯=-故选:D .【点睛】题目主要考查一元一次方程的应用,理解题意,列出方程是解题关键.8.D【分析】设甲、乙一共用x 天完成,根据题意,列出方程,即可求解.【详解】解:设甲、乙一共用x 天完成,根据题意得:101012520x -+=. 故选:D【点睛】本题主要考查了一元一次方程的应用,明确题意,准确得到等量关系是解题的关键.9.C【分析】根据原价和售价的关系,列方程计算即可.【详解】解:设原价为x 元,由题意,得(1+10%)×95%·x =83.6,解得:x =80.故选:C .【点睛】此题考查了一元一次方程的应用—打折销售,解题的关键是确定等量关系列方程求解.10.B【分析】设小红答对的个数为x 个,根据抢答题一共20个,记分规则如下:每答对一个得5分,每答错或不答一个扣1分,列出方程求解即可.【详解】解:设小红答对的个数为x 个,由题意得()52070x x --=,解得15x =,故选B .【点睛】本题主要考查了一元一次方程的应用,正确理解题意是列出方程求解是解题的关键.11.C【分析】根据题意设出房间数,进而表示出总人数得出等式方程求出即可.【详解】设该店有x 间客房,则7x+7=9x-9,故选:C.【点睛】本题考查了一元一次方程的应用,熟练掌握一元一次方程的解题方法是解题的关键.12.B【分析】买鸡的人数为x 人,根据“如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.”列出方程,即可求解.【详解】解:买鸡的人数为x 人,根据题意得:911616x x -=+ ,解得:9x = ,∴鸡的价钱为911991170x -=⨯-= ,答:买鸡的人数为9人,鸡的价钱为70文.故选:B【点睛】本题主要考查了一元一次方程的应用,明确题意,准确得到等量关系是解题的关键.13.B【分析】由点的运动,可知点E 从点A 运动到点D ,用时2s ,点F 从点A 到点B ,用时2s ,从点B 运动到点C ,用时1s,从点C运动到点D,用时2s,y与x的函数图象分三段:①当0≤x≤2时,②当2<x≤3时,③当3<x≤5时,根据每种情况求出△AEF的面积.【详解】解:点E从点A运动到点D,用时2s,点F从点A到点B,用时2s,从点B运动到点C,用时1s,从点C 运动到点D,用时2s,∴y与x的函数图象分三段:①当0≤x≤2时,AE=2x,AF=4x,•2x•4x=4x2,∴y=12这一段函数图象为抛物线,且开口向上,由此可排除选项A和选项D;②当2<x≤3时,点F在线段BC上,AE=4,×4×8=16,此时y=12③当3<x≤5时,×4×(4+8+4−4x)=32−8x,由此可排除选项C.y=12故选:B.【点睛】本题考查了动点问题的函数图象,二次函数图象,三角形的面积,矩形的性质,根据题意理清动点的时间分段,并根据三角形的面积公式列出函数关系式是解题的关键,难度不大.14.D【分析】设买鸡的人数为x,根据鸡的价格不变,建立等量关系,列出相关方程即可.【详解】解:设买鸡的人数为x,则由题意有:-,=+x x911616故选:D.【点睛】本题考查了一元一次方程的实际应用,准确找到等量关系是解题的关键.15.D【分析】设小王的行车时间为x分钟,小张的行车时间为y分钟,根据计价规则计算出小王的车费和小张的车费,建立方程求解.【详解】设小王的行车时间为x分钟,小张的行车时间为y分钟,依题可得:1.8×6+0.3x=1.8×8.5+0.3y+0.8×(8.5-7),10.8+0.3x=16.5+0.3y,0.3(x-y)=5.7,x-y=19,故答案为D.【点睛】本题考查列方程解应用题,读懂表格中的计价规则是解题的关键.16.D【分析】利用到商店时间+停留时间可确定A ,利用爸爸所用时间+2分与路程3300米可求小明速度可确定B ,利用设爸爸开始时车速为x 米/分,列方程求解即可确定C ,利用小明和爸爸行走路程一样,设t 分爸爸追上小明,列方程求解可知D .【详解】解:A .12517a +==,故A 正确,不合题意;B .小明的速度为330022150÷=米/分,故B 正确,不合题意;C .设爸爸开始时车速为x 米/分,()()1225603300x x -++=,解得200x =米/分,故爸爸从家到商店的速度为200米/分钟正确,不合题意;D .设y 分爸爸追上小明,()1502200y y +=,解得:6y =,故9t =时,爸爸追上小明,选项不正确,符合题意故选:D .【点睛】本题考查行程问题的函数图像,会看图像,能从中获取信息,掌握速度,时间与路程三者关系,把握基准时间是解题关键.17.B【分析】直接根据题中等量关系列方程即可.【详解】解:根据题意,7x +4 = 9x -8,故选:B .【点睛】本题考查一元一次方程的应用,理解题意,正确列出方程是解答的关键.18.B【分析】一竖列上相邻的三个数的关系是:上面的数总是比下面的数小7.可设中间的数是x ,则上面的数是x-7,下面的数是x+7.则这三个数的和是3x ,因而这三个数的和一定是3的倍数.【详解】设中间的数是x ,则上面的数是x-7,下面的数是x+7,则这三个数的和是(x-7)+x+(x+7)=3x ,因而这三个数的和一定是3的倍数,则,这三个数的和都为3的倍数,观察只有51与75是3的倍数,但75÷3=25,25+7=32不符合题意,所以这三个数的和可能为51,故选B .。
解一元一次方程二去括号与去分母

变式训练 解下列方程:
解:去分母(方程两边乘6),得 (x-1) -2(2x+1) = 6.
去括号,得 x-1-4x-2 = 6. 移项,得 x-4x = 6+2+1. 合并同类项,得 -3x = 9. 系数化为1,得 x = -3.
解:整理方程,得
去分母(方程两边乘30),得 6 (4x+9) -10(3+2x) = 15(x-5).
做一做
清人徐子云《算法大成》中有一首诗: 巍巍古寺在山林,不知寺中几多僧. 三百六十四只碗,众僧刚好都用尽. 三人共食一碗饭,四人共吃一碗羹. 请问先生名算者,算来寺内几多增?
诗的意思: 3个僧人吃一碗饭,四个僧人吃一碗羹,刚好用了 364只碗,请问寺内有多少僧人?
解:设寺内有x个僧人,依题意得
移项,得
2x+x = 8+2 -2+4.
合并同类项,得 3x = 12.
系数化为1,得 x = 12.
解:去分母(方程两边乘6),得 18x+3(x-1) =18-2 (2x -1).
去括号,得 18x+3x-3 =18-4x +2.
移项,得
18x+3x+4x =18 +2+3. 合并同类项,得
25x = 23. 系数化为1,得
讲授新课
一 解含分母的一元一次方程
合作探究
解方程:
想一想 1. 若使方程的系数变成整系数方程, 方程两边应该同乘以什么数?
2. 去分母时要注意什么问题?
去分母(方程两边同乘各分母的最小公倍数)
去括号 移项 合并同类项
小心漏乘, 记得添括号!
系数化为1
5.2 解一元一次方程课时1-合并同类项 课件(共30张PPT)

420
书.
新课讲解
练一练
2. 某工厂的产值连续增长,2022年是2021年的1.5倍,2023年是2022年的2倍,
这三年的总产值为550万元.2021年的产值是多少万元?
解:设2021年的产值是x万元,则2022年的产值是1.5x万元,2023年的
13=-x
D. 由 6x-2-4x+2=0,得 2x=0.
当堂小练
2
2. 将方程− = 1的系数化为1时,下列做法正确的是( C )
3
A.方程两边同时加上
1
3
C.方程两边同时除以−
B.方程两边同时减去
2
3
2
3
D.方程两边同时乘以−
2
3
当堂小练
3. 解下列方程:
(1)2x + 3x + 4x = 18
解:合并同类项,得
9x = 18
系数化为1,得
x=2
(2)13x - 15x + x = -3
解:合并同类项,得
-x = -3
系数化为1,得
x=3
当堂小练
3. 解下列方程:
(3)2.5y + 10y - 6y = 15 - 21.5
解:合并同类项,得
6.5y = - 6.5
系数化为1,得
y = -1
解:设前年购买计算机x台,则去年购买计算机2x台,今年购买计算机4x台.
列得方程得 + 2 + 4 = 140.
把含有x的项合并同类项,得 7 = 140.
系数化为1,得x=20.
答:前年这所学校购买了20台计算机.
4.2 解一元一次方程的算法

4.2 解一元一次方程的算法42 解一元一次方程的算法在数学的世界里,方程就像是一座桥梁,连接着已知和未知。
而一元一次方程,作为方程家族中的“基础成员”,其解法有着重要的地位和广泛的应用。
今天,咱们就来好好聊聊解一元一次方程的算法。
一元一次方程,形式通常是 ax + b = 0 (其中 a 和 b 是常数,且 a ≠ 0)。
解这样的方程,其实就是找出那个能让等式成立的未知数 x 的值。
先来说说最基本的思路。
我们的目标是把方程逐步变形,最终让 x 单独在等式的一边。
比如说,对于方程 3x + 5 = 14,第一步,我们要把常数项 5 移到等式右边,变成 3x = 14 5,这一步依据的是等式的基本性质:等式两边同时加上或减去同一个数,等式仍然成立。
接下来,计算 14 5 得到 3x = 9。
然后,为了让 x 单独出现,因为3 乘以 x 等于 9,所以 x 就等于 9 除以 3,即 x = 3。
这一步的依据是等式两边同时乘以或除以同一个非零数,等式仍然成立。
再举个例子,方程-2x + 7 = 1,先把 7 移到右边得到-2x = 1 7,也就是-2x =-6。
这时,两边同时除以-2,算出 x = 3。
有时候,方程可能会稍微复杂一点,比如有括号。
像 2(x 3) + 5 =11,这时候我们先运用乘法分配律把括号去掉,得到 2x 6 + 5 = 11,整理一下就是 2x 1 = 11。
然后把-1 移到右边变成 2x = 11 + 1,即2x = 12,最后得出 x = 6。
还有分母的情况,比如(x + 1) / 2 = 3。
这时候要先把分母去掉,两边同时乘以 2,得到 x + 1 = 6,接着算出 x = 5。
解一元一次方程的过程,其实就是不断运用等式的基本性质,进行变形和化简。
通过这些步骤,我们就能找到那个神秘的 x 的值。
在实际应用中,一元一次方程的解法用处可大了。
比如说,我们在计算物品的单价、行程问题中的速度、工程问题中的工作效率等等,都可能会用到一元一次方程。
一元一次方程的算法---配方法(1)

解法2:由平方根的定义,得:x 3 1 x 3 1, x1 4, x2 2
思考:把方程:(x-3)2=1化为X2-6x+8=0,怎样解 方程 X2-6x+8=0 呢?
• 【思路】把X2-6x+8=0化为(x-3)2=1,就可以 用直接开平方法求解了。
2x-5=0, (2).x2-4x+1=0
方法归纳:
例2代数式A=2m2+3m+7, B=m2+5m+5试比较代 数式A与B的大小。 • 解:A-B=(2m2+3m+7)-( m2+5m+5) • =2m2+3m+7- m2-5m-5 • = m2-2m+2 • =(m-1)2+1>0, • 所以,A>B
解: 第一步:把常数项移到等号右边:X2-6x=-8 第二步:两边同加上一次项系数一半的平方: X2-6x+32=-8+32, 第三步:配方,得:(x-3)2=1, 第四步:用直接开平方法求得:∴x-3=±1,x1=4,x2=2
配方法的定义
回顾:
(a±b)2 这个式子有什么特点呢? • a2±2ab+b2=_________ 把这个式子写成:a2±2ba+b2= (a±b)2,请 你观察这个式子有什么特点?
作业:P 19 3
同学们再见!
2 2 2
2
规律总结:
x
2
p px __ 2
2
p 2 x __ 2
尝试:用配方法解一元二次方程:
x 6x 4 0
一元一次方程的算法---直接开平方法(1)

解方程: 35 2 x
2
900
这种方法叫因式分解法,它的思路是:把一元二次 方程化为(ax+b)(cx+d)=0的形式,然后利用两个因式 相乘,至少有一个因式等于0,得到方程:ax+b=0, 或cx+d=0.
试试看
B
C
D
DBຫໍສະໝຸດ (3)方程有实数解。练习:
解方程:
小结:
1.2.1 因式分解法, 直接开平方法(1)
湖南省新邵县酿溪中学王军旗
学习目标
• 1 .知道解一元一次方程的基本思路是“降 次”----化二次为一次。 • 2. 能熟练地通过降次化一元二次方程为一 元一次方程。
复习:
x 1 2x 1 • 解方程: 1 1 2( x 3) 5 0, 2 2 3 解: 2 x 6 5 0, 1 去括号,得:
合并,得:2x 1 1 两边同除以2,得:x 2 2 两边同乘以6,得:3 x 1 2 2 x 1 6
去括号,得: 3x 3 4 x 2 6 合并得:7x 7, 两边同除以7, 得:x 1
解一元一次方程一般步骤:去分母,去括号,移项合 并同类项,未知数系数化“1”.
怎样解一元二次方程呢?
• 问题1.解方程: 35 2 x 900
2
回顾: 平方根 的平方根记作:____ 4 若x2 4, 那么x叫4的 _______,4
因此,x= 4 平方根 的平方根记作: 若x 2 a(a 0), 那么x叫a的 ______,a __ a x a 因此,x ____
解一元一次方程的算法去分母市公开课一等奖省优质课获奖课件
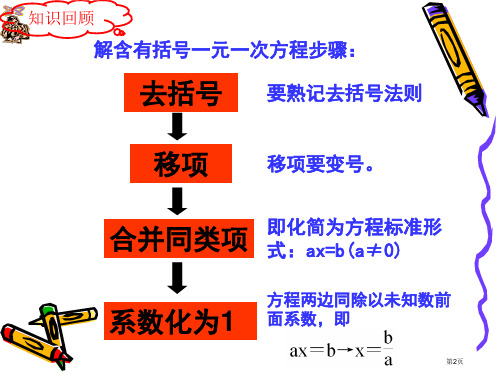
解含有括号一元一次方程步骤:
去括号 要熟记去括号法则
移项
移项要变号。
合并同类项
即化简为方程标准形 式:ax=b(a≠0)
系数化为1
方程两边同除以未知数前 面系数,即
第2页
动脑筋
一件工作,甲单独做需要15天完成,乙单独做需 要12天完成,现在甲先单独做1天,接着乙又单独 做4天,剩下工作由甲、乙两人合做,问合做多少 天能够完成全部工作任务? 等量关系 :
ax=b(a≠0)
系数化为1
方程两边同除以未知数前面系数,即
第5页
例
第6页
判断下面解题过程是否正确并更正:
解方程 2 x 2 x 3
5
2
解:去分母,得 2(2-x)=2-5(x+3)
去括号,得 4-2x=2-5x-15
移项,得
-2x+5x=2-15-4 合并同类项,得
3x=-17 系数化为1,得
甲完成工作量+乙完成工作量=工作总量. 设工作总量为1,剩下工作两人合做需x天完成,
第3页
解方程
第4页
解含有分母一元一次方程步骤:
去分母
方程两边同乘以各分母最小公倍数.注意不可漏乘 某一项,尤其是不含分母项,分子是代数式要加括 号。
去括号 要熟记去括号法则
移项
移项要变号。
合并同类项 即化简为方程标准形式:
x 17 3
第7页
解以下方程
(1) x x 1 1 x 2
2
3
(2) 5x 1 3x 1 2 x
4
2
3
第8页
解含有分母一元一次方程步骤:
去分母
方程两边同乘以各分母最小公倍数.注意不可漏乘 某一项,尤其是不含分母项,分子是代数式要加括 号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解一元一次方程的算法(1)
教学目标
1.在现实情景中深刻理解等式的性质,并能正确运用等式的性质.
2.熟练掌握移项法则,利用移项法则解一元一次方程.
教学重、难点
重点:等式的基本性质,移项法则
难点:对等式性质的理解和用移项的法则解方程.
教学过程
一激情引趣,导入新课
解方程 :2x-5=3x+6
你能说出你解这个方程每一步的依据吗?(一个加数等于和减去_______.)(导入新课:在小学我们学习了解方程,依据是加数与和的关系,因数与积的关系,还有没有别的依据呢?)
二合作交流,探究新知
1 等式的性质
问题1 (一)班的学生人数等于(二)班的学生人数,现在每班增加2名学生,那么(一)班与(二)班的学生人数还相等吗?如果每班减少了3名学生,那么两个班的学生人数还相等吗?
如果(-)班人数为a人,(二)班人数为b人,上面问题用含有a、b的式子怎样表示?
问题2如果甲筐米的重量=乙筐米的重量,现在把甲、乙两筐的米分别倒出一半,那么甲,乙两筐剩下的米的重量相等吗?
如果设甲筐米的重量为a,乙筐米的重量为b,上面问题用式子怎么表示?
从上面两个问题,可以发现等式有什么性质?
等式的性质 1 等式两边都______(或者减去)_________(或同一个式子)所得结果仍是____.
等式的性质2 等式两边都______(或者除以)_________(或同一个式子)(除数或者除式不能为0),所得结果仍是____.
你能用式子表达等式的性质吗?
2 尝试练习
做一做
(1)说一说下面等式变形的根据
①从x=y 得到 x+4=y+4, ②从a=b 得到 a+10=b+10
③从2x=3x-6得到 2x-3x=3x-6-3x ④从3x=9得到x=3, ⑤从1
4
2
x 得到
x=8
用等式的性质解方程:4x+4=3x+12
归纳:(1)什么叫移项?把方程的某一项改变____后从方程的一边移到另一边叫______
看看下面的变形是移项吗?
2x+5-3x+6=9,解 :2x-3x+5+6=9
练一练
用移项的方法解方程
1 2x=x+3
2 3x-1=40+2x
三 应用迁移,巩固提高
1 实际应用
例1 (我国古代数学问题)用绳子量井深,把绳子3折来量,井外余绳子4尺;把绳子4折来量,井外余绳子1尺,于是量井人说:“我知道这口井有多深了”。
你能算出这口井的深度吗?(做完后交流讨论)
2 游戏:请你任意圈出下面日历中竖列上三个相邻的数,求
出它们的和并告诉我,我就知道你圈出的是哪三个数。
四 课堂练习 ,巩固提高
1 如果单项式121-2
n a b +与213n m a b -是同类项,则n=___,m=____ 2 如果代数式3x-5与1-2x 的值互为相反数,那么x=____
3 若方程3x-5=4x+1与3m-5=4(m+x)-2m 的解相同,求()
200820m +的值
P 109 1,2
五 反思小结,拓展提高
这一节你有什么收获?
作业 p 118,1 、 2、3。
