第11章 存储论
第11章--存储论资料讲解

图所示
Q
假定每
足t时间的需求Rt,记订
t
货量为Q,Q=Rt,订购费
为C3,货物单价为K,则 订货费为C3+KRt;t时间
的平均订货费为 C3 KR t
模型一:不允许缺货,补充时间极短
专门研究这类有关存储问题的科学,构成 运筹学的一个分支,叫作存储论(inventory Theory),也称库存论。
本章所介绍的存储问题,模型并不复杂, 原理也容易掌握,应用这些原理可以从一 个方面改善企业的经营管理,以达到节约 资金,获得更多利润的目的。
1.2 存储论的基本概念
• 存贮系统 是一个由补充、存贮、需求三个环节 紧密构成的运行系统。
备货时间可能很长,也可能很短,可能是随机性 的,也可以是确定性的。
2. 补充(订货或生产)
存储论要解决的问题是:多少时间补充一次, 每次补充的数量应该是多少。决定多少时间 补充一次以及每次补充数量的策略称为存储 策略。
存储策略的优劣如何衡量呢?最直接的衡量 标准,是计算该策略所耗用的平均费用多少。 为此有必要对费用进行详细的分析。
第11章--存储论
第1节 存储论的基本概念 1.1 存储问题的提出
人们在生产和日常生活活动中往往将所需的物资、 用品和食物暂时地储存起来,以备将来使用或消 费。这种储存物品的现象是为了解决供应(生产) 与需求(消费)之间的不协调的一种措施,这种不 协调性一般表现为供应量与需求量和供应时期与 需求时期的不一致性上,出现供不应求或供过于 求。人们在供应与需求这两环节之间加入储存这 一环节,就能起到缓解供应与需求之间的不协调, 以此为研究对象,利用运筹学的方法去解决最合 理、最经济地储存问题。
费用
(3) 生产费,补充存储时,如果不需向外厂订 货,由本厂自行生产,这时仍需要支出两项费 用。一项是装配费用(准备结束费用),如组 织和调整生产线的费用,它是一次性的费用, 或称为固定费用,也用C3表示。另一项是与生 产产品的数量有关的费用如材料费、加工费等 (可变费用)。
存储论简介

2.清朝黄遵宪曾作诗曰:“钟声一及时,顷刻不少留。虽
有万钧柁,动如绕指柔。”这是在描写
()
A.电话
B.汽车
C.电报
D.火车
解析:从“万钧柁”“动如绕指柔”可推断为火车。
答案:D
[典题例析]
[例1] 上海世博会曾吸引了大批海内外人士利用各种
交通工具前往参观。然而在19世纪七十年代,江苏沿江
居民到上海,最有可能乘坐的交通工具是
3.发展 (1)原因: ①甲午战争以后列强激烈争夺在华铁路的 修。筑权 ②修路成为中国人 救的亡强图烈存愿望。 (2)成果:1909年 京建张成铁通路车;民国以后,各条商路修筑 权收归国有。 4.制约因素 政潮迭起,军阀混战,社会经济凋敝,铁路建设始终未入 正轨。
二、水运与航空
1.水运 (1)1872年,
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办
()
A.打破了外商对中国航运业的垄断
B.阻止了外国对中国的经济侵略
C.标志着中国近代化的起步
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵 制了列强的经济侵略,但是并未能阻止其侵略。故B、C、D 三项表述都有错误。 答案:A
TC(t)
KRt
C3
C1Rt 2
2
AC(t) KRt C3 C1Rt 2 / t tt 2
Q Q*
AC(t) KRt C3 C1Rt 2 / t tt 2
运筹学11-存储论

第11章存储论存储论也称库存论(Inventory theory),是研究物资最优存储策略及存储控制的理论。
物资的存储是工业生产和经济运转的必然现象。
任何工商企业,如果物资存储过多,不但积压流动资金,而且还占用仓储空间,增加保管费用。
如果存储的物资是过时的或陈旧的,会给企业带来巨大经济损失;反之,若物资存储过少企业就会失去销售机会而减少利润,或由于缺少原材料而被迫停产,或由于缺货需要临时增加人力和费用。
寻求合理的存储量、订货量和订货时间是存储论研究的重要内容。
§1 确定型经济订货批量模型本节假定在单位时间内(或称计划期)的需求量为已知常数,货物供应速率、订货费、存储费和缺货费已知,其订货策略是将单位时间分成n等分的时间区间t,在每个区间开始订购或生产相同的货物量,形成t循环储存策略。
在建立储存模型时定义了下列参数及其含义。
D:需求速率,单位时间内的需求量(Demand per unit time)。
P:生产速率或再补给速率(Production or replenishment rate)。
A:生产准备费用(Fixed ordering or setup cost)。
C:单位货物获得成本(Unit acquisition cost)。
H:单位时间内单位货物持有(储存)成本(Holding cost per unit per unit time)。
B:单位时间内单位货物的缺货费用(Shortage cost per unit short per unit time)。
π:单位货物的缺货费用,与时间无关(Shortage cost per unit short, independent of time)。
t:订货区间(Order interval),周期性订货的时间间隔期,也称为订货周期。
L:提前期(order lead time),从提出订货到所订货物且进入存储系统之间的时间间隔,也称为订货提前时间或拖后时间。
《运筹学》存储论、库存论培训课件

一、ABC库存管理技术 ABC库存管理技术是一种简单,有效的库存 管理技术,它通过对品种,规格极为繁多的 库存物资进行分类,使得企业管理人员把主 要注意力集中在 金额较大,最需要加以重视 的产品上,达到节约资金的目的。
A类物资的特点:品种较少,但因年耗用
量特别大,或价格高,因而年金额特别大, 占用资金很多。通常它占总品种的10%以下 ,年金额占全部库存物资的年金额的60%到 70%。A 类物资往往是企业生产过程中主要 原材料和燃料。它是节约企业库存资金的重 点和关键。
存贮论(存储论,库存论) (Inventory theory)
引言 经济订货批量的存贮模型 具有约束条件的存贮模型 具有价格折扣优惠的存贮模型 单时期的随机存贮模型
第一节 引言
在生产和生活中,人们经常进行着各种个样的存 贮活动,这是为了解决供应(或生产)与需求(或消 费)之间不协调或矛盾的一种手段.例如,一场战 斗在很短时间内可能消毫几十万发炮弹,而兵工 厂不可能在这么短的时间内生产那么多炮弹,这 就是供需矛盾,为了解决这一矛盾,只能将军火 工厂每天生产的炮弹储存到军火库内,以备战争 发生时的需要.
ⅲ(s,S)策略:设s为定货点(或保险存储量,安全 存储量,警戒点等).当存储余额为I,若I>s则不
对存储进行补充;若I s时,则对存储进行补
充,补充数量Q=S-I.补充后的数量达到最大存 储量S. ⅳ(t,s,S)策略:在很多情况下,实际存储量需要 通过盘点才能得知,若每隔一个固定时间t盘 点一次,得知存储量为I,再根据I是否超过定货 点s决定是否定货.
(t3
t4) .
t1 t2 t3 t4
t1 t2 t3 t4
因为S1 Pt1 Dt1 (P D)t1 Dt2
存储论的基本概念

存储论的基本概念库存管理的对象•库存管理的对象是很多的,广而言之,它可以包括:商业企业库存的商品、图书馆库存的图书、博物馆库存的展品等等。
库存管理的意义•企业作为一个微观的经济系统,它必然要以宏观的经济系统作为自己的依存环境,在供、产、销、储、运等等方面搞好内部与外部的协调和配合,才能获得良好的社会效益和经济效益,才能保持企业的生存与发展。
•企业库存管理的目标可概括为下列两点:–保证企业按科学的计划实现均衡生产,不要因缺少原材料或其他物资而停工停产。
–使库存管理的总费用达到最低。
存储论主要解决两个问题•当我们补充存储物资时,我们每次补充数量是多少?•我们应该间隔多长时间来补充我们的存储物资?存储论的基本概念•需求/输出需求只需要从货存中取出的货物数量,即存储系统的输出•进货/输入补充指需要存入仓库的货物数量,即存储系统的输入•定购费/订货费–进一次货所需要的固定费用–如果供应源来自企业外部,它就包括采购人员工资,差旅费,手续费等,如果供应源来自企业内部,例如工厂,它就包括更换模具、夹具、设备的调整及检验所需的费用。
定购费/订货费与所订货的数量无关。
存储论的基本概念•购进费–是指货物本身的价格、运费等,它与进货多少有关–应该注意的是,如果不考虑折扣,当需求量一定时,无论分几批进货,也无论每批的数量多少,总购进费是一个常数。
•存储费/库存费–有每单位商品的存储费和存储数量决定。
包括两个部分:(1)购买商品或生产商品占用的资金的利息。
若是银行贷款,即贷款利息;如是自有资金,也应考虑占用资金的机会成本,等同于银行的贷款利息。
(2)存储仓库的费用、保险费用、损耗费用、管理费用等。
存储论的基本概念•短缺费–它指的是当需求不能被满足时所引起的损失,如失去销售机会的损失,停工待料的损失,为补足拖欠订货所发生的额外成本支出,以及由于对顾客(如厂矿企业)延期交货而付给的罚金等。
存储模型的类型•确定性存储模型:模型中的数据皆为确定的数值。
存贮论(存储论,库存论)

1 2
(RT
Q1)2 R
C3)
Y 有两个变量T , Q ,利用多元函数求机制的方法求最小值。
C Q1
1 T
( C1Q1 R
RT Q1 R
C2 )
0
C T
1 T2
( Q12C1 2R
1 2
(RT
Q1)2 R
C2
C3 )
1 T
(C2 (RT
Q1))
0
得到:
T
2C3(C1 C2 ) C1C2 R
库存物资占用仓库面积而引起的一系列费 用,如货物的搬运费,仓库本身的固定资 产折旧,仓库维修费用,仓库及其设备的 租金,仓库的取暖、冷藏、照明等费用, 仓库管理人员等的工资、福利费用,仓库 的业务核算费用等。
库存管理中费用分类
2 订货费
它包括二项:一项是订货费用(固定费用 )如采购人员的各种工资、旅差费、订购 合同、邮电费用等 ,它与订购次数有关, 与订购数量无关。
2.过高的存贮量占用了流动资金使资金周转困 难,降低了资金利用率;
3.过量存贮降低了材料或产品的质量,甚至于 产品过时,变质损坏.
存贮量不足会有什么后果:
1.由于原料不足可能会造成停工,停产等重大 经济损失; 2.因缺货失去销售机会,失去顾客;
3.用频繁订货的方法以补充短缺的物资,这将 增加订购费用.
的最大缺货量,并设单位时间缺货费用为 C3 ,则T1 为存储量为正的时间
周期, T2 为存储量为负的时间周期(缺货周期)。所以在一个周期内的
订货量仍为 Q1 RT1
与 模 型 (2.1) 的 推 导 类 似 , 在 一 个 周 期 内 0 ~ T1 的 平 均 存 量 为
Q1 2
《运筹学》课程教学(自学)基本要求
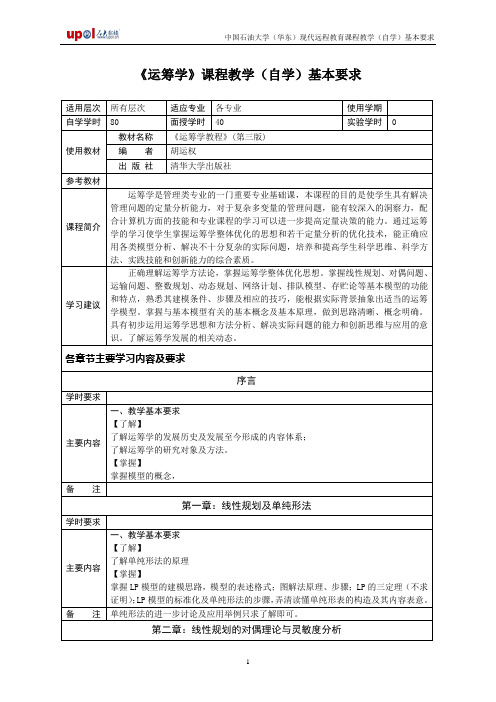
线性规划及其对偶问题的矩阵描述只求读懂
第三章:运输问题
学时要求
主要内容
一、教学基本要求
【了解】
了解如何应用表上作业法求解不平衡的运输问题
【掌握】
运输问题的数学模型;应用(最小元素法)表上作业法求解运输问题,掌握闭回路与位势法的异同,特别注意退化的运输问题的处理方式;
备注
有转运的运输问题不要求
第四章:目标规划
学习建议
正确理解运筹学方法论,掌握运筹学整体优化思想。掌握线性规划、对偶问题、运输问题、整数规划、动态规划、网络计划、排队模型、存贮论等基本模型的功能和特点,熟悉其建模条件、步骤及相应的技巧,能根据实际背景抽象出适当的运筹学模型。掌握与基本模型有关的基本概念及基本原理,做到思路清晰、概念明确。具有初步运用运筹学思想和方法分析、解决实际问题的能力和创新思维与应用的意识。了解运筹学发展的相关动态。
各章节主要学习内容及要求
序言
学时要求
主要内容
一、教学基本要求
【了解】
了解运筹学的发展历史及发展至今形成的内容体系;
了解运筹学的研究对象及方法。
【掌握】
掌握模型的概念,
备注
第一章:线性规划及单纯形法
学时要求
主要内容
一、教学基本要求
【了解】
了解单纯形法的原理
【掌握】
掌握LP模型的建模思路,模型的表述格式;图解法原理、步骤;LP的三定理(不求证明);LP模型的标准化及单纯形法的步骤,弄清读懂单纯形表的构造及其内容表意。
【掌握】
正确应用0—1变量、整数变量建立整数规划模型;
掌握分支定界技术、割平面法及匈牙利法求解整数规划的步骤,特别搞清分支定界技术及割平面法的原理。
运筹学教材习题答案详解

B1:2.0
3
需要量(套)
200
150
问怎样下料使得(1)用料最少;(2)余料最少.
【解】第一步:求下料方案,见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
(2)
【解】最优解X=(3/4,7/2);最优值Z=-45/4
(3)
【解】最优解X=(4,1);最优值Z=-10
(4)
【解】最优解X=(3/2,1/4);最优值Z=7/4
(5) 【解】最优解X=(3,0);最优值Z=3
(6)
【解】无界解。
(7)
【解】无可行解。
(8)
【解】最优解X=(2,4);最优值Z=13
【解】设x1、x2、x3分别为产品A、B、C的产量,则数学模型为
1.3建筑公司需要用6m长的塑钢材料制作A、B两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:
表1-23窗架所需材料规格及数量
型号A
型号B
每套窗架需要材料
长度(m)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Q
1 t 1 0 RTdT 2 Rt t
t
(此结果由图中利用几何知识易得出, 平均存储量为三角形高的二分之一) 单位时间内单位物品的存储费用为C1, t 时间内所需平均存储费用为 1 C 1 Rt
2
模型一:不允许缺货,补充时间极短
t 时间内总的平均费用为C(t)
C(t)= t时间内的平均订货费+ t时间内的平均存储费
例3
某医院药房每年需某种药品1600瓶,每次 订购费为5元,每瓶药品每年保管费0.1元, 试求每次应订多少瓶?
2.2 模型二:允许缺货(需补足缺货)、生产需 一定时间
假设条件除允许缺货生产需一定时间外, 其余条件皆与模型一相同,其存储变化如 图所示
A
A
2C3 C1 C2 P t* C1R C2 PR
例如
(1) 水电站在雨季到来之前,水库应蓄水多 少? (2) 工厂生产需用原料,如没有储存一定数 量的原料,会发生停工待料现象。 (3) 在商店里若存储商品数量不足,会发生 缺货现象,失去销售机会而减少利润;如 果存量过多,一时售不出去,会造成商品 积压,占用流动资金过多而且周转不开, 这样也会给商家造成经济损失。
模型一:不允许缺货,补充时间极短
由于Q*、t *皆与K无关,所以此后在费用函数中略 去K、R这项费用。如无特殊需要不再考虑此项费用, 略去后
C* C(t*) 2C1C3R (11.5)
模型一:不允许缺货,补充时间极短
例1:某商品的成本为5元,每天保管费为成 本的0.1%,每次订购费为10元。已知对该商 品的需求是100件/天,不允许缺货。假设该 商品的进货可以随时实现。问应该怎样组织 进货才最经济。 2C3 * t (11.2) C1R 2C3R Q* Rt* (11.3) C1
一个好的存储策略,既可以使总费用最小,又 可避免因缺货影响生产(或对顾客失去信用)
存储模型的两大类型:
一类叫作确定性模型,即模型中的数据皆 为确定的数值; 另一类叫作随机性模型,即模型中含有随 机变量,而不是确定的数值。 本章将按介绍一些常用的确定性存储模型, 并从中得出相应的存储策略。
第2节 确定性存储模型
费用
(3) 生产费,补充存储时,如果不需向外厂订 货,由本厂自行生产,这时仍需要支出两项费 用。一项是装配费用(准备结束费用),如组 织和调整生产线的费用,它是一次性的费用, 或称为固定费用,也用C3表示。另一项是与生 产产品的数量有关的费用如材料费、加工费等 (可变费用)。 (4) 缺货费C2,当存储供不应求时所引起的损 失。如失去销售机会的损失、停工待料的损失 以及不能履行合同而缴纳罚款等。 在不允许缺货的情况下,在费用上处理的方式 是缺货费为无穷大。
C2~∞
2C 3 P t* C1R P R
C2~∞
2C3R P t* C1 PR
C1 t 2* t* C1 C 2
R R t3* t * (1 )t 2 * P P
PR t 1* t* P
t2=0
t1=t2=0
R t3* t * P
A R(t * t 3*)
C* C(t*) 2C1C3R (11.5)
例2
某轧钢厂每月按计划需产角钢3000吨,每 吨每月需存储费5.3元,每次生产需调整机 器设备等,共需准备费25000元。若该厂每 月生产角钢一次,生产批量为3000吨。 每月需总费用 1/2×5.3×3000+25000=10450(元/月) 全年需费用 10450×12=125400(元/年) 然后按E.O.Q公式计算每次生产批量
2.1 模型一:不允许缺货,补充时间极短 假设:
(1) 需求是连续均匀的,即需求速度(单位时间内的需 求量)R是常数,则t时间的需求量为Rt; (2) 补充可以瞬时实现。当存储降至零时,可以立即得 到补充(即备货时间或生产时间很短,可以近似地看作 零); (3) 单位存储费(单位时间内单位物资的存储费)为C1 , 单位缺货费(单位时间内每缺少一单位物资的损失) C2为无穷大,订货费(每订购一次的固定费用)为C3 , 货物单价为K. (4)采用t-循环策略,补充时间为t,补充时存储已用完, 每次补充量为Q。
专门研究这类有关存储问题的科学,构成 运筹学的一个分支,叫作存储论(inventory Theory),也称库存论。 本章所介绍的存储问题,模型并不复杂, 原理也容易掌握,应用这些原理可以从一 个方面改善企业的经营管理,以达到节约 资金,获得更多利润的目的。
1.2 存储论的基本概念
• 存贮系统 是一个由补充、存贮、需求三个环节 紧密构成的运行系统。
得
2C3R Q* Rt* C1 (11.3)
C* C(t*) 2C1C3R KR (11.4)
按照t-循环策略,应当每隔t*时间补充存储量 Q*,这样平均总费用为C*,是最经济的。 式(11.3)即存储论中著名的经济订购批量 (economic ordering quantity)公式。简称 为E.O.Q公式,或经济批量(economic lot size)公式。
计算批量和批次
Q0 2 C3 (装配费) D(需求速度) C1 (存储费) 2 2500 3000 5.3 1682(吨)
300012 n0 21.4(次) Q0
计算需要的数据
两次生产相隔的时间t0=(365/21.4)≈17(天) 17天的单位存储费(5.3/30)×17=3.00(元/吨), 共需费用5.3/30×17×1682+2500≈5025(元)。 按全年生产21.5次(两年生产43次)计算,全年共 需费用5025×21.5=108037(元/年)。 两者相比较,该厂在利用E.O.Q公式求出经济批 量进行生产即可每年节约资金 125400 -108037=17363(元)
2. 补充(订货或生产)
存储论要解决的问题是:多少时间补充一次, 每次补充的数量应该是多少。决定多少时间 补充一次以及每次补充数量的策略称为存储 策略。 存储策略的优劣如何衡量呢?最直接的衡量 标准,是计算该策略所耗用的平均费用多少。 为此有必要对费用进行详细的分析。
3. 费用
主要包括:存储费、订货费、生产费、缺货费
第11章 存贮论
第11章 存贮论 (存储论) (Inventory Theory)
第1节 第2节 第3节 第4节 存贮论的基本概念 确定性存贮模型 随机性存贮模型 存贮论应用研究中的一些问题
第1节 存储论的基本概念 1.1 存储问题的提出
人们在生产和日常生活活动中往往将所需的物资、 用品和食物暂时地储存起来,以备将来使用或消 费。这种储存物品的现象是为了解决供应(生产) 与需求(消费)之间的不协调的一种措施,这种不 协调性一般表现为供应量与需求量和供应时期与 需求时期的不一致性上,出现供不应求或供过于 求。人们在供应与需求这两环节之间加入储存这 一环节,就能起到缓解供应与需求之间的不协调, 以此为研究对象,利用运筹学的方法去解决最合 理、最经济地储存问题。
(1) t循环策略,每隔t时间补充存储量Q。 (2) (t,S)策略,每隔固定的时间t补充一次,补充数量以 补足一个固定的最大存储量S为准。 (3) (s,S)策略,每当存储量x>s时不补充。当x≤s时补 充存储。补充量Q=S-x。S称为订货点(保险存储量、 安全存储量、警戒点等) (4) (t,s,S)混合策略,每经过t时间检查存储量x,当x> s时不补充。当x≤s时,补充存储量使之达到S。
补充
存
贮
需求
1.2 存储论的基本概念
需求、补充、费用、存贮策略 1. 需求
对存储来说,由于需求,从存储中取出一定的 数量,使存储量减少,这就是存储的输出。有 的需求是间断式的,有的需求是连续均匀的。
1. 需求
有的需求是确定性的,如钢厂每月按合同 卖给电机厂矽钢片10吨。有的需求是随机 性的,如书店每日卖出去的书可能是1000 本,也可能是800本。但是经过大量的统计 以后,可能会发现每日售书数量的统计规 律。
C2~∞
2C3R P t* C1 PR
C1 t 2* t* C1 C 2
R R t3* t * (1 )t 2 * P P
PR t 1* t* P
t2=0
t1=t2=0
R t3* t * P
A R(t * t 3*)
B Rt 1 * C* 2C 3 / t *
2.3 模型三:不允许缺货,补充需一定时间
在模型二的假设条件中,取消允许缺货条 件(即设C2~∞,t2=0),就成为模型三
在[0,T]区间内,存储以(P-R)速度增加,在 [T,t]区间内存储以速度R减少。
2C3 C1 C2 P t* C1R C2 PR
2C3R C1 C 2 P Q* C1 C2 PR
C3 1 C( t ) KR C1Rt t 2
求C(t)的最小值
(11.1)
模型一:不允许缺货,补充时间极短
只需对(11.1)式利用微积分求最小值的方法可 求出。
C3 1 dC( t ) 令: 2 C1R 0 dt t 2
2C3 得: t C1R
*
(11.2)
经济批量公式
(1) 存储费C1,包括货物占用资金应付的利息以及使用 仓库、保管货物、货物损坏变质等支出的费用,一般和 存储数量及时间成比例。 (2) 订货费,向外采购物资的费用。包括两项费用,一项 是订购费用C3 (固定费用,或一次性费用)如手续费、电 信往来、派人员外出采购等费用。订购费与订货次数有 关,而与订货数量无关。另一项是可变费用,它与订货 数量及货物本身的价格等有关,如货款、运费等。如货 物单价为K元,订购费用为C3元,订货数量为Q,则订 货费用为:C3+KQ。
模型一:不允许缺货,补充时间极短
