07试卷答案讲解学习
(浙江卷)2007年高考语文试卷及答案详细解析

[解析][这道题主要考查学生筛选和整合文中信息的能力。C项“味觉对象转移到琵琶声上”为无中生有,A、B两项在第二段有相关落脚点,D项信息在第三段。]
9文章开头说难以正面、直接回答什么样的琵琶声是好的,但最后一段叉说历来有正面、直接而具体的标准,下面对此分析正确的一项是
A起到先抑后扬的作用,从而强调“五字标准”的长赴。
太史公论《诗》,以为“《国风》好色而不淫,《小雅》怨诽而不乱。”以余观之,是特识变风、变雅耳,乌睹《诗》之正乎?昔先王之泽衰,然后变风发乎情,虽衰而未竭,是以犹止于礼义,以为贤于无所止者而已。若夫发于情止于忠孝者,其诗岂可同日而语哉!古今诗人众矣,而杜子美为首,岂非以其流落饥寒,终身不用,而一饭未尝忘君也欤。
B利害攸关而实话实说,连遇强手而毫不怯懦,检点省(shěng)察而幡然知耻,路见不平而拔刀相助:这就是勇敢。
c傅雷先生耻于蝇利蜗名之争,奋而辞职,闭门译述,翻译艺术日臻(zhēn)完美,终以卷帙浩繁的译著,享誉学界。
D《古文观止》是由康熙年间两位名不见经传的选家所编,他们披沙捡金,遴选了二百多篇琅琅(lǎng)上口、百读不厌的佳作。
7下面各项陈述中,最能说明“通感”特征的一项是
A弹拨乐器而具有某些打击乐器的发音效果。
B玉使人联想起悦耳的“乐音”有“水灵灵”的特性。
c珠与玉的光彩,有着东方人的含蓄之美。
D在中国民族乐器中,琵琶最具珠玉之美。
[答案]B
[解析][这道题主要考查学生理解文中重要词语的含义能力。“乐音”属于听觉,“水灵灵”属于视觉,根据第二段“把一类事物的特性比附到另一类不同的事物上去,或者说把一种感官对象的性质移到另一种感官对象上去”的信息可以得出答案。]
c同学们,考人大学仅仅是一个新的起点,让我们志存高远,学海无涯苦作舟,在老师们的推波助澜下,直挂云帆济沧梅!
2007年普通高等学校招生全国统一考试数学卷(广东.理)含答案

试卷类型:B2007年普通高等学校招生全国统一考试(广东卷)数 学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,选划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高.如果事件A B ,互斥,那么()()()P A B P A P B +=+. 如果事件A B ,相互独立,那么()()()P A B P A P B =.用最小二乘法求线性回归方程系数公式1221ni ii nii x y nx yb xnx==-=-∑∑,a y bx =-.一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合要求的. 1.已知函数()f x =M ,()ln(1)g x x =+的定义域为N ,则M N =( ) A .{|1}x x >-B .{|1}x x <C .{|11}x x -<<D .∅2.若复数(1)(2)bi i ++是纯虚数(i 是虚数单位,b 是实数),则b =( ) A .2B .12C .12-D .2-3.若函数21()sin ()2f x x x =-∈R ,则()f x 是( )A .最小正周期为π2的奇函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数D .最小正周期为π的偶函数4.客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达内地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( )s (km s (km s (km s (km5.已知数列{}n a 的前n 项和29n S n n =-,第k 项满足58k a <<,则k =( ) A .9B .8C .7D .66.图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为1210A A A ,,,(如2A 表示身高(单位:cm )在[)150155,内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm (含160cm ,不含180cm )的学生人数,那么在流程图中的判断框内应填写的条件是( ) A.6i <B.7i < C.8i < D.9i <1 2 3 60 8010t (1 2 3 6080 10t (1 2 3 6080 10t (1 2 36080 10t (A .B .C .D .0 0 0 45505560人数/人7.图3是某汽车维修公司的维修点环形分布图.公司在年初分配给A B C D ,,,四个维修点某种配件各50件.在使用前发现需将A B C D ,,,四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n 件配件从一个维修点调整到相邻维修点的调动件次为n )为( ) A.15B.16C.17D.188.设S 是至少含有两个元素的集合,在S 上定义了一个二元运算“*”(即对任意的a b S ∈,,对于有序元素对(a b ,),在S 中有唯一确定的元素*a b 与之对应).若对任意的a b S ∈,,有()**a b a b =,则对任意的a b S ∈,,下列等式中不恒成立的是( ) A .()**a b a a = B .[()]()****a b a a b a = C .()**b b b b =D .()[()]****a b b a b b =二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,图3考生只能选做二题,三题全答的,只计算前两题得分.9.甲、乙两个袋中装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球,2个白球,乙袋装有1个红球,5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球是红球的概率为 .(答案用分数表示)10.若向量,a b 满足1==a b ,a 与b 的夹角为120,则a a +a b = . 11.在平面直角坐标系xOy 中,有一定点(21)A ,,若线段OA 的垂直平分线过抛物线22(0)y px p =>的焦点,则该抛物线的准线方程是 .12.如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有()f n 对异面直线,则(4)f = ;()f n = .(答案用数字或n 的解析式表示) 13.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为33x t y t =+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2sin 2x y θθ=⎧⎨=+⎩(参数[)02θ∈π,),则圆C 的圆心坐标为 ,圆心到直线l 的距离为 .14.(不等式选讲选做题)设函数()213f x x x =-++,则(2)f -= ;若()5f x ≤,则x 的取值范围是 .图5图415.(几何证明选讲选做题)如图5所示,圆O 的直径6AB =,C 为圆周上一点,3BC =.过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D E ,,则DAC =∠ ,线段AE 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知ABC △顶点的直角坐标分别为(34)A ,,(00)B ,,(0)C c ,. (1)若5c =,求sin A ∠的值; (2)若A ∠是钝角,求c 的取值范围.17.(本小题满分12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y bx a =+;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=) 18.(本小题满分14分)在平面直角坐标系xOy,已知圆心在第二象限、半径为C 与直线y x =相切于坐标原点O .椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10.(1)求圆C 的方程;(2)试探究圆C 上是否存在异于原点的点Q ,使Q 到椭圆右焦点F 的距离等于线段OF 的长,若存在,请求出点Q 的坐标;若不存在,请说明理由. 19.(本小题满分14分)如图6所示,等腰ABC △的底边AB =,高3CD =,点E 是线段BD 上异于点B D ,的动点,点F 在BC 边上,且EF AB ⊥,现沿EF 将BEF △折起到PEF △的位置,使PE AE ⊥,记BE x =,()V x 表示四棱锥P ACFE -的体积. (1)求()V x 的表达式;(2)当x 为何值时,()V x 取得最大值?(3)当()V x 取得最大值时,求异面直线AC 与PF 所成角的余弦值. 20.(本小题满分14分)已知a 是实数,函数2()223f x ax x a =+--,如果函数()y f x =在区间[]11-,上有零图6P ED F BCA点,求a 的取值范围. 21.(本小题满分14分)已知函数2()1f x x x =+-,αβ,是方程()0f x =的两个根(αβ>),()f x '是()f x 的导数,设11a =,1()(12)()n n n n f a a a n f a +=-=',,. (1)求αβ,的值;(2)证明:对任意的正整数n ,都有n a α>; (3)记ln(12)n n n a b n a βα-==-,,,求数列{}n b 的前n 项和n S .绝密★启用前 试卷类型:B2007年普通高等学校招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分。
2007年高考语文试题及参考答案(海南卷)

(2)件装货物
(3)成组装货物(UNITIZED CARGO)
2、从货物形态的角度分 (1)包装货物 (2)裸装货物 (3)散装货物 3、从货物重量的角度分 (1)重量货物 (2)体积货物(1t,体积大于1立方米)
四、运输代理人
1、运输代理人的性质 2、运输代理人的种类 按照代理业务的性质和范围的不同分为 以下几类: (1)租船代理(charter agent) (2)船务代理(shipping agent) (3)货运代理(freight agent) (4)咨询代理(consulting agent)
2、班轮运输在国际海上货物运输中表现出了 明显的优点如下:
班轮运输的船舶技术性能较好,运输速度快 班轮运输的管理制度较为完善 班轮运输特别适合一般杂货和小批量货物的运输 需要
班轮运输有利于收、发货的合理安排
3、班轮运费的计收标准
(1)按重量吨(weight ton)计收。运价表上用 “W”表示。按货物毛重(公吨)计算,吨以下取 小数三位。适用于价值不高、体积小、重量大的货 物。
4、班轮运费的计算
当确定某商品装某船运往某港时: 1、首先查该船公司的运价本,查找所装商品等级和 计费标准 ; 2、再找出运往的目的港所属航线; 3、然后用商品的单位包装重量或尺码乘以基本运费, 加上附加费,得出单位包装重量或尺码的运费,再 乘以计费总件数,即得出该批货物应付的运费总额。 (如果是从价运费,按规定的百分比乘以FOB货值 即可。 )
每箱运费 =0.035×(76+5)= 2.835美元 应付船公司总运费=2.835×1000箱=2835美元。
4、班轮运费的计算
实例1:
某公司出口箱装货物,报价为每箱50美元CFR 伦敦。已知:该货物体积没箱长45CM、宽 40CM、高25CM,每箱毛重35KG,运费计算 标准为W/M,每运费吨基本运费为120美元, 并加收直航附加费20%,港口附加费10%。 英商要求该报FOB价,我方应报价多少?
物理(江苏卷)答案解析2007

2007年普通高等学校夏季招生考试物理(江苏卷)一、选择题 ( 本大题共 3 题, 共计 12 分)1、(4分) AB解析:电阻丝电阻值较小,为减小实验误差,应采用外接法,A正确.电源内阻较小,同理可知应采用外接法,B正确.描绘小灯泡的伏安特性曲线,变化范围大,应采用分压式,C错误.D电路图中应将电阻箱和滑动变阻器对调,才能利用“半偏法”测出电流表的内阻,D错误.2、(4分) BC解析:M=ρV=πd3ρ,向心力F向=G,当天体直径和天体间距均缩小到原来的一半时,,因此B对,A错.由可得T=2,由此式可见,当M变为原值的、r变为原来的时,周期T不变,C正确,D错误.3、(4分) CD解析:温度相同,分子平均动能相同,A错.由热力学第一定律W+Q=ΔU可知,系统绝热,对外无做功现象,因此系统内能不变,温度与初始状态相同,氢气的内能不变,B错.系统内部,氢气对氧气做功,内能减少,温度降低,氧气体积减小,温度升高,之后发生热交换,热量从氧气传递到氢气,因此,氧气的内能先增大后减小,C、D均正确.二、非选择题 ( 本大题共 8 题, 共计 112 分)1、(9分)(1) a(2)a) Pb)(3)解析:(1)由于阻值0~20 Ω的滑动变阻器b的额定电流为0.5 A,而并联支路的最大阻值将小于20 Ω,因此并联部分的最小电流为I min= A=0.6 A>0.5 A,因此,必须选a.(2)假设电压表接在O端,由于电压表内阻约为10 kΩ,因此,并联部分的电阻应小于10 kΩ,但由数据看出,当I=0.06 mA时,U=6.16 V,此时,并联电阻大于100 kΩ,显然,电压表应跨接在P端.(3)待测元件导通前电压均匀增大,导通后,电压基本不变.2、(13分) (1) 6 不明显,可忽略(2)斜面高度h滑块A的质量M及斜面的高度h,且使Mh不变(3)滑动摩擦力 arcsin 0.6 (arcsin 0.57 -arcsin 0.64都算对)0.3 (0.2~0.4都算对)解析:(1)a=≈m·s-2=6 m·s-2;由上滑及下滑的v-t图象的近似对称,a值近似相等知,摩擦力很小,可忽略.(2)改变斜面的高度,可改变物体所受的下滑力,即可验证a∝F(m一定时);同理,改变滑块质量M和斜面高度h,使Mh保持不变,可验证a∝的关系,因为Mg sinθ=Mg=Mh,Mh不变即物块所受合力不变.(3)由图象可知s1=0.64 m=s2t1=0.4 s,t2=0.6 s则s1=g(sinθ+μcosθ)t12 ①s2=g(sinθ-μcosθ)t22 ②联立可得θ=arcsin0.6,μ=0.3.3、(14分) (1)解法一由几何关系知由折射定律代入,得解得(1)解法二由几何关系知液面高度变化,折射角不变,由,得解得(2)4、(14分) 直升机取水,水箱受力平衡T1sinθ1-f=0 ①T1cosθ1-mg=0 ②由①②得 f=mgtanθ1③直升机返回,由牛顿第二定律T2sinθ2-f=(m+M)a ④T2cosθ2-(m+M)g=0 ⑤由④⑤得,水箱中水的质量 M=4.5×103kg.5、(15分) (1)设C在AB连线的延长线上距离B为l处达到平衡,带电量为Q 库仑定律平衡条件解得(舍去),l2=d所以,平衡位置l=d(2)不能(3)环C带电-q,平衡位置不变,拉离平衡位置一小位移x后C受力为利用近似关系化简得所以小环C将做简谐运动6、(15分) (1)设a粒子以速度v进入磁场,打在胶片上的位置距S的距离为x圆周运动①a粒子的动能②x=2R ③由①②③式可得由④可得化简可得(2)动能为E的a粒子沿角入射,轨道半径相同,设为R圆周运动a粒子的动能由几何关系得7、(16分) (1)线框MN边刚开始进入磁场区域时感应电动势 E=Blv0①感应电流②安培力③由①②③解得F=2.8N(2)设线框竖直下落时,线框下落了H,速度为v H能量守恒定律自由落体规律解得(3)解法一只有在线框进入和穿出条形磁场区域时,才产生感应电动势。
2007年普通高等学校招生全国统一考试数学卷(浙江.文)含答案

2007年普通高等学校招生全国统一考试(浙江卷)数学(文科)第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集{13568}U =,,,,,{16}A =,,{568}B ,,,则()UA B =( )A .{6}B .{58},C .{68},D .{3568},,,2.已知π3cos 22ϕ⎛⎫+=⎪⎝⎭,且π||2ϕ<,则tan ϕ=( ) A .33-B .33C .3-D .33.“1x >”是“2x x >”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.直线210x y -+=关于直线1x =对称的直线方程是( ) A.210x y +-= B.210x y +-= C.230x y +-=D.230x y +-=5.要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是( ) A.6 B.5 C.4 D.36.91x x ⎛⎫- ⎪⎝⎭展开式中的常数项是( )A .36-B .36C .84-D .847.若P 是两条异面直线l m ,外的任意一点,则( ) A .过点P 有且仅有一条直线与l m ,都平行 B .过点P 有且仅有一条直线与l m ,都垂直 C .过点P 有且仅有一条直线与l m ,都相交 D .过点P 有且仅有一条直线与l m ,都异面8.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜,根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是( )第5题A .0.216B .0.36C .0.432D .0.6489.若非零向量,a b 满足-=a b b ,则( ) A.22>-b a b B.22<-b a b C.2>-a 2a bD. 2<-a 2a b10.已知双曲线22221(00)x y a b a b-=>>,的左、右焦点分别为1F ,2F ,P 是准线上一点,且12PF PF ⊥,124PF PF ab =,则双曲线的离心率是( ) A.2B.3C.2D.3第II 卷(共100分)二、填空题:本大题共7小题,每小题4分,共28分.11.函数221x y x =+(x ∈R )的值域是 .12.若1sin cos 5θθ+=,则sin 2θ的值是 . 13.某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,彩用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 .14.2z x y =+中的x y ,满足约束条件250300x y x x y -+=⎧⎪-⎨⎪+⎩,≥,≥,则z 的最小值是 .15.曲线32242y x x x =--+在点(13)-,处的切线方程是 .16.某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是 (用数字作答). 17.已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=.若对于β内异于O 的任意一点Q ,都有45POQ ∠≥,则二面角AB αβ--的大小是.三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤. 18.(本题14分)已知ABC △的周长为21+,且sin sin 2sin A B C +=.(I )求边AB 的长; (II )若ABC △的面积为1sin 6C ,求角C 的度数. 19.(本题14分)已知数列{}n a 中的相邻两项212k k a a -,是关于x 的方程2(32)320k k x k x k -++=的两个根,且212(123)k k a a k -=≤,,,.(I )求1a ,3a ,5a ,7a 及2n a (4n ≥)(不必证明); (II )求数列{}n a 的前2n 项和2n S .20.(本题14分)在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点.(I )求证:CM EM ⊥;(II )求DE 与平面EMC 所成的角的正切值.21.(本题15分)如图,直线y kx b =+与椭圆2214x y +=交于A B ,两点,记AOB △的面积为S .(I )求在0k =,01b <<的条件下,S 的最大值;(II )当2AB =,1S =时,求直线AB 的方程.22.(本题15分)已知22()|1|f x x x kx =-++. (I )若2k =,求方程()0f x =的解;(II )若关于x 的方程()0f x =在(02),上有两个解12x x ,,求k 的取值范围,并证明12114x x +<.EDCMA(第20题)BAyxO B(第21题)2007年普通高等学校招生全国统一考试(浙江卷)数学(文科)试题参考答案一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分. 1.B 2.C 3.A 4.D 5.C 6.C7.B 8.D 9.A 10.B二、填空题:本题考查基本知识和基本运算.每小题4分,满分28分. 11.[01),12.2425-13.5014.53-15.520x y +-=16.26617.90三、解答题18.本题主要考查利用正弦定理、余弦定理来确定三角形边、角关系等基础知识和基本运算能力.满分14分.解:(I )由题意及正弦定理,得21AB BC AC ++=+,2BC AC AB +=,两式相减,得1AB =. (II )由ABC △的面积11sin sin 26BC AC C C =,得13BC AC =, 由余弦定理,得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--==, 所以60C =.19.本题主要考查等差、等比数列的基本知识,考查运算及推理能力.满分14分.(I )解:方程2(32)320k kx k x k -++=的两个根为13x k =,22k x =.当1k =时,13x =,22x =, 所以12a =;当2k =时,16x =,24x =, 所以34a =;当3k =时,19x =,28x =, 所以58a =;当4k =时,112x =,216x =, 所以712a =.因为当4n ≥时,23nn >,所以22(4)nn a n =≥.(II )解:2122k n S a a a =+++2(363)(222)n n =+++++++2133222n n n ++=+-.20.本题主要考查空间线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.满分14分. 方法一: (I )证明:因为AC BC =,M 是AB 的中点,所以CM AB ⊥.又因为EA ⊥平面ABC , 所以CM EM ⊥.(II )解:连结MD ,设AE a =,则2BD BC AC a ===, 在直角梯形EABD 中,22AB a =,M 是AB 的中点,所以3DE a =,3EM a =,6MD a =,因此DM EM ⊥.因为CM ⊥平面EMD , 所以CM DM ⊥,因此DM ⊥平面EMC ,故DEM ∠是直线DE 和平面EMC 所成的角. 在Rt EMD △中,6MD a =,3EM a =,tan 2MDDEM EM∠==. 方法二:如图,以点C 为坐标原点,以CA ,CB 分别为x 轴和y 轴,过点C 作与平面ABC 垂直的直线为z 轴,建立直角坐标系C xyz -,设EA a =,则(2)A a 00,,,(020)B a ,,,EDCMAByzxED C MAB(20)E a a ,,.(022)D a a ,,,(0)M a a ,,.(I )证明:因为()EM a a a =--,,,(0)CM a a =,,, 所以0EM CM =, 故EM CM ⊥.(II )解:设向量001y z (),,n =与平面EMC 垂直,则EM ⊥n ,CM ⊥n , 即0EM =n ,0CM =n .因为()EM a a a =--,,,(0)CM a a =,,, 所以01y =-,02x =-, 即112(--),,n =,因为(22)DE a a a =--,,, 6cos 3DE DE DE <>==,n n n, DE 与平面EMC 所成的角θ是n 与DE 夹角的余角,所以tan 2θ=.21.本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.满分15分.(I )解:设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,.由2214x y +=,解得21,221x b =±- 所以222121||21112S b x x b b b b =-=-≤+-= 当且仅当22b =时,.S 取到最大值1. (Ⅱ)解:由2214y kx b x y =+⎧⎪⎨+=⎪⎩得 222(41)8440k x kbx b +++-=2216(41)k b ∆=-+ ①|AB |=222212216(41)1||1241k b k x x kk -++-=+=+ ② 又因为O 到AB 的距离2||21||1b Sd AB k ===+ 所以221b k =+ ③ ③代入②并整理,得424410k k -+= 解得,2213,22k b ==,代入①式检验,△>0 故直线AB 的方程是2622y x =+或2622y x =-或2622y x =-+或2622y x =--. (22)本题主要考查函数的基本性质、方程与函数的关系等基础知识,以及综合运用所学知识、分类讨论等思想方法分析和解决问题的能力.满分15分. (Ⅰ)解:(1)当k =2时, 22()|1|20f x x x x =-++=① 当210x -≥时,x ≥1或x ≤-1时,方程化为22210x x +-= 解得132x -±=,因为13012-+<<,舍去, 所以132x --=. ②当210x -<时,-1<x <1时,方程化为210x += 解得12x =-, 由①②得当k =2时,方程()0f x =的解所以132x --=或12x =-. (II)解:不妨设0<x 1<x 2<2,因为22 1 ||1() 1 ||1x kx x f x kx x ⎧+->=⎨+≤⎩所以()f x 在(0,1]是单调函数,故()f x =0在(0,1]上至多一个解, 若1<x 1<x 2<2,则x 1x 2=-12<0,故不符题意,因此0<x 1≤1<x 2<2.由1()0f x =得11k x =-, 所以1k ≤-; 由2()0f x =得2212k x x =-, 所以712k -<<-; 故当712k -<<-时,方程()0f x =在(0,2)上有两个解. 因为0<x 1≤1<x 2<2,所以11k x =-,22221x kx +-=0 消去k 得 2121220x x x x --=即212112x x x +=, 因为x 2<2,所以12114x x +<.。
2007年普通高等学校招生全国统一考试(全国新课标)参考答案

1PD CBAAOSCB2007年普通高等学校招生全国统一考试(新课标全国卷)1.A 2.C 3.A 4.D 5.C 6.B7.C8.B9.C10.D11.D12.B13.3 14.1 15.44i - 16.121.【解析】由{}{}|1|22A x x B x x =>-=-<<,,可得A B = {}|2x x >-.答案:A 2.【解析】p ⌝是对p 的否定,故有:,x ∃∈R sin 1.x >答案:C3.【解析】π3()sin 2,32f ππ⎛⎫=-=- ⎪⎝⎭排除B、D,π()sin 20,663f ππ⎛⎫=⨯-= ⎪⎝⎭排除C。
也可由五点法作图验证。
答案:A 4.【解析】1322-=a b (12).-,答案:D 5.【解析】由程序知,15021222502502550.2S +=⨯+⨯++⨯=⨯⨯= 答案:C 6.【解析】曲线223y x x =-+的顶点是(12),,则:1, 2.b c ==由a b c d ,,,成等比数列知,12 2.ad bc ==⨯=答案:B7.【解析】由抛物线定义,2132()()(),222p p px x x +=+++即:2132FP FP FP =+.答案:C 8.【解析】如图,18000202020.33V =⨯⨯⨯=答案:B(8题图) (11题图)9.【解析】22cos 2cos sin 22(sin cos ),π22sin (sin cos )42αααααααα-==-+=-⎛⎫-- ⎪⎝⎭1cos sin .2αα⇒+=答案C10.【解析】:(),x x y e e ''⇒==曲线在点2(2)e ,处的切线斜率为2e ,因此切线方程为22(2),y e e x -=-2C BFAOyx则切线与坐标轴交点为2(1,0),(0,),A B e -所以:2211.22AOBe S e ∆=⨯⨯=答案:D 11.【解析】如图,2,90,2,AB r ACB BC r ⇒=∠==3111122,3323ABC V SO S r r r r ∆∴=⨯⨯=⋅⋅⋅⋅=三棱锥 333441,::4.333V r V V r r πππ=∴==球球三棱锥答案:D12.【解析】(78910)58.5,20x +++⨯== 甲2222215[(78.5)(88.5)(98.5)(108.5)]1.25,20s ⨯-+-+-+-== (710)6(89)48.5,20x +⨯++⨯==乙2222226[(78.5)(108.5)]4[(88.5)(98.5)]1.45,20s ⨯-+-+⨯-+-== (710)4(89)68.5,20x +⨯++⨯==丙2222234[(78.5)(108.5)]6[(88.5)(98.5)]1.05,20s ⨯-+-+⨯-+-== 22213213.s s s s s s >>>>2由得 答案:B13.【解析】如图,过双曲线的顶点A 、焦点F 分别向其渐近线作垂线, 垂足分别为B 、C ,则:||||63.||||2OF FC c OA AB a =⇒== 答案:3 14.【解析】(1)(1)2(1)0, 1.f f a a =-⇒+=∴=- 答案:-1 15.【解析】238i 2i 3i 8i i -2-3i +4+5i -6+7i +8=4-4i.++++= 答案:44i -16.【解析】46563,a a a +=⇒=1515135510 1.22a a a S a ++=⨯=⨯=⇒= 511.512a a d -∴==-答案:1217.解:在BCD △中,πCBD αβ∠=--.由正弦定理得sin sin BC CDBDC CBD=∠∠.所以sin sin sin sin()CD BDC s BC CBD βαβ∠==∠+·.在ABC Rt △中,tan sin tan sin()s AB BC ACB θβαβ=∠=+·.318.解:(Ⅰ)取AB 的中点E ,连结DE CE ,,因为ADB 是等边三角形,所以DE AB ⊥.当平面ADB ⊥平面ABC 时,因为平面ADB 平面ABC AB =,所以DE ⊥平面ABC ,可知DE CE ⊥ 由已知可得31DE EC ==,,在DEC Rt △中,222CD DE EC =+=.(Ⅱ)当ADB △以AB 为轴转动时,总有AB CD ⊥. 证明:(ⅰ)当D 在平面ABC 内时,因为AC BC AD BD ==,,所以C D ,都在线段AB 的垂直平分线上,即AB CD ⊥.(ⅱ)当D 不在平面ABC 内时,由(Ⅰ)知AB DE ⊥.又因AC BC =,所以AB CE ⊥. 又DE CE ,为相交直线,所以AB ⊥平面CDE ,由CD ⊂平面CDE ,得AB CD ⊥. 综上所述,总有AB CD ⊥.19.解:()f x 的定义域为32⎛⎫-+ ⎪⎝⎭,∞.(Ⅰ)224622(21)(1)()2232323x x x x f x x x x x ++++'=+==+++. 当312x -<<-时,()0f x '>;当112x -<<-时,()0f x '<;当12x >-时,()0f x '>.从而,()f x 分别在区间312⎛⎫-- ⎪⎝⎭,,12⎛⎫-+ ⎪⎝⎭,∞单调增加,在区间112⎛⎫--⎪⎝⎭,单调减少. (Ⅱ)由(Ⅰ)知()f x 在区间3144⎡⎤-⎢⎥⎣⎦,的最小值为11ln 224f ⎛⎫-=+ ⎪⎝⎭.又31397131149lnln ln 1ln 442162167226f f ⎛⎫⎛⎫⎛⎫--=+--=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0<. 所以()f x 在区间3144⎡⎤-⎢⎥⎣⎦,的最大值为117ln 4162f ⎛⎫=+ ⎪⎝⎭.20.解:设事件A 为“方程2220a ax b ++=有实根”.当0a >,0b >时,方程2220x ax b ++=有实根的充要条件为a b ≥.(Ⅰ)基本事件共12个:(00)(01)(02)(10)(11)(12)(20)(21)(22)(30)(31)(32),,,,,,,,,,,,,,,,,,,,,,,.其中第一个数表示a 的取值,第二个数表示b 的取值.事件A 中包含9个基本事件,事件A 发生的概率为93()124P A ==. (Ⅱ)试验的全部结束所构成的区域为{}()|0302a b a b ,,≤≤≤≤. 构成事件A 的区域为{}()|0302a b a b a b ,,,≤≤≤≤≥. EDBCA4所以所求的概率为2132222323⨯-⨯==⨯.21.解:(Ⅰ)圆的方程可写成22(6)4x y -+=,所以圆心为(60)Q ,,过(02)P ,且斜率为k 的直线方程为2y kx =+.代入圆方程得22(2)12320x kx x ++-+=,整理得22(1)4(3)360k x k x ++-+=.① 直线与圆交于两个不同的点A B ,等价于2222[4(3)]436(1)4(86)0k k k k ∆=--⨯+=-->, 解得304k -<<,即k 的取值范围为304⎛⎫- ⎪⎝⎭,. (Ⅱ)设1122()()A x y B x y ,,,,则1212()OA OB x x y y +=++ ,,由方程①,1224(3)1k x x k -+=-+ ②又1212()4y y k x x +=++.③ 而(02)(60)(62)P Q PQ =-,,,,,. 所以OA OB + 与PQ 共线等价于1212()6()x x y y +=+, 将②③代入上式,解得34k =-.由(Ⅰ)知304k ⎛⎫∈ ⎪⎝⎭,,故没有符合题意的常数k .22.A(Ⅰ)证明:连结OP OM ,. 因为AP 与O 相切于点P ,所以OP AP ⊥. 因为M 是O 的弦BC 的中点,所以OM BC ⊥. 于是180OPA OMA ∠+∠=°.由圆心O 在PAC ∠的内部,可知四边形APOM 的对角互补,所以A P O M ,,,四点共圆. (Ⅱ)解:由(Ⅰ)得A P O M ,,,四点共圆,所以OAM OPM ∠=∠.由(Ⅰ)得OP AP ⊥.由圆心O 在PAC ∠的内部,可知90OPM APM ∠+∠=°. 所以90OAM APM ∠+∠=°. 22.B解:以极点为原点,极轴为x 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.(Ⅰ)cos x ρθ=,sin y ρθ=,由4cos ρθ=得24cos ρρθ=. 所以224x y x +=.即2240x y x +-=为1O 的直角坐标方程. 同理2240x y y ++=为2O 的直角坐标方程.APO MCB5(Ⅱ)由22224040x y x x y y ⎧+-=⎪⎨++=⎪⎩,解得1100x y =⎧⎨=⎩,,2222x y =⎧⎨=-⎩. 即1O ,2O 交于点(00),和(22)-,.过交点的直线的直角坐标方程为y x =-. 22.C解:(Ⅰ)令214y x x =+--,则1521334254x x y x x x x ⎧---⎪⎪⎪=--<<⎨⎪⎪+⎪⎩, ,, ,, .≤≥...............3分作出函数214y x x =+--的图象,它与直线2y =的交点为(72)-,和523⎛⎫ ⎪⎝⎭,.所以2142x x +-->的解集为5(7)3x x ⎛⎫--+ ⎪⎝⎭,,.(Ⅱ)由函数214y x x =+--的图像可知,当12x =-时,214y x x =+--取得最小值92-.12- O 2y =4xy。
2007年全国卷二试卷超详细解析版
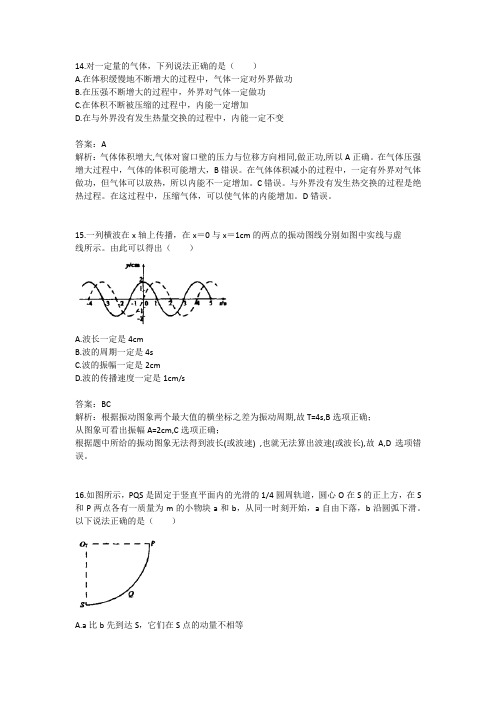
14.对一定量的气体,下列说法正确的是()A.在体积缓慢地不断增大的过程中,气体一定对外界做功B.在压强不断增大的过程中,外界对气体一定做功C.在体积不断被压缩的过程中,内能一定增加D.在与外界没有发生热量交换的过程中,内能一定不变答案:A解析:气体体积增大,气体对窗口壁的压力与位移方向相同,做正功,所以A正确。
在气体压强增大过程中,气体的体积可能增大,B错误。
在气体体积减小的过程中,一定有外界对气体做功,但气体可以放热,所以内能不一定增加。
C错误。
与外界没有发生热交换的过程是绝热过程。
在这过程中,压缩气体,可以使气体的内能增加。
D错误。
15.一列横波在x轴上传播,在x=0与x=1cm的两点的振动图线分别如图中实线与虚线所示。
由此可以得出()A.波长一定是4cmB.波的周期一定是4sC.波的振幅一定是2cmD.波的传播速度一定是1cm/s答案:BC解析:根据振动图象两个最大值的横坐标之差为振动周期,故T=4s,B选项正确;从图象可看出振幅A=2cm,C选项正确;根据题中所给的振动图象无法得到波长(或波速) ,也就无法算出波速(或波长),故A,D选项错误。
16.如图所示,PQS是固定于竖直平面内的光滑的1/4圆周轨道,圆心O在S的正上方,在S 和P两点各有一质量为m的小物块a和b,从同一时刻开始,a自由下落,b沿圆弧下滑。
以下说法正确的是()A.a比b先到达S,它们在S点的动量不相等B.a 与b 同时到达S ,它们在S 点的动量不相等C.a 比b 先到达S ,它们在S 点的动量相等D.b 比a 先到达S ,它们在S 点的动量不相等答案:A解析:解法一:利用分运动的独立性和分运动与合运动的同时性。
即分运动的运动时间和合运动的运动时间是相同的而分运动互不影响,所以分析a 和b 的竖直运动就可以判断两者谁先到达S :a 竖直方向为自由落体,加速度为g,而b 在竖直方向除了受到重力外,还有圆弧支持力的一个向上的分力,其加速的加速度小于g ,且先做加速度减小的加速再做加速度增大的减速,最大速度将小于a 到S 时的速度 ,故平均速度较小,所以b 将后到S 。
2007年海南高考数学(理科)试题详细解答

2007年普通高等学校招生全国统一考试海南理科数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第II 卷第22题为选考题,其他题为必考题.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回. 注意事项: 1.答题前,考生先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的准考证号、姓名,并将条形码粘贴在指定位置上.2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或炭素笔书写,字体工整,笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.作选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的标号涂黑. 参考公式:样本数据1x ,2x , ,n x 的标准差锥体体积公式s =13V Sh =其中x 为样本平均数 其中S 为底面面积、h 为高 柱体体积公式 球的表面积、体积公式V Sh =24πS R =,34π3V R =其中S 为底面面积,h 为高其中R 为球的半径第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知命题:p x ∀∈R ,sin 1x ≤,则( ) A.:p x ⌝∃∈R ,sin 1x ≥ B.:p x ⌝∀∈R ,sin 1x ≥ C.:p x ⌝∃∈R ,sin 1x >D.:p x ⌝∀∈R ,sin 1x >2.已知平面向量(11)(11)==-,,,a b ,则向量1322-=a b ( ) A.(21)--, B.(21)-,C.(10)-,D.(12)-,3.函数πsin 23y x ⎛⎫=-⎪⎝⎭在区间ππ2⎡⎤-⎢⎥⎣⎦,的简图是( )4.已知{}n a 是等差数列,1010a =,其前10项和1070S =,则其公差d =( ) A.23-B.13-C.13D.235.如果执行右面的程序框图,那么输出的S =( ) A.2450 B.2500C.2550D.26526.已知抛物线22(0)y px p =>的焦点为F ,点111222()()P x y P x y ,,,,333()P x y ,在抛物线上, 且2132x x x =+, 则有( ) A.123FP FP FP +=B.222123FP FP FP +=C.2132FP FP FP =+ D.2213FP FP FP =· 7.已知0x >,0y >,x a b y ,,,成等差数列,x c d y ,,,成等比数列,则2()a b cd+的最小值是( ) A.0 B.1C.2D.48.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是( )xA.B.C.D.正视图侧视图俯视图A.34000cm 3B.38000cm 3C.32000cmD.34000cm9.若cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭,则cos sin αα+的值为( )A.2-B.12-C.1210.曲线12e x y =在点2(4e ),处的切线与坐标轴所围三角形的面积为( ) A.29e 2B.24eC.22eD.2e123s s s ,,分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有( )A.312s s s >> B.213s s s >> C.123s s s >>D.231s s s >>12.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为1h ,2h ,h ,则12::h h h =( )2:222 第II 卷本卷包括必考题和选考题两部分,第13题-第21题为必考题,每个试题考生都必须做答,第22题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 .14.设函数(1)()()x x a f x x ++=为奇函数,则a = .15.i 是虚数单位,51034ii-+=+ .(用a bi +的形式表示,a b ∈R ,) 16.某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有种.(用数字作答)三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D .现测得BCD BDC CD s αβ∠=∠==,,,并在点C 测得塔顶A 的仰角为θ,求塔高AB .18.(本小题满分12分)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°,O 为BC 中点. (Ⅰ)证明:SO ⊥平面ABC ; (Ⅱ)求二面角A SC B --的余弦值.19.(本小题满分12分)在平面直角坐标系xOy中,经过点(0且斜率为k 的直线l 与椭圆2212x y +=有两个不同的交点P 和Q .(I )求k 的取值范围;(II )设椭圆与x 轴正半轴、y 轴正半轴的交点分别为A B ,,是否存在常数k ,使得向量OP OQ + 与AB共线?如果存在,求k 值;如果不存在,请说明理由.20.(本小题满分12分)如图,面积为S 的正方形ABCD 中有一个不规则的图形M ,可按下面方法估计M 的面积:在正方形ABCD 中随机投掷n 个点,若n 个点中有m 个点落入M 中,则M 的面积的估计值为mS n,假设正方形ABCD 的边长为2,M 的面积为1,并向正DC BA OSBC方形ABCD 中随机投掷10000个点,以X 表示落入M 中的点的数目.(I )求X 的均值EX ;(II )求用以上方法估计M 的面积时,M 的面积的估计值与实际值之差在区间(0.03)-0.03,内的概率. 附表:1000010000()0.250.75ktt t t P k C-==⨯⨯∑21.(本小题满分12分) 设函数2()ln()f x x a x =++(I )若当1x =-时,()f x 取得极值,求a 的值,并讨论()f x 的单调性; (II )若()f x 存在极值,求a 的取值范围,并证明所有极值之和大于eln2. 22.请考生在A B C ,,三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.A(本小题满分10分)选修4-1:几何证明选讲 的割如图,已知AP 是O 的切线,P 为切点,AC 是O 点线,与O 交于B C ,两点,圆心O 在PAC ∠的内部,M 是BC 的中点. (Ⅰ)证明A P O M ,,,四点共圆; (Ⅱ)求OAM APM ∠+∠的大小.22.B(本小题满分10分)选修4-4:坐标系与参数方程1O 和2O 的极坐标方程分别为4cos 4sin ρθρθ==-,.(Ⅰ)把1O 和2O 的极坐标方程化为直角坐标方程; (Ⅱ)求经过1O ,2O 交点的直线的直角坐标方程.22.C(本小题满分10分)选修45-;不等式选讲 设函数()214f x x x =+--. (I )解不等式()2f x >; (II )求函数()y f x =的最小值.2007年普通高等学校招生全国统一考试A理科数学试题参考答案(宁夏)一、选择题 1.C 2.D 3.A 4.D5.C6.C7.D8.B9.C10.D 11.B12.B二、填空题 13.314.1-15.12i +16.240三、解答题17.解:在BCD △中,πCBD αβ∠=--. 由正弦定理得sin sin BC CDBDC CBD=∠∠. 所以sin sin sin sin()CD BDC s BC CBD βαβ∠==∠+·. 在ABC Rt △中,tan sin tan sin()s AB BC ACB θβαβ=∠=+·.18.证明:(Ⅰ)由题设AB AC SB SC ====SA ,连结OA ,ABC△为等腰直角三角形,所以2OA OB OC SA ===,且A O B C ⊥,又SBC △为等腰三角形,故SO BC ⊥,且SO SA =,从而222OA SO SA +-.所以SOA △为直角三角形,SO AO ⊥. 又AO BO O = . 所以SO ⊥平面ABC . (Ⅱ)解法一:取SC 中点M ,连结AM OM ,,由(Ⅰ)知SO OC SA AC ==,,得OM SC AM SC ⊥⊥,.OMA ∠∴为二面角A SC B --的平面角.由AO BC AO SOSO BC O ⊥⊥= ,,得AO ⊥平面SBC . 所以AO OM ⊥,又2AM SA =,故sin 3AOAMO AM ∠===. 所以二面角A SC B --. 解法二:OSBCM以O 为坐标原点,射线OB OA ,分别为x 轴、y 轴的正半轴,建立如图的空间直角坐标系O xyz -. 设(100)B ,,,则(100)(010)(001)C A S -,,,,,,,,.SC 的中点11022M ⎛⎫- ⎪⎝⎭,,,111101(101)2222MO MA SC ⎛⎫⎛⎫=-=-=-- ⎪ ⎪⎝⎭⎝⎭,,,,,,,,. 00MO SC MA SC ==,∴··.故,MO SC MA SC MO MA ⊥⊥>,,<等于二面角A SCB --的平面角.cos MO MA MO MA MO MA <>==,·· 所以二面角A SC B --.19.解:(Ⅰ)由已知条件,直线l的方程为y kx =代入椭圆方程得22(12x kx +=.整理得221102k x ⎛⎫+++=⎪⎝⎭① 直线l 与椭圆有两个不同的交点P 和Q 等价于2221844202k k k ⎛⎫∆=-+=->⎪⎝⎭,解得k <或k >k的取值范围为22⎛⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭,,∞∞.(Ⅱ)设1122()()P x y Q x y ,,,,则1212()OP OQ x x y y +=++,,由方程①,12212x x k +=-+. ②又1212()y y k x x +=++ ③而(01)(A B AB =,,. 所以OP OQ + 与AB共线等价于1212)x x y y +=+,将②③代入上式,解得2k =.由(Ⅰ)知2k <-或2k >,故没有符合题意的常数k . 20.解:每个点落入M 中的概率均为14p =. 依题意知1~100004X B ⎛⎫ ⎪⎝⎭,. (Ⅰ)11000025004EX =⨯=. (Ⅱ)依题意所求概率为0.03410.0310000X P ⎛⎫-<⨯-< ⎪⎝⎭,0.03410.03(24252575)10000X P P X ⎛⎫-<⨯-<=<< ⎪⎝⎭2574100001000024260.250.75tt t t C-==⨯⨯∑2574242510000100001100001000024260.250.750.250.75tt ttt t t CC --===⨯⨯-⨯⨯∑∑0.95700.04230.9147=-=.21.解: (Ⅰ)1()2f x x x a'=++, 依题意有(1)0f '-=,故32a =. 从而2231(21)(1)()3322x x x x f x x x ++++'==++. ()f x 的定义域为32⎛⎫-+ ⎪⎝⎭,∞,当312x -<<-时,()0f x '>;当112x -<<-时,()0f x '<; 当12x >-时,()0f x '>. 从而,()f x 分别在区间31122⎛⎫⎛⎫---+ ⎪ ⎪⎝⎭⎝⎭,,,∞单调增加,在区间112⎛⎫-- ⎪⎝⎭,单调减少. (Ⅱ)()f x 的定义域为()a -+,∞,2221()x ax f x x a++'=+. 方程22210x ax ++=的判别式248a ∆=-.(ⅰ)若0∆<,即a <<()f x 的定义域内()0f x '>,故()f x 的极值.(ⅱ)若0∆=,则a 或a =若a =,()x ∈+∞,()f x '=当2x =-时,()0f x '=,当22x ⎛⎛⎫∈--+ ⎪ ⎪⎝⎭⎝⎭,∞时,()0f x '>,所以()f x 无极值.若a =)x ∈+∞,2()0f x '=>,()f x 也无极值.(ⅲ)若0∆>,即a >或a <,则22210x ax ++=有两个不同的实根12a x --=,2x =当a <12x a x a <-<-,,从而()f x '有()f x 的定义域内没有零点,故()f x 无极值.当a >时,1x a >-,2x a >-,()f x '在()f x 的定义域内有两个不同的零点,由根值判别方法知()f x 在12x x x x ==,取得极值.综上,()f x 存在极值时,a 的取值范围为)+∞. ()f x 的极值之和为2221211221()()ln()ln()ln 11ln 2ln 22e f x f x x a x x a x a +=+++++=+->-=.22.A(Ⅰ)证明:连结OP OM ,.因为AP 与O 相切于点P ,所以OP AP ⊥. 因为M 是O 的弦BC 的中点,所以OM BC ⊥. 于是180OPA OMA ∠+∠=°.由圆心O 在PAC ∠的内部,可知四边形APOM 的对角互补,所以A P O M ,,,四点共圆.(Ⅱ)解:由(Ⅰ)得A P O M ,,,四点共圆,所以OAM OPM ∠=∠. 由(Ⅰ)得OP AP ⊥.由圆心O 在PAC ∠的内部,可知90OPM APM ∠+∠=°. 所以90OAM APM ∠+∠=°. 22.B解:以极点为原点,极轴为x 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位. (Ⅰ)cos x ρθ=,sin y ρθ=,由4cos ρθ=得24cos ρρθ=. 所以224x y x +=.即2240x y x +-=为1O 的直角坐标方程. 同理2240x y y ++=为2O 的直角坐标方程.(Ⅱ)由22224040x y x x y y ⎧+-=⎪⎨++=⎪⎩,解得1100x y =⎧⎨=⎩,,2222x y =⎧⎨=-⎩. 即1O ,2O 交于点(00),和(22)-,.过交点的直线的直角坐标方程为y x =-. 22.C解:(Ⅰ)令214y x x =+--,则1521334254x x y x x x x ⎧---⎪⎪⎪=--<<⎨⎪⎪+⎪⎩, ,, ,, .≤≥...............3分作出函数214y x x =+--的图象,它与直线2y =的交点为(72)-,和523⎛⎫ ⎪⎝⎭,. 所以2142x x +-->的解集为5(7)3x x ⎛⎫--+ ⎪⎝⎭,,. A(Ⅱ)由函数214y x x =+--的图像可知,当12x =-时,214y x x =+--取得最小值92-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
201007试卷答案2010年7月江苏省高等教育自学考试02191机械制造技术一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题后的括号内。
(每小题1分,共10分)1.刃倾角的功能之一是控制切屑流向,若刃倾角为负,则切屑流向( A )A.已加工表面B.待加工表面C.过渡表面D.切削刃的法线方向2.装配尺寸链的封闭环是( B )A.精度要求最高的环B.要保证的装配精度C.尺寸最小的环D.基本尺寸为零的环3.工件采用心轴定位时,定位基准面是( B )A.心轴外圆柱面B.工件内圆柱面C.心轴中心线D.工件孔中心线4.切削用量对切削力的影响由大到小的是( D )5.在下列齿轮齿形加工方法中,属于成形法加工齿形的是( A )P147A.铣齿B.插齿C.剃齿D.珩齿6.在机械加工时,工件表面产生波纹的原因是( C )P268A.工件表面有裂纹B.残余应力C.切削过程中的振动D.塑性变形7.工件在车床三爪卡盘上一次装夹车削外圆及端面,加工后检验发现端面与外圆不垂直,其可能的原因是( C )A.车床主轴径向跳动B.主轴回转轴线与纵导轨不平行C.主轴回转轴线与横导轨不平行D.三爪卡盘装夹面与主轴轴线不同轴8.定位基准是指( C )vfaDfvaCpp、、、、..vafBafvApp、、、、..A.机床上的某些点、线、面B.夹具上的某些点、线、面C.工件上的某些点、线、面D.刀具上的某些点、线、面9.镗床上镗孔时主轴有角度摆动,镗出的孔将呈现( B )P218A.圆孔B.椭圆孔C.圆锥孔D.双曲线孔10.由一个工人在一台设备上对一个工件所连续完成的那部分工艺过程,称为( D )A.走刀B.工步C.工位D.工序二、填空题(每空1分,共10分)11.车削加工时,增大刀具的主偏角,会使表面粗糙度增加。
P6512.影响切削层参数、切削分力的大小和比例、刀尖强度及散热条件的刀具角度是Kr 。
P 46、P6413.磨削加工的实质是磨粒对工件进行刻划、滑擦和切削三种作用的综合过程。
P79-8014.切削铸铁时,刀具的磨损部位主要发生在主后刀面。
P5315.在正常条件下(采用符合标准的设备、工艺装备和标准技术等级的工人,不延长加工时间)所能保证的加工精度称为加工经济精度。
P30216.生产中,保证装配精度的装配方法有互换法、分组法、修配法和调整法。
P365-37317.在机械加工中,由于加工余量不均匀、材料硬度不均匀、夹紧力时大时小等原因引起的加工误差属随机误差。
P24218.车削加工时的切削力可分解为切削力F c、背向力F p和进给力F f,其中最大的分力是F c。
(是主切削力、P40)19.在粗基准选择中,为保证某重要加工表面余量均匀,应选择该重要表面作为粗基准。
P299 20.机械加工中选择机床时,要求机床的尺寸规格、精度等级、加工效率及机床功率与本工件加工工序要求相适应。
P318三、判断改错题(每小题2分,共10分),在题后的括号内,正确的打√,错误的打×,并在题下空处进行改正。
21.刀具的标注角度随着刀具的安装条件和进给量的大小变化而变化。
(×)答:标注角度是设计刀具用的,标注在图上的。
(刀具的工作角度(实际角度)随着刀具的安装条件和进给量的大小变化而变化)(P13)22.工序尺寸偏差一般采用“入体原则”标注,因此对于轴类外圆表面工序尺寸,应标成下偏差为零。
(×)答:工序尺寸偏差一般采用“入体原则”标注,因此对于轴类外圆表面工序尺寸,应标成上偏差为零。
P31423.镗床类机床的主轴采用滑动轴承结构时,主轴轴颈的圆度误差对加工精度影响较大,而轴承孔的圆度误差对加工精度影响较小。
(×)答:镗床类机床的主轴采用滑动轴承结构时,主轴轴颈的圆度误差对加工精度影响不大,而轴承孔的圆度误差对加工精度影响较大。
(P216)24.机床内、外联系传动链误差均会影响展成法加工工件的加工精度。
(×)答:(P137)内联系传动链误差会影响展成法加工工件的加工精度外联系传动链误差不会影响展成法加工工件的加工精度(联系两个执行件,以形成复合成形运动的传动链,称为内联系传动链。
它的作用是保证两个末端件之间的相对速度或相对位移保持严格的比例关系,以保证被加工表面的性质。
外联系传动链传动比的变化,只影响生产率或表面粗糙度,不影响加工表面的形状。
因此,外联系传动链不要求两末端件之间有严格的传动关系。
)25.在加工塑性材料时,随切削条件的不同会分别得到带状切屑、单元切屑和崩碎切屑。
(×)答:加工塑性材料时,随切削条件的不同会分别得到带状切屑、挤裂切屑和单元切屑,不会出现崩碎切屑(P34~35)四、名词解释题(每小题3分,共12分)26.主偏角KrP1227.刀具磨钝标注P5528.定位误差P184~18529.零件的结构工艺性P293五、简答题(每小题5分,共20分)30.在零件机械加工过程中,精基准选择原则有哪些?解:P300~30131.如题图31所示,工件以一个平面和一个短圆柱销和一个V形架定位。
试分析各定位元件分别限制了哪些自由度?有无过定位现象?怎样改进?题31图解:如图所示,平面限制的自由度Z移动、X和Y的转动;圆柱销限制的自由度X和Y移动V形块限制的自由度X的移动、Z的转动所以,出现了过定位现象。
改进方案:V形架改为活动可调,仅约束Z的转动自由度。
32.为什么要研究切削热的产生和传出?切削热产生得越多能否说明切削区的温度越高?解: P48 P49、P51切削热的产生和传出决定切削区的切削温度。
产生切削热的多少取决于切削功消耗的多少。
切削区的切削温度的高低不仅与产生的切削热多少有关,还与由刀具、切屑、工件及周围介质传出的热量多少有关。
如果产生的热量多于传出的热量,切削温度就升高,反之,切削温度就降低。
所以,仅以切削热产生的多少不能决定切削区的温度。
33.在粗加工、精加工中分别应如何选择切削用量? 解:P68~71 粗加工 精加工 a p 尽可能大 一次切完全部用量 f 尽可能大 合理选用,受工件精度和表面粗糙度影响 v c a p 、f 确定后,根据合理的刀具耐用度确定粗加工a p 、f 尽可能大,a p 、f 确定后,根据合理的刀具耐用度确定v c 。
精加工a p 一次切完全部用量,f 合理选用,受工件精度和表面粗糙度影响,a p 、f 确定后,根据合理的刀具耐用度确定v c六、分析题(每小题6分,共18分)34.题34图两种粗基准选择方案,图a )为以导轨面为粗基准,图b )为以床腿为粗基准。
指出哪种方案好,并说明理由。
a b 题34图 解:得分 评分人复查人图a方案较好,a方案先以导轨面为粗基准加工床腿,再以床腿为精基准加工导轨面,这样有利于导轨面的加工余量小且较均匀,提高导轨面的耐磨性。
P29935.如题35图所示,在卧式铣床上铣削键槽,经测量发现两端的深度大于中间的深度,且都比调整的深度尺寸小,试分析产生这一现象的原因?题35图解:原因:1.工件刚度低,特别是中段,将产生受力变形而让刀。
故两端深,中间段浅。
2.铣刀杆也会因受力变形而反向让刀。
36.某小轴上有一外圆,直径为Ф28h6,表面粗糙度为0.8 ,其加工方案为粗车-精车-淬火-磨削。
生产类型为成批生产,毛坯为普通的热轧圆钢,试计算粗车工序余量和各次加工的工序尺寸和公差,并填入题36表。
题36表m工序余量 工序尺寸公差 工序尺寸及偏差标注 磨削 0.3 0.013,h6精车 0.9 0.084,h10 粗车 2.8 0.28,h12 毛坯尺寸4(总余量)+0.40 -0.75七、计算题(每小题10分,共20分)37. 车床主轴上一双联齿轮的装配关系如题37图所示。
为保证齿轮的正常工作,要求其轴向间隙为0.05~0.20mm 。
当采用完全互换法装配时,试采用等公差法确定各组成环公差和偏差。
题37图得分 评分人复查人0015.0-5.2解:T0=0.2-0.05=0.15mmT2.5=0.015mmT104=T8.5=T115=(0.15-0.015)/3=0.045mm所以:38.一批圆柱销外圆的设计尺寸为 ,加工后测量发现外圆尺寸按正态规律分布,其均方根偏差为0.004mm ,曲线顶峰位置偏离公差带中心,向右偏移0.005mm 。
(1) 试绘出分布曲线图,并求出常值系统误差和工序能力系数。
(2) 是否产生废品?若产生,可采取哪些措施减少废品率?解:(1)绘制分布曲线图mm A mm A mm A 045.001050045.01040045.0-5.21051045.8+-===;;mm 02.0-04.0-60φΔ常=0.005mm,工序能力不足(2)产生废品,图中阴影区减少废品率措施: ①减小常值系统误差;②改进加工工艺;③提高机床精度。
183.0004.0602.06<=⨯==σT C p。
