高考2016届高考数学总复习 第五章 第4节 数列求和课件
合集下载
高考数学第五章数列求和-教学课件

[冲关锦囊] 分组求和常见类型及方法
(1)an=kn+b,利用等差数列前n项和公式直接求解; (2)an=a·qn-1,利用等比数列前n项和公式直接求解; (3)an=bn±cn,数列{bn},{cn}是等比数列或等差数列,
采用分组求和法求{an}的前n项和.
[精析考题] [例2] (2011·辽宁高考)已知等差数列{an}满足a2=0,a6+a8=-10. (1)求数列{an}的通项公式; (2)求数列{2an-n 1}的前n项和.
解:(1)因为{an}是首项为a1=19,公差为d=-2的等差数列,所以an= 19-2(n-1)=-2n+21. Sn=19n+nn2-1·(-2)=-n2+20n. (2)由题意知bn-an=3n-1,所以bn=3n-1+an=3n-1-2n+21. Tn=Sn+(1+3+…+3n-1)=-n2+20n+3n-2 1.
解析:∵Sn=2+2·22+3·23+…+n·2n① ∴2Sn=22+2·23+3·24+…+(n-1)·2n+n·2n+1② ①-②得 -Sn=2+22+23+…+2n-n·2n+1 =211--22n-n·2n+1=2n+1-2-n·2n+1, ∴Sn=(n-1)·2n+1+2.
答案:(n-1)·2n+1+2
n C.n-1
n+1 D. n
解析:∵f′(x)=mxm-1+a,∴m=2,a=1. ∴f(x)=x2+x,f(n)=n2+n, ∴f1n=n2+1 n=nn1+1=n1-n+1 1, ∴Sn=f11+f12+f13+…+fn-1 1+f1n =1-12+12-13+13-14+…+n-1 1-n1+n1-n+1 1 =1-n+1 1=n+n 1.
[自主解答] (1)设数列{an}的公比为q.由a23=9a2a6得 a23=9a24,所以q2=19.由条件可知q>0,故q=13. 由2a1+3a2=1,得2a1+3a1q=1,得a1=13. 故数列{an}的通项公式为an=31n.
【高考讲坛】2016届高考数学一轮复习 第5章 第4节 数列求和课件 理 苏教版

3
所以 bn-an=(b1-a1)qn-1=2n-1. 从而 bn=3n+2n-1(n=1,2,„).
(2)由(1)知 bn=3n+2n 1(n=1,2,„).
-
n 1 - 2 3 数列{3n}的前 n 项和为2n(n+1), 数列{2n-1}的前 n 项和为 1-2
=2n-1. 3 所以,数列{bn}的前 n 项和为2n(n+1)+2n-1.
固 基 础 · 自 主 落 实
第四节
数列求和
启 智 慧 · 高 考 研 析
提 知 能 · 典 例 探 究
课 后 限 时 自 测
内容 A 考纲传真 等差数列 等比数列
要求 B C √ √
1.公式法 直接利用等差数列、等比数列的前 n 项和公式求和 (1)等差数列的前 n 项和公式: na1+an nn-1 Sn= =na1+ 2 d; 2 (2)等比数列的前 n 项和公式: na1,q=1, Sn=a1-anq a11-qn = ,q≠1. 1 - q 1 - q
2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和 相等或等于同一个常数,可用倒序相加法求和,如等差数列的前 n 项和公式即是用此法推导的. 3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对 应项之积构成的,可用错位相减法求和.
4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以 相互抵消,从而求得其和. (2)裂项时常用的三种变形: 1 1 1 ① = - ; nn+1 n n+1 1 1 1 1 ② =22n-1-2n+1 ; 2n-12n+1 ③ 1 n+ n+1 = n+1- n.
【典例 3】 (2013· 江西高考)正项数列{an}的前 n 项和 Sn 满足:
所以 bn-an=(b1-a1)qn-1=2n-1. 从而 bn=3n+2n-1(n=1,2,„).
(2)由(1)知 bn=3n+2n 1(n=1,2,„).
-
n 1 - 2 3 数列{3n}的前 n 项和为2n(n+1), 数列{2n-1}的前 n 项和为 1-2
=2n-1. 3 所以,数列{bn}的前 n 项和为2n(n+1)+2n-1.
固 基 础 · 自 主 落 实
第四节
数列求和
启 智 慧 · 高 考 研 析
提 知 能 · 典 例 探 究
课 后 限 时 自 测
内容 A 考纲传真 等差数列 等比数列
要求 B C √ √
1.公式法 直接利用等差数列、等比数列的前 n 项和公式求和 (1)等差数列的前 n 项和公式: na1+an nn-1 Sn= =na1+ 2 d; 2 (2)等比数列的前 n 项和公式: na1,q=1, Sn=a1-anq a11-qn = ,q≠1. 1 - q 1 - q
2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和 相等或等于同一个常数,可用倒序相加法求和,如等差数列的前 n 项和公式即是用此法推导的. 3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对 应项之积构成的,可用错位相减法求和.
4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以 相互抵消,从而求得其和. (2)裂项时常用的三种变形: 1 1 1 ① = - ; nn+1 n n+1 1 1 1 1 ② =22n-1-2n+1 ; 2n-12n+1 ③ 1 n+ n+1 = n+1- n.
【典例 3】 (2013· 江西高考)正项数列{an}的前 n 项和 Sn 满足:
高考数学一轮总复习 第5章 数列 第4节 数列求和课件 理 新人教版
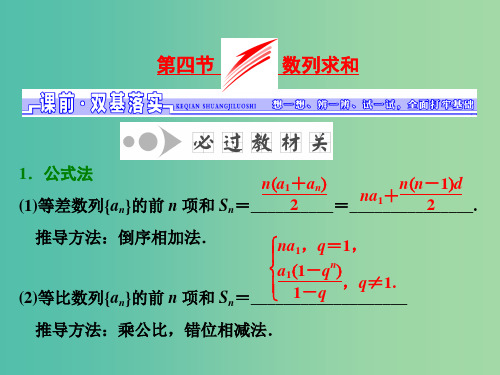
2.若等比数列{an}满足 a1+a4=10,a2+a5=20,则{an}的前 n 项和 Sn=________.
解析:由题意 a2+a5=q(a1+a4),得 20=q×10,故 q=2, 代入 a1+a4=a1+a1q3=10,得 9a1=10,即 a1=190. 故 Sn=19011--22n=190(2n-1). 答案:190(2n-1)
(2015·湖北高考)设等差数列{an}的公差为 d,前 n 项和为 Sn,等 比数列{bn}的公比为 q.已知 b1=a1,b2=2,q=d,S10=100. (1)求数列{an},{bn}的通项公式; (2)当 d>1 时,记 cn=abnn,求数列{cn}的前 n 项和 Tn.
解析
[由题悟法]
bn=3
an+1 2
,求数列an+2 1·bn的前
n
项和
Sn.
an+1
解:由(1)可得 bn=3 2 =3n,
所以an+2 1·bn=n·3n,
[即时应用]
已知等比数列{an}中,首项 a1=3,公比 q>1,且 3(an+2 +an)-10an+1=0(n∈N*). (1)求数列{an}的通项公式; (2)设bn+13an是首项为 1,公差为 2 的等差数列,求数列 {bn}的通项公式和前 n 项和 Sn.
解析
考点三 错位相减法求和 重点保分型考点——师生共研 [典例引领]
(3)错位相减法:如果一个数列的各项是由一个等差数列和 一个等比数列的对应项之积构成的,那么求这个数列 的前 n 项和即可用错位相减法求解.
(4)倒序相加法:如果一个数列{an}与首末两端等“距离” 的两项的和相等或等于同一个常数,那么求这个数列 的前 n 项和即可用倒序相加法求解.
2016版高考数学大一轮复习课件:第5章-第4节数列求和
名师金典·新课标高考总复习·理科数学
基 础 知 识 点
核 心 考 向
菜单
方 法 技 巧
第四节 数列求和
课 时 限 时 检 测
第一页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
基 础 知 识 点
方 法 技 巧
[考情展望] 1.考查等差、等比数列的求和.2.以数列求和 为载体,考查数列求和的各种方法和技巧.
用分组求和法求{an}的前 n 项和.
(2)通项公式为 an=bcnn,,nn为为偶奇数数, 的数列,其中数列 课
核
时
心 考
{bn},{cn}是等比数列或等差数列,可采用分组求和法求和.
限 时
向
检
测
菜单
第十七页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
对点训练 (2014·湖南高考)已知数列{an}的前 n 项和 Sn
限 时
向
=311--33n-211--22n=3n2+1-2n+1+12.
检 测
菜单
第十六页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
基 础 知 识 点
规律方法 1 分组转化法求和的常见类型
方 法
技
(1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采 巧
基 础
(2)由(1)知a2n-11a2n+1=3-2n11-2n
知
识 点
=122n1-3-2n1-1,
方 法 技 巧
从而数列a2n-11a2n+1的前 n 项和为
核
12-11-11+11-13+…+2n1-3-2n1-1
基 础 知 识 点
核 心 考 向
菜单
方 法 技 巧
第四节 数列求和
课 时 限 时 检 测
第一页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
基 础 知 识 点
方 法 技 巧
[考情展望] 1.考查等差、等比数列的求和.2.以数列求和 为载体,考查数列求和的各种方法和技巧.
用分组求和法求{an}的前 n 项和.
(2)通项公式为 an=bcnn,,nn为为偶奇数数, 的数列,其中数列 课
核
时
心 考
{bn},{cn}是等比数列或等差数列,可采用分组求和法求和.
限 时
向
检
测
菜单
第十七页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
对点训练 (2014·湖南高考)已知数列{an}的前 n 项和 Sn
限 时
向
=311--33n-211--22n=3n2+1-2n+1+12.
检 测
菜单
第十六页,编辑于星期五:二十三点 五十五分。
名师金典·新课标高考总复习·理科数学
基 础 知 识 点
规律方法 1 分组转化法求和的常见类型
方 法
技
(1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采 巧
基 础
(2)由(1)知a2n-11a2n+1=3-2n11-2n
知
识 点
=122n1-3-2n1-1,
方 法 技 巧
从而数列a2n-11a2n+1的前 n 项和为
核
12-11-11+11-13+…+2n1-3-2n1-1
苏教版高三数学复习课件5.4 数列的求和

答案: 答案:
5. (2010·南京市第九中学调研测试 已知数列 n}满足:an= . 南京市第九中学调研测试)已知数列 满足: 南京市第九中学调研测试 已知数列{a 满足 则数列{a 的前 的前100项的和是 项的和是________. 则数列 n}的前 项的和是 . 解析: 解析:an=
∴a1+a2+…+a100=
6.常见的拆项公式有: .常见的拆项公式有:
(1)
(2)
(3) 思考:用裂项相消法求数列前 项和的前提是什么 项和的前提是什么? 思考:用裂项相消法求数列前n项和的前提是什么? 提示:数列中的每一项均能分裂成一正一负两项,这是用裂项相消法的前提. 提示:数列中的每一项均能分裂成一正一负两项,这是用裂项相消法的前提.
第4课时 数列的求和
掌握数列求和的几种常见方法. 掌握数列求和的几种常见方法. 【命题预测】 命题预测】 数列的求和在近几年高考中,填空题与解答题都有出现 , 重点以容易题和中档 数列的求和在近几年高考中 , 填空题与解答题都有出现, 题为主,基本知识以客观题出现,综合知识则多以解答题体现, 题为主 , 基本知识以客观题出现 , 综合知识则多以解答题体现 , 主要是探索型 和综合型题目.复习时,要具有针对性地训练,并以“注重数学思想方法、 和综合型题目 . 复习时 , 要具有针对性地训练 , 并以 “ 注重数学思想方法 、 强 化运算能力、重点知识重点训练”的角度做好充分准备. 化运算能力、重点知识重点训练”的角度做好充分准备.
1. 数列 . 数列0.9,0.99,0.999,…, ,
项和为________. …的前n项和为 的前 项和为 .
解析:数列的通项公式为 其前n项和 解析:数列的通项公式为an=1-0.1n,其前 项和 -
高考数学一轮复习 第5篇 第4节 数列求和课件 文 新人教版

等比数列或等差数列,可采用分组求和法求和.
即时突破 1 (2013 包头模拟)已知数列{xn}的首项 x1=3,通项
xn=2 p+nq(n∈N ,p,q 为常数),且 x1,x4,x5 成等差数列.求: (1)p,q 的值; (2)数列{xn}前 n 项和 Sn. 解:(1)由 x1=3,得 2p+q=3, 4 5 又因为 x4=2 p+4q,x5=2 p+5q,且 x1+x5=2x4, 5 5 即 3+2 p+5q=2 p+8q,解得 p=1,q=1. (2)由(1),知 xn=2n+n, 所以 Sn=(2+2 +…+2 )+(1+2+…+n)=2 -2+
2 n-1
反思归纳
分组转化法求和的解题策略:
(1)数列求和应从通项入手,通过对通项变形,转化为等差数 列或等比数列或可求前 n 项和的数列求和. (2)分组转化法求和的常见类型 ①若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组 求和法求{an}的前 n 项和.
bn , n为奇数, ②通项公式为 an= 的数列,其中数列{bn},{cn}是 cn , n为偶数
100 1 100 2
2
=5050, 故选 C.
4.设数列{an}的通项公式为 an=2 ,令 bn=nan,则数列{bn}的 前 n 项和 Sn 为 . 2n-1 解析:由 bn=nan=n·2 知 Sn=1·2+2·23+3·25+…+n·22n-1, ① 从而 2 ·Sn=1·2 +2·2 +3·2 +…+n·2 ①-②得(1-22)·Sn =2+2 +2 +…+2
高考数学一轮复习第五章数列第4讲数列求和课件文

已知数列{an}的通项公式是 an=2·3n-1+ (-1)n(ln 2-ln 3)+(-1)nnln 3,求其前 n 项和 Sn. [解] Sn=2(1+3+…+3n-1)+[-1+1-1+…+(-1)n](ln 2 -ln 3)+[-1+2-3+…+(-1)nn]ln 3, 所以当 n 为偶数时, Sn=2×11--33n+n2ln 3=3n+n2ln 3-1; 当 n 为奇数时,
分组转化法求和的常见类型 (1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分 组转化法求{an}的前 n 项和. (2)通项公式为 an=bcnn,,nn为为偶奇数数的数列,其中数列{bn},{cn} 是等比数列或等差数列,可采用分组转化法求{an}的前 n 项 和.
3.等比数列{an}的首项为 a,公比为 q,Sn 为其前 n 项的和, 求 S1+S2+…+Sn. [解] 当 q=1 时,an=a,Sn=na, 所以 S1+S2+…+Sn=(1+2+…+n)a=n(n2+1)a. 当 q≠1 时, 因为 Sn=a(11--qqn),所以 S1+S2+…+Sn
Tn=11-12+12-13+13-14+…+n1-n+1 1=1-n+1 1=
n n+1.
利用裂项相消法求和时,应注意抵消后并不一定只剩下第一 项和最后一项,也有可能前面剩两项,后面也剩两项,再就 是将通项公式裂项后,有时候需要调整前面的系数,使裂开 的两项之差和系数之积与原通项公式相等.
2Tn=3×[2×23+3×24+…+(n+1)×2n+2], 两 式 作 差 , 得 - Tn = 3×[2×22 + 23 + 24 + … + 2n + 1 - (n +
1)×2n+2]=3×4+4(11--22n)-(n+1)×2n+2
2016年高考数学总复习课件:第五章 第4讲 数列的求和

则求和时,可采用分组求和,即先分别求和,再将各部分合并.
第十页,编辑于星期五:二十三点 二十八分。
【互动探究】 1.(2013 年重庆)设数列{an}满足 a1=1,an+1=3an,n∈N*. (1)求{an}的通项公式及前 n 项和 Sn; (2)已知{bn}是等差数列,前 n 项和为 Tn,且 b1=a2,b3= a1+a2+a3,求 T20.
4.数列{an}的通项公式为 an=
1 n+
n+1,若前
n
项的和
为 10,则项数 n=______12_0_.
第七页,编辑于星期五:二十三点 二十八分。
考点 1 公式或分组法求和 例 1:(2014 年湖南)已知数列{an}的前 n 项和 Sn=n2+2 n, n∈N*. (1)求数列{an}的通项公式; (2)设 bn=2an +(-1)nan,求数列{bn}的前 2n 项和.
第八页,编辑于星期五:二十三点 二十八分。
解:(1)当 n=1 时,a1=S1=1+2 1=1. 由 Sn=n2+2 n,得 Sn-1=n-12+2 n-1. ∴当 n≥2 时,an=Sn-Sn-1=n2+2 n -n-12+2 n-1=n. 经检验,首项 a1 也满足 an=n. ∴数列{an}的通项公式为 an=n.
第二十一页,编辑于星期五:二十三点 二十八 分。
(2)由bn=3n-1知,an=(2n-1)3n-1, 于是数列{an}的前n项和 Sn=1×30+3×31+5×32+…+(2n-1)×3n-1, 3Sn=1×31+3×32+…+(2n-3)×3n-1+(2n-1)×3n, 两式相减,得-2Sn=1+2×(31+32+…+3n-1)- (2n-1)×3n=-2-(2n-2)×3n. ∴Sn=(n-1)3n+1.
第十页,编辑于星期五:二十三点 二十八分。
【互动探究】 1.(2013 年重庆)设数列{an}满足 a1=1,an+1=3an,n∈N*. (1)求{an}的通项公式及前 n 项和 Sn; (2)已知{bn}是等差数列,前 n 项和为 Tn,且 b1=a2,b3= a1+a2+a3,求 T20.
4.数列{an}的通项公式为 an=
1 n+
n+1,若前
n
项的和
为 10,则项数 n=______12_0_.
第七页,编辑于星期五:二十三点 二十八分。
考点 1 公式或分组法求和 例 1:(2014 年湖南)已知数列{an}的前 n 项和 Sn=n2+2 n, n∈N*. (1)求数列{an}的通项公式; (2)设 bn=2an +(-1)nan,求数列{bn}的前 2n 项和.
第八页,编辑于星期五:二十三点 二十八分。
解:(1)当 n=1 时,a1=S1=1+2 1=1. 由 Sn=n2+2 n,得 Sn-1=n-12+2 n-1. ∴当 n≥2 时,an=Sn-Sn-1=n2+2 n -n-12+2 n-1=n. 经检验,首项 a1 也满足 an=n. ∴数列{an}的通项公式为 an=n.
第二十一页,编辑于星期五:二十三点 二十八 分。
(2)由bn=3n-1知,an=(2n-1)3n-1, 于是数列{an}的前n项和 Sn=1×30+3×31+5×32+…+(2n-1)×3n-1, 3Sn=1×31+3×32+…+(2n-3)×3n-1+(2n-1)×3n, 两式相减,得-2Sn=1+2×(31+32+…+3n-1)- (2n-1)×3n=-2-(2n-2)×3n. ∴Sn=(n-1)3n+1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.15 B.12 C.-12 D.-15
[解析] ∵an=(-1)n(3n-2), ∴a1+a2+…+a10=(-1+4)+(-7+10)+…+(-25+28)=
3×5=15.
[答案] A
A
9
4.数列{an}中,an=n(n1+1),若{an}的前 n 项和为22 001145,则项 数 n 为( ) A.2 013 B.2 014 C.2 015 D.2 016 [解析] 因为 an=n(n1+1)=1n-n+1 1, 所以 Sn=a1+a2+…+an =1-12+12-13+…+1n-n+1 1=n+n 1, 由已知得 Sn=n+n 1=22 001145,解得 n=2 014.
(2)通项公式为 an=bcnn,,nn为为奇偶数数,的数列,其中数列{bn},{cn}
是等比数列或等差数列,可采用分组求和法求和.
A
15
【变式训练 1】(2014·北京高考)已知{an}是等差数列,满足 a1=3, a4=12,数列{bn}满足 b1=4,b4=20,且{bn-an}为等比数列. (1)求数列{an}和{bn}的通项公式; (2)求数列{bn}的前 n 项和.
A
4
4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和. (2)裂项时常用的三种变形:
①nபைடு நூலகம்n1+1)=1n-n+1 1;
②(2n-1)1(2n+1)=122n1-1-2n1+1;
1 ③ n+ n+1= n+1- n.
5.分组转化求和法 一个数列的通项公式是由若干个等差数列或等比数列或可求和的 数列组成,则求和时可用分组求和法,分别求和后相加减.
A
12
[解析]
(1)an=1+12+14+…+21n-1=1-121n
1-2
=21-21n,
∴Sn=21-12+1-212+…+1-21n =2(1+1+…+1)n个-12+212+…+21n =2n-1-21n=2n-2+21n-1.
[答案]
2n-2+2n1-1
A
13
(2)①当 n=1 时,a1=S1=1; 当 n≥2 时,an=Sn-Sn-1=n2+2 n-(n-1)2+2 (n-1)=n. 故数列{an}的通项公式为 an=n. ②由①知 an=n,故 bn=2n+(-1)nn. 记数列{bn}的前 2n 项和为 T2n,则 T2n=(21+22+…+22n)+(-1+2-3+4-…+2n).
乘以 a 即可根据错位相减法求得.( )
(4)如果数列{an}是周期为 k(k 为大于 1 的正整数)的周期数列,
那么 Skm=mSk.( )
[答案] (1)√ (2)√ (3)× (4)√
A
7
2.(教材改编)一个球从 100 m 高处自由落下,每次着地后又跳回到 原高度的一半再落下,当它第 10 次着地时,经过的路程是( ) A.100+200×(1-2-9) B.100+100(1-2-9) C.200(1-2-9) D.100(1-2-9)
A
5
1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误
的打“×”)
(1)如果数列{an}为等比数列,且公比不等于 1,则其前 n 项和
Sn=a11--aqn+1.(
)
A
6
(2)当 n≥2 时,n2-1 1=12n-1 1-n+1 1.(
)
(3)求 Sn=a+2a2+3a3+…+nan 之和时只要把上式等号两边同时
(1)等差数列的前 n 项和公式:
Sn=n(a1+ 2 an)= na1 +
n(n-1) 2d
.
A
3
2(2)等比数列的前 n 项和公式: na1,q=1,
Sn=a11--aqnq=a1(11--qqn),q≠1W. 2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和相等 或等于同一个常数,那么求这个数列的前 n 项和即可用倒序相加 法,如等差数列的前 n 项和公式即是用此法推导的. 3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项 之积构成的,这个数列的前 n 项和可用错位相减法.
[答案] C
A
11
考向 1 分组转化法求和
【典例 1】(1)数列 1,1+12,1+12+14,…,1+12+14+…+2n1-1
的前 n 项和 Sn=________. (2)(2014·湖南高考)已知数列{an}的前 n 项和 Sn=n2+2 n,n∈N*.
①求数列{an}的通项公式;
②设 bn=2an+(-1)nan,求数列{bn}的前 2n 项和
[解析] 第 10 次着地时,经过的路程为 100+2(50+25+…+100×2-9) =100+2×100×(2-1+2-2+…+2-9)
2-1(1-2-9) =100+200× 1-2-1 =100+200(1-2-9).
[答案] A
A
8
3.若数列{an}的通项公式是 an=(-1)n(3n-2),则 a1+a2+…+ a10=( )
固
启
基
智
础
慧
·
·
自
高
主
考
落 实
第四节 数列求和
研 析
提
知
课
能
后
·
限
典
时
例
自
探
测
究
A
1
[考纲传真]
1.熟练掌握等差、等比数列的前 n 项和公式. 2.掌握非等差、 等比数列求和的几种常见方法. 3.能在具体的问题情境中识别 数列的等差关系或等比关系,并能用相关知识解决相应的问题.
A
2
1.公式法
直接利用等差数列、等比数列的前 n 项和公式求和
记 A=21+22+…+22n,B=-1+2-3+4-…+2n,则
A=2(11--222n)=22n+1-2,
B=(-1+2)+(-3+4)+…+[-(2n-1)+2n]=n,
故数列{bn}的前 2n 项和 T2n=A+B=22n+1+n-2.
A
14
【规律方法】
分组转化法求和的常见类型:
(1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组 求和法求{an}的前 n 项和;
[答案] B
A
10
5.若数列{ an} 的通项公式为 an=2n+2n-1,则数列{ an} 的前 n 项和 Sn 为( )
A.2n+n2-1 B.2n+1+n2-1 C.2n+1+n2-2 D.2n+n2-2
[解析] Sn=(2+22+23+…+2n)+(1+3+5+…+(2n-1)) =2(11- -22n)+n(1+22n-1)=2n+1-2+n2.
[解析] ∵an=(-1)n(3n-2), ∴a1+a2+…+a10=(-1+4)+(-7+10)+…+(-25+28)=
3×5=15.
[答案] A
A
9
4.数列{an}中,an=n(n1+1),若{an}的前 n 项和为22 001145,则项 数 n 为( ) A.2 013 B.2 014 C.2 015 D.2 016 [解析] 因为 an=n(n1+1)=1n-n+1 1, 所以 Sn=a1+a2+…+an =1-12+12-13+…+1n-n+1 1=n+n 1, 由已知得 Sn=n+n 1=22 001145,解得 n=2 014.
(2)通项公式为 an=bcnn,,nn为为奇偶数数,的数列,其中数列{bn},{cn}
是等比数列或等差数列,可采用分组求和法求和.
A
15
【变式训练 1】(2014·北京高考)已知{an}是等差数列,满足 a1=3, a4=12,数列{bn}满足 b1=4,b4=20,且{bn-an}为等比数列. (1)求数列{an}和{bn}的通项公式; (2)求数列{bn}的前 n 项和.
A
4
4.裂项相消法 (1)把数列的通项拆成两项之差,在求和时中间的一些项可以相互 抵消,从而求得其和. (2)裂项时常用的三种变形:
①nபைடு நூலகம்n1+1)=1n-n+1 1;
②(2n-1)1(2n+1)=122n1-1-2n1+1;
1 ③ n+ n+1= n+1- n.
5.分组转化求和法 一个数列的通项公式是由若干个等差数列或等比数列或可求和的 数列组成,则求和时可用分组求和法,分别求和后相加减.
A
12
[解析]
(1)an=1+12+14+…+21n-1=1-121n
1-2
=21-21n,
∴Sn=21-12+1-212+…+1-21n =2(1+1+…+1)n个-12+212+…+21n =2n-1-21n=2n-2+21n-1.
[答案]
2n-2+2n1-1
A
13
(2)①当 n=1 时,a1=S1=1; 当 n≥2 时,an=Sn-Sn-1=n2+2 n-(n-1)2+2 (n-1)=n. 故数列{an}的通项公式为 an=n. ②由①知 an=n,故 bn=2n+(-1)nn. 记数列{bn}的前 2n 项和为 T2n,则 T2n=(21+22+…+22n)+(-1+2-3+4-…+2n).
乘以 a 即可根据错位相减法求得.( )
(4)如果数列{an}是周期为 k(k 为大于 1 的正整数)的周期数列,
那么 Skm=mSk.( )
[答案] (1)√ (2)√ (3)× (4)√
A
7
2.(教材改编)一个球从 100 m 高处自由落下,每次着地后又跳回到 原高度的一半再落下,当它第 10 次着地时,经过的路程是( ) A.100+200×(1-2-9) B.100+100(1-2-9) C.200(1-2-9) D.100(1-2-9)
A
5
1.(夯基释疑)判断下列结论的正误.(正确的打“√”,错误
的打“×”)
(1)如果数列{an}为等比数列,且公比不等于 1,则其前 n 项和
Sn=a11--aqn+1.(
)
A
6
(2)当 n≥2 时,n2-1 1=12n-1 1-n+1 1.(
)
(3)求 Sn=a+2a2+3a3+…+nan 之和时只要把上式等号两边同时
(1)等差数列的前 n 项和公式:
Sn=n(a1+ 2 an)= na1 +
n(n-1) 2d
.
A
3
2(2)等比数列的前 n 项和公式: na1,q=1,
Sn=a11--aqnq=a1(11--qqn),q≠1W. 2.倒序相加法 如果一个数列{an}的前 n 项中首末两端等“距离”的两项的和相等 或等于同一个常数,那么求这个数列的前 n 项和即可用倒序相加 法,如等差数列的前 n 项和公式即是用此法推导的. 3.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项 之积构成的,这个数列的前 n 项和可用错位相减法.
[答案] C
A
11
考向 1 分组转化法求和
【典例 1】(1)数列 1,1+12,1+12+14,…,1+12+14+…+2n1-1
的前 n 项和 Sn=________. (2)(2014·湖南高考)已知数列{an}的前 n 项和 Sn=n2+2 n,n∈N*.
①求数列{an}的通项公式;
②设 bn=2an+(-1)nan,求数列{bn}的前 2n 项和
[解析] 第 10 次着地时,经过的路程为 100+2(50+25+…+100×2-9) =100+2×100×(2-1+2-2+…+2-9)
2-1(1-2-9) =100+200× 1-2-1 =100+200(1-2-9).
[答案] A
A
8
3.若数列{an}的通项公式是 an=(-1)n(3n-2),则 a1+a2+…+ a10=( )
固
启
基
智
础
慧
·
·
自
高
主
考
落 实
第四节 数列求和
研 析
提
知
课
能
后
·
限
典
时
例
自
探
测
究
A
1
[考纲传真]
1.熟练掌握等差、等比数列的前 n 项和公式. 2.掌握非等差、 等比数列求和的几种常见方法. 3.能在具体的问题情境中识别 数列的等差关系或等比关系,并能用相关知识解决相应的问题.
A
2
1.公式法
直接利用等差数列、等比数列的前 n 项和公式求和
记 A=21+22+…+22n,B=-1+2-3+4-…+2n,则
A=2(11--222n)=22n+1-2,
B=(-1+2)+(-3+4)+…+[-(2n-1)+2n]=n,
故数列{bn}的前 2n 项和 T2n=A+B=22n+1+n-2.
A
14
【规律方法】
分组转化法求和的常见类型:
(1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组 求和法求{an}的前 n 项和;
[答案] B
A
10
5.若数列{ an} 的通项公式为 an=2n+2n-1,则数列{ an} 的前 n 项和 Sn 为( )
A.2n+n2-1 B.2n+1+n2-1 C.2n+1+n2-2 D.2n+n2-2
[解析] Sn=(2+22+23+…+2n)+(1+3+5+…+(2n-1)) =2(11- -22n)+n(1+22n-1)=2n+1-2+n2.
