昆明理工大学理论力学练习册答案第七章后
昆明理工大学理论力学B练习册题解答
(∨)
1.1.17凡是两端用铰链连接的直杆都是二力杆。(×)
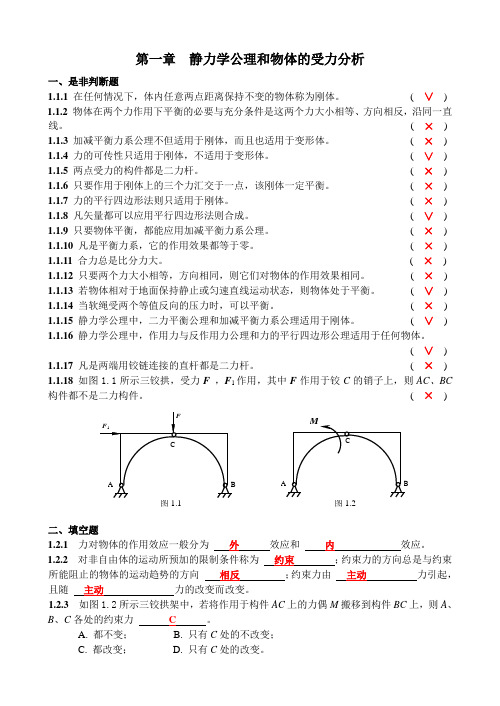
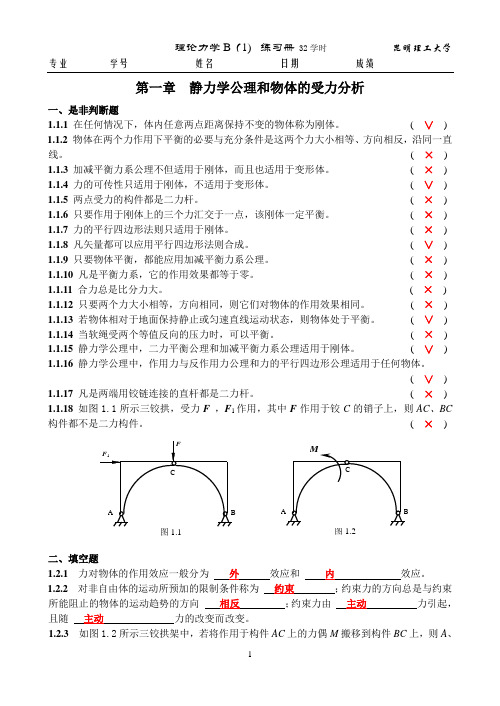
1.1.18如图1.1所示三铰拱,受力F,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。(×)
二、填空题
1.2.1力对物体的作用效应一般分为外效应和内效应。
三、受力图
1.3.1画出各物体的受力图。下列各图中所有接触均处于光滑面,各物体的自重除图中已标出的外,其余均略去不计。
1.3.2画出下列各物体系中各指定研究对象的受力图。接触面为光滑,各物自重除图中已画出的外均不计。
第二章 平面力系(汇交力系与平面偶系)
一、 是非判断题
2.1.1当刚体受三个不平行的力作用时,只要这三个力的作用线汇交于同一点,则刚体一定处于平衡状态。(×)
2.1.1一个任意力系的合力矢是主矢。(×)
2.1.2某平面任意力系向A、B两点简化的主矩皆为零,即MA=MB=0,此力系简化的最终结果为:
A、可能简化为一个力。(∨)
B、可能简化为一个力偶。(×)
C、可能平衡。(∨)
2.1.3若平面平行力系平衡,可以列出三个独立的平衡方程。(1个)(×)
2.1.4平面任意力系的三个独立平衡方程不能全部采用投影方程。(∨)
322板abcd由六根杆支承如图所示受任意已知力系而处于平衡为保证所列的每个方f1fcd三计算题331在图示力系中f1100nf2300nf3200n各力作用线位置如图所示求力系cos3002002002003453n100131001005f?rx300cos03f0xmx?rz01300f2cos300300100132496cos30003100131002001001056n02f1sin02100010z03f2sio3f3cos03300332如图所示的空间构架由三根杆件组成在my20030020010013200032003453i2496j1056k1005179nm1003664nm200032005179i3664j10359knm若各杆自重不计求各杆的内力
理论力学课后习题答案 第7章 质点动力学

习题7-2图习题7-3图习题7-1图(a) g m NF s F a(b)θs F N F gm a 第7章 质点动力学7-1 图示滑水运动员刚接触跳台斜面时,具有平行于斜面方向的速度40.2km/h ,忽略摩擦,并假设他一经接触跳台后,牵引绳就不再对运动员有作用力。
试求滑水运动员从飞离斜面到再落水时的水平长度。
解:接触跳台时 171136001024030..v =⨯=m/s 设运动员在斜面上无机械能损失7688442892171122020....gh v v =⨯⨯-=-=m/s 1418.cos v v x ==θm/s, 2563.sin v v y ==θm/s 5410221.g v h y ==m 33201.gv t y ==s 220121)(gt h h =+780.08.9)44.2541.0(2)(2012=+=+=g h h t s112.121=+=t t t s0591*******...t v x x =⨯==m7-2 图示消防人员为了扑灭高21m 仓库屋顶平台上的火灾,把水龙头置于离仓库墙基15m 、距地面高1m 处,如图所示。
水柱的初速度250=υm/s ,若欲使水柱正好能越过屋顶边缘到达屋顶平台,且不计空气阻力,试问水龙头的仰角α应为多少?水柱射到屋顶平台上的水平距离s 为多少? 解:(1) αcos v t 0115=(1) 2021sin 2110=-⋅gt t v α (2) (1)代入(2),得01.44cos sin 375cos 5002=+-ααα ααα22cos 1cos 3751.44cos 500-=+ 081.1944cos 96525cos 39062524=+-αα 22497.0cos 2=α, ︒=685.61α(2) gv t αsin 02=(到最高点所经过时间) 26.232)15cos (20=⨯-⋅=t v S αm7-3 图示三角形物块置于光滑水平面上,并以水平等加速度a 向右运动。
昆明理工大学--2008年《理论力学》工程力学班试题A答案

昆明理工大学2007~2008学年第一学期《理论力学》期末考试试卷(A 卷)答案1. 是非判断题(每题2分,共20分。
)1、×';2、×;3、√;4、×;5、×;6、×;7、√;8、√;9、√;10、√二、选择题(每题3分,共12分)ACD;AAA;C;C;三、填空题 (本题共13分)1. (本题6分)图(a )的 ω = 0 ,α =R a /; 图(b ) 的ω =R a /cos θ,α =R a /sin θ; 图(c ) 的ω =R a /,α = 0 。
2. (本题4分) L 2m ω(1分); ωω222224652322131mL L m L m mL =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+(1分);画出方向(共2分)3. (本题2分) PL/24. (本题2分)5四、计算题1. (本题10分)如图4.1所示横梁,F 1= F 2= F 3=F 用虚位移原理求解系统B 和D 处反力。
解:(1)把B 点约束力视作为主动力。
设给系统虚位移如图(图2分)。
系统虚功方程为:021=---δϕδδδM y F y F y F F E B B(2分) ==>567111MF F B +=(1分)(2)把D 点约束力视作为主动力。
设给系统虚位移如图(图2分)。
系统虚功方程为:032=++G F D D y F y F y F δδδ(2分) ==>F F B 2827=(1分)2. (本题15分)3. 弯成直角的曲杆OAB 以角速度ω= 常数绕O 点作逆时针转动。
在曲杆的AB 段装有滑筒C ,滑筒与在滑道内运动的铅直杆DC 铰接于C ,O 点与DC 位于同一铅垂线上。
设曲杆的OA段长为r ,求当φ=30°时DC 杆的速度和加速度。
(解):如图,在点O 建立参考基和曲杆连体基1e e 和。
对于曲杆OAB ,CD 杆上的C 点为动点。
昆明理工大学材料力学习题册1-14概念答案

第一章绪论一、是非判断题材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 内力只作用在杆件截面的形心处。
( × )杆件某截面上的内力是该截面上应力的代数和。
( × )确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ )根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ )根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ )同一截面上正应力σ与切应力τ必相互垂直。
( ∨ )同一截面上各点的正应力σ必定大小相等,方向相同。
( × )同一截面上各点的切应力τ必相互平行。
( × )应变分为正应变ε和切应变γ。
( ∨ )应变为无量纲量。
( ∨ )若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ )若物体内各点的应变均为零,则物体无位移。
( × )平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ )题图所示结构中,AD杆发生的变形为弯曲与压缩的组合变形。
( ∨ )题图所示结构中,AB杆将发生弯曲与压缩的组合变形。
( × )B题图题图二、填空题材料力学主要研究 受力后发生的,以及由此产生的 。
拉伸或压缩的受力特征是 ,变形特征是 。
剪切的受力特征是 ,变形特征是。
扭转的受力特征是 ,变形特征是 。
弯曲的受力特征是 ,变形特征是 。
组合受力与变形是指 。
构件的承载能力包括 , 和 三个方面。
所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
根据固体材料的性能作如下三个基本假设 , , 。
认为固体在其整个几何空间内无间隙地充满了组成该物体的物质,这样的假设称为 。
根据这一假设构件的 、 和 就可以用坐标的连续函数来表示。
填题图所示结构中,杆1发生 变形, 杆2发生 变形,杆3发生 变形。
理论力学 陈立群 第7章习题解答

第七章 质点动力学 习题解答7-1 质量为40 g 的小球M 以初速度v =8 j (m/s)从点A (0, 0, 0.3m)抛出后,受到沿i 方向恒定的电磁力作用,其大小F = 0.8 kN ,如图所示。
求小球M 到达xy 平面点B 时,点B 的坐标和小球的速度。
解:取小球M 为研究对象,小球所受到的主动力为 k i F mg F R -=由质点运动微分方程R F m =r ,写出投影式F x m = ,0=ym ,mg z m -= 初始条件为000====t t y x ,3.00==t z ;000====t t z x,v y t ==0 解得质点的速度方程为t mFx= ,v y = ,gt z -= 质点的运动方程为 22t m F x =,vt y =,3.022+-=t gz 当0=z 时,小球到达xy 平面,由03.022=+-=t g z 解得s 247.01=t ,于是小球到达xy 平面时的各速度分量为m/s 7.494811===t mFxt t ,m/s 81===v y t t ,m/s 425.211-=-==gt z t t . 各坐标为m 2.6122211===t m F x t t ,m 979.111===vt y t t ,m 137.23.02211-=+-==t gz tt .7-2 图示A ,B 两物体的质量分别为m A 和m B ,二者用一细绳连接,此绳跨过一定滑轮,滑轮半径为r 。
运动开始时,两物体的高度差为h ,且m A > m B ,不计滑轮质量。
求由静止释放后,两物体达到相同高度时所需的时间。
解:分别取A 和B 物体为研究对象,受力图如图示,列出动力学方程TA A A A F W x m -= , TB B B B F W x m -= , 式中g m W A A =,g m W B B =,根据题意,有TB TA F F =,B A x x -=,B A xx -= 初始条件00==t A x ,h x t B ==0,00==t A x,00==t B x . 解以上初值问题,得题7-2图g m m m m xBA B A A +-= , ()22gt m m m m x B A BA A +-=g m m m m x B A B A B +--= , ()h gt m m m m x B A BA B ++--=22令B A x x =,即()()h gt m m m m gt m m m m B A BA B A B A ++--=+-2222解得当两物体达到相同高度时 ()()gm m h m m t B A B A -+=...7-3 质量为m 的质点M 受到引力F = -k 2m r 的作用,其中k 为常量,运动开始时,质点M在轴x 上,OM 0 = b ,初速度v 0与轴x 的夹角为β,如图所示。
理论力学 第六版部分习题答案 第七章
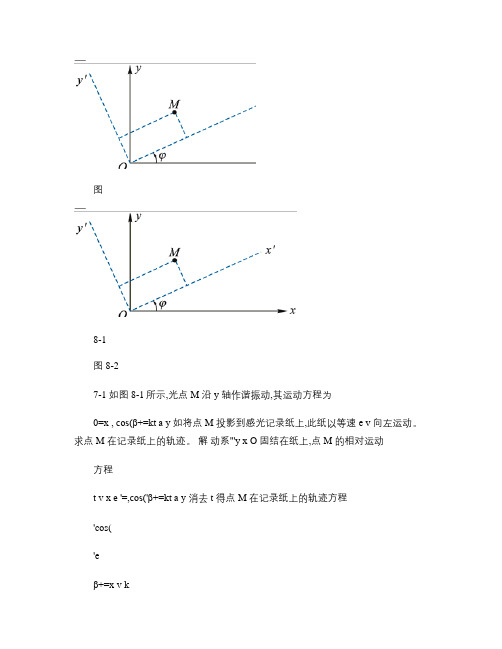
图8-1图8-27-1 如图8-1所示,光点M 沿y 轴作谐振动,其运动方程为0=x , cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解动系'''y x O 固结在纸上,点M 的相对运动方程t v x e '=,cos('β+=kt a y 消去t 得点M 在记录纸上的轨迹方程'cos('eβ+=x v ka y 7-2 如图8-2所示,点M 在平面''y Ox 中运动,运动方程为cos 1(40't x −=,t y sin 40'= 式中t 以s 计,'x 和'y 以mm 计。
平面''y Ox 又绕垂直于该平面的轴O 转动,转动方程为rad t =ϕ,式中角ϕ为动系的'x 轴与定系的x 轴间的交角。
求点M 的相对轨迹和绝对轨迹。
解由点M 的相对运动方程可改写为t yt x sin 40cos 140''=−=⎟⎟⎠⎞⎜⎜⎝⎛−上2式两边平方后相加,得点M 的相对轨迹方程 1600'40'(22=+−y x 由题得点M 的坐标变换关系式ϕϕsin 'cos 'y x x −= ϕϕcos 'sin 'y x y +=将t =ϕ和相对运动方程代入,消去t 得点M 的绝对轨迹方程160040(22=++y x7-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成°=60β角,如图8-3a 所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
′′v(a (b图8-3解水轮机工作轮入口处的1滴水为动点M ,动系固结于工作轮,定系固结于机架/地面(一般定系可不别说明,默认为固结于机架,下同;牵连运动为定轴转动,相对运动与叶片曲面相切,速度分析如图8-3b 所示,设θ为r v 与'x 轴的夹角。
昆明理工大学理论力学B练习册题+解答
第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学1-7章答案【精选】

习题7-1图Oυ(a)υυ(b)习题7-3图第7章 点的复合运动7-1 图示车A 沿半径R 的圆弧轨道运动,其速度为v A 。
车B 沿直线轨道行驶,其速度为v B 。
试问坐在车A 中的观察者所看到车B 的相对速度v B /A ,与坐在车B 中的观察者看到车A 的相对速度v A /B ,是否有B A A B //v v -=?(试用矢量三角形加以分析。
)答:B A A B //v v -≠1.以A 为动系,B 为动点,此时绝对运动:直线;相对运动:平面曲线;牵连运动:定轴转动。
为了定量举例,设R OB 3=,v v v B A ==,则v v 3e =∴ ⎩⎨⎧︒==6021/θv v A B2.以B 为动系,A 为动点。
牵连运动为:平移;绝对运动:圆周运动;相对运动:平面曲线。
此时⎪⎩⎪⎨⎧︒==4522/θv v B A ∴ B A A B //v v -≠7-3 图示记录装置中的鼓轮以等角速度0ω转动,鼓轮的半径为r 。
自动记录笔连接在沿铅垂方向并按)sin(1t a y ω=规律运动的构件上。
试求记录笔在纸带上所画曲线的方程。
解:t r x 0ω= (1) )sin(1t a y ω=(2)由(1)0ωr xt =代入(2),得)sin(01r xa y ωω=7-5 图示铰接四边形机构中,O 1A = O 2B = 100mm ,O 1O 2 = AB ,杆O 1A 以等角速度ω= 2rad/s 绕轴O 1转动。
AB 杆上有一套筒C ,此套筒与杆CD 相铰接,机构的各部件都在同一铅垂面内。
试求当ϕ= ︒60,CD 杆的速度和加速度。
解:1.动点:C (CD 上),动系:AB ,绝对:直线,相对:直线,牵连:平移。
2.r e a v v v +=(图a ) v e = v A01.02121.0cos e a =⨯⨯==ϕv v m/s (↑)3. r e a a a a +=(图b )4.021.022e =⨯==ωr a m/s 2 346.030cos e a =︒=a a m/s 2(↑)习题7-5图习题7-7图习题7-9图υ(a) (b)(a)7-7 图示瓦特离心调速器以角速度ω绕铅垂轴转动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 点的合成运动一、是非题7.1.1动点的相对运动为直线运动,牵连运动为直线平动时,动点的绝对运动必为直线运动。
( × ) 7.1.2无论牵连运动为何种运动,点的速度合成定理r e av v v +=都成立。
( ∨ ) 7.1.3某瞬时动点的绝对速度为零,则动点的相对速度和牵连速度也一定为零。
( × ) 7.1.4当牵连运动为平动时,牵连加速度等于牵连速度关于时间的一阶导数。
( ∨ ) 7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。
( × ) 7.1.6( × ) 7.1.7只要动点的相对运动轨迹是曲线,就一定存在相对切向加速度。
( × ) 7.1.8在点的合成运动中,判断下述说法是否正确:(1)若r v 为常量,则必有r a =0。
( × ) (2)若e ω为常量,则必有e a =0.( × )(3)若e r ωv //则必有0=C a 。
( ∨ ) 7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
( × ) 7.1.10当牵连运动为定轴转动时一定有科氏加速度。
( × )二、 填空题7.2.1 牵连点是某瞬时 动系 上与 动点 重合的那一点。
7.2.2e a v v =大小为,在一般情况下,若已知v e 、v r ,应按a 的大小。
三、选择题:7.3.1 动点的牵连速度是指某瞬时牵连点的速度,它相对的坐标系是( A )。
A 、 定参考系B 、 动参考系C 、 任意参考系 7.3.2 在图示机构中,已知t b a s ωsin +=, 且t ωϕ=(其中a 、b 、ω均为常数),杆长为L ,若取小球A 为动点,动系固结于物块B ,定系固结于地面,则小球的牵连速度v e 的大小为( B )。
A 、 ωLB 、 t b ωωcosC 、 t L t b ωωωωcos cos +D 、ωωωL t b +cos四、计算题7.4.1 杆OA 长L ,由推杆BC 通过套筒B 推动而在图面内绕点O 转动,如图所示。
假定推杆的速度为v ,其弯头高为b 。
试求杆端A 的速度的大小(表示为由推杆至点O 的距离x 的函数)。
7.4.2 在图a 和b 所示的两种机构中,已知s rad mm b O O /3,200121===ω。
求图示位置时杆A O 2的角速度。
7.4.3 图示四连杆平行形机构中,m m 10021==B O A O ,A O 1以等角速度rad/s 2=ω绕1O 轴转动。
杆AB 上有一套筒C ,此筒与滑杆CD 相铰接。
机构的各部件都在同一铅直面内。
求当60=ϕ时,杆CD 的速度和加速度。
解:取滑块C为动点,动系固连在杆AB 上;则动点的绝对运动为铅垂方向的直线运动,相对运动为沿AB 杆的直线运动,牵连运动平动。
re a v v v+=)式:由(7-7sm A O v v A e /2.01=⋅==ω其中:)(/1.0cos ↑===s m v v v e a CD ϕ则:re a +=由(137-22214.021.0s m A O a a n A e =⨯=⋅==ω其中: 60sin 4.0sin ⨯=⋅==ϕe a CD a a a 则:)(346.032.02↑==s m 解:(a) 取滑块A 为动点,动系固连在杆O 1A 上;则动点的绝对运动为绕O 2点的圆周运动,相对运动为沿O 1A 杆的直线运动,牵连运动为绕O 1点的定轴转动。
re a v v v+=)式:由(7-7111其中:ωωb A O v e =⋅=030cos /:则e a v v =由几何关系02102230cos 2)30cos 2()30cos 2(/2ωω====b v b v A O v e a a A o )(/24323逆时时s rad =⨯=(b) 取滑块A 为动点,动系固连在杆O 2A 上;则动点的绝对运动为绕O 1点的圆周运动,相对运动为沿O 2A 杆的直线运动,牵连运动为绕O 2点的定轴转动。
re a v v v+=)式:由(7-7030cos :则a e v v =由几何关系)逆时(/5.12)2()30cos 2(/1022针s rad b v b v A O v a e e A o =====ωω111其中:ωωb A O v a =⋅=7.4.4 径为R 的半圆形凸轮C 等速u 水平向右运动,带动从动杆AB 沿铅直方向上升,如图所示。
求 30=ϕ时7.4.5 如图所示,半径为r 的圆环内充满液体,液体按箭头方向以相对速度v 在环内作匀速运动。
如圆环以等1和2处液体的绝对加速度的大小。
7.4.6 图示直角曲杆OBC 绕O 轴转动,使套在其上的小环M 沿固定直杆OA 滑动。
已知:m 1.0=OB ,OB 与BC 垂直,曲杆的角速度 rad/s 5.0=ω,角加速度为零。
求当 60=ϕ时,小环M 的速度和加速度。
re a v v v +=)式:由(7-7a t r a re a v v v+=u v v e r 332cos /==ϕn r t r e a a a a a ++=R u R v a nr 3422==R u a a nr t r 934tan 2=⨯=ϕ解:取小环M 为动点,动系固连在直角杆OBC 上。
则动点的绝对运动为沿OA 杆的直线运动,相对运动为沿BC 杆的直线运动,牵连运动为绕O 点的定轴转动。
ϕωωcos 其中:OB OM v e ⋅=⋅=)(/1732.031.0则:→=⨯===s m tg v v v e a M ϕsm /1.021.05.0=⨯⨯=)(/2.021.0cos 方向如图s m v v e r =⨯==ϕϕωωcos ,0其中:22OB OM a a n e te⋅=⋅==r r e c v v a ωω22==将(a )式向x 轴投影得: c ne a a a a ++-=0cos cos ϕϕr a v OB a ωω222+⋅-=⇒)(35.04222→==+⋅-==⇒s m v OB a a r a M ωω1、2处的液体为动点,动系固连在圆环上。
则动点的绝对运动为曲线运动,相对运动为沿圆环的匀速圆周运动,牵连运动为绕O 点的匀速定轴转动。
c r e a a a a a ++=)式:20-7由(21其中:ωr a n e =)(a a a a a c n r n e a ++=⇒v a c ω21=225ωr a n e =v a c ω22=)(2221111↑++-=++-=v r v r a a a a c n r n e a ωω轴投影得: vr v r a a a a c n r ne x a ωωϕ2sin 222222---=---=2222cos ωϕr a a n e y a -=-=42222222224)2(ωωωr v r v r a a aya x a a +++=+=∴4222222224)2(2cos ωωωωωαr v r v r v r v r a a a xa +++++-==r v a n r 22=v a n r 21=y 轴投影得: 52cos 51sin ==ϕϕ,422222224)2(2cos ωωωωβr v r v r r a a a y a +++-==)()式:207由(a a a a a a cr n e t e a +++=-第八章 刚体的平面运动一、是非题8.1.1刚体运动时,若已知刚体内任一点的运动,则可由此确定刚体内其它各点的运动。
( × ) 8.1.2刚体作平面运动时,其上任意一点的轨迹为平面曲线。
( ∨ ) 8.1.3平面图形的速度瞬心只能在图形内。
( × ) 8.1.4当平面图形上A 、BAB( ∨ ) 8.1.5平面图形上A 、B( × )8.1.60=α。
( × ) 8.1.7刚体作瞬时平动时,刚体上各点的加速度都是相等的。
( × ) 8.1.8只要角速度不为零,作平面运动的刚体上的各点一定有加速度。
( × ) 8.1.9刚体作平面运动时,平面图形内两点的速度在任意轴上的投影相等。
( × )二、填空题8.2.1刚体的平面运动可以简化为一个___平面图形_____在自身平面内的运动。
平面图形的运动可以分解为随基点的__平动__和绕基点的_转动___。
其中,__平动______部分为牵连运动,它与基点的选取__有__关;而__转动____部分为相对运动,它与基点的选取_无___关。
8.2.2如图8.1所示,圆轮半径为R 轮缘上M 点牵连速度的大小为 v O,相对速度的大小为 v O ,方向在图上标出。
8.2.3边长为L 的等边三角形板在其自身平面内运动。
在图8.2A 点的速度大小为v A ,沿AC方向,B 点的速度沿CB C 点的速度大小为_______。
8.2.4如图8.3所示,塔轮沿直线轨道作纯滚动,外轮半径为R ,内轮半径为r ,轮心的速度和加速度为v O 、a O 。
则外轮缘上A 、B 、C 、D 四点的加速度分别为 ____________=A a ,____________=B a ,___________=Ca , ____________=D a 。
R v O =ω AABC ABC C v CC v 2=⋅=ω3300Ltg AC AC ABC =⋅= 3230cos 0L AC CC ABC ==L v AC v A ABC A ABC 3==∴ωA v 2O MO v R v ==∴ωMv ra r v 00,==αωO Ax a R a -=2ωOOa rv R -=22r a R R a O Ay --==α222222)(r a R a r v R a O O O A +-=222r v RR a O Bx-=-=ω)(O O O By a raR a R a +-=--=α22222)1()(++=rR a r v R a O O B 222222)(r a R a r v R O O O +-22222)1()(++r R a r v R O O 222222)(r a R a r v R O O O ++22222)1()(-+r R a r v RO O tBA n BA A B a a a a ++=刚体作平面运动xy三、选择题8.3.1某瞬时,平面图形(图8.4)上任意两点A 、B 的速度分别为v A 和v B ,则此时该两点连线中点D 的速度为( B )。
