分治算法实验报告
分治算法实验报告(C语言)

实验1、《分治算法实验》一、实验目的1. 了解分治策略算法思想2. 掌握快速排序、归并排序算法3. 了解其他分治问题典型算法二、实验内容1.编写一个简单的程序,实现归并排序。
2. 编写一段程序,实现快速排序。
3. 编写程序实现循环赛日程表。
设有n=2k个运动员要进行网球循环赛。
现要设计一个满足以下要求的比赛日程表:(1)每个选手必须与其它n-1个选手各赛一次(2)每个选手一天只能赛一场(3)循环赛进行n-1天三、算法思想分析1.归并排序先是将待排序集合分成两个大小大致相同的集合,分别对每个集合进行排序,递归调用归并排序函数,再是调用合并函数,将两个集合归并为一个排好序的集合。
2.快速排序先是选择关键数据作为比较量,然后将数组中比它小的数都放到它的左边,比它大的数放大右边,再对左右区间重复上一步,直至各个区间只有一个数。
3.循环赛日程表先将选手分为两部分,分别排序,再将两部分合并,合并时由于循环赛的规律得知直接将左上角的排序表复制到右下角,左下角的排序表复制到右上角即可。
分成两部分时需要利用递归不断分下去直至只剩下一位选手。
四、实验过程分析1.通过归并算法我对分治算法有了初步的实际操作经验,快速排序与归并算法有很大的相似点,但是在合并时的方法不一样,而循环赛日程表则是思路问题,这个题目编程难点应该在于合并时数组调用的for循环的次数以及起始位置问题。
2.对于分治算法一般是将大规模问题分解为小问题,通过递归不断分下去,然后对每个小规模用一个函数去求解。
适用于小规模独立且易解,可以合并到大问题具有最优子结构的问题。
3.归并排序和快速排序熟悉书本及PPT基本没有问题,循环赛日程表则是纠结了很久,一开始算法思路并不是十分清晰所以错了很多次,后来想了很久再观察PPT的循环赛日程表得知最终算法,编写代码中遇到了一个小问题,有一部分选手未排序,如图所示:图中有部分选手未排序,即左下角排序出现了问题,后来直接静态调试,自己按照代码用实际数据去试了一遍,发现是排序时的for循环的次数不对。
分治算法实验

分治算法实验(用分治法查找数组元素的最大值和最小值)算法分析与设计实验报告第一次实验实验步骤关键代码}else//当数组中元素个数少于2时,直接赋值处理1. 先解决小规模的问题,如数组中只有1个元素或者只有两个元素时候的情况。
2. 将问题分解,如果数组的元素大于等于3个,将数组分为两个小的数组。
3. 递归的解各子问题,将中分解的两个小的数组再进行以上两个步骤最后都化为小规模问题。
4. 将各子问题的解进行比较最终得到原问题的解。
//分治法处理整个数组,求出最大值与最小值void merge( int a[], int left, int right, int &Max, int &Min){int max1=0,min 1=0,max2=0,min2=0;if (right-left>2) //当数组中元素个数大于3时,才实行分治法{int mid=(right+left)/2;merge(a,left,mid,max1,mi n1);//左半边递归调用自身,求岀最大值与最小值,分别保存在max1,min1中merge(a,mid+1,right,max2,mi n2);//右半边递归调用自身,求岀最大值与最小值,分别保存在max2,min2中if (max1>=max2)Max=max1; //子序列两两合并,求岀最大值与最小值elseMax=max2; //分别保存在Max与Minif (min1<=min2)Min=mi n1;elseMin=mi n2;测试结果实验心得Max=compmax(a,left,right);Min=compmi n( a,left,right);}}利用分治法(递归实现):非递归实现:请输入数据克1000093 32767The tine is1990003276? 9The tine is1000032767 0TJ IE tine is1000 32767 9The time is3276? RThe tine is內.0060-004TO通解,明白了分治法到底是怎样的一个过程,在代码实现分治法的时候,也使我加深了对于自己构造函数的理解,明白了分治法利用代码是怎样实现的,以及构造函数的传参与返回值等等地方需要注意的F;\鮒实验沁[p || B附录:完整代码(分治法)#include <iostream>#inelude <time.h>#include <iomanip> using namespacestd;//当数组中的元素个数小于3时,处理最大值int compmax(int A[], int start, int end) {int max;if (start<end) //有两个元素{if (A[start]<=A[end]) max=A[e nd];elsemax=A[start];}else //有一个元素max=A[start];return max;}//当数组中元素的个数小于2时,处理最小值int compmin(int A[], int start, int end){int min;if (start<end) //有两个元素{if (A[start]<=A[end]) mi n= A[start];elsemin= A[e nd];}else //有一个元素mi n=A[start];return mi n;}//分治法处理整个数组,求最大值与最小值void merge( int a[], int left, int right, int &Max,int &Min) 〃Max,Min 用来保存最大值与最小值//之所以使用&引用,是由于如果只是简单的使用变量,并不会改变Ma>与Min的值,使用指针也可以{int max1=0,min 1=0,max2=0,min2=0;if (right-left>2) //当数组中元素个数大于等于3时,进行分治{int mid=(right+left)/2;merge(a,left,mid,max1,min1); //左半边递归调用自身,求出最大值最小值,分别保存在max1,min1中merge(a,mid+1,right,max2,min2); //右半边递归调用自身,求出最大值最小值,分别保存在max2,min2中if (max1>=max2) //子序列两两合并,求出最大值与最小值,保存在Max与Mi n 中Max=max1;elseMax=max2;if (min 1<=min2)Min=min1;elseMin=min 2;}else //数组中元素个数小于3时的情况,直接赋值{Max=compmax(a,left,right);Mi n=compmi n( a,left,right);}}void ran( int *input, int n) //随机生成数组元素函数{int i;sran d(time(0)); for(i=0;i<n;i++) input[i]=ra nd();input[i]= '\0';}int a[1000000]; //定义全局变量用来存放要查找的数组int main(){int n;int i;int max;int min;coutvv "请输入要查找的序列个数:"<<e ndl;for (i=0;i<5;i++){cin>>n;ran (a,n);start=clock();en d=clock();over=end-start;start=clock();//调用分治法算法merge(a,0, n-1,max,min);coutvvmax<<‘ " vvminvvendl;en d=clock();printf( "The time is %6.3f" ,( double )(end-start-over)/CLK_TCK); //显示运行时间}system( "pause"); // 停止运行窗口return 0;}完整代码(非递归方法)#include <iostream>#include <time.h>#include <iomanip> usingnamespacestd;void ran( int *input, int n) {//随机生成数组元素函数int i;sran d(time(0));for (i=0;i<n;i++)in put[i]=ra nd();input[i]= '\0';}int a[1000000];int main(){int max=a[0],min=a[0];int i,j,n;cout<<"请输入数据规模: "<<e ndl;for (j=0;j<5;j++){cin»n;ran( a, n);clock_t start,e nd,over;//计算程序运行时间的算法start=clock();en d=clock();start=clock(); for(i=1;i<n;i++) {if (a[i]>max)max=a[i];if (a[i]<min) min=a[i];}coutvvmax<<‘ " vvminvvendl;en d=clock();printf( "The time is %6.3f" ,( double )(end-start-over)/CLK_TCK); // 显示运行时间}system( "pause");return 0;}。
分治算法的实验报告

一、实验背景分治算法是一种常用的算法设计方法,其基本思想是将一个复杂问题分解成若干个相互独立的小问题,然后将小问题递归求解,最终将子问题的解合并为原问题的解。
分治算法具有高效性、可扩展性和易于实现等优点,被广泛应用于各个领域。
本实验旨在通过实现分治算法解决实际问题,掌握分治算法的设计思想,并分析其时间复杂度。
二、实验目的1. 理解分治算法的基本思想;2. 掌握分治算法的递归实现方法;3. 分析分治算法的时间复杂度;4. 应用分治算法解决实际问题。
三、实验内容本实验选择两个分治算法:快速排序和合并排序。
1. 快速排序快速排序是一种高效的排序算法,其基本思想是将待排序序列分为两个子序列,其中一个子序列的所有元素均小于另一个子序列的所有元素,然后递归地对两个子序列进行快速排序。
(1)算法描述:① 选择一个基准值(pivot),通常取序列的第一个元素;② 将序列分为两个子序列,一个子序列包含所有小于基准值的元素,另一个子序列包含所有大于基准值的元素;③ 递归地对两个子序列进行快速排序。
(2)代码实现:```cvoid quickSort(int arr[], int left, int right) {if (left < right) {int pivot = arr[left];int i = left;int j = right;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);}}```2. 合并排序合并排序是一种稳定的排序算法,其基本思想是将待排序序列分为两个子序列,分别对两个子序列进行排序,然后将排序后的子序列合并为一个有序序列。
分治法实验报告

一. 实验目的及实验环境实验目的:熟练掌握运用分治法解决问题。
实验环境:windows下的Ubuntu虚拟机二. 实验内容利用分治法求一个数组的最大值、最小值(要求:数组的大小和数组的长度随机产生)三.方案设计分治法解决问题就是要将原问题分解成小问题,再将小问题分解成更小的问题,以此类推,直到最终分解的问题能够一步解决即可。
代码要求最后要输出数组的最大值、最小值。
所以,在用分治法求最值的函数max_min()中,需要将设置参数int *max,int *min。
即void max_min(int a[],int m,int n,int *max,int *min)。
这样就可以直接得到最大值、最小值。
该函数使用递归来实现,而递归的终止条件是最后分得的数组中只有一个或两个元素,当分得的数组元素个数大于2时,就进行递归调用。
四.测试数据及运行结果正确的3组运行结果:出现的错误:若将代码中的随机数函数返回值的类型改变,则会出现错误结果,甚至编译不通过。
五.总结1.实验过程中遇到的问题及解决办法;实验过程中,用分治法求最大值、最小值时,如果用返回值求最大值和最小值,则需要两个函数。
这样就会导致代码冗余,不会达到代码的复用性功能。
所以要将两个功能用一个函数直接实现就可以使用参数指针的形式。
2.对设计及调试过程的心得体会。
算法设计的课内实验既要实现实验的功能,还要讲究代码中算法的精妙、简单以及它的效率。
不能同其他高级语言的课内实验一样仅仅考虑如何完成该实验的功能,这样就可以真正地体验到算法与设计这门课的意义。
平时做实验时我们可以用不同算法实现,这样不仅可以积累平常上课学到的知识,还可以为以后的算法设计能力奠定基础。
平常更多地进行思考,可以让我们在求职时更受益。
六.附录:源代码(电子版)#include<stdio.h>#include<stdlib.h>#include<time.h>void max_min(int a[],int m,int n,int *max,int *min){int middle,hmax,hmin,gmax,gmin;if(m==n){ *max=a[m];*min=a[m];}else if(m==n-1){if(a[m]>a[n]){*max=a[m];*min=a[n];}else{*max=a[n];*min=a[m];}}else{max_min(a,m,middle,&gmax,&gmin);max_min(a,middle+1,n,&hmax,&hmin);if(gmax>hmax)*max=gmax;else*max=hmax;if(gmin<hmin)*min=gmin;else*min=hmin;}}int main(){int i;int max,min;srand((unsigned)time(NULL));int n=rand()%10+1;printf("数组的个数:%d\n",n);int a[n];for(i=0;i<n;i++){a[i]=rand()%50+1;printf("%d\t",a[i]);}max_min(a,0,n-1,&max,&min);printf("最大数:%d,最小数:%d\n",max,min);retur n 0;}。
分治算法实验报告
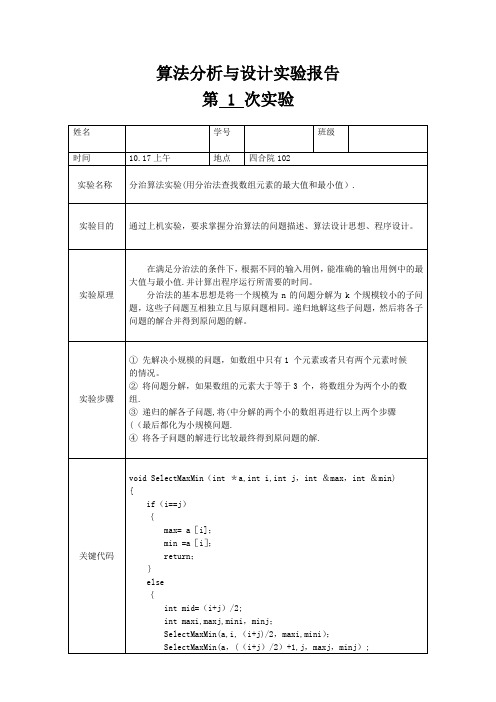
算法分析与设计实验报告第 1 次实验if(maxi>maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}srand((unsigned int)time(NULL));cout <〈”随机产生的数据(0—100):”;for(int i=0; i〈m; i++)a[i] = rand()%100;测试结果附录:完整代码SelectMaxMin.cpp:#include <iostream>#include <ctime>#include 〈cstdio>#include <iomanip>#include 〈cstdlib〉using namespace std;void SelectMaxMin(int *a,int i,int j,int &max,int &min) {if(i==j){max= a[i];min =a[i];return;}else{int mid=(i+j)/2;int maxi,maxj,mini,minj;SelectMaxMin(a,i,(i+j)/2,maxi,mini);SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);if(maxi〉maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}int main(){clock_t start,end,over;start=clock();end=clock();over=end—start;start=clock();//freopen("in。
txt",”r",stdin);//freopen(”out。
txt”,”w",stdout);int m;cout 〈<"Please input the number : ”;cin>〉 m;int a[m];srand((unsigned int)time(NULL));cout 〈〈 "随机产生的数据(0-100):";for(int i=0; i〈m; i++)a[i] = rand()%100;for(int i=0; i〈m; i++)cout <〈 a[i] 〈< " ";cout 〈< endl;int max,min;SelectMaxMin(a,0,m-1,max,min);cout 〈< "max = " 〈〈 max 〈〈 endl;cout <〈”min = " <〈 min 〈〈 endl;end=clock();printf(”The time is %6.3f”,(double)(end-start—over)/CLK_TCK); }。
分治算法实验报告.doc

一、实验目的1.加深对分治算法的基本思想、基本步骤和一般形式的理解,掌握分治算法设计的基本方法。
2.用分治法设计L型组件填图问题的算法,分析其复杂性,并实现;3.用分治法设计求数列中的第1~k小元素的算法,分析其复杂性,并实现。
二、实验内容(一)L型组件填图问题1.问题描述设B是一个n×n棋盘,n=2k,(k=1,2,3,…)。
用分治法设计一个算法,使得:用若干个L型条块可以覆盖住B的除一个特殊方格外的所有方格。
其中,一个L型条块可以覆盖3个方格。
且任意两个L型条块不能重叠覆盖棋盘。
例如:如果n=2,则存在4个方格,其中,除一个方格外,其余3个方格可被一L型条块覆盖;当n=4时,则存在16个方格,其中,除一个方格外,其余15个方格被5个L型条块覆盖。
2. 具体要求输入一个正整数n,表示棋盘的大小是n*n的。
输出一个被L型条块覆盖的n*n棋盘。
该棋盘除一个方格外,其余各方格都被L型条块覆盖住。
为区别出各个方格是被哪个L型条块所覆盖,每个L型条块用不同的数字或颜色、标记表示。
3. 测试数据(仅作为参考)输入:8输出:A 2 3 3 7 7 8 82 2 13 7 6 6 84 1 15 9 96 104 45 5 0 9 10 1012 12 13 0 0 17 18 1812 11 13 13 17 17 16 1814 11 11 15 19 16 16 2014 14 15 15 19 19 20 204. 设计与实现的提示对2k×2k的棋盘可以划分成若干块,每块棋盘是原棋盘的子棋盘或者可以转化成原棋盘的子棋盘。
注意:特殊方格的位置是任意的。
而且,L型条块是可以旋转放置的。
为了区分出棋盘上的方格被不同的L型条块所覆盖,每个L型条块可以用不同的数字、颜色等来标记区分。
5. 扩展内容可以采用可视化界面来表示各L型条块,显示其覆盖棋盘的情况。
(二) 求第k小项三、程序清单及实验过程和结果分析(一)#include "stdafx.h"#include "stdio.h"#define M 1024int table[M][M];int index;void LFill( int startx , int starty , int width , int x , int y ){int half=width/2;if( width==2 ){//填充if( table[startx][starty]==0 ) table[startx][starty]=index;if( table[startx+1][starty]==0 ) table[startx+1][starty]=index;if( table[startx][starty+1]==0 ) table[startx][starty+1]=index;if( table[startx+1][starty+1]==0 ) table[startx+1][starty+1]=index;index++;}else{//判断x,y方块位置//根据该位置用L填充if( x < startx+half ){if( y < starty+half ) //左上{table[startx+half-1][starty+half]=index; //左下table[startx+half][starty+half-1]=index; //右上table[startx+half][starty+half]=index; //右下index++;LFill(startx,starty,half,x,y);LFill(startx,starty+half,half,startx+half-1,starty+half);//左下LFill(startx+half,starty,half,startx+half,starty+half-1);//右上LFill(startx+half,starty+half,half,startx+half,starty+half);//右下}else{//左下table[startx+half-1][starty+half-1]=index; //左上table[startx+half][starty+half-1]=index; //右上table[startx+half][starty+half]=index; //右下index++;LFill(startx,starty,half,startx+half-1,starty+half-1);//左上LFill(startx,starty+half,half,x,y);LFill(startx+half,starty,half,startx+half,starty+half-1);//右上LFill(startx+half,starty+half,half,startx+half,starty+half);//右下}}else{if( y<starty+half )//右上{table[startx+half-1][starty+half]=index;table[startx+half-1][starty+half-1]=index;table[startx+half][starty+half]=index;index++;LFill(startx,starty,half,startx+half-1,starty+half-1);//左上LFill(startx,starty+half,half,startx+half-1,starty+half);//左下LFill(startx+half,starty,half,x,y);LFill(startx+half,starty+half,half,startx+half,starty+half);//右下}else{//右下table[startx+half][starty+half-1]=index;table[startx+half-1][starty+half-1]=index;table[startx+half-1][starty+half]=index;index++;LFill(startx,starty,half,startx+half-1,starty+half-1);//左上LFill(startx,starty+half,half,startx+half-1,starty+half);//左下LFill(startx+half,starty,half,startx+half,starty+half-1);//右上LFill(startx+half,starty+half,half,x,y);}}}}int main(){index=1;int n,i,j,p,q;printf("输入n的大小(n=2^k):");scanf("%d",&n);for(i=0;i<n;i++)for(j=0;j<n;j++)table[i][j]=0;printf("输入特殊位置坐标:");scanf("%d%d",&p,&q);table[p][q]=-1;LFill(0,0,n,p,q);for(i=0;i<n;i++){for(j=0;j<n;j++){if(i==p&&j==q) printf(" A");elseprintf("%5d",table[i][j]);}printf("\n");}}(二)#include "stdafx.h"#include "stdio.h"#define M 100void sort(int a[],int n){int i,j,t;for(i=1;i<=n;i++)for(j=i+1;j<=n;j++)if(a[i]>a[j]){t=a[i];a[i]=a[j];a[j]=t;}}int select(int a[],int low,int high,int k){int pp=low+high-1;if(pp<44){sort(a,high);return a[k];}int b[50],c[50];int i=1,j=1,t=1;for(i=1;i<=high;i++)//对每组排序后分别取中项存于数组c中,再对数组c排序{b[j++]=a[i];if( i % (high/5) ==0 || i==high){sort(b,j-1);c[t++]=b[j/2];j=1;}}int mid=t/2;sort(c,t-1);int aa[50],bb[50],cc[50];int p=1,q=1,r=1;for(i=1;i<=high;i++){if(a[i]>c[mid]) cc[r++]=a[i];else if(a[i]<c[mid]) aa[p++]=a[i];else if(a[i]==c[mid]) bb[q++]=a[i];}p--;q--;r--;if(p>=k) return select(aa,1,p,k);else if( (p+q) >=k) return c[mid];else return select(cc,1,r,k-p-q);}int main(){int n,a[100],i,k;scanf("%d",&n);for(i=1;i<=n;i++)scanf("%d",&a[i]);scanf("%d",&k);printf("第%d小项为:%d\n",k,select(a,1,n,k) );return 0;}。
分治策略算法实验报告

分治策略算法实验报告引言分治策略是一种经典的算法设计策略,也是算法设计中最重要的思想之一。
其基本思想是将大问题划分成小的、相互独立的子问题,再将子问题合并求解,最终得到原问题的解。
本实验将通过实际例子,验证分治策略算法的有效性。
实验内容本实验选择两个经典的算法问题进行实现和验证,分别是二分查找和快速排序。
这两个问题在算法领域都有重要的应用价值,也是实践分治算法的好例子。
问题1:二分查找二分查找是一种在有序数组中查找特定元素的算法,其基本思想是将数组分为两部分,然后判断目标值在哪一部分,并且逐步缩小问题的规模。
具体实现如下:pythondef binary_search(arr, target):low = 0high = len(arr) - 1while low <= high:mid = (low + high) 2if arr[mid] == target:return midelif arr[mid] < target:low = mid + 1else:high = mid - 1return -1问题2:快速排序快速排序是一种高效的排序算法,其基本思想是通过一趟划分将待排序序列分割成两个独立的子序列,然后递归地对子序列进行排序,最终得到有序序列。
具体实现如下:pythondef quicksort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) 2]left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quicksort(left) + middle + quicksort(right)实验结果为了验证分治策略算法的有效性,我们分别对上述两个问题进行了测试。
分治算法实验(用分治法实现快速排序算法)

算法分析与设计实验报告第四次附加实验while(a[--j]>x);if(i>=j){break;}Swap(a[i],a[j]);}a[p] = a[j]; //将基准元素放在合适的位置a[j] = x;return j;}//通过RandomizedPartition函数来产生随机的划分template<class Type>int RandomizedPartition(Type a[],int p,int r){int i = Random(p,r);Swap(a[i],a[p]);return Partition(a,p,r);}较小个数排序序列的结果:测试结果较大个数排序序列的结果:附录:完整代码(分治法)// 随机后标记元素后的快速排序#include <iostream>#include <ctime>#include <time.h>#include <iomanip>using namespace std;int a[1000000]; //定义全局变量用来存放要查找的数组template <class Type>void Swap(Type &x,Type &y); //声明swap 函数inline int Random(int x, int y); //声明内联函数template <class Type>int Partition(Type a[],int p,int r); //声明Partition 函数更大个数排序序列的结果:实验心得快速排序在之前的数据结构中也是学过的,在几大排序算法中,快速排序和归并排序尤其是重中之重,之前的快速排序都是给定确定的轴值,所以存在一些极端的情况使得时间复杂度很高,排序的效果并不是很好,现在学习的一种利用随机化的快速排序算法,通过随机的确定轴值,从而可以期望划分是较对称的,减少了出现极端情况的次数,使得排序的效率挺高了很多,与后面的随机化算法想呼应,而且关键的是对于随机生成函数,通过这一次的实验和自己的学习终于弄明白是怎么回事了,不错。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
算法分析与设计实验报告
第 1 次实验
if(maxi>maxj)
max=maxi;
else
max=maxj;
if(mini<minj)
min=mini;
else
min=minj;
return;
}
}
srand((unsigned int)time(NULL));
cout << "随机产生的数据(0-100):";
for(int i=0; i<m; i++)
a[i] = rand()%100;
测试结果
附录:完整代码
SelectMaxMin.cpp:
#include <iostream>
#include <ctime>
#include <cstdio>
#include <iomanip>
#include <cstdlib>
using namespace std;
void SelectMaxMin(int *a,int i,int j,int &max,int &min) {
if(i==j)
{
max= a[i];
min =a[i];
return;
}
else
{
int mid=(i+j)/2;
int maxi,maxj,mini,minj;
SelectMaxMin(a,i,(i+j)/2,maxi,mini);
SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);
if(maxi>maxj)
max=maxi;
else
max=maxj;
if(mini<minj)
min=mini;
else
min=minj;
return;
}
}
int main()
{
clock_t start,end,over;
start=clock();
end=clock();
over=end-start;
start=clock();
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
int m;
cout <<"Please input the number : ";
cin>> m;
int a[m];
srand((unsigned int)time(NULL));
cout << "随机产生的数据(0-100):";
for(int i=0; i<m; i++)
a[i] = rand()%100;
for(int i=0; i<m; i++)
cout << a[i] << " ";
cout << endl;
int max,min;
SelectMaxMin(a,0,m-1,max,min);
cout << "max = " << max << endl;
cout << "min = " << min << endl;
end=clock();
printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); }。
