竖曲线
竖曲线计算公式

竖曲线计算公式第三节竖曲线纵断⾯上两个坡段的转折处,为⽅便⾏车,⽤⼀段曲线来缓和,称为竖曲线。
可采⽤抛物线或圆曲线。
⼀、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.⼆次抛物线基本⽅程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很⼩)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任⼀点竖距h:竖曲线外距:⼆、竖曲线最⼩半径(三个因素)1.缓和冲击对离⼼加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2⽐较合适。
我国取a=0.278,则Rmin=V2/3.6 或 Lmin=V2ω/3.62.⾏驶时间不过短 3s的⾏程Lmin=V.t/3.6=V/1.23.满⾜视距的要求分别对凸凹曲线计算。
(⼀)凸形竖曲线最⼩半径和最⼩长度按视距满⾜要求计算1.当LLmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第⼆个公式计算值⼤,作为有效控制。
按缓和冲击、时间⾏程和视距要求(视距为最不利情况)计算各⾏车速度时的最⼩半径和最⼩长度,见表4-13。
表中:(1)⼀般最⼩半径为极限最⼩半径的1.5~2倍;(2)竖曲线最⼩长度为3s⾏程的长度。
(⼆)凹曲线最⼩半径和长度1.夜间⾏车前灯照射距离要求:1)L2) L≥STLL≥STω /26.92 (4-15)3s时间⾏程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最⼩长度L=V/1.2例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始⾼程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线⾼程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m 设计⾼程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线⾼程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m 设计⾼程=431.18 - 6.40=424.78m。
竖曲线计算

竖曲线:竖曲线是指在线路纵断面上,以变坡点为交点,连接两相邻坡段的曲线。
竖曲线有凸形和凹形两种。
道路纵断面线经常采用直线(又叫直坡段)、竖曲线两种线形,二者是纵断面线形的基本要素。
竖曲线常采用抛物线,因为在设计和计算上,抛物线比圆曲线更方便。
在道路纵断面上两个相邻纵坡线的交点,被称为变坡点。
为了保证行车安全、舒适以及视距的需要,在变坡处设置竖曲线。
竖曲线的主要作用是:缓和纵向变坡处行车动量变化而产生的冲击作用,确保道路纵向行车视距;将竖曲线与平曲线恰当地组合,有利于路面排水和改善行车的视线诱导和舒适感。
竖曲线技术指标主要有竖曲线半径和竖曲线长度。
凸形的竖曲线的视距条件较差,应选择适当的半径以保证安全行车的需要。
凹形的竖曲线,视距一般能得到保证,但由于在离心力作用下汽车要产生增重,因此应选择适当的半径来控制离心力不要过大,以保证行车的平顺和舒适。
一般城市干路相邻坡段的坡度小于0.5%或外距小于5cm 时,可以不设置竖曲线。
竖曲线的最小半径与设计速度有关,凹形竖曲线最小半径为100M,凸形竖曲线为100M。
拉坡后,坡度差已知,变坡点高程已知,切线上各点和高程也就知道了。
选定竖曲线半径R,用竖距计算公式求出切线上各点的竖距,切线高程减竖距就是竖曲线高程。
竖距公式如下:h=距离的平方除以两倍的半径高速公路计算在公路纵断面设计过程中,竖曲线设计的本质就是根据纵坡变化的大小、设计车速、行车视距来确定竖曲线的长度。
在满足《公路路线设计规范》(以下简称《规范》)要求且造价增加不大的情况下,适当选择较大的竖曲线对于保证纵坡度的平滑过渡、行车安全,畅通是非常有利的。
就行车舒适、高速运行的角度考虑,要求纵坡小一些为好,但从路面排水的角度考虑,又要求有一定的纵坡。
按照《规范》要求,公路纵坡不宜小于0.3%,横向排水不畅的路段或长路堑路段,采用平坡0%或小于0.3%的纵坡时,其边沟应做纵向排水设计。
竖曲线内任意点纵坡的分析1)竖曲线表达式路线设计中的竖曲线,可采用抛物线形式,也可采用圆曲线形式,但为了简化计算,圆曲线方程最终还是可简化为抛物线方程,因此,竖曲线的方程采用抛物线方程是没有异议的。
竖曲线

竖曲线是在变坡点处,为了行车平顺的需要而设置的一段曲线。
竖曲线的形状,通常采用圆曲线或二次抛物线两种。
在设计和计算上抛物线比圆曲线更为方便,故一般采用二次抛物线。
在纵坡设计时,由于纵断面上只反映水平距离和竖直高度,因此竖曲线的切线长与弧长是其在水平面上的投影,切线支距是竖直的高程差,相邻两条纵坡线相交角用坡度差表示。
一、竖曲线要素计算如图3-3所示,设变坡处相邻两纵坡度分别为i1和i2,坡度差以ω表示,则坡度差ω为i1和i2的代数差,即ω= i1-i2:当ω>0时,则为凸形竖曲线;当ω<0时,则为凹形竖曲线。
图3-3竖曲线示意图1、竖曲线的基本方程二次抛物线作为竖曲线的基本形式是我国目前常用的一种形式。
如图3-4所示,用二次抛物线作为竖曲线的基本方程:3-4 竖曲线要素示意图竖曲线上任意一点的斜率为:当x=0时:k= i1,则b= i1;当x=L,r=R时:,则:因此,竖曲线的基本方程式为:或 (3-19)2、竖曲线的要素计算曲线长:(3-20)切线长:(3-21)外距:(3-22)曲线上任意一点的竖距(改正值):(3-23)二、竖曲线设计标准竖曲线的设计标准包括竖曲线的最小半径和最小长度。
1、竖曲线设计的限制因素(1)缓和冲击汽车在竖曲线上行驶时会产生径向离心力,在凸形竖曲线上行驶会减重,在凹形竖曲线上行驶会增重,如果这种离心力达到某种程度时,乘客就会有不舒适的感觉,同时对汽车的悬挂系统也有不利影响,故应对径向离心力加速度加以控制。
根据试验得知,离心加速度a限制在0.5~0.7m/s2比较合适。
汽车在竖曲线上行驶时其离心加速度为:(3-24)《标准》中确定竖曲线半径时取a=0.278 m/s2。
或(3-25)(2)行程时间不宜过短汽车从直坡段驶入竖曲线时,如果其竖曲线长度过短,汽车倏忽而过,冲击力大,旅客会感到不舒适,太短的竖曲线长度从视觉上也会感到线形突然转折。
因此,应限制汽车在竖曲线上的行程时间,一般不宜小于3s。
竖曲线

竖曲线1、竖曲线要素计算1.)变坡角δ:相邻两纵坡i1,i2,由于公路纵坡的允许值不大,故可以认为变坡角δ为:δ=△i= i1-i2(若不考虑近似情况,该值δ=arctan (i1)-arctan(i2)。
需要注意的是假设坡度上升为正时,δ计算结果会有正有负,但其绝对值的大小却与变坡角的角度相等。
但若不考虑正负差异,会造成最终的计算结果出错。
)2.)切线长T:(变坡角δ和圆心角大小相等。
)由于δ很小,可认为故(若不考虑近似情况,,δ值的正负号需注意。
)3.)曲线长L的计算由于变坡角δ很小,可认为L=2T(若不考虑近似情况,因为δ等于该弧所对应的圆周角,那么L=R*δ,其中δ应换算成弧度。
注意在利用CASIO计算器计算时的中间、最终结果的角度弧度问题。
)4.)外矢距E的计算由于变坡角δ很小,可认为y坐标与半径方向一致,它是切线上与曲线上的高程差。
从而得(R+y)2=R2+x2展开2Ry=x2-y2又因y2 与x2相比较,y2的值很小,略去y2,则2Ry= x2即当x=T时,y值最大,约等于外矢距E,所以(若不考虑近似情况,y2+2Ry-x2=0,,其中E >0,。
)2、竖曲线的测设算例:已知:某竖曲线半径R=2000米,相邻坡段的坡度i1=-2.95%,i2=-5.0628%,变坡点里程桩号为K0+760,其高程为428.312米。
(设计给出T=21.128,E=0.112。
)求:K0+730、K0+740、K0+750、K0+760、K0+770、K0+780、K0+790的线路坡度高程和设计高程。
解:步骤一:由已知条件知δ= i1-i2=-0.0295+0.050628=0.021128弧度(若不考虑近似情况δ=(arctan(i1)-arctan(i2))=1°12′30.82″=0.0210940493155弧度)1、)切线长=1000*(-0.0295+0.050628)=21.128米(若不考虑近似情况,=21.0942米)2、)曲线长L=2T=21.128*2=42.256米(若不考虑近似情况L=R*δ=2000*(arctan(i1)-arctan(i2))=2000*1°12′30.82″*π/180°=42.1867米)3、)外矢距=21.128^2/4000=0.1116米(若代入T=21.0942,计算结果=0.1112)(若不考虑近似情况 =0.1112米,其中T=21.0942。
竖曲线

竖曲线计算竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高。
其要点是:首先根据转坡点处的地面线与相邻设计直线坡段情况,按上述竖曲线中的有关规定和要求,合理地选定竖曲线半径。
其次,根据转坡点相邻纵坡度i1、i2和已确定的半径R,计算出竖曲线的基本要素w、L、T、E及竖曲线起、终点桩号。
第三,分别计算出指定桩号的切线设计标高,指定桩号至竖曲线起(或终)点间的平距l和指定桩号的竖距h。
则指定桩号的路基设计标高为:(1)凸形竖曲线:路基设计标高=切线设计标高-h(2)凹形竖曲线:路基设计标高=切线设计标高+h例.某山岭区二级公路,转坡点设在K6+140桩号处,其高程为428.90,两相邻坡段的前坡i1=+4.0%,后坡 i2=-5.0%,选用竖曲线半径R=2000m。
试计算竖曲线要素及桩号K6+080和K6+160处的路基设计标高。
1.计算竖曲线要素转坡角:w= i1- i2=(0.04)-(-0.05)=0.09w>0,为凸形竖曲线。
曲线长:L=R w=2000*0.09=180m切线长:T=L/2=180/2=90m外距:E=T2/(2R)= 902/(2*2000)=2.03m2.计算起、终点桩号竖曲线起点桩号=(K6+140)-90=K6+050竖曲线终点桩号=(K6+140)+90=K6+2303.计算路基设计标高桩号K6+080处:平距(平距是竖曲线上任意一点至起点或终点的水平距离)l=(K6+080)-(K6+050)=30m竖距(竖距是切线上任意一点至竖曲线上的竖向距离)h= l2/(2R)= 302/(2*2000)=0.23m切线标高=428.9-60*0.04=426.50m设计标高=426.50-0.23=426.27m桩号K6+160处:平距l=(K6+230)-(K6+160)=70m竖距h=l2/(2R)= 702/(2*2000)=1.23m切线标高=428.9-20*0.05=427.90m设计标高=427.90-1.23=426.67m。
竖曲线计算公式

竖曲线计算公式竖曲线是一种重要的曲线,它存在于大多数物理曲线中,例如比较一个物体施加力和物体受到力的关系,我们可以用竖曲线来描述。
在数学中,需要根据曲线的特性来计算曲线上某一点的坐标,而这就要求我们弄清竖曲线的计算公式。
首先,我们来讨论竖曲线的定义,竖曲线是指按照特定的模式画出的曲线,即x轴和y轴的关系。
这种模式可以用多项式来描述。
一般来说,竖曲线可以用一阶或更高阶多项式拟合,也就是说,可以用y=ax+b来描述一阶多项式,而用y=ax2+bx+c来描述二阶多项式。
其次,我们来讨论竖曲线的计算公式。
首先,如果要求一阶多项式拟合的曲线,则可以使用最小二乘法来求解。
根据最小二乘法的原理,我们需要将曲线上的点分别求出,然后根据两点之间的距离计算出曲线的系数a和b,最后将a和b代入y=ax+b求得该曲线的一阶多项式拟合曲线。
再比如要求二阶多项式拟合的曲线,也可以使用最小二乘法。
但在这种情况下,我们需要将曲线上的点分别求出,然后根据三点之间的距离计算出曲线的系数a、b和c,最后将a、b和c代入y=ax2+bx+c 求得该曲线的二阶多项式拟合曲线。
有时候,曲线的系数不可能精确地求出,例如曲线系数b和c有可能接近于0,此时,使用“拟合法”来求解曲线的系数就会比较简单。
拟合法的基本思想是,我们可以将曲线上的点拟合到一条直线上,这就是一阶多项式拟合,然后以一阶多项式拟合的直线为基础,得出曲线系数b和c,最后再将b和c代入y=ax2+bx+c求得该曲线的二阶多项式拟合曲线。
拟合法可以节省计算的时间和空间,而且它的效果比较准确。
另外,对于特殊形状的竖曲线,例如指数形状、正弦形状、余弦形状等,可以使用除最小二乘法外的其他方法来求解曲线系数,例如加权最小二乘法、最小均方误差法等。
综上所述,竖曲线的计算公式可以分为2类:一阶多项式拟合和二阶多项式拟合。
对于前者,我们可以使用最小二乘法来求解;而对于后者,我们可以使用拟合法或其他方法来求解。
竖曲线计算
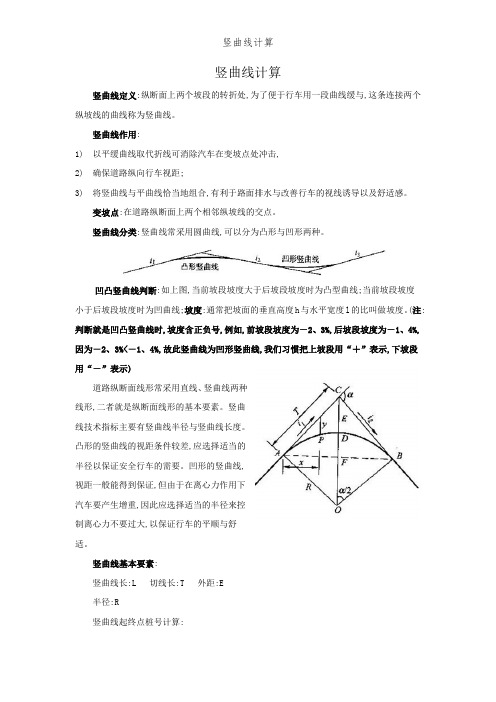
竖曲线计算竖曲线定义:纵断面上两个坡段的转折处,为了便于行车用一段曲线缓与,这条连接两个纵坡线的曲线称为竖曲线。
竖曲线作用:1)以平缓曲线取代折线可消除汽车在变坡点处冲击,2)确保道路纵向行车视距;3)将竖曲线与平曲线恰当地组合,有利于路面排水与改善行车的视线诱导以及舒适感。
变坡点:在道路纵断面上两个相邻纵坡线的交点。
竖曲线分类:竖曲线常采用圆曲线,可以分为凸形与凹形两种。
凹凸竖曲线判断:如上图,当前坡段坡度大于后坡段坡度时为凸型曲线;当前坡段坡度小于后坡段坡度时为凹曲线;坡度:通常把坡面的垂直高度h与水平宽度l的比叫做坡度。
(注:判断就是凹凸竖曲线时,坡度含正负号,例如,前坡段坡度为-2、3%,后坡段坡度为-1、4%,因为-2、3%<-1、4%,故此竖曲线为凹形竖曲线,我们习惯把上坡段用“+”表示,下坡段用“-”表示)道路纵断面线形常采用直线、竖曲线两种线形,二者就是纵断面线形的基本要素。
竖曲线技术指标主要有竖曲线半径与竖曲线长度。
凸形的竖曲线的视距条件较差,应选择适当的半径以保证安全行车的需要。
凹形的竖曲线,视距一般能得到保证,但由于在离心力作用下汽车要产生增重,因此应选择适当的半径来控制离心力不要过大,以保证行车的平顺与舒适。
竖曲线基本要素:竖曲线长:L 切线长:T 外距:E半径:R竖曲线起终点桩号计算:竖曲线起点桩号:变坡点桩号-T竖曲线终点桩号:变坡点桩号+T如右图所示,两个相邻的纵坡为i1与i2,竖曲线半径为R,则测设元素为:曲线长L=R ×α由于竖曲线的转角α很小,故可以认为:α=i1-i2;所以L=R(i1-i2)切线长T=Rtan 2α 因为α很小,tan2α=2α;所以可以推出: T=R ·2α=2L =21R(i1-i2) 又因为α很小,可以认为:DF=E;AF=T根据三角形ACO与三角形ACF相似,根据相似三角形“边角边”定理得出:R:T=T:2E; 于就是如上图外距E=RT 22, 同理可导出竖曲线上任意一点P距切线纵距的计算公式:y =Rx 22式中:x —竖曲线上任意一点P 到竖曲线起点或终点的水平距离Y —值在凹形竖曲线中为正号,在凸形竖曲线中为负号。
竖曲线计算原理

2.竖曲线诸要素计算公式 (1)竖曲线长度L或竖曲线半径R: 竖曲线长度L或竖曲线半径R L = xA - xB
L = Rω , R= L
ω
(2)竖曲线切线长T: 竖曲线切线长T 因为T 因为T = T1 = T2,则
L Rω T= = 2 2
B
i
2
(3)竖曲线外距E: 竖曲线外距E
式中: 式中:R——抛物线顶点 抛物线顶点 处的曲率半径
A
B
一、竖曲线要素的计算公式 竖曲线的基本方程式: 1.竖曲线的基本方程式:设变坡点相邻两纵坡坡 度分别为i 抛物线竖曲线有两种可能的形式: 度分别为i1和i2。抛物线竖曲线有两种可能的形式: 包含抛物线底( (1)包含抛物线底(顶)部; 不含抛物线底( (2)不含抛物线底(顶)部。
抛物线上任一点的曲率半径为r 抛物线上任一点的曲率半径为r,
dy 2 r = [1 +( ) dx
]3 / 2 /
d2y dx 2
dy d2y 1 = i, = 2 k dx dx
抛物线上任一点的曲率半径 r = k(1+i2)3/2 竖曲线底部的切线坡度i 较小, 竖曲线底部的切线坡度 i1 较小 , 故 i12 可略去不 计 ,则竖曲线底部的曲率半径R为: 则竖曲线底部的曲率半径R R = r ≈ k 二次抛物线竖曲线基本方程式(通式) 二次抛物线竖曲线基本方程式(通式)为
2.时间行程不过短 .时间行程不过短 最短应满足3 行程。 最短应满足3s行程。
Lmin V V = t= 3.6 1.2 则 Rmin V = = ω 1.2ω L min
3.满足视距的要求: 满足视距的要求: 凸形竖曲线: 凸形竖曲线:坡顶视线受阻 凹形竖曲线: 凹形竖曲线:下穿立交 4. 凸形竖曲线主要控制因素:行车视距。 凸形竖曲线主要控制因素:行车视距。 凹形竖曲线的主要控制因素:缓和冲击力。 凹形竖曲线的主要控制因素:缓和冲击力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竖曲线
竖曲线【vertical curve】在线路纵断面上,以变坡点为交点,连接两相邻坡段的曲线称为竖曲线。
竖曲线有凸形和凹形两种。
道路纵断面线形常采用直线(又叫直坡段)、竖曲线两种线形,二者是纵断面线形的基本要素。
竖曲线常采用圆曲线,可以分为凸形和凹形两种。
在道路纵断面上两个相邻纵坡线的交点,被称为变坡点。
为了保证行车安全、舒适以及视距的需要,在变坡处设置竖曲线。
竖曲线的主要作用是:缓和纵向变坡处行车动量变化而产生的冲击作用,确保道路纵向行车视距;将竖曲线与平曲线恰当地组合,有利于路面排水和改善行车的视线诱导和舒适感。
竖曲线技术指标主要有竖曲线半径和竖曲线长度。
凸形的竖曲线的视距条件较差,应选择适当的半径以保证安全行车的需要。
凹形的竖曲线,视距一般能得到保证,但由于在离心力作用下汽车要产生增重,因此应选择适当的半径来控制离心力不要过大,以保证行车的平顺和舒适。
鐵路線路採用的豎曲綫,按其形狀可分為一下三種:
1 圓曲綫形豎曲綫
2 抛物線形豎曲綫
3 連續短坡(鏈條坡)
目前採用最多的為抛物線形豎曲綫。
這種豎曲綫,在離開切線后,其曲度逐漸變更,將一端的坡度緩緩變化而成為他端的坡度,因其圖形與拋體運動的軌道形狀相同,故稱為拋物線形豎曲綫。
關於豎曲綫的有關規定
相鄰坡度的坡度代數差應儘量小些,最大不得超過重車方向的限制坡度值。
Ⅰ、Ⅱ级铁路相邻地段的坡度差大于3‰,Ⅲ级铁路大于4‰时,应以竖曲线连接。
竖曲线半径:Ⅰ、Ⅱ级铁路应为10000m,Ⅲ级铁路应为5000m。
竖曲线不应与缓和曲线重叠,也不应设在无碴桥的桥面上。
竖曲线不宜与道岔重叠,困难条件下必须重叠时,竖曲线半径不应小于10000m。
這裡我們可以這樣分析:如果豎曲綫與道岔重疊時,豎曲綫半徑採用10000米,按我國現行標準道岔來考慮,在尖軌長為7.7及6.25米的範圍內,豎曲綫的影響值為3及2毫米;而在道岔全長範圍內,豎曲綫的影響值為3及2毫米;而在道岔全廠範圍內,其坡度變化如下表所列數值。
應當注意:除非確實困難條件,一般不採用上述規定。
竖曲线的計算
如图所示,设相邻两纵坡坡度分别为i1和i2,则相邻两坡度的代数差即转坡角为ω= i1-i2,其中i1、i2为本身之值,当上坡时取正值,下坡时取负值。
当i1- i2为正值时,则为凸形竖曲线。
当i1 - i2为负值时,则为凹形竖曲线。
竖曲线基本方程式
我国采用的是二次抛物线形作为竖曲线的常用形式。
其基本方程为:
Py x 22=
若取抛物线参数P 为竖曲线的半径 R ,则有:
Ry x 22
= R x y 22
= 竖曲线要素计算公式
竖曲线计算图示
1、切线上任意点与竖曲线间的竖距h 通过推导可得:
==PQ h )()(2112li y l x R
y y A A q p ---=-R l 22= 2、竖曲线曲线长:
L=R ω 3、竖曲线切线长: T= TA =TB ≈ L/2 =2ω
R
4、竖曲线的外距: E =R T 22
5、线上任意点至相应切线的距离:
R x y 22
式中:x —为竖曲任意点至竖曲线起点(终点)的距离m ; R —为竖曲线的半径m 。
對稱式抛物線形豎曲綫的分析
以上三個是我們計算豎曲綫的常用公式。
不對稱抛物線形豎曲綫的分析。
