高等数学(定积分的应用)习题及解答
定积分典型例题20例答案
定积分典型例题20例答案定积分典型例题20例答案例1 求33322321lim(2)n n n n n →∞+++．分析将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解将区间[0,1]n 等分，则每个小区间长为1i x n ?=，然后把2111n n n=?的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即33322321lim(2)n n n n n →∞+++=333112lim ()n n n n nn →∞+++=13034xdx =?．例2 2202x x dx -?=_________．解法1 由定积分的几何意义知，2202x x dx -?等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故2202x x dx -?=2π．解法2 本题也可直接用换元法求解．令1x -=sin t （2 2t ππ-≤≤），则222x x dx -?=2221sin cos t tdt ππ--?=2221sin cos t tdt π-?=2202cos tdt π=2π 例3 （1）若22()x t xf x e dt -=?，则()f x '=___；（2）若0()()xf x xf t dt =?，求()f x '=___．分析这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ''=-?．解（1）()f x '=422x x xe e ---；（2）由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =?，则可得()f x '=0()()xf t dt xf x +?．例4 设()f x 连续，且31()x f t dt x -=?，则(26)f =_________．解对等式310()x f t dt x -=?两边关于x 求导得32(1)31f x x -?=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =．例5 函数11()(3)(0)x F x dt x t =->?的单调递减开区间为_________．解 1()3F x x'=-，令()0F x '<得13x >，解之得109x <<，即1(0,)9为所求．例6 求0()(1)arctan xf x t tdt =-?的极值点．解由题意先求驻点．于是()f x '=(1)arctan x x -．令()f x '=0，得1x =，0x =．列表如下：故1x =为()f x 的极大值点，0x =为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()xt g x e dt -=?，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．分析两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ''=．解由已知条件得2(0)(0)0t f g e dt -===?，且由两曲线在(0,0)处切线斜率相同知2(arcsin )2(0)(0)11x x e f g x -=''===-．故所求切线方程为y x =．而()(0)3lim ()lim33(0)330n n f f n nf f n n→∞→∞-'=?==-．例8 求 22000sin lim(sin )x x xtdtt t t dt→-??；分析该极限属于型未定式，可用洛必达法则．解 22000sin lim (sin )x x xtdtt t t dt→-?=2202(sin )lim (1)(sin )x x x x x x →-??-=220()(2)lim sin x x x x →-?-=304(2)lim 1cos x x x→-?-x(,0)-∞0 (0,1)1 (1,)+∞()f x '＋－=2012(2)lim sin x x x→-?=0．注此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b ，使等式2201lim1sin x x t dt x b x a t→=-+?成立．分析易见该极限属于型的未定式，可用洛必达法则．解 20201lim sin x x t dt x b x a t →-+?=220lim 1cos x x a x b x →+-=22001lim lim 1cos x x x b x a x →→?-+201lim 11cos x x b x a →==-，由此可知必有0li m(1cos )0x b x →-=，得1b =．又由2012lim 11cos x x x a a→==-，得4a =．即4a =，1b =为所求．例10 设sin 20()sin x f x t dt =?，34()g x x x =+，则当0x →时，()f x 是()g x 的（）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小．D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→?=+ 2200cos sin(sin )lim lim34x x x x x x →→=?+ 22011lim 33x x x →==．故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++．例11 计算21||x dx -?．分析被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -?＝0210()x dx xdx --+??＝220210[][]22x x --+＝52．注在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=?，则是错误的．错误的原因则是由于被积函数21 x 在0x =处间断且在被积区间内无界.例12 设()f x 是连续函数，且10()3()f x x f t dt =+?，则()________f x =．分析本题只需要注意到定积分()baf x dx ?是常数（,a b 为常数）．解因()f x 连续，()f x 必可积，从而10()f t dt ?是常数，记1()f t dt a =?，则()3f x x a =+，且11(3)()x a dx f t dt a +==??．所以2101[3]2x ax a+=，即132a a +=，从而14a =-，所以 3()4f x x =-．例13 计算2112211x x dx x-++-?．分析由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解 2112211x x dx x-++-?=211112221111x x dx dx x x--++-+-?．由于22211x x+-是偶函数，而211x x+-是奇函数，有112011xdx x-=+-?, 于是2112211x x dx x -++-?=2102411x dx x +-?=22120(11)4x x dx x--?=11200441dx x dx --?? 由定积分的几何意义可知12014x dx π-=, 故211122444411x x dx dx xππ-+=-?=-+-?．例14 计算220()xd tf x t dt dx -?，其中()f x 连续．分析要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解由于220()xtf x t dt -?=2221()2x f x t dt-?．故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()x tf x t dt -?=201()()2x f u du -?=201()2x f u du ?，故220()x d tf x t dt dx -?=201[()]2x d f u du dx ?=21()22f x x=2()xf x ．错误解答220()x d tf x t dt dx -?22()(0)xf x x xf =-=．错解分析这里错误地使用了变限函数的求导公式，公式()()()xad x f t dt f x dx 'Φ==?中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．例15 计算30sin x xdx π．分析被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．解30s i n x x d x π30(c o s )x d x π=-?33[(c o s )](c o s )x x x d x ππ=?---? 30cos 6xdx ππ=-+?326π=-．例16 计算120ln(1)(3)x dx x +-?．分析被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-?=101ln(1)()3x d x +-?=1100111[ln(1)]3(3)(1)x dx x x x +-?--+? =101111ln 2()2413dx x x-++-?11ln 2ln324=-．例17 计算20sin x e xdx π．分析被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解由于2sin xe xdx π20sin xxde π=?220[sin ]cos xx e x e xdx ππ=-?220cos x e e xdx ππ=-?，（1）而20cos xe xdx π20cos xxde π=?220[cos ](sin )xx e x e x dx ππ20sin 1x e xdx π=-?，（2）将（2）式代入（1）式可得20sin xe xdx π220[sin 1]x e e xdx ππ=--?,故20sin xe xdx π21(1)2e π=+．例18 计算1arcsin x xdx ?．分析被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解 10arcsin x xdx ?210arcsin ()2x xd =?221100[arcsin ](arcsin )22x x x d x =?-?21021421x dx x π．（1）令sin x t =，则2121x dx x-?222sin sin 1sin td t tπ=-?220sin cos cos ttdt t π=??220sin tdt π=?201cos22t dt π-==?20sin 2[]24t t π-4π=．（2）将（2）式代入（1）式中得1arcsin x xdx =8π．例19设()f x [0,]π上具有二阶连续导数，()3f π'=且0[()()]cos 2f x f x xdx π''+=?，求(0)f '．分析被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．解由于0[()()]cos f x f x xdx π''+?00()sin cos ()f x d x xdf x ππ'=+??{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx ππππ'''=-++??()(0)2f f π''=--=．故(0)f '=2()235f π'--=--=-．例20 计算243dxx x +∞++?．分析该积分是无穷限的的反常积分，用定义来计算．解2043dx x x +∞++?=20lim 43t t dx x x →+∞++?=0111lim ()213t t dx x x →+∞-++? =011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32．。
高等数学第05章 定积分及其应用习题详解
0
x 1 sin tdt 0dt 1 ， 2
b a
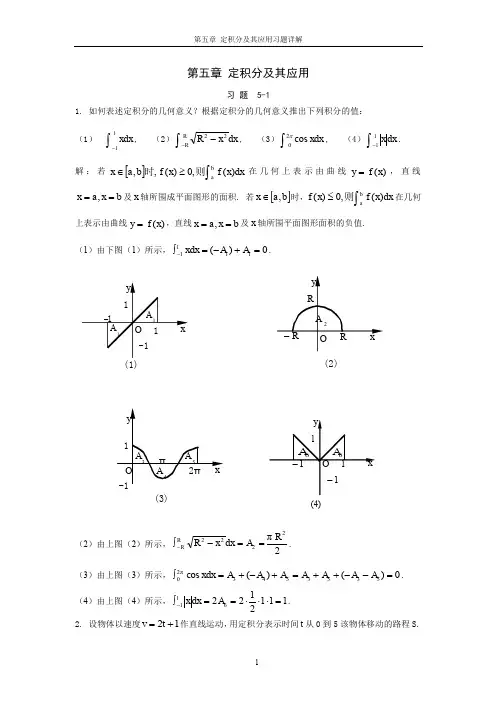
f ( x)dx 在 几 何 上 表 示 由 曲 线 y f ( x) ， 直 线
x a, x b 及 x 轴所围成平面图形的面积. 若 x a, b时，f ( x) 0, 则 b f ( x)dx 在几何 a
上表示由曲线 y f ( x) ，直线 x a, x b 及 x 轴所围平面图形面积的负值. （1）由下图（1）所示， 1 xdx ( A1 ) A1 0 .
n
2
i
i 1
n
2
1 1 1 1 1 n(n 1)(2n 1) = (1 )(2 ) 3 n 6 6 n n 1 1 2 当 0时 （即 n 时 ） ，由定积分的定义得： x d x = ． 0 3
= 5. 利用定积分的估值公式，估计定积分
4 3
1 1
(4 x 4 2 x 3 5) dx 的值.
上任取一点 i 作乘积 f ( i ) xi 的和式：
n
f ( i ) xi c ( xi xi1 ) c(b a) ,
i 1 i 1
n
n
记 max{xi } , 则
1i n
b a
cdx lim f ( i ) xi lim c(b a) c(b a) .
x
0
(t 1)dt ，求 y 的极小值
解： 当 y x 1 0 ，得驻点 x 1 ， y '' 1 0. x 1 为极小值点， 极小值 y (1)
( x 1)dx - 2
高等数学(同济大学第五版)第六章 定积分的应用
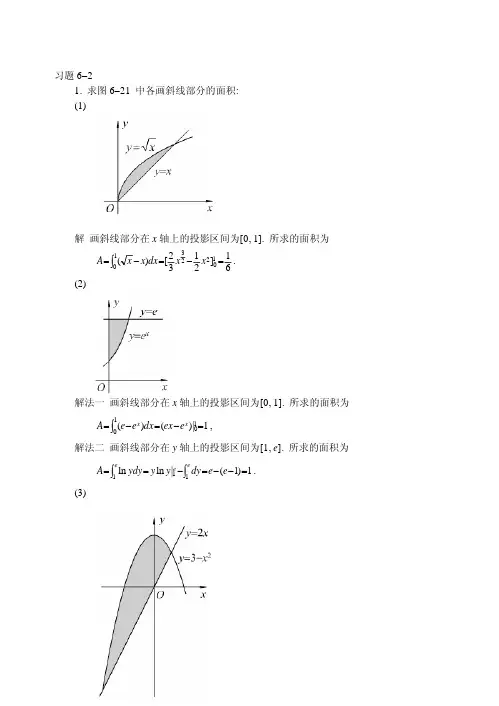
习题6−21. 求图6−21 中各画斜线部分的面积:(1)解 画斜线部分在x 轴上的投影区间为[0, 1]. 所求的面积为61]12[)(12231=−=−=x x dx x x A . 2300∫ 解法一x 轴上的投影区间为[0, 1]. 所求的面积为0 画斜线部分在y 轴上的区间为[1, e ]. 所求的面积为(2)画斜线部分在 1|)()(11=−=−=∫x x e ex dx e e A ,0 解法二投影 1)1(|ln ln =−−=−==∫∫e e dy y y ydy A e e e . 111(3)解 画斜线部分在x 轴上的投影区间为[−3, 1]. 所求的面积为332]2)3[(132=−−=∫−dx x x A . (4)解 [−1, 3]. 所求的面积为画斜线部分在x 轴上的投影区间为 332|)313()32(3132312=−+=−+=−−∫x x x dx x x A . 2. 求由下列各曲线所围成的图形的面积:(1) 221x y =与x 2+y 2=8(两部分都要计算); 解:388282)21222228(2020020221−−=−−=−−=∫∫∫∫dx x dx x dx x dx x x A 323cos 16402+=−=∫πtdt . 48π346)212−=−ππS . 2(2=A (2)xy =1与直线y =x 及x =2; 解:所求的面积为∫=A −=−202ln 23)1(dx x x . e x , y =e −x 与直线x =1;解:所求的 (3) y =面积为∫−+=−=−1021)(e e dx e e A x x . (4)y =ln x , y 轴与直线y =ln a , y =ln b (b >a >0).解所求的面积为a b e dy e A ba yb a y −===∫ln ln ln ln3. 求抛物线y =−x 2+4x −3及其在点(0, −3)和(3, 0)处的切线所围成的图形的面积. 解: 过点(0, −3)处的切线的斜率为4, 切线方程为y =4(x −3)., 切线方程为y =−2x +6.y ′=−2 x +4.过点(3, 0)处的切线的斜率为−2两切线的交点为)3 ,23(, 所求的面积为 49]34(62[)]34(34[2302332=−+−−+−+−+−−−=∫∫dx x x x x x x A . 4. 求抛物线y 2=2px 及其在点),2(p p 处的法线所围成的图形的面积. 解2y ⋅y ′=2p .在点处, 1),2(==′p p y p y ,),2(p p 法线的斜率k =−1, 法线的方程为)2(p x p y −−=−, 即y p x −=23.),2(p p 求得法线与抛物线的两个交点为和)3,29(p p −. 法线与抛物线所围成的图形的面积为233232316)612123()223(p y p y y p dy p y y p A p p pp =−−=−−=−−∫. 5. 求由下列各曲线 所围成的图形的面积;(1)ρ=2a cos θ ;解:所求的面积为∫∫==2221πθθ −202cos 4)cos 2(2ππθθd a d a A =πa 2. a cos 3t , y =a sin 3t ;解2(2)x =所求的面积为∫∫∫===204220330sin cos 34)cos ()sin (44ππtdt t a t a d t a ydx A a 2206204283]sin sin [12a tdt tdt a πππ=−=∫∫.(3)ρ=2 解所求的面积为a (2+cos θ ) 2202220218)cos cos 44(2)]cos 2(221a d a d a A πθθθθθππ=++=+=∫∫. 6. 求由摆线x =a (t −sin t ), y =a (1−cos t )的一拱(0≤t ≤2π)与横轴 所围成的图形的面积. 解:所求的面积为∫∫∫−=−−==a a a dt t a dt t a t a ydx A 20222020)cos 1()cos 1()cos 1(ππ22023)2cos 1cos 21(a dt t t a a =++−=∫. 7. 求对数螺线ρ=ae θ(−π≤θ≤π)及射线θ=π所围成的图形面积.解所求的面积为)(42)(2ππ−−∫∫e d e a d ae 11222222πππθπθθθ−−===e a . 8. 求下列各曲线所围成图形的公共部分的面积.(1)ρ=3cos θ 及ρ=1+cos θ解曲线ρ=3cos θ 与ρ=1+cos θ 交点的极坐标为A)3,23(πA , )3,23(π−B . 由对称性, 所求的面积为 πθθθθπππ45])cos 3(21)cos 1(21[2232302=++=∫∫d d A . (2)θρsin 2=及解θρ2cos 2=.6,22(π.曲线θρsin 2=与θρ2cos 2=的交点M 的极坐标为M 所求的面积为 2316]2cos 21)sin 2(21[24602−+=+=∫∫πθθθθπππd d A .于曲线e x 下方, 9. 求位y =该曲线过原点的切线的左方以及x 轴上方之间的图形的面积. 解 设直线y =kx 与曲线y =e x 相切于A (x 0, y 0)点, 则有x y e y kx y x x 00)(0000, , y 0=e , k =e .所求面 ⎪⎩⎪⎨⎧==′==ke 求得x 0=1积为21ln 21)ln 1(00020e dy y y y y y e dy y y e e e e e=⋅+−=−∫∫. 10. 求由抛物线y 2=4ax 与过焦点的弦所围成的图形的面积的最小值. 解 设弦的倾角为α. 由图可以看出, 抛物线与过焦点的弦所围成的图形的面积为10A A A +=. 显然当2πα=时1=0; 当, A 2πα1因此, 抛物线与过焦点的弦所围成的图形的面积的最小值为 <时, A >0. 20300383822a x a dx ax A a a ===∫. 1. 把抛物线y 2=4ax 及直线x =x 0(x 0>0)所围成的图形绕x 轴旋转, 计算得旋转体的体积.1所 解 所得旋转体的体积为20022224000x a axdx dx y V xx x πππ====∫ 00x a π∫. 12. 由y =x 3, x =2, y =0所围成的图形, 分别绕x 轴及y 轴旋转, 计算所得转所得旋转体的体积为两个旋转体的体积.解 绕x 轴旋πππ712871207206202====∫∫x dx x dx y V x . 绕y 轴旋转所得旋转体的体积为∫∫−=−⋅⋅=803280223282dy y dy x V y ππππ ππ56453328035=−=y . 所围成的图形, 绕x 轴旋, 计算所得旋转体的体积. 解 由对称性, 所求旋转体的体积为13. 把星形线转3/23/23/2a y x =+ dx x a dx y V a a ∫=2222π∫−=0333)(2π 0 3024224210532)33(2a dx x x a x a a a π=−+−=∫.14. 用积分方法证明图中球缺的体积为)(2H R H V −=π.3证明 ∫∫−−−==R H R RH R dy y R dy y x V )()(222ππ)3()1(32y y R R H R =−=−ππ 32H R H −.15. 求下列已知曲线所围成的图形, 按指定的轴旋转所产生的体积:(1的旋转体)2x y =,2y x =, 绕y 轴; πππ)(22=−=∫∫dy y ydy V 解 103)5121(10521010=−y y . (2)ax a y ch =, x =0, x =a , y =0, 绕x 轴; 解 ∫∫∫===102ch udu 302202 ch )(a x dx a x a dx x y V a aπππ令 au1022)()2(u u u du e e −=++=∫2231032122144u e u e a a −−+ππ )2sh 2(43+a π= . (3)216)5(2=−y , 绕x 轴.解 +x ∫∫−−−−−−+=44224422)165()165(dx x dx x Vππ 24021601640π∫=−=dx x .x =(t −sin t ),=a (1−cos t )的一拱, y =0, 绕直线y =2a . 解 a dy y a dx a V02202)2()2( 23237)8πππa t a a =+−=. 16. 求圆盘 (4)摆线a y a 2∫∫−−=ππππ∫−+−=πππ202223)sin (])cos 1([8t t da t a a 0sin cos 1(tdt a ∫232222a y x ≤+绕x =−b (b >a >0)旋转所成旋转体 解 的体积.∫∫−−−−−−+=a a a a dy y a b dy y a b V222222)()(ππ 2202228ππb a dy y a b a=−=∫.17. 设有一截锥体, 其高为h , 上、下底均为椭圆, 椭圆的轴2a 、2b 和2A 、求这截锥体的体积.解 建立坐标系如图. 过y 轴上y 点作垂直于y 轴的平面, 则 易得其长分别为2B , 平面与截锥体的截面为椭圆,长短半轴分别为y h a A A −−, y hb B B −−. 积为π)()(y 截面的面h h B B y a A A −⋅b −−−.于是截锥体的体积为])(2[61)()(b V h=∫0AB a h dy y h b B B y h a A A +++=−−⋅−−π.计算底面是半径为R 的圆, 而垂直于底面上一条固定直径的所有截面都是等边三角.x 且垂直于x () 件知, 它是边长为bA aB 18. 形的立体体积 解 设过点轴的截面面积为A x ,由已知条xR −2的等边三角形的面积, 其值为)(3)(22x R x A −=, 322334)(3R dx x R VR=−=∫R所以 − a.如图, 在x 处取一宽为dx 的边梯形, 小曲边梯形绕y 积近似为2πx ⋅f (x )dx , 这就是体积元素, 即 dV =2πx ⋅f (x )dx ,y 轴旋转所成的旋转体的体积为==bab dx x xf dx x xf V)(2)(2ππ.用题19和结论, 计算曲线y =sin x (0≤x ≤π)和x 轴所围成的图形绕y 轴旋转所得旋转体的体积. 解.19. 证明 由平面图形0≤a ≤x ≤b , 0≤y ≤f (x )绕y 轴旋转所成的旋转体的体积为=bdx x xf V )(2π∫ 证明 小曲轴旋转所得的旋转体的体于是平面图形绕 ∫a∫ 20. 利2002)sin cos (2cos 2sin 2πππππππ=+−=−==∫∫x x x x xd xdx x V .y =ln x 上相应于83≤≤ 21. 计算曲线x 的一段弧的长度.解 ∫∫∫+=+=′+=82838x32321)1(1)(1dx x x dx dx x y s ,t 12−=t x ,x +21=, 即 则令23ln 211111113223232222322+=−+=t s −=−⋅−=∫∫∫∫dt t dt d t t dt t tt t .)3(x − 22. 计算曲线3弧的长度. x y =上相应于1≤x ≤3的一段 解x x x y 3−=, 1x y 2−=′,x 121x x y 4112+−=′, 214)(12x y +=′+,121x为所求弧长3432)232(21)1(213131−=+=+=∫x x x dx xx s .23. 计算半立方抛物线被抛物线32x y =32)1(32−=x y 截得的一段弧的长度.解 由⎪⎩⎪⎨⎧=−=3)1( 32232x y x y 得两曲线的交点的坐标为36 ,2(, )36 ,2(−. 所求弧长为∫′+=21212dx y s .因为2y x y 2)1(−=′,)1(23)1()134−=−2)1(2−=′y y x ,32()1(242−−==′y x y 所以 x x x . ]1)25[(98)1)1−x 3(13232(231232121−=−=−+=∫∫d x dx x s . 抛物线y 2=2px 从顶点到这曲线上的一点M (x , y )的弧长.24. 计算∫∫∫+=+=′+=y yydy sy p p dy p y dy y x 02202021)(1)(1 解y y p y p p 2222])2[+++=y p y 02ln(21+p 2y p y py p py 2222ln2++++=.25. 计算星形线t a x 3cos =, 的全长.解 用参数方程的弧长公式.t a y 3sin = dt t y t x s =∫′+′2022)()(4π∫⋅+−⋅=202222]cos sin 3[)]sin (cos 3[4πdt t t a t t aa tdt t 6cos sin 1220==∫π.26. 将绕在圆(半径为a )上的细线放开拉直, 使细线与圆周始终相切, 细线端点画出的轨迹叫做圆的渐伸线, 它的方程为 )sin (cos t t t a x +=, )cos (sin t t t a y −=.计算这曲线上相应于t 从0变到π的一段弧的长度. 解 由参数方程弧长公式∫∫+=′+′=ππ022022)sin ()cos ()]([)]([dtt at t at dt t y t x s 0∫22ππa tdt a ==.cos t )上求分摆线第一拱成1: 3 解 设t 从0变化到t 0时摆线第一拱上对应的弧长为s (t 0), 则 27. 在摆线x =a (t −sin t ), y =a (1−的点的坐标.∫∫+−=′+′=0220220]sin [)]cos 1([)]t ([)]([)(t t dt t a t a dt y t x t s)2cos 1(42sin 2000ta dt t a t −==∫.当t 0=2π时, 得第一拱弧长s (2π)=8a . 为求分摆线第一拱为1: 3的点为A (x , y ), 令a ta 22cos 1(40=−,32解得0π=t , 因而分点的坐标为:a a x )32()2sin 2(−=−=πππ, 横坐标23 纵坐标33a a y 23)32cos1(=−=π,故所求分点的坐标为)23 ,)2332((a a −π. ρθa e =相应于自θ=0到的一段弧长 28. 求对数螺线θ=ϕ. 解 用极坐标的弧长公式. θθθρθρϕθθϕd ae e d a a ∫∫+=′+=22022)()()()(s )1−θ(11202+=+=∫ϕθθa a e aa d e a .29线1相应于自 . 求曲ρθ=43=θ至34=θ.的一段弧长 极坐标公式可得所求的弧长 解 按∫∫−+=′+=344322234322)1()1()()(θθθθθρθρd d s23ln 1251134322+=+=∫θθθd .30. 求心形线ρ=a (1+cos θ )的全长. 解 用极坐标的弧长公式. θθθθθρθρππd a a d s ==2 ∫∫−++′+0222022)sin ()cos 1()()(2a d a 82∫cos 4==πθθ.习题6−31. 由实验知道, 弹簧在拉伸过程中, 需要的力F (单位: N )与伸长量s (单位: cm)成正比, 即F =ks (k 为比例常数). 如果把弹簧由原长拉伸6cm , 计算所作的功.解 将弹簧一端固定于A , 另一端在自由长度时的点O 为坐标原点, 建立坐标系. 功元素为dW =ksds , 所求功为18216260===∫s k ksds W k(牛⋅厘米).2. 直径为20cm 、高80cm 的圆柱体内充满压强为10N/cm 2的蒸汽. 设温度保持不变, 要使蒸汽体积缩小一半, 问需要作多少功？ 解 由玻−马定律知:ππ80000)8010(102=⋅⋅==k PV .设蒸气在圆柱体内变化时底面积不变, 高度减小x 厘米时压强 为P (x )牛/厘米2, 则ππ80000)]80)(10[()(2=−⋅x x P , π−=80800)(x P .功元素为dx x P dW )()10(2⋅=π,所求功为 2ln 8008018000080800)10(400402πππππ=−=−⋅⋅=∫∫dx dx W(J).3. (1)证明: 把质量为m 的物体从地球表面升高到h 处所作的功是 hR mgRhW +=,其中g 是地面上的重力加速度, R 是地球的半径;(2)一颗人造地球卫星的质量为173kg , 在高于地面630km 处进入轨道. 问把这颗卫星从地面送到630的高空处, 克服地球引力要作多少功？已知g =9.8m/s 2, 地球半径R =6370km .证明 (1)取地球中心为坐标原点, 把质量为m 的物体升高的功元素为dy ykMm dW 2=, 所求的功为 )(2h R R mMh k dy y kMm W hR R+⋅==∫+.(2)533324111075.910)6306370(106370106301098.51731067.6×=×+×××××⋅×=−W (kJ).4. 一物体按规律3ct x =作直线运动, 媒质的阻力与速度的平方成正比. 计算物体由x =0移至x =a 时, 克服媒质阻力所作的功. 解 因为3ct x =, 所以23)(cxt x v =′=, 阻力4229t kc kv f −=−=. 而32)(cx t =, 所以34323429)(9)(x kc cx kc x f −=−=. 功元素dW =−f (x )dx , 所求之功为 37320343203432072799)]([a kc dx x kcdx x kc dx x f Wa aa ===−=∫∫∫. 5. 用铁锤将一铁钉击入木板, 设木板对铁钉的阻力与铁钉击入木板的深度成正比, 在击第一次时, 将铁钉击入木板1cm . 如果铁锤每次打击铁钉所做的功相等, 问锤击第二次时, 铁钉又击入多少？解 设锤击第二次时铁钉又击入h cm , 因木板对铁钉的阻力f 与铁钉击入木板的深度x (cm)成正比, 即f =kx , 功元素dW =f dx =kxdx , 击第一次作功为 k kxdx W 21101==∫,击第二次作功为 )2(212112h h k kxdx W h+==∫+.因为, 所以有 21W W =)2(21212h h k k +=, 解得12−=h (cm).6. 设一锥形贮水池, 深15m , 口径20m , 盛满水, 今以唧筒将水吸尽, 问要作多少功？解 在水深x 处, 水平截面半径为x r 3210−=, 功元素为dx x x dx r x dW 22)3210(−=⋅=ππ,所求功为 ∫−=1502)3210(dx x x Wπ∫+−=15032)9440100(dx x x x π =1875(吨米)=57785.7(kJ).7. 有一闸门, 它的形状和尺寸如图, 水面超过门顶2m . 求闸门上所受的水压力. 解 建立x 轴, 方向向下, 原点在水面. 水压力元素为xdx dx x dP 221=⋅⋅=, 闸门上所受的水压力为21252252===∫x xdx P (吨)=205. 8(kN).8. 洒水车上的水箱是一个横放的椭圆柱体, 尺寸如图所示. 当水箱装满水时, 计算水箱的一个端面所受的压力.解 建立坐标系如图, 则椭圆的方程为11)43()43(2222=+−y x .压力元素为dx x x dx x y x dP 22)43()43(38)(21−−⋅=⋅⋅=,所求压力为∫∫−⋅⋅+=−−⋅=222322cos 43cos 43)sin 1(4338)43()43(38ππtdx t t dx x x Pππ169cos 49202==∫tdx (吨)=17.3(kN). (提示: 积分中所作的变换为t x sin 4343=−)9. 有一等腰梯形闸门, 它的两条底边各长10m 和6m , 高为20m . 较长的底边与水面相齐. 计算闸门的一侧所受的水压力.解 建立坐标系如图. 直线AB 的方程为x y 1015−=,压力元素为dx x x dx x y x dP )5110()(21−⋅=⋅⋅=,所求压力为1467)5110(200=−⋅=∫dx x x P (吨)=14388(千牛).10. 一底为8cm 、高为6cm 的等腰三角形片, 铅直地沉没在水中, 顶在上, 底在下且与水面平行, 而顶离水面3cm , 试求它每面所受的压力. 解 建立坐标系如图.腰AC 的方程为x y 32=, 压力元素为dx x x dx x x dP )3(34322)3(+=⋅⋅⋅+=,所求压力为168)2331(34)3(34602360=+=+=∫x x dx x x P (克)=1.65(牛).11. 设有一长度为l 、线密度为μ的均匀细直棒, 在与棒的一端垂直距离为a 单位处有一质量为m 的质点M , 试求这细棒对质点M 的引力.解 建立坐标系如图. 在细直棒上取一小段dy , 引力元素为dy ya Gm y a dy m G dF 2222+=+⋅=μμ, dF 在x 轴方向和y 轴方向上的分力分别为dF r a dF x −=, dF rydF y =.2202222022)(1)(l a a l Gm dy y a y a aGm dy y a Gm r a F l lx +−=++−=+⋅−=∫∫μμμ,)11()(12202222022l a a Gm dy y a y a Gm dy y a Gm r y F l ly +−=++=+⋅=∫∫μμμ. 12. 设有一半径为R 、中心角为 ϕ 的圆弧形细棒, 其线密度为常数 μ . 在圆心处有一质量为m 的质点F . 试求这细棒对质点M 的引力. 解 根据对称性, F y =0.θμcos 2⋅⋅⋅=Rdsm G dF xθθμθθμd R Gm R Rd Gm cos cos )(2=⋅=,θθμϕϕd R Gm F x ∫−=2cos2sin 2cos 220ϕμθθμϕR Gm d R Gm ==∫. 引力的大小为2sin 2ϕμR Gm , 方向自M 点起指向圆弧中点.总 习 题 六1. 一金属棒长3m , 离棒左端xm 处的线密度为11)(+=x x ρ (kg/m ). 问x 为何值时, [0, x ]一段的质量为全棒质量的一半? 解 x 应满足∫∫+=+300112111dt t dt t x.因为212]12[110−+=+=+∫x t dt t x x, 112[2111213030=+=+∫t dt t ,所以1212=−+x ,45=x (m).2. 求由曲线ρ=a sin θ, ρ=a (cos θ+sin θ)(a >0)所围图形公共部分的面积. 解∫++⋅=43222)sin (cos 21)2(21ππθθθπd a a S24322241)2sin 1(28a d a a −=++=∫πθθπππ.3. 设抛物线c bx ax y ++=2通过点(0, 0), 且当x ∈[0, 1]时, y ≥0. 试确定a 、b 、c 的值, 使得抛物线与直线x =1, y =0所围图形的面积为c bx ax y ++=294,且使该图形绕x 轴旋转而成的旋转体的体积最小.y c bx ax +=+ 解 因为抛物线2y 通过点(0, 0), 所以c =0, 从而 bx ax +=2.bx ax y +=2与直线x =1, y =0所围图形的面积为抛物线23)(102b a dx bx ax S +=+=∫. 令9423=+b a , 得968a b −=. 该图形绕x 轴旋转而成的旋转体的体积为 )235()(221022ab b a dx bx ax V ++=+=∫ππ)]968(2)968(315[22a a a a −+−+=π. 令0)]128(181********[=−+−⋅+2=a a a ddV π, 得35−=a , 于是b =2. 4. 求由曲线23x y =与直线x =4, x 轴所围图形绕y 轴旋转而成的旋转体的体积.解 所求旋转体的体积为πππ751272224027403=⋅=⋅=∫x dx x x V . 5. 求圆盘1)2(22≤+−y x 绕y 轴旋转而成的旋转体的体积.解 )2(122312∫−−⋅⋅=dx x x Vπ 2224cos )sin 2(4 sin 2ππππ=+=−∫−tdt t t x 令.6. 抛物线221x y =被圆322=+y x 所需截下的有限部分的弧长. 解 由⎪⎩⎪⎨⎧==+222213x y y x 解得抛物线与圆的两个交点为)1 ,2(−, )1 ,2(, 于是所求的弧长为2022202])1ln(2112[212x x x x dx x s ++++=+=∫ )32ln(6++=.,解 建立坐标系如图. 将球从水中取出时, 球的各点上升的高度均为2r . 在x 处取一厚度为dx 的薄片, 在将球从水中取出的过程中, 薄片在水下上升的高度为r +x ,在水上上升的高度为r −x . 在水下对薄片所做的功为零,在水上对薄片所做的功为dx x r x r g dW ))((22−−=π,对球所做的功为g r x d x r x r g W rr 22234))((ππ=−−=∫−. 8. 边长为a 和b 的矩形薄板, 与液面成α 角斜沉于液体内,长边平行于液面而位于深h 处, 设a >b , 液体的比重为ρ, 试求薄板每面所受的压力.解 在水面上建立x 轴, 使长边与x 轴在同一垂面上, 长边的在x 轴上的投影区间为[0, b cos α], 在x 处x 轴到薄板的距离为h +x tan α. 压力元素为 上端点与原点对应. 长边dx x h ga dx a x h g dP )tan (cos cos )tan (ααρααρ+=⋅⋅+⋅=, 薄板各面所受到的压力为)sin 2(21)tan (cos cos 0αρααραb h gab dx x h ga P b +=+=∫. 9. 设星形线t a x 3cos =,t a y 3sin =上每一点处的线密度的大小等于该点到原点距离的立方, 在原点O 处有一单位质点, 求星形线在第一象限的弧段对这质点的引力. 解 取弧微分ds 为质点, 则其质量为ds y x ds y x 322322)()(+=+, 其中tdt t a dt t a t a ds cos sin 3])sin [(])cos [(2323=′+′=.设所求的引力在x 轴、y 轴上的投影分别为F x 、F y , 则有∫+⋅++⋅⋅=202222322)()(1πds y x x y x y x G F x 2204253sin cos 3Ga tdt t Ga ==∫π, ∫+⋅++⋅⋅=22222322)()(1πds y x y y x y x G F x 2204253sin cos 3Ga tdt t Ga ==∫π, 所以)53 ,53(22Ga Ga =F .。
定积分典型例题20例解答
定积分典型例题20例答案例1求33322321lim(2)n n n n n®¥+++．分析将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．解将区间[0,1]n 等分，则每个小区间长为1i x n D =，然后把2111n n n =×的一个因子1n乘入和式中各项．于是将所求极限转化为求定积分．即33322321lim (2)n n n n n®¥+++=333112lim ()n n n n n n ®¥+++=13034xdx =ò．例2222x x dx -ò=_________．解法1由定积分的几何意义知，222x x dx -ò等于上半圆周22(1)1x y -+= (0y ³)与x 轴所围成的图形的面积．故222x x dx -ò=2p ．解法2本题也可直接用换元法求解．令1x -=sin t （22t pp-££），则222x x dx -ò=2221sin cos t tdt pp --ò=2221sin cos t tdt p -ò=222cos tdt p ò=2p例3（1）若22()xtxf x e dt -=ò，则()f x ¢=___；（2）若0()()xf x xf t dt=ò，求()f x ¢=___．分析这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ¢¢=-ò．解（1）()f x ¢=422x x xee---；（2）由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =ò，则可得()f x ¢=()()xf t dt xf x +ò．例4 设()f x 连续，且310()x f t dt x -=ò，则(26)f =_________．解对等式31()x f t dt x -=ò两边关于x 求导得32(1)31f x x -×=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =． 例5 函数11()(3)(0)x F x dt x t =->ò的单调递减开区间为_________． 解 1()3F x x¢=-，令()0F x ¢<得13x >，解之得109x <<，即1(0,)9为所求．为所求．例6 求0()(1)arctan xf x ttdt =-ò的极值点．的极值点． 解 由题意先求驻点．于是()f x ¢=(1)arctan x x -．令()f x ¢=0，得1x =，0x =．列表如下：如下：故1x =为()f x 的极大值点，0x =为极小值点．为极小值点．例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中处的切线相同，其中 2arcsin0()x tg x e dt -=ò，[1,1]x Î-，试求该切线的方程并求极限3lim()n nf n®¥． 分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ¢¢=．解 由已知条件得由已知条件得2(0)(0)0t f g e dt-===ò，且由两曲线在(0,0)处切线斜率相同知处切线斜率相同知2(arcsin )2(0)(0)11x x ef g x-=¢¢===-．故所求切线方程为y x =．而．而3()(0)3lim ()lim33(0)330n n f f n nf f nn®¥®¥-¢=×==-． 例8 求 22sin lim (sin )xx xtdtt t t dt®-òò；分析 该极限属于00型未定式，可用洛必达法则．型未定式，可用洛必达法则．解 2200sin lim (sin )xx x tdtt t t dt®-òò=2202(sin )lim (1)(sin )x x x x x x ®-××-=220()(2)lim sin x x x x ®-×-=304(2)lim 1cos x xx ®-×- x(,0)-¥0 (0,1)1 (1,)+¥()f x ¢- 0 ＋ 0 －=2012(2)lim sin x x x®-×=0． 注 此处利用等价无穷小替换和多次应用洛必达法则．此处利用等价无穷小替换和多次应用洛必达法则．例9 试求正数a 与b ，使等式221lim 1sin x x tdt x b x a t®=-+ò成立．成立．分析 易见该极限属于型的未定式，可用洛必达法则． 解 221lim sin x x tdt x b xa t®-+ò=22lim 1cos x xa xb x ®+-=221lim lim 1cos x x xb xa x ®®×-+201lim 11cos x x b xa ®==-， 由此可知必有0lim(1cos )0x b x ®-=，得1b =．又由．又由 2012lim 11cosx xx a a ®==-， 得4a =．即4a =，1b =为所求．为所求．例10 设sin 20()sin x f x t dt=ò，34()g x x x =+，则当0x ®时，()f x 是()g x 的（的（ ）． A ．等价无穷小．．等价无穷小． B ．同阶但非等价的无穷小．．同阶但非等价的无穷小． C ．高阶无穷小．．高阶无穷小． D ．低阶无穷小．解法1 由于由于 22300()sin(sin )cos lim lim ()34x x f x x x g x x x ®®×=+ 2200cos sin(sin )lim lim 34x x x x xx ®®=×+ 22011lim 33x xx ®==． 故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到的幂级数，再逐项积分，得到sin 223370111()[()]sin sin 3!342xf x t t dt x x =-+=-+ò，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x xx®®®®-+-+===++．例11 计算21||x dx -ò．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -ò＝0210()x dx xdx--+òò＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时在使用牛顿－莱布尼兹公式时,,应保证被积函数在积分区间上满足可积条件．如应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=ò，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界积区间内无界. .例12 设()f x 是连续函数，且1()3()f x x f t dt=+ò，则()________f x =．分析 本题只需要注意到定积分()baf x dx ò是常数（,a b 为常数）．解 因()f x 连续，()f x 必可积，从而1()f t dt ò是常数，记1()f t dt a =ò，则，则()3f x x a =+，且110(3)()x a dx f t dt a+==òò．所以所以211[3]2x ax a +=，即132a a +=，从而14a =-，所以，所以 3()4f x x =-．例13 计算2112211x xdx x-++-ò．分析 由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解 2112211x x dx x -++-ò=211112221111xx dx dx x x --++-+-òò．由于22211x x +-是偶函数，而211xx+-是奇函数，有112011xdx x-=+-ò, 于是于是2112211x xdx x -++-ò=2102411x dx x +-ò=22120(11)4x x dx x --ò=11200441dx x dx --òò 由定积分的几何意义可知12014x dx p -=ò, 故2111022444411x x dx dx xp p -+=-×=-+-òò． 例14 计算220()xdtf x t dt dx -ò，其中()f x 连续．连续． 分析 要求积分上限函数的导数，要求积分上限函数的导数，但被积函数中含有但被积函数中含有x ，因此不能直接求导，因此不能直接求导，必须先换必须先换元使被积函数中不含x ，然后再求导．，然后再求导．解 由于由于220()xtf x t dt -ò=22201()2xf x t dt -ò． 故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以，所以22()xtf x t dt -ò=201()()2x f u du -ò=201()2xf u du ò，故22()xd tf x t dt dx -ò=21[()]2x d f u du dx ò=21()22f x x ×=2()xf x ．错误解答 220()xd tf x t dt dx -ò22()(0)xf x x xf =-=． 错解分析 这里错误地使用了变限函数的求导公式，公式这里错误地使用了变限函数的求导公式，公式()()()xa d x f t dtf x dx ¢F ==ò中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．导，而应先换元．例15 计算3sin x xdx pò．分析 被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法． 解3s i n x x d xpò3(c o s )x d x p=-ò3300[(c o s )](co s )x x x d x p p=×---ò3cos 6xdx pp=-+ò326p=-． 例16 计算12ln(1)(3)x dx x +-ò．分析 被积函数中出现对数函数的情形，可考虑采用分部积分法．被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-ò=101ln(1)()3x d x +-ò=1100111[ln(1)]3(3)(1)x dx x x x +-×--+ò =101111ln 2()2413dx x x-++-ò 11ln 2ln324=-． 例17 计算2sin xe xdx pò．分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法．解 由于2sin xe xdx pò2sin x xde p=ò22[sin ]cos xxe x e xdx p p=-ò220cos xe e xdx pp=-ò， （（1）而2cos xe xdx pò2cos xxdep=ò22[cos ](sin )xx e x e x dx pp=-×-ò2sin 1x e xdx p =-ò， （（2）将（将（22）式代入（）式代入（11）式可得）式可得2sin xe xdx pò220[sin 1]xe e xdx pp=--ò,故2sin xe xdx pò21(1)2e p=+．例18 计算1arcsin x xdx ò．分析 被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法． 解 10arcsin x xdxò210arcsin ()2x xd =ò221100[arcsin ](arcsin )22x x x d x =×-ò 21021421xdx xp=--ò． （1） 令sin x t =，则，则2121xdx x-ò2202sin sin 1sin t d ttp =-ò220sin cos cos t tdt t p=×ò220sin tdt p=ò201cos 22tdt p -==ò20sin 2[]24t t p-4p =． （2）将（将（22）式代入（）式代入（11）式中得）式中得10arcsin x xdx =ò8p． 例19设()f x [0,]p 上具有二阶连续导数，()3f p ¢=且[()()]cos 2f x f x xdx p¢¢+=ò，求(0)f ¢．分析分析 被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．解 由于0[()()]cos f x f x xdx p¢¢+ò00()sin cos ()f x d x xdf x p p¢=+òò[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx pppp¢¢¢=-++òò()(0)2f f p ¢¢=--=．故 (0)f ¢=2()235f p ¢--=--=-．例20 计算2043dxx x +¥++ò．分析 该积分是无穷限的的反常积分，用定义来计算． 解 2043dx x x +¥++ò=20lim 43t t dx x x ®+¥++ò=0111lim ()213t t dx x x ®+¥-++ò =011lim [ln ]23t t x x ®+¥++=111lim (ln ln )233t t t ®+¥+-+ =ln 32．。
定积分典型例题20例标准答案
定积分典型例题20例答案例1 求33322321lim(2)n n n n n®¥+++．分析 将这类问题转化为定积分主要是确定被积函数和积分上下限．若对题目中被积函数难以想到，可采取如下方法：先对区间[0,1]n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限．找出被积函数与积分上下限．解 将区间[0,1]n 等分，则每个小区间长为1i x nD =，然后把2111n n n =×的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即入和式中各项．于是将所求极限转化为求定积分．即33322321lim (2)n n n n n ®¥+++=333112lim ()n n n n nn ®¥+++=13034xdx =ò．例2 2202x x dx -ò=_________．解法1 由定积分的几何意义知，2202x x dx -ò等于上半圆周22(1)1x y -+= (0y ³) 与x 轴所围成的图形的面积．故2202x x dx -ò=2p． 解法2 本题也可直接用换元法求解．令1x -=sin t （22t pp-££），则，则222x x dx -ò=2221sin cos t tdt pp --ò=22021sin cos t tdt p-ò=2202cos tdt pò=2p例3 （1）若22()x t x f x e dt -=ò，则()f x ¢=___；（2）若0()()xf x xf t dt =ò，求()f x ¢=___．分析 这是求变限函数导数的问题，利用下面的公式即可这是求变限函数导数的问题，利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ¢¢=-ò．解 （1）()f x ¢=422x x xee---；（2） 由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =ò，则可得可得()f x ¢=()()xf t dt xf x +ò．例4 设()f x 连续，且31()x f t dt x -=ò，则(26)f =_________．解 对等式310()x f t dt x -=ò两边关于x 求导得求导得32(1)31f x x -×=，故321(1)3f x x-=，令3126x -=得3x =，所以1(26)27f =．例5 函数11()(3)(0)xF x dt x t =->ò的单调递减开区间为_________．解 1()3F x x ¢=-，令()0F x ¢<得13x>，解之得109x <<，即1(0,)9为所求．为所求． 例6 求0()(1)arctan xf x t tdt =-ò的极值点．的极值点． 解 由题意先求驻点．于是()f x ¢=(1)arctan x x -．令()f x ¢=0，得1x =，0x =．列表如下：如下： 故1x =为()f x 的极大值点，0x =为极小值点．为极小值点． 例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中处的切线相同，其中2arcsin 0()xt g x e dt -=ò，[1,1]x Î-，试求该切线的方程并求极限3lim ()n nf n ®¥．分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同，隐含条件(0)(0)f g =，(0)(0)f g ¢¢=．解 由已知条件得由已知条件得2(0)(0)0tf g e dt -===ò，且由两曲线在(0,0)处切线斜率相同知处切线斜率相同知2(arcsin )2(0)(0)11x x e f g x-=¢¢===-．故所求切线方程为y x =．而．而3()(0)3lim ()lim33(0)330n n f f n nf f n n®¥®¥-¢=×==-．例8 求 22sin lim(sin )x x x tdt t t t dt®-òò；分析 该极限属于型未定式，可用洛必达法则．型未定式，可用洛必达法则． 解 22000sin lim (sin )x x xtdtt t t dt ®-òò=2202(sin )lim(1)(sin )x x x x x x ®-××-=220()(2)lim sin x x x x ®-×-=304(2)lim 1cos x x x ®-×- =2012(2)lim sin x x x®-×=0．注 此处利用等价无穷小替换和多次应用洛必达法则．此处利用等价无穷小替换和多次应用洛必达法则．x (,0)-¥(0,1)1 (1,)+¥()f x ¢-＋－例9 试求正数a 与b ，使等式2021lim1sin xx t dt x b x a t®=-+ò成立．成立．分析 易见该极限属于型的未定式，可用洛必达法则． 解 20201lim sin x x t dt x b x a t ®-+ò=220lim 1cos x x a x b x ®+-=22001lim lim 1cos x x x b x a x ®®×-+201lim 11cos x x b xa ®==-，由此可知必有0lim(1cos )0x b x ®-=，得1b =．又由．又由 2012lim11cos x x xaa®==-，得4a =．即4a =，1b =为所求．为所求． 例10 设sin 20()sin xf x t dt =ò，34()g x x x =+，则当0x ®时，()f x 是()g x 的（的（）． A ．等价无穷小．．等价无穷小． B ．同阶但非等价的无穷小．．同阶但非等价的无穷小． C ．高阶无穷小．．高阶无穷小．D ．低阶无穷小． 解法1 由于由于 22300()sin(sin )cos lim lim ()34x x f x x x g x x x ®®×=+ 2200cos sin(sin )lim lim 34x x x x x x ®®=×+ 22011lim 33x x x ®==． 故()f x 是()g x 同阶但非等价的无穷小．选B ．解法2 将2sin t 展成t 的幂级数，再逐项积分，得到的幂级数，再逐项积分，得到sin223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+ò，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f xg x x x x ®®®-+-+===++．例11 计算21||x dx -ò．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分．解 21||x dx -ò＝0210()x dx xdx --+òò＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时在使用牛顿－莱布尼兹公式时,,应保证被积函数在积分区间上满足可积条件．如应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=ò，则是错误的．错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界积区间内无界. .例12 设()f x 是连续函数，且1()3()f x x f t dt =+ò，则()________f x =．分析 本题只需要注意到定积分()baf x dx ò是常数（,a b 为常数）．解 因()f x 连续，()f x 必可积，从而1()f t dt ò是常数，记1()f t dt a =ò，则，则()3f x x a =+，且11(3)()x a dx f t dt a +==òò．所以所以2101[3]2x ax a +=，即132a a +=，从而14a =-，所以，所以 3()4f x x =-．例13 计算2112211x xdx x-++-ò． 分析 由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性． 解2112211x x dx x -++-ò=211112221111xxdx dx x x--++-+-òò．由于22211x x +-是偶函数，而211xx +-是奇函数，有112011x dx x-=+-ò, 于是于是 2112211x xdx x-++-ò=212411x dx x+-ò=2212(11)4x x dx x--ò=11200441dx x dx --òò由定积分的几何意义可知12014x dx p-=ò, 故2111022444411x xdx dx x p p -+=-×=-+-òò．例14 计算22()x d tf x t dt dx -ò，其中()f x 连续．连续． 分析 要求积分上限函数的导数，要求积分上限函数的导数，但被积函数中含有但被积函数中含有x ，因此不能直接求导，因此不能直接求导，必须先换必须先换元使被积函数中不含x ，然后再求导．，然后再求导．解 由于由于220()xtf x t dt -ò=22201()2xf x t dt -ò．故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以，所以22()x tf x t dt -ò=201()()2xf u du -ò=21()2x f u du ò，故220()x d tf x t dt dx -ò=201[()]2x d f u du dx ò=21()22f x x ×=2()xf x ． 错误解答 22()x d tf x t dt dx -ò22()(0)xf x x xf =-=．错解分析 这里错误地使用了变限函数的求导公式，公式这里错误地使用了变限函数的求导公式，公式()()()xa d x f t dt f x dx¢F ==ò中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．导，而应先换元． 例15 计算3sin x xdx pò．分析 被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法．被积函数中出现幂函数与三角函数乘积的情形，通常采用分部积分法． 解 3s i n x x d x pò3(c o s )x d x p=-ò330[(c o s )](co s )x x x d x pp=×---ò 30cos 6xdx pp=-+ò326p=-． 例16 计算1200ln(1)(3)x dx x +-ò． 分析 被积函数中出现对数函数的情形，可考虑采用分部积分法．被积函数中出现对数函数的情形，可考虑采用分部积分法．解 120ln(1)(3)x dx x +-ò=101ln(1)()3x d x +-ò=1100111[ln(1)]3(3)(1)x dx x x x +-×--+ò =101111ln 2()2413dx x x-++-ò 11ln 2ln324=-．例17 计算20sin x e xdx pò．分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法． 解 由于2sin xe xdx pò20sin xxde p=ò220[sin ]cos xxe x e xdx p p=-ò220cos xe e xdx p p=-ò，（1） 而2cos xe xdx pò20cos xxde p=ò2200[cos ](sin )xxe x e x dx p p=-×-ò 2sin 1xe xdx p=-ò， （2）将（将（22）式代入（）式代入（11）式可得）式可得2sin xe xdx pò220[sin 1]xe e xdx p p=--ò,故20sin xe xdx pò21(1)2e p=+．例18 计算10arcsin x xdx ò．分析 被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．被积函数中出现反三角函数与幂函数乘积的情形，通常用分部积分法．解10arcsin x xdx ò210arcsin ()2x xd =ò221100[arcsin ](arcsin )22x x x d x =×-ò 21021421x dx x p=--ò． （1） 令sin x t =，则，则2121x dx x-ò2202sin sin 1sin t d t tp =-ò220sin cos cos t tdt tp=×ò220sin tdt p=ò 201cos 22t dt p-==ò20sin 2[]24t t p-4p =． （2） 将（将（22）式代入（）式代入（11）式中得）式中得1arcsin x xdx =ò8p ．例19设()f x [0,]p 上具有二阶连续导数，()3f p ¢=且0[()()]cos 2f x f x xdx p¢¢+=ò，求(0)f ¢．分析分析 被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解．被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解． 解 由于0[()()]cos f x f x xdx p ¢¢+ò00()sin cos ()f x d x xdf x p p¢=+òò[]0000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx pppp¢¢¢=-++òò()(0)2f f p ¢¢=--=． 故 (0)f ¢=2()235f p ¢--=--=-．例20 计算2043dx x x +¥++ò． 分析 该积分是无穷限的的反常积分，用定义来计算．解 2043dx x x +¥++ò=20lim 43t t dx x x ®+¥++ò=0111lim ()213t t dx x x ®+¥-++ò =011lim [ln ]23t t x x ®+¥++=111lim (ln ln )233t t t ®+¥+-+ =ln 32．。
定积分典型例题20例答案
定积分典型例题20例答案例1求lim 丄(循2丁2『L Vn 3) •n n分析将这类问题转化为定积分主要是确定被积函数和积分上下限. 若对题目中被积函数难以想到，可采取如下方法：先对区间 [0, 1] n 等分写出积分和，再与所求极限相比较来找出被积函数与积分上下限.解 将区间[0, 1] n 等分，则每个小区间长为 ％ -,然后把1丄的一个因子-乘nn n nn入和式中各项•于是将所求极限转化为求定积分•即lim A (习n 2 ^2n 2 LVn 3) = lim -(^—L ^—) = VXdx - • n nnnn,n ,n ° 42 -- ------ r例 2o (2x x dx = ___________• 2 . ________解法1由定积分的几何意义知， °. 2x x 2dx 等于上半圆周(x 1)2 y 2 1 ( y 0)与x 轴所围成的图形的面积.故2,2x x 2dx = _ • 0 2'1 sin 2tcostdt = 2。
2J sin 2t costdt =2 ： cos 2 tdt^22x 2 2x例 3 (1)若 f (x) x e 七 dt ，则 f (x) = ________; (2)若 f (x) 0 xf (t)dt ,求 f (x)=分析这是求变限函数导数的问题，利用下面的公式即可(1) f (x) =2xe x e x可得xf (x) = 0 f (t)dt xf (x) •x 1例 4 设 f(x)连续，且。
f(t)dt x ，贝U f (26) = _________________O Ax 1解 对等式0 f(t)dtx 两边关于x 求导得3 2f(x 1) 3x 1,解法2本题也可直接用换元法求解.令x 1= Sint (2 t 2)，则d v(x)dx u(x)f(t)dt f[v(x)]v(x) f[u(x)]u (x) • (2) 由于在被积函数中x 不是积分变量，故可提到积分号外即xf (x) x 0 f (t)dt ，则x 2dx =3 1 令x 1 26得x 3，所以f (26)27故f(x 3 1) 丄3x 例5函数F(x)F (x)1 1，令F (x) 0得r 3，解之得xx1 10 x -，即(0,-)为所求.9 9f (x)x0 (1 t)arctan tdt 的极值点.f (x) = (1 x)arctan x .令 f (x) = 0，得 x 1 , x 0.列表如下:x(,0)0 (0,1) 1(1,)f (x)-0 +f (x)的极大值例7已知两曲线y f (x)与y g(x)在点(0,0)处的切线相同，其中arcs inxg(x) 0t 2e dt , x [ 1,1],试求该切线的方程并求极限 lim nf (?).n n分析两曲线y f (x)与y g(x)在点(0,0)处的切线相同，隐含条件f(0) g(0)，f (0)g (0) •解由已知条件得f(0)g(0)°e " dt且由两曲线在(0,0)处切线斜率相同知f (0)g(0)(arcsin x)2e1 x 2故所求切线方程为 y x .而lim nf (-) n nIim3nf(-) n3 0 nf(0) 一 3f (0) 3 •x 22sin tdtlim 0；x 0分析 该极限属于型未定式，可用洛必达法则. 0X 22sin tdt lim ------------------ = lim = ( 2) lim= ( 2)x 0：t (t sin t)dt x 0( 1) x (x sinx) 、7 x 0x sinx ' 丿2x(sin x 2)22 2(x ) 34x(x 0)的单调递减开区间为x 1(3点，x 0为极小值点.由题意先求驻点.于是12x=(2) lim =0 . x 0sinx注此处利用等价无穷小替换和多次应用洛必达法则.1 x t 2例9 试求正数a 与b ，使等式lim -------------------- dt 1成立.x 0x bsin x 0 ‘ ―t 2分析 易见该极限属于 0型的未定式，可用洛必达法则.1 x 2lim.a x 01 bcosx21 x lim3x 0x 2故f(x)是g(x)同阶但非等价的无穷小.2例11计算1|x|dx .分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分.2 220 2x 0 x 251|x|dx = 1( x)dx 0xdx = [ y] 1 [y]0 =-.在使用牛顿-莱布尼兹公式时，应保证被积函数在积分区间上满足可积条件.如[-]32丄，则是错误的.错误的原因则是由于被积函数 」2在x 0处间断且在被x 6 x 2lim__ x 0x bsin x 0 . a 2x_ _t 「dt = lim _— =lim 1f 2 x 01 bcosx x op x 2x 2limx 01 bcosx由此可知必有 lim(1 bcosx) 0，得 b 1 .又由得a 4 .即a 4 , si nx1xlim a x 01 cosxb 1为所求. 例10设f (x)sin t 2dt , g(x) x 3 x 4，则当0 时，f (x)是 g(x)的( ). A .等价无穷小.B .同阶但非等价的无穷小.解法1由于lim 型 lim si 门伽浪)cosxx 0g(x) x 0C .高阶无穷小.D .低阶无穷小.mo Hx3x 2 4x 3cosx3 4xmo Hxsin (sin x)x解法2 将sin t 2展成t 的幕级数, 1 2 3 3!(t)f (x) 0 sin x 2 [t 2 再逐项积分，得到1 si n 42L ]dt 1 . 3 一 sin xlim 少 x 0g(x).31sin x(- lim -1 . 4sin x 4234x x1 lim -x 01 ■ 4 . sin x L 42 1 xUdx x积区间内无界 例12设f(x)是连续函数，且f(x) 1x 3 0 f(t)dt ，则 f (x)所以 分析本题只需要注意到定积分因f (x)连续，f (x)必可积,从而a 1—,所以 4例13 计算12x21 分析 bf (x)dx 是常数(a, b 为常数).从而f (x) x 3a ，且f(x) x1 21[―X 2 3ax]0 23 2 .10 f (t)dt 是常数，记 10 f (t)dt a ，则1 o(x3a)dx3a a ,x dx. 1 1 x 2由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性. I 2x 2 x ------ dx = II 1 x 2 I 2x 2----- dxII .1 x 2 ___ dx .由于 11 1 x 2一是偶函数，而 1 1 x 2 旦古函数, 是奇 2 x 111=dx 2 x0,I2x 2 xII1 x 2dx = 4 由定积分的几何意义可知 例14计算肿(x 2 011 x 20 1x 2dx 1 2x 2 1 dx = 4 1x 2 (11x 2) 0x _= dx 1 1 x 2t 2)dt ，其中 分析 要求积分上限函数的导数, 元使被积函数中不含 ，然后再求导. 由于 x 2 otf(xx 2dx = 4 dx 4；FVdx故令x 2xdx 01 4 dx 0 f(x)连续. 但被积函数中含有 x ,因此不能直接求导，必须先换2 1 x2 2 2t )dt = 2 0f(x t )dt .2 20时u x ；当t x 时u 0，而dtx2 2 1tf(x t)dt=；222d 1 x tf(x t)dt= dx [2 0x 2f (U)( du)=idu ，所以x 2f (u)du ,f (u)du] =£ f(x 2) 2x = xf (x 2).错误解答 — tf(x 2 t 2)dtxf(x 2 x 2) xf(O).dx 0错解分析这里错误地使用了变限函数的求导公式，公式d x(x) a f (t)dt f (x)dx a中要求被积函数f(t)中不含有变限函数的自变量 x ，而f (x 2 t 2)含有x ，因此不能直接求导，而应先换元. 15 计算 3 xsinxdx .分析 被积函数中出现幕函数与三角函数乘积的情形，通常采用分部积分法.=1ln21 In3 .417计算2e si nxdx .分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法. 解 由于 02e x sin xdx；sin xde x [e x sinx]〕2e x cosxdxe^2e x cos xdx ,(1)而02 *cosxdx2cos xde x[e x cosx](?o2e x ( sin x)dx2e x sin xdx 01 , (2)将(2)式代入(1)式可得?e x s in xdx e 2[2 e x sin xdx 1],故2 e xsin xdx1 ~2-(e 2 1). 21例 18 计算 xarcsinxdx .解 3 xs in xdx 3 xd(0 0 '3cosx) [x ( COSX )]oo3( cos x) dx616计算0兽dx .3cosxdx¥ 6分析被积函数中出现对数函数的情形，可考虑采用分部积分法.1x)d(-3 xJdx= 1ln(1 0(3 x)2'1Fln(1x)】1(3 x) (1 x)dx1 In2 21 xarcsin xdx分析被积函数中含有抽象函数的导数形式，可考虑用分部积分法求解. 解 由于 0 [ f (x) f (x)]cos xdx 0 f (x)d sinxcosxdf (x){ f (x)sin x 00 f (x)sin xd" {[ f (x)cosx]° 0f (x)sin xd 冷f ( ) f (0) 2 .故 f (0) 2 f ( )2 3分析 该积分是无穷限的的反常积分，用定义来计算.解 dxtdx1 t 11 解2= lim 2= lim ()dxx 4x 3 t 0 x 4x 3 t 2 0 x 1 x 31 x 1 t 1 t 1 1 =lim [In ]0= lim (In In ) t2 x3 t 2 t 3 3分析 被积函数中出现反三角函数与幕函数乘积的情形，通常用分部积分法.1解xarcs in xdx1x20arcsinxd (一2x1[ arcsinx]。
济南大学高等数学C(一)5定积分及其应用-疑难解答
第六章 定积分及其应用习题6-1 定积分的概念下列定积分：利用定积分的定义计算.1⎰21;)1(-dx x[]等分个分点，把区间中插入在闭区间解：n n 12,1.10-- ,211210=<<<<<=--n n x x x x x.3)1(2Δn n x i =--= ).,,2,1(31n i i nx i =+-=[]，所以因为中取右端点为在每个区间x x f i nx ξx x i i i i =+-==-)(.31,.210.3)31(ΔΔ)(111∑∑∑===⋅+-==ni i n i i i n i i ni n x ξx ξf .2)1(939393Δ)(212121+⋅+-=+-=+-=∑∑∑===n n n i n i n x ξf n i ni i ni i 即{})Δ(232)1(93lim Δ)(lim .31210210n i i n i ni i λx max λn n n x ξf xdx ≤≤∞→=→-==⎥⎦⎤⎢⎣⎡+⋅+-==∑⎰其中⎰10.)2(dx e x[]等分个分点，把区间中插入在闭区间解：n n 11,0.10-,101210=<<<<<=-n n x x x x x.1Δn x i = ).,,2,1(0n i ni n i x i ==+=[]，所以因为中取右端点为在每个区间x i i i i e x f ni x ξx x ===-)(.,.210.1ΔΔ)(111∑∑∑===⋅==ni ni i n i ξi n i i ne x e x ξf i.1)1(1)(1Δ)(111211--⋅=++++=-=∑n nnn nn nni ni i e e e ne e e e nx ξf 即{})Δ(11)1(1lim Δ)(lim .311110100n i i n nn i ni i λxx max λe e e e n x ξf dx e ≤≤∞→=→=-=--⋅==∑⎰其中，说明下列等式：利用定积分的几何意义.2;12110⎰=x xd ）（ ;412102⎰=-πx d x ）（⎰-=ππx sinxd ；）（03 ⎰⎰-=2022.24πππx cosxd x cosxd ）（角形的面积，故表示如图所示的直角三）解：（⎰1021x xd.x xd 12121210=⋅⋅=⎰ ⎰-1024112圆的面积，故表示如图所示）（x d x.414111022⎰=⋅⋅=-ππx d x ⎰-ππx x sinxd 轴上方为正面积，的面积，其中表示如图所示阴影部分）（3轴下方为负面积，故x ⎰-=ππx sinxd .0⎰-2224ππx cosxd 倍，面积的的面积，它是第一象限表示如图所示阴影部分）（⎰⎰-=2022.2πππx cosxd x cosxd 故习题6-2 定积分的性质积分的大小：比较下列各题中的两个.2;,110421021dx x I dx x I ⎰⎰==）（ ;,221422121dx x I dx x I ⎰⎰==）（;)(ln ,ln 34332431dx x I dx x I ⎰⎰==）（ ;)1ln(,4102101dx x I dx x I ⎰⎰+==）（.)1(,5102101dx x I dx e I x ⎰⎰+==）（ ，只有有限个成立的解：)"(",10)1(42x x x x =≥∴≤≤ ,,42是连续函数又x x .,21104102I I dx x dx x >>⎰⎰即故是连续函数，，又只有有限个成立的4242,)"(",21)2(x x x x x x =≤∴≤≤ .,21214212I I dx x dx x <<⎰⎰即故是连续函数，，又33)(ln ,ln )(ln ln ,1ln ,43)3(x x x x x x <∴>∴≤≤ .,)(ln ln 2143343I I dx x dx x <<⎰⎰即故.,)1ln(),10()1ln(,0)0()()(10),10(111)(,)1ln()()4(211010I I dx x dx x x x x f x f x f x x xx f x x x f ><+∴≤<<+=<≤≤<<-+='-+=⎰⎰即即单调递减，故时，故当则设.,1,)1(,0)5(21I I e x x x n l x x >∴<+∴<+>时[]，证明：上连续在及设)(,)()(3b a b a x g x f .< [].0)(,0)(,0)(,)1(>≡/≥⎰ba dx x f x f x fb a 则且上，若在[][].0)(,,0)(,0)(,)2(≡=≥⎰x f b a dx x f x f b a ba 上，则在且上，若在[][]).()(,,)()(),()(,)3(x g x f b a dx x g dx x f x g x f b a ba ba ≡=≤⎰⎰上，在则且上，若在[]⎰≥∴≥ba dx x f x fb a ,0)(,0)(,)1(上，在证明：，假设⎰=ba dx x f 0)(上，知在由],[)2(b a ，0)(≡x f 矛盾，这与0)(≡/x f .0)(⎰>∴ba dx x f ，假设反证法0)())(2(≡/x f ，则至少存在一点],[b a ξ∈，使得0)(≠ξf ，0)(≥x f ，0)(>∴ξf []上连续，在b a x f ,)( 的区间包含ξ∴，],[],[21b a c c ⊆ ，可设0)(>x f ],[21c c x ∈，易知：⎰>210)(c c dx x f ， ，，而⎰⎰≥≥120)(0)(c abc dx x f dx x f ⎰⎰⎰⎰>++=∴ba c a c c bc dx x f dx x f dx x f dx x f 1212.0)()()()(矛盾，这与⎰=ba dx x f 0)([].0)(,≡∴x f b a 上，假设不成立，即在，令)()()()3(x f x g x F -=，],[)()(b a x x g x f ∈≤ .0)(≥∴x F，且⎰⎰⎰=-=b a b a ba dx x f dx x g dx x F 0)()()( ,0)()2(≡x F 知由).()(x f x g ≡即习题6-3 微积分的基本公式计算下列各导数：.1;11302dt t dx d x ⎰+）（ ;112422dt t dx d x x ⎰+）（ ⎰x x dt t πdx d cos sin 2)cos()3( ;1331162223x x x x +=⋅+=）（）原式解：（⎥⎦⎤⎢⎣⎡+-+=⎰⎰420022112x x t dt t dt dx d ）原式（ ⎰⎰+-+=24020211x x t dt dx d t dt dx d x x x x 2)(114)(1122324⋅+-⋅+= ;1214483xx x x +-+= []⎰⎰-=x x dt t πdt t πdxd cos 0sin 022)cos()cos()3(原式 ⎰⎰-=x x dt t πdxd dt t πdx d sin 02cos 02)cos()cos( [][]x x πx x πcos )(sin cos )sin ()(cos cos 22--= [][].cos )(sin cos sin )(cos cos 22x x πx x π--= 计算下列各积分：.2a ax x dx x x 02302|)21()3(1-=-⎰）（2321a a -=821|)3131()1(221334212=-=+-⎰x x dx x x ）（ 67|)2132()()1(30122301211-=+=+=+⎰⎰x x dx x x dx x x ）（⎰⎰⎰-+=ππππdx x nxdx si dx x 2020)sin (sin 11）（4|cos |cos 20=+-=πππx x 617|31|)21()(122131022010212=+=+=⎰⎰⎰x x dx x xdx dx x f ）（ :3求下列极限.;lim )1(02x dt e x t x ⎰→ .sin )sin (lim )2(0320220⎰⎰→x x x dtt t dt t;11lim )1(002===→e ex x 原式解： 320220320220sin 2lim sin sin sin 2lim )2(xx x dt t xx x dt t xx xx ⋅⋅=⋅=⎰⎰→→原式3020sin 2lim xdtt xx ⎰→=.323sin 2lim 22==→x x x .)(0cos 500dxdyx y y dt t dt e .xyt的导数所确定的隐函数求由方程==+⎰⎰求导，得对解：原方程左、右两边x0cos =+x dx dy e y .1sin cos cos -=-=∴x x e x dx dy y.)(602的极值求函数⎰-=xt dt te x f .2)(x xex f -='解： ，令02=-x xe0=x 得极值点 01)0(>=''f .f x f x 0)0()(0==∴有极小值时函数[]()，证明函数内可导且上连续，在在设0)(,,)(.7<'x f b a b a x f ().0)(,)(1)(<'-=⎰x F b a dt t f ax x F xa内的一阶导数在 2)()())(()(a x dtt f a x x f x F xa ---='⎰证明：)()())(())((2x ξa a x a x ξf a x x f ≤≤----= )())(()()(x ηξax ξx ηf a x ξf x f <<--'=--=，0,0,0)(>->-<'a x ξx ηf .0)(<'∴x F习题6-4 定积分的换元积分法计算下列定积分：.1;02121)3cos()3sin()1(33=-=+-=+⎰πππππx dx πx 解：;16921)49(81)49()49(41)49()2(122123123=+-=++=+-----⎰⎰x x d x x dx ;31cos 31cos cos cos sin )3(203202202=-=-=⎰⎰πππφφd φφd φφ;2)2sin 4121(22cos 1sin )cos 1()4(000202πθθθd θθd θθd θππππ=-=-==-⎰⎰⎰;232)2(31)2(2212)5(202322202202=--=---=-⎰⎰x x d x dx x x;1)6(2102dx x x -⎰,cos ),20(sin tdt dx πt t x =≤≤=令.164sin 41812141241cos cos cos 20202202202202πt t dtt os4c dt t sin tdt t sin tdt t t sin πππππ=-=-===⋅⋅=⎰⎰⎰⎰）（）（原式;45)7(11⎰--xxdx;2,45,452dt tdx t x t x -=-==-则令;61)53(8185)2(45133131322=-=-=--=⎰⎰t t dt t dt t tt 原式;1)8(41⎰+xdx,2,,2tdt dx t x t x ===则令;23ln 22)1ln (2)111(212212121-=+-=+-=+=⎰⎰t t dt t t tdt 原式;2121)]21([)(21)9(11021010222---=-=--=⎰⎰--e e t d e dt te tt t;212ln 2)ln 1(2)ln 1()ln 1(ln 1ln ln 1)10(212121212121-+=+=++=+=+⎰⎰⎰-x x d x xxd x x dx .41arctan )2arctan(1)2(54)11(12122122πx x dx x x dx ==+=++=++------⎰⎰ ;32)31(31)sin 3sin 31(21)cos 3(cos 212cos cos )12(222222=--=+=+=---⎰⎰ππππππx x dx x x xdx x .34)(cos 32)(cos 32cos cos cos cos sin cos )sin (cos sin cos )cos 1(cos cos cos )13(202302232002200222222223=-=-=⋅+-==-⋅=-------⎰⎰⎰⎰⎰⎰⎰ππππππππππππx x xd x x d x xdx x dx x x dxx x dx x x dx x x .22sin 2sin 2cos 2cos 2cos 2cos 22cos 1)14(2202200020=-=-===+⎰⎰⎰⎰⎰πππππππππx x dx x dx x dxx dx x dx x 列定积分：利用函数奇偶性计算下.2;1arcsin 1212122dx xx ⎰--）（）（.12sin )2(552432dx x x x x ⎰-++ 为偶函数，故）（解：221arcsin )()1(xx x f -=;324arcsin 32arcsin 21arcsin 232103210221022πx x arcsin d x dx xx ===-=⎰⎰）（）（）（原式.012sin )()2(2432=++=为奇函数，故原式x x x x x f 证明下列各题：.3;)0(11)1(11212⎰⎰>+=+xx x xdx x dx ;)1()1()2(1010dx x x dx x x mnnm⎰⎰-=-.cos 2cos )3(2010010dx x dx x ππ⎰⎰=右边；左边令证明：=+=+=+-=-==⎰⎰⎰xx x x dx t dt t dt t dt t dx t x 1121121122211111,1,1)1( 右边；左边，则令=-=-=--=-=-==-⎰⎰⎰dx x x dt t t dt t t dt dx t x t x nmnmnm101001)1()1()()1(,,11)2(,cos cos cos )3(2102010010xdx xdx xdx ππππ⎰⎰⎰+=则令,,dt dx t πx -=-=,cos cos )(cos cos 201020100210210xdx tdt dt t xdx πππππ⎰⎰⎰⎰==-= .cos 2cos cos cos 201020102010010xdx xdx xdx xdx ππππ⎰⎰⎰⎰=+=故习题6-5 定积分的分部积分法计算下列定积分：.1);1(414121121ln 21)21(ln ln )2(21221212121+=-=⋅-==⎰⎰⎰e xe dx x x x x x xd xdx x e e e ee;2sin 2)cos (cos )cos (sin )3(2020202020πx πdx x x x x xd xdx x πππππ-=+-=---=-=⎰⎰⎰;2ln 33cos ln 33cos cos 133cos sin 33tan tan tan sec cos )4(303030303030302302-=+=+=-=-===⎰⎰⎰⎰⎰⎰πx πx d x πdx x x πdx x x x x d x dx x x dx xx ππππππππ;ln )5(41dx xx ⎰,2,2tdt dx t x t x ===，则令;42ln 8)22ln 4(2)214ln 2(2)ln ln (2ln 22ln 212221212212212-=-=⋅⋅-=-===⎰⎰⎰⎰dt t tt t d t t t dt t tdt t t 原式.214)arctan (218)111(2181121arctan 21)21()6(10102102210210210-=--=+--=+⋅-==⎰⎰⎰⎰πx x πdx x πdx x x x x x arctamxd xarctamxdx ).2(51cos ,2cos 5cos 42)2cos cos (2)cos (22sin sin sin cos )7(202202202202202202202202202202-=∴-=--=⋅-+=--=⋅-==⎰⎰⎰⎰⎰⎰⎰⎰ππx ππxπx ππx πxππxππx πxπxπxe xdx e e xdx e xdxe e dx e x x e e x d e e dxe x x e x d e xdx e 故;)sin(ln )8(1⎰edx x,,dt e dx e x t x ln t t ===，则令,sin 11cos 1sin )sin cos (1sin cos 1sin cos sin sin sin )sin(ln 101010101110101dt e t e e dt e t t e e tde e dt e t t e tde dt e t dx x t tt t tttte⎰⎰⎰⎰⎰⎰⎰⋅-+-=⋅+-=-=⋅-==⋅=.21)1cos 1(sin sin )sin(ln ,1)1cos 1(sin sin 210110+-=⋅=+-=⋅∴⎰⎰⎰e dt e t dx x e dt e t tet 故.12ln 23ln 31ln ln )1ln()9(32323221--=⋅-==+⎰⎰⎰dt t t t t tdt dx x ;sin )10(20dx x π⎰,2,2tdt dx t x t x ===，则令.2sin 22cos 2cos 2)cos (22sin 00000πtπdt t t t t d t dt t t πππππ=+=+-=-=⋅=⎰⎰⎰原式.22)1(111ln ln ln )ln (ln )11(1111111111e e e e e dxx x dx x x dx x dx x dx x eeeee e e e -=--+-+-=-++-=+-=⎰⎰⎰⎰⎰利用递推公式计算：.2.)1()2(;sin )1(299102990100100dx x J xdx x J π⎰⎰-==.212,)12(2)12()12(sin )12(sin )12(sin cos ]cos )12([sin cos sincos )cos (sin sin ,sin )1()1(22)1(222)1(2020220120120120120122022----------=∴-=---=---+=-++-=-===⎰⎰⎰⎰⎰⎰⎰m m m m mm πmπm πm 2-2m πm πm πm πm m πm m J mm J J m mJ J m J m xdxx m xdx x m xdx x dxx x sin m x x x x x x x xd x xdx sin x x J xdx x J 故则设解：.2196959897100999897100991009910011000482492492502100J J J J J J ⋅⋅⋅⋅==⋅==-==⨯⨯⨯⨯ 故.224969810013959799,22100200πJ πxdx J π⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅===⎰ 故而.224969810013959799sin )sin ()(sin ,sin ]2,0[,cos )2(10020990299πdt t dt t t J tdt dx πt t x ππ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅==-=-=∈=⎰⎰ ，则令习题6-6 广义积分算广义积分的值：收敛性，如果收敛，计判别下列各广义积分的.1;4141)4(41)3(040404=-=--=∞+-∞+-∞+-⎰⎰xx xex d e dx e.21sin ,1sin 2,sin 1]sin sin [1sin 1cos 1cos cos )cos (sin )4(00000000000==∴-=+-=-=-=-+-=-=⎰⎰⎰⎰⎰⎰⎰⎰⎰∞+-∞+-∞+-∞+-∞+-∞+-∞+-+∞-+∞-+∞-+∞-dx x e dx x e dx x e dx x e x e x d e dx x e dxx e xe x d e dx x e xxxx xxxx xxx 故.)2(2)2arctan(1)2(54)5(22πππx x dx x x dx =--=+=++=++∞+∞-∞+∞-∞+∞-⎰⎰ .1]1)1([lim 1)1(21lim 1)6(21210221102=+--=---=---→→⎰⎰b x x d dx x x b b b ;1()7(203⎰-）x dx .1(1,1,1111,,11203103013103013113113发散）都发散，原式，则令⎰⎰⎰⎰⎰⎰⎰-∴+==-=-=-==-----x dx dt t dt t dt tdt t dt t dt t dt dx t x t x.1)8(21⎰-x xdx.38)3(2)1(22)1(,2,1,1110310210222=+=+=+==+==-=-⎰⎰t t dt t dt t t t tdt dx t x t x t x 原式，则令 )1()(ln 111ln ln )(ln )(ln 212≠+⋅-==-∞+⎰⎰⎰k C x k x x d x x dx k k x x dxk .k k k k 解：取得最小值？为何值时，这广义积分当发散？为何值时，这广义积分收敛？当为何值时，广义积分当时，当1=k ⎰x x dx ln C x xxd +==⎰ln ln ln ln⎪⎩⎪⎨⎧≠⋅-==∴∞+-+∞∞+⎰1|)(ln 1111|ln ln )(ln 2122k x k k x x x dx k k时，当1)1(=k .，原广义积分发散原式+∞= 时，当1)2(<k .,|)(ln 1121发散原式+∞=-=∞+-k x k=>时，原式当1)3(k .,)2(ln 111|)(ln 111121收敛-∞+--=⋅-k k k x k 时，当1>k 则记,)2ln 1(11)(1--=k k k f12)2(ln 1)1(1)(---='k k k f )2ln 1ln()2ln 1(111--+k k ).2ln ln 11()2(ln 1)1(11+---=-k k k ，令0)(='k f ，1>k 从而,0)2ln 1(111≠-∴-k k,02ln ln 11=+-k ,2ln ln 11-=k 即.值为唯一驻点此k时，当2ln ln 11->k 时，即02ln ln 11<+-k .0)(>'k f时，当2ln ln 11-<k .0)(该驻点是极小值点，∴<'k f时，即当1>k .)(),1(处的极小值就是最小值故唯一驻点没有边界值进行比较，时，在此区间上k f k ∞+∈习题6-7 定积分的几何应用形的面积：求由下列各曲线所围图.1 ).0(ln ,ln ,0,ln )7(;1,,)6(;2,1)5(;(8,2)4(;2,3)3(;,0,)2(;,)1(2222>>===========+==-======-a b b y a y x x y x e y e y x x y xy x y x y x y x y e y x e y x y x y x x x 与两部分都要计算）.61)()1(10⎰=-=dx x x S 面积解：.1)()2(10⎰=-=dx e e S x 面积 .332)23(),6,3(),2,1(32)3(1322⎰-=--=--⇒⎩⎨⎧-==dx x x S B A x y x y 面积.342)218()4(22221⎰+=--=-πdx x x S 阴影部分的面积 .346)34282-=+-=πππS （另一部分的面积.2ln 23)1()5(21⎰-=-=dx x x S 面积.21)()6(10⎰-+=-=-ee dx e e S xx 面积.)0(,ln )7(ln ln ⎰-=-==⇒=ba yy a b dy e S e x x y 面积转的旋转体的体积：围平面图形绕指定轴旋求下列各题中的曲线所.2轴；轴绕y x x y x y ,,2,0,)1(3=== 轴；绕y y x x y ,,)2(22== 轴；绕x y x ,16)5()3(22=-+ ).0(,)4(222>>==+a b b x a y x 绕,7128)()1(2203πdx x πV x ==⎰解：,33y x x y =⇒=dy y πdy πV y ⎰⎰⋅-⋅=8023802)(2.56459632πππ=-=,)2(2y x x y =⇒=.10352)()(1022102πππdy y πdy y πV y =-=⋅-⋅=⎰⎰,165,165:16)5()3(222122x y x y y x --=-+==-+得由dx y y πdx y πdx y πV x )(22442144224421-=⋅-⋅=⎰⎰⎰---.160162102442πdx x π=-⋅=⎰-,,,:)4(22222122222y a b R y a b R y a x a y x --=-+=-±==+设得由dy R πdy R πV aa aa b ⎰⎰---=2221dy R R πaa )(2221-=⎰-dy y a b πaa 2222-⋅⋅=⎰-b a π222=.3列各题中立体的体积的立体体积公式计算下用平行截面面积为已知..)1(的正劈锥体为高底圆直径的线段为顶，的圆为底，平行且等于以半径为H R .)()2(的球缺的球体中高为半径为R H H R <.)20(1)3(2222的平面所截的劈形立体轴且与底面夹角的椭圆柱体被通过底面为椭圆πααx b y a x <<≤+ 截面的面积为：解：)1( [],,,221)(2222R R x x R h h x R x A -∈-=-⋅=：故此正劈锥体的体积为.21)(222h R πdx x R h dx x A V R R R R ⎰⎰--=-==截面的面积为：)2( [],,),()(22R H R y y R πy A -∈-=故球缺的体积为：).31()(222H R H πy d y R πV RH R -=-=⎰- 截面的面积为：)3( [],,,tan 1121)(2222ααx αax b a x b x A -∈-⋅-=故劈形立体的体积为： .tan 32tan )1(21)(2222αab dx αa x b dx x A V a a a a ⎰⎰--=-==习题6-8 定积分的经济应用.1000257)(1，求总成本函数，固定成本为已知边际成本为xx C .+=' .5071000)257(1000)()0()(00⎰⎰++=++='+=x x x x dx xdx x C C x C 解：.30202100)(.3应追加的成本数时，增加到，求当产量由已知边际成本==-='x x x x C：解：应追加的成本数为.500)2100()(30203020=-='⎰⎰dx x dx x C.0260)(430)(.4）（设固定成本为，求最大利润，边际收益为已知边际成本x x R x x C -='+=').0(230230)430()(22固定成本为解：x x C x x dx x x C +=++=+=⎰.60)260()(2C x x dx x x R +-=-=⎰,60)(,0,0)0(2x x x R C R -=∴=∴=,33023060)()()(222x x x x x x x C x R x L -=---=-=∴ ,06)(,5,0630)(<-=''==-='x L x x x L .75)5(5=-=L x 利润为时，有最大利润，最大故当 支出增加多少？费亿元时，购买冰箱的消亿元增加至，当居民收入由的函数，的变化率是居民总收入消费支出某地区居民购买冰箱的942001)()(.5xx W x x W =').(10012001)(9494亿解：=='⎰⎰dx xdx x W .1001亿增加故购买冰箱的消费支出.20)3(20)2()1(.10100106价值万元时，求收益的资本当应满足的方程）；万元时，求内部利率（当本？为何值时，公司不会亏元收入年后报废，公司每年可备使用万元购买某设备，该设（连续复利）贷款某公司按利率==b b b b %.年后的总收益：：年后这笔贷款的本利和解：10,10010010)1(101.0e e =⨯),1(101001)10(1.0⎰---=e eb dt e b t ),1(101001--=e eb e 若公司不亏本，则.1101--=eb 则 ，则设内部利率为ρ)2(),1(202010010100ρtρe ρdt e ---==⎰.1510ρe ρ--=即投入资金的现值收益流现值资本价值-=)3( 100201001.0-=⎰-dt e t.20010010020020011---=--=e e总习题六计算下列极限：.1.1lim 11lim )1(11111e edt e x xx x t x ==-→→⎰ .111)(1lim 21121)(lim .1)(lim )(,1)(lim )2(2220=⋅=+=⋅+==++∞→+∞→+∞→+∞→⎰x f xx xx x f t f t f x dt t f x x t xx 原式连续且其中计算下列积分：.2.22ln 2ln 2cos 1sin ,2ln )cos 1ln(cos 1)cos 1(cos 1sin ,2ln 22tan 2tan 2tan 22sec 2sec 22cos 2cos 1,cos 1sin cos 1cos 1sin )1(2020202020202020220220220202020ππdx x x x x x x d dx x x πdx x x x x d x x dx x dx x x dx x x dx x x dx x x dx x x dx x x x ππππππππππππππ=+-=++=+-=++-=+-=-=====++++=++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰故而而 ;42)2(22⎰-+xdx.122tan 22sec 2122cos 212)cos 111(cos 1cos cos 22cos 2,cos 2]2,0[,sin 220202202202020-=-=-=-=+-=+=+==∈=⎰⎰⎰⎰⎰πt πdt t πdtt πdt t t tdt t tdt tdt dx πt t x ππππππ原式，则令).12(2)sin cos ()cos (sin )cos (sin )sin (cos cos sin )cos (sin cos sin 2cos sin 2sin 1)3(2440244020202202220-=--++=-+-=-=-=-+=-⎰⎰⎰⎰⎰⎰ππππππππππx x x x dx x x dx x x dx x x dxx x dx x x x x dx x .22)tan 2arctan(211)tan 2(tan 2211tan 2tan 1tan 2sec 1tan 21tan sin 2cos cos sin sin 1)4(202022022022222202222202πx x x d x x d dx x x dx x x x x xdx x x dx πππππππ==+=+=+=++=++=+⎰⎰⎰⎰⎰⎰ 且说明理由：指出下列计算中的错误4..01lim 1)3(;01,11)2(;2]1[arctan )1(1)1(1)1(4343112112111211112112=+=+=+∴+-=+-=-=+-=+⎰⎰⎰⎰⎰⎰⎰-+∞→∞∞---=----b bb tx xdx x x dx x x dx t dt x dx πx x x d x dx.0)1(2x x 以，故不能分子分母同除可以取为第一步到第二步错，因解：.2)4(4arctan 111112πππx x dx =--==+⎰--正确的做法： .x tx 0,1)2(就取不到因为这样不能令=.)3(是没有关系的限设法错误，因为它们第二步中定积分的上下解下列几何问题：.5；轴旋转的旋转体的体积所围图形绕求由y y x x y 0,4,)1(23===；轴旋转的旋转体的体积绕求圆盘y y x 1)2()2(22≤+- .940,1,,.0]1,0[)0,0()3(22积最小轴旋转而成的旋转体体，且使图形绕为所围图形的面积与直线的值，使抛物线试确定时，，且当过原点设抛物线x y x c bx ax y c b a y x c bx ax y ==++=≥∈++=应取何值？所围图形面积最小时，与抛物线）点，当直线过（已知直线b a x y b ax y b ax y ,1,0)4(2=+=+=.7512128)(4)1(80348023280212πdy y ππdy y πdy πV V V =-=⋅-⋅=-=⎰⎰⎰解：故旋转体的体积为，得由],1,1[121)2()2(222-∈-±==+-y y x y x.418124)12()12(211211221122112πdy y πdyy πdy y πdy y πV =-=-⋅=----+=⎰⎰⎰⎰----,896,94)(,0)3(1022=+=++==⎰b a dx bx ax bx ax y c 故，故由已知轴旋转体的体积绕x ),235()(22102abb a πdx bx ax πV ++=+=⎰)],98(12131)98(1801[),98(61222b b b b πV b a -++-=∴-=.0,35,2,0151,2,0]152151[22满足条件时，故当故=-==>⋅===-=c a b πdb V d b b πdb dV ）（即由已知11)4(=+=b ax y ，即它所围面积，则两交点的横坐标为与抛物线设直线⎰-+=<=+=21)1()(,1221212x x dx x ax A x x x x x y ax y ),(31)()(23132122122x x x x x x a A ---+-=,01122=--⇒⎩⎨⎧=+=ax x xy ax y 是此方程的两根，有设21,x x ,1,2121-==+x x a x x ,44)(2)(221212212122212+=-+=-+=-a x x x x x x x x x x ,4))(()(,4212122122212+=-+=-+=-a a x x x x x x a x x 又 .)4(64)1(314421),1(4]))[((232222222221212123132+=++-+++=++=-+-=-a a a a a a A a a x x x x x x x x 故.1,0480,0,0)4(18212=====+=b a A a a a a dadA ，故有最小值时，故当则令解下列经济应用问题：.6？台的平均利润各为多少台与后台时，前售出台电视机的总利润售出试求的边际利润为已知某商场销售电视机需求出满足的方程）万元，求内部利率（只年，每年收益厂投产期万元扩建一个工厂，该某企业投资少？单位时，总成本减少多单位减少到由问当产量成本已知生产某产品的边际303060.2.401),20(10250)()3(.2020232)2(312,30183)()1(2.x xx L x x x x C ≥-='+-='.11120232)2(.756)30183()()1(202001232123ρtρeρ.6dt e ρdx x x dx x C C --⎰⎰⎰-===+-='=，解得：，则设内部利润为减少的成本解：,20250)10250()(.1)3(2C x x dx x x L +-=-=⎰,20250)(,0,0)0(2x x x L C L -=∴=∴=.9920)40(40=L 台电视机的总利润为：售出,5.24830745530)30(,7455)30(.2===L L ,5.24530)30()60(,7365)30()60(,14820)60(=-=-=L L L L L.5..5245302483060台的平均利润为，后台的平均利润为台时，前故售出（注：本资料素材和资料部分来自网络，仅供参考。
(完整版)定积分应用题附答案
《定积分的应用》复习题一．填空：1．曲线ln ,ln ,ln (0)y x y a y b a b y ===<<及轴所围成的平面图形的面积为A =ln ln by ae dy ⎰=b-a______2.2y x y ==曲线和 ____13____二．计算题：1．求由抛物线 y 2 = 2x 与直线 2x + y – 2 = 0 所围成的图形的面积。
解：（1）确定积分变量为y ，解方程组2222y x y x ⎧=⎨=-+⎩ 得12121/22,12x x y y ==⎧⎧⎨⎨==-⎩⎩ 即抛物线与直线的交点为（21，1）和( 2 , - 2 ).故所求图形在直线y = 1和y = - 2 之间，即积分区间为［－2，1 ］。
（2）在区间［－2，1］上，任取一小区间为［ y , y + dy ］,对应的窄条面积近似于高为［(１－21y ）-21y 2 ］,底为dy 的矩形面积，从而得到面积元素 dA = [(１－21y)- 21y 2 ]dy (3)所求图形面积 A =⎰-12[（1- 21y ）-21y 2 ]dy = [y - 41y 2 – 61y 3]12-= 942．求抛物线 y = - x 2 + 4x - 3 及其在点（0，- 3）和（3，0）处的切线所围成的图形的面积。
解：由y = - x 2 + 4x – 3 得 '24,'(0)4,'(3)2y x y y =-+==-。
抛物线在点（0，- 3）处的切线方程为 y = 4x – 3 ;在点（3，0）处的切线方程为 y = - 2x + 6 ; 两切线的交点坐标为 （ 32，3 ）。
故 面积A =332223029[(43)(43)][(26)(43)]4x x x dx x x x dx --+-+-+-+-=⎰⎰3．求由摆线 x = a (t – sint) , y = a( 1- cost) 的一拱（02t π≤≤）与横轴所围成的图形的面积。