现代数字信号处理仿真作业
现代数字信号matlab处理仿真题
3.17（1）相关函数仿真代码：A1=getAk(SNR1);A2=getAk(SNR2);A3=getAk(SNR3); %求得信号的幅度；noise=randn(1,N) + j*randn(1,N); % 构建高斯白噪声；s1=getSk(A1,f1,N);s2=getSk(A2,f2,N);s3=getSk(A3,f3,N);; %产生3个复正弦信号vn=s1+s2+s3+noise;vk=fft(vn,2*N); %对v(n)补N个零，然后做2N点FFTswk=((abs(vk)).^2)/N; %计算功率谱估计S(ω)r0=ifft(swk); %对S(k)做ifft得到r=[r0(N+2 : 2*N) , r0(1 : N)]; %根据教程3.1.8式可得r1=xcorr(vn, N-1,'biased'); %直接计算自相关函数%%%%%%%%%%%%%%%%%%%%%%%%%取序列实部，虚部%%%%%% real_r=real(r);imag_r=imag(r);real_r1=real(r1);imag_r1 = imag(r1);subplot(2,2,1);stem(real_r);xlabel('基于FFT的自相关函数的实部');ylabel('实部');subplot(2,2,2);stem(imag_r);xlabel('基于FFT的自相关函数的虚部');ylabel('虚部');subplot(2,2,3);stem(real_r1);ylabel('实部');xlabel('估计的自相关函数的实部');subplot(2,2,4);stem(imag_r1);xlabel('估计的自相关函数的虚实部');ylabel('虚部');function AK=getAk(SNR) %求得幅度%%%%%%%%%%%%%%%%%%%由SNR=10log(A^2/2*σ^2) %%%%%%% AK=((10^(SNR/10))*2)^0.5;function Sk=getSk(Ak,fk,N)Sk=Ak * exp(j * 2 * pi * fk *(0:N-1));仿真波形：（2）BT 法和周期法估计 仿真程序： clear all; clc;%设定N 值可以改变抽样信号的点数，设定M 值可以设定加窗的大小，设定N3可以补零，确定实际求fft 的点数。
现代数字信号处理及其应用 第六章仿真题
6.12clc;clear;M=15;Lb=10;% hb=[0.407 0.815 0.407];hb=[0.04 -0.05 0.07 -0.21 -0.5 0.72 0.36 0 0.21 0.03 0.07]; Hb=zeros(2*M+1,2*M+Lb+1);for k=1:2*M+1Hb(k,k:1:k+Lb)=hb;endEA1 = zeros(2000, 1);EA2 = zeros(2000, 1);for k=1:100sigma=1e-3;N=2000;s=randsrc(2*M+Lb+N,1);vn=sqrt(sigma)*randn(2*M+N,1);S=zeros(2*M+Lb+1,N);V=zeros(2*M+1,N);for k=1:NS(:,k)=s(2*M+Lb+k:-1:k);V(:,k)=vn(2*M+k:-1:k);endUb=Hb*S+V;errb_LMS=zeros(N,1);wb_LMS=zeros(2*M+1,N);wb_LMS(M+1,1)=1;dn=S(M+Lb+1,:);errb_LMS(1)=dn(1)-wb_LMS(:,1)'*Ub(:,1);mu=0.025;for k=1:N-1wb_LMS(:,k+1)=wb_LMS(:,k)+mu*Ub(:,k)*conj(errb_LMS(k)); errb_LMS(k+1)=dn(k+1)-wb_LMS(:,k+1)'*Ub(:,k+1);endMSEb_LMS=abs(errb_LMS).^2;EA1=EA1+MSEb_LMS;lambda=0.99;delta=0.004;wb_RLS=zeros(2*M+1,N+1);wb_RLS(M+1,1)=1;epsilon=zeros(N,1);P1=eye(2*M+1)/delta;for k=1:NPIn=P1*Ub(:,k);deno=lambda+Ub(:,k)'*PIn;kn=PIn/deno;epsilon(k)=dn(k)-wb_RLS(:,k)'*Ub(:,k);wb_RLS(:,k+1)=wb_RLS(:,k)+kn*conj(epsilon(k)); P1=P1/lambda-kn*Ub(:,k)'*P1/lambda;endMSEb_RLS=abs(epsilon).^2;EA2=EA2+MSEb_RLS;endM=15;Lb=2;hb=[0.407 0.815 0.407];Hb=zeros(2*M+1,2*M+Lb+1);for k=1:2*M+1Hb(k,k:1:k+Lb)=hb;endEA3 = zeros(2000, 1);EA4 = zeros(2000, 1);for k=1:100sigma=1e-3;N=2000;s=randsrc(2*M+Lb+N,1);vn=sqrt(sigma)*randn(2*M+N,1);S=zeros(2*M+Lb+1,N);V=zeros(2*M+1,N);for k=1:NS(:,k)=s(2*M+Lb+k:-1:k);V(:,k)=vn(2*M+k:-1:k);endUb=Hb*S+V;errb_LMS=zeros(N,1);wb_LMS=zeros(2*M+1,N);wb_LMS(M+1,1)=1;dn=S(M+Lb+1,:);errb_LMS(1)=dn(1)-wb_LMS(:,1)'*Ub(:,1);mu=0.025;for k=1:N-1wb_LMS(:,k+1)=wb_LMS(:,k)+mu*Ub(:,k)*conj(errb_LMS(k)); errb_LMS(k+1)=dn(k+1)-wb_LMS(:,k+1)'*Ub(:,k+1);endMSEb_LMS=abs(errb_LMS).^2;EA3=EA3+MSEb_LMS;lambda=0.99;delta=0.004;wb_RLS=zeros(2*M+1,N+1);wb_RLS(M+1,1)=1;epsilon=zeros(N,1);P1=eye(2*M+1)/delta;for k=1:NPIn=P1*Ub(:,k);deno=lambda+Ub(:,k)'*PIn;kn=PIn/deno;epsilon(k)=dn(k)-wb_RLS(:,k)'*Ub(:,k);wb_RLS(:,k+1)=wb_RLS(:,k)+kn*conj(epsilon(k));P1=P1/lambda-kn*Ub(:,k)'*P1/lambda;endMSEb_RLS=abs(epsilon).^2;EA4=EA4+MSEb_RLS;end% figureplot(EA1/100);hold onplot(EA2/100);hold onplot(EA3/100);hold onplot(EA4/100);6.15clc;clear;EA1 = zeros(999, 1);A1 = zeros(2, 1000);for i=1:100a1=0.99;sigma=0.995;N=1000;vn=sqrt(sigma)*randn(N,1);nume=1;deno=[1 a1];u0=zeros(length(deno)-1,1);xic=filtic(nume,deno,u0);un=filter(nume,deno,vn,xic);n0=1;M=2;b=un(n0+1:N);L=length(b);un1=[zeros(M-1,1).',un.'];A=zeros(M,L);for k=1:LA(:,k)=un1(M-1+k:-1:k);enddelta=0.004;lambda=0.98;w=zeros(M,L+1);epsilon=zeros(L,1);P1=eye(M)/delta;for k=1:LPIn=P1*A(:,k);denok=lambda+A(:,k)'*PIn;kn=PIn/denok;epsilon(k)=b(k)-w(:,k)'*A(:,k);w(:,k+1)=w(:,k)+kn*conj(epsilon(k)); P1=P1/lambda-kn*A(:,k)'*P1/lambda; endMSE=abs(epsilon).^2;EA1=EA1+MSE;A1=A1+w;endplot(EA1/100);A2=A1/500;plot(A2(1,:));。
ADSP现代数字信号处理仿真实验报告
目录仿真一：LMS算法和RLS算法 (1)1 自适应滤波的基本原理 (1)1.1 自适应最小均方（LMS）算法 (1)1.2 递归最小二乘方（RLS）算法 (2)2 仿真实验 (4)3 结果分析 (6)仿真二：P阶Levinson-Durbin算法 (8)1 要求： (8)2 算法描述 (8)2.1 产生信号 (8)2.2 L-D算法 (9)2.3 对比信号谱功率和LD算法谱估计 (10)3 结果分析 (11)3.1 AR模型 (11)3.2 MA模型 (12)3.3 总结 (13)仿真一：LMS 算法和RLS 算法1 自适应滤波的基本原理自适应滤波器由参数可调的数字滤波器/自适应处理器和自适应算法两部分组成，如图1所示。
输入信号x(n)通过参数可调数字滤波器后产生的输出信号为y(n)，将其与参考信号d(n)进行比较，得到误差信号e(n)。
误差信号e(n)经过一定的自适应算法后反馈到参数可调数字滤波器，对滤波器进行参数调整（有时还需要利用x(n)），以使得e(n)最终的均方值最小。
这是一种自动控制理论，因此，滤波器在设计时不需要事先知道输入信号和噪声的统计特性，而能够根据输入信号的统计特性变化自动跟踪这种变化，自动调整参数，使滤波器性能达到最佳。
图 1 自适应滤波器框图图1所示自适应滤波器，输入信号为：x(n)和d(n)，两个输出为：y(n)和e(n)。
当误差信号e(n)的均方误差达到最小的时候，可以证明信号y(n)是信号d(n)的最佳估计。
1.1 自适应最小均方（LMS ）算法最陡下降法每次迭代都需要知道性能曲面上某点的梯度值，而梯度值只能根据观测数据进行估计。
LMS 算法是一种有用简单的估计梯度的方法，其最核心的思想是采用平方误差最小代替均方误差最小准则。
信号基本关系：()()()()()()(1)()2()()T y n W n X n e n d n y n W n W n e n X n μ==-+=+式中，W(n) 为 n 时刻自适应滤波器的权矢量，011()[(),(),....()]TN W n w n w n w n -=，下一时刻权矢量 W(n +1) 等于当前权矢量 W (n ) 加上一个修正量，该修正量是误差信号e (n )的加权值，加权系数 2μx(n) 正比于当前的输入信号 x(n)。
现代数字信号处理仿真作业
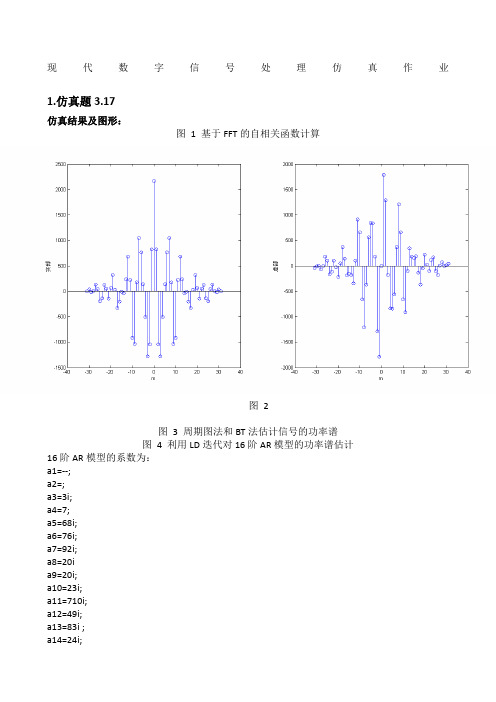
现代数字信号处理仿真作业1.仿真题3.17仿真结果及图形：图 1 基于FFT的自相关函数计算图 2图 3 周期图法和BT法估计信号的功率谱图 4 利用LD迭代对16阶AR模型的功率谱估计16阶AR模型的系数为：a1=--;a2=;a3=3i;a4=7;a5=68i;a6=76i;a7=92i;a8=20ia9=20i;a10=23i;a11=710i;a12=49i;a13=83i ;a14=24i;a16=3i.仿真程序（3_17）:clear allclc%% 产生噪声序列N=32; %基于FFT的样本长度%N=256; %周期图法，BT法，AR模型功率谱估计的长度vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);%%产生复正弦信号f=[0.15 0.17 0.26]; %归一化频率SNR=[30 30 27]; %信噪比A=10.^(SNR./20); %幅度signal=[A(1)*exp(1i*2*pi*f(1)*(0:N-1)); %复正弦信号 A(2)*exp(1i*2*pi*f(2)*(0:N-1));A(3)*exp(1i*2*pi*f(3)*(0:N-1))];%% 产生观察样本un=sum(signal)+vn;%% 利用3.1.1的FFT估计Uk=fft(un,2*N);Sk=(1/N)*abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];%%r2=xcorr(un,N-1,'biased');% 画图k=-N+1:N-1;figure(1)subplot(1,2,1)stem(k,real(r1))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r1))xlabel('m');ylabel('虚部');figure(2)subplot(1,2,1)stem(k,real(r2))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r2))xlabel('m');ylabel('虚部');%% 周期图法NF=1024;Spr=fftshift((1/NF)*abs(fft(un,NF)).^2);kk=-0.5+(0:NF-1)*(1/(NF-1));Spr_norm=10*log10(abs(Spr)/max(abs(Spr)));M=64;r3=xcorr(un,M,'biased');BT=fftshift(fft(r3,NF));BT_norm=10*log10(abs(BT)/max(abs(BT)));figure(3)subplot(1,2,1)plot(kk,Spr_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('周期图法')subplot(1,2,2)plot(kk,BT_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('BT法')%% LD迭代算法p=16;r0=xcorr(un,p,'biased');r4=r0(p+1:2*p+1); %计算自相关函数a(1,1)=-r4(2)/r4(1);sigma(1)=r4(1)-(abs(r4(2))^2)/r4(1);for m=2:p %LD迭代算法k(m)=-(r4(m+1)+sum(a(m-1,1:m-1).*r4(m:-1:2)))/sigma(m-1);a(m,m)=k(m);for i=1:m-1a(m,i)=a(m-1,i)+k(m)*conj(a(m-1,m-i));endsigma(m)=sigma(m-1)*(1-abs(k(m))^2);endPar=sigma(p)./fftshift(abs(fft([1,a(p,:)],NF)).^2); %p阶AR模型的功率谱Par_norm=10*log10(abs(Par)/max(abs(Par)));figure(4)plot(kk,Par_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('16阶AR模型')2.仿真题3.20仿真结果及图形：单次Root-MUSIC算法中最接近单位圆的两个根为：对应的归一化频率为：相同信号的MUSIC谱估计结果如下图 5 对3.20信号进行MUSIC谱估计的结果仿真程序（3_20）:clear allclc%% 信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand); %复正弦信号 exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%% 计算自相关矩阵M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endR=xs*xs'/(N-M);%% 自相关矩阵的特征值分解[U,E]=svd(R);%% Root-MUSIC算法的实现G=U(:,3:M);Gr=G*G';co=zeros(2*M-1,1);for m=1:Mco(m:m+M-1)=co(m:m+M-1)+Gr(M:-1:1,m);endz=roots(co);ph=angle(z)/(2*pi);err=abs(abs(z)-1);%% 计算MUSIC谱En=U(:,2+1:M);NF=2048;for n=1:NFAq=exp(-1i*2*pi*(-0.5+(n-1)/(NF-1))*(0:M-1)');Pmusic(n)=1/(Aq'*En*En'*Aq);endkk=-0.5+(0:NF-1)*(1/(NF-1));Pmusic_norm=10*log10(abs(Pmusic)/max(abs(Pmusic)));plot(kk,Pmusic_norm)xlabel('w/2*pi');ylabel('归一化功率谱/dB')3.仿真题3.21仿真结果及图形：单次ESPRIT算法中最接近单位元的两个特征值为：对应的归一化频率为：仿真程序（3_21）:clear allclc%% 信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand); %复正弦信号 exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%% 自相关矩阵的计算M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endRxx=xs(:,1:end-1)*xs(:,1:end-1)'/(N-M-1);Rxy=xs(:,1:end-1)*xs(:,2:end)'/(N-M-1);%% 特征值分解[U,E]=svd(Rxx);ev=diag(E);emin=ev(end);Z=[zeros(M-1,1),eye(M-1);0,zeros(1,M-1)];Cxx=Rxx-emin*eye(M);Cxy=Rxy-emin*Z;%% 广义特征值分解[U,E]=eig(Cxx,Cxy);z=diag(E);ph=angle(z)/(2*pi);err=abs(abs(z)-1);4.仿真题4.18仿真结果及图形：步长为0.05时失调参数为m1=0.0493；步长为0.005时失调参数为m2=0.0047。
数字信号处理matlab仿真
数字信号处理matlab仿真数字信号处理作业设计报告一、目的1.增进对Matlab的认识，加深对数字信号处理理论方面的理解。
2.掌握数字信号处理中IIR和FIR滤波器的设计。
3.了解和掌握用Matlab实现IIR和FIR滤波器的设计方法、课程，为以后的设计打下良好基础。
二、设计内容1.IIR（无限脉冲响应）模拟滤波器设计（1）设计题目：椭圆型模拟带通IIR滤波器技术指标：通带下截止频率fpl=2kHz，上截止频率fph=5kHz，通带内最大衰减ap=1dB；阻带下截止频率fsl=1.5kHz上截止频率fsh=5.5kHz,阻带最小衰减as=40dB. 设计原理：①确定模拟带通滤波器的技术指标，并对边界频率做归一化处理；②确定归一化低通技术要求；③设计归一化低通G(p)；④将低通G(p)转换成带通H(s)。
Matlab原程序如下：clear all;fp=[2000,5000];ap=1;fs=[1500,5500];as=40;wp=2*pi*fp;ws=2*pi*fs;%归一化的截止频率[N,wn]=ellipord(wp,ws,ap,as, 's');%求椭圆形滤波器的最小阶数和归一化截止频率[B,A]=ellip(N,ap,as,wn, 's');%求传递函数的分子分母系数[H,w]=freqs(B,A);%频率响应函数f=0:8000;1w=2*pi*f;H=freqs(B,A,w);%求系统在指定频率点w上的频响Hplot(f,20*log10(abs(H)));%绘图显示axis([0 7000 -80 0])仿真波形图如下：（2）设计题目：巴特沃斯低通模拟滤波器技术指标：通带截止频率fp=5kHz，通带内最大衰减ap=2dB；阻带截止频率fs=12kHz，阻带最小衰减as=30dB。
设计原理：①确定模拟带通滤波器的技术指标，并对边界频率做归一化处理；②确定归一化低通技术要求并求出归一化低通原型系统函数Ga(p);③将Ga(p)去归一化。
现代信号处理及其应用仿真
仿真作业周子超200820003043 3.17(1)clear allclose allf1=0.15;f2=0.17;f3=0.26;v=randn(1,256);A1=10^(30/20);A2=10^(30/20);A3=10^(30/27);t=0:255;x1=A1*exp(j*2*pi*f1*t);x2=A2*exp(j*2*pi*f2*t);x3=A3*exp(j*2*pi*f3*t);u=v+x1+x2+x3;u=u(:,1:32);u1=[u,zeros(1,32)];uk=fft(u1);for i=1:64uuk(i)=(1/32)*uk(i)*conj(uk(i));endr0=ifft(uuk);rr1=[r0(1,34:64),r0(1,1:32)];r=0;r10=0;r1=zeros(1,63);u=[u,zeros(1,32)];for n=1:32r=(1/32)*u(n)*conj(u(n));r10=r+r10;endfor m=1:31for n=m+1:32r=(1/32)*u(n)*conj(u(n-m));r1(1,m)=r1(1,m)+r;endendfor m=32:62for n=1:31r=(1/32)*u(n)*conj(u(n+m-31));r1(1,m)=r1(1,m)+r;endendrr2=[r1(1,62:-1:32),r10,r1(1,1:31)];通过上面的计算可以发现基于FFT的自相关函数快速算法估计的自相关函数和式(3.1.2)估计出的自相关函数相等。
(2)clear allclose allf1=0.15;f2=0.17;f3=0.26;v=randn(1,256);A1=10^(30/20);A2=10^(30/20);A3=10^(27/20);t=0:255;x1=A1*exp(j*2*pi*f1*t);x2=A2*exp(j*2*pi*f2*t);x3=A3*exp(j*2*pi*f3*t);u=v+x1+x2+x3;U=fft(u);for i=1:256SPER(i)=abs(U(i)*conj(U(i)))/256;endSPER=10*log(SPER);n=0:length(u)-1;k=n/(length(u)-1);figureplot(k,SPER)xlabel('归一化频率')ylabel('功率谱(dB)')title('周期图法')u=u(:,1:256);r=0;r10=0;r1=zeros(1,511);u=[u,zeros(1,256)];for n=1:256r=(1/256)*u(n)*conj(u(n));r10=r+r10;endfor m=1:255for n=m+1:256r=(1/256)*u(n)*conj(u(n-m));r1(1,m)=r1(1,m)+r;endendfor m=256:510for n=1:255r=(1/256)*u(n)*conj(u(n+m-255));r1(1,m)=r1(1,m)+r;endendrr=[r1(1,510:-1:256),r10,r1(1,1:255)];rr=rr(1,193:319);k=-63:63;w=pi*k/63+pi;Sbtw=rr*(exp(-j)).^(k'*w);SBTW=abs(Sbtw);P=10*log(SBTW);figureplot(w/(2*pi),P)xlabel('归一化频率')ylabel('功率谱(dB)')title('BT 法')00.10.20.30.40.50.60.70.80.91-40-2020406080100120140归一化频率功率谱（d B ）周期图法00.10.20.30.40.50.60.70.80.9160708090100110120归一化频率功率谱（d B ）BT 法(3)clear allclose allf1=0.15;f2=0.17;f3=0.26;v=randn(1,256);A1=10^(30/20);A2=10^(30/20);A3=10^(27/20);t=0:255;x1=A1*exp(j*2*pi*f1*t);x2=A2*exp(j*2*pi*f2*t);x3=A3*exp(j*2*pi*f3*t);u=v+x1+x2+x3;r=0;r10=0;r1=zeros(1,511);u=[u,zeros(1,256)];for n=1:256r=(1/256)*u(n)*conj(u(n));r10=r+r10;endfor m=1:255for n=m+1:256r=(1/256)*u(n)*conj(u(n-m));r1(1,m)=r1(1,m)+r;endendr00=0;r11=0;a=zeros(16,16);delta=zeros(16);r=[r10,r1(1,1:16)];a(1,1)=-r(2)/r(1);delta(1)=r(1)-r(2)*conj(r(2))/r(1);for m=2:16r11=0;for i=1:m-1r00=a(i,m-1)*r(m+1-i);r11=r11+r00;endk=-(r(m+1)+r11)/delta(m-1);a(m,m)=k;for i=1:m-1a(i,m)=a(i,m-1)+k*conj(a(m-i,m-1));enddelta(m)=delta(m-1)*(1-abs(k)^2);endap=a(:,16).';delta=delta(16);ap=[1,ap,zeros(1,1007)];i=1;for w=0:2*pi/1023:2*pie=exp(-j*w.*(0:1023));AP=ap*e.';SARW(i)=delta/((1+AP)*conj(1+AP)); i=i+1;endP=abs(10*log10(SARW));w=0:1/1023:1;figureplot(w,P)xlabel('归一化频率')ylabel('功率谱(dB)')title('Levinson-Durbin迭代算法')00.10.20.30.40.50.60.70.80.91归一化频率功率谱（d B ）Lev inson-Durbin 迭代算法3.20clear allclose allM=8;N=1000;n=1:N;x=exp(j*2*pi*0.25*n)+exp(j*2*pi*0.6*n)+randn(size(n));Rxx=zeros(M,M);for n=M:NX=zeros(1,M);X=x(n:-1:n-M+1);Rxx=Rxx+X'*X;endRxx=(1/(N-M+1))*Rxx;[V D]=eig(Rxx,'nobalance');weights=diag(D);weights=weights(1:6);for k=1:6;noise_eigenvects(:,k)=V(:,k);end% root-musicP=0;for i=1:length(weights),P=P+conv(noise_eigenvects(:,i),conj(flipud(noise_eigenvects(:,i)))); endroots_P=roots(P);roots_P1=roots_P(abs(roots_P)<1);[not_used,indx]=sort(abs(abs(roots_P1)-1));sorted_roots=roots_P1(indx);if(angle(sorted_roots(1))>0)f1rootmusic=angle(sorted_roots(1))/(2*pi);elsef1rootmusic=(angle(sorted_roots(1))+2*pi)/(2*pi);endif(angle(sorted_roots(2))>0)f2rootmusic=angle(sorted_roots(2))/(2*pi);elsef2rootmusic=(angle(sorted_roots(2))+2*pi)/(2*pi);endfrootmusic=[f1rootmusic f2rootmusic];% musici1=1;for w=0:2*pi/1023:2*piaw=[1 exp(j*w) exp(j*2*w) exp(j*3*w) exp(j*4*w) exp(j*5*w) exp(j*6*w) exp(j*7*w)].';Pmusic(i1)=1/abs(aw'*noise_eigenvects*noise_eigenvects'*aw);Pmusic(i1)=10*log10(Pmusic(i1));i1=i1+1;endw=0:1/1023:1;plot(w,Pmusic)xlabel('归一化频率')ylabel('功率谱(dB)')title('Music算法')通过上面的计算，Root-Music算法估计的频率为f1=0.25，f2=0.5999，而Music 算法的估计结果为f1=0.248，f2=0.63，所以Root-Music算法估计的频率较Music 算法估计的准确。
现代信号处理仿真作业一(318谐波恢复)
现代信号处理仿真作业一(3.18谐波恢复)班级：自研42 姓名：李琳琳 学号：2004211068一． 谐波恢复的基本理论和方法：1． Pisarenko 谐波分解理论谐波过程可用差分方程描述，首先利用Pisarenko 谐波分解理论推导谐波过程所对应的差分方程。
对单个正弦波()sin(2)x n fn πθ=+利用三角函数恒等式，有：()2cos(2)(1)(2)0x n f x n x n π--+-=对上式作z 变换，得： 12[12cos(2)]()0f z z X z π---+=得到特征多项式：1212cos(2)0f z z π---+=。
由此可见，正弦波的频率可以由相应特征方程的一对共轭根来决定：|arctan[Im()/Re()]|/2i i i f z z π=将单个正弦波推广到多个正弦波的情形，得：如果p 个实的正弦波信号没有重复频率的话，则这p 个频率应该由特征多项式1(21)212110p p p a z a z z -----++++= (1)的根决定。
由此可得到p 个实正弦波所组成的谐波过程可以用以下的差分方程进行描述：21()()0pi i x n a xn i =+-=∑这是一个无激励的AR 过程。
2. 谐波恢复的ARMA 建模法在无激励的AR 模型差分方程21()()0pi i x n a x n i =+-=∑两边同乘()x n k -，并取数学期望，则有：21()()0,px i x i R k a R k i k =+-=∀∑ (2)正弦波过程一般是在加性白噪声中被观测的，设加性白噪声为()w n ，即观测过程为： 1()()()sin(2)()pi i i i y n x n w n A f n w n πθ==+=++∑，其中()w n 为0均值的高斯白噪声。
由于谐波过程和加性白噪声统计独立，所以有：2()()()()()y x w x w R k R k R k R k k σδ=+=+ (3)将(3)式代入(2)式得： 21()()0,2py i y i R k a R k i k p =+-=>∑..................... . (4)这就是加性白噪声中观测到的p 个正弦信号所组成的谐波信号的ARMA 过程的所服从的法方程。
现代信号处理仿作业（谐波恢复）
现代信号处理仿作业（谐波恢复）现代信号处理仿作业(谐波恢复)————————————————————————————————作者：————————————————————————————————日期：现代信号处理仿真作业一(3.18谐波恢复)班级：自研42 姓名：李琳琳学号：2004211068一．谐波恢复的基本理论与方法：1． Pisarenko 谐波分解理论谐波过程可用差分方程描述，首先利用Pisarenko 谐波分解理论推导谐波过程所对应的差分方程。
对单个正弦波()sin(2)x n fn πθ=+利用三角函数恒等式，有：()2cos(2)(1)(2)0x n f x n x n π--+-=对上式作z 变换，得：12[12cos(2)]()0f z z X z π---+=得到特征多项式：1212cos(2)0f z z π---+=。
由此可见，正弦波的频率可以由相应特征方程的一对共轭根来决定：|arctan[Im()/Re()]|/2i i i f z z π=将单个正弦波推广到多个正弦波的情形，得：如果p 个实的正弦波信号没有重复频率的话，则这p 个频率应该由特征多项式1(21)212110p p p a z a z z -----++++=K (1)的根决定。
由此可得到p 个实正弦波所组成的谐波过程可以用以下的差分方程进行描述：21()()0pi i x n a x n i =+-=∑这是一个无激励的AR 过程。
2. 谐波恢复的ARMA 建模法在无激励的AR 模型差分方程21()()0pi i x n a x n i =+-=∑两边同乘()x n k -，并取数学期望，则有：21()()0,px i x i R k a R k i k =+-=?∑ (2)正弦波过程一般是在加性白噪声中被观测的，设加性白噪声为()w n ，即观测过程为： 1()()()sin(2)()pi i i i y n x n w n A f n w n πθ==+=++∑，其中()w n 为0均值的高斯白噪声。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
现代数字信号处理仿真作业1.仿真题3.17仿真结果及图形：图基于FFT的自相关函数计算图图周期图法和BT法估计信号的功率谱图利用LD迭代对16阶AR模型的功率谱估计16阶AR模型的系数为：a1=--;a2=;a3=3i;a4=7;a5=68i;a6=7+6i;a7=9-2i;a8=2-0ia9=2+0i;a10=2+3i;a11=7-10i;a12=4-9i;a13=8-3i ;a14=2+4i;a15=2+1i;a16=3i.仿真程序（3_17）:clear allclc%%产生噪声序列N=32;%基于FFT的样本长度%N=256;%周期图法，BT法，AR模型功率谱估计的长度vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);%%产生复正弦信号f=[0.150.170.26];%归一化频率SNR=[303027];%信噪比A=10.^(SNR./20);%幅度signal=[A(1)*exp(1i*2*pi*f(1)*(0:N-1));%复正弦信号A(2)*exp(1i*2*pi*f(2)*(0:N-1));A(3)*exp(1i*2*pi*f(3)*(0:N-1))];%%产生观察样本un=sum(signal)+vn;%%利用3.1.1的FFT估计Uk=fft(un,2*N);Sk=(1/N)*abs(Uk).^2;r0=ifft(Sk);r1=[r0(N+2:2*N),r0(1:N)];%%r2=xcorr(un,N-1,'biased');%画图k=-N+1:N-1;figure(1)subplot(1,2,1)stem(k,real(r1))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r1))xlabel('m');ylabel('虚部');figure(2)subplot(1,2,1)stem(k,real(r2))xlabel('m');ylabel('实部');subplot(1,2,2)stem(k,imag(r2))xlabel('m');ylabel('虚部');%%周期图法NF=1024;Spr=fftshift((1/NF)*abs(fft(un,NF)).^2);kk=-0.5+(0:NF-1)*(1/(NF-1));Spr_norm=10*log10(abs(Spr)/max(abs(Spr)));%%BT法M=64;r3=xcorr(un,M,'biased');BT=fftshift(fft(r3,NF));BT_norm=10*log10(abs(BT)/max(abs(BT)));figure(3)subplot(1,2,1)plot(kk,Spr_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('周期图法')subplot(1,2,2)plot(kk,BT_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('BT法')%%LD迭代算法p=16;r0=xcorr(un,p,'biased');r4=r0(p+1:2*p+1);%计算自相关函数a(1,1)=-r4(2)/r4(1);sigma(1)=r4(1)-(abs(r4(2))^2)/r4(1);for m=2:p%LD迭代算法k(m)=-(r4(m+1)+sum(a(m-1,1:m-1).*r4(m:-1:2)))/sigma(m-1);a(m,m)=k(m);for i=1:m-1a(m,i)=a(m-1,i)+k(m)*conj(a(m-1,m-i));endsigma(m)=sigma(m-1)*(1-abs(k(m))^2);endPar=sigma(p)./fftshift(abs(fft([1,a(p,:)],NF)).^2);%p阶AR模型的功率谱Par_norm=10*log10(abs(Par)/max(abs(Par)));figure(4)plot(kk,Par_norm)xlabel('w/2pi');ylabel('归一化功率谱/DB');title('16阶AR模型')2.仿真题3.20仿真结果及图形：单次Root-MUSIC算法中最接近单位圆的两个根为：+-对应的归一化频率为：相同信号的MUSIC谱估计结果如下图对3.20信号进行MUSIC谱估计的结果仿真程序（3_20）:clear allclc%%信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand);%复正弦信号exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%%计算自相关矩阵M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endR=xs*xs'/(N-M);%%自相关矩阵的特征值分解[U,E]=svd(R);%%Root-MUSIC算法的实现G=U(:,3:M);Gr=G*G';co=zeros(2*M-1,1);for m=1:Mco(m:m+M-1)=co(m:m+M-1)+Gr(M:-1:1,m);endz=roots(co);ph=angle(z)/(2*pi);err=abs(abs(z)-1);%%计算MUSIC谱En=U(:,2+1:M);NF=2048;for n=1:NFAq=exp(-1i*2*pi*(-0.5+(n-1)/(NF-1))*(0:M-1)');Pmusic(n)=1/(Aq'*En*En'*Aq);endkk=-0.5+(0:NF-1)*(1/(NF-1));Pmusic_norm=10*log10(abs(Pmusic)/max(abs(Pmusic))); plot(kk,Pmusic_norm)xlabel('w/2*pi');ylabel('归一化功率谱/dB')3.仿真题3.21仿真结果及图形：单次ESPRIT算法中最接近单位元的两个特征值为：+-对应的归一化频率为：仿真程序（3_21）:clear allclc%%信号样本和高斯白噪声的产生N=1000;vn=(randn(1,N)+1i*randn(1,N))/sqrt(2);signal=[exp(1i*0.5*pi*(0:N-1)+1i*2*pi*rand);%复正弦信号exp(-1i*0.3*pi*(0:N-1)+1i*2*pi*rand)];un=sum(signal)+vn;%%自相关矩阵的计算M=8;for k=1:N-Mxs(:,k)=un(k+M-1:-1:k).';endRxx=xs(:,1:end-1)*xs(:,1:end-1)'/(N-M-1);Rxy=xs(:,1:end-1)*xs(:,2:end)'/(N-M-1);%%特征值分解[U,E]=svd(Rxx);ev=diag(E);emin=ev(end);Z=[zeros(M-1,1),eye(M-1);0,zeros(1,M-1)];Cxx=Rxx-emin*eye(M);Cxy=Rxy-emin*Z;%%广义特征值分解[U,E]=eig(Cxx,Cxy);z=diag(E);ph=angle(z)/(2*pi);err=abs(abs(z)-1);4.仿真题4.18仿真结果及图形：步长为0.05时失调参数为m1=0.0493；步长为0.005时失调参数为m2=0.0047。
图步长为0.05时权向量的收敛曲线图步长为0.005时权向量的收敛曲线图步长分别为0.05和0.005时100次独立实验的学习曲线仿真程序（4_18）:clear allclc%%产生100组独立样本序列data_len=512;trials=100;n=1:data_len;a1=-0.975;a2=0.95;sigma_v_2=0.0731;v=sqrt(sigma_v_2)*randn(data_len,1,trials);u0=[00];num=1;den=[1,a1,a2];Zi=filtic(num,den,u0);u=filter(num,den,v,Zi);%产生100组独立信号%%LMS迭代mu1=0.05;mu2=0.005;w1=zeros(2,data_len,trials);w2=w1;for m=1:100;temp=zeros(data_len,1);e1(:,:,m)=temp;e2(:,:,m)=temp;d1(:,:,m)=temp;d2(:,:,m)=temp;for n=3:data_len-1w1(:,n+1,m)=w1(:,n,m)+mu1*u(n-1:-1:n-2,:,m)*conj(e1(n,1,m));w2(:,n+1,m)=w2(:,n,m)+mu2*u(n-1:-1:n-2,:,m)*conj(e2(n,1,m));d1(n+1,1,m)=w1(:,n+1,m)'*u(n:-1:n-1,:,m);d2(n+1,1,m)=w2(:,n+1,m)'*u(n:-1:n-1,:,m);e1(n+1,1,m)=u(n+1,:,m)-d1(n+1,1,m);e2(n+1,1,m)=u(n+1,:,m)-d2(n+1,1,m);endendt=1:data_len;w1_mean=zeros(2,data_len);w2_mean=w1_mean;e1_mean=zeros(data_len,1);e2_mean=e 1_mean;for m=1:100w1_mean=w1_mean+w1(:,:,m);w2_mean=w2_mean+w2(:,:,m);e1_mean=e1_mean+e1(:,:,m).^2;e2_mean=e2_mean+e2(:,:,m).^2;endw1_mean=w1_mean/100;%100次独立实验权向量的均值w2_mean=w2_mean/100;e1_100trials_ave=e1_mean/100;%100次独立实验的学习曲线均值e2_100trials_ave=e2_mean/100;figure(1)plot(t,w1(1,:,90),t,w1(2,:,90),t,w1_mean(1,:),t,w1_mean(2,:))xlabel('迭代次数');ylabel('权向量')title('步长=0.05')figure(2)plot(t,w2(1,:,90),t,w2(2,:,90),t,w2_mean(1,:),t,w2_mean(2,:))xlabel('迭代次数');ylabel('权向量')title('步长=0.005')%%计算剩余误差和失调参数wopt=zeros(2,trials);Jmin=zeros(1,trials);sum_eig=zeros(trials,1);for m=1:trialsrm=xcorr(u(:,:,m),'biased');R=[rm(512),rm(513);rm(511),rm(512)];p=[rm(511);rm(510)];wopt(:,m)=R\p;[v,d]=eig(R);Jmin(m)=rm(512)-p'*wopt(:,m);sum_eig(m)=d(1,1)+d(2,2);endsJmin=sum(Jmin)/trials;Jex1=e1_100trials_ave-sJmin;%剩余均方误差mu1Jex2=e2_100trials_ave-sJmin;%剩余均方误差mu2sum_eig_100trials=sum(sum_eig)/100;Jexfin1=mu1*sJmin*(sum_eig_100trials/(2-mu1*sum_eig_100trials));Jexfin2=mu2*sJmin*(sum_eig_100trials/(2-mu2*sum_eig_100trials));M1=Jexfin1/sJmin;%失调参数m1M2=Jexfin2/sJmin;%失调参数m2figure(3)plot(t,e1_100trials_ave,'*',t,e2_100trials_ave)xlabel('迭代次数');ylabel('均方误差')legend('u1=0.05','u2=0.005')axis([0,600,0,1])5.仿真题5.10仿真结果及图形：(1)M=2时，210.99,0.93627a σ=-=，求解Yule-Walker 方程可得到自相关矩阵相应的计算程序为r2=inv([1,-0.99;-0.99,1])*[0.93627;0];R2=[r2(1),r2(2);r2(2),r2(1)];%M=2(2)M=3时，2120.99,0,0.93627a a σ=-==，求解Yule-Walker 方程可得到自相关矩阵为相应的计算程序为r3=inv([1,-0.99,0;-0.99,1,0;0,-0.99,1])*[0.93627;0;0];R3=[r3(1),r3(2),r3(3);r3(2),r3(1),r3(2);r3(3),r3(2),r3(1)];%M=3(3)计算特征值扩展%%特征值分解eig_value_1=eig(R2);eig_value_2=eig(R3);%%特征值扩展eig_spread_1=max(eig_value_1)/min(eig_value_1);eig_spread_2=max(eig_value_2)/min(eig_value_2);M=2时特征值扩展是199.0000；M=3时特征值扩展是444.2790。