现代数字信号处理作业
数字信号处理习题及答案4
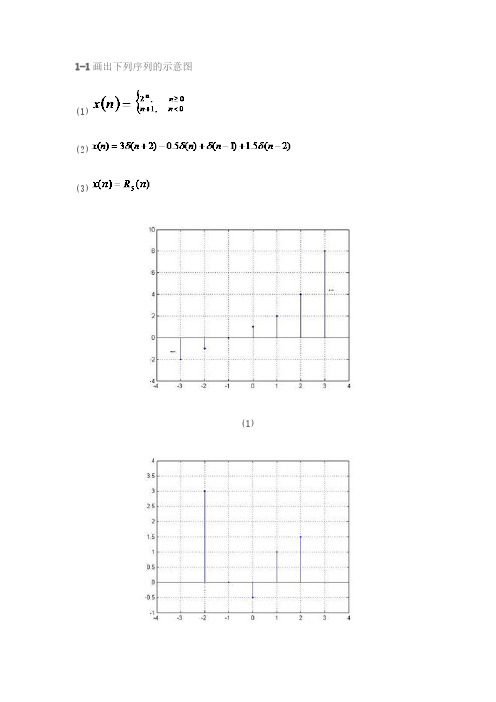
习题及答案4一、填空题（每空1分， 共10分）1．序列()sin(3/5)x n n π=的周期为 .2．线性时不变系统的性质有 律、 律、 律. 3．对4()()x n R n =的Z 变换为 ，其收敛域为 。
4．抽样序列的Z 变换与离散傅里叶变换DFT 的关系为 。
5．序列x(n ）=(1，-2，0，3;n=0，1,2，3）， 圆周左移2位得到的序列为 。
6．设LTI 系统输入为x （n ） ,系统单位序列响应为h （n ）,则系统零状态输出y （n ）= . 7．因果序列x （n ），在Z →∞时，X(Z ）= 。
二、单项选择题（每题2分， 共20分）1．δ(n)的Z 变换是 （ ）A.1 B 。
δ(ω） C 。
2πδ(ω) D 。
2π2．序列x 1(n)的长度为4，序列x 2（n ）的长度为3，则它们线性卷积的长度是 （ )A. 3 B. 4 C 。
6 D 。
73．LTI 系统，输入x （n)时，输出y （n ）；输入为3x （n —2),输出为 （ ) A. y （n-2） B.3y （n —2) C 。
3y （n ） D.y(n ）4．下面描述中最适合离散傅立叶变换DFT 的是 （ ）A.时域为离散序列,频域为连续信号B 。
时域为离散周期序列，频域也为离散周期序列C 。
时域为离散无限长序列,频域为连续周期信号D 。
时域为离散有限长序列,频域也为离散有限长序列5．若一模拟信号为带限，且对其抽样满足奈奎斯特条件，理想条件下将抽样信号通过 即可完全不失真恢复原信号 （ ）A.理想低通滤波器 B 。
理想高通滤波器 C 。
理想带通滤波器 D 。
理想带阻滤波器6．下列哪一个系统是因果系统 （ ）A.y(n)=x (n+2) B 。
y （n ）= cos （n+1）x （n ） C 。
y （n ）=x (2n ） D.y （n)=x （— n ）7．一个线性时不变离散系统稳定的充要条件是其系统函数的收敛域包括 ( ) A 。
(优选)数字信号处理课后习题答案全章.
将x(n)的表示式代入上式， 得到 1 y(n)=－2δ(n+2)－δ(n+1)－0.5δ(2n)+2δ(n－1)+δ(n－2)
+4.5δ(n－3)+2δ(n－4)+δ(n－5)
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况，
所以
T［ax1(n)+bx2(n)］=aT［x1(n)］+bT［x2(n)］
（2） 令输入为
输出为
x(n－n0)
y′(n)=2x(n－n0)+3 y(n－n0)=2x(n－n0)+3=y′(n) 故该系统是非时变的。 由于
T［ax1(n)+bx2(n)］=2ax1(n)+2bx2(n)+3 T［ax1(n)］=2ax1(n)+3 T［bx2(n)］=2bx2(n)+3 T［ax1(n)+bx2(n)］≠aT［x1(n)］+bT［x2(n)］ 故该系统是非线性系统。
m0
1 0.55 1 0.51
0.5n
31 0.5n
最后写成统一表达式：
y(n)=(2－0.5n)R5(n)+31×0.5nu(n－5)
9． 证明线性卷积服从交换律、 结合律和分配律， 即证明下面等式成立： （1） x(n)*h(n)=h(n)*x(n) （2） x(n)*(h1(n)*h2(n))=(x(n)*h1(n))*h2(n) （3） x(n)*(h1(n)+h2(n))=x(n)*h1(n)+x(n)*h2(n) 证明： （1） 因为
1 2 ［x(n)+x(－n)］， 并画出xe(n)波形； 1 ［x(n)－x(－n)］， 并画出xo(n)波形; 2
数字信号处理大题+小题(空白)
已知序)()(5n R n x ,求x(n)的8点DFT 变换。
已知模拟滤波器的传输函数 ，用脉冲响应不变法将其转换为数字滤波器，设T=2。
已知采样周期T=2，用双线性变换法将其转换成数字滤波器，说明双线性变换法的有点和缺点。
已知 ，在Z 平面上画出零极点分布图。
已知FIR滤波器的单位脉冲响应为：N=7,h(n)=[3,-2,1,0,1,-2,3] ，说明其相位特性，求群时延。
利用Z变换法求解差分方程描述系统的系统函数H(z)。
1,0)(),(05.0)1(9.0)(-≤==--nnynunyny写出图中流图的系统函数表达式。
已知序列x(n)如图所示，画x((n-2))5R5(n)的图形。
(选做)y(n)1/2 -83 1/4x(n)2Z-1Z-1Z-1求有限长序列x(n)= 的N点DFT。
用脉冲不变法将转换为H(z),采样周期T。
五、计算题(每题12分，共24分)如图所示的RC低通滤波器(1)用脉冲响应不变法转换成数字滤波器。
并画出相应的网络结构图(2)用双线性变换法转换成数字滤波器。
并画出相应的网络结构图(3)以上两种方法所设计的滤波器各自存在那种失真？已知，求两个序列的N=5的循环卷积。
已知系统的差分方程为)2(31)1(32)2()1(2)()(-+---+-+=n y n y n x n x n x n y ， (1)求出系统函数(2)画出直接II 型网络结构(3)画出全部一阶节的级联型结构 (4)画出一阶节的并联结构已知序列}4,3,2,1{)(1=n x ，}1,1,1,1{)(2=n x ，求两个序列的线性卷积，和N=5及N=7点的循环卷积。
一个FIR线性相位滤波器的单位脉冲响应是实数的，且n<0 和n>6 时h(n)=0。
如果H(0)=1且系统函数在z=0.5e jπ/3和z=3 各有一个零点，H(z)的表达式是什么？假如x(n)的z变换代数表示式为：（1）求出系统函数所有的零极点；（2）X（z）可能有多少个不同的收敛域？（3）画出不同情况的收敛域图。
数字信号处理作业-2012
《数字信号处理Ⅰ》作业姓名：学号：学院：2012 年春季学期第一章 时域离散信号和时域离散系统月 日一 、判断：1、数字信号处理和模拟信号处理在方法上是一样的。
（ ）2、如果信号的取值和自变量都离散，则称其为模拟信号。
（ ）3、如果信号的取值和自变量都离散，则称其为数字信号。
（ ）4、时域离散信号就是数字信号。
（ ）5、正弦序列都是周期的。
（ ）6、序列)n (h )n (x 和的长度分别为N 和M 时，则)n (h )n (x *的长度为N+M 。
（ ）7、如果离散系统的单位取样响应绝对可和，则该系统稳定。
（ ）8、若满足采样定理，则理想采样信号的频谱是原模拟信号频谱以s Ω（采样频率）为周期进行周期延拓的结果。
（ ）9、序列)n (h )n (x 和的元素个数分别为21n n 和，则)n (h )n (x *有（1n n 21-+）个元素。
（ ）二、选择1、R N (n)和u(n)的关系为（ ）：A. R N (n)=u(n)-u(n-N)B. R N (n)=u(n)+u(n-N)C. R N (n)=u(n)-u(n-N-1)D. R N (n)=u(n)-u(n-N+1)2、若f(n)和h(n)的长度为别为N 、M ，则f(n)*h(n)的长度为 （ ）： A.N+M B.N+M-1 C.N-M D.N-M+13、若模拟信号的频率范围为[0，1kHz],对其采样，则奈奎斯特速率为（ ）： A.4kHz B. 3kHz C.2kHz D.1kHz4、LTIS 的零状态响应等于激励信号和单位序列响应的（ ）： A.相乘 B. 相加 C.相减 D.卷积5、线性系统需满足的条件是（ ）：A.因果性B.稳定性C.齐次性和叠加性D.时不变性 6、系统y(n)=f(n)+2f(n-1)(初始状态为0)是（ ）： A. 线性时不变系统 B. 非线性时不变系统 C. 线性时变系统 D. 非线性时变系统7、、若模拟信号的频率范围为[0，Fs],对其采样，则奈奎斯特间隔为（ ）：A.1/4FsB. 1/3FsC.1/2FsD.1/Fs 三、填空题1、连续信号的（ ）和（ ）都取连续变量。
数字信号处理课后习题答案
（修正：此题有错，
(3)系统的单位脉冲响应 而改变，是两个复序列信号之和）
(4)
（修正： 随上小题答案
（修正：此图错误，乘系数应该为 0.5，输出端 y(n)应该在两个延迟器 D 之间）
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数 ； (2)画出系统的一种模拟框图； (3)求使系统稳定的 A 的取值范围。 解：(1)
(2)
(3)
解：（1）
（2）
（3）
1-7 若采样信号 m(t)的采样频率 fs=1500Hz，下列信号经 m(t)采样后哪些信号不 失真？ (1) (2) (3) 解：
(1)
采样不失真
(2)
采样不失真
(3)
，
采样失真
1-8 已知
,采样信号 的采样周期为 。
(1) 的截止模拟角频率 是多少？
(2)将 进行 A/D 采样后， 如何？
（3）最小阻带衰减 5-4
由分式（5.39）根据 A 计算 ，如下： 由表 5.1 根据过度带宽度 计算窗口：
单位脉冲响应如下：
单位脉冲响应如下：
其中 为凯泽窗。 5-5 答：减小窗口的长度 N，则滤波器的过度带增加，但最小阻带衰减保持不变。 5-6：图 5.30 中的滤波器包括了三类理想滤波器，包括了低通，带通和高通，其响应的单位
(1)
，
(2)
1-18 若当 时
；时
(1)
，其中
(2) 证明：
，收敛域
,其中 N 为整数。试证明： ，
(1) 令 其中
，则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下： ，
(1)试求零输入响应 ，零状态响应 ，全响应 ； (2)画出系统的模拟框图 解： (1)零输入响应
中科院数字信号处理作业维纳滤波
中科院数字信号处理作业维纳滤波数字信号处理实验⼀⼀、实验⽬的1、掌握FIR 维纳滤波器的基本原理2、设计FIR 维纳滤波器，对加噪声的信号进⾏滤波处理；⼆、实验原理设期望信号为()S n ，噪声信号为()V n ，则观测信号为()()()X n S n V n =+，为了设计滤波器的最佳传递函数，要先求出期望信号与观测数据的互相关函数xs R 和观测数据的⾃相关函数xx R ，然后利⽤公式-1opt h xs xs R R =求出最佳传递函数，再对信号进⾏()X n 进⾏滤波处理。
三、实验内容及要求1、在直⾓坐标系产⽣⼀个围绕原点做半径为1的圆；2、产⽣均值为0，⽅差分别为0.05和0.06的⾼斯噪声500个；3、将两种杂声分别加在圆的x 、y ⽅向；4、设计FIR 滤波器，根据要求的误差范围不断改变滤波器的阶数，直⾄满⾜误差允许值；5、分别绘制出x ⽅向和y ⽅向的期望信号、噪声信号、观测信号、滤波后的信号、误差信号的曲线图；6、在同⼀幅图中绘制出期望信号、观测信号和滤波后点⽬标的运动轨迹四、实验结果及分析1、在滤波器阶数分别为100和400时，X 轴⽅向的期望信号、噪声信号、观测信号、滤波后信号和误差信号分别如图1和图2所⽰。
图1 X 轴⽅向各个信号滤波器阶数为100图2 X轴⽅向各个信号滤波器阶数为4002、在滤波器阶数分别为100和400时，Y轴防线的期望信号、噪声信号、观测信号、滤波后信号和误差信号如图2所⽰。
图3 Y轴⽅向各个信号滤波器阶数为100图4 Y轴⽅向各个信号滤波器阶数为4003、在滤波器阶数分别为100和400时，期望信号、观测信号和滤波信号在⼀张图中显⽰的结果如图5和图6所⽰，其中红⾊的线为期望信号、绿⾊的线为加噪后的信号、蓝⾊的线为滤波后的信号。
图5 滤波器阶数为100 图6 滤波器阶数为4004、滤波器的阶数与误差的关系表如表1所⽰表1 滤波器阶数与误差对照表滤波器阶数 50 100 200 300 400 x ⽅向误差 0.028512 0.014955 0.012172 0.008156 0.007988 y ⽅向误差 0.0291100.018449 0.005544 0.006908 0.006098 总误差 0.040747 0.023749 0.013375 0.010688 0.010050由实验结果可以看出，滤波器的阶数越⾼，滤波的效果越好。
数字信号处理试题及答案
数字信号处理试题及答案一、选择题（每题2分，共20分）1. 数字信号处理中，离散时间信号的数学表示通常采用______。
A. 连续时间函数B. 离散时间序列C. 连续时间序列D. 离散时间函数答案：B2. 在数字信号处理中，采样定理是由谁提出的？A. 傅里叶B. 拉普拉斯C. 香农D. 牛顿答案：C3. 下列哪一项不是数字滤波器的类型？A. 低通滤波器B. 高通滤波器C. 带通滤波器D. 线性滤波器答案：D4. 数字信号处理中，傅里叶变换的离散形式称为______。
A. 傅里叶级数B. 傅里叶变换C. 离散傅里叶变换（DFT）D. 快速傅里叶变换（FFT）答案：C5. 在数字信号处理中，频域分析通常使用______。
A. 时域信号B. 频域信号C. 频谱D. 波形答案：C二、填空题（每题2分，共20分）1. 数字信号处理中，对连续信号进行采样后得到的信号称为______。
答案：离散时间信号2. 离散时间信号的傅里叶变换是______的推广。
答案：连续时间信号的傅里叶变换3. 数字滤波器的系数决定了滤波器的______特性。
答案：频率响应4. 在数字信号处理中，信号的采样频率必须大于信号最高频率的______倍。
答案：25. 快速傅里叶变换（FFT）是一种高效的算法，用于计算______。
答案：离散傅里叶变换（DFT）三、简答题（每题10分，共30分）1. 简述数字信号处理与模拟信号处理的主要区别。
答案：数字信号处理涉及离散时间信号，而模拟信号处理涉及连续时间信号。
数字信号处理使用数字计算机进行信号处理，模拟信号处理则使用模拟电路。
2. 解释什么是采样定理，并说明其重要性。
答案：采样定理指出，为了能够无失真地从其样本重构一个带限信号，采样频率必须大于信号最高频率的两倍。
这一定理的重要性在于它为信号的数字化提供了理论基础。
3. 描述离散傅里叶变换（DFT）与快速傅里叶变换（FFT）之间的关系。
答案：离散傅里叶变换是将时域信号转换到频域的数学工具，而快速傅里叶变换是一种高效计算DFT的算法。
现代数字信号处理何子述课后
现代数字信号处理何子述课后现代数字信号处理是一门极为重要的学科，它对于现代通信、信息处理乃至于音视频处理都具有非常重要的意义。
何子述教授的课程内容涵盖广泛，是掌握现代数字信号处理知识的必修课程，下面就以何子述课后为主题展开论述。
第一步：认识现代数字信号处理的基础知识现代数字信号处理的基础知识主要包括数字信号、数字系统等。
数字信号是指通过离散化时间和幅度的信号，它可以进行数字系统的处理。
数字系统是通过数字信号处理电路实现数字信号的转换、处理以及存储等。
要掌握现代数字信号处理的知识，首先需要对这些基础知识有一个全面的认识。
第二步：了解数字信号处理的处理流程数字信号处理的处理流程主要包括采样、量化、编码、传输等过程。
采样是指将连续时间的模拟信号转换为离散信号的过程。
量化是指将连续的模拟信号转换为离散的数值，编码是将离散的数值转换为符号。
传输是指将数字信号传输至接收端。
只有了解了数字信号处理的处理流程，才能更好地理解数字信号处理的具体实现。
第三步：学习数字信号处理的具体技术数字信号处理的技术主要包括滤波器设计、时域处理、频域处理、自适应处理等。
滤波器设计是数字信号处理中的基础，其目的是去除或改变信号中的某些成分。
时域处理是指直接对信号进行处理，如加减乘除等。
频域处理是指对信号进行傅里叶变换，对其在频域上进行处理。
自适应处理是另一种常用的数字信号处理技术，其目的是通过自适应反馈，让系统自适应其输入和输出之间的关系。
第四步：实践数字信号处理的实际应用数字信号处理的实际应用十分广泛，涵盖通信、音视频处理乃至于医学影像等领域。
在实践数字信号处理的实际应用过程中，需要根据具体的应用场景选择不同的数字信号处理技术，进行系统设计和实现。
以上就是关于现代数字信号处理何子述课后的分步骤解析。
通过学习该课程，可了解数字信号处理的基本知识，理解数字信号处理的处理流程，掌握数字信号处理的技术和应用，为将来在相关领域进行数字信号处理提供基础和指引，是一门非常有价值的课程。