解析几何初步精品PPT课件
合集下载
解析几何初步ppt(42份) 北师大版12

2 2 2 xOy平面的距离为d= 00 00 03 3 .
答案:3
【要点探究】
知识点
空间两点间距离公式
对空间两点间距离公式的两点说明
(1)空间两点间距离公式是平面内两点间距离公式的延伸、推
广,而平面内两点间距离公式又是空间两点间距离公式的特例.
(2)公式的推导
A .3 3 B . 2 C . 2
)
D .5
(2)如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3, |AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中 点,求M,N两点间的距离.
【解题探究】1.题(1)中如何求AB中点P的坐标?
2.题(2)中,M点的坐标如何确定?
广,其形式和结构特征是相同的,只是多出一组坐标.
【即时练】 1.已知点A(0,1,1),B(-2,0,2),则线段AB的长为 (
A . 3 B . 2 C . 2 D . 6
)
2.已知A(-2,1,m),B(-2,2,0),若|AB|=1,则m=_____.
【解析】1.选D.|AB|=
0 2 1 0 1 2 1 16 . 4
点P在对角线AB上运动时”,你能求出|PQ|的最小值吗?
1 P(x,x,z),则 【解析】依题意Q ( 0 , 1 ,设 ), 2
1 1 1 2 2 2 2 2 1 |PQ|= x x 1 ( z ) 2 ( x ) ( z ) , 2 2 2 2
1 时,|PQ| = 2 , 所以当x=z= min 2
【变式训练】如图所示,PA,AB,AD两两互
相垂直,四边形ABCD为矩形,M,N分别为AB,
答案:3
【要点探究】
知识点
空间两点间距离公式
对空间两点间距离公式的两点说明
(1)空间两点间距离公式是平面内两点间距离公式的延伸、推
广,而平面内两点间距离公式又是空间两点间距离公式的特例.
(2)公式的推导
A .3 3 B . 2 C . 2
)
D .5
(2)如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3, |AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中 点,求M,N两点间的距离.
【解题探究】1.题(1)中如何求AB中点P的坐标?
2.题(2)中,M点的坐标如何确定?
广,其形式和结构特征是相同的,只是多出一组坐标.
【即时练】 1.已知点A(0,1,1),B(-2,0,2),则线段AB的长为 (
A . 3 B . 2 C . 2 D . 6
)
2.已知A(-2,1,m),B(-2,2,0),若|AB|=1,则m=_____.
【解析】1.选D.|AB|=
0 2 1 0 1 2 1 16 . 4
点P在对角线AB上运动时”,你能求出|PQ|的最小值吗?
1 P(x,x,z),则 【解析】依题意Q ( 0 , 1 ,设 ), 2
1 1 1 2 2 2 2 2 1 |PQ|= x x 1 ( z ) 2 ( x ) ( z ) , 2 2 2 2
1 时,|PQ| = 2 , 所以当x=z= min 2
【变式训练】如图所示,PA,AB,AD两两互
相垂直,四边形ABCD为矩形,M,N分别为AB,
解析几何初步 PPT课件 (42份) 北师大版4

x-2y+5=0与直线2x+3y-18=0交点的直线系(不包括直线2x+3y-
18=0),无论a取何值,它都过两直线的交点,由
解得
x y
3, 4.
x 2y5 0, 2x 3y18 0,
所以直线必过定点(3,4).
【拓展类型】两直线交点的综合应用 【备选例题】(1)直线ax+2y+8=0,x+3y-4=0和5x+2y+6=0相交 于一点,则a的值为________. (2)是否存在m,使得三条直线3x-y+2=0,2x+y+3=0,mx+y=0能 够构成三角形?若存在,请求出m的取值范围;若不存在,请 说明理由.
得
3,
x y
2, 1,
即交点P(-2,1).
由题意知,所求直线的斜率存在且不为0.
设直线l:y-1=k(x+2).
令x=0,得y=1+2k;
令y=0,得x=-2- 1 .
k
由1+2k=-2- 1 ,得k=-1或k=- 1 .
k
2
故所求直线方程为x+y+1=0或x+2y=0.
方法二:设所求直线方程为x+2+λ(2x+y+3)=0,
即(1+2λ)x+λy+2+3λ=0,(※)
令x=0,得 y= 2 3;
令y=0,得 x= 2 3 .
1 2
由题意得 23=23,
12
得λ=- 2 或λ=-1.代入(※)式得所求直线方程为x+2y=0或
第六讲 解析几何初步ppt课件

(二)解析几何具体结构
(二)解析几何具体结构
(三)高中解析几何主要思想与方法
高中解析几何既是一种重要的数学思想,也 是一种重要的数学方法,其核心是“数形结合”的 思想方法.同时,由于解析几何内容的综合性,在解 决问题的过程中,就必然还要用到其它的思想方法, 如函数与方程、特殊与一般、分类与整合的思想, 以及待定系数法、换元法等等.
2.考点分析
(1)平面解析几何试题统计表 • 表(一) 2009~2013福建高考(理科)解
析几何试题的总体分布
• 表(二) 2009~2013福建高考(理科)解 析几何试题的总体分布
(2)统计分析
(结合2013年全国各高考卷和福建近五年试卷)
① 题型、题量、难易度与分值
统计表明,在2013 年的解析几何试题 中,从所考查的题量分值上看,绝大多数试 卷的圆锥曲线题量都保持着一小一大或两小 一大的格局,分值约在17~23 分之间 ); 从 试题所处的位置看,绝大多数解答题都设置 在后三题的位置上,其把关题的作用依旧突 出;
福建5年而言,题型、题量与分值与全国 情况基本类似(理科考查权重
(2)统计分析
②内容、知识点
从考查内容看,重点考查圆锥曲线的 定义 方程和几何性质的地位依然不变,其 中大多数大题的背景仍以椭圆居多,抛物 线次之,双曲线最少,且都以小题为主; 从所考查的知识点看,在注重考查基本概 念和几何性质的基础上,加大了学科内的 知识综合;
• 评注1:以抛物线的基础知识为背景,考查圆的一 般方程,只需求得圆心和半径即可。
• 评注2:第(I)问已知直线的方程及直线和圆相 切,求圆的方程,主要考查待定系数法求圆的方 程。
• 评注3:第(Ⅱ)问和上一题相比较,考查的内容 相同,都是求圆的方程,但条件呈现的形式不同, 此时的直线是抛物线的准线要自己求得。
解析几何初步ppt(33份) 北师大版15
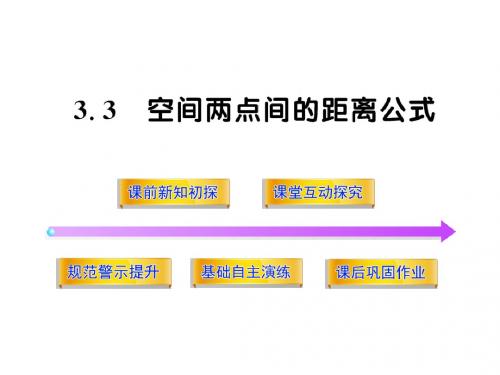
由点A的坐标是 ( 3 ,1 及点 , 0 ) D的坐标求AD中点的坐标,进
2 2
而可求得点D到AD中点的距离.
【解析】因点D在平面yOz上,可设点D的坐标为(0,y,z), 在Rt△BCD中BC=2且∠BDC=90°,∠DCB=30°, 则 z 3,y 1 . ∴点D的坐标为 (0, 1 , 3 ).
2 2 2 2 ∵点A的坐标是 ( 3 , 1 , 0 ) . 2 2 ∴AD中点的坐标为 ( 3 , 0 , 3 ) 4 4
∴点D到AD中点的距离为
3 2 1 3 3 1 0 2 2 ( 0 ) ( 0 ) ( ) . 4 2 4 2 4
【挑战能力】 (10分)在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3), 试问 (1)在y轴上是否存在点M,满足|MA|=|MB|? (2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,
【解析】选D.由两点间的距离公式可得
2 A B 31 3 2 m 3 m 3 5 .
2
2
2
C D 0 2 11 01 . 5
2 2 2
所以|AB|≥|CD|.
2.已知△ABC的三个顶点A(3,3,2),B(4,-3,7),C(0,5,1),则
【解题提示】利用该定点到三个坐标平面的距离都是1 求出点的坐标,然后用空间两点间的距离公式求解. 【解析】选B.一定点到三个坐标平面的距离都是1,则该点
的坐标可为(1,1,1)
∴该点到原点的距离为
3.
二、填空题(每题4分,共8分)
5.已知长方体的长宽高分别为3,4,5.则该长方体的对角线
长为__________.
解析几何初步 PPT课件 (42份) 北师大版11

B.xOy平面上
D.xOz平面上
(2)在空间直角坐标系中,作出点M(6,-2,4).
【解题探究】1.题(1)中点的y坐标是0,说明什么距离一定为0?
2.题(2)中点M到三个坐标轴的距离分别为多少?
【探究提示】1.说明点到xOz平面的距离一定为0.
2.点M到yOz平面,xOz平面,xOy平面的距离分别为6,2,4.
§3 空间直角坐标系
3.1 空间直角坐标系的建立 3.2 空间直角坐标系中点的坐标
1.如何建立空间坐标系?建系原则是什么?
问题 引航 它又有哪些构成要素? 2.空间中的点由几个坐标参数确定?如何确 定空间中的点的位置?
1.空间直角坐标系 垂直 的轴、 (1)建系方法:过空间任意的一点O作三条两两互相_____ 相同 的长度单位. 有_____ (2)建系原则:本书建立的坐标系都是右手直角坐标系.伸出右 垂直 ,并使四指先指向____ x轴 正方向,然后 手,让四指与大拇指_____ 90° 指向____ y轴 正方向,此时大拇指的指 让四指沿握拳方向旋转_____ z轴 正向. 向即为____
(2)反之,对任意一个有序实数组(x,y,z),在x轴,y轴,z
轴上分别作出点P,Q,R,使它们在x轴,y轴,z轴上的坐标分
别是x,y,z,再分别过这些点作垂直于各自所在的坐标轴的
平面,这三个平面的交点即为所求的点A.
2.空间中点的对称规律 点M(x,y,z)是空间直角坐标系中的一点,则有 (1)与M点关于x轴对称的点为(x,-y,-z). (2)与M点关于y轴对称的点为(-x,y,-z). (3)与M点关于z轴对称的点为(-x,-y,z). (4)与M点关于原点对称的点为(-x,-y,-z). (5)与M点关于xOy平面对称的点为(x,y,-z). (6)与M点关于yOz平面对称的点为(-x,y,z).
解析几何初步 PPT课件 (42份) 北师大版9

;y2=0与直线y=x+b没有交点,则b的取值范围是
__________________.
【解析】1.因为(x-1)2+(y-1)2=a2与两坐标轴恰有两个交点,
所以圆与坐标轴相切,所以|a|=1,a=±1.
答案:±1
2.圆x2+2x+y2=0可化为(x+1)2+y2=1,
杂,则用代数法较简单.
【变式训练】(2014·西城区高一检测)在同一坐标系下,直
线ax+by=ab和圆(x-a)2+(y-b)2=r2(ab≠0,r>0)的图象可能 是( )
【解析】选D.直线ax+by=ab在x轴,y轴上的截距分别为b和a, 圆心横坐标为a,纵坐标为b. 在A中,由直线位置可得b<0,而由圆的位置可得b>0,这不可 能,故A不正确. 在B中,由直线位置可得a>0,而由圆的位置可得a<0,这不可
所以直线方程为x+y=0,
0 2 圆心(1,0)到直线x+y=0的距离为 d1 < r 2 , 2 2
所以直线与圆相交.
答案:相交
【要点探究】
知识点1
直线与圆的位置关系
对直线与圆的位置关系的两点说明
(1)直线与圆的位置关系可以按照由远及近的顺序记忆:
相离(没有公共点)→相切(只有一个公共点)→相交(两个公共 点).
2.3 直线与圆、圆与圆的位置关系 第1课时 直线与圆的位置关系
问题 引航
1.平面几何中学过的直线与圆的位置关系
有几种?
2.如何判断直线与圆的位置关系?
直线与圆的位置关系及判断
直线Ax+By+C=0(A2+B2≠0),圆(x-a)2+(y-b)2=r2(r>0)
__________________.
【解析】1.因为(x-1)2+(y-1)2=a2与两坐标轴恰有两个交点,
所以圆与坐标轴相切,所以|a|=1,a=±1.
答案:±1
2.圆x2+2x+y2=0可化为(x+1)2+y2=1,
杂,则用代数法较简单.
【变式训练】(2014·西城区高一检测)在同一坐标系下,直
线ax+by=ab和圆(x-a)2+(y-b)2=r2(ab≠0,r>0)的图象可能 是( )
【解析】选D.直线ax+by=ab在x轴,y轴上的截距分别为b和a, 圆心横坐标为a,纵坐标为b. 在A中,由直线位置可得b<0,而由圆的位置可得b>0,这不可 能,故A不正确. 在B中,由直线位置可得a>0,而由圆的位置可得a<0,这不可
所以直线方程为x+y=0,
0 2 圆心(1,0)到直线x+y=0的距离为 d1 < r 2 , 2 2
所以直线与圆相交.
答案:相交
【要点探究】
知识点1
直线与圆的位置关系
对直线与圆的位置关系的两点说明
(1)直线与圆的位置关系可以按照由远及近的顺序记忆:
相离(没有公共点)→相切(只有一个公共点)→相交(两个公共 点).
2.3 直线与圆、圆与圆的位置关系 第1课时 直线与圆的位置关系
问题 引航
1.平面几何中学过的直线与圆的位置关系
有几种?
2.如何判断直线与圆的位置关系?
直线与圆的位置关系及判断
直线Ax+By+C=0(A2+B2≠0),圆(x-a)2+(y-b)2=r2(r>0)
解析几何初步ppt(33份) 北师大版16

2 2
值为
最小值为
对称问题
1.对称问题的分类
2.对称问题的求解策略 (1)点关于点的对称问题,是对称问题中最基础最重要的一类, 其余几类对称问题均可以化归为点关于点的对称进行求解.熟 练掌握和灵活运用中点坐标公式是处理这类问题的关键. (2)点关于直线的对称问题是点关于点的对称问题的延伸,处
y 即 k ,y=kx.当直线y=kx与圆(x-2)2+y2=3相切时, x 斜率k取得最大值与最小值,此时 2k 0 解得 3, 2 k 1 y 故 的最大值为 最小值为 3; 3, k 3 . x
(1)设
(2)设y-x=b,即y=x+b,当直线y=x+b与圆相切时,直线在
y轴
在使用斜截式判断直线的位置关系时,注意直 线斜率不存在的情形.
【例2】已知两直线l1:x+m2y+6=0,l2:(m-2)x+3my+2m=0, 当m为何值时,l1与l2
(1)相交;(2)平行;(3)重合.
【审题指导】对直线的斜率存在与否,进行讨论,转化为
“斜截式”后,才能使用相关结论.
【规范解答】当m=0时,l1:x+6=0, l2:x=0. ∴l1∥l2. 当m≠0时,则两直线化为斜截式方程分别为: l1: y
理这类问题主要抓住两个方面:①两点连线与已知直线斜率
乘积等于-1,②两点的中点在已知直线上.
(3)直线关于点的对称问题,可转化为直线上的点关于此点对 称的问题,这里需要注意到的是两对称直线是平行的.我们往 往利用平行直线系去求解.
【例7】已知直线l∶x+2y-3=0 (1)求点A(1,3)关于直线l的对称点A′的坐标. (2)求直线l关于点A(1,3)对称的直线l′的方程. 【审题指导】(1)因为A,A′关于直线对称,所以直线l是线段 AA′的垂直平分线.(2)直线l′与直线l关于点A(1,3)对称,则直 线l与直线l′相互平行且点A到两直线的距离相等.
值为
最小值为
对称问题
1.对称问题的分类
2.对称问题的求解策略 (1)点关于点的对称问题,是对称问题中最基础最重要的一类, 其余几类对称问题均可以化归为点关于点的对称进行求解.熟 练掌握和灵活运用中点坐标公式是处理这类问题的关键. (2)点关于直线的对称问题是点关于点的对称问题的延伸,处
y 即 k ,y=kx.当直线y=kx与圆(x-2)2+y2=3相切时, x 斜率k取得最大值与最小值,此时 2k 0 解得 3, 2 k 1 y 故 的最大值为 最小值为 3; 3, k 3 . x
(1)设
(2)设y-x=b,即y=x+b,当直线y=x+b与圆相切时,直线在
y轴
在使用斜截式判断直线的位置关系时,注意直 线斜率不存在的情形.
【例2】已知两直线l1:x+m2y+6=0,l2:(m-2)x+3my+2m=0, 当m为何值时,l1与l2
(1)相交;(2)平行;(3)重合.
【审题指导】对直线的斜率存在与否,进行讨论,转化为
“斜截式”后,才能使用相关结论.
【规范解答】当m=0时,l1:x+6=0, l2:x=0. ∴l1∥l2. 当m≠0时,则两直线化为斜截式方程分别为: l1: y
理这类问题主要抓住两个方面:①两点连线与已知直线斜率
乘积等于-1,②两点的中点在已知直线上.
(3)直线关于点的对称问题,可转化为直线上的点关于此点对 称的问题,这里需要注意到的是两对称直线是平行的.我们往 往利用平行直线系去求解.
【例7】已知直线l∶x+2y-3=0 (1)求点A(1,3)关于直线l的对称点A′的坐标. (2)求直线l关于点A(1,3)对称的直线l′的方程. 【审题指导】(1)因为A,A′关于直线对称,所以直线l是线段 AA′的垂直平分线.(2)直线l′与直线l关于点A(1,3)对称,则直 线l与直线l′相互平行且点A到两直线的距离相等.
解析几何初步 PPT课件 (33份) 北师大版18
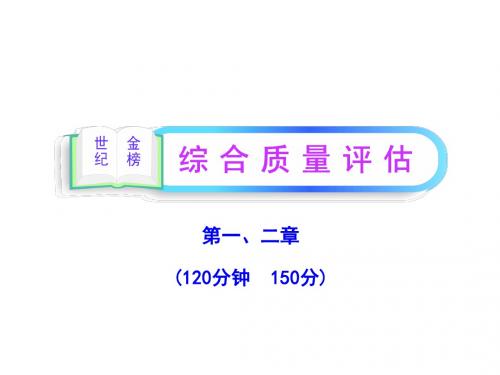
∵ABCD为正方形,∴E为BD中点.
又F为PD中点,∴EF 又AM 1 PB,∴AM
2
1 PB.
2
EF.
∴AEFM为平行四边形.
∴MF∥AE.
∵PB⊥平面ABCD, AE 平面ABCD, ∴PB⊥AE.∴MF⊥PB. 因为ABCD为正方形,∴AC⊥BD.∴MF⊥BD. 又PB∩PD=P,∴MF⊥平面PBD. 又MF 平面PMD.∴平面PMD⊥平面PBD.
①y=x+1
②y=2
③4x-3y=0
④y=2x+1
【解题提示】只要点到直线的距离d≤4便可.
【解析】点M(5,0)到直线y=x+1的距离为
510 3 24
2
不合题意;点M(5,0)到直线y=2的距离为2<4合题意;点
M(5,0)到直线4x-3y=0的距离为4合题意;点M(5,0)到直线
y=2x+1的距离为 10 1 0 4 不合题意.
∴1=2×(-2)+b,b=5.∴k=2,b=5.
(2)圆心(-4,2)到2x-y+5=0的距离为
2425
d
5.
5
而圆的半径为2 5 , ∴∠AOB=120°.
22.(12分)(2011·常熟高二检测)如图, 四边形ABCD是正方形,PB⊥平面ABCD, MA⊥平面ABCD,PB=AB=2MA. 求证:(1)平面AMD∥平面BPC; (2)平面PMD⊥平面PBD.
7.(2011·蚌埠高二检测)已知点P(3,2)与点Q(1,4)关于
直线l对称,则直线l的方程为( )
(A)x-y+1=0
(B)x-y=0
(C)x+y+1=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
斜率的计算公式. 能根据两条直线的斜率判定这两条直线 平行或垂直.掌握直线方程的几种形式,掌握三种距离. 会直线与圆的位置关系的判定;直线与圆中的度量(弦长、 距离等)分析;直线与圆的方程等;强化了求弦长、求圆 的切线方程、求圆的方程、直线与圆的位置关系判定、圆 与圆的位置关系判定等技能与技巧的考查;同时,关注对 图形几何特征的代数转化、数形结合化归与转化、分类讨 论、待定系数法等基本数学思想与方法的渗透。
化、例子)
(2)统计分析
②内容、知识点
从考查内容看,重点考查圆锥曲线的定义 方程和几 何性质的地位依然不变,其中大多数大题的背景仍以椭圆 居多,抛物线次之,双曲线最少,且都以小题为主;从所 考查的知识点看,在注重考查基本概念和几何性质的基础 上,加大了学科内的知识综合;
福建近5年试卷,若考虑理科的选修4-4的参数方程与 极坐标,几乎各块都有考,只是不同的交汇形式而已。但 解答题背景以椭圆、抛物线,文科以抛物线、圆为主.
解析几何的基本思想
解析几何的基本思想是在平面上引进所 谓“坐标”的概念,并借助这种坐标在平面 上的点和有序实数对之间建立一一对应的关 系.使几何代数与几何实现了有机的统一.
解析几何的研究方法
交流内容
一、梳理知识 二、聚焦考点 三、赏析试题 四、复习建议
一、解析几何知识梳理
(一)总体结构
直角
解
坐标系
(2)统计分析
⑤解析几何与不同模块知识的大交汇
解析几何与不同模块知识的结合,常常是视角别致、 情境新颖,为高考解析几何试题的命制拓宽了思路,是实 现在知识网络交汇点处设计试题的良好的素材,较好地体 现了解析内容的综合性.表中显示,解析几何常与函数、 导数、向量、平几、不等式的结合综合考查,其中以函数、 向量、平几的结合最为常见,其实质是解析几何内容特点 的反映,较好地体现了解几内容在高考选拔中的作用.
2.考点分析
(1)平面解析几何试题统计表 • 表(一) 2009~2013福建高考(理科)解析几何试题的总体
分布
• 表(二) 2009~2013福建高考(理科)解析几何试题的总体 分布
(2)统计分析
(结合2013年全国各高考卷和福建近五年试卷)
① 题型、题量、难易度与分值
统计表明,在2013 年的解析几何试题中,从所考查的题 量分值上看,绝大多数试卷的圆锥曲线题量都保持着一小一 大或两小一大的格局,分值约在17~23 分之间 ); 从试题所 处的位置看,绝大多数解答题都设置在后三题的位置上,其 把关题的作用依旧突出;
三、赏析试题
下面结合2013年全国高考试题以及福建 09~13年的部分试题,对解析几何的知识 思想方法和能力考核目标分类加以细化分析。
(一)直线与圆考核目标细化分析。 (二)椭圆的考核目标细化解析。 (三)双曲线的考核目标细化解析 (四)抛物线的考核目标细化解析 (五)亮点试题推荐
三、赏析试题
(一)直线与圆考核目标细化分析 理解直线的倾斜角和斜率的概念,掌握过两点的直线
析
几
何 基
坐标法
曲线与 方程
本
思
想
极坐标系
知曲线 求方程 用方程 研究曲线
知方程 画曲线 用曲线 研究方程
平面曲 线(直线、 圆、椭 圆、抛 物线、 双曲线 的专题 研究)
(二)解析几何具体结构
(二)解析几何具体结构
(三)高中解析几何主要思想与方法
高中解析几何既是一种重要的数学思想,也是一 种重要的数学方法,其核心是“数形结合”的思想 方法.同时,由于解析几何内容的综合性,在解决问 题的过程中,就必然还要用到其它的思想方法,如 函数与方程、特殊与一般、分类与整合的思想,以 及待定系数法、换元法等等.
• 评注1:以抛物线的基础知识为背景,考查圆的一 般方程,只需求得圆心和半径即可。
• 评注2:第(I)问已知直线的方程及直线和圆相 切,求圆的方程,主要考查待定系数法求圆的方 程。
(2)统计分析
③数学思想和方法
从所考查的数学思想方法看,在重视解析几何本质的 同时,既强调通性通法,淡化特殊技巧,又注重提供灵活 运用坐标法解题的空间;解析几何的基本思想突出表现为 坐标法、向量法的应用.用斜率公式、两点间距离公式、点 到直线距离公式、弦长公式、联立方程等代数工具来刻画 图形的几何性质、描述直线与圆锥曲线(椭圆、抛物线) 的位置关系,求解轨迹方程、探究最值、定值、范围等问 题,通常以解答题的形式呈现,是解析几何最重要的考查 点。
(四)高中解析几何的能力要求
高中解析几何课程具有培养学生的运算求 解能力、推理论证能力、抽象概括能力的功 效,也是培养学生数学综合能力、应用意识 与创新意识的好场所.
二、聚焦考点
1. 考试要求
(1)新课程《考试大纲》与我省《考试说明》的差异比较
理科:
(了解) 掌握抛物线的定义、几何图形、
标准方程及其简单性质;
福建5年而言,题型、题量与分值与全国情况基本类似 (理科考查权重18+16)/324=11%,应考分值16.5;文科考查 权重(18+12)/250=12%,应考分值18,实际考查与考查权重 基本上相吻合);难度而言从2009到2011年解析几何的难度 明显下降,2012年突然加大难度,2013年有所回归.(去模式
(2)统计分析
④ 同一套试卷文科、理科的差异置处理或姊妹题的背景或设问方式 处理,使得整体的考查内容既有较高的相似度,又符合 文理科的考纲要求,较好地反映了文理科学生学习基础、 水平上的差异,体现了《标准》中“高中数学课程应具 有多样性与选择性,使不同的学生在数学上得到不同的 发展”的理念.
(无说明)掌握直线与圆锥曲线的位置关系;
(了解)能解决圆锥曲线的简单应用问题.
文科:
(无说明)理解直线与圆锥曲线的位置关系;
•
(没变化)了解圆锥曲线的简单应用.
1.考试要求
(2)高中平面解析几何的内容要求的层次分析
理科:双曲线与方程、曲线与方程的概念; 文科:抛物线与方程、双曲线与方程、圆锥
曲线 的简单应用,界定为了解水平, 其余都在理解、掌握的水平上,可见这块知 识的重要性.这方面知识的考查在难题、中档 题都有可能出现.
化、例子)
(2)统计分析
②内容、知识点
从考查内容看,重点考查圆锥曲线的定义 方程和几 何性质的地位依然不变,其中大多数大题的背景仍以椭圆 居多,抛物线次之,双曲线最少,且都以小题为主;从所 考查的知识点看,在注重考查基本概念和几何性质的基础 上,加大了学科内的知识综合;
福建近5年试卷,若考虑理科的选修4-4的参数方程与 极坐标,几乎各块都有考,只是不同的交汇形式而已。但 解答题背景以椭圆、抛物线,文科以抛物线、圆为主.
解析几何的基本思想
解析几何的基本思想是在平面上引进所 谓“坐标”的概念,并借助这种坐标在平面 上的点和有序实数对之间建立一一对应的关 系.使几何代数与几何实现了有机的统一.
解析几何的研究方法
交流内容
一、梳理知识 二、聚焦考点 三、赏析试题 四、复习建议
一、解析几何知识梳理
(一)总体结构
直角
解
坐标系
(2)统计分析
⑤解析几何与不同模块知识的大交汇
解析几何与不同模块知识的结合,常常是视角别致、 情境新颖,为高考解析几何试题的命制拓宽了思路,是实 现在知识网络交汇点处设计试题的良好的素材,较好地体 现了解析内容的综合性.表中显示,解析几何常与函数、 导数、向量、平几、不等式的结合综合考查,其中以函数、 向量、平几的结合最为常见,其实质是解析几何内容特点 的反映,较好地体现了解几内容在高考选拔中的作用.
2.考点分析
(1)平面解析几何试题统计表 • 表(一) 2009~2013福建高考(理科)解析几何试题的总体
分布
• 表(二) 2009~2013福建高考(理科)解析几何试题的总体 分布
(2)统计分析
(结合2013年全国各高考卷和福建近五年试卷)
① 题型、题量、难易度与分值
统计表明,在2013 年的解析几何试题中,从所考查的题 量分值上看,绝大多数试卷的圆锥曲线题量都保持着一小一 大或两小一大的格局,分值约在17~23 分之间 ); 从试题所 处的位置看,绝大多数解答题都设置在后三题的位置上,其 把关题的作用依旧突出;
三、赏析试题
下面结合2013年全国高考试题以及福建 09~13年的部分试题,对解析几何的知识 思想方法和能力考核目标分类加以细化分析。
(一)直线与圆考核目标细化分析。 (二)椭圆的考核目标细化解析。 (三)双曲线的考核目标细化解析 (四)抛物线的考核目标细化解析 (五)亮点试题推荐
三、赏析试题
(一)直线与圆考核目标细化分析 理解直线的倾斜角和斜率的概念,掌握过两点的直线
析
几
何 基
坐标法
曲线与 方程
本
思
想
极坐标系
知曲线 求方程 用方程 研究曲线
知方程 画曲线 用曲线 研究方程
平面曲 线(直线、 圆、椭 圆、抛 物线、 双曲线 的专题 研究)
(二)解析几何具体结构
(二)解析几何具体结构
(三)高中解析几何主要思想与方法
高中解析几何既是一种重要的数学思想,也是一 种重要的数学方法,其核心是“数形结合”的思想 方法.同时,由于解析几何内容的综合性,在解决问 题的过程中,就必然还要用到其它的思想方法,如 函数与方程、特殊与一般、分类与整合的思想,以 及待定系数法、换元法等等.
• 评注1:以抛物线的基础知识为背景,考查圆的一 般方程,只需求得圆心和半径即可。
• 评注2:第(I)问已知直线的方程及直线和圆相 切,求圆的方程,主要考查待定系数法求圆的方 程。
(2)统计分析
③数学思想和方法
从所考查的数学思想方法看,在重视解析几何本质的 同时,既强调通性通法,淡化特殊技巧,又注重提供灵活 运用坐标法解题的空间;解析几何的基本思想突出表现为 坐标法、向量法的应用.用斜率公式、两点间距离公式、点 到直线距离公式、弦长公式、联立方程等代数工具来刻画 图形的几何性质、描述直线与圆锥曲线(椭圆、抛物线) 的位置关系,求解轨迹方程、探究最值、定值、范围等问 题,通常以解答题的形式呈现,是解析几何最重要的考查 点。
(四)高中解析几何的能力要求
高中解析几何课程具有培养学生的运算求 解能力、推理论证能力、抽象概括能力的功 效,也是培养学生数学综合能力、应用意识 与创新意识的好场所.
二、聚焦考点
1. 考试要求
(1)新课程《考试大纲》与我省《考试说明》的差异比较
理科:
(了解) 掌握抛物线的定义、几何图形、
标准方程及其简单性质;
福建5年而言,题型、题量与分值与全国情况基本类似 (理科考查权重18+16)/324=11%,应考分值16.5;文科考查 权重(18+12)/250=12%,应考分值18,实际考查与考查权重 基本上相吻合);难度而言从2009到2011年解析几何的难度 明显下降,2012年突然加大难度,2013年有所回归.(去模式
(2)统计分析
④ 同一套试卷文科、理科的差异置处理或姊妹题的背景或设问方式 处理,使得整体的考查内容既有较高的相似度,又符合 文理科的考纲要求,较好地反映了文理科学生学习基础、 水平上的差异,体现了《标准》中“高中数学课程应具 有多样性与选择性,使不同的学生在数学上得到不同的 发展”的理念.
(无说明)掌握直线与圆锥曲线的位置关系;
(了解)能解决圆锥曲线的简单应用问题.
文科:
(无说明)理解直线与圆锥曲线的位置关系;
•
(没变化)了解圆锥曲线的简单应用.
1.考试要求
(2)高中平面解析几何的内容要求的层次分析
理科:双曲线与方程、曲线与方程的概念; 文科:抛物线与方程、双曲线与方程、圆锥
曲线 的简单应用,界定为了解水平, 其余都在理解、掌握的水平上,可见这块知 识的重要性.这方面知识的考查在难题、中档 题都有可能出现.
