大学物理课件麦克斯韦方程组
合集下载
大学物理章 麦克斯韦方程组(老师课件)

James ClerkMaxwell (1831-1879)
麦克斯韦简介
英国物理学家、数学家麦克斯韦15岁就在“爱丁 堡皇家学报”发表论文,1854年从剑桥大学毕业, 1874年任卡文迪许实验室的首任主任。他是气体动理 论的创始人之一,也是经典电磁理论的奠基人。麦克 斯韦虽然只活了49岁,但他却写了100多篇有价值的论 文。爱因斯坦在纪念麦克斯韦100周年的文集中对他作 出了很高的评价“这是自牛顿奠定理论物理学的基础 以来,物理学公理基础的最伟大的变革,„这样一次 伟大的变革是同法拉第、麦克斯韦和赫兹的名字永远 联在一起的。这次革命的最大部分出自麦克斯韦。”
答案:(A)
2. 如图,电量Q均匀分布在半径R、长L(LR) 的绝缘圆筒上,一单匝矩形线圈的一边与圆筒 轴线重合.若圆筒以角速度=0(1-t/t0)线性减 速旋转,则线圈中的感应电流为 解: 磁感应线位于包含圆筒轴 线的各个平面内,穿过线圈 的磁通始终为零 i=0Ii=0.
3. 在感应电场中电磁感应定律可写成 d E k dl m L dt 式中 E k 为感应电场的电场强度,此式表明 (A)闭合曲线上 E k 处处相等. (B)感应电场是保守力场. (C)感应电场的电力线不是闭合曲线. (D)在感应电场中不能像对静电场那样引入电势 的概念.
Ⅱ、磁场的性质 在任意磁场中,通过任意闭合曲面的磁 通量都等于零。 B dS 0
S
Ⅲ、变化的电场与磁场的关系
由全电流的安培环路定律
D d D H dl I 0 ( j0 ) dS S dt t
L
Ⅳ、变化的磁场与电场的关系 dΦ m L E静 dl 0 L E涡 dl dt B dΦ m dS E E静 E涡 L E dl S t dt
大学物理 6.5麦克斯韦方程组
6.5 麦克斯韦方程组
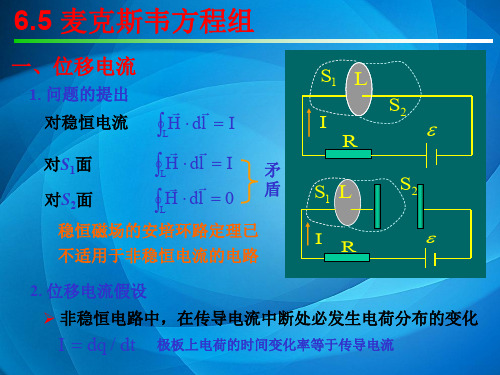
一、位移电流
1. 问题的提出
对稳恒电流 LH dl I
对S1面 对S2面
LH
dl
I
矛 盾
LH dl 0
稳恒磁场的安培环路定理已
不适用于非稳恒电流的电路
S1 L
I R
S2
S1 L
S2
IR
2. 位移电流假设 非稳恒电路中,在传导电流中断处必发生电荷分布的变化
电位移通量的变化率等于传导电流强度 位移电流密度 jD
一般情况位移电流
位移电流与传导电流连接起来恰好构成连续的闭合电流
麦克斯韦提出全电流的概念
ID
I
R
电流在空间永远是连续不中断的,并且构成闭合回路 麦克斯韦将安培环路定理推广
(全电流安培环路定理)
若传导电流为零
3. 位移电流、传导电流的比较
(1) 位移电流具有磁效应 —与传导电流相同
(2) 位移电流与传导电流不同之处 • 产生机理不同 • 存在条件不同
I dΦD dt
B
位移电流可以存在于真空中、导体中、介质中
(3) 位移电流不产生焦耳热,传导电流产生焦耳热
例1设平行板电容器极板为圆板,半径为R ,两极板间距为d,
用缓变电流 IC 对电容器充电
0
B
dS
S t
表明:静电场是保守场,变化磁场可以激发涡旋电场
4. 全电流安培环路定理
H dl
L
L (H1 H2 ) dl
Ii
D
dS
一、位移电流
1. 问题的提出
对稳恒电流 LH dl I
对S1面 对S2面
LH
dl
I
矛 盾
LH dl 0
稳恒磁场的安培环路定理已
不适用于非稳恒电流的电路
S1 L
I R
S2
S1 L
S2
IR
2. 位移电流假设 非稳恒电路中,在传导电流中断处必发生电荷分布的变化
电位移通量的变化率等于传导电流强度 位移电流密度 jD
一般情况位移电流
位移电流与传导电流连接起来恰好构成连续的闭合电流
麦克斯韦提出全电流的概念
ID
I
R
电流在空间永远是连续不中断的,并且构成闭合回路 麦克斯韦将安培环路定理推广
(全电流安培环路定理)
若传导电流为零
3. 位移电流、传导电流的比较
(1) 位移电流具有磁效应 —与传导电流相同
(2) 位移电流与传导电流不同之处 • 产生机理不同 • 存在条件不同
I dΦD dt
B
位移电流可以存在于真空中、导体中、介质中
(3) 位移电流不产生焦耳热,传导电流产生焦耳热
例1设平行板电容器极板为圆板,半径为R ,两极板间距为d,
用缓变电流 IC 对电容器充电
0
B
dS
S t
表明:静电场是保守场,变化磁场可以激发涡旋电场
4. 全电流安培环路定理
H dl
L
L (H1 H2 ) dl
Ii
D
dS
麦克斯韦方程组

给电容为C的平行板电容器充电 电流i=0.2e-t(SI) , 的平行板电容器充电,电流 例:给电容为 的平行板电容器充电 电流 时电容器极板上无电荷, 设 t = 0时电容器极板上无电荷,求: 时电容器极板上无电荷 的变化关系; (1)极板间电压 随时间 t 的变化关系; )极板间电压U (2)t时刻极板间总的位移电流 Id . ) 时刻极板间总的位移电流 解:给平板电容器充电 i = 0.2et (SI) t = 0 极板间上 q0 = 0 t dq (1) i = ∴ q ( t ) = ∫ i d t = 0 .2 ( 1 e t )
特指静电场和恒定磁场的方程组 特指静电场和恒定磁场的方程组 静电场和恒定磁场
而当
S
q = 0;
I =0
V
∫∫ D dS = ∫∫∫ ρdV = 0 ∫∫ B dS = 0
B ∫LE d l = ∫∫S t d S D ∫LH dl = ∫∫S t dS 这时空间存在变化的电磁场(自由电磁场) 这时空间存在变化的电磁场(自由电磁场) 电磁波 表明变化电场与变化磁场相互激发,相互依存的关系! 表明变化电场与变化磁场相互激发,相互依存的关系!
dt
0
0 .2 ( 1 e t ) q( t ) = U = C C
d U d (Φ 0 ) d ( Sε ) ( SεE ) = = (2) I d = dt d dt dt dU dq(t) = C = = i = 0 .2 e t dt dt
平行板电容极板为圆形,半径R,间距为d. 例:平行板电容极板为圆形,半径 ,间距为 充电。 点处的磁场强度H。 用缓变电流( 用缓变电流(IC)充电。求P1,P2 点处的磁场强度 。 缓变电流, 解:缓变电流,极板间可视为匀强 非静电场, 非静电场,通常称库仑电场 设:极板间位移电流也是均匀分布
第2讲 麦克斯韦方程组ppt课件

dS
r E t
r )dS
C
S t
rr
Ñ S
B
dS
0
rr1
Ñ S
E
dS
0
V
ρdV
v v dq
ÑS JgdS dt
第二讲 麦克斯韦方程组
二、介质中的麦克斯韦方程
媒质对电磁场的响应可分为三种情况:极化、磁化和传导。 极化:媒质在电场作用下呈现宏观电荷(束缚电荷)分布 磁化:媒质在磁场作用下呈现宏观电流(磁化电流)分布 描述媒质电磁特性的参数为:介电常数、磁导率和电导率。
第二讲 麦克斯韦方程组
四、静态场与时变场的麦克斯韦方程
宏观电磁场的普遍规律是Maxwell方程组,而静态场是
时变场的特殊情况。
Maxwell方程组
H
E
J
D
t
B
t
B 0
D
0 t
静态场方程
静电场
E
0
( J = 0 ) D
J 0
恒定电场 (J≠0)
第二讲 麦克斯韦方程组
一、真空中的麦克斯韦方程
麦克斯韦方程组(Maxwell’s equations)
r B
r E r
微分形式
r 0(J
r B
t
0
r E t
)
B 0
r
E / 0
r gJ
t
Ñ
Ñ
C
r B r E
r dl
r dl
积分形式
r
0
(J
S
r
B
0 r
麦克斯韦第二方程,表明时变磁 场产生电场
麦克斯韦第三方程,表明磁场是 无源场,磁力线总是闭合曲线
r E t
r )dS
C
S t
rr
Ñ S
B
dS
0
rr1
Ñ S
E
dS
0
V
ρdV
v v dq
ÑS JgdS dt
第二讲 麦克斯韦方程组
二、介质中的麦克斯韦方程
媒质对电磁场的响应可分为三种情况:极化、磁化和传导。 极化:媒质在电场作用下呈现宏观电荷(束缚电荷)分布 磁化:媒质在磁场作用下呈现宏观电流(磁化电流)分布 描述媒质电磁特性的参数为:介电常数、磁导率和电导率。
第二讲 麦克斯韦方程组
四、静态场与时变场的麦克斯韦方程
宏观电磁场的普遍规律是Maxwell方程组,而静态场是
时变场的特殊情况。
Maxwell方程组
H
E
J
D
t
B
t
B 0
D
0 t
静态场方程
静电场
E
0
( J = 0 ) D
J 0
恒定电场 (J≠0)
第二讲 麦克斯韦方程组
一、真空中的麦克斯韦方程
麦克斯韦方程组(Maxwell’s equations)
r B
r E r
微分形式
r 0(J
r B
t
0
r E t
)
B 0
r
E / 0
r gJ
t
Ñ
Ñ
C
r B r E
r dl
r dl
积分形式
r
0
(J
S
r
B
0 r
麦克斯韦第二方程,表明时变磁 场产生电场
麦克斯韦第三方程,表明磁场是 无源场,磁力线总是闭合曲线
麦克斯韦方程组最新PPT资料

并由1式得到关于E的方程:
模2仿B 上述 过 2tB程2 :可得到关于B的方程:
上式中的符号2称为拉普拉斯算符2 2 2 2 x2 y2 z 2
(4)
j Eபைடு நூலகம்
电导率
D E
介电常数
H
1
B
磁导率
第二节 电磁场的波动性
对4式两端对时间求导数,则
B
2 E
t
t 2
对上式左端变换求导顺序,并考虑到第(3)
式:
B
t
(
E)
2E t 2
第二节 电磁场的波动性
利用公式(363页附录)
2E(E)2tE2 ( E) 2E
(5): E 位移电流强度与位移电流密度联系 t 第二节 电磁场的波动性
(6): (7): (8):
• D
•B 0
H j
D
t
第一节 麦克斯韦方程组
符号的意义: 哈密顿算符:
i
j
k
x y z
具有矢量和求导的双重功能。
散度
•D
:
是“标量积”
•D
Dx
Dy
Dz
x y z
法拉第电磁感应定律 :d
dt
d dt
B•
d
B t
•
d
感应电动势的定义:单位正电荷沿闭合回路移动一
周时,涡旋电场所作 的功。即
E • dl
因此得到:
E • dl
B t
• d
此式即为法拉第电磁感应定律的数学表达式
第一节 麦克斯韦方程组
麦克斯韦认为(猜想): (1)感应电动势的产生是一种电场对线圈中自由电
Q
0
大学物理 麦克斯韦方程组

S
S
M dS L M dl 斯托克斯公式 S E dS L E dl S B 环路定理 d S L E dl s t B 比较上两式,可得 E t D 同理由公式 d S L H d l t s D 可得 H t
L
R Q Q P P R dydz dzdx dxdy y z z x x y S R Q Q P P R cos cos cos dS y z z x x y S N dS M dS
D H t
B E t
高斯公式
(P cos Q cos R cos )dS
S
P Q R dxdydz x y z V 设矢量 M Pi Qj Rk dS (dS cos )i (dS cos ) j (dS cos )k
S
N i j k y z z x x y
矢量乘法: A Ai x A y j Ak z
B Bi x B y j Bk z
Ax Ay Az AB Bx By Bz (Ay Bz Az By )i (Az Bx AxBz ) j (AxBy Ay Bx )k i j k
s
B dS 0
s
v
( 2) D d S L H d l t S
16-麦克斯韦方程组ppt

7
) IS ( t e2.0 i
例:给电容为C的平行板电容器充电,电流为
,
例:平行板电容极板为圆形,半径R,间距为d.用缓变
电流(IC)充电。求P1,P2点处的磁场强度H. 解:缓变电流,极板间可视为匀强 非静电场,通常称库仑电场 设:极板间位移电流也是均匀分布
IC D 位移电流密度 j D t R 2
S
dV
V
通量
d B LE dl dt S t dS D LB dl 0[S jC dS S t dS ]
环流
10
一. 电场的性质
1 有源特性,高斯定律: E dS
S
B dS 0
S
V
通量
环流
13
特别是: 当 B 0; D 0 t t
D dS dV q S V B dS 0 S d B LE dl dt S t dS 0
—— 传导电流
—— 位移电流 变化的电场等效地也是一种“电流” D j D ——位移电流面密度 t I C I D ——全电流 jC jD ——全电流密度
3
三. 全电流(安培)定律
传导电流 麦克斯韦提出全电流概念 运流电流 位移电流
CBiblioteka S1L S2
全电流在空间永远是连续的闭合电流 D H dl IC I D jC dS dS L S S t
1
矢量式
S EH
EH
坡印廷矢量
19
w 1 3.电磁场的质量: m 2 2 ( D E B H ) c 2c w 1 4.电磁场的动量: p ( D E B H ) c 2c wc S w c 2 2 c c c c 如何计算? 辐射压强“光压”的产生——类似于碰撞, w S 注意到: p 2 (动量密度) c c
) IS ( t e2.0 i
例:给电容为C的平行板电容器充电,电流为
,
例:平行板电容极板为圆形,半径R,间距为d.用缓变
电流(IC)充电。求P1,P2点处的磁场强度H. 解:缓变电流,极板间可视为匀强 非静电场,通常称库仑电场 设:极板间位移电流也是均匀分布
IC D 位移电流密度 j D t R 2
S
dV
V
通量
d B LE dl dt S t dS D LB dl 0[S jC dS S t dS ]
环流
10
一. 电场的性质
1 有源特性,高斯定律: E dS
S
B dS 0
S
V
通量
环流
13
特别是: 当 B 0; D 0 t t
D dS dV q S V B dS 0 S d B LE dl dt S t dS 0
—— 传导电流
—— 位移电流 变化的电场等效地也是一种“电流” D j D ——位移电流面密度 t I C I D ——全电流 jC jD ——全电流密度
3
三. 全电流(安培)定律
传导电流 麦克斯韦提出全电流概念 运流电流 位移电流
CBiblioteka S1L S2
全电流在空间永远是连续的闭合电流 D H dl IC I D jC dS dS L S S t
1
矢量式
S EH
EH
坡印廷矢量
19
w 1 3.电磁场的质量: m 2 2 ( D E B H ) c 2c w 1 4.电磁场的动量: p ( D E B H ) c 2c wc S w c 2 2 c c c c 如何计算? 辐射压强“光压”的产生——类似于碰撞, w S 注意到: p 2 (动量密度) c c
清华大学_大学物理课件.第21章.麦克斯韦方程组和电磁辐射

32
【演示】
电磁波的辐射和接收
【TV】
电磁波
33
中英文名称对照表
位移电流 — displacement current 麦克斯韦方程组 — Maxwell equations 电磁波 — electromagnetic wave 能量密度 — energy density 能流密度 — energy flow density 坡印廷矢量 — Poynting vector 动量密度 — momentum density 电磁辐射 — electromagnetic radiation 同步辐射 — synchrotron radiation
彗星的彗尾总是向背离 阳光的方向伸展。
27
§21.4 电磁辐射
q(t)
C
I(t)
C
L
L
H
-q(t) E
电磁场封闭在 LC 振荡电路中
电磁场较开放
电偶极振子天线 电磁场完全开放
偶极振子 E线 H线
28
在开放的空间,电磁场的变化和相互激发 可以传播出去,形成脱离场源的电磁辐射。
电磁场在辐射区(r >> l, )特点:
第二十一章结束
34
L
Id内
S
D
d
s
t
πr 2 d E
dt
HP
r
2
dE dt
BP
HP
r
2
dE dt
11
§21.2 麦克斯韦方程组
设空间既有自由电荷和传导电流,又有变化 的电场和磁场,同时还有电介质和磁介质。
一. 麦克斯韦方程组的积分形式
由
L
E静
d和l
E
L
【演示】
电磁波的辐射和接收
【TV】
电磁波
33
中英文名称对照表
位移电流 — displacement current 麦克斯韦方程组 — Maxwell equations 电磁波 — electromagnetic wave 能量密度 — energy density 能流密度 — energy flow density 坡印廷矢量 — Poynting vector 动量密度 — momentum density 电磁辐射 — electromagnetic radiation 同步辐射 — synchrotron radiation
彗星的彗尾总是向背离 阳光的方向伸展。
27
§21.4 电磁辐射
q(t)
C
I(t)
C
L
L
H
-q(t) E
电磁场封闭在 LC 振荡电路中
电磁场较开放
电偶极振子天线 电磁场完全开放
偶极振子 E线 H线
28
在开放的空间,电磁场的变化和相互激发 可以传播出去,形成脱离场源的电磁辐射。
电磁场在辐射区(r >> l, )特点:
第二十一章结束
34
L
Id内
S
D
d
s
t
πr 2 d E
dt
HP
r
2
dE dt
BP
HP
r
2
dE dt
11
§21.2 麦克斯韦方程组
设空间既有自由电荷和传导电流,又有变化 的电场和磁场,同时还有电介质和磁介质。
一. 麦克斯韦方程组的积分形式
由
L
E静
d和l
E
L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L1
L1
L2
[C]
有一圆形平行平板电容器,R=3.0cm。现对其充电,使 电路上的传导电流 I c dQ dt 2.5 A 。现有一点P处于两 极板间,离开轴线的距离r=2.0cm,若略去边缘效应。 求: (1)两极板间的位移电流;
(2)P点处的磁感应强度 。
五、电磁波的产生与传播
0
发射
接收
如图,平板电容器(忽略边缘效应)充电时,沿环 路L1、L2磁场强度H的环流中,必有:
( A) (B) (C ) ( A)
dl H dl LH 1 L2 dl H dl LH 1 L2 dl H dl LH 1 L2 H dl 0
1 LC
L
C
L
C
辐射能与频率 的4次方成正比
+ -
L
C
- +
偶极振子的辐射 ——最重要的电磁辐射模型
2 4 p0 辐射功率:P 3 12 0c
p p0 cost
电磁波的传播机制
变化的电场 —— 磁场 变化的磁场 —— 电场 地位对称 变化率也随时间变化 变化的电场、磁场同时存在, 又以对方存在为前提
全电流总是连续的
电流的连续性问题得到解决
三、位移电流的磁场
位移电流的引入,更重要的意义是提出了位移电流 也在周围空间激发磁场!
dΦD I B d l I H d l I I c c d L L dt E LH dl I c t dS
H dl I c I d L
麦克斯韦方程组
积分形式
d m LE dl dt
SD dS V dV B dS 0
S
dΦD LH dl I dt
预 言 了 电 磁 波 的 存 在
微分形式
电磁场——互相依存、同时存在的变化的电场和磁场
E B
E B
E
E
B
E、B、k 三矢量成右手螺旋
B
波速 u 1
k
E、B同相位(同号、同步)
c 光的折射率 n r r u
00 r
1
真空中 c
0 0
电磁波谱
光 、X射线、放射性辐射等都是电磁波,只是频 率或波长有很大差别。 按波长或频率的顺序把电磁波排列起来 ——电磁 波谱。以真空中的波长作为电磁波谱的标度。 无线电波: 长波:几千米; 中波: 103m-50m; 短波: 50m-10m; 微波:10m-1mm 红外线: 10-2cm-760nm; 可见光:760nm-400nm; 紫外线: 400nm—5 nm ; X 射线: 1nm-10-3nm; γ射线: 0.1nm
变化的电场在其周围空间激发磁场!
传导电流与位移电流的比较:
相同点: 都在空间激发磁场 不同点: 传导电流 运动的电荷 位移电流 变化的电场
四、麦克斯韦方程组
电磁基本规律的归纳 1. 电场高斯定理:
S
q E0 dS
Ei dS 0
q S ( E0 Ei ) dS
dq 由 I dt
电容冲放电过程的特点: 0 D 0 q S 0 SD E
d ( SD ) 得: I dt
q
-
q
I
+ + + +
D
- - - -
dΦ D I dt
——传导电流等于电容器极板间 电位移通量的变化率。
如果把极板间电场的变化看作相当于某种电流在流动, 则整个电路的电流仍可视为连续的! 麦克斯韦的位移电流概念: 变化的电场相当于某种电流 ——位移电流 Id
4. 磁场环路定理:
d m B dS E dl S t L dt
L
H 0 dl I c
dΦ D L H i dl I d dt
dΦD I dt D dS H dl jc dS L S S dt
dΦ D 电流强度: I d dt
dD 电流密度: jd dt
二、全电流
通常,导体中以传导电流为主, 介质中以位移电流为主。
q
-
qLeabharlann I+ + + +D
- - - -
一般情况下,传导电流、位移电流可能同时通过某一 截面。
麦克斯韦全电流概念:
通过某截面的电流应是两种电流的代数和——全电流
I=I c I d
S1
L
S2
LB dl I
H dl I
L
L所包围的电流I,可以理解为穿过 以L为边界的任意曲面的电流。 电容冲放电过程的安培环路定理:
S1 I
S2 K
S1面: LH dl I S2面: LH dl 0
安培环路定理仅适于稳恒电路
第二十一章 麦克斯韦方程组和电磁辐射
电磁学的对称性与完整性:
电场
静电场 静止电荷 稳恒磁场 恒定电流
起因
磁场
感生电场 dB dt 感生磁场?
起因
dE ? dt
Maxwell 从电流的连续性入手得到了突破
一、 位移电流 ( 17.7 与变化电场相联系的磁场)
I L 稳恒电流,安培环路定理成立
D B 0 B E t D H j t
解决电磁场空间 分布问题
解决有限空间电磁场问题
1831年 法拉第(1791-1867)
发现电磁感应
1865年 麦克斯韦(1831-1879) 完善电磁方程 1888年 赫兹验证了电磁波的发射与传播 赫兹实验
S
2. 磁场高斯定理: S B0 dS 0 Bi dS 0
S
D dS q dV
S
q E dS
S
V
B dS 0
S
3. 电场环路定理:
L
E 0 dl 0
d m L Ei dl dt
L1
L2
[C]
有一圆形平行平板电容器,R=3.0cm。现对其充电,使 电路上的传导电流 I c dQ dt 2.5 A 。现有一点P处于两 极板间,离开轴线的距离r=2.0cm,若略去边缘效应。 求: (1)两极板间的位移电流;
(2)P点处的磁感应强度 。
五、电磁波的产生与传播
0
发射
接收
如图,平板电容器(忽略边缘效应)充电时,沿环 路L1、L2磁场强度H的环流中,必有:
( A) (B) (C ) ( A)
dl H dl LH 1 L2 dl H dl LH 1 L2 dl H dl LH 1 L2 H dl 0
1 LC
L
C
L
C
辐射能与频率 的4次方成正比
+ -
L
C
- +
偶极振子的辐射 ——最重要的电磁辐射模型
2 4 p0 辐射功率:P 3 12 0c
p p0 cost
电磁波的传播机制
变化的电场 —— 磁场 变化的磁场 —— 电场 地位对称 变化率也随时间变化 变化的电场、磁场同时存在, 又以对方存在为前提
全电流总是连续的
电流的连续性问题得到解决
三、位移电流的磁场
位移电流的引入,更重要的意义是提出了位移电流 也在周围空间激发磁场!
dΦD I B d l I H d l I I c c d L L dt E LH dl I c t dS
H dl I c I d L
麦克斯韦方程组
积分形式
d m LE dl dt
SD dS V dV B dS 0
S
dΦD LH dl I dt
预 言 了 电 磁 波 的 存 在
微分形式
电磁场——互相依存、同时存在的变化的电场和磁场
E B
E B
E
E
B
E、B、k 三矢量成右手螺旋
B
波速 u 1
k
E、B同相位(同号、同步)
c 光的折射率 n r r u
00 r
1
真空中 c
0 0
电磁波谱
光 、X射线、放射性辐射等都是电磁波,只是频 率或波长有很大差别。 按波长或频率的顺序把电磁波排列起来 ——电磁 波谱。以真空中的波长作为电磁波谱的标度。 无线电波: 长波:几千米; 中波: 103m-50m; 短波: 50m-10m; 微波:10m-1mm 红外线: 10-2cm-760nm; 可见光:760nm-400nm; 紫外线: 400nm—5 nm ; X 射线: 1nm-10-3nm; γ射线: 0.1nm
变化的电场在其周围空间激发磁场!
传导电流与位移电流的比较:
相同点: 都在空间激发磁场 不同点: 传导电流 运动的电荷 位移电流 变化的电场
四、麦克斯韦方程组
电磁基本规律的归纳 1. 电场高斯定理:
S
q E0 dS
Ei dS 0
q S ( E0 Ei ) dS
dq 由 I dt
电容冲放电过程的特点: 0 D 0 q S 0 SD E
d ( SD ) 得: I dt
q
-
q
I
+ + + +
D
- - - -
dΦ D I dt
——传导电流等于电容器极板间 电位移通量的变化率。
如果把极板间电场的变化看作相当于某种电流在流动, 则整个电路的电流仍可视为连续的! 麦克斯韦的位移电流概念: 变化的电场相当于某种电流 ——位移电流 Id
4. 磁场环路定理:
d m B dS E dl S t L dt
L
H 0 dl I c
dΦ D L H i dl I d dt
dΦD I dt D dS H dl jc dS L S S dt
dΦ D 电流强度: I d dt
dD 电流密度: jd dt
二、全电流
通常,导体中以传导电流为主, 介质中以位移电流为主。
q
-
qLeabharlann I+ + + +D
- - - -
一般情况下,传导电流、位移电流可能同时通过某一 截面。
麦克斯韦全电流概念:
通过某截面的电流应是两种电流的代数和——全电流
I=I c I d
S1
L
S2
LB dl I
H dl I
L
L所包围的电流I,可以理解为穿过 以L为边界的任意曲面的电流。 电容冲放电过程的安培环路定理:
S1 I
S2 K
S1面: LH dl I S2面: LH dl 0
安培环路定理仅适于稳恒电路
第二十一章 麦克斯韦方程组和电磁辐射
电磁学的对称性与完整性:
电场
静电场 静止电荷 稳恒磁场 恒定电流
起因
磁场
感生电场 dB dt 感生磁场?
起因
dE ? dt
Maxwell 从电流的连续性入手得到了突破
一、 位移电流 ( 17.7 与变化电场相联系的磁场)
I L 稳恒电流,安培环路定理成立
D B 0 B E t D H j t
解决电磁场空间 分布问题
解决有限空间电磁场问题
1831年 法拉第(1791-1867)
发现电磁感应
1865年 麦克斯韦(1831-1879) 完善电磁方程 1888年 赫兹验证了电磁波的发射与传播 赫兹实验
S
2. 磁场高斯定理: S B0 dS 0 Bi dS 0
S
D dS q dV
S
q E dS
S
V
B dS 0
S
3. 电场环路定理:
L
E 0 dl 0
d m L Ei dl dt
