流体力学-第十章管路水力计算
《管道的水力计算》PPT课件

(1)按ΣQi=0分配流量 从A点和最远点F点分配,可假设
(2)计算各管段损失并填表 注意正负号 hi SiQi2
(3)计算校正流量ΔQ
注意公共段CD
环网计算表
环 管 假定流
路 段 量Qi
Si
管段校 校正后 校正后
hi
hi /Qi
ΔQ
正流量 的流量Qi 的hi
AB +0.15 59.76 +1.3346 8.897
vB2 2g
zA
zB
pA pB
g
v
2 A
2g
1 vB2Biblioteka 2gH0——作用水头
H0
1
vB2 2g
流速
vB
1
1
2gH0 2gH0
对锐缘进口的管嘴,ζ=0.5, 1 0.82
1 0.5
流量 Q vB A A 2gH0 A 2gH0
Qi 0 b.由流量确定各管段管径
d 4Qi ve
ve——经济流速(规范要求)
c.由控制线确定作用压力
p pi pc Spi Qi2 pc 或 H hi hc Shi Qi2 hc
d.阻力平衡,调整支管管径
(2)管网布置和作用压力已定,求di——校核计 算,扩建管网
短管的作用水头
H0
1
l d
v2 2g
1→突扩ζ=1,H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入,得
流体力学孔口管嘴出流与管路水力计算

流体力学孔口管嘴出流与管路水力计算流体力学是研究流体运动和力学性质的物理学科。
在水力学中,孔口管嘴出流和管路水力计算是流体力学的一个重要应用。
1.孔口管嘴出流孔口管嘴出流是指在一定压力差下,流体从孔口或管嘴中流出的现象。
它是一种自由射流,不受管道限制,流速和流量可以自由变化。
对于理想流体来说,根据贝努利定律和连续性方程,可以得出孔口管嘴出流速度的计算公式:v = √(2gh)其中,v为出流速度,g为重力加速度,h为液面距离孔口或管嘴的高度差。
可以看出,出流速度与液面高度差成正比,与重力加速度的平方根成正比。
对于真实流体来说,考虑到粘性和摩擦等因素,出流速度会稍有减小。
此时,可以使用液体流量系数进行修正。
液体流量系数是指实际流量与理论流量之比,一般使用实验数据来确定。
根据实验结果,可以通过乘以液体流量系数来修正出流速度的计算。
管路水力计算是指在给定管道材料、管径和流体性质的条件下,计算流体在管路中的流动状态、压力损失以及流量等参数。
管路水力计算是实际工程中常见的问题,它可以帮助我们了解管道的输送性能和节能问题。
管道中的流体运动受到多个因素的影响,包括管道长度、管道粗糙度、流速、流量等。
在水力学计算中,一般常用的公式有达西公式和罗斯诺-魏谢巴赫公式。
达西公式可以用来计算管道中流体的摩阻损失,它的计算公式为:ΔP=λ(L/D)(v^2/2g)其中,ΔP为管道中的压力损失,L为管道长度,D为管道直径,v为流速,g为重力加速度,λ为摩阻系数,也称为达西摩阻系数。
罗斯诺-魏谢巴赫公式则可以用来计算管路中流体的水力损失,它的计算公式为:ΔP=ρ(h_f+h_m)其中,ΔP为管路中的总压力损失,ρ为流体密度,h_f为摩阻压力损失,也称为莫阿P(Moody)摩阻,h_m为各种表面或局部的附加压力损失。
除了达西公式和罗斯诺-魏谢巴赫公式,还有一些经验公式和图表可以用来计算管路的压力损失和流量。
这些公式和图表都是根据实验数据和经验总结得出的,可以帮助工程师在实际应用中进行快速计算。
管内流动和水力计算

2.紊流
流体质点运动彼此混杂、互相干扰,完全无 规则的流动状态。
3.上临界速度和下临界速度:
随着水流速度的增大,水流将由层流状态过渡到紊流状态。由
层流过渡到紊流的临界状态下的流体速度称为上临界速度,用
Vcr′表示。
当玻璃管内的水流已经是紊流运动,此时逐渐关小阀门K,使 水流速度逐渐减小,当水流速度减小到一定程度时,紊乱的红 色液体又将重新成为一条明晰的红色直线流,即紊流又转变为 层流。但是,由紊流转变为层流的临界速度比上临界速Vcr′更 低,称为下临界速度,用Vcr表示。
当Re>Recr,惯性力起主导作用,粘性力控制减弱, 不足以控制和约束外界扰动,惯性力将微小扰动不断 扩大,形成紊流。
第三节 管道进口段中粘性流体的流动
一、圆管内层流流动的起始段
d
L
层流边界层
充分发展的流动
紊流边界层
d
L
粘性底层
由于流体的粘性作用,自圆管入口起,在管壁附近形成一层 有速度梯度存在的流体薄层,该流体薄层内壁面上流体的速 度为零,薄层外边界上的流速为u (x)。这一有速度梯度存在 的流体层称为附面层或边界层。
说明
(1)当流体的流速超过上临界速度(V>Vcr′), 管内 水流一定是紊流状态;
(2)当流体的流速低于下临界速度时(V<Vcr) ,管 内水流一定是层流状态;
(3)当流体的流速介于上临界速度和下临界速度之间时 (Vcr<V<Vcr′),管内水流可能是层流,也可能是紊 流。如果流速是由小增大时,流动是层流,如果流速 是由大变小时,则流动是紊流。
实验表明,这两种情况下的流动状态都不稳定,并且取决于实验的起始
5.4--管路的水力计算

解(1)首先取两过流断面1—1和2—2,以右侧水面 为零基准面,在两断面之间建立伯努利方程,计算点 取在各断面的液面上,其压强均为大气压强,相对压 强为零
H1
hw
l d
v2 2g
( 进
b
出)
v2 2g
v 2.05m / s
q 16.1103 m3 / s 16.1L / s
(2)管道最高点A处的真空度为最大,在1—1段面和管 道A断面之间建立伯努利方程,并仍以左侧水面为零基准 面,有
H hw12
hf
l
hj
d
v2 2g
管中流速v
1
2gH
l
d
流量系数c
1
l
d
,流量Q
c A
2gH
自由出流
c
1
1
l d
进口+2 折角
Q A 2gH cΒιβλιοθήκη 淹没出流c 1
l d
进口+2 折角+出口
Q A 2gH c
淹没出流的流量系数与自由出流的流量系数 虽计算公式不同,但同一个管路系统的计算结果 相等。
c
4
0.4254 m2 / s
例2 水箱供水,l=20m,d=40mm,λ=0.03 ,总
局部水头损失系数为15。求流量Q=2.75L/s时的作 用水头H。
解:
v
Q
d2
2.75 103
0.042
2.188m / s
4
4
H
1
l d
v2 2g
(1 0.03 20 15) 2.1882 5.126m
损失系数:进口ζe=0.5 ,出口ζs=1.0 ,弯头1的 ζ1 =0.2。弯头2、3的ζ2 = ζ3 =0.4,弯头ζ4 =0.3,B点高出上游水面4.5m,试求流经虹吸管的
流体力学管路水力的计算
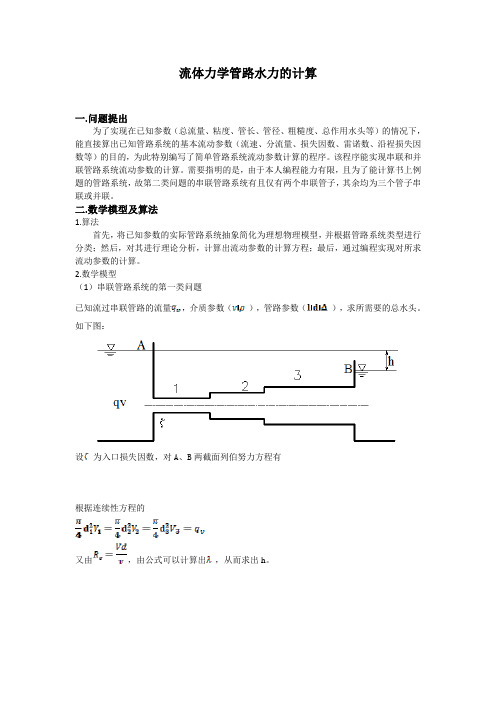
流体力学管路水力的计算一.问题提出为了实现在已知参数(总流量、粘度、管长、管径、粗糙度、总作用水头等)的情况下,能直接算出已知管路系统的基本流动参数(流速、分流量、损失因数、雷诺数、沿裎损失因数等)的目的,为此特别编写了简单管路系统流动参数计算的程序。
该程序能实现串联和并联管路系统流动参数的计算。
需要指明的是,由于本人编程能力有限,且为了能计算书上例题的管路系统,故第二类问题的串联管路系统有且仅有两个串联管子,其余均为三个管子串联或并联。
二.数学模型及算法1.算法首先,将已知参数的实际管路系统抽象简化为理想物理模型,并根据管路系统类型进行分类;然后,对其进行理论分析,计算出流动参数的计算方程;最后,通过编程实现对所求流动参数的计算。
2.数学模型(1)串联管路系统的第一类问题已知流过串联管路的流量,介质参数(),管路参数(),求所需要的总水头。
如下图:设为入口损失因数,对A、B两截面列伯努力方程有根据连续性方程的又由,由公式可以计算出,从而求出h。
(2)串联管路系统的第二类问题已知总水头h,介质参数(),管路参数(),求通过的流量如下图:设为入口损失因数,对A、B两截面列伯努力方程有根据连续性方程的由此可得又,,由公式可以计算出。
将算出的与所取得对比,若二者之差均满足所取得精度,则计算结束,否则令作为新的重新计算为止。
最终可得流量(3)并联管路系统的第一类问题已知两点间的压力降(即能量损失)h,介质参数(),管路参数(),求总流量如下图:先取const,(i=1,2,3,下同);由达西公式可求得所以由公式可以计算出,将算出的与所取得对比,若二者之差均满足所取得精度,则计算结束,否则令作为新的重新计算为止。
则(4)并联管路系统的第二类问题已知总流量,介质参数(),管路参数(),求各分支管路的流量及能量损失h如下图:根据经验,先取h=const;由此h值根据并联管路第一类问题计算出各分支管路的流量(i=1,2,3,下同);则蒋总流量按如下分配用计算出的流量,结合公式、,可以计算出,从而求出;若中任两个之差满足给定精度,则h为所求值,否则令h=,从头重新计算,直到满足精度为止。
水力计算公式选用

水力计算公式选用水力计算是指利用水的流动性质进行流量、压力和速度等相关参数的计算。
在水力学中,常用的水力计算公式主要有流量计算公式、速度计算公式和压力计算公式。
下面将介绍几种常用的水力计算公式。
一、流量计算公式:1.泊松公式:流量计算公式是通过测定流速和截面积的方式来计算流量。
泊松公式是最常用的流量计算公式之一,其公式为:Q=A×v其中,Q为流量,A为流体通过的截面积,v为流速。
2.管道流量公式:当涉及到管道流量计算时,可以使用伯努利公式来计算流量,伯努利公式为:Q=π×r²×v其中,Q为流量,r为管道的半径,v为流速。
3.梯形槽流量公式:当涉及到梯形槽流量计算时,可以使用曼宁公式来计算流量,曼宁公式为:Q=(1.49/A)×R^(2/3)×S^(1/2)其中,Q为流量,A为梯形槽的横截面积,R为梯形槽湿周和横截面积之比,S为梯形槽的比降,1.49为曼宁系数。
二、速度计算公式:1.波速计算公式:在涉及到波浪速度计算时,可以使用波速公式进行计算,波速公式的一般形式为:c=λ×f其中,c为波速,λ为波长,f为频率。
2.重力加速度和液体高度差计算公式:当涉及到重力加速度和液体高度差计算时,可以使用水头计算公式,水头计算公式的一般形式为:H=v²/2g+z其中,H为水头,v为速度,g为重力加速度,z为液体的高度。
三、压力计算公式:1.应力计算公式:当涉及到液体对物体的压力计算时,可以使用应力计算公式,应力计算公式的一般形式为:P=F/A其中,P为压力,F为受力大小,A为受力的面积。
2.流体静压力计算公式:当涉及到流体的静压力计算时,可以使用静压力计算公式,静压力计算公式的一般形式为:P=ρ×g×h其中,P为压力,ρ为流体密度,g为重力加速度,h为液体的高度。
以上是一些常用的水力计算公式,可以根据不同的情况和具体要求选择合适的公式进行计算。
管路的水力计算

为保证虹吸管能通过设计流量,工程上一般限制管中最 大允许的真空度为[hv]=7~8.5m。
.
[例1] 如图所示虹吸管,通过虹吸作用将左侧水流引向下游。 已知虹吸管管径d=100mm,H1=2.5m,H2=3.7m,l1=5m,l2=5m。 管道沿程损失因素λ=0.025,进口设有滤网,其局部损失因 素ζe=8,弯头阻力因素ζb=0.15。试求: (1) 通过虹吸管流量; (2) 计算虹吸管最高处A点的真空度。
.
解(1)首先取两过流断面1—1和2—2,以右侧水面 为零基准面,在两断面之间建立伯努利方程,计算点 取在各断面的液面上,其压强均为大气压强,相对压 强为零
H1
hw
l d
v2 2g
( 进
b
出)
v2 2g
v 2.05m / s
q 16.1103 m3 / s 16.1L / s
.
(2)管道最高点A处的真空度为最大,在1—1段面和管 道A断面之间建立伯努利方程,并仍以左侧水面为零基准 面,有
H1
pa
g
(H1
H2)
pA
g
v2 2g
( 进
b
l1 ) d
v2 2g
pa pA
g
H2
(1 进
b
l1 ) d
v2 2g
pv pa pA 5.93m
.
短管水力计算的问题
例1 已知短管l=200m,d=400mm,H=10m,相同
的两个弯头局部水头损失系数为0.25,闸门全开的
《管道的水力计算》课件

日常工作中需要注意管道流量、阻力和维护等问题,确保系统正常运行。
3 管道水力计算的应用前景
在工程建设、水资源管理和环境保护等领域具有广阔的应用前景。
ቤተ መጻሕፍቲ ባይዱ
3
管道保养的注意事项
4
保养时需要注意使用正确的材料和方法, 遵守相关规定和标准。
维护工作的必要性
管道的维护可以保证管道系统的正常运 行和延长使用寿命。
管道的保养措施
保养包括防锈、防腐、除垢、消毒等措 施,可以延缓管道老化和减少故障。
总结
1 管道水力计算知识的重要性
掌握管道水力计算知识可以提高工作效率和减少系统故障。
《管道的水力计算》PPT 课件
# 管道的水力计算
管道流量的计算
1
流量的定义
流量是单位时间内通过管道的液体或气
流速与断面积的关系
2
体的体积。
流速是单位时间内通过断面的液体或气
体的体积,与断面积成反比。
3
流量计算公式
流量(Q)= 流速(V)× 断面积(A)
实际管道流量实例
4
通过实例计算管道流量,考虑测量误差 和流体性质变化。
泥沙径流的特点
泥沙径流是带有泥沙的水流,通过计算降雨量和土 壤侵蚀来估算泥沙径流。
泥沙径流计算公式
泥沙径流(Qs)= 雨量(P)× 土壤侵蚀量(E)
径流计算实例
通过实例计算管道的径流,考虑降雨强度和土壤类 型。
管道的维护与保养
1
管道维护的注意事项
2
维护时需要注意安全、定期检查和清洁、
修复漏水等问题。
管道阻力的计算
阻力的定义
阻力是管道内液体或气体流动时受到的阻碍力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,不能在总管路与支管 之间列方程 ,应对某一分支 列(按并联)。如2、3、4线
h h f1 h f2 h f7 h f3
hf 6 hf 7 hf 8 , hf 8 hf 2 hf 4 hf 4 hf 3
qv2 qv3 qv4 qv7 qv2 qv5
V1 0,
p1 p2 pa
hw
由于等径,连续,V不变,
2 V2 h
2g
lV V hw i i 2dg 2g 2 li V2 ( i i ) d 2g 2 li V h (1 i i ) d 2g li 令 s i i d
h
l
称单位长度作用水头,称水力坡度。
K相当于水力坡度为1时的流量。
K f d ,
由于流动为阻力平方区。
f 故
在一般工程手册上可以查到 K f d
K f , d
通常 一定。
第三节
串联管路的计算
因各段管路均按长管计算,只有沿程损失,故
q h fi l K
2
2 i 2
2 2
16qv 1 V h (1 s ) (1 s ) 2 4 2g d 2g qv 2 或 h 0.0827(1 s ) 4 d
2
s 包括管路入口、转弯、阀门阻力和沿程。
若流入大容器,作用水头h为二液面高度差, 阻力应加上出口阻力。 若不等径,只需将各处阻力系数(包括沿 程)换算至同一速度。
内部流量为qv2 , qv3 , qv4
并联特点:(1)阻力相等
h f 2 h f3 h f 4
q l K
2 vi i 2 i
i=2、3、4
(2)流量 :在支线上分流
qv1 qv2 qv3 qv4 qv5
第五节 枝状管路的水力计算
h fi q l K
2 vi i 2 i
第十章
• 短管水力计算
管路水力计算
• 简单长管的水力计算
• 串联管路的计算
• 并联长管的水力计算
• 枝状管路的水力计算
• 环状管路的水力计算
• 均匀泄流的水力计算
• 有压管路的水击
本章是应用能量方程和阻力计算来确定流速、 流量,或已知管径、流量,确定阻力,即qv、 Δp。工程中,一般是设计时,qv已知,预知 结构,计算Δp阻力。选择机械如泵、风机。 在计算中,要用到连续方程,动量方程, 能量方程,阻力计算公式。
l 1 0.0827l 以qv为例 : h 2 d 2 2g d d 4
或
l 1 h l d d 2g g d K 8
2 16qv 2 4 2 qv 2 5 2 lqv 2
2 qv
2 qv 5
K
gd 8
5
为流量模数
m s
3
h qv K l
h li
(1)
2 Ki
当有泄漏时,
qi 0
qi 1 qi qvi
可列(i-1)个方程,与(1)式联立可解。
第四节 并联长管的水力计算
qv 2 ,l2 , d 2
qv1 ,l1 , d1
A
qv3 ,l3 , d3 qv 4 ,l4 , d 4
qv 5 ,l5 , d 5
B
分流前流量为qv1,合流后为qv5
限制:恒定流,设α=1。
1、几个概念:
(1)管路系统:构成流体流动限制,并保 证流体流动畅通的管件组合,简称管路。 按能量损失型式将管路分为长管和短管: (2)长管 :凡局部损失和出流速度水头 之和与管路的沿程阻力的和比较小,一般 小于5%,这样的管路称长管或水力长管。 长管只计算沿程损失而忽略局阻损失和出 流速度头。是工程上的简化。
第二节
简单长管的水力计算
以等径水平长管为例:
L d
h
p1 V 1 p2 V 2 hw 列能量方程: h g 2 g g 2 g
2 V2 h
2
2
2
l 2g d 2g
2 V2
V2 长管出流 : 0 2g 2 lV ∴ h hw d 2g
即全部能头h被阻力消耗。
(3)短管:各项损失和出流速度头均需 计及的管路,也称水力短管。 管路也可按结构分为简单管路和复杂管路: (4)简单管路:等径,无分支。 (5)复杂管路:简单管路以外的管路,即 不等径,或有分支或二者兼之。 (a)串联管路:首尾相连管径不同,无分支 的管路。 (b)并联管路:有分支,但有共同的汇合和 起始点。
供液水头H(自身流动) (2)已知L、d,H或允许Δp,求qv (3)已知qv 、H、L,确定d 前两种为校核计算,后一种为设计计算
第一节 短管水力计算
以等径管路为例,说明计算方法。
1 1
(h)
hቤተ መጻሕፍቲ ባይዱ
2
0
2
V2
0
假设液体自管端流入大气,即自由出流。 以0—0为基准,对自由液面1—1和出流断 面2—2列能量方程 p1 V12 p2 V22 h hw g 2g g 2g
(c)枝状管路:枝状管路起始点不同, 而汇合点相同。 (d)网状管路:起始和汇合均不同的 不规则管路。
2、设计管路的目的
尽量减少动消耗,即能耗,节约能源,节约 原材料,降低成本。 为达到上述目的,需计算确定qv,尺寸(L、 d),损失Δp。
3、设计方法
(1)已知qv和L、d,求Δp(外力流动)或
qv1 qv7 qv6
第六节 环状管路的水力计算
通常网络布局已知。即各管的长度 li 已知, qvi 已知,求各管段的流量和设计各管的 直径d 。如图。
各节点,根据连续性, 流入qvi=流出qvo
若以流入为正,流出 为负则节点方程:
qvi 0
按阻力:两节点间阻力相等。若已顺时针为 正,逆时针为负,则节点间。 计算时一般采用逼近方法,即予先取,分配 流量及流向,选择管径,求各段阻力,验证, 否则重分配流量。一般是管路长,流量大。 阻力小,流量小。
2 v 2 i i
h
l1 , d1
l2 , d 2
l3 , d3
qv1
qv 2
在无泄漏时:
qi qv
h h fi
(忽略出流速度头)
2 l1 qv 2 K 1
2 h qv
2 li 2 Ki
li 2 2 K2 Ki l2
qv
