qualitative theory of dynamical systems的tex模板
DYNAMICAL SYSTEMS, STABILITY, AND CHAOS

In this expository and resources chapter we review selected aspects of the mathematics of dynamical systems, stability, and chaos, within a historical framework that draws together two threads of its early development: celestial mechanics and control theory, and focussing on qualitative theory. From this perspective we show how concepts of stability enable us to classify dynamical equations and their solutions and connect the key issues of nonlinearity, bifurcation, control, and uncertainty that are common to time-dependent problems in natural and engineered systems. We discuss stability and bifurcations in three simple model problems, and conclude with a survey of recent extensions of stability theory to complex networks.
a The
Greek word for governor is kubernetes, from which the mathematician Norbert Wiener (1894–1964) coined the term cybernetics as a name for the collective field of automated control and information theory.
应用数学SCI期刊排名

67
SCIENCES
MATHEMATICS AND COMPUTERS IN
68
SIMULATION
INTERNATIONAL JOURNAL OF COMPUTER
69
MATHEMATICS
NONLINEAR ANALYSIS-THEORY METHODS &
70
APPLICATIONS
71
Journal of Applied Analysis and Computation
JOURNAL OF COMPUTATIONAL AND APPLIED
43
MATHEMATICS
APPLIED MATHEMATICS AND MECHANICS-
44
ENGLISH EDITION
45
INVERSE PROBLEMS
46
APPLIED NUMERICAL MATHEMATICS
9,060 2,147 12,329
0.008660 0.005070 0.017780 0.001960 0.012640 0.016660 0.041770 0.020120 0.000760 0.008740 0.000900 0.004490 0.002400 0.009950 0.004570 0.015210 0.019680 0.001340 0.015760 0.013550 0.002100 0.006410 0.007300 0.007490 0.018340 0.002950 0.000890 0.010070 0.000900 0.006910 0.001820 0.016410 0.004000 0.015090 0.016100 0.004330 0.007850 0.012280 0.007550 0.000920 0.008740 0.003890 0.020410 0.002440 0.009630 0.005990
上海交通大学数学科学学院2018年博士生导师及招生专业和
几何力学、哈密尔顿动力学 Geometric Mechanics ; Hamiltonian Dynamics
复分析与动力系统(多变量复分析与复动
Feng RONG /
Professor
基础数学 Pure Mathematics
分方程定性理论)Complex Analysis and Dynamical Systems (Complex Analysis and Dynamics in Several Variables; Qualitative Theory of
Ordinary Differential Equations)
唐敏 / 特别研究员
应用数学
23
Min TANG /Special
Applied Mathematics
Researcher
计算数学和生物数学(输运方程,反应扩散方程的数值 求解和生物建模)Computatioal Mathematics and Mathematical Biology(Transport Equations and Reaction Diffusion Equations, Their Numerical Schemes and Biology Modeling)
金融数学和概率统计、随机控制 Mathematical Finance and Probability Theory and Statistics; Stochastic Controls
Tudor Stefan RATIU
基础数学
21
/讲席教授
Pure Mathematics
Chair Professor
Applied Mathematics
Professor
Differential equation
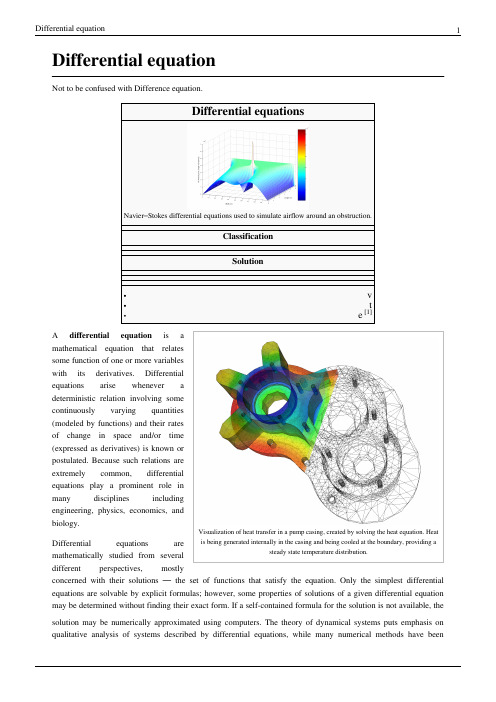
Differential equationNot to be confused with Difference equation.Stokes differential equations used to simulate airflow around an obstruction.ClassificationSolutionVisualization of heat transfer in a pump casing, created by solving the heat equation. Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution.A differential equation is amathematical equation that relatessome function of one or more variableswith its derivatives. Differentialequations arise whenever adeterministic relation involving somecontinuously varying quantities(modeled by functions) and their ratesof change in space and/or time(expressed as derivatives) is known orpostulated. Because such relations areextremely common, differentialequations play a prominent role inmany disciplines includingengineering, physics, economics, andbiology.Differential equations aremathematically studied from severaldifferent perspectives, mostlyconcerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form. If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have beendeveloped to determine solutions with a given degree of accuracy.ExampleFor example, in classical mechanics, the motion of a body is described by its position and velocity as the time value varies. Newton's laws allow one (given the position, velocity, acceleration and various forces acting on the body) to express these variables dynamically as a differential equation for the unknown position of the body as a function of time.In some cases, this differential equation (called an equation of motion) may be solved explicitly.An example of modelling a real world problem using differential equations is the determination of the velocity of a ball falling through the air, considering only gravity and air resistance. The ball's acceleration towards the ground is the acceleration due to gravity minus the acceleration due to air resistance. Gravity is considered constant, and air resistance may be modeled as proportional to the ball's velocity. This means that the ball's acceleration, which is a derivative of its velocity, depends on the velocity (and the velocity depends on time). Finding the velocity as a function of time involves solving a differential equation and verifying its validity.Directions of studyThe study of differential equations is a wide field in pure and applied mathematics, physics, and engineering. All of these disciplines are concerned with the properties of differential equations of various types. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of the methods for approximating solutions. Differential equations play an important role in modelling virtually every physical, technical, or biological process, from celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems may not necessarily be directly solvable, i.e. do not have closed form solutions. Instead, solutions can be approximated using numerical methods.Mathematicians also study weak solutions (relying on weak derivatives), which are types of solutions that do not have to be differentiable everywhere. This extension is often necessary for solutions to exist.The study of the stability of solutions of differential equations is known as stability theory.NomenclatureThe theory of differential equations is well developed and the methods used to study them vary significantly with the type of the equation.Ordinary and partial•An ordinary differential equation (ODE) is a differential equation in which the unknown function (also known as the dependent variable) is a function of a single independent variable. In the simplest form, the unknown function is a real or complex valued function, but more generally, it may be vector-valued or matrix-valued: this corresponds to considering a system of ordinary differential equations for a single function.Ordinary differential equations are further classified according to the order of the highest derivative of the dependent variable with respect to the independent variable appearing in the equation. The most important cases for applications are first-order and second-order differential equations. For example, Bessel's differential equation(in which y is the dependent variable) is a second-order differential equation. In the classical literature a distinction is also made between differential equations explicitly solved with respect to the highest derivative and differential equations in an implicit form. Also important is the degree, or (highest) power, of the highest derivative(s) in the equation (cf. : degree of a polynomial). A differential equation is called a nonlinear differential equation if its degree is not one (a sufficient but unnecessary condition).• A partial differential equation (PDE) is a differential equation in which the unknown function is a function of multiple independent variables and the equation involves its partial derivatives. The order is defined similarly to the case of ordinary differential equations, but further classification into elliptic, hyperbolic, and parabolic equations, especially for second-order linear equations, is of utmost importance. Some partial differentialequations do not fall into any of these categories over the whole domain of the independent variables and they are said to be of mixed type.Linear and non-linearBoth ordinary and partial differential equations are broadly classified as linear and nonlinear.• A differential equation is linear if the unknown function and its derivatives appear to the power 1 (products of the unknown function and its derivatives are not allowed) and nonlinear otherwise. The characteristic property of linear equations is that their solutions form an affine subspace of an appropriate function space, which results in much more developed theory of linear differential equations. Homogeneous linear differential equations are a further subclass for which the space of solutions is a linear subspace i.e. the sum of any set of solutions or multiples of solutions is also a solution. The coefficients of the unknown function and its derivatives in a linear differential equation are allowed to be (known) functions of the independent variable or variables; if these coefficients are constants then one speaks of a constant coefficient linear differential equation.•There are very few methods of solving nonlinear differential equations exactly; those that are known typically depend on the equation having particular symmetries. Nonlinear differential equations can exhibit verycomplicated behavior over extended time intervals, characteristic of chaos. Even the fundamental questions of existence, uniqueness, and extendability of solutions for nonlinear differential equations, and well-posedness of initial and boundary value problems for nonlinear PDEs are hard problems and their resolution in special cases is considered to be a significant advance in the mathematical theory (cf. Navier–Stokes existence and smoothness).However, if the differential equation is a correctly formulated representation of a meaningful physical process, then one expects it to have a solution.Linear differential equations frequently appear as approximations to nonlinear equations. These approximations are only valid under restricted conditions. For example, the harmonic oscillator equation is an approximation to the nonlinear pendulum equation that is valid for small amplitude oscillations (see below).ExamplesIn the first group of examples, let u be an unknown function of x, and c and ω are known constants.•Inhomogeneous first-order linear constant coefficient ordinary differential equation:•Homogeneous second-order linear ordinary differential equation:•Homogeneous second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:•Inhomogeneous first-order nonlinear ordinary differential equation:•Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:In the next group of examples, the unknown function u depends on two variables x and t or x and y.•Homogeneous first-order linear partial differential equation:•Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:•Third-order nonlinear partial differential equation, the Korteweg–de Vries equation:Related concepts• A delay differential equation (DDE) is an equation for a function of a single variable, usually called time, in which the derivative of the function at a certain time is given in terms of the values of the function at earlier times.• A stochastic differential equation (SDE) is an equation in which the unknown quantity is a stochastic process and the equation involves some known stochastic processes, for example, the Wiener process in the case of diffusion equations.• A differential algebraic equation (DAE) is a differential equation comprising differential and algebraic terms, given in implicit form.Connection to difference equationsSee also: Time scale calculusThe theory of differential equations is closely related to the theory of difference equations, in which the coordinates assume only discrete values, and the relationship involves values of the unknown function or functions and values at nearby coordinates. Many methods to compute numerical solutions of differential equations or study the properties of differential equations involve approximation of the solution of a differential equation by the solution of a corresponding difference equation.Universality of mathematical descriptionMany fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics, differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed together with the sciences where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second-order partial differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat, the theory of which was developed by Joseph Fourier, is governed by another second-order partial differential equation, the heat equation. It turns out that many diffusion processes, while seemingly different, are described by the same equation; the Black–Scholes equation in finance is, for instance, related to the heat equation.Notable differential equationsPhysics and engineering•Newton's Second Law in dynamics (mechanics)•Euler–Lagrange equation in classical mechanics•Hamilton's equations in classical mechanics•Radioactive decay in nuclear physics•Newton's law of cooling in thermodynamics•The wave equation•Maxwell's equations in electromagnetism•The heat equation in thermodynamics•Laplace's equation, which defines harmonic functions•Poisson's equation•Einstein's field equation in general relativity•The Schrödinger equation in quantum mechanics•The geodesic equation•The Navier–Stokes equations in fluid dynamics•The Diffusion equation in stochastic processes•The Convection–diffusion equation in fluid dynamics•The Cauchy–Riemann equations in complex analysis•The Poisson–Boltzmann equation in molecular dynamics•The shallow water equations•Universal differential equation•The Lorenz equations whose solutions exhibit chaotic flow.Biology•Verhulst equation – biological population growth•von Bertalanffy model – biological individual growth•Lotka–Volterra equations – biological population dynamics•Replicator dynamics – found in theoretical biology•Hodgkin–Huxley model – neural action potentialsEconomics•The Black–Scholes PDE•Exogenous growth model•Malthusian growth model•The Vidale–Wolfe advertising modelReferences•P. Abbott and H. Neill, Teach Yourself Calculus, 2003 pages 266-277•P. Blanchard, R. L. Devaney, G. R. Hall, Differential Equations, Thompson, 2006• E. A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955• E. L. Ince, Ordinary Differential Equations, Dover Publications, 1956•W. Johnson, A Treatise on Ordinary and Partial Differential Equations[2], John Wiley and Sons, 1913, in University of Michigan Historical Math Collection [3]• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.•R. I. Porter, Further Elementary Analysis, 1978, chapter XIX Differential Equations•Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems[4]. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.[1]/w/index.php?title=Template:Differential_equations&action=edit[2]/cgi/b/bib/bibperm?q1=abv5010.0001.001[3]/u/umhistmath/[4]http://www.mat.univie.ac.at/~gerald/ftp/book-ode/External links•Lectures on Differential Equations (/courses/mathematics/18-03-differential-equations-spring-2010/video-lectures/) MIT Open CourseWare Videos•Online Notes / Differential Equations (/classes/de/de.aspx) Paul Dawkins, Lamar University•Differential Equations (/diffeq/diffeq.html), S.O.S. Mathematics•Differential Equation Solver (/tools/differential_equation_solver/) Java applet tool used to solve differential equations.•Introduction to modeling via differential equations (/mat/u-u/en/ differential_equations_intro.htm) Introduction to modeling by means of differential equations, with critical remarks.•Mathematical Assistant on Web (http://user.mendelu.cz/marik/maw/index.php?lang=en&form=ode) Symbolic ODE tool, using Maxima•Exact Solutions of Ordinary Differential Equations (http://eqworld.ipmnet.ru/en/solutions/ode.htm)•Collection of ODE and DAE models of physical systems (/research/models.htm) MATLAB models•Notes on Diffy Qs: Differential Equations for Engineers (/diffyqs/) An introductory textbook on differential equations by Jiri Lebl of UIUC•Khan Academy Video playlist on differential equations (/math/ differential-equations) Topics covered in a first year course in differential equations.•MathDiscuss Video playlist on differential equations (/category/courses/ solutions-differential-equations/homogeneous-linear-systems/)Article Sources and Contributors8Article Sources and ContributorsDifferential equation Source: /w/index.php?oldid=610771276 Contributors: 17Drew, After Midnight, Ahoerstemeier, Alarius, Alfred Centauri, Amahoney, AndreiPolyanin, Andres, AndrewHowse, Andycjp, Andytalk, AngryPhillip, Anonymous Dissident, Antoni Barau, Antonius Block, Anupam, Apmonitor, Arcfrk, Asdf39, Asyndeton, Attilios,Babayagagypsies, Baccala@, Baccyak4H, Bejohns6, Bento00, Berland, Bidabadi, Bigusbry, BillyPreset, Bob.v.R, Bolatbek, Brandon, Bryanmcdonald, Btyner, Bygeorge2512,Callumds, Charles Matthews, Christian75, Chtito, Cispyre, Cmprince, Coginsys, ConMan, Cxz111, Cybercobra, DAJF, Danski14, Dbroadwell, Ddxc, Delaszk, DerHexer, Dewritech, Difu Wu, Djordjes, DominiqueNC, Donludwig, Dpv, Dr sarah madden, Drmies, DroEsperanto, Duoduoduo, Dysprosia, EconoPhysicist, Elwikipedista, Epicgenius, EricBright, Erin.Annette.Brown,Estudiarme, F=q(E+v^B), Fintor, Fioravante Patrone, Fioravante Patrone en, Flameturtle, Friend of the Facts, FutureTrillionaire, Gabrielleitao, Gandalf61, Gauss, Genedronek, Geni, Giftlite,GoingBatty, Gombang, Grenavitar, Haham hanuka, Hamiltondaniel, Harry, Haruth, Haseeb Jamal, Heikki m, Holmes1900, Ilya Voyager, Iquseruniv, Iulianu, Izodman2012, J arino, J.delanoy, Ja 62, Jak86, JamesBWatson, Jao, Jarble, Jauhienij, Jayden54, Jeancey, Jersey Devil, Jim Sukwutput, Jim.belk, Jim.henderson, JinJian, Jitse Niesen, JohnOwens, Johndoeisnotmyname, JorisvS,Julesd, K-UNIT, Kayvan45622, KeithJonsn, Kensaii, Khalid Mahmood, Klaas van Aarsen, Kr5t, Krushia, LOL, Lambiam, Lavateraguy, Lethe, LibLord, Linas, Lumos3, Madmath789, Mandarax, Mankarse, MarSch, Martastic, Martynas Patasius, Maschen, Math.geek3.1415926, Matqkks, Mattmnelson, Maurice Carbonaro, Maxis ftw, Mazi, McVities, Mduench, Mets501, Mh, MichaelHardy, Mindspillage, MisterSheik, Mohan1986, Mossaiby, Mpatel, MrOllie, Mtness, Mysidia, Nik-renshaw, Nkayesmith, Norm mit, Okopecz, Oleg Alexandrov, Opelio, Pahio, Parusaro, Paul August, Paul Matthews, Paul Richter, PavelSolin, Pgk, Phoebe, Pine, Pinethicket, Pratyya Ghosh, PseudoSudo, Qwerty Binary, Qzd800, R'n'B, Rama's Arrow, Randomguess, Reallybored999, RexNL, Reyk, RichMorin, Robin S, Romansanders, Rosasco, Ruakh, SDC, SFC9394, SakeUPenn, Salix alba, Sam Staton, Sampathsris, Sardanaphalus, Senoreuchrestud, Silly rabbit, Siroxo,Skakkle, Skypher, SmartPatrol, Snowjeep, Spirits in the Material, Starwiz, Suffusion of Yellow, Sverdrup, Symane, TVBZ28, TYelliot, Tannkrem, Tbhotch, Tbsmith, TexasAndroid, Tgeairn, The Hybrid, The Thing That Should Not Be, Timelesseyes, Tranum1234567890, Tsirel, Tuseroni, User A1, Vanished User 0001, Vishwanathnm, Vthiru, Waffleguy4, Waldir, Waltpohl, Wavelength, Wclxlus, Wihenao, Willtron, Winterheart, Wsears, XJaM, Yafujifide, Zepterfd, ﺪﺟﺎﺳ ﺪﺠﻣﺍ ﺪﺟﺎﺳ, 363 anonymous editsImage Sources, Licenses and ContributorsFile:Airflow-Obstructed-Duct.png Source: /w/index.php?title=File:Airflow-Obstructed-Duct.png License: Public Domain Contributors: Original uploader was User A1 at en.wikipediaFile:Elmer-pump-heatequation.png Source: /w/index.php?title=File:Elmer-pump-heatequation.png License: Creative Commons Attribution-Sharealike 3.0Contributors: Christian1985, Crimerob, Kri, User A1, 2 anonymous editsLicenseCreative Commons Attribution-Share Alike 3.0///licenses/by-sa/3.0/。
常微分方程中的英文单词和短语

常微分方程
Ordinary Differential Equtions
第一章 基本概念
Chapter 1 Basic Concepts
常微分方 程
阶 线性 非线性 偏微分方 程
通解 特解 初值条件 初值问题 柯西问题 几何解释 积分曲线 线素 线素场 方向场 等斜线 对称形式 奇异点 通积分
boundary finite closed interval open set finite semi-open interval
Lagrange formula
l ocal finite covering theorem
bar area monotone decreasing sectorial area comparability solution minimum solution maximum solution sl ope
topological dynamical system
differential dynamical system
stability of solution Liapunov stability
asymptotic stability asymptotic stability field attraction domain globe asymptotic stability
第六章 线 性 微 分 方 程 组
Chapter 6 Linear Differential Equations
存在和唯一 性定理 齐次线性微 分方程组 基本解组 朗斯基行列 式 刘维尔公 式 解矩阵 基解矩阵 常数矩阵 非齐次线性 微分方程 组 常数列向 量 常数变异公 式 计算公式 结构公式 常系数线性 微分方程 组 矩阵指数函 数 标准基解矩 阵 若尔当标准 型 矩阵函数 实值解 复值解 代数余子 式 特征方程 算子式 算子多项 式 拉普拉斯逆 变换
国际关系英语专业术语(较完整)

缓冲国buffer state治国术statecraftcomprehensive power 综合国力双重国籍dual nationality东道国host country附庸国vassal stateprotectorate 保护国战败国 a defeated country卫星国satellite state战胜国 victorious nation中立国neutrality stated, neutral country永久中立国neutralized statedAxis Powers 轴心国不结盟国家nonaligned state缔约国 signatory state of the treaty (convention) hegemonic state霸权国策源国政治学political science比较政治学comparative politics低级政治low politics高级政治high politics规模政治politics of scaleRealpolitik 现实政治官僚政治bureaucratic politics政治地理political geography政治化politicization政治精神心理学 political psychophysiology生态政治学ecopolitics政治精英political elitezero-sum game 零和游戏nonzero-sum game 非零和游戏game theory 博弈论two-level game or two-tier game双层博弈 paradigm 范式本土化localization不可逆转性irreversibilityconvention 常规解构deconstructionbalance of power 均势联系协定association agreementexclusivity排他性批判理论critique theoriesequilibrium 平衡globalization全球化identity 认同或特性外溢spill-overrelative gain相对收益absolute gain 绝对收益相互依赖interdependence效忠转移loyalty-transferring边际成本marginal costpublic domain 公共领域公共选择理论public choice theory国家间交易成本 interstate transaction cost交易收益transaction benefit利益集团interests group囚徒困境prisoner’s dilemma权利让渡transferring rightsanarchy 无政府状态constitutionalism宪政信息不对称 asymmetric information定量分析quantitative analysis定性分析qualitative analysis交流理论transactionism复合相互依赖 complex interdependencecase study 个案研究理论体系theoretical framework辩证法dialectical method世界体系理论world system theoryalienation 异化物竞天择natural selectionpagan 异教徒证伪falsificationappeasement 绥靖不对称战略 asymmetrical strategy代议制政府 representative forms of government dependency theory 依附理论电讯革命 telecommunications revolution遏制政策containment policy反主流文化counterculture非西方化dewesternization非线性nonlinearity功利主义哲学utilitarian philosophysupply-side economics供应学派经济学理性行为体模型rational actor model古典自由主义学派classical liberal schooldecentralization分散化乌托邦理论utopian theorynormative theory 规范理论value judgment 价值判断阶级斗争class strugglemirror image 镜像比较研究comparative study控制论cybernetic theory; cyberneticspredictability可预测性跨文化比较分析cross-cultural comparative analysis边缘化marginalization确保摧毁assured destruction知识产权intellectual property同质文明[,hɔmə'dʒi:niəs, ,həu-] homogeneous civilizationhomogenization 同质化Heterogeneou 异质化[,hetərəu'dʒi:njəs]futurology 未来学文明的冲突clash of civilizationstheoretical foundation理论基础grand theory 大理论信息革命information revolution意识形态冲突ideological conflictbarbarism 野蛮状态lobbying 游说nonwhite people 有色人种metaphysics 形而上学长周期理论long-circle theoryresource theory资源理论autonomous 自治case study 案例研究cyclical theory周期理论共同观念shared ideas全球治理global governancethe nature of man人性认知心理学cognitive psychologycivil society市民社会ideology 意识形态智囊团brain trustbandwagon 搭便车autarky 自给自足, 闭关自守democratization民主化宪政民主constitutional democracy当代史方法current history approachend of history历史终结社会化socialization自我实现的预言self-fulfilling prophecy结构性暴力structural violence适者生存survival of the fittestxenophobia 仇外, 排外ontology 本体论Copenhagen School 哥本哈根学派结构二重性duality of structure内化internalization制度化institutionalization世俗化secularizationthink tank 思想库public goods 公共物品非关税壁垒non-tariff barrier非正式协议informal agreement关税减让tariffs reduction关税同盟Tariffs Union互惠reciprocityGreat Depression 大萧条Industrial Revolution工业革命工业时代Industrial Age反托拉斯法antitrust law工业化industrialization股票市场崩溃stock market clash浮动汇率floating exchange rate固定汇率fixed exchange rate外汇汇率currency exchange rategold standard金本位金融机构financial institutioneconomic determinism 经济决定论economic globalization经济全球化economic sanction 经济制裁经济周期economic circletransnational corporation, multinational corporation跨国公司 money laundering 洗钱能源危机energy crisisUruguay Round 乌拉圭回合剩余价值surplus value贸易平衡balance of trade贸易赤字trade deficit公债treasury bond中央银行central bankfree market system自由市场体系城市化urbanizationeconomic growth 经济增长可持续发展 sustainable development customs union 关税同盟emerging market 新兴市场滞胀stagflationnondiscrimination非歧视原则非关税壁垒 nontariff barriers (NTBs) package deal 一揽子交易市场失灵market failurebourgeoisie 资产阶级民族自决 national self-determination民族解放 national liberation种族问题racial issue民族身份ethnic identity种族冲突ethnic conflictgeopolitics地缘政治sea power 海权land power 陆权air power 空权Balkan 巴尔干Age of Exploration地理大发现时代 Geoeconomics 地缘经济学 Indochina 印度支那Formosa 福摩萨Pacific Rim 环太平洋地区 heartland 大陆心脏Latin American 拉丁美洲马六甲海峡Strait of Malacca大陆国家 continental countryKashmir 克什米尔地理位置 geographic locationSerbia 塞尔维亚破碎地带shatterbeltNetherlands 尼德兰Eurasia 欧亚大陆lebensraum 生存空间中心-边缘模式core-periphery modelGlobal North 北方世界Global South 南方世界人名Karl W. Deutsch 卡尔•多伊奇Francis Fukuyama 弗朗西斯•福山Hans J. Morgenthau 汉斯•摩根索Jean Monnet 让•莫内Joseph S. Nye 约瑟夫•奈Kenneth N. Waltz 肯尼思•沃尔兹Hugo Grotius 雨果•格劳秀斯Jean Bodin 让•博丹William Olson 威廉•奥尔森John Ikenberry 约翰•伊肯伯里Harold Nicolson 哈罗德•尼科尔森 《外交学》弗朗切斯科•圭恰迪尼 《意大利史》 Francesco GuicciardiniThomas Hobbes 托马斯•霍布斯Henry Kissinger 亨利•基辛格Robert Gilpin 罗伯特•吉尔平Arnord Wolfers 阿诺德•沃尔弗斯Edward Karl 爱德华•卡尔彼得•卡赞斯坦Peter KatzensteinGeorge Kennan 乔治•凯南Stephen Krasner 史蒂芬•克拉斯纳Paul Kennedy 保罗•肯尼迪John Ruggie 约翰•鲁杰Niccol Machiavelli马基雅维利John Mearsheirmer 约翰•米尔斯海默Adam Smith 亚当•斯密David A. Baldwin 大卫•鲍德温Thucydides 修昔底德Raymond Aron 雷蒙•阿隆Stephen Walt 斯蒂芬•沃尔特Martin Wight 马丁•怀特Max Weber 马克斯•韦伯(德国社会学家)Alexander Wendt 亚历山大•温特Brace Russett 布鲁斯•拉西特伊曼纽尔•沃勒斯坦Immanuel Wallerstein让•雅克•卢梭Jean-Jaques Rousseau欧内斯特•萨道义爵士 《外交实践指南》 Sir Ernest SatowJohn Locke 约翰•洛克Jeremy Bentham 杰里米•边沁France Bacon 弗朗西斯•培根Hedley Bull 赫德利•布尔赫伯特•巴特菲尔德Herbert ButterfieldGeorge Canning 乔治•坎宁Socrates 苏格拉底Plato 柏拉图本尼迪克特•德•斯宾诺莎Benedict de SpinozaDante 但丁Lassa Oppenheim 拉萨•奥本海约瑟夫•A•熊彼特Joseph A. SchumpeterHans Kelsen 汉斯•凯尔森Voltaire 伏尔泰Montesquieu 孟德斯鸠John Courtney Murray 约翰•考特尼•默里Reinhold Niebuhr 莱因霍尔德•尼布尔John Dowey 约翰•杜威Denis Diderot 丹尼斯•狄德罗Erasmus 伊拉斯谟Ludwig Feuerbach 路德维希•费尔巴哈本杰明•富兰克林Benjamin FranklinHomer 荷马Graham T. Allison 格雷汉姆•艾利森Tommaso Campanella 托马索•康帕内拉David Hume 大卫•休谟Jack S. Levy 杰克•列维Walter Lippmann 沃尔特•李普曼Quincy Wright 昆西•赖特Susan Strange 苏珊•斯特兰奇Richard Ashley 理查德•阿什利David Mitrany 戴维•米特兰尼Charles de Visscher查理•德维舍Michael W. Doyle 迈克尔•多伊尔John Hertz 约翰•赫茨Fredric Latzel弗里德里希•拉采尔鲁道夫•契伦Rudolf KjellenKarl Haushofer 卡尔•豪斯霍夫Nicolas Spykman 尼古拉斯•斯皮克曼Sir Halford Mackinder麦金德Douhet 杜黑Alfred Thayer Mahan 艾尔弗雷德•马汉David Mitrany 戴维•米特兰尼Alexander Hamilton 亚历山大•汉密尔顿Stanley Hoffmann 斯坦利•霍夫曼Kenneth W. Thompson 肯尼思•汤普逊Robert O. Keohane 罗伯特•基欧汉Robert Cox 罗伯特•考克斯弗里德里希•冯•哈耶克Friedrich von HayekJohn W. Burton 约翰•伯顿Morton Kaplan 莫顿•卡普兰John Ikenberry 约翰•埃肯伯里Arnold Toynbee 阿诺德•汤因比弗朗索瓦•德•卡利埃 《外交的艺术》 Francois de CallieresAbraham de Wicquefort 亚伯拉罕•德•威克福 ,《大使及其职能》 Robbery Jervis 罗伯特•杰维斯Barry Buzan 巴里•布赞Joseph Grieco 约瑟夫•格里科Sigmund Freud 西蒙•弗洛伊德Jurgen Habermas 尤尔根•哈贝马斯George W. F. Hegal 黑格尔Immanuel Kant 伊曼纽尔•康德Walter Lippmann 沃尔特•李普曼Thomas Aquinas 托马斯•阿奎那Fernand Braudel 费尔南•布罗代尔凯尔•冯•克劳塞维茨Karl von ClausewitzChristopher Columbus 克里斯托弗•哥伦布Auguste Comte 奥古斯特•孔德Herodotus 希罗多德Martin Luther 马丁•路德Richelieu 黎塞留John L. Gaddis 约翰•加迪斯Herbert Spencer 赫伯特•斯宾塞(英国社会学家)Oswald Spengler 奥斯瓦尔德•施宾格勒(德国历史哲学家) Talleyrand 塔列朗Caliphate 哈里发斯大林Joseph StalinDwight D. Eisenhower 德怀特•艾森豪威尔Eisenhower Doctrine 艾森豪威尔主义Harry Truman 哈里•杜鲁门Truman Doctrine 杜鲁门主义Jimmy Carter 吉米•卡特Ronald Reagan 罗纳德•里根Thomas Jefferson 托马斯•杰斐逊Coolidge 柯立芝Monroe Doctrine 门罗主义Richard Nixon 理查德•尼克松Nixon Doctrine 尼克松主义温斯顿•丘吉尔Winston ChurchillWoodrow Wilson 伍德罗•威尔逊Wilsonianism 威尔逊主义内维尔•张伯伦Neville Chamberlain阿道夫•希特勒Adolf HitlerOtto von Bismarch 奥托•冯•俾斯麦Napoleon Bonaparte 拿破仑•波拿巴亚历山大大帝Alexander the GreatAristotle 亚里士多德Augustine 奥古斯丁腓特烈大帝Frederick the Great梅特涅亲王Prince Metternich戴高乐Charles de Gaulle阿拉法特Yassir Arafat凯撒Julius CaesarBrezhnev Doctrine 勃列日涅夫主义Abbas I 阿拔斯一世君士坦丁(拜占庭皇帝)Constantine (Byzantine emperor)Hideyoshi 丰臣秀吉Oliver Cromwell 奥利弗•克伦威尔伊凡雷帝Ivan the Terrible (Tsar)Justinian 查士丁尼Genghis Khan 成吉思汗Mahomet 穆罕默德Peter the Great彼得大帝威廉一世 William I (Duke of Normandy, the Conqueror, King of England) Yoshida Doctrine 吉田主义Robespierre 罗伯斯庇尔Catherine the Great 叶卡捷琳娜大帝Charlemagne 查理曼大帝Sun Yat-sen 孙中山Khrushchev 赫鲁晓夫军事基地military basemilitary coup军事政变军费开支military expenditures军事援助military assistance军事一体化military integration军事干预military intervention军事挑衅military provocation军事技术革命military-technical revolution相互威慑mutual deterrence外层空间的非军事化demilitarization of outer spacearmed force 军队, 武装力量大规模报复massive retaliationWMD, Weapons of mass destruction大规模杀伤性武器preemption 先发制人巡航导弹cruise missileballistic missile defense弹道导弹防御洲际弹道导弹intercontinental ballistic missile中程弹道导弹intermediate-range ballistic missiletheater missile defense(TMD) (战区)导弹防御系统低烈度冲突low-intensity conflict第一次打击战略first-strike strategy第二次打击能力second-strike capacityatomic bomb 原子弹战略武器strategic weapon战术武器tactical weaponnaval blockade 海上封锁海军naval force空军air forceland force 陆军arms race 军备竞赛arms control 军备控制海军实力naval capabilityPentagon 五角大楼维和行动peace keeping operation防务政策defense policyguerilla war游击战信息战information warfare (IW), infowarmercenary 雇佣军open sea 公海 high seas international waters 公海;国际水域 outer space 外层空间领土完整territorial integrity领土管辖权territorial jurisdiction领水territorial water领空territorial air领海territorial sea领海范围limits of territorial sea增长极限论limits-to-growth propositionPersian Gulf War 海湾战争印巴战争Indo-Pakistani WarVietnam War 越南战争常规战争conventional warwar by proxy 代理人战争Indo-Chinese War 中印战争just war 正义战争有限核战争limited nuclear war预防性战争preventive warpostmodern war 后现代战争total war 总体战争Korean War 朝鲜战争preemptive war 先发制人的战争Crimean War 克里米亚战争[krai'miən]Falklands War 马岛战争Franco-Prussian 普法战争Russo-Japanese War 日俄战争Opium War 鸦片战争['əupiəm]Great Northern War 北方战争太平洋战争War of PacificThirty Years War 三十年战争the Peloponnesian War伯罗奔尼撒战争[,peləpə'ni:ʃən] Boer War 布尔战争Boer ['bəuə; bɔ:]nuclear weapons 核武器nuclear free zone无核区不首先使用(核武器)non-first usenonlethal weapon 非致使武器切尔诺贝利核事故 Chernobyl nuclear accident核查verification反核运动antinuclear movements核威慑nuclear deterrence核冬天nuclear winter核技术nuclear technologynuclear age 核时代全面禁止核试验CTB, Comprehensive test ban全面禁止核试验条约 Comprehensive Test Ban Treaty和平解决争端 peaceful settlement of disputes和平红利peace dividend和平共处peaceful coexistence民主和平论democratic peaceinstitutional peace theory 制度和平论partnership of peace 和平伙伴关系genocide 种族屠杀apartheid 种族隔离racial discrimination 种族歧视ethnic cleansing 种族清洗ethnocentrism 种族优越感国际组织:The Andean Pact 安第斯条约集团NAFTA, the North American Free Trade Agreement 北美自由贸易协定the Council of Ministers (欧盟)部长理事会(即 欧盟理事会)the COREPER, Committee of Permanent Representatives 常驻代表委员会the Dayton Peace Accords 代顿协议ASEAN, the Association of Southeast Asian nations 东南亚国家联盟community sense 共同体意识economic integration 经济一体化EMU, Economic and Monetary Union 经济与货币联盟ECJ, the European Court of Justice 欧洲法院EC, European Community 欧洲共同体the European Council 欧洲委员会(Council of Europe-------注:1)Council of the European Union :欧盟理事会2(俗称欧盟部长理事会the C ouncil of Ministers )1 Council of Europe:欧洲委员会,是由爱尔兰、比利时、丹麦、法国、荷兰、卢森堡、挪威、瑞典、意大利和英国通过1949年5月5日在伦敦签订《欧洲委员会法规》所成立,具有国际法地位、并且为联合国观察员身份的国际组织,是欧洲整合东欧进程中最早成立的机构。
人工智能与机器学习-教务处-东华大学

东华大学暑期课程手册教务处二零一八年六月为进一步深化教育教学改革,实现学生多样化的学习体验,今年暑期继续面向本科生开设暑期国际课程及专业大师课程。
本次开设18门课程。
课程开设目标如下:1. 拓展视野,提升学生综合素质通过暑期国际课程及专业大师课程,我校学生不用跨出校门,可以有机会聆听国内外知名教师(工程师)授课,拓宽学术视野,提高独立思考能力、科研能力,并培养专业兴趣。
2. 推动教学方式变革,丰富人才培养模式来自国内外的知名教师(工程师)能够将先进的教学方式、教学内容带到暑期课堂,扩展教学环节,使教学模式多样化,以此将大幅提升学生课堂参与度,对学生创造性思维和独立研究能力的培养发挥重要作用。
3. 鼓励教师旁听课程,加快师资培养步伐暑期课程期间,我校教师将得以方便地旁听国内外的知名教师(工程师)所开的课程,能够为教师提供一个全新的学习交流平台,对于提升教师素质,推动教师创新教学方式方法发挥积极作用。
1.概率论与计量金融 (4)2.微纳光电及标准化 (5)3.纺织品和服装的全球消费 (7)4.仿生学和纺织品技术 (8)5.服装系列样衣制作 (9)6.创意设计工具包 (10)7.服饰手工艺工作坊 (12)8.印花和T恤设计:现代T恤印花设计与制作 (14)9.产品服务设计 (15)10.供应链金融 (16)11.数据同化 (18)12.业务流程和企业资源计划 - 使用SAP的ERP (19)13.企业价值评估与投资分析 (20)14.服务运营管理 (22)15.人工智能技术及在设计和制造中的应用 (23)16.现代人工智能技术的应用及前景 (25)17.能源变革与智能电网 (27)18.全球市场纺织服装技术法规要求 (28)19.高分子化学与物理 (30)20.人工智能与机器学习 (32)21.物联网 (33)22.环境毒理学与物理辐射 (34)23.可持续建筑技术应用 (35)概率论与计量金融课程名称:概率论与计量金融开课学院:理学院开课教师:John Appleby 职称:教授课程代码:012611 学分:1选修人数:50教师简介:Professor John Appleby received his doctoral degree in Applied Mathematical Sciences from Dublin City University, Ireland in 1999. He has been a lecturer and researcher for 18 years in the School of Mathematical Sciences, Dublin City University, Ireland. He can offer many courses in probability and differential equations (both at undergraduate and graduate levels). He has published more than 100 papers in stochastic and deterministic dynamical systems, and has given around 100 talks at conferences and university colloquia worldwide. He has supervised successfully 10 PhD stud ents, been awarded around €1m in external funding support for his research. He is an associate editor of the Electronic Journal of the Qualitative Theory of Differential Equations and has acted as a reviewer for many of the important journals in differential equations and stochastic analysis (See attached Resume).课程简介:该短期课程的目标是向同学们展示:金融市场中的衍生证券可以采用一种所有市场参与者都认同的方式来定价,尽管大家在对初级证券价格变化的认识上存在着分歧。
1研究生课程中英文对照表

2
激光物理学
Laser Physics
3
1
原子光谱学
Atomic spectroscopy
3
1
量子光学
Quantum Optics
3
1
激光原理
Principle of Lasers
3
2
粒子物理理论
Theory on Particle Physics
3
1
量子场论基础
Basic on Quantum Field Theory
3
2
李群在微分方程中的应用
Applications of Lie Groups to Differential Equations
.
3,4
变分学
Calculus of variations
3
2
抽象代数
Abstract Algebra
6
1,2
代数拓扑学
Algebraic Topology
4
非线性发展方程
3
2
高等有机化学实验
Advanced Organic Chemistry Experiments
3
2
有机结构分析
organic Structural Analysis
3
2
有机合成专论
Organic Synthesis
3
2
有机合成实验
Advanced Organic Synthesis Experiment
3
3
正负法数控绘图
Positive-Negative Algorithm for Drawing Graphs with Digital
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
qualitative theory of dynamical systems的tex模板
摘要:
一、引言
1.定性理论动力学系统简介
2.动力学系统在各个领域的应用
3.本文的目的和结构安排
二、定性理论动力学系统的基本概念
1.动力学系统的定义
2.定性理论的定义
3.动力学系统的稳定性分析
三、定性理论动力学系统的数学模型
1.动力学系统的数学表示
2.定性理论的数学描述
3.数学模型的构建与分析
四、定性理论动力学系统的应用
1.物理学中的应用
2.生物学中的应用
3.经济学中的应用
4.其他领域中的应用
五、定性理论动力学系统的实例分析
1.实例介绍
2.定性理论动力学分析
3.结果与讨论
六、结论
1.定性理论动力学系统的研究现状与展望
2.对未来研究的建议
正文:
一、引言
定性理论动力学系统(qualitative theory of dynamical systems)是一个研究动力学系统稳定性和行为的数学分支。
动力学系统在物理学、生物学、经济学等多个领域都有广泛应用。
本文将介绍定性理论动力学系统的基本概念、数学模型、应用实例以及研究现状与展望。
二、定性理论动力学系统的基本概念
动力学系统是由一组状态变量和一组非线性的演化方程组成的。
这些状态变量随时间变化,并遵循一定的演化规律。
定性理论主要研究动力学系统的稳定性、平衡点、吸引子和排斥子等性质。
三、定性理论动力学系统的数学模型
动力学系统的数学模型通常由一组非线性方程构成,可以通过数值模拟和符号计算进行研究。
定性理论的数学描述主要关注系统的吸引子和排斥子,以及它们的结构和稳定性。
四、定性理论动力学系统的应用
定性理论动力学系统在多个领域都有广泛应用,如物理学中的混沌现象、生物学中的生态系统建模、经济学中的金融市场波动等。
这些应用有助于我们
更好地理解自然和社会现象,为决策提供理论支持。
五、定性理论动力学系统的实例分析
本文以一个简单的物理系统为例,运用定性理论动力学方法对其进行稳定性分析。
通过计算吸引子和排斥子,我们可以了解系统的稳定性和动态行为。
六、结论
定性理论动力学系统的研究现状和应用表明,该领域具有广泛的研究价值和应用前景。
