等腰三角形的性质优质课课件
合集下载
等腰三角形的性质(八下优质课件)

等边对等角 三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底 边上的高和中线才有这一性 质.而腰上高和中线与底角 的平分线不具有这一性质.
∵AB=AC, ∠1=∠2(已知),
12
∴BD=CD,AD⊥BC(等腰三角形三线合一). B D C
∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC, AD⊥BC(已知), ∴BD=CD, ∠1=∠2(等腰三角形三线合一).
典例精析
例1 如图,在△ABC中 ,AB=AC,点D在AC上, 且BD=BC=AD,求△ABC各角的度数.
角∠BAC的角平分线、底边BC上的高线 .
总结归纳
定理:等腰三角形的两个底角相等(等边对等角).
如图,在△ABC中, ∵AB=AC(已知), ∴∠B=∠C(等边对等角).
A
B
C
推论:等腰三角形顶角的平分线、底边上的中线及 底边上的高线互相重合(三线合一).
证明后的结论,以后可以直接运用.
A 综上可得:如图,在△ABC中,
(1)若AD=AE,求证:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,求证:
AF⊥BC.
A
A
B
D GE
B C
DF E
C
图①
图②
解析:(1)过A作AG⊥BC于G,根据等腰三角形的性质
得出BG=CG,DG=EG即可证明;(2)先证BF=CF,
再根据等腰三角形的性质证明.
A
A
B
D GE
B C
1.两点确定一条直线;
2.两点之间线段最短; 3.同一平面内,过一点有且只有一条直线与已知直线
等腰三角形全国优质课一等奖完美PPT课件

20
直角三角形相关知识回顾
直角三角形的定义
有一个内角为90°的三角形 称为直角三角形。
2024/1/28
直角三角形的性质
直角三角形的两个锐角互 余,斜边是直角三角形的 最长边,且满足勾股定理 。
直角三角形的判定
若一个三角形满足有一个 内角为90°或满足勾股定理 ,则该三角形为直角三角 形。
21
相似三角形相关知识拓展
02
若一个三角形中有一个角为90度 ,且这个三角形的两条直角边相 等,则这个三角形是等腰直角三 角形。
13
其他特殊情况下判定方法
若一个三角形的三条边满足勾股定理, 即其中两条边的平方和等于第三条边的 平方,则这个三角形是直角三角形。若 此时直角边相等,则为等腰直角三角形
。
2024/1/28
若一个三角形的三条边满足 a:b:c=1:1:√2的关系(a、b为直角边, c为斜边),则这个三角形是等腰直角
顶角与底角的关系
顶角的度数是底角度数的两倍,即顶角 = 2 × 底 角。
3
高、中线与角平分线的关系
在等腰三角形中,高、中线和顶角的角平分线互 相重合。
2024/1/28
9
等腰三角形性质总结
对称性
等腰三角形是Hale Waihona Puke 对称图形,对 称轴是底边的垂直平分线。
2024/1/28
边角关系
在等腰三角形中,两底角相等 ,且顶角的度数是底角度数的 两倍。
3
课程背景与意义
三角形是初中数学的重要内容 ,等腰三角形作为特殊三角形 ,具有独特的性质和广泛的应 用。
2024/1/28
学习等腰三角形有助于学生理 解三角形的基本性质,掌握证 明方法,提高几何推理能力。
直角三角形相关知识回顾
直角三角形的定义
有一个内角为90°的三角形 称为直角三角形。
2024/1/28
直角三角形的性质
直角三角形的两个锐角互 余,斜边是直角三角形的 最长边,且满足勾股定理 。
直角三角形的判定
若一个三角形满足有一个 内角为90°或满足勾股定理 ,则该三角形为直角三角 形。
21
相似三角形相关知识拓展
02
若一个三角形中有一个角为90度 ,且这个三角形的两条直角边相 等,则这个三角形是等腰直角三 角形。
13
其他特殊情况下判定方法
若一个三角形的三条边满足勾股定理, 即其中两条边的平方和等于第三条边的 平方,则这个三角形是直角三角形。若 此时直角边相等,则为等腰直角三角形
。
2024/1/28
若一个三角形的三条边满足 a:b:c=1:1:√2的关系(a、b为直角边, c为斜边),则这个三角形是等腰直角
顶角与底角的关系
顶角的度数是底角度数的两倍,即顶角 = 2 × 底 角。
3
高、中线与角平分线的关系
在等腰三角形中,高、中线和顶角的角平分线互 相重合。
2024/1/28
9
等腰三角形性质总结
对称性
等腰三角形是Hale Waihona Puke 对称图形,对 称轴是底边的垂直平分线。
2024/1/28
边角关系
在等腰三角形中,两底角相等 ,且顶角的度数是底角度数的 两倍。
3
课程背景与意义
三角形是初中数学的重要内容 ,等腰三角形作为特殊三角形 ,具有独特的性质和广泛的应 用。
2024/1/28
学习等腰三角形有助于学生理 解三角形的基本性质,掌握证 明方法,提高几何推理能力。
等腰三角形课件ppt

边与角的相互影响
边长变化对角度的影响
当等边的长度增加或减少时,底角α的大小会发生变化。这是因为角度α与基边的长度成 反比。
角度变化对边长的影响
当底角α的大小发生变化时,基边的长度也会相应地增加或减少。这是因为角度的变化会 影响到三角形的周长,从而影响基边的长度。
Part
03
等腰三角形的判定与证明
04
等腰三角形的面积与周长
面积的计算
1 2
面积公式
等腰三角形的面积可以通过底边长度和对应的高 来计算,公式为 (S = frac{1}{2} times text{底边 长度} times text{高})。
面积与底边和高
等腰三角形的面积与底边长度和高有关,当底边 长度和高发生变化时,面积也会相应地变化。
等腰三角形与勾股定理
总结词
勾股定理是几何学中的重要定理之一 ,它可以应用于等腰三角形,特别是 等腰直角三角形。
详细描述
勾股定理表明在一个直角三角形中, 直角边的平方和等于斜边的平方。对 于等腰直角三角形,两条直角边长度 相等,因此它们的平方和等于斜边的 平方。
详细描述
等腰三角形是两边相等的三角形,根据等腰三角形的性质,两个底角相等,并且 三角形的内角和为180度,因此每个底角的大小为(180度 - 顶角度数)/ 2。
等腰三角形的外角和定理
总结词
等腰三角形的外角和定理表明等腰三角形的一个外角等于它 不相邻的两个内角之和。
详细描述
根据三角形外角定理,一个三角形的外角等于它不相邻的两 个内角之和,对于等腰三角形来说,由于两个底角相等,所 以一个底角的外角等于另一个底角。
等腰三角形课件
• 等腰三角形的定义与性质 • 等腰三角形的边与角 • 等腰三角形的判定与证明 • 等腰三角形的面积与周长 • 等腰三角形的拓展知识
13. 等腰三角形的性质 PPT课件(华师大版)

分析:由上述操作可以得到启示,即添加
等腰三角 形的顶角平分线AD,然
后证明△ABD≌ △ACD.
证明:画∠ABC的平分线AD. 在 △ABD和 △ACD中, ∵ AB=AC (已知), ∠ 1 = ∠ 2(角平分线的定义), AD =AD (公共边), ∴ △ABD≌ △ACD(S.A.S.). ∴ ∠B=∠C(全等三角形的对应角相等)•
2.等腰三角形“三线合一”的性质常常可以用来证明角相 等、线段相等和线段垂直.在遇到等腰三角形的问题 时, 尝试作这条辅助线,常常会有意想不到的效果.
例4 如图 13.3.4,在△ABC中, AB=AC ,D是BC 边上的中点, ∠B =30°.求 :
(1)∠ADC的大小; (2)∠1的大小. 解: (1)∵ AB=AC ,BD=DC (已知),
3 (中考·丹东)如图,在△ABC中,AB=AC,∠A=30° ,E为BC的延长线上一点,∠ABC与∠ACE的平 分线交于点D,则∠D的度数为( ) A.15° B.17.5° C.20° D.22.5°
知识点 2 等腰三角形的轴对称性:三线合一
探索
由前面的“做一做”,你还可以发现什么结论?请 写 出你的发现:
例2 已知:在△ABC中, AB=AC , ∠B =80°.求 ∠C和∠A的大小.
解: ∵ AB=AC (已知), ∴ ∠C=∠B = 80°(等边对等角). 又∵ ∠A + ∠B + ∠C = 180°(三角形的内角和 等于 180 °), ∴ ∠A = 180 °- ∠B - ∠C (等式的性质) = 180°- 80°- 80°= 20°.
做
一
做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角 形的大小和形状可以不一样,如图13.3.2,把纸片对折,让
等腰三角 形的顶角平分线AD,然
后证明△ABD≌ △ACD.
证明:画∠ABC的平分线AD. 在 △ABD和 △ACD中, ∵ AB=AC (已知), ∠ 1 = ∠ 2(角平分线的定义), AD =AD (公共边), ∴ △ABD≌ △ACD(S.A.S.). ∴ ∠B=∠C(全等三角形的对应角相等)•
2.等腰三角形“三线合一”的性质常常可以用来证明角相 等、线段相等和线段垂直.在遇到等腰三角形的问题 时, 尝试作这条辅助线,常常会有意想不到的效果.
例4 如图 13.3.4,在△ABC中, AB=AC ,D是BC 边上的中点, ∠B =30°.求 :
(1)∠ADC的大小; (2)∠1的大小. 解: (1)∵ AB=AC ,BD=DC (已知),
3 (中考·丹东)如图,在△ABC中,AB=AC,∠A=30° ,E为BC的延长线上一点,∠ABC与∠ACE的平 分线交于点D,则∠D的度数为( ) A.15° B.17.5° C.20° D.22.5°
知识点 2 等腰三角形的轴对称性:三线合一
探索
由前面的“做一做”,你还可以发现什么结论?请 写 出你的发现:
例2 已知:在△ABC中, AB=AC , ∠B =80°.求 ∠C和∠A的大小.
解: ∵ AB=AC (已知), ∴ ∠C=∠B = 80°(等边对等角). 又∵ ∠A + ∠B + ∠C = 180°(三角形的内角和 等于 180 °), ∴ ∠A = 180 °- ∠B - ∠C (等式的性质) = 180°- 80°- 80°= 20°.
做
一
做
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角 形的大小和形状可以不一样,如图13.3.2,把纸片对折,让
人教版数学等腰三角形的性质公开课PPT课件
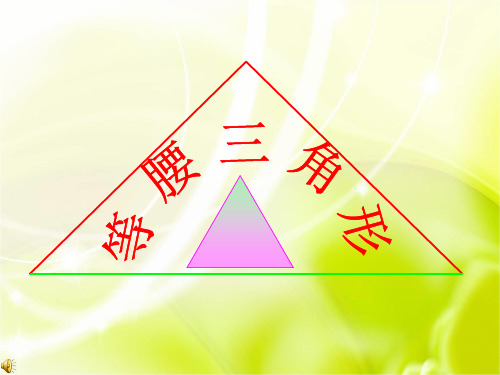
性质2 等腰三角形的顶角平分线与底边上的中线, 底边上的高互相重合. (简写成“三线合一” )
几何语言:
A
(1)∵ AB=AC, AD⊥BC,
∴∠ 1 = ∠ 2 , BD = CD .
12
(2) ∵ AB=AC, BD=CD,
∴ AD ⊥ BC ,∠ 1 =∠ 2 .
∟
(3) ∵ AB=AC, ∠1= ∠ 2,
谢 谢 指 导!
如图,AOB是一钢架,且∠AOB=10°,为使钢
架更加坚固,需在其内部添一些钢管EF、FG、 GH……,添加的钢管长度都与OE相等,则∠M
HA = 50 °,最多能添加这样的钢管8 根。
B
G
M
40° 60°
60°808°0°
E
20° 40°
20°
10°
10° 30°
30° 50° 50°70°70°90°
13.3.1 等腰三角形(第1课时)
如图所示,把一张长方形的纸按图中虚线对折,然 后画出一条裁剪线,并剪去阴影部分,再把它展开,得 到的△ABC 有什么特点?
底角 腰
B
A
D
底 边
顶角
C
腰
底角
定义:有两边相等的三角形,叫做等腰三角形.ຫໍສະໝຸດ 在△ABC 中,AB=AC
把剪出的等腰三角形ABC 沿折痕对折,找出其中相等
体验了什么数学思想? 分类思想 方程思想
想进一步研究的问题是
A
.................
B
C
等边三角形
如图,点B,D,E,C在同一直线上,AB=AC , AD=AE. 求证:BD=CE.
A
方法:求有关等腰三角 形的问题,作顶角平分 线、底边中线,底边的 高是常用的辅助线
等腰三角形性质PPT课件
M
7A
E
2
10°
1
3
6
4
5
8
O
F
H
B
老师,这个题我明白了,会做了!
第27页/共29页
(1)本节课里你学到了什么???
有两边相等的三角形 概念
腰、底、顶角、底角 等腰三角形
性质 等边对等角 三线合一
(2)等腰三角形中常作的辅助线: 作顶角的平分线、底边上的高或底边上的中线
第28页/共29页
感谢您的观看!
所以这个三角形的边为4 ,4 ,2
第25页/共29页
5.如图,AOB是一钢架,且∠AOB=10°, 为使钢架更加坚固,需在其内部添一些钢管EF、FM、 MH……,添加的 钢管长度都与OE相等, 添加这样的钢管4根时,则∠AHB 的度数为___5_0_°_
M
A
E
10°
O
F
H
B
第26页/共29页
如图,AOB是一钢架,且∠AOB=10°, 为使钢架更加坚固,需在其内部添一些钢管EF、FM、 MH……,添加的 钢管长度都与OE相等, 添加这样的钢管4根时,则∠AHB的度数为__5_0_°__
如图,在下列等腰三角形中, 分别求出其它两个角的度数。
A
A
36°
120°
B
30°
72° 72°
B
C
30°
C
第21页/共29页
1.填空题 巩固练习
(1)如果等腰三角形的一个底角为500,则其余 两个角为_8_0_0_和_5_0_0_.
(2)如果等腰三角形的顶角为800,则它的一个 底角为_5_0_0_. (3)如果等腰三角形的一个角为800,则其余两 个角为__8_0_0和__2_0_0___或_5_0_0_和__5_0_0. (4)如果等腰三角形的一个角为1000,则其余两 个角为__4_0_0和__4_0_0_.
等腰三角形的性质PPT授课课件

HK版 八年级上
第三章 声的世界
第2节 声音的特性
第2课时 噪声的防治
习题链接
提示:点击 进入习题
1 噪声;空气 4 dB;不能
答案呈现
7 人耳 10 见习题
2D
5D
8C
3C
6 声源;传播过程 9 B
基础巩固练
8.[中考·山东潍坊]将教室的门窗关闭,室内同学听到的 室外噪声减弱。对该现象说法正确的是( C ) A.室外噪声不再产生 B.噪声音调大幅降低 C.在传播过程中减弱了噪声 D.噪声在室内的传播速度大幅减小
AB=AC,
∵
BD=CD,
AD=AD,
∴△BAD ≌△CAD (SSS).
∠B=∠C.
这样,我们就证明了性质1
感悟新知
归纳
知1-讲
我们可以发现等腰三角形的性质: 性质1 等腰三角形的两个底角相等(简写成“等边 对顶角”.
感悟新知
例 1 如图,在△ABC中,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数.
16 B
答案呈现
17 B 18 见习题 19 见习题
基础巩固练
1.某市已经明令禁止在城区内燃放烟花爆竹,因为燃放 烟花爆竹除了会造成空气污染外,燃放烟花爆竹时的 巨大声音还是一种___噪__声___(填“乐音”或“噪声”),爆 竹的巨大声音是__空__气____的振动产生的。
基础巩固练
7.[安徽霍邱月考]如图所示,在女子10 m气手枪比赛中,射 击时,很多运动员在耳朵里放一个耳塞或戴上耳罩,这 主要是在___人__耳___处减弱噪声。
能力提升练
解:(1)据题可知,“控制音量”是在声源处减弱噪声, 控制的是噪声的响度。
《等腰三角形的性质》优秀课件

全等识别
若两个三角形三边及三角分别相等,则这两个三角形全等。在等腰三角形中, 若两个等腰三角形的底边和腰长分别相等,则这两个等腰三角形全等。
2024/1/26
21
对后续知识点(如圆、三角函数)的铺垫作用
对圆的知识点铺垫
等腰三角形的性质与圆的性质有密切联系。例如,在等腰三角形中,底边上的中垂线同时也是底边所 在圆的直径;此外,在等腰三角形中引入外接圆和内切圆的概念,可以进一步探讨三角形的性质。
SAS全等判定
若两个三角形两边和夹角分别相等,则这两个三 角形全等。
3
HL全等判定(直角三角形)
在直角三角形中,若斜边和一条直角边分别相等 ,则这两个三角形全等。
2024/1/26
5
与其他特殊三角形关系
与等边三角形的关系
等边三角形是特殊的等腰三角形,三 边都相等。
与相似三角形的关系
若两个等腰三角形的顶角和底角分别 相等,则这两个三角形相似。
8
边角关系
等腰三角形中,两个等腰边所 对的两个底角相等,即等边对 等角。
2024/1/26
等腰三角形的顶角平分线、底 边上的中线、底边上的高相互 重合,即“三线合一”。
等腰三角形中,若有一个角是 60度,则这个三角形是等边三 角形。
9
面积计算公式
等腰三角形的面积可以通过以下公式计算
面积 = (底边长度 × 高) / 2。其中,底边长度是两个等腰边所夹的底边的长度, 高是从顶点到底边的垂直距离。
《等腰三角形的性质》 优秀课件
2024/1/26
1
目录
2024/1/26
• 等腰三角形基本概念 • 等腰三角形性质探究 • 等腰三角形在生活中的应用 • 等腰三角形相关定理证明 • 等腰三角形在几何变换中的地位和作用 • 典型例题解析与课堂互动环节
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A C
D
C
如图,是西安半坡博物馆屋顶的截面图, 如图,是西安半坡博物馆屋顶的截面图,已经知道它 的两边AB AC是相等的 AB和 是相等的. 的两边AB和AC是相等的.建筑工人师傅对这个建筑物 做出了两个判断: 做出了两个判断: 工人师傅在测量了∠ 37°以后,并没有测量∠ ①工人师傅在测量了∠B为37°以后,并没有测量∠C , 就说∠ 的度数也是37 37° 就说∠C 的度数也是37°. 工人师傅要加固屋顶,他们通过测量找到了横梁BC ②工人师傅要加固屋顶,他们通过测量找到了横梁BC 的中点D 然后在AD两点之间钉上一根木桩, AD两点之间钉上一根木桩 的中点D,然后在AD两点之间钉上一根木桩,他们认 为木桩是垂直横梁的. 为木桩是垂直横梁的.
A
1 2 1 2 B C D
思考:
(1)等腰三角形的对称轴怎样回答? 等腰三角形的对称轴怎样回答? 等腰三角形的对称轴怎样回答 等腰三角形是轴对称图形.对称轴是底边上 等腰三角形是轴对称图形 对称轴是底边上 的中线(顶角平分线 底边上的高)所在直线 顶角平分线,底边上的高 的中线 顶角平分线 底边上的高 所在直线 (2)等腰三角形底角的平分线与它所对边上的 等腰三角形底角的平分线与它所对边上的 中线和高线重合么? 中线和高线重合么?
下课了!
等腰三角形的有关概念
A
顶 角
腰
腰
B
C
返回
A 的中线AD 证明: 作△ABC 的中线
则有 BD= CD = 在△ABD和△ACD中 和 AB= AB=AC C B D BD=CD = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SSS) ≌ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
A 的高线AD 证明: 作△ABC 的高线
例1、如图,在△ABC中 ,AB=AC,点D在AC上,且 、如图, 中 , 在 上 BD=BC=AD,求△ABC各角的度数。 各角的度数。 , 各角的度数
A
解:∵AB=AC,BD=BC=AD, AB=AC,BD=BC=AD, ∴∠ABC=∠ ∠ ∴∠ABC=∠C=∠BDC,∠A=∠ABD ABC= , ∠ 等边对等角) (等边对等角 设∠A=x,则∠BDC= ∠A+ ∠ABD=2x, 则 从而∠ 从而∠ABC= ∠C= ∠BDC=2x,
等 腰 三 角 形 的 性 质
心灵手巧
如图:把一张长方形纸片按图中的虚线对折 如图:把一张长方形纸片按图中的虚线对折, 并剪去红线下方的部分,再把它展 并剪去红线下方的部分 再把它展 开,得△ABC 得
B
A C
D
观察
AC和AB有什么关系 这个三角形有什么特点 和 有什么关系 这个三角形有什么特点? 有什么关系?这个三角形有什么特点
C
2x B
⌒ ⌒ ⌒ ⌒ x D 2x
于是在△ 于是在△ABC中,有 中 ∠A+∠ABC+∠C=x+2x+2x=180°, ∠ ∠ ° 解得x=36°, ° 解得
在△ABC中, ∠A=36°,∠ABC=∠C=72° 中 ° ∠ °
4 :△ ABC是等腰直角三角形 是等腰直角三角形 (AB=AC, ∠ BAC=90°), 是底 , °),AD是底 上的高, 边BC上的高,标出∠ B, ∠ C, 上的高 标出∠ , , 的度数? ∠ BAD, ∠ DAC的度数? , 的度数 B 答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45° ° 5:在△ ABC中,AB=AD=DC, : 中 , ∠BAD=16°,求∠ B和∠ C的度数 ° 和 的度数 答:∠ B= 82° ,∠ C =41° ° ° B A D
∠1=∠2=55 等式性质)。 ∴ ∠1=∠2=550(等式性质)。 ∵AB=AC(已知) (2)在△ABC ∵AB=AC(已知) AD是 ABC的中线 已知) 的中线( 又∵AD是△ABC的中线(已知) AD⊥BC(等腰三角形底边上的中线垂直底边)。 ∴ AD⊥BC(等腰三角形底边上的中线垂直底边)。 ∵AB=AC(已知) (1)解:在△ABC ∵AB=AC(已知)
C
归纳结论
性质2:
等腰三角形的顶角平分线与底边上的中线,底边上 等腰三角形的顶角平分线与底边上的中线,底边上 顶角平分线 上的中线 的高互相重合 的高互相重合 (等腰三角形三线合一) 用符号语言表示为: 用符号语言表示为:
在△ABC中,AB =AC, 点 D在BC上 中 在 上 1、∵AD ⊥ BC 、 BD = CD 。 ∴∠ 1 = ∠ 2 , 2、∵AD是中线, 是中线, 、 是中线 ∴ AD⊥ BC ,∠ 1 =∠ 2 。 ∠ 3、∵AD是角平分线, 是角平分线, 、 是角平分线 。 ∴ AD ⊥ BC , BD= CD
则有 ∠ADB=∠ADC =90º = 在Rt△ABD和Rt△ACD中 △ 和 △ AB= AB=AC 公共边) (公共边)B AD=AD =
D
C
∴ Rt△ABD≌Rt△ACD (HL) △ ≌ △ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
归纳结论
性质1
等腰三角形的两个底角相等。 等腰三角形的两个底角相等。 (等边对等角) 用符号语言表示为: 用符号语言表示为:
C
一题多解 如图, 的边BC上 如图,点D、E在△ABC的边 上, 、 在 的边 且AB=AC,AD=AE,此时 与CE有 , ,此时BD与 有 何关系?请说明理由。 何关系?请说明理由。
谈谈你的收获! 谈谈你的收获!
轴对称图形
性质一:两个底角相等(等边对角) 等边对角) 性质一:
性质二:顶角平分线、底边上的中线、 性质二:顶角平分线、底边上的中线、 互相重合( 和底边上的高互相重合(三线合 一)
ABC是等腰三角形 AC=AB, △ABC是等腰三角形
(1)什么是等腰三角形?
有两条边相等的三角形叫做等腰三角形. 有两条边相等的三角形叫做等腰三角形
(2)等腰三角形的有关概念 (3)三角形中学过哪些重要线段?
三角形的中线、 三角形的中线、角平分线和高线 如图:中线 角平分线AE,高AF 如图:中线AD,角平分线 角平分线 高
B D C
大胆猜想
等腰三角形除了两腰相等以外, 等腰三角形除了两腰相等以外, 你还能发现它的其他性质吗? 你还能发现它的其他性质吗?
猜想与论证
猜想
等腰三角形的两个底角相等。 等腰三角形的两个底角相等。 已知:△ABC中,AB=AC
A
求证:∠B=∠C
分析: 如何证明两个角相等 如何证明两个角相等? 分析:1.如何证明两个角相等? 2.如何构造两个全等的 2.如何构造两个全等的 三角形? 三角形?
A
在△ABC中, 中 ∵ AC=AB(已知) (已知) 等边对等角) ∴ ∠B=∠C (等边对等角) ∠
C
B
看谁算得快 如图,在下列等腰三角形中, 如图,在下列等腰三角形中,分别求 出它们的底角的度数。 出它们的底角的度数。 A A
36° ° 120° °
B B C
C
巩固练习(1)
⒈等腰三角形一个底角为75°,它的另外两个 等腰三角形一个底角为75° 75 75°, __; 角为_____ 角为_____ 30° ; __ ⒉等腰三角形一个角为70°,它的另外两个角 等腰三角形一个角为70° 70 70°,40°或55°,55° 为___________________; ___________________; ⒊等腰三角形一个角为110°,它的另外两个角 等腰三角形一个角为110° 110 35°,35° __。 为______ __。
等腰三角形是轴对称图形吗? 等腰三角形是轴对称图形吗?
把剪出的等腰三角形ABC沿折痕对折, 沿折痕对折, 把剪出的等腰三角形 沿折痕对折 找出其中重合的线段和角. 找出其中重合的线段和角
重合的线段
重合的角
A
AB=AC = BD=CD = AD=AD =
∠B = ∠C.
∠BAD = ∠CAD ∠ADB = ∠ADC
论证猜想
作顶角的平分线AD, 证明: 作顶角的平分线 ,
则有∠ = 则有∠1= ∠2
A 12
在△ABD和△ACD中 和 AB= AB=AC B D ∠1=∠2 = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SAS) ≌ ) ° ∴ BD=CD ∠ADB =∠ADC= 90° =
B D
C
A 作顶角的平分线AD, 证明: 作顶角的平分线 ,
则有∠ = 则有∠1= ∠2
12
在△ABD和△ACD中 和 AB= AB=AC C B D ∠1=∠2 = AD=AD (公共边) = 公共边) ∴ △ABD≌ △ACD (SAS) ≌ ) ∴ ∠B=∠C 全等三角形对应角相等) = (全等三角形对应角相等)
请同学们想想,工人师傅的说法对吗?请说明理由. 请同学们想想,工人师傅的说法对吗?请说明理由.A(学以致用)B
D
C
我思,我进步 我思 我进步1
如图,已知AB=AC, AD是 ABC的中 如图,已知AB=AC,∠BAC=1100,AD是△ABC的中 AB=AC 线。 A 的度数; (1)求∠1和∠2的度数; 1 2 AD⊥BC吗 为什么? (2)AD⊥BC吗?为什么? B D 又∵AD是△ABC的中线(已知) AD是 ABC的中线(已知) 的中线 1 ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角) ∴ ∠1=∠2= ∠BAC(等腰三角形底边上的中线平分顶角) 2 ∠BAC=110 已知) ∵ ∠BAC=1100(已知)
想一想: 想一想:
刚才的证明除了能得到∠ = 刚才的证明除了能得到∠B=∠C 你 还能发现什么? 还能发现什么
重合的线段 AB=AC = BD=CD = AD=AD = 重合的角
