天圆地方的计算公式
天圆地方工程量计算方法

天圆地方工程量计算方法
1. 嘿,你知道天圆地方的工程量咋计算吗?就好比你要建个小城堡,那得把每一块砖的用量都算清楚呀!像算它的体积,不就跟算一个大盒子的体积差不多嘛!
2. 哎呀呀,天圆地方的面积计算可不能小瞧!就像你给自己房间铺地毯,总得量好尺寸吧!难道你能随随便便就买块不合适的呀?
3. 喂,想过没,天圆地方的周长计算有多重要?这就好像你要围着操场跑一圈,得知道操场周长有多长呀!可不能瞎跑一通吧!
4. 嘿,天圆地方的角度计算也得弄明白呀!好比你要调整自行车的把手角度,要刚刚好才骑得舒服,不是吗?
5. 哎呀,那计算天圆地方的各项数据真得细心点!就跟你数自己宝贝玩具一样,一个都不能落下呀!
6. 知道吗,精确计算天圆地方工程量就像医生治病一样严格!稍微有点差错可不行,这不是闹着玩的呀!
7. 天圆地方工程量计算方法可得好好掌握呀!这就像掌握一门独特的技能,让你在建筑世界里游刃有余,难道你不想吗?
我的观点结论就是:天圆地方工程量计算方法非常重要,一定要认真对待,仔细研究,这样才能在相关工程中做到准确无误。
天圆地方的计算方法
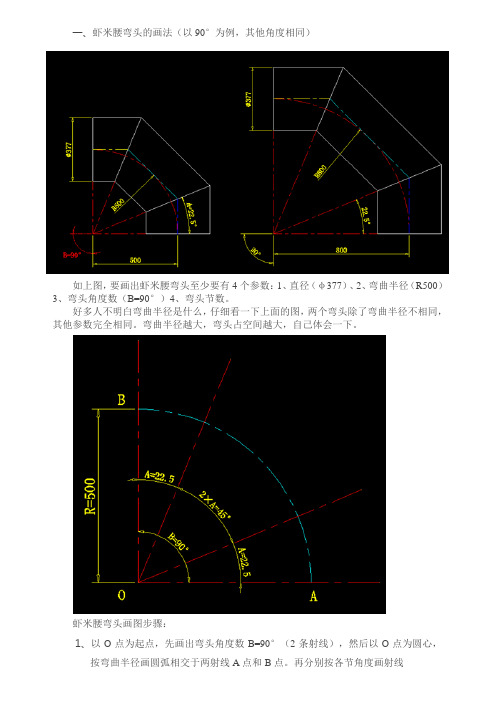
一、虾米腰弯头的画法(以90°为例,其他角度相同)如上图,要画出虾米腰弯头至少要有4个参数:1、直径(φ377)、2、弯曲半径(R500)3、弯头角度数(B=90°)4、弯头节数。
好多人不明白弯曲半径是什么,仔细看一下上面的图,两个弯头除了弯曲半径不相同,其他参数完全相同。
弯曲半径越大,弯头占空间越大,自己体会一下。
虾米腰弯头画图步骤:1、以O点为起点,先画出弯头角度数B=90°(2条射线),然后以O点为圆心,按弯曲半径画圆弧相交于两射线 A点和B点。
再分别按各节角度画射线重点:第一节的夹角A=22.5°的计算公式:需要注意的是:虾米腰弯头各节的角度不是总角度除以节数,这是错误的!不论多少节的虾米腰弯头都应这样分节:第一节和最后一节的角度是中间节角度的一半,因此可推导出上面的公式。
2、以A点为中点,画出弯头的直径(377),并在两端点画垂直于直径线的2条线;相交于第一节的“节线”E和E’点。
3、同样步骤画出第三节,并连接各个交点,完成弯头的尺寸图4、如果是3节以上的弯头(如上图为5节),中间节角度必定是第一节和最后一节角度的2倍。
然后以OE和OE’为半径截取各个角度的射线,连接各个交点,即可画出完整的虾米腰弯头。
二、放样展开通俗讲展开就是将一个空间面“拍平”到一个平面。
如下图(第一节的半部分,将直径377圆等分12等份),将左面黄线部分的空间曲面“拍平”后到右边的平面。
请仔细观察一下各个点之间的关系虾米腰弯头各节经过扭转对齐后可组成一个直管(如下图),由于第一节、最后一节是中间节的一半,所以只需展开第一节就可以了。
从点1处将第一节“剪开”,“拍平”后,其长度为377*3.1416=1184.38 ,等分为12等份(图上只画出一半),向上画12条垂直线,其高度从左面第一节各个点量出后,在对应的垂线上截取。
平滑连接得到的各个点,完成展开图。
有的放样展开是这样形状的(下图):其实只是剖切的点不同,上图剖切点在第一节的最短处(1点),下图剖切点在点4处三、弯头厚度的处理以上放样展开过程没有厚度问题,在薄壁弯头时可以。
天圆地方操作方法

天圆地方操作方法天圆地方,一种传统的数学计算方法,是中国古代数学的重要成果之一。
它的基本思想是将地球看作一个球体,而在球体上进行计算。
以下是天圆地方的操作方法:一、天圆天圆是指在地理坐标系中以地球为球心,在其表面上建立的圆形坐标系。
具体步骤如下:1.建立基准面在地球表面上选择一个基准面,通常选取赤道或零子午线作为基准面。
2.确定经纬度以基准面为参考面,确定地点的经度和纬度。
经度是以零子午线为基准,由东向西计算;纬度是以赤道为基准,由南向北计算。
3.建立天圆坐标系以地球为球心,在地球表面上建立天圆坐标系。
在该坐标系中,以基准面为赤道,以地球中心与地点的连线为极轴,建立圆形坐标系。
4.转换为平面坐标系为方便计算,将天圆坐标系转换为平面坐标系。
在平面坐标系中,以基准面为X轴,以地点的子午线为Y轴,建立直角坐标系。
二、地方地方是指在地理坐标系中以地球上某一点为中心建立的平面坐标系。
具体步骤如下:1.建立基准面在地球表面上选择一个基准面,通常选取赤道或零子午线作为基准面。
2.确定经纬度以基准面为参考面,确定地点的经度和纬度。
3.建立地方坐标系以地点为中心,在地球表面上建立地方坐标系。
在该坐标系中,以地点的子午线为X轴,以地点所在纬度的平行圆为Y轴,建立直角坐标系。
4.转换为天圆坐标系为方便计算,将地方坐标系转换为天圆坐标系。
在天圆坐标系中,以赤道为基准面,以地方坐标系中的X轴为天圆坐标系中的Y轴,以地方坐标系中的Y轴为天圆坐标系中的X轴,建立圆形坐标系。
三、计算方法在天圆地方中进行计算时,需要掌握以下几种计算方法:1.求两点间距离可以通过天圆坐标系或地方坐标系计算。
在天圆坐标系中,可以通过余弦定理求得;在地方坐标系中,则可以通过勾股定理求得。
2.求两点间方位角在天圆坐标系中,可以通过正切公式求得;在地方坐标系中,则可以通过正切公式或余切公式求得。
3.求距离和方位角的增量在天圆坐标系中,可以通过正弦公式和余弦公式求得;在地方坐标系中,则可以通过正切公式和余切公式求得。
天圆地方放样方法

1.天圆地方及其放样过程概述天圆地方又名方圆变径管,被广泛应用于圆断面与矩形断面的风管与设备间的连接。
如圆通风管与风机出口,空调机组与风机进口等场合的连接。
其放样过程简要如下:(1)先将上圆均分为若干等分,并将上圆各等分点与矩形角点依次相连,即将其分成若干个小三角形(如图1)。
(2)利用直角三角形定理先求出其在投影面上的长,再利用该值与天圆地方的高求出各连线空间实长。
并同时求出圆上任意两个相邻点间的弧长。
(3)用(2)中求得的空间实长与圆上任意两个相邻点间的弧长作展开图(如图2)。
由上述步骤可知传统放样过程的确较为繁琐,当天圆地方为偏心或制作精度要求较高的情形时则更为繁琐。
因此,寻找其快捷方式具有一定的现实意义。
2. 计算公式的推导本文以两个方向偏心的天圆地方为例进行推导,以求出天圆地方放样参数的通用公式。
假设现需制作一天圆地方,其上圆半径为r,矩形长为a 宽为b,其上下端面在长边方向上的偏心矩为e1,在短边方向上的偏心矩e2,天圆地方的高为h,同时结合实际将上圆等分数定为n(n一般为4的倍数,图中取为12)。
建立三维坐标本文通过建立三维坐标将原来所需的两次计算减为经一次计算即可得出结果。
先以X轴平行于矩形长边,Y轴平等于矩形短边,Z轴过圆心并平行于天圆地方的高,建立三维直角坐标系。
同时根据实际情况将圆周进行n等分,并将各等分点与矩形角点相连(如图1)。
则各相关点的坐标分别为:A(,,0);B(,,0);C(,,0);D(,,0);E(,0,0);Fi(rcosiθ,rsiniθ,h)其中i=0,1,…n;θ=2π/n。
如图所示A、B、C、D为矩形角点,E为AD与X轴的交点,F为圆上等分点。
公式推导:结合上述各点坐标再利用空间两点间的距离公式可求出各连线在空间实长:AFi= 其中i=0,1,…,n/4;BFi= 其中i=n/4,n/4+1,…,n/2;CFi= 其中i=n/2,n/2+1,…,n/4;DFi= 其中i=3n/4,3n/4+1,…,n;EF0= ;FiFi+1= 其中i=0,1,…,n-1。
天圆地方面积计算公式(二)

天圆地方面积计算公式(二)天圆地方面积计算公式1. 圆的面积计算公式圆的面积计算公式是基于圆的半径的长度r:A=πr2其中,A表示圆的面积,π是圆周率(约等于),r是圆的半径。
例子:如果圆的半径为5cm,那么它的面积可以通过公式计算:A=π⋅(5cm)2≈2所以,圆的面积约为平方厘米。
2.正方形的面积计算公式正方形的面积计算公式是基于正方形的边长a:A=a2其中,A表示正方形的面积,a是正方形的边长。
例子:如果正方形的边长为6cm,那么它的面积可以通过公式计算:A=(6cm)2=36cm23. 矩形的面积计算公式矩形的面积计算公式是基于矩形的长l和宽w:A=l⋅w其中,A表示矩形的面积,l是矩形的长,w是矩形的宽。
例子:如果矩形的长为10cm,宽为8cm,那么它的面积可以通过公式计算:A=10cm⋅8cm=80cm2所以,矩形的面积为80平方厘米。
4.三角形的面积计算公式三角形的面积计算公式是基于三角形的底长b和高ℎ:A=12⋅b⋅ℎ其中,A表示三角形的面积,b是三角形的底长,ℎ是三角形的高。
例子:如果三角形的底长为6cm,高为4cm,那么它的面积可以通过公式计算:A=12⋅6cm⋅4cm=12cm2总结以上是常见几何形状的面积计算公式:圆、正方形、矩形和三角形。
通过这些公式,我们可以方便地计算出不同形状的区域面积。
在实际应用中,我们可以将这些公式运用到建筑设计、土地测量和其他几何学相关领域中。
无论是计算自然界中的地理面积,还是设计人造物体的形状,这些公式都能提供重要的计算工具。
天圆地圆折弯角度计算公式

天圆地圆折弯角度计算公式在日常生活中,我们经常会遇到需要计算角度的情况,比如在建筑设计、工程施工、地理测量等领域。
而在这些领域中,天圆地圆折弯角度计算公式是一个非常重要的工具,它可以帮助我们准确地计算出角度,从而保证工程的准确性和可靠性。
天圆地圆折弯角度是指在地球表面上两点之间的曲线路径所形成的角度。
在地理测量中,我们经常需要计算两个地理位置之间的角度,以便确定方向和距离。
而天圆地圆折弯角度计算公式就是用来计算这种角度的工具。
天圆地圆折弯角度计算公式是基于地球的球面几何原理推导而来的,它可以帮助我们在地球表面上准确地计算出两点之间的角度。
这个公式的推导过程比较复杂,涉及到大量的数学知识和地理知识,但是在实际应用中,我们只需要记住这个公式就可以了。
天圆地圆折弯角度计算公式的表达形式如下:cosθ = sinφ1sinφ2 + cosφ1cosφ2cos(λ2-λ1)。
其中,θ表示两点之间的角度,φ1和φ2分别表示两点的纬度,λ1和λ2分别表示两点的经度。
这个公式可以帮助我们在给定两个地理位置的经纬度的情况下,准确地计算出这两个地理位置之间的角度。
在实际应用中,我们可以通过这个公式来计算出两个地理位置之间的角度,然后根据这个角度来确定两点之间的方向和距离。
这对于地理测量和导航来说是非常重要的,可以帮助我们准确地确定出行的方向和距离,从而避免迷失方向和浪费时间。
除了在地理测量和导航中的应用,天圆地圆折弯角度计算公式还可以在建筑设计和工程施工中发挥重要作用。
在建筑设计中,我们经常需要计算出建筑物之间的角度,以便确定建筑物的布局和朝向。
而在工程施工中,我们也需要计算出工程设施之间的角度,以便确定施工的方向和距离。
总之,天圆地圆折弯角度计算公式是一个非常重要的工具,它可以帮助我们在地球表面上准确地计算出两点之间的角度,从而在地理测量、建筑设计、工程施工等领域发挥重要作用。
掌握这个公式可以帮助我们更好地进行地理测量和导航,更准确地确定建筑物的布局和朝向,更有效地进行工程施工。
天圆地方

小议天圆地方中图分类号:[f287.2] 文献标识码:a 文章编号:小议天圆地方前言在钣金展开放样中,有一类方圆过渡接头,俗称“天圆地方”。
这种构件广泛存在于各类工业管道中,是常用构件之一,那么它是如何方圆过渡的呢?1、正天圆地方下面以一个正天圆地方来说明它的成形原理。
首先画出天圆地方如图1,图中a、d点为圆的象限点,b、c为线段bc的端点。
连接ab、ac、cd,因为是正天圆地方,其余处于此处相同,因此只讨论此处成形原理即可。
2、天圆地方成形原理我们知道一个点和一个直线可以确定一个平面,因此点a与线段bc可以确定一个平面,abc是一个平面三角形。
ad这段曲线是1/4圆弧,它与c点所形成的面只能是曲面。
这个曲面在一些钣金展开放样的书籍中认为是不可展曲面,还有些书中只是说明如何展开,没有说明这是一个什么曲面。
要想说明这个曲面,我们先回顾一下有关的基础知识:a、曲面上相邻两素线如果平行或相交,则该曲面为可展曲面,否则为不可展曲面。
b、一直母线沿一曲导线运动并始终通过一定点所形成的曲面称为锥面。
c、当锥面的曲导线为圆,锥顶点与圆心的连线又不垂直于圆时,所形成的锥面称为椭圆锥面。
d、由于锥面上相邻两素线为过锥顶的相交两直线,所以锥面是可展曲面。
再来看看天圆地方的曲面部分,它是一直母线沿曲导线圆并始终通过一定点c所形成的曲面,oc连线不垂直于圆,因此这个曲面是椭圆锥面。
从图1可以看出这个曲面是椭圆锥面的一部分。
图13、天圆地方的构成通过以上分析,我们可以得到这样的结论:天圆地方是由四个三角形和四个曲面组成,其中曲面是椭圆锥的一部分,是可展曲面。
4、天圆地方的展开天圆地方的展开方法在有关钣金展开的书籍中都有详细介绍,在此不做讨论,下面介绍一些有别于传统的展开方法。
4.1、在autocad中做展开。
在autocad中也可以按照传统方法展开,只不过放样是在电脑上进行,其他都没有什么变化。
但在autocad中还有一种简单快捷的方法:立体线框法。
天圆地方的计算方法

一、虾米腰弯头的画法(以90°为例,其他角度相同)如上图,要画出虾米腰弯头至少要有4个参数:1、直径(φ377)、2、弯曲半径(R500)3、弯头角度数(B=90°)4、弯头节数。
好多人不明白弯曲半径是什么,仔细看一下上面的图,两个弯头除了弯曲半径不相同,其他参数完全相同。
弯曲半径越大,弯头占空间越大,自己体会一下。
虾米腰弯头画图步骤:1、以O点为起点,先画出弯头角度数B=90°(2条射线),然后以O点为圆心,按弯曲半径画圆弧相交于两射线 A点和B点。
再分别按各节角度画射线重点:第一节的夹角A=22.5°的计算公式:需要注意的是:虾米腰弯头各节的角度不是总角度除以节数,这是错误的!不论多少节的虾米腰弯头都应这样分节:第一节和最后一节的角度是中间节角度的一半,因此可推导出上面的公式。
2、以A点为中点,画出弯头的直径(377),并在两端点画垂直于直径线的2条线;相交于第一节的“节线”E和E’点。
3、同样步骤画出第三节,并连接各个交点,完成弯头的尺寸图4、如果是3节以上的弯头(如上图为5节),中间节角度必定是第一节和最后一节角度的2倍。
然后以OE和OE’为半径截取各个角度的射线,连接各个交点,即可画出完整的虾米腰弯头。
二、放样展开通俗讲展开就是将一个空间面“拍平”到一个平面。
如下图(第一节的半部分,将直径377圆等分12等份),将左面黄线部分的空间曲面“拍平”后到右边的平面。
请仔细观察一下各个点之间的关系虾米腰弯头各节经过扭转对齐后可组成一个直管(如下图),由于第一节、最后一节是中间节的一半,所以只需展开第一节就可以了。
从点1处将第一节“剪开”,“拍平”后,其长度为377*3.1416=1184.38 ,等分为12等份(图上只画出一半),向上画12条垂直线,其高度从左面第一节各个点量出后,在对应的垂线上截取。
平滑连接得到的各个点,完成展开图。
有的放样展开是这样形状的(下图):其实只是剖切的点不同,上图剖切点在第一节的最短处(1点),下图剖切点在点4处三、弯头厚度的处理以上放样展开过程没有厚度问题,在薄壁弯头时可以。
