矩形高层建筑横风向风振动力反应分析计算
超高层建筑在正弦风荷载作用下的横向振动

随着 社会 经济 以及 建筑 学 的不 断 发展 , 高层 建
第1 0卷 第 l 期
21 0 1年 2月
江 南 大 学 学 报 (自 然 科 学 版 )
J u n l f in n nUnv ri ( t r l ce c dt n o r a a g a ie st Nau a in eE i o ) oJ y S i
V0 .1 N0 1 0 .1
i v si a e n e tg t d.Th o d r s u d t e o i e f r a d t e wo k i s me o b o y wi d. e l a s a e a s me o b fsn o m n h r sas u d t e d ne b n
c 0 di a e a e s l e r m h a h m ai a o e . The t e r tca e uls s o t a i r to o r n t s c n b ov d fo t e m t e tc lm d 1 h o e i lr s t h w h tv b a i n
F . eb 2 01l
超高 层 建 筑 在 正 弦 风 荷 载作 用下 的横 向振 动
李 成
( 中国科 学技 术 大 学 苏 州 研 究 院 , 国科 学 技 术 大 学 一 港 城 市 大 学联 合 高 等研 究 中心 , 苏 中 香 江
苏州 , 1 13 252 ) 摘 要 : 究 了超 高层建 筑在 变化 的风荷 载作 用下的振 动 响应 。 风荷 载假 设 为正 弦变化 的外 力 . 研 将
The v ra i ns o br to r qu n y n ta s e s s l e n t e pe t t i a e g t a i to fvi a i n fe e c a d r n v r e dip ac me t wih r s c o tme nd h i h
[应用]高层建筑结构在风荷载作用下的振动分析[1]
![[应用]高层建筑结构在风荷载作用下的振动分析[1]](https://img.taocdn.com/s3/m/471aa4489b6648d7c1c746f2.png)
高层建筑结构在风荷载作用下的振动分析[1]致振动。
脉动风压是由于大气的湍流运动形成的动荷载。
建筑物周围脉动风压作用见图3[ 4 ]。
致振动。
脉动风压是由于大气的湍流运动形成的动荷载。
建筑物周围脉动风压作用见图3[ 4 ]。
第34卷第24期山西建筑Vol. 34 No. 24·86·2008年8月SHANXI ARCHITECTUREAug. 2008·结构·抗震·文章编号:100926825 (2008) 2420086202高层建筑结构在风荷载作用下的振动分析秦力张学礼徐德永摘要:通过介绍我国高层建筑结构风荷载设计方法、风荷载作用形式及由风荷载引起的结构振动,结合工程实例,进行了较详细的结构振动反应计算,以供同类型风荷载作用下的振动分析参考借鉴。
关键词:高层建筑结构,脉动风压,结构振动中图分类号:TU312. 10 引言高层建筑上作用的水平荷载包括风荷载和水平地震作用。
风的作用是不规则的,风压随着风速、风向的紊乱变化而不断的变化。
风荷载是随时间波动的动力荷载。
对高层建筑而言,动力荷载是引起结构毁灭性破坏的主要原因,因此,在高层建筑结构设计和安全性评价时,进行结构的动力反应分析是非常必要的。
为简,对高度大且较柔的高层建筑,必须考虑其动力效应影响[1]化起见,某些结构设计规范或结构动力反应分析中的抗风分析采用一些拟静力计算方法[2] ,如风压采用等效静力形式,但仍必须进行结构的动力分析。
对于高层和超高层建筑的风振动力反应主要有以下3方面的考虑:1)由风振产生的惯性力在结构中引起附加应力;2)建筑结构振动加速度会使生活和工作在其中的人产生不舒适感[3] ;3)由于风振反应发生的频度较高,有可能使结构产生疲劳效应[2]。
文中通过介绍我国高层建筑结构风荷载设计方法、风荷载的作用形式及由风荷载引起的结构振动,详细论述了结构在顺风向、横风向脉动风荷载作用下和二者共同作用下产生的扭转作用的处理过程和引起结构振动反应分析的最新研究。
矩形高层建筑横风向动力风荷载解析模型

1 风 洞 试 验
本次 豉验在 中 国空气 动力研 究与 发展 中心 低速 所进行 , 试验风洞 为 宽I4 高 14 .m、 m
收稿 日期 :o 1 1l; 修 订 日期 : O —53 2 0 o 9 2 l a8 O o 基 盒项 目 : 象 自然 科 学 基 盘 资 助项 目 f 准 5 8. j 圈 批 %7 00 5 作 者简 介 : 舡 粜 f90) . ^学 木 建筑 工 学 院教 授 . 事缩 } 动 力学 、 梅 抗 研 究 弛 15- . 武 从 茸 墙
面 的 建 筑 物 涡 潋 磷 风 力 的 主 要 和 可靠 手 段 。 自 8 0年 代 来 , 工 程 界 对 矩 形 建 筑 物 的 横 风
风 向动力风荷 载作 了不少 的风洞试 验研 究 , 只局 限于少数截 面 长宽 比。 此基础 上提 出 但 在 的横 风力 谱解 析 函数也不 够准确 完善 , 其是高 频部 分下 降太 h, 尤 央 与试验结 果不符 。本 文 作者 在对边 界层 风 洞 中不 同长宽 比 、 宽 此的矩形 截 面刚性 模 型 脉动 风 压测 量数 据 的 处 高 理 、 析的基础 上 . 出适用 于各种 长宽 比、 分 提 高宽 比矩形 建筑 物 的横 风力功率谱 密度 函数 、 均方根 升力 系数 和 S oh l 的经验 公式 , ) ua 数 r 井给 出相 干 函数 的表 达式及其参 数 的建议值
片如 图 2
。 04 02 n
模 型 为木 制 , 自振 频率 远 远 超 出风 的 其 频率范 围 , 以认 为删 可 , 考虑 由于模 不 啦
证 明它是合理有效的 . 可在此基础上建立高 层建筑横风 向动力响应 的频域计算方法:
关 键 词 : 层建 筑 ; 荷载 ; 洞 试 验 i 力 系 数 ; 厥 力 谱 高 风 风 升 横
风荷载计算软件方法与要求规范方法进行比较

风荷载是空气流动对工程结构所产生的压力。
风荷载也称风的动压力,是空气流动对工程结构所产生的压力。
风荷载与基本风压、地形、地面粗糙度、距离地面高度,及建筑体型等诸因素有关。
中国的地理位置和气候条件造成的大风为:夏季东南沿海多台风,内陆多雷暴及雹线大风;冬季北部地区多寒潮大风。
其中沿海地区的台风往往是设计工程结构的主要控制荷载。
台风造成的风灾事故较多,影响范围也较大。
雷暴大风可能引起小范围内的风灾事故。
一《建筑结构荷载规范》GB50009-2012中所规定的顺风向风荷载的具体计算1 顺风向风荷载2012规范关于顺风向风荷载的计算公式没有形式上的变化,仍然采用平均风压乘以风振0ωμμβωκz s z = (1)其中: k ω— 风荷载标准值(kN/m 2); z β— 高度z 处的风振系数;s μ— 风荷载体型系数;z μ— 风压高度变化系数; 0ω— 基本风压。
如果不考虑结构在风荷载作用下的动力响应,则由平均风压引起的静荷载取决于体型系数、风压高度变化系数及基本风压这三项因素,下面讨论顺风向作用下的静荷载计算:1.1 基本风压中国规定的基本风压w 0 以一般空旷平坦地面、离地面10米高、风速时距为10分钟平均的最大风速为标准,按结构类别考虑重现期(一般结构重现期为30年,高层建筑和高耸结构为50年,特别重要的结构为100年),统计得最大风速v (即年最大风速分布的96.67%分位值,并按w 0=ρv 2/2确定。
式中ρ为空气质量密度;v 为风速)。
根据统计,认为离地面10米高、时距为10分钟平均的年最大风压,统计分布可按极值I 型考虑。
基本风压因地而异,在中国的分布情况是:台湾和海南岛等沿海岛屿、东南沿海是最大风压区,由台风造成。
东北、华北、西北的北部是风压次大区,主要与强冷气活动相联系。
青藏高原为风压较大区,主要由海拔高度较高所造成。
其他内陆地区风压都较小。
风速风速随时间不断变化,在一定的时距Δt 内将风速分解为两部分:一部分是平均风速的稳定部分;另一部分是指风速的脉动部分。
2012新规范风荷载计算及其在PKPM软件中的实现

度变化系数 及基本风压 这三项因素,下面首先讨论顺风向作用下的静荷载计算:
1.1 基本风压
2012 规范在 2001 规范数据的基础上进行了重新统计,部分城市在补充新的气象资料重新统计后,基本 风压有所提高。
1.2 体型系数
2012 规范中表 8.3.1 中增加了第 31 项,对于高度超过 45m 的矩形截面高层建筑需考虑深宽比 D/B 对背 风面体型系数的影响。当平面深宽比 D/B≤1.0 时,背风面的体型系数由-0.5 增加到-0.6,矩形高层建 筑的风力系数也由 1.3 增加到 1.4 。 8.3.2 条还增加了矩形平面高层建筑的相互干扰系数取值。 在 PKPM 软件中,基本风压和体型系数由设计人员直接指定,以上两项变化需由设计人员确认并在软 件参数中体现,软件不做改变。
1.3 风压高度变化系数
2012 规范在保持划分 4 类粗糙度类别不变的情况下,适当提高了 C、D 两类粗糙度类别的梯度风高度,
由 400m 和 450m 分别修改为 450m 和 550m。B 类风速剖面指数由 0.16 修改为 0.15,适当降低了标准
场地类别的平均风荷载,具体变化如下:
2001规范
图4 从图 4 对比可知 2012 规范四类场地的风振系数均比 2001 规范明显提高,为比较相对变化规律,对于
100 米、200 米和 400 米的结构,分别比较了不同高度处风振系数 2012 规范相比 2001 规范的百分比差 异,以 C 类地区为例,仍然假定基本风压 0.5KN/m2,阻尼比 5%,高宽比等于 5,考虑结构基本周期
≥ 0.74
µ
C z
= 0.544
z
0.44
10
µ
C z
≥
高层建筑风振加速度计算、计算案例、风振控制系统性能参数的确定

(A.1.3)
式中:
——迎风面体型系数;
——背风面体型系数;
【条文说明】根据广东省《建筑结构荷载规范》(DBJ 15-101-2014),对于高度超过45m的矩形截面高层建筑,迎风面及背风面体型系数可按下表取值:
D/B
≤1
1.2
2
≥4
迎风面体型系数
+0.8
背风面体型系数
-0.6
-0.5
-0.4
空气密度 也可根据所在地的海拔高度按下式近似估算:
式中: ——海拔高度(m);
当取 时,式(A.1.1-2)可以转换为:
将上式代入式(A.1.1-1)可得:
A.1.2
(A.1.2)
式中:
——顺风向一阶频率(Hz),可按照《建筑结构荷载规范》(DBJ 15-101-2014)附录F.2近似确定;
【条文说明】峰值因子为与结构自振频率相关的量,根据本公式计算高层结构周期1~7s时对应的加速度峰值因子数值介于3.18~3.74之间,大于国标标准《建筑结构荷载规范》(GB50009)和广东省《建筑结构荷载规范》(DBJ 15-101-2014)峰值因子2.5。
——湍流尺度 在参考高度H处的值(m);
——建筑顶部H处风速(m/s),按本规程式(A.1.1-2)计算;
——迎风面宽度(m);
——建筑顶部高度(m)。
A.1.7
(A.1.7)
式中:
——楼层总数;
——第 层质量(kg);
——第 层顺风向一阶振型系数。
【条文说明】当无法获得实际振型系数 、 、 时,可取 进行计算,其中 为 层高度。
附录A
1 顺风向风振加速度计算
A.1.1
(A.1.1-1)
高层建筑顺风向和横风向风振加速度计算
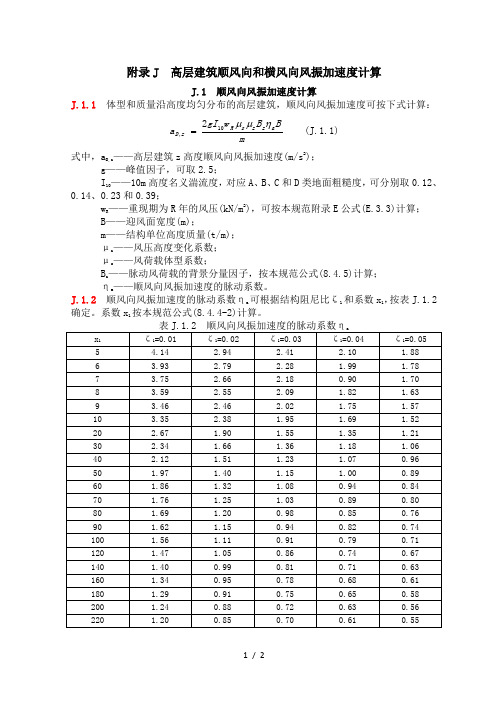
附录J 高层建筑顺风向和横风向风振加速度计算J.1 顺风向风振加速度计算J.1.1 体型和质量沿高度均匀分布的高层建筑,顺风向风振加速度可按下式计算:mBB w gI a a z z s R z D ημμ10,2=(J.1.1)式中,a D,z ——高层建筑z 高度顺风向风振加速度(m/s 2);g ——峰值因子,可取2.5; I 10——10m 高度名义湍流度,对应A 、B 、C 和D 类地面粗糙度,可分别取0.12、0.14、0.23和0.39;w R ——重现期为R 年的风压(kN/m 2),可按本规范附录E 公式(E.3.3)计算; B ——迎风面宽度(m);m ——结构单位高度质量(t/m); μz ——风压高度变化系数; μs ——风荷载体型系数;B z ——脉动风荷载的背景分量因子,按本规范公式(8.4.5)计算; ηa ——顺风向风振加速度的脉动系数。
J.1.2 顺风向风振加速度的脉动系数ηa 可根据结构阻尼比ζ1和系数x 1,按表J.1.2确定。
系数x 1按本规范公式(8.4.4-2)计算。
J.2.1 体型和质量沿高度均匀分布的矩形截面高层建筑,横风向风振加速度可按下式计算:)(2)(8.211110,a smFL L H R z L C S z mBw gI a ςςπφμ+=(J.2.1)式中:a L,z ——高层建筑z 高度横风向风振加速度(m/s 2);g ——峰值因子,可取2.5;W R ——重现期为R 年的风压(kN/m 2),可按本规范附录E 第E.3.3条的规定计算; B ——迎风面宽度(m);m ——结构单位高度质量(t/m);μH ——结构顶部风压高度变化系数;S FL ——无量纲横风向广义风力功率谱,可按本规范附录H 第H.2.4条确定; C sm ——横风向风力谱的角沿修正系数,可按本规范附录H 第H.2.5条的规定采用;φL1(z)——结构横风向第1阶振型系数; ζ1——结构横风向第1阶振型阻尼比;ζa1_——结构横风向第1阶振型气动阻尼比,可按本规范附录H 公式(H.2.4-3)计算。
矩形截面结构横风向风振校核

矩形截面结构横风向风振校核1 规范依据一旦在参数中勾选“考虑横风向风振”并选取了“规范矩形截面结构”,程序将无条件依据《建筑结构荷载规范》(GB 50009-2012)第8.5.2-3条的方法计算结构的横风向风振等效风荷载,计算程序不作关于规范适用性的判断,任何结构,尤其是平面或立面体型较复杂的结构,都应在确有依据的前提下,再慎重采用程序计算结果。
要特别注意:该版本所有计算和校核结果都仅适用于单塔结构。
以下校核结果依据规范H.2.1条,仅供初步设计参考,不作为最终设计依据。
2 已知条件结构总高度(不计入地下室)H=18m,结构2/3高度处楼层为第3层,该层迎风面宽度B=21.60m, 平面进深D=54.60m,X向横风向第1阶自振周期T Lx=0.30, Y向横风向第1阶自振周期T Ly=0.30,(请注意确认此项周期值是否正确!)基本风压W0=0.31(kN/m2), 地面粗糙度类别为B类,3 校核过程H/SQRT(BD)=18/SQRT(21.60×54.60)=0.52 ,深宽比D/B=54.60/21.60=2.53结构顶部风压高度变化系数μH=1.19,空气密度ρ=1.25(kg/m3),根据公式(8.5.3-3),结构顶部风速V H=sqrt(2000×μH×W0/ρ)=sqrt(2000×1.19×0.31/1.25)=24.13V H T Lx/SQRT(BD)=24.13×0.30/sqrt(21.60×54.60)=0.21,V H T Ly/SQRT(BD)=24.13×0.30/sqrt(21.60×54.60)=0.21,4 结论深宽比D/B=2.53不满足0.5~2,高宽比H/SQRT(BD)=0.52不满足4~8; V H T Lx/SQRT(BD)=0.21,满足≤10的要求;V H T Ly/SQRT(BD)=0.21,满足≤10的要求;以上仅供参考,请参照荷载规范H.2.1条自行进行完整判断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∂U i ∂ u ′j 形 ∂X j ∂X i
式的项(即“紊动-剪切”)项,使分析工作得到简化 而又能保证必要的精度, 并展开源项, 再运用 Taylor 关于湍流冻结假定[10,11]得: 1 ∂ 2 p′ ∂ 2 p′ + 2 = U c2 ∂t 2 ∂ y
Fig.1
图 1 风压谱公式计算结果与足尺观测数据 Wind pressure spectrum data from suggested equation and from full scale measureement
摘
要:从湍流理论的基本方程出发,根据 Taylor 关于湍流的“冻结”假定,导出了湍流脉动风压谱密度函数的
解析计算公式。在分析过程中考虑了压力控制方程源项中全部“紊动-剪切”项的影响。若取用合适的湍流积分尺 度,则由此公式得出的横风向脉动风压谱密度函数值与足尺观测数据相吻合。在接近建筑物第一阶自振频率附近 谱值函数高于由风洞实验得出的结果。因此根据湍流脉动风压谱密度函数计算得出的结构横风向风振动力反应位 移值与加速度值均高于由日本规范公式等计算得出的值。 关键词:脉动风压;谱密度函数;湍流;傅氏变换;对流速度;相关函数;随机过程 中图分类号:O357.5; TU311.3 文献标识码:A
EVALUATION OF ACROSS-WIND DYNAMIC RESPONSE FOR RECTANGULAR HIGH RISE BUILDINGS
*
GE Nan1 , HOU Ai-bo2 , ZHOU Xi-yuan1
(1. China Academy of Building Science, Beijing 100013, China; 2. Department of Architecture, Beijing Polytechnic University, Beijing 100022, China)
距距建筑物表面距离 建筑物表面距离 / m/ m
~ 关 于 脉 动 风 压 p ′( x , y , z , t ) 傅 氏 变 换 P ( x , y , z,ω ) 的 常 微 分 方 程 , 再 根 据 边 界 条 件 求 出 ~ ~ P ( x, y, z,ω ) , 并利用 P ( x , y , z , ω ) 与脉动风压 谱密度函数 S ( x, y , z , ω ) 之间的关系就可以求出建
α1 = 0.5 [8];U 0 ( z ) :离地面 z 高度处剪切区外自由
⎛z⎞ 来风风速/(m/s);U 0 ( z ) = U 0 ⎜ ⎟ ,U 0 :建筑物顶 ⎝h⎠
α
82
工
程
力
学
部自由来风风速/(m/s); z :距地面高度/m;h:建 筑物高度/m;α :地面粗糙度指数;ρ :空气密度, 0.00129 t/m3;t:时间/s。带有上标“−”的表示是 对时间取平均值的量;带有上标“'”的表示是脉 动的量。 若在式(1)两端取对时间的傅氏变换, 使其成为
Abstract: According to Taylor’s Frozen Assumption about turbulence, an analytical solution of spectral density function of pressure fluctuation in across-wind direction was derived from the governing equation of flow movement in turbulence theory. All of the turbulence-mean components in the source term of pressure governing equation had been taken into account. If an appropriate turbulence integral scale is adopted, the spectrum density function value will correspond well to the results from full scale measurements. The function value near the basic natural frequency of building is larger than that from wind tunnel test. The displacement and the acceleration value evaluated with this fluctuating pressure load are larger than those from Japanese design code. Key words: fluctuating wind pressure; spectral density function; turbulence; Fourier transform; convective velocity; correlation function; stochastic process 在建筑物正向来风时, 结构同时受到顺风向与横 风向脉动风荷载的作用。由于横风向脉动风荷载的 复杂性,目前还没有建立其解析形式的模型。现在 一般处理这个问题的基本方法是采用风洞试验与 原型观测。到目前为止国内外已做过不少这方面的 试验与理论研究并取得了一定的成果,但是尚不能 满足工程应用的实际需要,例如加拿大西安大略大 ———————————————
当来风风速小于共振风速时,结构传递函数也 有可能与较高风压谱密度值区域重合,使结构的风 振反应值放大。这时若应用以上的风压谱值计算风 振动力反应, 有可能低估其数值。 在建筑物风场中, 由漩涡脱落引起的横向扰力与湍流脉动风压是同 时存在的,可能是一种因素占据主导地位而另一种 因素占据次要的地位。周围的湍流对于建筑物的影 响是不可忽略的。应建立尽可能符合实际情况的横
b 是结构面迎风向宽度; S t 是结构斯特卢哈数,它
反映了结构尾流中漩涡脱落的频率与风速和结构 横向尺寸之间的关系。因此横风向脉动风压谱密度 函数应为在这一频率处的窄带函数。但是由于风场 的高度复杂性,建筑物背后的漩涡脱落频率也有可 能是随机值而非某一固定值,其统计样本中占优势 的值为与漩涡脱落对应的斯特卢哈数所对应的频 率值。 有些足尺观测结果反映了与以上风洞实验数 据的不同特性[8],在观测得到的横风向风压谱曲线 中没有出现上述曲线中的峰值(见图 1), 并且当频率 较高以至于接近建筑结构第一阶自振频率时,谱值 可能仍然处于较高的水平。
[7] 6
风向脉动风荷载模型。 参考文献[3]归纳总结了过去 的研究给出的横风向激励力谱密度函数的数学描 述公式,并指出虽然这些公式都经过了风洞试验的 检验,也存在有不足之处,试验结果都表明湍流的 影响明显地改变了谱密度函数的形状,提出了将涡 激力谱与湍流的影响分离开研究的想法。 本文从湍流理论出发建立了横风向脉动风荷 载谱密度函数解析模型,从机理上分析了横风向湍 流脉动风压的形成机制,并与风洞试验数据及足尺 观测数据做了对比、分析和验证。最后根据结构随 机振动理论谱分析方法计算了建筑物在湍流脉动 风压作用下的风振动力反应值,并与日本公式的计 算结果作了对比。工程力学 Nhomakorabea81
及动力反应内容最为详细的是日本的建筑规范[6], 其中给出了由尾流中的漩涡脱落引起的横风向脉 动风荷载计算公式与风振动力反应计算方法。对高 层建筑横风向振动有影响的风速都处于跨临界风 速的范围(即流动雷诺数 Re≥3.5×10 , 与此雷诺数 相应的来风平均风速下限值仅为 2m/s~5m/s。事实 上对结构有影响的风速远高于此下限值)。 已有的风 洞试验数据表明 : 当来风速度处于跨临界范围时, 结构背后的尾流十分紊乱,但总的来说呈现有规律 的漩涡脱落。在这个范围内尾流漩涡按某一固定的 频率 n 脱落( n = S t × v / b )。v 是流场中的特征风速;
式。由于在式 (2) 中要用到脉动风速的时间相关函 数,根据 Taylor 关于湍流冻结假定,用脉动风速空 间相关函数代替了时间相关函数[10]。 为了计算方便,将整理后的式(2)无量纲化,引 ˆ ,V ˆ, x ˆ, y ˆ, β , 其中: 入如下无量纲参数: ξ ,η , ζ , f , γ ,U
第 24 卷第 10 期 2007 年 10 月
Vol.24 No.10 Oct. 2007
工
程
力
学 80
ENGINEERING MECHANICS
文章编号:1000-4750(2007)10-0080-07
矩形高层建筑横风向风振动力反应分析计算
*
葛 楠 1,侯爱波 2,周锡元 1
(1. 中国建筑科学研究院,北京 100013;2. 北京工业大学建筑工程学院,北京 100022)
筑物横向边墙上任一点 ( x,0, z ) 处的脉动风压谱密 度函数[12]:
150
100
~ ~ P ( x,0, z , ω ) P * ( x,0, z , ω ) S ( x, z , ω ) = lim (2) T →∞ 2πT ~ ~ 其中 P * ( x , 0 , z , ω ) 是 P ( x , 0 , z , ω ) 的复共轭形
1 湍流脉动风压谱密度函数的计算 公式
