2013东城区高三一模文科数学试卷及答案
【推荐】北京2013届高三文科试题分类汇编(含9区一模及上学期期末试题)专题12：算法
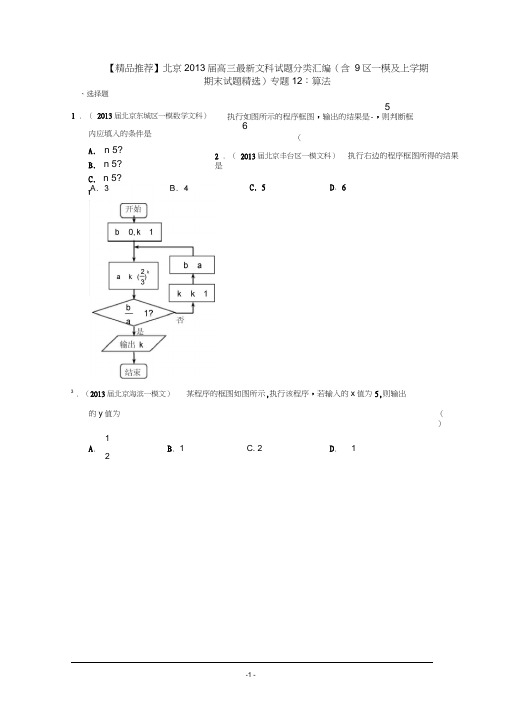
【精品推荐】北京2013届高三最新文科试题分类汇编（含 9区一模及上学期期末试题精选）专题12：算法、选择题5执行如图所示的程序框图，输出的结果是-，则判断框6（2 . （ 2013届北京丰台区一模文科） 执行右边的程序框图所得的结果是3. （2013届北京海滨一模文）某程序的框图如图所示,执行该程序，若输入的x 值为5,则输出的y 值为 （）1A .B . 1 C. 2 D . 121 . （ 2013届北京东城区一模数学文科）内应填入的条件是A.n 5? B. n 5? C. n 5? D.n 5?C. 5D . 64 . （2013届北京大兴区一模文科）执行如图所示的程序框图5 .（2013届北京西城区一模文科）执行如图所示的程序框图A. -42B. -21C. 11D. 43n A.- 6 B.nC.-3D..若n 4,则输出s的值是.若输出y .3,则输入角F y=审口1 f/输缶〃6 . （2013届房山区一模文科数学）执行如图所示的程序框图.若输出S 15,可以填入A. n4B. n8C. n16 则框图中①处（）D. n 167 .（北京市石景山区2013届高三上学期期末考试数学文试题）3, 则可输入的实数X值的个数为A. 1B. 2C. 3执行右面的框图, 若输出结果为（）D. 48 .（北京市朝阳区2013届高三上学期期末考试数学文试题）执行如图所示的程序框图. 若输入x 3，则输出k的值是x=x+5f t*箱束QA. 3B. 4 c. 5 D. 69 .（北京市东城区2013届高三上学期期末考试数学文科试题）执行如图所示的程序框图,（）输出10.11 .12. 的k的值为A. 4（北京市丰台区的S值为. A. 3（北京市海淀区序，若输入的/馆出七/B. 5C. 6 2013届高三上学期期末考试数学文试题）B. 6C. 7 2013届高三上学期期末考试数学文试题）p为24，则输出的n,S的值分别为A. n 4,S 30 C. n 5,S 30D. 7执行如图所示的程序框图,（）则输出D. 10某程序的框图如图所示，（）执行该程■开始n 1, S 0入PS =•n___S是' 1 r1 /输岀n，S /t ___结束B. n 4,SD. n 5,S4545（北京市通州区2013届高三上学期期末考试数学文试题）执行如图所示的程序框图, 输出的13.（北京市西城区2013S=S^C. 251 1D. 250 1届高三上学期期末考试数学文科试题）执行如图所示的程序框图, 则输/辑出占/. a•结東.A. 2、填空题B. 6C. 15D. 3114 . （2013届北京市延庆县一模数学文）执行如图的程序框图,如果输入p 6 ,则输出的15. （2013届北京门头沟区一模文科数学）如右图所示的程序框图，执行该程序后输出的结果是开始i 1，s 2| H = 74■厂16.（北京市东城区普通高中示范校2013届高三3月联考综合练习（二）(7W5=97=1^=1 （文）试题）某程序框图如图所示，该程序运行后输出的n的值是S=S+T17.（北京市昌平区2013届高三上学期期末考试数学文试题）已知某算程图如图所示，则程序运行结束时输出的结果为___________ .TET 工—■］即=7¥+ H/输出邸/法的流18.（北京市房山区2013届高三上学期期末考试数学文科试题（解析版）运行相应的程序，则输出n的值为•）阅读右边的程序框图,【精品推荐】北京 2013届高三最新文科试题分类汇编（含9区一模及上学期期末试题精选）专题12：算法参考答案选择题 A A A C D ； B 【答案】Cx ? 1x2解：本程序为分段函数 y' ，当x 2时，由x 2 1 3得，x 2 4，所以log 2x, x 2x 2。
2013届北京市东城区普通校高三11月联考数学(文)试卷
东城区普通校2012-2013学年第一学期联考试卷高三数学（文科）命题校：北京市崇文门中学 2012年11月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 150 分，考试用时 120分钟。
考试结束后，将本试卷和答题卡一并交回。
祝各位考生考试顺利！第Ⅰ卷一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．1. 设集合{x x U =}3<， {}1<=x x A ，则A C U = （ ）A ．{}31<≤x xB ．{}31≤<x xC ．}{31<<x x D ．{}1x x ≥2. 下列函数中在区间)(0,+∞上单调递增的是 （ ）A. sinx y =B. 2-x y =C. x y 3log =D. x)21(y =3. 设⎩⎨⎧<>=)0(,3)0(log )(3x x x x f x ，则)]3([-f f等于 ( )A. 3B. 3-C.31D. 1- 4. 已知二次函数()x f 的图象如图1所示 , 则其导函数()x f '的图象大致形状是（ ）5.“3=a ”是“函数22)(2+-=ax x x f 在区间[)+∞,3内单调递增”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件6．函数2)(-+=x e x f x的零点所在的区间是 （ ）A. （-2,-1）B. （-1,0）C. （1,2）D. （0,1）7. 将函数x y 2cos =的图象先向左平移2π个单位长度，再向上平移1个单位长度，所得图象对应的函数解析式是 ( ) A. x y 2sin -= B. x y 2cos -= C. x y 2sin 2= D. 22cos y x =-8. 某企业投入100万元购入一套设备．该设备每年的运转费用是0.5万元，此外每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元．为使该设备年平均费用最低，该企业（ ）年后需要更新设备. A. 10 B. 11 C. 13 D. 21第Ⅱ卷二、填空题：本大题共6小题，每小题5分，共30分． 9．已知),2(,135sin ππαα∈=，则=αtan . 10. 若数列{}n a 满足11=a ，)(2*1N n a a n n ∈=+，则3a = ；前5项的和5S = . 11. 已知)(x f 是定义在R 上的偶函数，并满足)()4(x f x f =+，当21≤≤x 时，2)(-=x x f ，则=)5.6(f .12. 设2log 31=a ，3log 2=b ，3.0)21(=c ，则a 、b 、c 从小到大的顺序是 .13. 已知命题021,:0200≤++∈∃x ax R x p . 若命题p 是假命题，则实数a 的取值范围是 .14. 已知函数)(x f 的定义域为A ，若其值域也为A ，则称区间A 为)(x f 的保值区间．若x m x x f ln )(-+=的保值区间是[,)e +∞，则m 的值为 .三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤. 15. (本小题满分12分)在锐角△ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，且32sin cA a =(Ⅰ) 确定角C 的大小；（Ⅱ）若c ＝7,且△ABC 的面积为233，求22b a +的值. 16. (本小题满分13分)已知函数2()cos 2sin f x x x x =-.（Ⅰ）若角α的终边与单位圆交于点)54,53(p ，求()f α的值； （Ⅱ）若[,]63x ππ∈-，求()f x 最小正周期和值域.17. (本小题满分13分)已知等差数列{}n a 满足：25a =，4622a a +=.{}n a 的前n 项和为n S . （Ⅰ）求n a 及n S ； （Ⅱ）若21()1f x x =- ,()n n b f a =（*n N ∈），求数列{}n b 的前n 项和n T . 18. （本小题满分14分）已知函数)1,0)(1(log )(),1(log )(≠>-=+=a a x x g x x f a a 且其中 （Ⅰ）求函数)()(x g x f +的定义域；（Ⅱ）判断函数)()(x g x f -的奇偶性，并予以证明；（Ⅲ）求使0)()(<+x g x f 成立的x 的集合.19. （本小题满分14分）已知322()2f x x ax a x =+-+．（Ⅰ）若1a =，求曲线)(x f y =在点))1(,1(f 处的切线方程； （Ⅱ）若0,a ≠ 求函数()f x 的单调区间； （Ⅲ）若不等式22ln ()1x x f x a '≤++恒成立，求实数a 的取值范围．20．（本小题满分14分).数列}{n a 的前n 项和为3,1=a S n 若，n S 和1+n S 满足等式,111+++=+n S nn S n n （Ⅰ）求2S 的值；（Ⅱ）求证：数列}{nS n是等差数列； （Ⅲ）若数列}{n b 满足n a n n a b 2⋅=，求数列}{n b 的前n 项和n T ；（Ⅳ）设322+=n n n T C ，求证：.272021>+⋅⋅⋅++n C C C东城区普通校2012-2013学年第一学期联考试卷高三数学（文科）参考答案（以下评分标准仅供参考，其它解法自己根据情况相应地给分）15.（本小题满分12分）解：（Ⅰ）解：∵ 32sin c A a = 由正弦定理得C c c A a sin 23sin == ………2分 ∴23sin =C ………………4分 ∵ ABC ∆是锐角三角形， ∴ 3π=C ………………6分（Ⅱ）解: 7=c , 3π=C 由面积公式得2333sin 21=πab ………………8分 ∴ 6ab = ………………9分由余弦定理得73cos222=-+πab b a ……………11分∴ 1322=+b a ………………12分 16．（本小题满分13分）解：（Ⅰ）∵ 角α的终边与单位圆交于点)54,53(p∴ 54sin =α，53cos =α， ………………2分 ∴2()cos 2sin f αααα=-24342()555=⨯-⨯=. ………………4分（Ⅱ）2()cos 2sin f x x x x =-cos 21x x =+-2sin(2)16x π=+- ………………8分∴最小正周期T=π ………………9分∵ [,]63x ππ∈-，所以65626πππ≤+≤-x ， ……………10分 ∴ 1sin(2)126x π-≤+≤， ………………12分 ∴ ()f x 的值域是[2,1]-. ………………13分 17．（本小题满分13分）解. （Ⅰ）设等差数列｛a n ｝的首项为a 1，公差为d∵ 25a =，4622a a +=∴ 2282,511=+=+d a d a ………………2分 解得 2,31==d a ………………4分 ∴ 12+=n a n n n S n 22+=, ………………6分 （Ⅱ）∵ 21()1f x x =-,()n n b f a = ∴ 211n n b a =- ………………7分 ∵12+=n a n ∴ )1(412+=-n n a n ∴ )1(41+=n n b n 111()41n n =-+ ………………9分n n b b b b T +⋅⋅⋅+++=321=14(1- 12+ 12- 13+…+1n -11n +) ………………11分=14(1-11n +) =4(1)n n +所以数列{}n b 的前n 项和n T =4(1)nn + . ………………13分18．（本小题满分14分）解：（Ⅰ）)()(x g x f +)1(log )1(log x x a a -++=由⎩⎨⎧>->+0101x x 11x -<<得………………2分所求定义域为{}R x x x ∈<<-,11| ………………3分 （Ⅱ）令)()()(x g x f x h -=1log (1)log (1)log 1a a ax x x x+=+--=- ………………4分 定义域为{}R x x x ∈<<-,11|()()x h xx a x x x x a x h -=-+-=-⎪⎭⎫⎝⎛-+=+-=-11log111log 11log∴ ()()f x g x -为奇函数 ……………8分 （Ⅲ）()1log 01log )1)(1(log )()(2a a a x x x x g x f =<-=-+=+……………9分 2101-x 1,-1001a x x ∴><<<<<<当时，得或当2011a <<>时，1-x . 不等式解集为空集综上： {}1101a x x >-<<<<当时，不等式的解集为或0 当01a <<时， 不等式的解集为空集 ……………14分 19．（本小题满分14分）解：（Ⅰ） ∵ 1=a ∴2)(23+-+=x x x x f ∴ 123)(2-+='x x x f …………1分∴ =k 4)1(='f ， 又3)1(=f ，所以切点坐标为)3,1( ∴ 所求切线方程为)1(43-=-x y ，即014=--y x . …………4分（Ⅱ）22()32()(3)f x x ax a x a x a '=+-=+-由()0f x '= 得x a =- 或3ax =…………5分 (1)当0a >时，由()0f x '<， 得3aa x -<<．由()0f x '>， 得x a <-或3ax >此时()f x 的单调递减区间为(,)3a a -，单调递增区间为(,)a -∞-和(,)3a+∞.…………7分 (2)当0a <时，由()0f x '<，得3ax a <<-． 由()0f x '>，得3ax <或x a >-此时()f x 的单调递减区间为(,)3a a -，单调递增区间为(,)3a -∞和(,)a -+∞. 综上：当0a >时，()f x 的单调递减区间为(,)3a a -，单调递增区间为(,)a -∞-和(,)3a+∞当0a <时，()f x 的单调递减区间为(,)3aa -单调递增区间为(,)3a-∞和(,)a -+∞.…………9分 （Ⅲ）依题意),0(+∞∈x ，不等式22ln ()1x x f x a '≤++恒成立, 等价于123ln 22++≤ax x x x 在(0,)+∞上恒成立可得xx x a 2123ln --≥在(0,)+∞上恒成立 ………………11分 设()x x x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=………………12分令0)(='x h ，得11,-3x x ==（舍）当10<<x 时，0)(>'x h ；当1>x 时，0)(<'x h当x 变化时，)(),(x h x h '变化情况如下表：∴ 当1=x 时,()x h 取得最大值, ()x h max =-2 2-≥∴a∴ a 的取值范围是[)+∞-,2. ………14分 20．（本小题满分14分）解：（I ）由已知:21122228S S a =+=+= …………2分 （II ）∵111n n n S S n n++=++ 同除以11:,11=-+++nS n S n nn 则有 …………4分}{nS n数列∴是以3为首项，1为公差的等差数列. …………6分（III ）由（II ）可知, 2*2()n S n n n =+∈N ……………7分113n a ∴==当时， 当12,21n n n n a S S n -≥=-=+时经检验，当n=1时也成立 ∴21(*)n a n n N =+∈ ………………9分211213521212(21)2,3252(21)2(21)2na n n n n n n nn n n b a b n T b b b b T n n +--+=⋅∴=+⋅=++⋅⋅⋅++∴=⋅+⋅+⋅⋅⋅+-⋅++⋅32121252)12(2)12(2)32(234++-⋅++⋅-+⋅-+⋅⋅⋅+⋅=n n n n n n n T …………10分解得：.982)9132(32-⋅+=+n n n T…………11分（Ⅳ）∵232111()23994n n n n T n C +==+-⋅ 411])41(1[4191912)1(3221--⋅-⋅++⋅=+⋅⋅⋅++∴n n n n n C C C n n n )41(2712719432⋅+-+=.2720271972719432=-≥-+>n n…………14分。
北京市东城区2012-2013第一学期高三期末数学统一练习文科 含答案
东城区2012-2013学年度第一学期期末教学统一检测高三数学 （文科）学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。
考试时长120分钟。
考生务必将答案答在答题卡上，在试卷上作答无效。
考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）设集合{1,2,3,4,5}U =，{1,2,3}A =，{2,3,4}B =，则()U A B I ð等于 (A) {2,3} (B) {1,4,5} (C) {4,5} (D) {1,5} （2）复数21i-等于 （A ）1i -- (B) 1i -+ ( C) 1i - ( D) 1i + （3）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d 等于（A ）1 （B ）53（C ）2 （D ）3 （4）执行如图所示的程序框图，输出的k 的值为（A ）4 （B ）5（C ）6 （D ）7（5）“2230x x -->成立”是“3x >成立”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件（6）已知x ，y 满足不等式组28,28,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩ 则目标函数3z x y =+的最大值为(A)332 (B)12 (C)8 (D)24（7）已知抛物线22y px =的焦点F 到其准线的距离是8，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且|||AK AF =，则AFK ∆的面积为（A ）32 （B ）16 （C ）8 （D ）4（8）给出下列命题：①在区间(0,)+∞上，函数1y x -=,12y x =,2(1)y x =-, 3y x =中有三个是增函数；②若log 3log 30m n <<，则01n m <<<；③若函数()f x 是奇函数，则(1)f x -的图象关于点(1,0)A 对称；④若函数()323xf x x =--，则方程()0f x =有2个实数根，其中正确命题的个数为（A ）1 （B ）2 （C ）3 （D ）4第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。
2013年北京市东城区高三数学文科一模试题及答案
北京市东城区2012-2013学年度第二学期高三综合练习（一）数学 （文科）第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）已知全集{1,2,3,4}U =，集合{1,2}A =，那么集合U A ð为（A ）{3}（B ）{3,4} （C ）{1,2} （D ）{2,3}（2） “1a =”是“直线20x y +=与直线(1)40x a y +++=平行”的（A ） 充分不必要条件 （B ） 必要不充分条件 （C ） 充要条件 （D ） 既不充分也不必要条件（3）已知ABCD 为平行四边形，若向量AB =a ，AC =b ，则向量BC 为（A ）-a b （B ）a +b（C ）-b a （D ）--a b（4）执行如图所示的程序框图，输出的结果是56，则判断框内应填入的条件是 （A ）5?n ≤ （B ）5?n < （C ）5?n > （D ）5?n ≥（5）已知一个几何体的三视图如图所示(单位：cm)， 那么这个几何体的侧．面积是（A ）2（B ）2（C ）2(4 （D ）2（6）已知点(2,1)A ，抛物线24y x =的焦点是F ，若抛物线上存在一点P ，使得PA PF +最小，则P 点的坐标为 （A ）(2,1)（B ）(1,1)（C ）1(,1)2（D ）1(,1)4（7）对于函数)(x f y =，部分x 与y 的对应关系如下表：数列n 满足1，且对任意，点1+n n 都在函数)(x f y =的图象上，则201320124321x x x x x x ++++++ 的值为（A ）9394 （B ）9380 （C ）9396 （D ）9400（8）已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23xf x =-.若函数()f x 在区间(1,)k k -（k ∈Z ）上有零点，则k 的值为2（A ）2或7- （B ）2或8- （C ）1或7- （D ）1或8-第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。
北京市东城区2013届高三数学11月联考试题 文 新人教A版
东城区普通校2012-2013学年第一学期联考试卷高三数学（文科）命题校：北京市崇文门中学 2012年11月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 150 分，考试用时 120分钟。
考试结束后，将本试卷和答题卡一并交回。
祝各位考生考试顺利！第Ⅰ卷一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求． 1. 设集合{xx U =}3<， {}1<=x x A ，则A C U = （ ）A ．{}31<≤x xB ．{}31≤<x xC ．}{31<<x x D ．{}1x x ≥2. 下列函数中在区间)(0,+∞上单调递增的是 （ ）A. sinx y =B. 2-x y =C. x y 3log =D. x)21(y =3. 设⎩⎨⎧<>=)0(,3)0(log )(3x x x x f x ，则)]3([-f f等于 ( )A. 3B. 3-C.31D. 1- 4. 已知二次函数()x f 的图象如图1所示 , 则其导函数()x f '的图象大致形状是（ ）5.“3=a ”是“函数22)(2+-=ax x x f 在区间[)+∞,3内单调递增”的（ ）A ．充分而不必要条件B ．必要而不充分条件w.w.w.k.s.C ．充分必要条件 w.w. .D ．既不充分也不必要条件6．函数2)(-+=x e x f x的零点所在的区间是 （ ）A. （-2,-1）B. （-1,0）C. （1,2）D. （0,1）7. 将函数x y 2cos =的图象先向左平移2π个单位长度，再向上平移1个单位长度，所得图象对应的函数解析式是 ( )A. x y 2sin -=B. x y 2cos -=C. x y 2sin 2= D. 22cos y x =-8. 某企业投入100万元购入一套设备．该设备每年的运转费用是0.5万元，此外每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元．为使该设备年平均费用最低，该企业（ ）年后需要更新设备. A. 10 B. 11 C. 13 D. 21第Ⅱ卷二、填空题：本大题共6小题，每小题5分，共30分． 9．已知),2(,135sin ππαα∈=，则=αtan . 10. 若数列{}n a 满足11=a ，)(2*1N n a a n n ∈=+，则3a = ；前5项的和5S = .11. 已知)(x f 是定义在R 上的偶函数，并满足)()4(x f x f =+，当21≤≤x 时，2)(-=x x f ，则=)5.6(f .12. 设2log 31=a ，3log 2=b ，3.0)21(=c ，则a 、b 、c 从小到大的顺序是 .13. 已知命题021,:0200≤++∈∃x ax R x p . 若命题p 是假命题，则实数a 的取值范围是 .14. 已知函数)(x f 的定义域为A ，若其值域也为A ，则称区间A 为)(x f 的保值区间．若x m x x f ln )(-+=的保值区间是[,)e +∞，则m 的值为 .三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤. 15. (本小题满分12分)在锐角△ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，且32sin cA a = (Ⅰ) 确定角C 的大小；（Ⅱ）若c ＝7,且△ABC 的面积为233，求22b a +的值. 16. (本小题满分13分)已知函数2()cos 2sin f x x x x =-.（Ⅰ）若角α的终边与单位圆交于点)54,53(p ，求()f α的值； （Ⅱ）若[,]63x ππ∈-，求()f x 最小正周期和值域. 17. (本小题满分13分)已知等差数列{}n a 满足：25a =，4622a a +=.{}n a 的前n 项和为n S . （Ⅰ）求n a 及n S ； （Ⅱ）若21()1f x x =- ,()n n b f a =（*n N ∈），求数列{}n b 的前n 项和n T . 18. （本小题满分14分）已知函数)1,0)(1(log )(),1(log )(≠>-=+=a a x x g x x f a a 且其中 （Ⅰ）求函数)()(x g x f +的定义域； （Ⅱ）判断函数)()(x g x f -的奇偶性，并予以证明；（Ⅲ）求使0)()(<+x g x f 成立的x 的集合.19. （本小题满分14分）已知322()2f x x ax a x =+-+．（Ⅰ）若1a =，求曲线)(x f y =在点))1(,1(f 处的切线方程； （Ⅱ）若0,a ≠ 求函数()f x 的单调区间； （Ⅲ）若不等式22ln ()1x x f x a '≤++恒成立，求实数a 的取值范围．20．（本小题满分14分).数列}{n a 的前n 项和为3,1=a S n 若，n S 和1+n S 满足等式,111+++=+n S nn S n n （Ⅰ）求2S 的值； （Ⅱ）求证：数列}{nS n是等差数列；（Ⅲ）若数列}{n b 满足n an n a b 2⋅=，求数列}{n b 的前n 项和n T ； （Ⅳ）设322+=n n n T C ，求证：.272021>+⋅⋅⋅++n C C C东城区普通校2012-2013学年第一学期联考试卷高三数学（文科）参考答案（以下评分标准仅供参考，其它解法自己根据情况相应地给分）解：（Ⅰ）解：∵ 32sin c A a = 由正弦定理得Cc c A a sin 23sin == ………2分 ∴23sin =C ………………4分 ∵ ABC ∆是锐角三角形， ∴ 3π=C ………………6分（Ⅱ）解: 7=c , 3π=C 由面积公式得2333sin 21=πab ………………8分 ∴ 6ab = ………………9分由余弦定理得73cos222=-+πab b a ……………11分∴ 1322=+b a ………………12分 16．（本小题满分13分）解：（Ⅰ）∵ 角α的终边与单位圆交于点)54,53(p∴ 54sin =α，53cos =α， ………………2分 ∴2()cos 2sin f αααα=-2434322()55525=⨯-⨯=. ………………4分（Ⅱ）2()cos 2sin f x x x x =-cos 21x x =+-2sin(2)16x π=+- ………………8分∴最小正周期T=π ………………9分∵ [,]63x ππ∈-，所以65626πππ≤+≤-x ， ……………10分 ∴ 1sin(2)126x π-≤+≤， ………………12分 ∴ ()f x 的值域是[2,1]-. ………………13分 17．（本小题满分13分）解. （Ⅰ）设等差数列｛a n ｝的首项为a 1，公差为d∵ 25a =，4622a a +=∴ 2282,511=+=+d a d a ………………2分 解得 2,31==d a ………………4分∴ 12+=n a n n n S n 22+=, ………………6分（Ⅱ）∵ 21()1f x x =-,()n n b f a = ∴ 211nn b a =- ………………7分 ∵12+=n a n ∴ )1(412+=-n n a n ∴ )1(41+=n n b n 111()41n n =-+ ………………9分n n b b b b T +⋅⋅⋅+++=321=14(1- 12+ 12- 13+…+1n -11n +) ………………11分=14(1-11n +) =4(1)n n +所以数列{}n b 的前n 项和n T =4(1)nn + . ………………13分18．（本小题满分14分）解：（Ⅰ）)()(x g x f +)1(log )1(log x x a a -++=由⎩⎨⎧>->+0101x x 11x -<<得………………2分所求定义域为{}R x x x ∈<<-,11| ………………3分 （Ⅱ）令)()()(x g x f x h -=1log (1)log (1)log 1a a ax x x x+=+--=- ………………4分 定义域为{}R x x x ∈<<-,11|()()x h xx a x x x x a x h -=-+-=-⎪⎭⎫⎝⎛-+=+-=-11log111log 11log∴ ()()f x g x -为奇函数 ……………8分（Ⅲ）()1log 01log )1)(1(log )()(2a a a x x x x g x f =<-=-+=+……………9分 2101-x 1,-1001a x x ∴><<<<<<当时，得或当2011a <<>时，1-x . 不等式解集为空集综上： {}1101a x x >-<<<<当时，不等式的解集为或0 当01a <<时， 不等式的解集为空集 ……………14分 19．（本小题满分14分）解：（Ⅰ） ∵ 1=a ∴2)(23+-+=x x x x f ∴ 123)(2-+='x x x f …………1分∴ =k 4)1(='f ， 又3)1(=f ，所以切点坐标为)3,1( ∴ 所求切线方程为)1(43-=-x y ，即014=--y x . …………4分 （Ⅱ）22()32()(3)f x x ax a x a x a '=+-=+-由()0f x '= 得x a =- 或3ax =…………5分 (1)当0a >时，由()0f x '<， 得3aa x -<<．由()0f x '>， 得x a <-或3ax >此时()f x 的单调递减区间为(,)3a a -，单调递增区间为(,)a -∞-和(,)3a+∞.…………7分 (2)当0a <时，由()0f x '<，得3ax a <<-． 由()0f x '>，得3ax <或x a >- 此时()f x 的单调递减区间为(,)3a a -，单调递增区间为(,)3a-∞和(,)a -+∞.综上：当0a >时，()f x 的单调递减区间为(,)3aa -，单调递增区间为(,)a -∞-和(,)3a+∞当0a <时，()f x 的单调递减区间为(,)3aa -单调递增区间为(,)3a-∞和(,)a -+∞.…………9分 （Ⅲ）依题意),0(+∞∈x ，不等式22ln ()1x x f x a '≤++恒成立, 等价于123ln 22++≤ax x x x 在(0,)+∞上恒成立可得xx x a 2123ln --≥在(0,)+∞上恒成立 ………………11分 设()x x x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=………………12分令0)(='x h ，得11,-3x x ==（舍）当10<<x 时，0)(>'x h ；当1>x 时，0)(<'x h当x 变化时，)(),(x h x h '变化情况如下表：∴ 当1=x 时,()x h 取得最大值, ()x h m ax =-2 2-≥∴a∴ a 的取值范围是[)+∞-,2. ………14分 20．（本小题满分14分）解：（I ）由已知:21122228S S a =+=+= …………2分 （II ）∵111n n n S S n n++=++ 同除以11:,11=-+++nS n S n nn 则有 …………4分 }{nS n数列∴是以3为首项，1为公差的等差数列. …………6分（III ）由（II ）可知, 2*2()n S n n n =+∈N ……………7分113n a ∴==当时， 当12,21n n n n a S S n -≥=-=+时经检验，当n=1时也成立 ∴21(*)n a n n N =+∈ ………………9分211213521212(21)2,3252(21)2(21)2na n n n n n n nn n n b a b n T b b b b T n n +--+=⋅∴=+⋅=++⋅⋅⋅++∴=⋅+⋅+⋅⋅⋅+-⋅++⋅32121252)12(2)12(2)32(234++-⋅++⋅-+⋅-+⋅⋅⋅+⋅=n n n n n n n T …………10分解得：.982)9132(32-⋅+=+n n n T…………11分（Ⅳ）∵232111()23994n n n n T n C +==+-⋅ 411])41(1[4191912)1(3221--⋅-⋅++⋅=+⋅⋅⋅++∴n n n n n C C C n n n )41(2712719432⋅+-+=.2720271972719432=-≥-+>n n…………14分。
【精品推荐】北京2013届高三最新文科试题分类汇编(含9区一模及上学期期末试题精选)专题12：算法
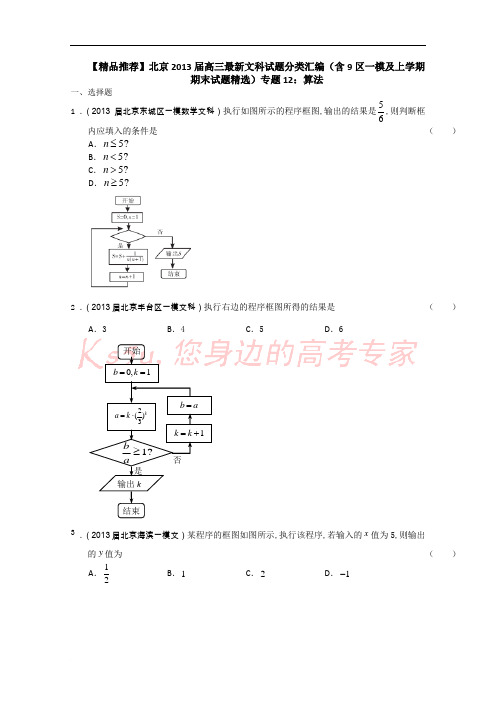
【精品推荐】北京2013届高三最新文科试题分类汇编（含9区一模及上学期期末试题精选）专题12：算法一、选择题1 ．（2013届北京东城区一模数学文科）执行如图所示的程序框图,输出的结果是56,则判断框内应填入的条件是（）A．5?n≤B．5?n<C．5?n>D．5?n≥2 ．（2013届北京丰台区一模文科）执行右边的程序框图所得的结果是（）A．3 B．4 C．5 D．63．（2013届北京海滨一模文）某程序的框图如图所示,执行该程序,若输入的x值为5,则输出的y值为（）A．12B．1C．2D．1-- 2 -4 ．（2013届北京大兴区一模文科）执行如图所示的程序框图.若4n =,则输出s 的值是（ ）A ．-42B ．-21 C ．11 D ．435 ．（2013届北京西城区一模文科）执行如图所示的程序框图.若输出y =则输入角=θ （ ）A ．π6B ．π6-C ．π3D ．π3--3 -6 ．（2013届房山区一模文科数学）执行如图所示的程序框图.若输出15S =, 则框图中① 处可以填入（ ）A ．4n >B ．8n >C ．16n >D ．16n <7 ．（北京市石景山区2013届高三上学期期末考试数学文试题）执行右面的框图，若输出结果为3， 则可输入的实数x 值的个数为 （ ）A ．1B ．2C ．3D ．4-4 -8 ．（北京市朝阳区2013届高三上学期期末考试数学文试题）执行如图所示的程序框图．若输入3x ，则输出k 的值是（ ）A ．3B ．4C ．5D ．69 ．（北京市东城区2013届高三上学期期末考试数学文科试题）执行如图所示的程序框图，输出-5 -的k 的值为（ ）A ．4B ．5C ．6D ．710．（北京市丰台区2013届高三上学期期末考试数学文试题）执行如图所示的程序框图，则输出的S 值为.（ ）A ．3B ．6C ．7D ．1011．（北京市海淀区2013届高三上学期期末考试数学文试题）某程序的框图如图所示, 执行该程序，若输入的p 为24的,n S 的值分别为（ ）A ．4,30n S ==B ．4,45n S ==C ．5,30n S ==D ．5,45n S ==12．（北京市通州区2013届高三上学期期末考试数学文试题）执行如图所示的程序框图，输出的- 6 -S 值为（ ）A ．5122-B ．5022-C ．5121-D ．5021-13．（北京市西城区2013届高三上学期期末考试数学文科试题）执行如图所示的程序框图，则输出S =（ ）A ．2B ．6C ．15D ．31二、填空题14．（2013届北京市延庆县一模数学文）执行如图的程序框图,如果输入6=p ,则输出的-7 -S=____.15．（2013届北京门头沟区一模文科数学）如右图所示的程序框图,执行该程序后输出的结果是____________.16．（北京市东城区普通高中示范校2013届高三3月联考综合练习（二）数学（文）试题）某程序框图如图所示,该程序运行后输出的n的值是___________.17．（北京市昌平区2013届高三上学期期末考试数学文试题）已知某算法的流程图如图所示，则程序运行结束时输出的结果为．-8 -18．（北京市房山区2013届高三上学期期末考试数学文科试题（解析版））阅读右边的程序框图，运行相应的程序，则输出n 的值为.- 9 -【精品推荐】北京2013届高三最新文科试题分类汇编（含9区一模及上学期期末试题精选）专题12：算法参考答案一、选择题 1. A 2. A 3. A 4. C 5. D; 6. B 7. 【答案】C解：本程序为分段函数2212log 2x x y x x ⎧-≤=⎨>⎩，，，当2x ≤时，由213x -=得，24x =，所以2x =±。
北京市2013高考数学 一模试题解析分类汇编系列五 2 函数 文
【解析分类汇编系列五：北京2013高三（一模）文数】2：函数1．（2013（ ）A ．9B ．91C ．9-D ．91-B2 ．（2013届北京大兴区一模文科）设0.70.45 1.512314,8,()2y y y -===,则（ ）A ．312y y y >> (B )213y y y >>C ．123y y y >>D ．132y y y >>A0.7 1.4142y ==，0.45 1.35282y ==， 1.5 1.531()22y -==，所以312y y y >>，选A.3．（2013届北京市朝阳区一模数学文）已知函数*()21,f x x x =+∈N .若*0,x n ∃∈N ，使000()(1)()63f x f x f x n +++++= ，则称0(,)x n 为函数()f x 的一个“生成点”.函数()f x 的“生成点”共有A. 1个 B .2个 C .3个 D .4个 B由题意知0000212(1)12()1(1)(21)63x x x n n x n ++++++++=+++= ，因为0,x n N ∈ ，所以12n +≥，021+1x n n ++>。
因为79=321=63⨯⨯，所以当13n +=时，00212321x n x ++=+=，此时解得02,9n x ==，生成点为(9,2)。
当17n +=时，0021279x n x ++=+=，此时解得06,1n x ==，生成点为(1,6)。
所以函数()f x 的“生成点”共有2个，选B.4．（2013届北京市延庆县一模数学文）已知函数)(2)()(2b a ab x b a x x f <+++-=的两个零点为)(,βαβα<,则实数βα,,,b a 的大小关系是（ ）A ．b a <<<βαB ．b a <<<βαC ．βα<<<b aD ．βα<<<b a A2()()2()()2f x x a b x ab x a x b =-+++=--+，所以()()20f a f b ==>，且)(,βαβα<是函数的两个零点，所以a b αβ<<<，选A.5．（2013届北京东城区一模数学文科）已知定义在R 上的函数()f x 的对称轴为3x =-,且当3x ≥-时,()23xf x =-.若函数()f x 在区间(1,)k k -(k ∈Z )上有零点,则k 的值为（ ）A ．2或7-B ．2或8-C ．或7-D ．或8-A当3x ≥-时，由()230xf x =-=，解得2log 3x =，因为21log 32≤≤，即函数的零点所在的区间为(1,2)，所以2k =。
北京市2013各区数学一模试题--数列及解析几何
2013年北京市各区高三一模试题编--数列一填空选择(2013年东城一模文科)（7）对于函数)(x f y =，部分x 与y 的对应关系如下表：x 1 2 3 4 5 6 7 8 9 y7 4 5 8 1 3 5 2 6数列}{n x 满足21=x ，且对任意*n ∈N ，点),(1+n n x x 都在函数)(x f y =的图象上，则201320124321x x x x x x ++++++ 的值为（A ）9394 （B ）9380 （C ）9396 （D ）9400 （2013年东城一模文科理科）（14）数列{a n }的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若n n a a =(0)a ≠， 则位于第10行的第8列的项等于 ，2013a 在图中位于 ．（填第几行的第几列）（2013年东城一模理科）（5）已知数列{}n a 中，12a =，120n n a a +-=，2log n n b a =，那么数列{}n b 的前10项和等于（A ）130 （B ）120 （C ）55 （D ）50(2013西城一模文科理科)4．设等比数列{}n a 的公比为q ，前n 项和为n S ，且10a >．若232S a >，则q 的取值范围是（A ）1(1,0)(0,)2- （B ）1(,0)(0,1)2-（C ）1(,1)(,)2-∞-+∞（D ）1(,)(1,)2-∞-+∞(2013西城一模文科)14．已知数列{}n a 的各项均为正整数，其前n 项和为n S ．若1, ,231,,nn n nn a a a a a +⎧⎪=⎨⎪+⎩是偶数是奇数且329S =，则1a =______；3n S =______. (2013西城一模理科)10．设等差数列{}n a 的公差不为0，其前n 项和是n S ．若23S S =，0k S =，则k =______．(2013海淀一模文科)2.等差数列{}n a 中, 2343,9,a a a =+= 则16a a 的值为 A. 14 B. 18 C. 21 D.2(2013海淀一模理科)10.等差数列{}n a 中,34259,18a a a a +==, 则16_____.a a = (2013丰台一模文科理科)3. 设n S 为等比数列{}n a 的前n 项和，3420a a +=，则31S a （ ）(A) 2 (B) 3 (C) 4 (D) 5（2013年石景山一模文科理科）11．在等差数列{a n }中，a l =-2013，其前n 项和为S n ，若10121210S S -=2，则2013S 的值等于 。
2013届北京市东城区高三一模数学文科试题(WORD解析版)
北京市东城区2012-2013学年度第二学期高三综合练习（一）数学 （文科）学校_____________班级_______________姓名______________考号___________本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。
考试时长120分钟。
考生务必将答案答在答题卡上，在试卷上作答无效。
考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）已知全集{1,2,3,4}U =，集合{1,2}A =，那么集合U A ð为（A ）{3} （B ）{3,4} （C ）{1,2} （D ）{2,3}【答案】B【解析】因为{1,2}A =，所以={3,4}U A ð，选B.（2） “1a =”是“直线20x y +=与直线(1)40x a y +++=平行”的（A ） 充分不必要条件 （B ） 必要不充分条件 （C ） 充要条件 （D ） 既不充分也不必要条件 【答案】C【解析】因为两直线平行，则有1112a +=，解得1a =。
所以1a =是“直线20x y +=与直线(1)40x a y +++=平行”的充要条件，选C 。
（3）已知ABCD 为平行四边形，若向量AB = a ，AC = b ，则向量BC为（A ）-a b （B ）a +b （C ）-b a （D ）--a b 【答案】C【解析】因为=BC AC AB - ，所以=BC b a -，选C.（4）执行如图所示的程序框图，输出的结果是56，则判断框内应填入的条件是（A ）5?n ≤ （B ）5?n <（C ）5?n > （D ）5?n ≥ 【答案】A 【解析】本程序计算的是1111223(1)S n n =+++⨯⨯+ ，因为1111111=122311S n n n =-+-++--++ ，由15116S n =-=+，解得5n =。
北京市东城区2012-2013第一学期高三期末数学统一练习文科
意. ……………………………9 分
当 m 0时， f (x) 的单调递减区间是 (3m,m) ，若
f (x) 在区间 (2,3) 上是减函数，
则
解 3m 2,
m 3.
得
m 3 .……………………………………………11
分
当 m 0 时， f (x) 的单调递减区间是 (m,3m) ，若
f (x) 在区间 (2,3) 上是减函数，
（Ⅱ）由（Ⅰ）得 bn nan n 2n1，设数列{bn}的前 n 项
和为Tn .
则 . Tn 11 2 2 3 22 4 23 n 2n1
①
. ② 2Tn 1 2 2 22 3 23 (n 1) 2n1 n 2n
①
-
②
得
……………………9 分 Tn 111 2 1 22 1 2n1 n 2n
至 2 页，第Ⅱ卷 3 至 5 页，共 150 分。考试时长
120 分钟。考生务必将答案答在答题卡上，在试
卷上作答无效。考试结束后，将本试卷和答题卡
一并交回。
第Ⅰ卷（选择题 共 40 分）
一、本大题共 8 小题，每小题 5 分，共 40 分。
在每小题列出的四个选项中，选出符合题目
要求的一项。
（ 1 ） 设 集 合 U ， {1, 2,3, 4,5} ， A {1, 2,3} B {2,3, 4}， 则
x
，
y
满足不等式组
2x y
x
0,
8,
则目标函数
y 0,
z 3x y 的最大值为 (A) 32
3
(B) 12
(C) 8
(D) 24
3
（7）已知抛物线 y2 2px 的焦点 F 到其准线的距离
北京市东城区2013届高三数学一模试题 文(含解析)北师大版
2013年北京市东城区高考数学一模试卷（文科）参考答案与试题解析一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）（2013•东城区一模）已知全集U={1，2，3，4}，集合A={1，2}，那么集合∁U A为（）A．{3} B．{3，4} C．{1，2} D．{2，3}考点：补集及其运算．专题：计算题．分析：直接利用补集的定义，求出A的补集即可．解答：解：因为全集U={1，2，3，4}，集合A={1，2}，那么集合∁U A={3，4}．故选B．点评：本题考查补集的运算，补集的定义，考查基本知识的应用．2．（5分）（2013•东城区一模）“a=1”是“直线x+2y=0与直线x+（a+1）y+4=0平行”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：直线与圆．分析：当a=1 时，经检验，两直线平行，故充分性成立；当两直线平行时，由斜率相等得到a=1，故必要性也成立．解答：解：当a=1 时，直线x+（a+1）y+4=0即x+2y+4=0，显然两直线平行，故充分性成立．当直线x+2y=0与直线x+（a+1）y+4=0平行，由斜率相等得﹣=﹣，a=1，故由直线x+2y=0与直线x+（a+1）y+4=0平行，能推出a=1，故必要性成立．综上，“aa=1”是“直线x+2y=0与直线x+（a+1）y+4=0平行”的充分必要条件，故选C．点评：本题考查两直线平行的条件和性质，充分条件、必要条件的定义和判断方法．3．（5分）（2013•东城区一模）已知ABCD为平行四边形，若向量，，则向量为（）A．﹣B．+C．﹣D．﹣﹣考点：平面向量的基本定理及其意义．专题：平面向量及应用．分析：如图所示，利用向量的减法法则即可得出．解答：解：如图所示，由向量的减法法则可得：==．故选C．点评：熟练掌握向量的减法法则是解题的关键．4．（5分）（2013•东城区一模）执行如图所示的程序框图，输出的结果是，则判断框内应填入的条件是（）A．n≤5？B．n＜5？C．n＞5？D．n≥5？考点：程序框图．专题：图表型．分析：本循环结构是经过n次循环，计算S=++…+，由此能求出结果．解答：解：经过n次循环，计算S=++…+=1﹣=，∵程序框图输出的结果是，∴=，∴n=5．∴n=6时，跳出循环．故选A．点评：本题考查循环结构的应用，是基础题．解题时要认真审题，仔细解答．5．（5分）（2013•东城区一模）已知一个几何体的三视图如图所示（单位：cm），那么这个几何体的侧面积是（）A．B．C．D．考点：由三视图求面积、体积．专题：计算题．分析：由题可知，图形是一个放倒的底面是直角梯形的四棱柱的三视图，求出表面积即可．解答：解：由题可知，三视图复原的几何体是一个放倒的底面是直角梯形的四棱柱，所以几何体的侧面积S==4+（cm2）．故选C．点评：本题考查学生的空间想象能力，是基础题．6．（5分）（2013•东城区一模）已知点A（2，1），抛物线y2=4x的焦点是F，若抛物线上存在一点P，使得|PA|+|PF|最小，则P点的坐标为（）A．（2，1）B．（1，1）C．D．考点：抛物线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：利用抛物线的定义，得|PA|+|PF|=|PA|+|PQ|．因此问题转化为求|PA|+|PQ|取最小值时P点的坐标，再利用P、A、Q三点共线时距离最小，即可求出满足条件的P点坐标．解答：解：根据抛物线的定义，点P到焦点F的距离等于它到准线l的距离设点P到准线l：x=﹣1的距离为PQ，则所求的|PA|+|PF|最小值，即|PA|+|PQ|的最小值；根据平面几何知识，可得当P、A、Q三点共线时|PA|+|PQ|最小，∴|PA|+|PQ|的最小值为A到准线l的距离；此时P的纵坐标为1，代入抛物线方程得P的横坐标为，得P故选：D点评：本题的考点是抛物线的简单性质，主要考查抛物线的定义，考查距离最小问题，关键是利用抛物线的定义，将点P到焦点的距离转化为它到准线的距离．7．（5分）（2013•东城区一模）对于函数y=f（x），部分x与y的对应关系如下表：x 1 2 3 4 5 6 7 8 9y 7 4 5 8 1 3 5 2 6数列{x n}满足x1=2，且对任意n∈N*，点（x n，x n+1）都在函数y=f（x）的图象上，则x1+x2+x3+x4+…+x2012+x2013的值为（）A．9394 B．9380 C．9396 D．9400考点：数列的求和．专题：计算题．分析：利用已知函数的关系求出数列的前几项，得到数列是周期数列，然后求出通过周期数列的和，即可求解本题．解答：解：因为数列{x n}满足x1=2，且对任意n∈N*，点（x n，x n+1）都在函数y=f（x）的图象上，x n+1=f（x n）所以x1=2，x2=4，x3=8，x4=2，x5=4，x6=8，x7=2，x8=4…所以数列是周期数列，周期为3，一个周期内的和为14，所以x1+x2+x3+x4+…+x2012+x2013=671×（x1+x2+x3）=9394．故选A．点评：本题考查函数与数列的关系，周期数列求和问题，判断数列是周期数列是解题的关键．8．（5分）（2013•菏泽二模）已知定义在R上的函数f（x）的对称轴为x=﹣3，且当x≥﹣3时，f（x）=2x﹣3．若函数f（x）在区间（k﹣1，k）（k∈Z）上有零点，则k的值为（）A．2或﹣7 B．2或﹣8 C．1或﹣7 D．1或﹣8考点：根的存在性及根的个数判断．专题：函数的性质及应用．分析：先作出当x≥﹣3时函数f（x）=2x﹣3的图象，观察图象的交点所在区间，再根据对称性得出另一个交点所在区间即可．解答：解：作出当x≥﹣3时函数f（x）=2x﹣3的图象，观察图象的交点所在区间在（1，2）．∵f（1）=21﹣3=﹣1＜0，f（2）=22﹣3=1＞0，∴f（1）•f（2）＜0，∴有零点的区间是（1，2），因定义在R上的函数f（x）的对称轴为x=﹣3，故另一个零点的区间是（﹣8，﹣7），则k的值为2或﹣7．故选A．点评：本题主要考查了根的存在性及根的个数判断．二分法是求方程根的一种基本算法，其理论依据是零点存在定理：一般地，若函数y=f（x）在区间[a，b]上的图象是一条不间断的曲线，且f（a）f（b）＜0，则函数y=f（x）在区间（a，b）上有零点．二、填空题：本大题共6小题，每小题5分，共30分．9．（5分）（2013•东城区一模）已知i是虚数单位，那么i（1+i）等于﹣1+i ．考点：复数代数形式的乘除运算．专题：计算题．分析：利用复数的运算法则即可得出．解答：解：i（1+i）=i﹣1=﹣1+i．故答案为﹣1+i．点评：熟练掌握复数的运算法则和i2=﹣1是解题的关键．10．（5分）（2013•东城区一模）如图是甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图，则甲5次测试成绩的平均数是84 ，乙5次测试成绩的平均数与中位数之差是2 ．考点：茎叶图；众数、中位数、平均数．专题：图表型．分析：先从茎叶图中分析出甲、乙两人的成绩数据，再根据中位数和平均数的求法进行运算即得．解答：解：由图可知，甲，乙两人共有5次测试成绩，分别是：甲：76、83、84、87、90乙：79、80、82、88、91则甲、乙两人5次体育测试成绩的中位数分别为84、82，平均数分别为==84，==84故乙5次测试成绩的平均数与中位数之差是 2．故答案为：84，2．点评：茎叶图的茎是高位，叶是低位，所以本题中“茎是十位”，叶是个位，从图中分析出参与运算的数据，代入相应公式即可解答．从茎叶图中提取数据是利用茎叶图解决问题的关键．11．（5分）（2013•东城区一模）不等式组表示的平面区域为D，则区域D的面积为 2 ，z=x+y的最大值为 2 ．考点：简单线性规划．专题：不等式的解法及应用．分析：先画出可行域，再利用三角形面积公式求第一问；第二问需由z=x+y，再变形为y=﹣x+z，则过点B时z最大．解答：解：不等式组所表示的平面区域如图所示解得A（2，﹣2）、B（2，0）、C（0，0），所以S△ABC=×2×2=2；由z=x+y，则y=﹣x+z，所以直线经过点B时x+y取得最大值，最大值为2+0=2．故答案为：2，2．点评：本类题是解决线性规划问题，本类题常用的步骤有两种：一是：由约束条件画出可行域，求出可行域各个角点的坐标，将坐标逐一代入目标函数，验证，求出最优解．二是：画出可行域，标明函数几何意义，确定最优解．12．（5分）（2013•东城区一模）从1，3，5，7这四个数中随机地取两个数组成一个两位数，则组成的两位数是5的倍数的概率为．考点：古典概型及其概率计算公式．专题：概率与统计．分析：根据所抽取的数据拼成两位数，得出总数及是5的倍数的数，求概率．解答：解：如下表，任意抽取两个不同数字组成一个两位数，共12种情况，其中是5的倍数的有15，35，75三种，∴组成两位数能被3整除的概率为=．1 3 5 71 13 15 173 31 35 375 51 53 577 71 73 75故答案为：．点评：本题考查了求概率的方法：列表法和树状图法．关键是通过画表格（图）求出组成两位数的所有可能情况及符合条件的几种可能情况．13．（5分）（2013•东城区一模）函数的图象为C，有如下结论：①图象C关于直线对称；②图象C关于点对称；③函数f（x）在区间内是增函数，其中正确的结论序号是①②③．（写出所有正确结论的序号）考点：命题的真假判断与应用．专题：计算题．分析：由题意可解出该函数的所有对称轴，对称区间和单调递增区间，取整数k的特殊值，比较选项即可得答案．解答：解：由=kπ+，可得x=kπ+，k∈Z，当k=0时，可得其中一条对称轴为x=，故①正确；由=kπ，可得x=kπ+，k∈Z，当k=1时，可得其中一个对称点的横坐标为x=，故②正确；由2kπ﹣≤≤2kπ+得2kπ﹣≤x≤2kπ+，k∈Z，当k=0时，可得其中一个单调递增区间为[，]，因为真包含于[，]，所以函数在上单调递增，故③正确．故答案为：①②③点评：本题考查命题真假的判断，涉及三角函数的对称性和单调性，属基础题．14．（5分）（2013•东城区一模）数列{a n}的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若（a≠0），则位于第10行的第8列的项等于a89，a2013在图中位于第45行的第77列．（填第几行的第几列）考点：数列的函数特性；等比数列的通项公式．专题：等差数列与等比数列．分析：①由于每行的所有数的个数形成等差数列，故可得到前9行的数的个数，从而得出答案；②由①可知前k行所有a i的个数为b1+b2+…b k=1+3+…（2k﹣1）=k2．解出（k﹣1）2≤2013即可得出答案．解答：解：①设每行的数的个数为数列{b n}，则此数列为首项为1，公差为2的等差数列，∴b n=1+（n﹣1）×2=2n﹣1．于是前9行所有a n的个数为b1+b2+…+b9==81．∴位于第10行的第8列的项等于a81+8=．②由①可知：前k行所有a i的个数为b1+b2+…b k=1+3+…（2k﹣1）=k2．由（k﹣1）2＜2013，解得，而442＜2013＜452，∴k＜1+44=45．∴前44行的所有数a i的个数为442=1936．而1936+77=2013，∴a2013在图中位于第45行的第77 列．故答案分别为a89，第45行的第77 列．点评：正确理解每行的所有数的个数形成等差数列，利用等差数列的通项公式和前可知前k 行所有a i的个数为b1+b2+…b k=1+3+…（2k﹣1）=k2是解题的关键．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）（2013•东城区一模）在△ABC中，三个内角A，B，C的对边分别为a，b，c，且．（Ⅰ）求角B；（Ⅱ）若，求ac的最大值．考点：正弦定理；余弦定理．专题：解三角形．分析：（Ⅰ）因为，由正弦定理求得，从而求得B的值．（Ⅱ）由余弦定理求得12=a2+c2﹣ac，再利用基本不等式求得ac的最大值．解答：解：（Ⅰ）因为，由正弦定理可得．因为在△ABC中，sinA≠0，所以．又0＜B＜π，所以．（Ⅱ）由余弦定理 b2=a2+c2﹣2accosB，因为，，所以12=a2+c2﹣ac．因为a2+c2≥2ac，所以ac≤12．当且仅当时，ac取得最大值12．点评：本题主要考查正弦定理、余弦定理以及基本不等式的应用，属于中档题．16．（14分）（2013•东城区一模）如图，已知AD⊥平面ABC，CE⊥平面ABC，F为BC的中点，若．（Ⅰ）求证：AF∥平面BDE；（Ⅱ）求证：平面BDE⊥平面BCE．考点：平面与平面垂直的判定；直线与平面平行的判定．专题：空间位置关系与距离．分析：（I）取BE的中点G，连接GF，GD．利用三角形的中位线定理即可得到GF∥EC，．由AD⊥平面ABC，CE⊥平面ABC，利用线面垂直的性质定理即可得到AD∥EC，进而即可判断四边形AFGD 为平行四边形，得到AF∥DG，再利用线面平行的判定定理即可证明；（II）利用等腰三角形的性质即可得到AF⊥BC，再利用线面垂直的性质得到GF⊥AF，利用线面垂直的判定定理即可证明AF⊥平面BEC，而DG∥AF，得到DG⊥平面BEC，利用面面垂直的定理即可证明结论．解答：证明：（Ⅰ）取BE的中点G，连接GF，GD．∵F是BC的中点，则GF为△BCE的中位线．∴GF∥EC，．∵AD⊥平面ABC，CE⊥平面ABC，∴GF∥EC∥AD．又∵，∴GF=AD．∴四边形GFAD为平行四边形．∴AF∥DG．∵DG⊂平面BDE，AF⊄平面BDE，∴AF∥平面BDE．（Ⅱ）∵AB=AC，F为BC的中点，∴AF⊥BC．∵EC∥GF，EC⊥平面ABC，∴GF⊥平面ABC．又AF⊂平面ABC，∴GF⊥AF．∵GF∩BC=F，∴AF⊥平面BCE．∵AF∥DG，∴DG⊥平面BCE．又DG⊂平面BDE，∴平面BDE⊥平面BCE．点评：熟练掌握三角形的中位线定理、线面垂直的判定定理和性质定理、等腰三角形的性质、平行四边形的判定和性质、面面垂直的判定定理是解题的关键．17．（13分）（2013•东城区一模）为了解高三学生综合素质测评情况，对2000名高三学生的测评结果进行了统计，其中优秀、良好、合格三个等级的男、女学生人数如下表：优秀良好合格男生人数x 380 373女生人数y 370 377（Ⅰ）若按优秀、良好、合格三个等级分层，在这2000份综合素质测评结果中随机抽取80份进行比较分析，应抽取综合素质测评结果是优秀等级的多少份？（Ⅱ）若x≥245，y≥245，求优秀等级的学生中男生人数比女生人数多的概率．考点：列举法计算基本事件数及事件发生的概率；分层抽样方法．专题：计算题；概率与统计．分析：（I）根据样本容量为2000，运用减法算出优秀等级的学生人数为500，再由分层抽样的公式即可算出应抽取综合素质测评结果是优秀等级的份数；（II）设“优秀等级的学生中男生人数比女生人数多”为事件A，分别列举出（x，y）的所有可能情况和满足x＞y的数组（x，y）的情况，再用随机事件的概率公式即可算出优秀等级的学生中男生人数比女生人数多的概率．解答：解：（Ⅰ）由表可知，优秀等级的学生人数为x+y=2000﹣（380+373+370+377）=500．因此，应抽取综合素质测评结果是优秀等级的份数为，即在优秀等级的学生中应抽取20份．（Ⅱ）设“优秀等级的学生中男生人数比女生人数多”为事件A．∵x+y=500，x≥245，y≥245，且x，y为正整数，∴数组（x，y）的可能取值为：（245，255），（246，254），（247，253），…，（255，245），共11个．其中满足x＞y的数组（x，y）的所有可能取值为：（255，245），（254，246），（253，247），（252，248），（251，249）共5个，即事件A包含的基本事件数为5．因此，所求概率为．答：（I）应抽取综合素质测评结果是优秀等级的20份；（II）优秀等级的学生中男生人数比女生人数多的概率为．点评：本题给出学生成绩统计的表格，求抽取综合素质测评结果是优秀生的份数和优秀等级的学生中男生人数比女生人数多的概率，着重考查了随机事件的概率和分层抽样计算公式等知识，属于基础题．18．（14分）（2013•东城区一模）已知函数f（x）=mlnx+（m﹣1）x（m∈R）．（Ⅰ）当m=2时，求曲线y=f（x）在点（1，f（1））处的切线方程；（Ⅱ）讨论f（x）的单调性；（ III）若f（x）存在最大值M，且M＞0，求m的取值范围．考点：利用导数求闭区间上函数的最值；利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．专题：综合题；分类讨论；导数的综合应用．分析：（Ⅰ）当m=2时求出导数f′（x），则切线斜率k=f′（1），f（1）=1，利用点斜式即可求得切线方程；（Ⅱ）先求出函数定义域，在定义域内分m≤0，m≥1，0＜m＜1三种情况解不等式f′（x）＞0，f′（x）＜0即可；（ III）分情况进行讨论：当m≤0或m≥1时f（x）单调，最值情况易判断；当0＜m＜1时，由单调性易求得其最大值，令其大于0，解出即可；解答：解：（Ⅰ）当m=2时，f（x）=2lnx+x．．所以f'（1）=3．又f（1）=1，所以曲线y=f（x）在点（1，f（1））处的切线方程是y﹣1=3（x﹣1），即3x﹣y﹣2=0．（Ⅱ）函数f（x）的定义域为（0，+∞），．当m≤0时，由x＞0知恒成立，此时f（x）在区间（0，+∞）上单调递减．当m≥1时，由x＞0知恒成立，此时f（x）在区间（0，+∞）上单调递增．当0＜m＜1时，由f'（x）＞0，得，由f'（x）＜0，得，此时f（x）在区间内单调递增，在区间内单调递减．（ III）由（Ⅱ）知函数f（x）的定义域为（0，+∞），当m≤0或m≥1时，f（x）在区间（0，+∞）上单调，此时函数f（x）无最大值．当0＜m＜1时，f（x）在区间内单调递增，在区间内单调递减，所以当0＜m＜1时函数f（x）有最大值，最大值．因为M＞0，所以有，解之得．所以m的取值范围是．点评：本题考查利用导数研究函数的单调性、最值及切线问题，考查分类讨论思想，考查学生分析解决问题的能力，属中档题．19．（13分）（2013•东城区一模）已知椭圆C：（a＞b＞0）的两个焦点分别为F1，F2，离心率为，且过点．（Ⅰ）求椭圆C的标准方程；（Ⅱ）M，N，P，Q是椭圆C上的四个不同的点，两条都不和x轴垂直的直线MN和PQ分别过点F1，F2，且这两条直线互相垂直，求证：为定值．考点：直线与圆锥曲线的综合问题；椭圆的标准方程．专题：综合题；圆锥曲线中的最值与范围问题．分析：（Ⅰ）由离心率为，即可得a2=2b2，从而C：，再把点代入椭圆方程即可求得b2，进而得到a2．（Ⅱ）由（Ⅰ）写出焦点F1，F2的坐标，设直线MN的方程为y=k（x+2），由直线MN 与直线PQ互相垂直得直线PQ的方程为，设M（x1，y1），N（x2，y2）．联立直线MN与椭圆方程消掉y得x的二次方程，由韦达定理及弦长公式可用k表示|MN|，同理可表示出|PQ|，计算即可得到为定值．解答：（Ⅰ）解：由已知，得．所以a2=2b2．所以C：，即x2+2y2=2b2．因为椭圆C过点，所以，得b2=4，a2=8．所以椭圆C的方程为．（Ⅱ）证明：由（Ⅰ）知椭圆C的焦点坐标为F1（﹣2，0），F2（2，0）．根据题意，可设直线MN的方程为y=k（x+2），由于直线MN与直线PQ互相垂直，则直线PQ的方程为．设M（x1，y1），N（x2，y2）．由方程组消y得（2k2+1）x2+8k2x+8k2﹣8=0．则，．所以|MN|===．同理可得|PQ|=．所以==．点评：本题考查直线与圆锥曲线的综合问题及椭圆方程的求解，韦达定理及弦长公式是解决该类题目的基础，应熟练掌握．20．（13分）（2013•东城区一模）设A是由n个有序实数构成的一个数组，记作：A=（a1，a2，…，a i，…，a n）．其中a i（i=1，2，…，n）称为数组A的“元”，S称为A的下标．如果数组S中的每个“元”都是来自数组A中不同下标的“元”，则称A=（a1，a2，…，a n）为B=（b1，b2，…b n）的子数组．定义两个数组A=（a1，a2，…，a n），B=（b1，b2，…，b n）的关系数为C（A，B）=a1b1+a2b2+…+a n b n．（Ⅰ）若，B=（﹣1，1，2，3），设S是B的含有两个“元”的子数组，求C（A，S）的最大值；（Ⅱ）若，B=（0，a，b，c），且a2+b2+c2=1，S为B的含有三个“元”的子数组，求C（A，S）的最大值．考点：平均值不等式在函数极值中的应用；排序不等式及应用．专题：新定义；不等式的解法及应用．分析：（Ⅰ）依据题意中“元”的含义，可知当S=（﹣1，3）时，C（A，S）取得最大值为2．（Ⅱ）对0是不是S中的“元”进行分类讨论：①当0是S中的“元”时，由于A的三个“元”都相等，及B中a，b，c三个“元”的对称性，利用平均值不等式计算的最大值，②当0不是S中的“元”时，只须计算的最大值即可，最后综上即可得出C（A，S）的最大值．解答：解：（Ⅰ）依据题意，当S=（﹣1，3）时，C（A，S）取得最大值为2．（Ⅱ）①当0是S中的“元”时，由于A的三个“元”都相等，及B中a，b，c三个“元”的对称性，可以只计算的最大值，其中a2+b2+c2=1．由（a+b）2=a2+b2+2ab≤2（a2+b2）≤2（a2+b2+c2）=2，得．当且仅当c=0，且时，a+b达到最大值，于是．②当0不是S中的“元”时，计算的最大值，由于a2+b2+c2=1，所以（a+b+c）2=a2+b2+c2+2ab+2ac+2bc≤3（a2+b2+c2）=3，当且仅当a=b=c时，等号成立．即当时，a+b+c取得最大值，此时．综上所述，C（A，S）的最大值为1．点评：本小题主要考查排序不等式及应用、平均值不等式在函数极值中的应用等基础知识，考查运算求解能力，考查化归与转化思想．属于中档题．。
北京市2013高考数学 一模试题解析分类汇编系列五 15 复数 文
【解析分类汇编系列五：北京2013高三（一模）文数】15：复数1．（2013届北京市朝阳区一模数学文）i 为虚数单位，复数11i -的虚部是A ．12 B ．12- C ．1i 2- D . 1i 2 A111111(1)(1)222iii i i i ++===+--+，所以虚部是12，选A.2．（2013届北京市石景山区一模数学文）若复数2(-)a i 在复平面内对应的点在y 轴负半轴上，则实数a 的值是（ ）A ． 1B ．-1CD ．A22()12a i a ai -=--,对应点的坐标为2(1,2)a a --，由题意知210,20a a -=-<，解得1a =，选A.3．（2013届北京丰台区一模文科）复数z=1i i -在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 A211111i ii i i i -=-=-=+,所以复数对应点的坐标为(1,1)，为第一象限，选A.4．（2013届北京大兴区一模文科）复数2(1i)+的值是 （ ）A ．2B ．2-C ．2iD ．2i -C22(1)122i i i i +=++=，选C.5．（2013届北京西城区一模文科）复数 1ii -+=（ ）A ．1i +B ．1i -+C ．1i --D ．1i - A1i (1)11i 11i i i i -+-+--===+--，选A.6．（2013届北京市延庆县一模数学文）若复数i m m m z )1()2(2+++-=(为虚数单位)为纯虚数,其中m R ∈,则=m _____.2因为复数为纯虚数，所以220,10m m m --=+≠，解得2m =。
7．（2013届北京东城区一模数学文科）已知i 是虚数单位,那么i(1i)+等于___. 1i -+2(1)=1i i i i i ++=-+.8．（2013届北京海淀一模文）在复平面上,若复数1+i b (b ∈R )对应的点恰好在实轴上,则b =_______.因为复数1+i b （b ∈R ）对应的点恰好在实轴上，所以0b =。
北京东城13上学期期末高三数学文科试题
东城区2012-2013学年度第一学期期末教学统一检测高三数学 （文科）2013.01 第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）设集合{1,2,3,4,5}U =，{1,2,3}A =，{2,3,4}B =，则()U A B ð等于 (A) {2,3} (B) {1,4,5} (C) {4,5} (D) {1,5} （2）复数21i-等于（A ）1i -- (B) 1i -+ ( C) 1i - ( D) 1i +（3）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d 等于（A ）1 （B ）53（C ）2 （D ）3（4）执行如图所示的程序框图，输出的k 的值为（A ）4（B ）5 （C ）6（D ）7（5）“2230x x -->成立”是“3x >成立”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件（6）已知x ，y 满足不等式组28,28,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩ 则目标函数3z x y =+的最大值为(A)332 (B)12 (C)8 (D)24（7）已知抛物线22y px =的焦点F 到其准线的距离是8，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且|||AK AF =，则AFK ∆的面积为（A ）32 （B ）16 （C ）8 （D ）4（8）给出下列命题：①在区间(0,)+∞上，函数1y x -=,12y x =,2(1)y x =-, 3y x =中有三个是增函数；②若log 3log 30m n <<，则01n m <<<；③若函数()f x 是奇函数，则(1)f x -的图象关于点(1,0)A 对称；④若函数()323xf x x =--，则方程()0f x =有2个实数根，其中正确命题的个数为 （A ）1 （B ）2 （C ）3 （D ）4第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。
2013年北京市东城区高考数学一模试卷(文科)(附答案解析)
2013年北京市东城区高考数学一模试卷（文科）一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1. 已知全集U ={1, 2, 3, 4}，集合A ={1, 2}，那么集合∁U A 为（ ） A.{3} B.{3, 4} C.{1, 2} D.{2, 3}2. “a =1”是“直线x +2y =0与直线x +(a +1)y +4=0平行”的（ ） A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3. 已知ABCD 为平行四边形，若向量AB →=a →，AC →=b →，则向量BC →为（ ） A.a →−b →B.a →+b →C.b →−a →D.−a →−b →4.执行如图所示的程序框图，输出的结果是56，则判断框内应填入的条件是（ ）A.n ≤5？B.n <5？C.n >5？D.n ≥5？5. 已知一个几何体的三视图如图所示（单位：cm ），那么这个几何体的侧面积是（ ）A.(1+√2)cm 2B.(3+√2)cm 2C.(4+√2)cm 2D.(5+√2)cm 26. 已知点A(2, 1)，抛物线y 2=4x 的焦点是F ，若抛物线上存在一点P ，使得|PA|+|PF|最小，则P 点的坐标为（ ） A.(2, 1) B.(1, 1)C.(12，1)D.(14，1)7.对于函数y =f(x)，部分x 与y 的对应关系如下表：数列{x n 1(x n , x n+1)都在函数y =f(x)的图象上，则x 1+x 2+x 3+x 4+...+x 2012+x 2013的值为（ ） A.9394 B.9380C.9396D.94008. 已知定义在R 上的函数f(x)的对称轴为x =−3，且当x ≥−3时，f(x)=2x −3．若函数f(x)在区间(k −1, k)(k ∈Z)上有零点，则k 的值为（ ） A.2或−7B.2或−8C.1或−7D.1或−8二、填空题：本大题共6小题，每小题5分，共30分．已知i 是虚数单位，那么i(1+i)等于________．如图是甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图，则甲5次测试成绩的平均数是________，乙5次测试成绩的平均数与中位数之差是________．不等式组{x −2≤0y ≤0x +y ≥0表示的平面区域为D ，则区域D 的面积为________，z =x +y 的最大值为________．从1，3，5，7这四个数中随机地取两个数组成一个两位数，则组成的两位数是5的倍数的概率为________．函数f(x)=sin (x −π3)的图象为C ，有如下结论：①图象C 关于直线x =5π6对称；②图象C 关于点(4π3，0)对称；③函数f(x)在区间[π3，5π6]内是增函数，其中正确的结论序号是________．（写出所有正确结论的序号）数列{a n }的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若a n =a n(a ≠0)，则位于第10行的第8列的项等于________，a 2013在图中位于________．（填第几行的第几列）三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，且b sin A =√3a cos B ． (Ⅰ)求角B ；(Ⅱ)若b =2√3，求ac 的最大值．如图，已知AD ⊥平面ABC ，CE ⊥平面ABC ，F 为BC 的中点，若AB =AC =AD =12CE ．（1）求证：AF // 平面BDE ；（2）求证：平面BDE ⊥平面BCE ．为了解高三学生综合素质测评情况，对2000名高三学生的测评结果进行了统计，其中优秀、良好、合格三个等级的男、女学生人数如下表：（1）若按优秀、良好、合格三个等级分层，在这2000份综合素质测评结果中随机抽取80份进行比较分析，应抽取综合素质测评结果是优秀等级的多少份？（2）若x ≥245，y ≥245，求优秀等级的学生中男生人数比女生人数多的概率．已知函数f(x)=m ln x +(m −1)x(m ∈R)．（1）当m =2时，求曲线y =f(x)在点（1, f(1)）处的切线方程；（2）讨论f(x)的单调性；（3）若f(x)存在最大值M ，且M >0，求m 的取值范围．已知椭圆C:x 2a+y 2b =1(a >b >0)的两个焦点分别为F 1，F 2，离心率为√22，且过点(2,√2)．（1）求椭圆C 的标准方程；（2）M ，N ，P ，Q 是椭圆C 上的四个不同的点，两条都不和x 轴垂直的直线MN 和PQ 分别过点F 1，F 2，且这两条直线互相垂直，求证：1|MN|+1|PQ|为定值．设A 是由n 个有序实数构成的一个数组，记作：A =(a 1, a 2,…,a i ,…,a n )．其中a i (i =1, 2,…,n)称为数组A 的“元”，S 称为A 的下标．如果数组S 中的每个“元”都是来自 数组A 中不同下标的“元”，则称A =(a 1, a 2,…,a n )为B =(b 1, b 2,…b n )的子数组．定义两个数组A =(a 1, a 2,…,a n )，B =(b 1, b 2,…,b n )的关系数为C(A, B)=a 1b 1+a 2b 2+...+a n b n ．（1）若A =(−12，12)，B =(−1, 1, 2, 3)，设S 是B 的含有两个“元”的子数组，求C(A, S)的最大值；（2）若A =(√33，√33，√33)，B =(0, a, b, c)，且a 2+b 2+c 2=1，S 为B 的含有三个“元”的子数组，求C(A, S)的最大值．参考答案与试题解析2013年北京市东城区高考数学一模试卷（文科）一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1.【答案】 B【考点】 补集及其运算 【解析】直接利用补集的定义，求出A 的补集即可． 【解答】解：因为全集U ={1, 2, 3, 4}，集合A ={1, 2}，那么集合∁U A ={3, 4}． 故选B ． 2.【答案】 C【考点】必要条件、充分条件与充要条件的判断 【解析】当a =1 时，经检验，两直线平行，故充分性成立；当两直线平行时，由斜率相等得到a =1，故必要性也成立． 【解答】解：当a =1 时，直线x +(a +1)y +4=0即x +2y +4=0，显然两直线平行，故充分性成立． 当直线x +2y =0与直线x +(a +1)y +4=0平行，由斜率相等得−12=−1a+1，a =1， 故由直线x +2y =0与直线x +(a +1)y +4=0平行，能推出a =1，故必要性成立． 综上，“aa =1”是“直线x +2y =0与直线x +(a +1)y +4=0平行”的充分必要条件， 故选C ． 3.【答案】 C【考点】平面向量的基本定理及其意义 【解析】如图所示，利用向量的减法法则即可得出． 【解答】解：如图所示，由向量的减法法则可得： BC →=AC →−AB →=b →−a →．故选C ．4. 【答案】 A 【考点】 程序框图 【解析】本循环结构是经过n 次循环，计算S =11×2+12×3+...+1n(n+1)，由此能求出结果．【解答】解：经过n 次循环， 计算S =11×2+12×3+...+1n(n+1)=1−1n+1=nn+1，∵ 程序框图输出的结果是56， ∴ nn+1=56，∴ n =5．∴ n =6时，跳出循环． 故选A ． 5.【答案】 C【考点】由三视图求体积 【解析】由题可知，图形是一个放倒的底面是直角梯形的四棱柱的三视图，求出表面积即可． 【解答】解：由题可知，三视图复原的几何体是一个放倒的底面是直角梯形的四棱柱， 所以几何体的侧面积S =(1+1+2+√2)×1=4+√2 (cm 2)． 故选C ． 6.【答案】 D【考点】 抛物线的求解 【解析】利用抛物线的定义，得|PA|+|PF|=|PA|+|PQ|．因此问题转化为求|PA|+|PQ|取最小值时P 点的坐标，再利用P 、A 、Q 三点共线时距离最小，即可求出满足条件的P 点坐标．【解答】解：根据抛物线的定义，点P 到焦点F 的距离等于它到准线l 的距离设点P 到准线l:x =−1的距离为PQ ，则所求的|PA|+|PF|最小值，即|PA|+|PQ|的最小值；根据平面几何知识，可得当P 、A 、Q 三点共线时|PA|+|PQ|最小， ∴ |PA|+|PQ|的最小值为A 到准线l 的距离；此时P 的纵坐标为1，代入抛物线方程得P 的横坐标为14，得P(14，1)故选：D 7. 【答案】A【考点】数列的求和【解析】利用已知函数的关系求出数列的前几项，得到数列是周期数列，然后求出通过周期数列的和，即可求解本题．【解答】解：因为数列{x n }满足x 1=2，且对任意n ∈N*，点(x n , x n+1)都在函数y =f(x)的图象上，x n+1=f(x n )，所以x 1=2，x 2=4，x 3=8，x 4=2，x 5=4，x 6=8，x 7=2，x 8=4…所以数列是周期数列，周期为3，一个周期内的和为14，所以x 1+x 2+x 3+x 4+...+x 2012+x 2013=671×(x 1+x 2+x 3)=9394． 故选A ． 8. 【答案】A【考点】根的存在性及根的个数判断【解析】先作出当x ≥−3时函数f(x)=2x −3的图象，观察图象的交点所在区间，再根据对称性得出另一个交点所在区间即可．【解答】解：作出当x ≥−3时函数f(x)=2x −3的图象，观察图象的交点所在区间在(1, 2)．∵ f(1)=21−3=−1<0，f(2)=22−3=1>0，∴ f(1)⋅f(2)<0，∴ 有零点的区间是(1, 2)，因定义在R 上的函数f(x)的对称轴为x =−3，故另一个零点的区间是(−8, −7)，则k 的值为2或−7．故选A ．二、填空题：本大题共6小题，每小题5分，共30分．【答案】−1+i 【考点】复数代数形式的乘除运算【解析】利用复数的运算法则即可得出．【解答】解：i(1+i)=i −1=−1+i ．故答案为−1+i ．【答案】84,2【考点】茎叶图众数、中位数、平均数【解析】 先从茎叶图中分析出甲、乙两人的成绩数据，再根据中位数和平均数的求法进行运算即得．【解答】解：由图可知，甲，乙两人共有5次测试成绩，分别是：甲：76、83、84、87、90乙：79、80、82、88、91则甲、乙两人5次体育测试成绩的中位数分别为84、82，平均数分别为 甲¯=76+83+84+87+905=84，乙¯=79+80+82+88+915=84 故乙5次测试成绩的平均数与中位数之差是 2．故答案为：84，2．【答案】2,2【考点】简单线性规划【解析】先画出可行域，再利用三角形面积公式求第一问；第二问需由z =x +y ，再变形为y =−x +z ，则过点B 时z最大． 【解答】解：不等式组所表示的平面区域如图所示 解得A(2, −2)、B(2, 0)、C(0, 0)， 所以S △ABC=12×2×2=2；由z =x +y ，则y =−x +z ，所以直线经过点B 时x +y 取得最大值，最大值为2+0=2．故答案为：2，2．【答案】1 【考点】古典概型及其概率计算公式 【解析】根据所抽取的数据拼成两位数，得出总数及是5的倍数的数，求概率． 【解答】解：如下表，任意抽取两个不同数字组成一个两位数，共12种情况，其中是5的倍数的有15，35，75三种， ∴ 组成两位数能被3整除的概率为312=14．故答案为：14．【答案】 ①②③ 【考点】命题的真假判断与应用 【解析】由题意可解出该函数的所有对称轴，对称区间和单调递增区间，取整数k 的特殊值，比较选项即可得答案． 【解答】解：由x −π3=kπ+π2，可得x =kπ+5π6，k ∈Z ， 当k =0时，可得其中一条对称轴为x =5π6，故①正确；由x −π3=kπ，可得x =kπ+π3，k ∈Z ， 当k =1时，可得其中一个对称点的横坐标为x =4π3，故②正确；由2kπ−π2≤x −π3≤2kπ+π2得2kπ−π6≤x ≤2kπ+5π6，k ∈Z ，当k =0时，可得其中一个单调递增区间为[−π6, 5π6]， 因为[π3，5π6]真包含于[−π6, 5π6]，所以函数在[π3，5π6]上单调递增，故③正确．故答案为：①②③ 【答案】a 89,第45行的第77列 【考点】数列的函数特性 等比数列的通项公式【解析】①由于每行的所有数的个数形成等差数列，故可得到前9行的数的个数，从而得出答案；②由①可知前k 行所有a i 的个数为b 1+b 2+...b k =1+3+…(2k −1)=k 2．解出(k −1)2≤2013即可得出答案． 【解答】解：①设每行的数的个数为数列{b n }，则此数列为首项为1，公差为2的等差数列，∴ b n =1+(n −1)×2=2n −1．于是前9行所有a n 的个数为b 1+b 2+...+b 9=9(1+2×9−1)2=81．∴ 位于第10行的第8列的项等于a 81+8=a 89=a 89．②由①可知：前k 行所有a i 的个数为b 1+b 2+...b k =1+3+…(2k −1)=k 2．由(k −1)2<2013，解得k <1+√2013， 而442<2013<452，∴ k <1+44=45． ∴ 前44行的所有数a i 的个数为442=1936． 而1936+77=2013，∴ a 2013在图中位于第45行的第77列． 故答案为：a 89，第45行的第77列．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 【答案】（1）因为b sin A =√3a cos B ，由正弦定理可得sin B sin A =√3sin A cos B ． 因为在△ABC 中，sin A ≠0，所以tan B =√3． 又0<B <π，所以B =π3．（2）由余弦定理b2＝a2+c2−2ac cos B，因为B=π3，b=2√3，所以12＝a2+c2−ac．因为a2+c2≥2ac，所以ac≤12．当且仅当a=c=2√3时，ac取得最大值12．【考点】余弦定理正弦定理【解析】(Ⅰ)因为b sin A=√3a cos B，由正弦定理求得tan B=√3，从而求得B的值．(Ⅱ)由余弦定理求得12＝a2+c2−ac，再利用基本不等式求得ac的最大值．【解答】（1）因为b sin A=√3a cos B，由正弦定理可得sin B sin A=√3sin A cos B．因为在△ABC中，sin A≠0，所以tan B=√3．又0<B<π，所以B=π3．（2）由余弦定理b2＝a2+c2−2ac cos B，因为B=π3，b=2√3，所以12＝a2+c2−ac．因为a2+c2≥2ac，所以ac≤12．当且仅当a=c=2√3时，ac取得最大值12．【答案】证明：（1）取BE的中点G，连接GF，GD．∵F是BC的中点，则GF为△BCE的中位线．∴GF // EC，GF=12CE．∵AD⊥平面ABC，CE⊥平面ABC，∴GF // EC // AD．又∵AD=12CE，∴GF=AD．∴四边形GFAD为平行四边形．∴AF // DG．∵DG⊂平面BDE，AF⊄平面BDE，∴AF // 平面BDE．（2）∵AB=AC，F为BC的中点，∴AF⊥BC．∵EC // GF，EC⊥平面ABC，∴GF⊥平面ABC．又AF⊂平面ABC，∴GF⊥AF．∵GF∩BC=F，∴AF⊥平面BCE．∵AF // DG，∴DG⊥平面BCE．又DG⊂平面BDE，∴平面BDE⊥平面BCE．【考点】平面与平面垂直的判定直线与平面平行的判定【解析】（1）取BE的中点G，连接GF，GD．利用三角形的中位线定理即可得到GF // EC，GF=12CE．由AD⊥平面ABC，CE⊥平面ABC，利用线面垂直的性质定理即可得到AD // EC，进而即可判断四边形AFGD为平行四边形，得到AF // DG，再利用线面平行的判定定理即可证明；（2）利用等腰三角形的性质即可得到AF⊥BC，再利用线面垂直的性质得到GF⊥AF，利用线面垂直的判定定理即可证明AF⊥平面BEC，而DG // AF，得到DG⊥平面BEC，利用面面垂直的定理即可证明结论．【解答】证明：（1）取BE的中点G，连接GF，GD．∵F是BC的中点，则GF为△BCE的中位线．∴GF // EC，GF=12CE．∵AD⊥平面ABC，CE⊥平面ABC，∴GF // EC // AD．又∵AD=12CE，∴GF=AD．∴四边形GFAD为平行四边形．∴AF // DG．∵DG⊂平面BDE，AF⊄平面BDE，∴AF // 平面BDE．（2）∵AB=AC，F为BC的中点，∴AF⊥BC．∵EC // GF，EC⊥平面ABC，∴GF⊥平面ABC．又AF⊂平面ABC，∴GF⊥AF．∵GF∩BC=F，∴AF⊥平面BCE．∵AF // DG，∴DG⊥平面BCE．又DG⊂平面BDE，∴平面BDE⊥平面BCE．【答案】（1）应抽取综合素质测评结果是优秀等级的20份；（2）优秀等级的学生中男生人数比女生人数多的概率为511．【考点】列举法计算基本事件数及事件发生的概率分层抽样方法【解析】（1）根据样本容量为2000，运用减法算出优秀等级的学生人数为500，再由分层抽样的公式即可算出应抽取综合素质测评结果是优秀等级的份数；（2）设“优秀等级的学生中男生人数比女生人数多”为事件A，分别列举出(x, y)的所有可能情况和满足x>y 的数组(x, y)的情况，再用随机事件的概率公式即可算出优秀等级的学生中男生人数比女生人数多的概率．【解答】解：（1）由表可知，优秀等级的学生人数为x+y=2000−(380+373+370+377)=500．因此，应抽取综合素质测评结果是优秀等级的份数为500×802000=20，即在优秀等级的学生中应抽取20份．（2）设“优秀等级的学生中男生人数比女生人数多”为事件A．∵x+y=500，x≥245，y≥245，且x，y为正整数，∴数组(x, y)的可能取值为：(245, 255)，(246, 254)，(247, 253)，…，(255, 245)，共11个．其中满足x>y的数组(x, y)的所有可能取值为：(255, 245)，(254, 246)，(253, 247)，(252, 248)，(251, 249)共5个，即事件A包含的基本事件数为5．因此，所求概率为P(A)=511．答：（1）应抽取综合素质测评结果是优秀等级的20份；（2）优秀等级的学生中男生人数比女生人数多的概率为511．【答案】解：（1）当m=2时，f(x)=2ln x+x．f′(x)=2x +1=x+2x．所以f′(1)=3．又f(1)=1，所以曲线y=f(x)在点（1, f(1)）处的切线方程是y−1=3(x−1)，即3x−y−2=0．（2）函数f(x)的定义域为(0, +∞)，f′(x)=mx +m−1=(m−1)x+mx．当m≤0时，由x>0知f′(x)=mx+m−1<0恒成立，此时f(x)在区间(0, +∞)上单调递减．当m≥1时，由x>0知f′(x)=mx+m−1>0恒成立，此时f(x)在区间(0, +∞)上单调递增．当0<m<1时，由f′(x)>0，得x<m1−m，由f′(x)<0，得x>m1−m，此时f(x)在区间(0,m1−m)内单调递增，在区间(m1−m，+∞)内单调递减．( III)由（2）知函数f(x)的定义域为(0, +∞)，当m≤0或m≥1时，f(x)在区间(0, +∞)上单调，此时函数f(x)无最大值．当0<m<1时，f(x)在区间(0,m1−m)内单调递增，在区间(m1−m，+∞)内单调递减，所以当0<m<1时函数f(x)有最大值，最大值M=f(m1−m)=m ln m1−m−m．因为M>0，所以有m ln m1−m−m>0，解之得m>e1+e．所以m的取值范围是(e1+e，1)．【考点】导数求函数的最值利用导数研究函数的单调性利用导数研究曲线上某点切线方程【解析】（1）当m=2时求出导数f′(x)，则切线斜率k=f′(1)，f(1)=1，利用点斜式即可求得切线方程；（2）先求出函数定义域，在定义域内分m≤0，m≥1，0<m<1三种情况解不等式f′(x)>0，f′(x)<0即可；( III)分情况进行讨论：当m≤0或m≥1时f(x)单调，最值情况易判断；当0<m<1时，由单调性易求得其最大值，令其大于0，解出即可；【解答】解：（1）当m=2时，f(x)=2ln x+x．f′(x)=2x+1=x+2x．所以f′(1)=3．又f(1)=1，所以曲线y=f(x)在点（1, f(1)）处的切线方程是y−1=3(x−1)，即3x−y−2=0．（2）函数f(x)的定义域为(0, +∞)，f′(x)=mx+m−1=(m−1)x+mx．当m≤0时，由x>0知f′(x)=mx+m−1<0恒成立，此时f(x)在区间(0, +∞)上单调递减．当m≥1时，由x>0知f′(x)=mx+m−1>0恒成立，此时f(x)在区间(0, +∞)上单调递增．当0<m <1时，由f ′(x)>0，得x <m1−m ，由f ′(x)<0，得x >m1−m ， 此时f(x)在区间(0,m 1−m)内单调递增，在区间(m 1−m，+∞)内单调递减．( III)由（2）知函数f(x)的定义域为(0, +∞)，当m ≤0或m ≥1时，f(x)在区间(0, +∞)上单调，此时函数f(x)无最大值． 当0<m <1时，f(x)在区间(0,m1−m )内单调递增，在区间(m1−m ，+∞)内单调递减， 所以当0<m <1时函数f(x)有最大值，最大值M =f(m1−m )=m ln m1−m −m ． 因为M >0，所以有m ln m1−m −m >0，解之得m >e1+e ． 所以m 的取值范围是(e 1+e，1)．【答案】（1）解：由已知e =ca =√22，得b 2a 2=a 2−c 2a 2=1−e 2=12．所以a 2=2b 2．所以C:x 22b 2+y 2b 2=1，即x 2+2y 2=2b 2． 因为椭圆C 过点(2,√2)，所以22+2(√2)2=2b 2， 得b 2=4，a 2=8． 所以椭圆C 的方程为x 28+y 24=1．（2）证明：由（1）知椭圆C 的焦点坐标为F 1(−2, 0)，F 2(2, 0)．根据题意，可设直线MN 的方程为y =k(x +2)，由于直线MN 与直线PQ 互相垂直，则直线PQ 的方程为y =−1k (x −2)． 设M(x 1, y 1)，N(x 2, y 2)．由方程组{y =k(x +2)x 28+y 24=1消y 得(2k 2+1)x 2+8k 2x +8k 2−8=0．则 x 1+x 2=−8k 22k 2+1，x 1x 2=8k 2−82k 2+1． 所以|MN|=√1+k 2|x 1−x 2|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=4√2(1+k 2)2k 2+1． 同理可得|PQ|=4√2(1+k 2)k 2+2． 所以1|MN|+1|PQ|=24√2(1+k 2)24√2(1+k 2)=24√2(1+k 2)=3√28． 【考点】直线与椭圆结合的最值问题 椭圆的标准方程 【解析】（1）由离心率为√22，即c a=√22可得a 2=2b 2，从而C:x 22b 2+y 2b 2=1，再把点(2,√2)代入椭圆方程即可求得b 2，进而得到a 2．（2）由（1）写出焦点F 1，F 2的坐标，设直线MN 的方程为y =k(x +2)，由直线MN 与直线PQ 互相垂直得直线PQ 的方程为y =−1k (x −2)，设M(x 1, y 1)，N(x 2, y 2)．联立直线MN 与椭圆方程消掉y 得x 的二次方程，由韦达定理及弦长公式可用k 表示|MN|，同理可表示出|PQ|，计算即可得到1|MN|+1|PQ|为定值． 【解答】（1）解：由已知e =c a=√22，得b 2a2=a 2−c 2a 2=1−e 2=12．所以a 2=2b 2． 所以C:x 22b2+y 2b 2=1，即x 2+2y 2=2b 2．因为椭圆C 过点(2,√2)，所以22+2(√2)2=2b 2，得b 2=4，a 2=8． 所以椭圆C 的方程为x 28+y 24=1．（2）证明：由（1）知椭圆C 的焦点坐标为F 1(−2, 0)，F 2(2, 0)． 根据题意，可设直线MN 的方程为y =k(x +2)，由于直线MN 与直线PQ 互相垂直，则直线PQ 的方程为y =−1k (x −2)．设M(x 1, y 1)，N(x 2, y 2)．由方程组{y =k(x +2)x 28+y 24=1消y 得(2k 2+1)x 2+8k 2x +8k 2−8=0．则 x 1+x 2=−8k 22k 2+1，x 1x 2=8k 2−82k 2+1． 所以|MN|=√1+k 2|x 1−x 2|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=4√2(1+k 2)2k 2+1． 同理可得|PQ|=4√2(1+k 2)k 2+2． 所以1|MN|+1|PQ|=24√2(1+k 2)24√2(1+k 2)=24√2(1+k 2)=3√28． 【答案】 解：（1）依据题意，当S =(−1, 3)时，C(A, S)取得最大值为2．（2）①当0是S 中的“元”时，由于A 的三个“元”都相等，及B 中a ，b ，c 三个“元”的对称性，可以只计算C(A,S)=√33(a +b)的最大值，其中a 2+b 2+c 2=1．由(a +b)2=a 2+b 2+2ab ≤2(a 2+b 2)≤2(a 2+b 2+c 2)=2， 得 −√2≤a +b ≤√2． 当且仅当c =0，且a =b =√22时，a +b 达到最大值√2，于是C(A,S)=√33(a +b)=√63．②当0不是S 中的“元”时，计算C(A,S)=√33(a +b +c)的最大值，由于a 2+b 2+c 2=1，所以(a +b +c)2=a 2+b 2+c 2+2ab +2ac +2bc ≤3(a 2+b 2+c 2)=3， 当且仅当a =b =c 时，等号成立． 即当a =b =c =√33时，a +b +c 取得最大值√3，此时C(A,S)=√33(a +b +c)=1．综上所述，C(A, S)的最大值为1． 【考点】平均值不等式在函数极值中的应用 排序不等式及应用【解析】（1）依据题意中“元”的含义，可知当S =(−1, 3)时，C(A, S)取得最大值为2．（2）对0是不是S 中的“元”进行分类讨论：①当0是S 中的“元”时，由于A 的三个“元”都相等，及B 中a ，b ，c 三个“元”的对称性，利用平均值不等式计算C(A,S)=√33(a +b)的最大值，②当0不是S 中的“元”时，只须计算C(A,S)=√33(a +b +c)的最大值即可，最后综上即可得出C(A, S)的最大值．【解答】解：（1）依据题意，当S =(−1, 3)时，C(A, S)取得最大值为2．（2）①当0是S 中的“元”时，由于A 的三个“元”都相等，及B 中a ，b ，c 三个“元”的对称性，可以只计算C(A,S)=√33(a +b)的最大值，其中a 2+b 2+c 2=1．由(a +b)2=a 2+b 2+2ab ≤2(a 2+b 2)≤2(a 2+b 2+c 2)=2， 得 −√2≤a +b ≤√2． 当且仅当c =0，且a =b =√22时，a +b 达到最大值√2，于是C(A,S)=√33(a +b)=√63． ②当0不是S 中的“元”时，计算C(A,S)=√33(a +b +c)的最大值，由于a 2+b 2+c 2=1，所以(a +b +c)2=a 2+b 2+c 2+2ab +2ac +2bc ≤3(a 2+b 2+c 2)=3， 当且仅当a =b =c 时，等号成立． 即当a =b =c =√33时，a +b +c 取得最大值√3，此时C(A,S)=√33(a +b +c)=1．综上所述，C(A, S)的最大值为1．。
北京高三最新文科试题分类汇编含9区一模及上学期期末试题精选专题4平面向量
北京2013届高三最新文科试题分类汇编（含9区一模及上学期期末试题精选）专题4:平面向量、选择题1 . （2013届北京东城区一模数学文科）已知ABCD为平行四边形,若向量AB7C二b,则向量£为A. a -b C. b ~ aB. a + b D. ~a - b.（2013届房山区一模文科数学）在正三角形ABC中，AB = 3,D 是BC 上一点，且£ = 3BD ,则AB AD =15A .兀.（北京市石景山区2013届高三上学期期末考试数学文试题）AB =(2,4), AC =(1,3),贝VAD =A. (2,4) B . (3,7) C (1,1)（北京市昌平区2013 届高三上学期AC为平行四边形ABCD的一条对角线,D (-1,-1)考试数学文试题ABC中，BD =2DC •若AB 二a, AC = b，则AD=B.B5 .（北京市丰台区2013届高三上学期期末考试数学文试题）在平面直角坐标系xOy中，已知A（1,0）,B（0,1）,点C在第一象限内，JI《AOC ，且|OC|=2,6若OC =，OA •」OB，则，』的值是A . '3 , 1B . 1,3C .空,13D 一逅D . 1,36 .（北京市海淀区2013届高三上学期期末考试数学文试题）向量a二（1,1）,b二（2, t）,若a_b,则实数t的值为( )A . -2B . -1C . 1D . 27 .（北京市西城区2013届高三上学期期末考试数学文科试题）2 2过点M （2,0）作圆x y =1的两条切线MA ,()( )MB (A ,B为切点），则MA MB二5血A.2B. 5 C.婕D. 3 222（北京市房山区2013届高三上学期期末考试数学文科试题（解析版））已知平面向量a,b夹角为=,且6■44a {a + b)=6 , a ，则|耳等于( )A. M'3 B 2^3 C 2品D2•3填空题（2013届北京市延庆县一模数学文）已知・|a|=1, | b|==2 ,向量a与b的夹角为60 =,则| a + b |= .（2013届北京丰台区一模文科） 在直角梯形 ABCD 中 ,AD // BC / A=90° ,A .B=AD=1,BC=2,E 是CD 的中点，则 —I TCD BE = ________ .（2013届北京海滨一模文） 若向量a ,b 满足丨a 冃b 冃a+b^1,则a ，b 的值为.（2013届北京门头沟区一模文科数学）设向量a 二a 「a 2, b = b 1,b 2,定义一种向量-,3 i, n = — ,0 i,点 P 在 y = sinx 的图象上 辽丿 i6丿运动，点Q 在y = f （x ）的图象上运动，且满足OQ =m ： OP + n （其中0为坐标原点）,则y=f （x ）的最 大值是 ______________ .（2013届北京大兴区一模文科）已知矩形 ABCD 中 , AB= 2 , AD = 1 , E 、F 分别是 BC CD 的中点,则T T T（AE+ AF ） ?AC 等于 _______ .（2013届北京西城区一模文科）已知向量i 二（1,0）, j = （0,1）.若向量i …j 与 j 垂直，则实数（北京市东城区普通高中示范校 2013届高三3月联考综合练习（二）数学（文）试题）已知a = 1, b = 2,且a+b 与a 垂直，则向量a 与b 的夹角大小是 _____________ .（北京市朝阳区 2013届高三上学期期末考试数学文 试题）在直角三角形 ABC 中，.ACB=90，T T T TAC 二BC =2，点P 是斜边AB 上的一个三等分点，则 CP CB CP CA 二 _____________ .（北京市东城区2013届高三上学期期末考试数学文科试题）若向量a , b 满足a =1 , b = 2，且a , b 的夹角为二，则 a b= ____ , a +b =—.3 — —8 . T、9 .10.11 .12 .13.14 .15.16 .17.积：a ： b = @, a 2 i £ b, b 2 =36,a 2b 2 .已知 m =18. (北京市通州区2013届高三上学期期末考试数学文试题)在边长为1的等边ABC中，D为BC边上一动点，则AB AD的取值范围是 _ .19. (北京市西城区2013届高三上学期期末考试数学文科试题)已知向量a= (1,3)，b = (m,2m —1).若向量a与b共线，则实数m= ______ .7-1 ;1. 2. 3.4.5.6.7.8._ 、9.10.11.7-1 ;【精品推荐】北京 2013届高三最新文科试题分类汇编(含 9区一模及上学期期末试题精选)专题 4 :平面向量参考答案 选择题C A 【答案】 解：因为 AB = (2,4),AC = (1,3),所以 BC = AC —届=(—1,—1)，即 斯=£ = (—1,—1)，选D .【答案】解:因为BD.2DC ，所以忌五。
北京市东城区2013届高三上学期期末教学统一检测数学文试题
北京市东城区2013届高三上学期期末教学统一检测数学文试题学校_____________班级_______________姓名______________考号___________本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。
考试时长120分钟。
考生务必将答案答在答题卡上，在试卷上作答无效。
考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）设集合{1,2,3,4,5}U =，{1,2,3}A =，{2,3,4}B =，则()U AB ð等于(A) {2,3} (B) {1,4,5} (C) {4,5} (D) {1,5} （2）复数21i-等于 （A ）1i -- (B) 1i -+ ( C) 1i - ( D) 1i +（3）已知{}n a 为等差数列，其前n 项和为n S ，若36a =，312S =，则公差d 等于（A ）1 （B ）53（C ）2 （D ）3 （4）执行如图所示的程序框图，输出的k 的值为（A ）4 （B ）5 （C ）6 （D ）7（5）“2230x x -->成立”是“3x >成立”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件（6）已知x ，y 满足不等式组28,28,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩ 则目标函数3z x y =+的最大值为(A)332 (B)12 (C)8 (D)24（7）已知抛物线22y px =的焦点F 到其准线的距离是8，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且|||AK AF =，则AFK ∆的面积为（A ）32 （B ）16 （C ）8 （D ）4（8）给出下列命题：①在区间(0,)+∞上，函数1y x -=,12y x =,2(1)y x =-, 3y x =中有三个是增函数；②若log 3log 30m n <<，则01n m <<<；③若函数()f x 是奇函数，则(1)f x -的图象关于点(1,0)A 对称；④若函数()323x f x x =--，则方程()0f x =有2个实数根，其中正确命题的个数为（A ）1 （B ）2 （C ）3 （D ）4第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。
2013北京东城区高三一模数学试题答案(文)
北京市东城区2012-2013学年度第二学期高三综合练习（一）数学参考答案（文科）一、选择题（本大题共8小题，每小题5分，共40分）（1）B （2）C （3）C （4）A （5）C （6）D （7）A （8）A 二、填空题（本大题共6小题，每小题5分，共30分）（9）1i -+ （10）84 2 （11）2，2 （12）14（13）①②③ （14）89a 第45行的第77列 注：两个空的填空题第一个空填对得3分，第二个空填对得2分． 三、解答题（本大题共6小题，共80分） （15）（共13分）解：（Ⅰ）因为sin cos b A B =，由正弦定理可得sin sin cos B A A B =， 因为在△ABC 中，sin 0A ≠，所以tan B =又0B <<π， 所以3B π=. （Ⅱ）由余弦定理 2222cos b a c ac B =+-，因为3B π=，b =， 所以2212a c ac =+-. 因为222a c ac +≥， 所以12ac ≤.当且仅当a c ==ac 取得最大值12. （16）（共14分）证明：（Ⅰ）取BE 的中点G ，连结GF ，GD . 因为F 是BC 的中点，则GF 为△BCE 的中位线． 所以//GF EC ，12GF CE =．因为AD ⊥平面ABC ，CE ⊥平面ABC ， 所以////GF EC AD ．又因为12AD CE =，所以GF AD =．所以四边形GFAD 为平行四边形． 所以//AF DG ．因为DG ⊂平面BDE ，AF ⊄平面BDE ， 所以//AF 平面BDE ．（Ⅱ）因为AB AC =，F 为BC 的中点， 所以AF BC ⊥．因为//EC GF ，EC ⊥平面ABC ， 所以GF ⊥平面ABC ． 又AF ⊂平面ABC ， 所以GF AF ⊥． 因为GF BC F =I ， 所以AF ⊥平面BCE ． 因为//AF DG ， 所以DG ⊥平面BCE ． 又DG ⊂平面BDE ， 所以平面BDE ⊥平面BCE ． （17）（共13分）解：（Ⅰ）由表可知，优秀等级的学生人数为： 2000(380373370377)500x y +=-+++=． 因为80500202000⨯=， 故在优秀等级的学生中应抽取20份．（Ⅱ）设“优秀等级的学生中男生人数比女生人数多”为事件A ． 因为500x y +=，245x ≥，245y ≥，且x ，y 为正整数， 所以数组(,)x y 的可能取值为：(245,255)，(246,254)，(247,253)，…，(255,245)，共11个． 其中满足x y >的数组(,)x y 的所有可能取值为：(255,245)，(254,246)，(253,247)，(252,248)，(251,249)共5个，即事件AABCDEFG包含的基本事件数为5． 所以5()11P A =． 故优秀等级的学生中男生人数比女生人数多的概率为511． （18）（共14分）解：（Ⅰ）当2m =时，()2ln f x x x =+．22()1x f x x x+'=+=． 所以(1)3f '=． 又(1)1f =，所以曲线()y f x =在点(1,(1))f 处的切线方程是13(1)y x -=-， 即320x y --=．（Ⅱ）函数()f x 的定义域为(0,)+∞，(1)()1m m x mf x m x x-+'=+-=． 当0m ≤时，由0x >知()10mf x m x '=+-<恒成立，此时()f x 在区间(0,)+∞上单调递减． 当m ≥1时，由0x >知()10mf x m x'=+->恒成立， 此时()f x 在区间(0,)+∞上单调递增．当01m <<时，由()0f x '>，得1m x m <-，由()0f x '<，得1mx m>-， 此时()f x 在区间(0,)1m m -内单调递增，在区间(,)1mm+∞-内单调递减．（III ）由（Ⅱ）知函数()f x 的定义域为(0,)+∞，当0m ≤或m ≥1时，()f x 在区间(0,)+∞上单调，此时函数()f x 无最大值． 当01m <<时，()f x 在区间(0,)1m m -内单调递增，在区间(,)1mm+∞-内单调递减， 所以当01m <<时函数()f x 有最大值． 最大值()ln 11m mM f m m m m==---．因为0M >，所以有ln 01m m m m ->-，解之得e1em >+． 所以m 的取值范围是e(,1)1e+． （19）（共13分）（Ⅰ）解：由已知2c e a ==， 所以222222112b ac e a a -==-=.所以222a b =.所以C ：222212x y b b+=，即22222x y b +=.因为椭圆C过点， 得24b =， 28a =.所以椭圆C 的方程为22184x y +=. （Ⅱ）证明：由（Ⅰ）知椭圆C 的焦点坐标为1(2,0)F -，2(2,0)F . 根据题意， 可设直线MN 的方程为(2)y k x =+，由于直线MN 与直线PQ 互相垂直，则直线PQ 的方程为1(2)y x k=--. 设11(,)M x y ，22(,)N x y .由方程组22(2),184y k x x y =+⎧⎪⎨+=⎪⎩消y 得2222(21)8880k x k x k +++-=.则 21228,21k x x k -+=+21228821k x x k -=+. 所以MN=22)21k k ++.同理可得PQ =22)2k k ++.所以11||||MN PQ +2=228==. （20）（共13分）解：（Ⅰ）依据题意，当)3,1(-=S 时，(,)C A S 取得最大值为2．（Ⅱ）①当0是S 中的“元”时，由于A 的三个“元”都相等，及B 中c b a ,,三个“元”的对称性，可以只计算(,))3C A S a b =+的最大值，其中1222=++c b a ． 由22222222()22()2()2a b a b ab a b a b c +=++≤+≤++=，得 a b ≤+≤当且仅当0c =，且a b =b a +，于是(,)()33C A S a b =+=．②当0不是S 中的“元”时，计算(,)()3C A S a b c =++的最大值， 由于1222=++c b a ，所以bc ac ab c b a c b a 222)(2222+++++=++． 3)(3222=++≤c b a ， 当且仅当c b a ==时，等号成立．即当33===c b a 时，c b a ++(,))13C A S a b c =++=． 综上所述，(,)C A S 的最大值为1．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京市东城区2012-2013学年度第二学期高三综合练习（一）数学 （文科） 2013.4学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。
考试时长120分钟。
考生务必将答案答在答题卡上，在试卷上作答无效。
考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。
在每小题列出的四个选项中，选出符合题目要求的一项。
（1）已知全集{1,2,3,4}U=，集合{1,2}A =，那么集合U A ð为（A ）{3}（B ）{3,4} （C ）{1,2} （D ）{2,3}（2） “1a =”是“直线20x y +=与直线(1)40x a y +++=平行”的（A ） 充分不必要条件 （B ） 必要不充分条件 （C ） 充要条件 （D ） 既不充分也不必要条件（3）已知ABCD 为平行四边形，若向量AB = a ，AC = b ，则向量BC 为（A ）-a b （B ）a+b （C ）-b a （D ）--a b（4）执行如图所示的程序框图，输出的结果是56， 则判断框内应填入的条件是 （A ）5?n ≤ （B ）5?n < （C ）5?n > （D ）5?n ≥（5）已知一个几何体的三视图如图所示(单位：cm)， 那么这个几何体的侧．面积是（A ）2（B ）2（C ）2 （D ）2（6）已知点(2,1)A ，抛物线24y x =的焦点是F ，若抛物线上存在一点P ，使得PA PF +最小，则P 点的坐标为 （A ）(2,1) （B ）(1,1)（C ）1(,1)2（D ）1(,1)4（7）对于函数)(x f y =，部分x 与y 的对应关系如下表：数列n 满足1，且对任意，点1+n n 都在函数的图象上，则201320124321x x x x x x ++++++ 的值为（A ）9394 （B ）9380 （C ）9396 （D ）9400 （8）已知定义在R 上的函数()f x 的对称轴为3x =-，且当3x ≥-时，()23x f x =-.若函数()f x 在区间(1,)k k -（k ∈Z ）上有零点，则k 的值为（A ）2或7- （B ）2或8- （C ）1或7- （D ）1或8-第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。
（9）已知i 是虚数单位，那么i(1i)+等于 ．（10）如图是甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图，则甲5次测试成绩的平均数是 ，乙5次测试成绩的平均数与中位数之差是 ．（11）不等式组20,0,0x y x y -≤⎧⎪≤⎨⎪+≥⎩表示的平面区域为D ，则区域D 的面积为 ，z x y =+的最大值为 ．（12）从1，3，5，7这四个数中随机地取两个数组成一个两位数，则组成的两位数是5的倍数的概率为 ． （13）函数()sin()3f x x π=-的图象为C ，有如下结论：①图象C 关于直线56x π=对称；②图象C 关于点4(,0)3π对称；③函数)(x f 在区间5[,]36ππ内是增函数，其中正确的结论序号是 ．(写出所有正确结论的序号)（14）数列{a n }的各项排成如图所示的三角形形状，其中每一行比上一行增加两项，若n na a =(0)a ≠， 则位于第10行的第8列的项等于 ，2013a 在图中位于 ．（填第几行的第几列）三、解答题：本大题共6小题，共80分。
解答应写出文字说明，演算步骤或证明过程。
（15）（本小题共13分）在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c ，且s i n s b A B ．（Ⅰ）求角B ；（Ⅱ）若b =ac 的最大值．（16）（本小题共14分）如图，已知AD ⊥平面ABC ，CE ⊥平面ABC ，F 为BC 的中点，若12AB AC AD CE ===．（Ⅰ）求证：//AF 平面BDE ；（Ⅱ）求证：平面BDE ⊥平面BCE ．ABCDEF（17）（本小题共13分）为了解高三学生综合素质测评情况，对2000名高三学生的测评结果进行了统计，其中（Ⅰ）若按优秀、良好、合格三个等级分层，在这2000份综合素质测评结果中随机抽取80份进行比较分析，应抽取综合素质测评结果是优秀等级的多少份？（Ⅱ）若245x ≥，245y ≥，求优秀等级的学生中男生人数比女生人数多的概率．（18）（本小题共14分）已知函数()ln (1)f x m x m x =+- ()m ∈R ．（Ⅰ）当2m =时，求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）讨论()f x 的单调性；（III ）若()f x 存在最大值M ，且0M >，求m 的取值范围．（19）（本小题共13分）已知椭圆C ：221x y a b +=(0)a b >>的两个焦点分别为1F ，2F ，离心率为2，且过点.（Ⅰ）求椭圆C 的标准方程；（Ⅱ）M ，N ，P ，Q 是椭圆C 上的四个不同的点，两条都不和x 轴垂直的直线MN 和PQ 分别过点1F ，2F ，且这两条直线互相垂直，求证：11||||MN PQ +为定值.（20）（本小题共13分）设A 是由n 个有序实数构成的一个数组，记作：12(,,,,,)i n A a a a a = .其中i a(1,2,,)i n = 称为数组A 的“元”，i 称为i a 的下标. 如果数组S 中的每个“元”都是来自 数组A 中不同下标的“元”，则称S 为A 的子数组. 定义两个数组12(,,,)n A a a a = ，12(,,,)n B b b b = 的关系数为1122(,)n n C A B ab a b a b =+++ . （Ⅰ）若11(,)22A =-，(1,1,2,3)B =-，设S 是B 的含有两个“元”的子数组，求(,)C A S 的最大值；（Ⅱ）若()333A =，(0,,,)B a b c =，且2221a b c ++=，S 为B 的含有三个“元”的子数组，求(,)C A S 的最大值.北京市东城区2012-2013学年度第二学期高三综合练习（一）数学参考答案（文科）一、选择题（本大题共8小题，每小题5分，共40分）（1）B （2）C （3）C （4）A （5）C （6）D （7）A （8）A 二、填空题（本大题共6小题，每小题5分，共30分）（9）1i -+ （10）84 2 （11）2，2（12）14（13）①②③ （14）89a 第45行的第77列 注：两个空的填空题第一个空填对得3分，第二个空填对得2分． 三、解答题（本大题共6小题，共80分） （15）（共13分）解：（Ⅰ）因为sin cos b A B ，由正弦定理可得sin sin cos B A A B ，因为在△ABC 中，sin 0A ≠，所以tan B 又0B <<π， 所以3B π=. （Ⅱ）由余弦定理 2222cos b a c ac B =+-，因为3B π=，b = 所以2212a c ac =+-.因为222ac ac +≥，所以12ac ≤.当且仅当a c ==ac 取得最大值12.（16）（共14分）证明：（Ⅰ）取BE 的中点G ，连结GF ，GD . 因为F 是BC 的中点，则GF 为△BCE 的中位线．所以//GF EC ，12GF CE =． 因为AD ⊥平面ABC ，CE ⊥平面ABC ，所以////GF EC AD ．又因为12AD CE =，所以GF AD =．所以四边形GFAD 为平行四边形． 所以//AF DG ．因为DG ⊂平面BDE ，AF ⊄平面BDE ， 所以//AF 平面BDE ．（Ⅱ）因为AB AC =，F 为BC 的中点， 所以AF BC ⊥．因为//EC GF ，EC ⊥平面ABC ， 所以GF ⊥平面ABC ． 又AF ⊂平面ABC ， 所以GF AF ⊥． 因为GF BC F = ， 所以AF ⊥平面BCE ． 因为//AF DG ， 所以DG ⊥平面BCE ． 又DG ⊂平面BDE ， 所以平面BDE ⊥平面BCE ． （17）（共13分）解：（Ⅰ）由表可知，优秀等级的学生人数为：2000(380373370377)x y +=-+++=． 因为80500202000⨯=， 故在优秀等级的学生中应抽取20份．（Ⅱ）设“优秀等级的学生中男生人数比女生人数多”为事件A ． 因为500x y +=，245x ≥，245y ≥，且x ，y 为正整数， 所以数组(,)x y 的可能取值为：(245,255，(246,254)，(247,253)，…，(255,245)，共11个．其中满足x y >的数组(,)x y 的所有可能取值为：ABCDEFG(255,245)，(254,246)，(253,247)，(252,248)，(251,249)共5个，即事件A包含的基本事件数为5． 所以5()11P A =． 故优秀等级的学生中男生人数比女生人数多的概率为511． （18）（共14分）解：（Ⅰ）当2m =时，()2ln f x x x =+．22()1x f x x x+'=+=．所以(1)3f '=．又(1)1f =，所以曲线()y f x =在点(1,(1))f 处的切线方程是13(1)y x -=-，即320x y --=． （Ⅱ）函数()f x 的定义域为(0,)+∞，(1)()1m m x m f x m x x-+'=+-=． 当0m ≤时，由0x >知()10mf x m x '=+-<恒成立，此时()f x 在区间(0,)+∞上单调递减．当m ≥1时，由0x >知()10mf x m x'=+->恒成立， 此时()f x 在区间(0,)+∞上单调递增．当01m <<时，由()0f x '>，得1m x m <-，由()0f x '<，得1mx m>-， 此时()f x 在区间(0,)1m m -内单调递增，在区间(,)1m m+∞-内单调递减． （III ）由（Ⅱ）知函数()f x 的定义域为(0,)+∞，当0m ≤或m ≥1时，()f x 在区间(0,)+∞上单调，此时函数()f x 无最大值．当01m <<时，()f x 在区间(0,)1m m -内单调递增，在区间(,)1mm+∞-内单调递减， 所以当01m <<时函数()f x 有最大值．最大值()ln 11m m M f m m m m==---．因为0M >，所以有ln 01m m m m ->-，解之得e 1e m >+． 所以m 的取值范围是e(,1)1e+． （19）（共13分）（Ⅰ）解：由已知2c e a ==， 所以222222112b ac e a a -==-=. 所以222ab =.所以C ：222212x y b b+=，即22222x y b +=.因为椭圆C过点，得24b=，28a =.所以椭圆C 的方程为22184x y +=. （Ⅱ）证明：由（Ⅰ）知椭圆C 的焦点坐标为1(2,0)F -，2(2,0)F . 根据题意， 可设直线MN 的方程为(2)y k x =+，由于直线MN 与直线PQ 互相垂直，则直线PQ 的方程为1(2)y x k=--. 设11(,)M x y ，22(,)N x y .由方程组22(2),184y k x x y =+⎧⎪⎨+=⎪⎩消y 得2222(21)8880k x k x k +++-=. 则 21228,21k x x k -+=+21228821k x x k -=+.所以MN =22)21k k ++.同理可得PQ =22)2k k ++.所以11||||MN PQ +2228==. （20）（共13分）解：（Ⅰ）依据题意，当)3,1(-=S 时，(,)C A S 取得最大值为2．（Ⅱ）①当0是S 中的“元”时，由于A 的三个“元”都相等，及B 中c b a ,,三个“元”的对称性，可以只计算(,)()3C A S a b =+的最大值，其中1222=++c b a ． 由22222222()22()2()2a b a b ab a b a b c +=++≤+≤++=，得a b ≤+当且仅当0c =，且a b =b a +于是(,))C A S a b +=．②当0不是S 中的“元”时，计算(,))C A S a b c =++的最大值， 由于1222=++c b a ，所以bc ac ab c b a c b a 222)(2222+++++=++．3)(3222=++≤c b a ，当且仅当c b a ==时，等号成立．即当33===c b a 时，c b a ++(,))1C A S a b c ++=． 综上所述，(,)C A S 的最大值为1．。