幂函数
幂函数的性质

幂函数的性质幂函数是数学中常见的一种函数形式,由x的幂次和常数项构成。
幂函数的一般形式可以表示为f(x) = ax^n + b,其中a、n和b为常数,且n为正整数。
幂函数具有独特的性质,包括定义域、值域、奇偶性、单调性以及图像特点等,下面将详细探讨幂函数的各种性质。
一、定义域幂函数的定义域取决于幂指数n的奇偶性:当n为奇数时,幂函数的定义域为实数集;当n为偶数时,幂函数的定义域取决于系数a的正负性:- 若a>0,则幂函数的定义域为非负实数集,即x ≥ 0;- 若a<0,则幂函数的定义域为空集,即不存在实数使幂函数的结果为负数。
二、值域幂函数的值域也与幂指数n的奇偶性和系数a的正负性相关:当n为奇数时,幂函数的值域为全体实数;当n为偶数时,幂函数的值域取决于系数a的正负性:- 若a>0,则幂函数的值域为非负实数集,即f(x) ≥ 0;- 若a<0,则幂函数的值域在实数轴上存在最大值,即存在一个唯一的实数C使得f(x) ≤ C。
三、奇偶性幂函数的奇偶性由幂指数n来决定:当n为偶数时,幂函数为偶函数,即f(x) = f(-x),图像关于y轴对称;当n为奇数时,幂函数为奇函数,即f(x) = -f(-x),图像关于原点对称。
四、单调性幂函数的单调性与幂指数n的奇偶性和系数a的正负性相关:当n为正整数且n为奇数时,幂函数在整个定义域上单调递增或单调递减;当n为正整数且n为偶数时,幂函数在定义域上存在极值点,若系数a>0,则为单调递增,若系数a<0,则为单调递减。
五、图像特点幂函数的图像具有一些特点:当n为正整数时:- 当n为奇数时,幂函数的图像经过点(0, 0)且从第三象限经过第一象限,右上倾斜;- 当n为偶数时,幂函数的图像经过点(0, 0),右侧在y轴上方且上升(a>0)或下降(a<0)。
综上所述,幂函数的性质主要包括定义域、值域、奇偶性、单调性以及图像特点。
幂函数

因为0 x1 x 2 , 所以x1 x2 0, x1
x2 0,
所以f ( x1 ) f ( x 2 ) 即幂函数f ( x ) x 在[0,)上的增函数 .
例3 若 m 4
1 2
3 2m ,
1 2
1 2
则求m的取值范围.
解: 幂函数f ( x) x 的定义域是(0, ) 且在定义域上是减函数, 0 3 2m m 4 1 3 m ,即为m的取值范围. 3 2
α<0
幂函数的图象及性质
对于幂函数,我们只讨论
1 =1,2,3, 2
,
-1时的情形。
五个常用幂函数的图像和性质
3 2 y x y x (1) (2) y x (3)
(4) y x
1 2
(5) y x
1
函数 y x 的图像
定义域: 值 域:
R R
奇偶性:在R上是奇函数
单调性:在R上是增函数
函数 y x 的图像
2
定义域:
R
值 域:[0, ) 奇偶性: 在R上是偶函数 单调性: 在[0,)上是增函数
在(,0]上是减函数
函数 y x
1
的图像
定义域:{x x 0} 值 域:{ y
y 0}
奇偶性:在{x x 0}上是奇函数
单调性: 在(0,)上是减函数
y=x 2
2
1
(-1,1)
-4 -2
(1,1)
2
y=x-1
4 6
-1
(-1,-1)
-2
-3
-4
练习:利用单调性判断下列各值的大小。 (1)5.20.8 与 5.30.8 (2)0.20.3-2 与 0.30.3 -2
幂函数的概念与性质

幂函数的概念与性质在数学中,幂函数是一种常见而重要的函数类型。
它是一种形如f(x) = x^n的函数,其中n是常数,x是自变量,而f(x)则是因变量。
幂函数的性质取决于n的值,下面将详细介绍幂函数的概念与性质。
一、幂函数的定义幂函数是一类特殊的单变量函数,其定义为f(x) = x^n,其中n是常数,x是自变量。
在这个函数中,自变量x的值经过幂指数n的运算而得到新的函数值f(x)。
当幂函数的指数n为正数时,函数图像会呈现出不同的特点。
例如当n为2时,幂函数为f(x) = x^2,它代表了二次函数的图像,是一个开口向上的抛物线。
当n为3时,幂函数为f(x) = x^3,它代表了一个呈现出S形曲线的三次函数。
同理,幂函数的指数n为负数时,函数图像也会呈现出不同的形状。
二、幂函数的性质1. 定义域和值域:幂函数的定义域为实数集R,除非指数n为分数时会有例外。
对于n为整数的幂函数,其值域为非负实数集R+;当n 为奇数时,幂函数的值域为整个实数集R。
2. 对称性:当幂函数的指数n为偶数时,函数图像关于y轴具有对称性。
当幂函数的指数n为奇数时,函数图像关于原点具有对称性。
3. 单调性:幂函数的单调性与指数n的正负性有关。
当n为正数时,幂函数是递增的;当n为负数时,幂函数是递减的。
4. 极限性质:幂函数具有一些特殊的极限性质。
当n大于0时,随着x趋于正无穷或负无穷,幂函数的值趋于正无穷;当n小于0时,随着x趋于正无穷或负无穷,幂函数的值趋于零。
5. 奇偶性:幂函数的奇偶性与指数n的奇偶性一致。
当n为偶数时,幂函数为偶函数;当n为奇数时,幂函数为奇函数。
6. 渐近线:幂函数的图像可以存在水平渐近线、斜渐近线和铅直渐近线。
具体的渐近线取决于指数n的正负和奇偶性。
7. 凸凹性:当指数n大于1时,幂函数的图像为凸函数;当指数n小于1时,幂函数的图像为凹函数。
综上所述,幂函数是一种常用且重要的函数类型,其性质与指数n的值密切相关。
幂函数的图象及性质
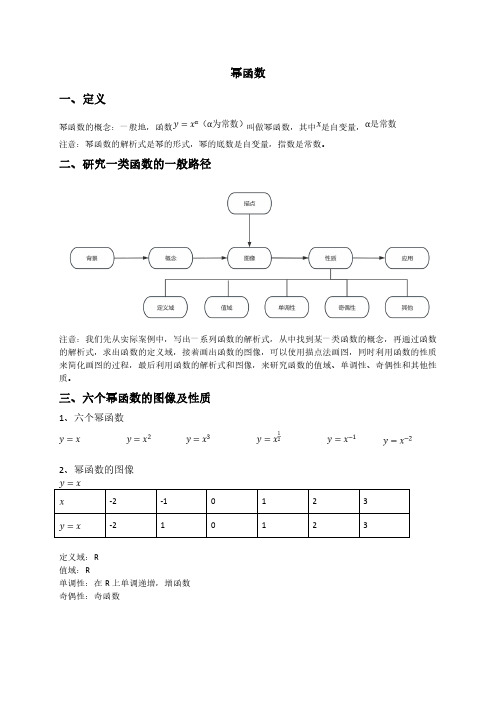
幂函数一、定义幂函数的概念:一般地,函数叫做幂函数,其中是自变量,注意:幂函数的解析式是幂的形式,幂的底数是自变量,指数是常数。
二、研究一类函数的一般路径注意:我们先从实际案例中,写出一系列函数的解析式,从中找到某一类函数的概念,再通过函数的解析式,求出函数的定义域,接着画出函数的图像,可以使用描点法画图,同时利用函数的性质来简化画图的过程,最后利用函数的解析式和图像,来研究函数的值域、单调性、奇偶性和其他性质。
三、六个幂函数的图像及性质1、六个幂函数2、幂函数的图像-2-10123-21123定义域:R 值域:R单调性:在R 上单调递增,增函数奇偶性:奇函数严禁复制-2-1012341149定义域:R 值域:单调性:在上单调递减,减函数,在上单调递增,增函数奇偶性:偶函数-2-10123-8-11827定义域:R 值域:R单调性:在R 上单调递增,增函数奇偶性:奇函数严禁复制124 012定义域:值域:单调性:在上单调递增,增函数奇偶性:非奇非偶函数严禁复制-2122定义域:值域:单调性:在上单调递减,减函数奇偶性:奇函数-2124定义域:值域:单调性:在上单调递减严禁复制奇偶性:偶函数从以上函数分析中,我们得到了6个幂函数的图像总结:6个幂函数具有的共同性质和不同性质1、函数的图像都经过。
2、函数在区间上单调递增,是增函数。
函数和严禁复制在区间上单调递减,是减函数。
在区间上单调递增,是增函数。
和在是单调递减,是减函数。
3、函数、和是奇函数,函数和是偶函数,函数是非奇非偶函数。
4、函数的图像经过原点,函数和的图像不经过原点。
5、已知幂函数,当时,函数在区间上单调递增,当时,函数在区间上单调递减。
四、题型1、幂函数的概念例题1已知幂函数f(x)过点,则f(9)的值为()(解析)设幂函数,因为过点,所以,解得a=,所以f(9)=。
例题2已知函数f(x)=为幂函数,则f()+f()=()(解析)因为函数f(x)=为幂函数,所以m-1=1,解得m=2,所以f(x)=,又因为函数f(x)为奇函数,有f()+f()=0。
幂函数知识点

幂函数知识点1. 幂函数的定义幂函数是一种特殊的函数,其形式为f(x) = ax^b,其中a 和b都是实数,且a不等于0。
在幂函数中,x是自变量,b 是幂指数,a是幂函数的系数。
2. 幂函数的图像根据幂函数的定义,可以推断出幂函数的图像特征: - 当幂指数b为正数时,幂函数呈现上升趋势。
当x趋近于无穷大时,幂函数的值也趋近于无穷大;当x趋近于零时,幂函数的值趋近于零。
- 当幂指数b为负数时,幂函数呈现下降趋势。
当x趋近于无穷大时,幂函数的值趋近于零;当x趋近于零时,幂函数的值趋近于无穷大。
- 当幂指数b为零时,幂函数为常数函数,图像为一条水平直线。
3. 幂函数的性质幂函数具有以下性质: - 幂函数的定义域为实数集,值域依赖于a的正负性质。
- 幂函数在定义域上是连续的。
- 当幂指数b为正偶数时,幂函数的值始终为正数。
- 当幂指数b为正奇数时,幂函数的值随着x的变化而变化,正负性取决于a 的正负性。
- 当幂指数b为负数时,幂函数的值随着x的变化而变化,正负性取决于a的正负性。
- 幂函数在x=0处存在一个驻点,即当x=0时,幂函数的导数为0。
- 当b>0时,幂函数对x的增长速度随着x的增大而增加;当b<0时,幂函数对x的增长速度随着x的增大而减小。
4. 幂函数的应用幂函数在数学和物理中有广泛的应用,例如: - 在生物学中,幂函数常被用来描述生物体量和身高的关系,以及种群增长和资源利用的关系。
- 在经济学中,幂函数常被用来描述产出与投入的关系,以及利润与销售量的关系。
- 在物理学中,幂函数常被用来描述力与位移的关系,以及电力消耗与电流的关系。
5. 幂函数的求导根据幂函数的定义,我们可以得出幂函数的导数公式: - 对于f(x) = ax^b,其中a不等于0且b不等于0,幂函数的导数为f’(x) = abx^(b-1)。
其中b-1为幂指数减一。
在求幂函数的导数时,需要注意幂指数b的取值范围,以及系数a的正负性。
幂函数的定义及性质

幂函数的定义及性质幂函数是数学中常见的一类函数形式,它的定义如下:定义:对于给定的实数a(a≠0)和非零实数b,幂函数f(x)=a⋅x^b。
其中,a称为幂函数的系数,b称为幂函数的指数,x称为幂函数的自变量,f(x)称为幂函数的因变量。
在幂函数的定义中,a是幂函数的系数,可以取任意非零实数。
系数a决定了函数的纵向伸缩变换,当a>0时,幂函数的图像在y轴上方,当a<0时,幂函数的图像在y轴下方。
指数b是幂函数的指数,决定了函数的横向伸缩变换以及函数的形状。
当b>1时,幂函数增长更为迅速;当0<b<1时,幂函数增长逐渐变缓;当b=1时,幂函数变为线性函数;当b<0时,幂函数变为倒数函数。
幂函数的性质如下:1. 定义域和值域:幂函数的定义域为所有使得指数函数值存在的实数。
当a>0且b>0时,幂函数的值域为(0,+∞);当a<0且b为奇数时,幂函数的值域为(-∞,0);当a<0且b为偶数时,幂函数的值域为[0,+∞)。
2. 对称性:a⋅(-x)^b = (-a)⋅x^b,即幂函数关于y轴对称。
3. 单调性:幂函数在定义域上单调递增或递减,取决于系数a和指数b的正负情况。
4. 奇偶性:当b为整数时,幂函数的奇偶性与系数a的奇偶性一致;当b为分数时,幂函数的奇偶性与a的正负性一致。
5. 渐近线:当b>0时,幂函数的图像有一条水平渐近线y=0;当b<0时,幂函数的图像有两条渐进线,分别是x轴和y轴。
6. 函数的图像:幂函数的图像形状随着系数a和指数b的取值而变化,可以是上凸、下凸、对称或非对称的。
以上是幂函数的定义及性质的介绍。
幂函数作为一类常见的函数形式,具有广泛的应用领域,在数学、物理、经济等学科中都有重要的作用。
通过对幂函数的研究和理解,我们可以更好地理解函数的变化规律和函数图像的特点,为解决实际问题提供数学工具和思路。
幂函数知识点

幂函数知识点一、幂函数的定义形如$y = x^{\alpha}$($\alpha$为常数)的函数,称为幂函数。
其中$x$是自变量,$\alpha$是常数。
需要注意的是,幂函数的底数是自变量$x$,指数是常数$\alpha$,这是幂函数的重要特征。
例如,$y = x^2$,$y = x^{1/2}$,$y= x^{-1}$等都是幂函数。
二、幂函数的图像和性质1、当$\alpha > 0$时(1)$\alpha$为偶数时,幂函数的图像关于$y$轴对称。
例如,$y = x^2$的图像是一个开口向上的抛物线,顶点在原点。
(2)$\alpha$为奇数时,幂函数的图像关于原点对称。
比如,$y = x^3$的图像是经过原点的单调递增曲线。
2、当$\alpha < 0$时(1)幂函数的图像在第一、二象限,在第一象限内,函数值随$x$的增大而减小。
例如,$y = x^{-1}$的图像是双曲线,位于第一、三象限。
(2)当$x > 1$时,幂函数的图像在$y = x$的下方;当$0 < x <1$时,幂函数的图像在$y = x$的上方。
3、当$\alpha = 0$时$y = 1$($x \neq 0$),图像是一条平行于$x$轴的直线,去掉点$(0, 1)$。
三、幂函数的单调性1、当$\alpha > 0$时(1)若$\alpha > 1$,幂函数在$0, +\infty)$上单调递增。
(2)若$0 <\alpha <1$,幂函数在$0, +\infty)$上单调递增,但增长速度较慢。
2、当$\alpha < 0$时幂函数在$(0, +\infty)$上单调递减。
四、幂函数的奇偶性1、若$\alpha$为整数(1)当$\alpha$为偶数时,幂函数为偶函数。
(2)当$\alpha$为奇数时,幂函数为奇函数。
2、若$\alpha$为分数将其化为最简分数形式$\frac{p}{q}$($p$,$q$互质)(1)若$q$为偶数,幂函数是非奇非偶函数。
幂函数的计算方法

幂函数的计算方法一、幂函数的基本概念。
1.1 幂函数长啥样呢?它的形式很简单,就是y = x^α(α是常数)。
这个α可不得了,它能决定幂函数的很多特性呢。
就像不同的性格能决定一个人的行事风格一样。
比如说,当α = 2的时候,函数y = x²,这就是一个很常见的幂函数啦。
1.2 幂函数的定义域也很有讲究。
这个定义域啊,得根据α的值来确定。
有时候是全体实数,有时候就得把某些数排除在外。
这就好比一个俱乐部的准入规则,不同的情况有不同的要求。
二、幂函数的计算要点。
2.1 幂的乘方。
这就像是给幂函数做“升级”。
比如说(x^m)^n,那结果就是x^(m n)。
这就好比是搭积木,一层一层往上加,规则很明确,按照这个来计算准没错。
这在幂函数的计算里可是相当重要的一个环节,就像盖房子打地基一样关键。
2.2 同底数幂相乘。
这个规则就是底数不变,指数相加。
像x^m x^n = x^(m + n)。
这多简单啊,就像把相同颜色的珠子串在一起,数量就相加了呗。
这也是幂函数计算里经常用到的规则,要是这个都不会,那计算幂函数就像没头的苍蝇——乱撞啦。
2.3 同底数幂相除。
这个规则是底数不变,指数相减。
例如x^m÷x^n = x^(m n)(x≠0)。
这也好理解,就像从一堆东西里拿走一部分,剩下的数量就是相减的结果嘛。
在幂函数的计算中,这个规则也不能忽视,不然就会算出错误的结果,那可就是竹篮打水——一场空了。
三、幂函数计算的实际例子。
3.2 再复杂一点的例子。
计算(x²)^3 x^4÷x^5。
根据幂的乘方规则,(x²)^3 = x^(2 3)= x^6。
然后,同底数幂相乘,x^6 x^4 = x^(6 + 4)= x^10。
同底数幂相除,x^10÷x^5 = x^(10 5)= x^5。
这整个过程就像走迷宫一样,每一步都得按照规则来,要是走错了,就找不到出口(正确结果)了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
底数相同,指数不同,考察指数函数.
探究二 在第一象限, 1、0 1、 0时,
函数的图象的变化趋势有何不同?
函数在第一象限的形状
如图所示,图中的曲线是幂函数y x
在第一象限的图象,已知取-
1 2
,1 2
,2三个值,则
B 对应于曲线C1,C2 ,C3的指数的值依次为( )
A. 1 , 1 , 2
其他函数_________________________________ 第三类函数有什么共同特征?
(1)指__数____是常数 (2)_底__数___是变量(3)都是 y___x_
的形式
温故知新,概念形成
幂函数定义
一般地,形如 y x R 的函数称为幂函数,其中
为常数.
y 2
y x-2
必 做
阅 读
必做:课后达标检测幂函数部分 选做:必修一课本79页2、3题
1.下列命题中正确的是( D ) A.幂函数在第一象限都是增函数
B.幂函数的图像都经过(0,0)和(1,1)点
C.若幂函数y x 是奇函数,则y x是定义域上的增函数
D.幂函数的图像不可能出现在第四象限
2.比较各题中两个幂的值的大小
1
1
(1)2.32 < 2.42
(2)( 2)-3 >
( 3)-3
y
22
B.2, 1 , 1 , 22
C. 1 , 2, 1 22
D. 1 , 2, 1
22
0
x
探究性质,学以致用
2
例2 讨论函数y x 5 的定义域、奇偶性,作出它的图象,
并根据图象说明函数的增减性.
2
y x3
y
(1,1)
0
函数在 0,+ 上单调递增,
x
在 -,0 上单调递减.
探究性质,学以致用
4
6
x
-2
探究性质,学以致用
(二)学生自主合作探究幂函数性质
探究一
0和 0时,幂函数
在第一象限的单调性有何不同?
探究性质,学以致用
★所有的幂函数在(0,+∞)都有定义,并且函数图 象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并 在(0,+∞)上为增函数.
★如果α<0,则幂函数的图象过点(1,1),并在 (0,+∞)上为减函数,以坐标轴为渐近线。
a
2
)
2 3
2
23
y
0
x
探究性质,学以致用
(3)设a 20.3,b 30.3, c 30.5,则( B )
A、a b c B、a b c C、a c b D、b a c
考察指数函数y 3x 函数在R上递增 又 0.3 0.5b c
a b c
小结: 底数不同,指数相同,考察幂函数.
2
解:函数y x 5 5 x 2 ,定义域是实数集 R
2
函数y x 5 是偶函数.
先作出幂函数在 0, 上的图象,
再根据函数的图象关于y轴对称,作出它在 ,0上的图象. 2 y x3 函数在 0,+ 上单调递增,
在 -,0 上单调递减.
(1,1)
0
探究性质,学以致用
总结:作幂函数图象的步骤 1、求定义域; 2、判断奇偶性; 3、作第一象限的图象; 4、利用奇偶函性,补全整个函数的图象.
探究性质,学以致用
例1 比较下列各题中两个值的大小:
11
(1)52 , 62;
(2)(a 1)1.5 , a1.5.
1
解:(1)考察幂函数 y x2 在区间0, 上是单调递增函数
1
1
52 62
(2)考察幂函数y x1.5 在区间0,+上是单调递增函数
y
a 1 a, (a 1)1.5 a1.5
1
1
; (3) y -x2; (4) y x2 ;
x2
(5) y 2x2;(6) y x3+2;
2. 幂函数 y (m 2)xm,则m=__-_1__
(-2,4)
y
4
y x3
y x2 (2,4)
3
yx
2
1
y x2
(-1,1)
1
(1,1)
-4
-2
2
o
(-1,-1)
-1
y x1
注意:将分数指数幂化成根式
探究性质,学以致用
练习 2 将图像相应解析式的序号写在括号内:
①
y
2
x3
②
y
3
x2
③
y
1
x 3;
④
y
1
x3
y
1
o
1
x
y 1 o1 x
( ③)
(① )
y 1 o1 x
( ④)
y 1 o1 x
(②)
总结反思,升华提高
幂函数的概念、图象和性质. 比较幂的大小;作图研究性质.
数形结合,转化思想.
0
x
探究性质,学以致用
练习1 比较下列各题中两个值的大小:
(1) 31.3, 21.3;
(2)
(2
a2
)
2 3
,
2
2 3
;
解:(1)考察幂函数y x1.3 ,在区间0, 上是单调递增函数 3 2,31.3 21.3
2
(2)考察幂函数 y x 3, 在区间0, 上是单调递减函数
2 a2
2,
(2
(1)y 2x (2)y log2 x(3)y x2 (4)y 3x (5)y x2 (6)y lg x
1
(7)y ln x (8)y 10x (9)y x3
指数函数_________________________________
对数函数_________________________________
1
y x2
2 -
y x 3
幂函数同指数函数、对数函数一样都是形式定义的函数. 前面的系数为1, 后面没有常数项
式子 指数函数: y=a x 幂函数: y= xα
名称
a
x
y
底数 指数位置 幂值
指数 底数位置 幂值
温故知新,概念形成
1.判断下列函数哪些是幂函数(:1)(2)(4)
(1)y x4; (2) y
